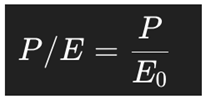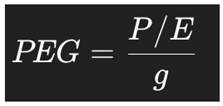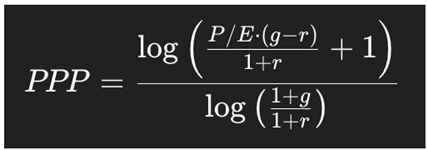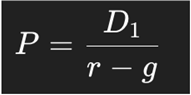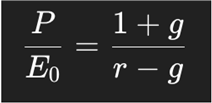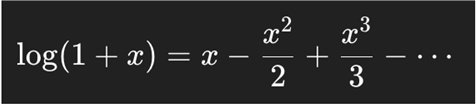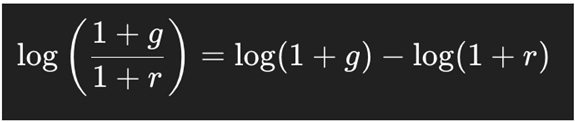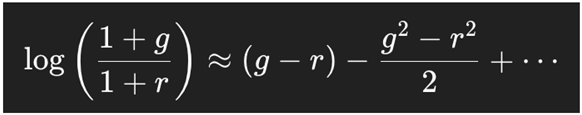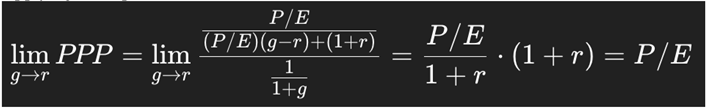1. Introduction
The Price/Earnings (P/E) ratio has long served as a popular indicator for evaluating stock prices relative to company earnings. However, this static metric fails to capture essential financial realities such as growth potential, discounting, and the time value of money. The PEG ratio, introduced as a growth-adjusted refinement, partially addresses the P/E ratio’s limitations by dividing it by the earnings growth rate. Yet, it still operates on a linear approximation and does not incorporate discounting or risk.
This article proposes that the Potential Payback Period (PPP) offers a more rigorous alternative. The PPP calculates the number of years theoretically required to recover a stock’s purchase price, assuming full distribution of future earnings, while accounting for growth, interest rates, and risk. We use Taylor expansion to explore how PPP overcomes the linear simplifications of PEG, draw connections to the Gordon Growth Model (GGM) to contextualize P/E, and apply L’Hospital’s Rule to demonstrate the PPP’s stability in limiting cases. The result is a valuation framework that better aligns with fundamental financial principles.
2. Mathematical Formulations
2.1. The Price/Earnings (P/E) Ratio
This ratio assumes constant earnings and no discounting, providing a basic estimate of how many years of earnings are needed to recoup the stock price.
2.2. The PEG Ratio
Where ggg is the expected earnings growth rate. The PEG ratio introduces growth but does so using a linear approximation, and it does not reflect the time value of money or risk.
2.3. The Potential Payback Period (PPP)
Where:
This formula gives the number of years required for the discounted, growing earnings to equal the current price, assuming full theoretical distribution.
3. Revisiting the P/E Ratio Through the Gordon Growth Model
The Gordon Growth Model (GGM) values a stock as the present value of an infinite stream of dividends growing at a constant rate:
Assuming full earnings payout D1 = E0(1 + g), we derive:
This growth-adjusted P/E ratio introduces basic elements of financial theory, but still rests on idealized assumptions: constant infinite growth, no retained earnings, and static discount rates. It also provides no explicit time horizon for investment recovery, unlike the PPP.
4. Taylor Expansion and Linear Approximations
4.1. Taylor Expansion in Valuation Metrics
The PPP uses logarithmic expressions that can be expanded using Taylor series:
The PEG ratio effectively retains only the first-order term (linear approximation). The PPP, in contrast, incorporates the full logarithmic structure, capturing nonlinear compounding effects.
4.2. Taylor Approximation of the PPP Denominator
Using Taylor expansion:
So:
The PEG ratio ignores higher-order terms, while the PPP includes them implicitly, offering a more accurate and theoretically consistent approach.
4.3. Stability of PPP Under Limiting Conditions: A L’Hospital’s Rule Approach
As g → r, the PPP becomes indeterminate:
Applying L’Hospital’s Rule:
Thus, PPP smoothly converges to P/E when g = r — showing that P/E is a special case of PPP, and confirming PPP’s mathematical stability.
In contrast, the PEG ratio diverges as g → 0, rendering it unstable and misleading in low-growth scenarios.
5. Conceptual Implications
5.1. Time Value and Risk
The PPP explicitly incorporates:
The discounting of future earnings (via r),
The risk premium (through CAPM-derived r),
The compounding of earnings (via g).
In doing so, it provides a valuation that is more aligned with core principles of modern finance.
5.2. Temporal Interpretability
The PPP offers a time-based interpretation of valuation: how many years of discounted earnings are needed to theoretically recover the stock’s price. Neither P/E nor PEG provide this temporal dimension.
5.3. A Generalized Framework
P/E is a degenerate case of PPP where g = r = 0
PEG is a crude linear simplification of the full PPP formula
PPP is a generalized, logarithmic, risk- and growth-adjusted model
It unifies and extends the insights from both traditional ratios, offering a more coherent framework.
6. Conclusions
This article has sought to demonstrate that the Potential Payback Period (PPP) offers a mathematically grounded and conceptually richer framework for stock valuation than the traditional P/E and PEG ratios. By drawing on tools such as Taylor expansion, the Gordon Growth Model, and L’Hospital’s Rule, we have shown that the PPP corrects some of the theoretical limitations inherent in the simpler ratios — notably their neglect of compounding growth, discounting, and the time value of money.
While the P/E and PEG ratios remain widely used for their simplicity and accessibility, the PPP provides a more nuanced and internally consistent estimate of valuation, particularly in cases involving high growth, variable risk, or long-term investment horizons. Its ability to express valuation in temporal terms — the number of years theoretically required to recover a stock’s price — adds interpretive clarity for investors seeking to understand a company’s earning power.
Though no single metric can capture all aspects of valuation, the PPP offers a compelling complement — and in many cases, a strong alternative — to traditional heuristics. Further empirical research and application across different market conditions could reinforce its usefulness and help refine its role in modern equity analysis.
References
- Bodie, Z., Kane, A., & Marcus, A. J. (2018). Investments (11th ed.). McGraw-Hill Education.
- Damodaran, A. (2012). Investment Valuation: Tools and Techniques for Determining the Value of Any Asset (3rd ed.). Wiley.
- Gordon, M. J. (1959). Dividends, Earnings, and Stock Prices. The Review of Economics and Statistics, 41(2), 99–105.
- Penman, S. H. (2013). Financial Statement Analysis and Security Valuation (5th ed.). McGraw-Hill.
- Sam, Rainsy. (2025). Extending the P/E and PEG Ratios: The Role of the Potential Payback Period (PPP) in Modern Equity Valuation. Preprints. [CrossRef]
- Sam, Rainsy. (2025). How to Adjust the P/E Ratio for Earnings Growth in Equity Valuation: PEG or PPP? SSRN. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=5241650.
- Sam, Rainsy. (2025). A Quantitative Revelation in Equity Valuation: The P/E Ratio is a Degenerate Case of the Potential Payback Period (PPP). SSRN. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=5268285.
- Sam, Rainsy. (2025). Proving that the P/E Ratio is Just a Limiting Case of the Potential Payback Period (PPP) When Earnings Growth and Interest Rate are Ignored. Preprints. [CrossRef]
- Sam, Rainsy. (2025). Generalizing the P/E Ratio Through the Potential Payback Period (PPP): A Dynamic Approach to Stock Valuation. SSRN. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=5261816.
- Stewart, J. (2015). Calculus: Early Transcendentals (8th ed.). Cengage Learning.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).