Proving that the P/E Ratio is Just a Limiting Case of the Potential Payback Period (PPP) When Earnings Growth and Interest Rate are Ignored

1. Introduction

The P/E ratio is a widely used tool in equity valuation, but it is limited by its static nature. It assumes earnings remain constant indefinitely and ignores the effects of growth, interest rates, and risk. The Potential Payback Period (PPP), addresses these limitations by introducing a more comprehensive framework. However, it is essential to verify that PPP remains consistent with P/E in appropriate special cases. One such case is when both the earnings growth rate and the discount rate are zero, which corresponds to the hypothetical scenario of a static world. Another important case occurs when the growth rate equals the discount rate, even if both are positive. In both instances, the PPP logically reduces to the simpler and more familiar P/E ratio.

2. The PPP Formula and the Limiting Case: When g = r = 0

The general form of the PPP is:

where:

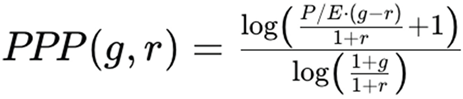
• P/E is the price-to-earnings ratio.
• g is the expected annual earnings growth rate.
• r is the discount rate, reflecting the time value of money and risk.

We first consider the fully static case when g = r = 0.

This case reflects a purely static world — no growth and no discounting — where time has no financial impact and future earnings are valued at face value.

Substitute g = r = 0 into the PPP formula:

This is an indeterminate form.

L’Hôpital’s Rule is a fundamental technique in calculus used to evaluate limits that result in indeterminate forms, such as 0/0 or ∞/∞. When both the numerator and the denominator of a fraction approach zero (or infinity) as the variable approaches a certain value, L’Hôpital’s Rule allows us to compute the limit by differentiating the numerator and denominator separately and then taking the limit of the resulting fraction.

We apply L’Hôpital’s Rule:

As g → 0

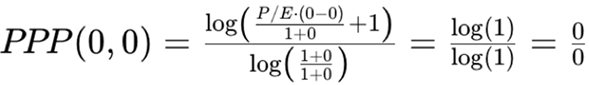
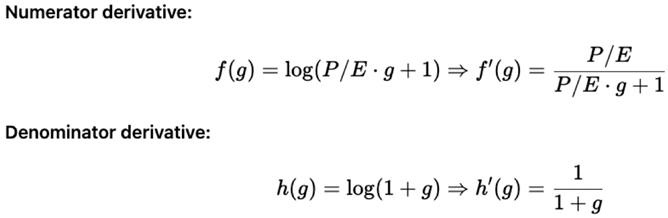
• Numerator → P/E
• Denominator → 1

So:

This confirms that in a completely static economic model, the PPP simplifies to the P/E ratio.

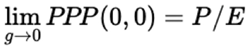
3. Secondary Case: When g = r ≠ 0

We now consider the case when the growth rate equals the discount rate, but both are nonzero. This is relevant in stable, low-growth, and low-interest-rate environments.

In this situation, the PPP formula again becomes:

Again, we apply L’Hôpital’s Rule:

This confirms that even when both rates are positive and equal, the PPP simplifies to the P/E ratio.

4. Far-Reaching Implications for Stock Valuation

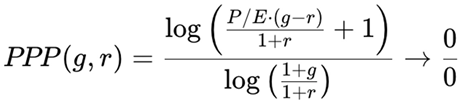
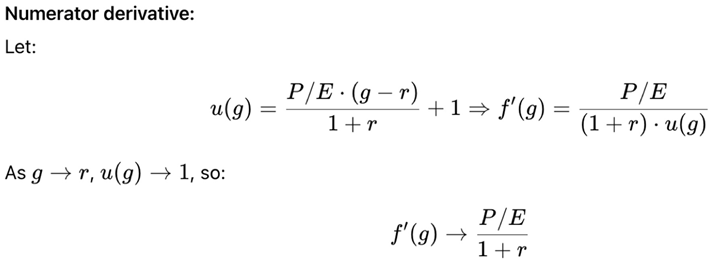
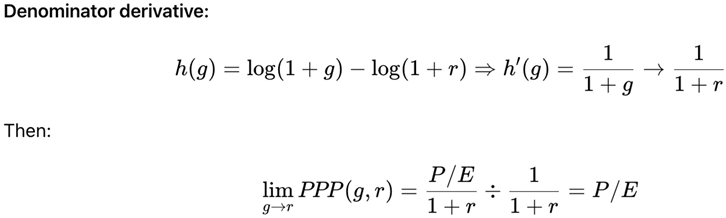
The demonstration that the P/E ratio is merely a special case of the more general PPP framework has several far-reaching implications for stock valuation:

• Unified Valuation Tool: PPP provides a seamless valuation method that applies both to static, no-growth contexts (where it aligns with the P/E ratio) and to dynamic contexts involving positive growth, discounting, and risk. This unification brings consistency and analytical clarity to financial modeling.
• Time-Sensitive Insight: By measuring how long it takes to potentially recover the price paid for a stock through discounted future earnings, PPP introduces a temporal dimension that the P/E ratio entirely overlooks. This makes the PPP far more informative for long-term investors.Bridge Between Stocks and Bonds: The PPP, through its embedded discounting mechanism, aligns stock valuation closer to bond valuation principles. This allows investors to compare expected returns across asset classes more precisely, particularly through the PPP-derived Stock Internal Rate of Return (SIRR).
• Risk-Adjusted Valuation: Unlike the P/E ratio, which ignores volatility and market risk, the PPP can incorporate a discount rate that reflects the stock’s risk profile (e.g., via the CAPM framework). This makes PPP particularly powerful for cross-company or cross-sector comparisons.
• Applicability to All Companies: The PPP can be applied even to companies with low or negative earnings, high-growth startups, or turnaround stories — cases where the P/E ratio becomes meaningless or misleading. This extends the analytical universe available to investors and analysts.
• Strategic Insights in Global Investing: By calculating PPP values across markets and comparing implied SIRRs to local interest rates, investors can identify undervalued regions or sectors. This opens up new frontiers in global asset allocation and equity screening.

5. Conclusion

We have provided a rigorous mathematical proof that the Potential Payback Period (PPP) reduces to the traditional Price-to-Earnings (P/E) ratio in two distinct but related special cases: when g = r = 0, and when g = r ≠ 0. In both scenarios, the PPP converges to P/E, confirming that the PPP is not an alternative to, but rather a generalization of, the P/E ratio. This insight highlights the theoretical robustness and practical adaptability of the PPP framework.

By incorporating earnings growth, discount rates, and risk, the PPP provides a much richer and more realistic model for valuing stocks. Yet, as shown here, it still respects the foundational simplicity of the P/E ratio under appropriate assumptions. This dual capability — flexibility in complex scenarios and consistency in simplified ones — underscores the PPP’s significance as a breakthrough valuation metric.