Benchmarking Students’ Tracking Rates in Undergraduate Higher Education with Different Time Windows: Retention Rates, Progression (Persistence) Rates, and Graduation (Completion) Rates

1. Nomenclature (in Alphabetical Order; Greek Symbols First)

$\Lambda$	Relaxation factor used in adjusting the progression rate to account for the effect of a foundation year (if applicable)
${\lambda }_{RR}$	Discount factor for extrapolating first-year retention rates, from 0 to 1
${\lambda }_{PR}$	Discount factor for extrapolating first-year progression rates, from 0 to 1
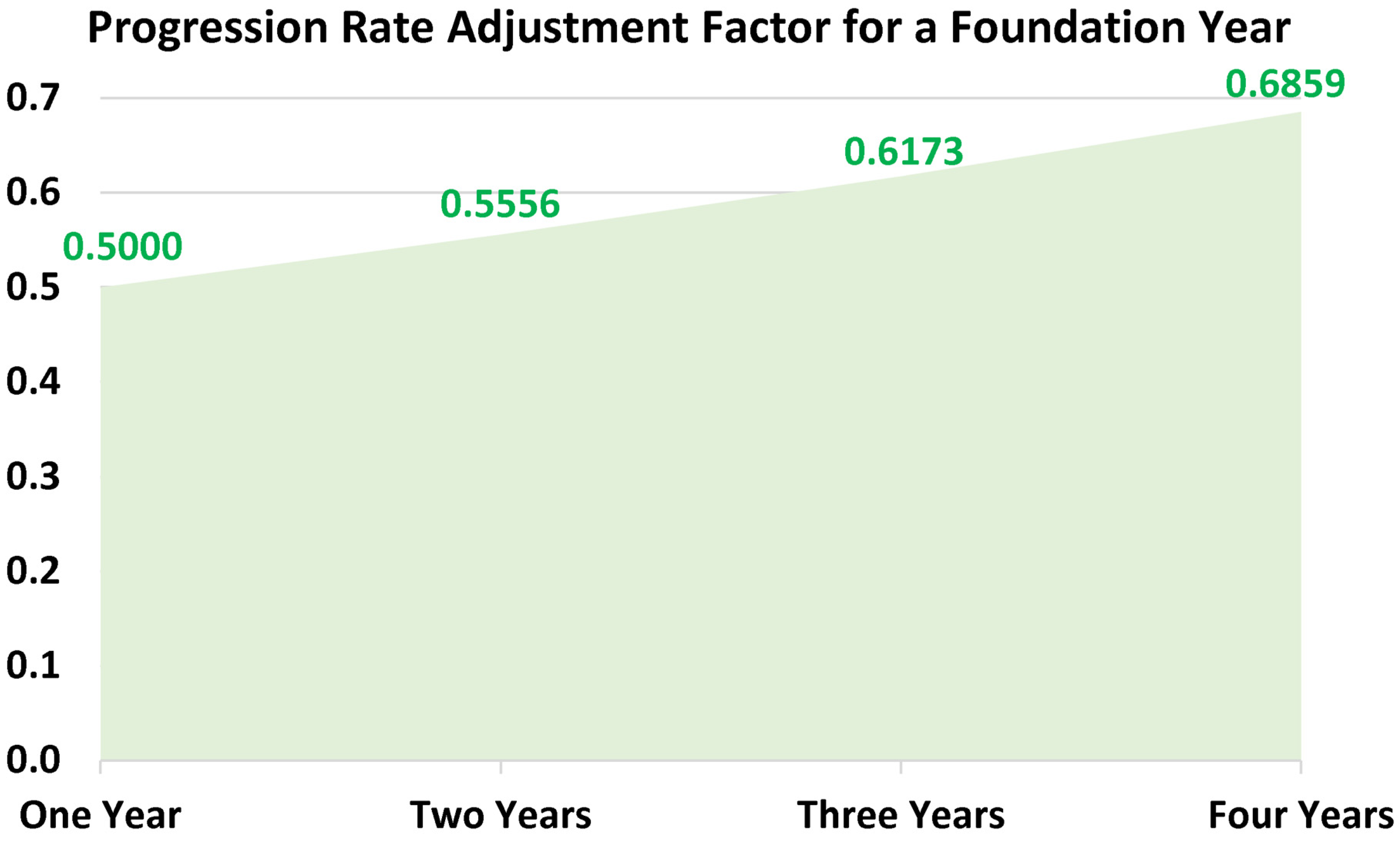
$\mu$	Progression rate adjustment factor (or penalty factor) to account for the effect of a foundation year (if applicable)
AR	Attrition rate (the complement of the retention rate; their sum is always 100%)
CR	Completion rate (same as the graduation rate)
CR′	Scaled completion rate for a perfect 0-100% range (proposed, but not used here)
DR	Dropout rate (same as the attrition rate)
ED	United States Department of Education
GR	Graduation rate, equivalently called “completion rate”
GR′	Scaled graduation rate for a perfect 0-100% range (proposed, but not used here)
HE	Higher education (equivalently “postsecondary education” or “tertiary education”)
HEI	Higher education institution (a university, academic institute, academy, or a standalone college)
IES	Institute of Education Sciences (part of ED)
NCEE	National Center for Education Evaluation and Regional Assistance (one of four centers under IES)
NCER	National Center for Education Research (one of four centers under IES)
NCES	National Center for Education Statistics (one of four centers under IES)
NCSER	National Center for Special Education Research (one of four centers under IES)
IPEDS	Integrated Postsecondary Education Data System (a system of annual data collection about higher education, conducted by NCES)
NSC-RC	National Student Clearinghouse – Research Center (located in the state of Virginia, USA)
PR	Progression rate (when defined as a modified version of the retention rate; we refer to this form of progression rate as the “expanded retention rate”), equivalently called “persistence rate” or “progress rate” (this is the type actually adopted in the date used by this study)
$\overline{\mathrm{P}\mathrm{R}}$	Average progression rate over four consecutive years
$\widehat{\mathrm{P}\mathrm{R}}$	Progression rate (when defined as a measure of the satisfactory pace of students’ advancement in their study within the same institution or degree program; we refer to this form of progression rate as the “within-institution/program study advancement” or simply the “within-institution/program”), equivalently called “persistence rate” or “progress rate” (explained, but not used here)
${\widehat{\mathrm{P}\mathrm{R}}}_{\mathrm{F}\mathrm{Y}}$	Adjusted $\widehat{\mathrm{P}\mathrm{R}}$for the influence foundation year
$\widehat{\mathrm{P}\mathrm{R}}$′	Scaled $\widehat{\mathrm{P}\mathrm{R}}$for a perfect 0-100% range (proposed, but not used here)
$\widehat{\mathrm{P}\mathrm{R}}$′′	Scaled performance-based $\widehat{\mathrm{P}\mathrm{R}}$(proposed, but not used here)
RR	Retention Rate
$\overline{\mathrm{R}\mathrm{R}}$	Average retention rate over four consecutive years

2. Introduction

2.1. Background

Undergraduate higher (postsecondary/tertiary) education, is an important stage of the qualifications framework, where many students are being prepared for starting their career and professional life, rather than for a subsequent stage of formal education [1,2,3,4]. Quality assurance in this stage involves a continuous improvement process, where several performance elements (qualitative indicators and quantitative metrics) are regularly evaluated and monitored against target levels or benchmarked with peers, such as the students-faculty ratio, retention rates (RR), progression rates (PR) – also known as persistence rates, graduation rates (GR) – also known as completion rates (CR), attrition rates (AR), students’ satisfaction, post-graduation job satisfaction, community engagement, institutional ranking, institutional affiliations, industrial collaboration and interaction with professional bodies, alignment with professional licensure, students’ scores on third-party standardized tests, practicum/field work and other experiential learning modes, entrepreneurial support, participation in competitions or innovation exhibitions, internationalization and students’ mobility, attractive students’ activities and campus life, and focus on sustainability [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50].

Students’ retention rates (RR), students’ progression rates (PR), and students’ graduation rates (GR) are three quantitative quality metrics for tracking students and assessing their success from the entry/admission point till the completion/graduation point, or for compliance with accreditation requirements [51,52,53,54,55,56,57].

Retention rates generally express the ability of an HEI or an academic degree program to retain its students; such that after a specified duration (one year for example), if a student remains enrolled (maintaining their active ID number) in the same HEI or program or earns a credential (academic degree) form it, then that student is considered “retained”. High retention rates (ideally 100%) are favored; as they show the attractiveness of the HEI or program, its stability, reputation, financial wellbeing, and a healthy relationship with its students that suggests a sense of belonging and an atmosphere of inclusion [58,59,60,61,62,63]. Mathematically, the retention rate is expressed as

$$\mathrm{R}\mathrm{R}={\displaystyle \frac{\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{r}\mathrm{e}\mathrm{t}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{d} \mathrm{s}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s}}{\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l} \mathrm{s}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s}}}$$

(1)

where the term “initial students” here refers to students at the beginning of the retention computation period; such as the beginning of the entire undergraduate degree program at the admission/entry point. Thus, if all initial students are retained, RR reaches its upper limit of 100%. With this expression, RR is guaranteed to lie exactly within the normalized range 0-100% as an inclusive interval of all possibilities, making it straightforward to interpret as any efficiency figure adopted for convenient performance characterization in energy systems or industrial processes [64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81].

The opposite (or complement) of retention is attrition or dropout, which refers to students who do not remain in their HEI or academic program, because of transferring out, withdrawal, or dismissal [82,83,84,85,86]. Thus, the attrition rate (AR) or dropout rate (DR) is 100% minus the retention rate (RR) as expressed in Equation (2). For example, a retention rate of 80% corresponds to an attrition rate (or a dropout rate) of 20%.

$$\mathrm{A}\mathrm{R}(\mathrm{o}\mathrm{r} \mathrm{D}\mathrm{R})=100\mathrm{\%}-\mathrm{R}\mathrm{R}$$

(2)

Or

$$\mathrm{A}\mathrm{R}\left(\mathrm{o}\mathrm{r} \mathrm{D}\mathrm{R}\right)={\displaystyle \frac{\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{u}\mathrm{t} \mathrm{s}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s}}{\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l} \mathrm{s}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s}}}={\displaystyle \frac{\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l} \mathrm{s}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s}-\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{r}\mathrm{e}\mathrm{t}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{d} \mathrm{s}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s}}{\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l} \mathrm{s}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s}}}$$

(3)

where the term “dropout students” here refers to all students who do not continue their enrollment in the HEI or program, because of transferring out, withdrawal, or dismissal. The ideal attrition rate is 0%; it is aimed to be minimized.

Progression rates (or persistence rates or progress rates) commonly refer to the ability of the students to advance through their academic program with a satisfactory rate that enables them to graduate within the normal duration of study (such as four years in a bachelor’s degree program) [87,88,89,90,91,92,93]. The portion of students who maintain a satisfactory pace of passing courses or earning credit hours over a specified period gives the progression rate (PR). Mathematically, the progression rate can be described as

$$\widehat{\mathrm{P}\mathrm{R}}={\displaystyle \frac{\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{s}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s} \mathrm{m}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{n}\mathrm{g} \mathrm{a} \mathrm{s}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{s}\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{r}\mathrm{y} \mathrm{p}\mathrm{a}\mathrm{c}\mathrm{e} \mathrm{o}\mathrm{f} \mathrm{a}\mathrm{d}\mathrm{v}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e} \mathrm{i}\mathrm{n} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{d}\mathrm{e}\mathrm{g}\mathrm{r}\mathrm{e}\mathrm{e} \mathrm{p}\mathrm{r}\mathrm{o}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{m}}{\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l} \mathrm{s}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s}}}$$

(4)

The circumflex (hat) notation is intentionally added to the above acronym of the progression (persistence) rate to emphasize that it is just one form of multiple forms in which it was defined in the literature. There is an alternative way to define the progression (persistence) rate, making it the result of augmenting the retention rate by including those students who transfer out to other institutions or complete a credential there (in this definition, a student is persistent or progressing if she or he continues studying regardless of where). Mathematically, this alternative definition of the progression (persistence) rate can be expressed as

$$\mathrm{R}\mathrm{R}={\displaystyle \frac{\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{r}\mathrm{e}\mathrm{t}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{d} \mathrm{s}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s} \mathrm{i}\mathrm{n} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{s}\mathrm{a}\mathrm{m}\mathrm{e} \mathrm{o}\mathrm{r} \mathrm{a}\mathrm{n}\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r} \mathrm{p}\mathrm{l}\mathrm{a}\mathrm{c}\mathrm{e}}{\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l} \mathrm{s}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s}}}$$

(5)

In fact, this alternative definition was adopted by the source of raw progression (persistence) rates we used here. This alternative definition of the progression (persistence) rate makes it less interesting to an individual higher education institution or academic program (it remains interesting at a country-level), and such a rate in this case does not qualify for institutional-level or program-level benchmarking and quality assessment, while the definition we expressed is much more useful and practicable. Despite this, all the progression (persistence) rates in our study refer to the alternative definition of being an “expanded retention rate” as per Equation (5), rather than being a “within-institution/program study advancement” as per Equation (4).

We also notice that some sources use the term “persistence rate” or “progression rate” with a similar meaning to what we call “retention rate”; but for the purpose of this study, these terms are different [94,95,96]. One study defined the progression rate during a college study in a different way as the duration of time to graduate following an anticipated progression pattern till graduation (for example, being a sophomore "second-year" student, then a junior "third-year" student, and then a senior "fourth-year" student) [97]. There are higher education institutions We understand that the term “progression” is easier to delineate in a school system with uniformly set sequential grades as compared to a college system where students have more freedom in deciding the sequence of courses they complete [98,99,100,101,102]. We also notice that there are higher education institutions or academic programs that do not monitor progression rates, but monitor retention rates and graduation rates; considering them sufficient for the tracking process [103,104,105].

Graduation rates (GR) or completion rates (CR) represent the portion of those students who successfully complete their graduation requirements within a specified period of time, which is commonly taken as 150% (one and half) times the nominal program’s completion period (normal or expected period for graduation); and this extension in the graduation window allows a less-biased and more-complete analysis, with accommodation for students who need additional study semesters, for example to balance their study with family or work commitments. This intentional time extension allows for accommodating such cases that otherwise penalize the HEI or program through low graduation rates driven mainly by a small number of exceptional students, reflecting a highly-skewed distribution of graduation durations [106,107,108,109,110,111,112,113,114]. Thus, for a four-year bachelor’s degree program, the graduation rate is the portion of students who complete the program within six years; while for a three-year undergraduate advanced diploma program, the graduation rate is the portion of students who complete the program within 54 months; and for a two-year diploma (associate degree) program, the graduation rate is the portion of students who complete the program within three years; and for a one-year undergraduate certificate program, the graduation rate is the portion of students who complete the program within 18 months; and other students who fail to graduate within that extended graduation window represent “non-completion” cases, and their portion is the a complementary non-completion rate (NCR), defined as [115,116,117,118,119,120,121,122,123,124]

$$\mathrm{N}\mathrm{C}\mathrm{R}=100\mathrm{\%}-\mathrm{G}\mathrm{R}(\mathrm{o}\mathrm{r} \mathrm{C}\mathrm{R})$$

(6)

Mathematically, the graduation (completion) rate can be expressed as

$$\mathrm{G}\mathrm{R}(\mathrm{o}\mathrm{r} \mathrm{C}\mathrm{R})={\displaystyle \frac{\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{s}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s} \mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{u}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d} \mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{i}\mathrm{n} \mathrm{a}\mathrm{n} \mathrm{e}\mathrm{x}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{d} \mathrm{p}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{d}}{\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l} \mathrm{s}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s}}}$$

(7)

where the term “extended period” refers here to 150% of the nominal period for completion.

Several approaches can improve students’ retention, progression, or graduation rates; such as advising and mentorship, customized educational environment, and student-centered learning [125,126,127,128,129,130,131,132]. For example, one study suggested innovative teaching techniques; such as project-based learning, peer teaching, and retrieval practice (which improves memory retention through 'active' recall of information in response to a question, as compared to 'passive' review methods); and such active learning strategies through systemic educational reforms boost an equitable and inclusive learner-centered environment and address learning barriers [133]. Another study found, through empirical research and hypotheses testing, that disparity in graduation rates among different higher education institutions is linked to the variations in institutional resources; and suggested that policy interventions can be adopted to remedy this issue where many higher education students are unable to earn a degree after enrolling in a four-year college [134]. In another study, offering a for-credit course titled “Psychology of Success” about positive psychology to academically-warned students after their first semester (with an option to drop this course after enrollment) was found to foster retention, progression, and graduation; based on results analyzed after four years of implementing this methodology [135].

2.2. Goal of the Study

This work was motivated by our experience with accreditation and administrative roles in higher education, particularly for undergraduate education, where the regular reporting of retention, progression, and graduation rates for a particular degree program is mandatory. While the computing of these rates can be automated through digital information systems, the evaluation of these rates remains a source of subjectiveness and perplexity if no clear targets or benchmarking standards exit. When attempting to compare the obtained students’ tracking rates (retention, progression, and graduation) with peer values, one can get highly misleading outcomes due to the variability in how these rates are computed. The problem becomes more pronounced in a higher education system that is based on credits (credit hours or credit points), rather than sequential semesters; because terms like “first year of study” and “second year of study” become not uniquely defined [136,137,138,139]. A student may be taking a course from the third year of the nominal study plan at the same time as taking a course from the second or even the third year, as long as the prerequisites are satisfied. Furthermore, undergraduate programs that involve a non-credit preparatory year (to be called here a ‘foundation year’) as a transition stage (a bridging step) between high school (secondary school) and the degree program in colleges need careful treatment when the student’s tracking rates are either computed or interpreted [140,141,142,143].

In the current study, we primarily aim at presenting general benchmarking value for the three students’ tracking rates (retention, progression, and graduation) based on selected and processed values, such that they may suit a wide range of higher education institutions as benchmarking standards for their particular situation.

3. Research Method

3.1. Data Sources

The present study is largely based on quantitative descriptive statistical analysis, with a small component involving inferential statistics and hypothesis testing.

The raw data about undergraduate students’ tracking rates were selected from two US-based sources, which are the National Center for Education Statistics (NCES), and the National Student Clearinghouse – Research Center (NSC-RC). The rationale behind using these particular sources is the robustness and reliability of their data being managed by well-established national-level entities having long specialized experiences in this process. The use of both sources, rather than only one of them, is because each source provides a certain set of data that partly fulfills the needs of our study; but both sources together provide all the data needed.

The National Center for Education Statistics (NCES) is one of the four centers belonging to the Institute of Education Sciences (IES) of the United States Department of Education (ED), and its mission traces back to the time when the Department of Education was instituted in 1867, and this mission involves collecting statistics and facts that describe the condition and progress of education in the several US states, as well as diffusing such data to allow people in the USA to establish and maintain efficient education systems [144,145]. The other three centers under IES are the National Center for Education Evaluation and Regional Assistance (NCEE), the National Center for Education Research (NCER), and the National Center for Special Education Research (NCSER) [146,147]. NCES is the main federal entity in the USA for collecting and analyzing data related to higher education, and it utilizes a robust and well-documented data system for the annual collection of data about higher education institutions in the USA, which include retention rates and graduation rates, among many other elements. This data system is the Integrated Postsecondary Education Data System (IPEDS), which represents 12 interrelated survey components that are conducted annually for gathering data from every college, university, and technical and vocational institution that participates in the federal student financial aid programs; and these data collections take place in the fall, winter, and spring semesters [148,149,150]. A free online portal called “College Navigator” was established by NCES, in which various metrics and indicators can be accessed for a particular higher education institution. However, since in our study we focus on aggregate national rates rather than individual institutions’ data, we use another free online data explorer, which is the Trend Generator [151,152].

The National Student Clearinghouse – Research Center (NSC-RC) is the research branch of the National Student Clearinghouse (NSC), and it works with higher education institutions and other educational organizations to better inform policymakers and practitioners about the educational pathways of students through reporting data outcomes. The Clearinghouse has been a non-profit education partner to colleges and universities in the USA since 1993, providing them with educational reports, studies on educational progress, and research services [153,154].

Table 1 lists the data we curated in the current study and their sources.

It should be noted that the seven disciplines selected here for additional discipline-specific analysis are not the exhaustive set of disciplines available in the NSC-RC data. Instead, we selected these disciplines as examples of personal interest that allow reasonable diversity in the coverage. Examples of additional available disciplines in the NSC-RC data are Agriculture, Biological/Biomedical Sciences, Communication/Journalism, Education, English Language, History, Liberal Arts, Mathematics/Statistics, Military Technologies, Parks/Recreation/Leisure/Fitness Studies, Philosophy and Religious Studies, Physical Sciences, Psychology, and Public Administration.

3.2. Retention and Progression Extrapolation

Because the reported retention rates in both sources used here (NCES or NSC-RC) and the progression rates (called persistence rates) reported by NSC-RC are based on the first year of college study; institutions that adopt longer time windows (such as the entire nominal duration of the program) for computing their retention rates should not compare their retention or progression rates with those directly reported by NCES or NSC-RC; as such comparison becomes misleading and unfair for those institutions because the retention or progression over a wider multi-year window is expected to be lower than those of the narrower first-year window. Therefore, we suggest a nonlinear extrapolation where either the first-year retention rate or the first-year progression rate is penalized when estimated for a multi-year period with a multiplicative “discount factor” ($\lambda$) that is the average of the square roots of the first-year retention rates (or the first-year progression rates) in the last four years. The rationale of our choice of this extrapolation mechanism combines both the simplicity of implementation (a single factor is involved in the extrapolation process) and the reasonable assumption that either progression or retention in subsequent years is better than their counterpart in the first year, where students might be experiencing a new college environment and education system that are different from those they are aware of during their earlier school study. Thus, instead of multiplying with the first-year rate itself, taking the square root brings the multiplicative factor closer to unity, and thus serves to weaken the anticipated decline in either the retention rate or the progression rate. After this, taking an average over four years helps in smoothening the computation and reduces the possibility of short-term irregularity due to exceptional rates in a particular year, such as during the COVID-19 pandemic [158,159,160,161,162,163].

Mathematically, if the first-year retention rates for the last four consecutive cohorts are RR₁ (oldest: corresponding to Fall 2019-20 in our study), RR₂, RR₃, and RR₄ (latest: corresponding to Fall 2022-23 in our study); then the discount factor for extrapolating the retention rate (${\lambda }_{\mathrm{R}\mathrm{R}}$) is

$${\lambda }_{\mathrm{R}\mathrm{R}}=0.25\left(\sqrt{\mathrm{R}{\mathrm{R}}_1}+\sqrt{\mathrm{R}{\mathrm{R}}_2}+\sqrt{\mathrm{R}{\mathrm{R}}_3}+\sqrt{\mathrm{R}{\mathrm{R}}_4}\right)$$

(8)

If the average retention rate for the four years is

$$\overline{\mathrm{R}\mathrm{R}}=0.25\left(\mathrm{R}{\mathrm{R}}_1+\mathrm{R}{\mathrm{R}}_2+\mathrm{R}{\mathrm{R}}_3+\mathrm{R}{\mathrm{R}}_4\right)$$

(9)

then, the extrapolation of the first-year retention rate is performed as

$$\mathrm{R}\mathrm{R}(\mathrm{o}\mathrm{n}\mathrm{e} \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r})=\overline{\mathrm{R}\mathrm{R}}$$

(10)

$$\mathrm{R}\mathrm{R}(\mathrm{t}\mathrm{w}\mathrm{o} \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{s})={\lambda }_{\mathrm{R}\mathrm{R}}\overline{\mathrm{R}\mathrm{R}}$$

(11)

$$\mathrm{R}\mathrm{R}(\mathrm{t}\mathrm{h}\mathrm{r}\mathrm{e}\mathrm{e} \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{s})={\lambda }_{\mathrm{R}\mathrm{R}}^2\overline{\mathrm{R}\mathrm{R}}$$

(12)

$$\mathrm{R}\mathrm{R}(\mathrm{f}\mathrm{o}\mathrm{u}\mathrm{r} \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{s})={\lambda }_{\mathrm{R}\mathrm{R}}^3\overline{\mathrm{R}\mathrm{R}}$$

(13)

$$\mathrm{R}\mathrm{R}(\mathrm{f}\mathrm{i}\mathrm{v}\mathrm{e} \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{s})={\lambda }_{\mathrm{R}\mathrm{R}}^4\overline{\mathrm{R}\mathrm{R}}$$

(14)

Similarly, if the first-year progression rates for the last four consecutive cohorts are PR₁ (oldest: based on the entering cohort of 2019-20 in our study), PR₂, PR₃, and PR₄ (latest: based on the entering cohort of 2022-23 in our study); then the discount factor for extrapolating the progression rate (${\lambda }_{\mathrm{P}\mathrm{R}}$) is

$${\lambda }_{\mathrm{P}\mathrm{R}}=0.25\left(\sqrt{\mathrm{P}{\mathrm{R}}_1}+\sqrt{\mathrm{P}{\mathrm{R}}_2}+\sqrt{\mathrm{P}{\mathrm{R}}_3}+\sqrt{\mathrm{P}{\mathrm{R}}_4}\right)$$

(15)

and the average progression rate for the four years is

$$\overline{\mathrm{P}\mathrm{R}}=0.25\left(\mathrm{P}{\mathrm{R}}_1+\mathrm{P}{\mathrm{R}}_2+\mathrm{P}{\mathrm{R}}_3+\mathrm{P}{\mathrm{R}}_4\right)$$

(16)

Then, the extrapolation of the first-year progression rate is performed as

$$\mathrm{P}\mathrm{R}(\mathrm{o}\mathrm{n}\mathrm{e} \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r})=\overline{\mathrm{P}\mathrm{R}}$$

(17)

$$\mathrm{P}\mathrm{R}(\mathrm{t}\mathrm{w}\mathrm{o} \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{s})={\lambda }_{\mathrm{P}\mathrm{R}}\overline{\mathrm{P}\mathrm{R}}$$

(18)

$$\mathrm{P}\mathrm{R}(\mathrm{t}\mathrm{h}\mathrm{r}\mathrm{e}\mathrm{e} \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{s})={\lambda }_{\mathrm{P}\mathrm{R}}^2\overline{\mathrm{P}\mathrm{R}}$$

(19)

$$\mathrm{P}\mathrm{R}(\mathrm{f}\mathrm{o}\mathrm{u}\mathrm{r} \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{s})={\lambda }_{\mathrm{P}\mathrm{R}}^3\overline{\mathrm{P}\mathrm{R}}$$

(20)

3.3. Progression Adjustment for Foundation Year

In the case that the progression (persistence) rate is a measure of the satisfactory pace of students’ advancement in their study within the same institution or degree program (we designate this form of progression rate by the symbol $\widehat{\mathrm{P}\mathrm{R}}$); then when computing the progression rates for an academic program that offers obligatory non-credit foundation year, the computation of such as progression rate becomes difficult as the transition from the foundation year to the college study is not necessarily happening concurrently at a single point; as some students may need more than one year to finish the foundation phase (for example because repeating a foundational course) or may need less than one year to finish it (for example, because the student transfers from another higher education institution in which the student completed part of the foundation requirement; or because the student can be exempted from part of the foundation requirement due to prior attained standardized certificate or due to receiving a high score in a placement test) [164,165]. The existence of such a foundation year does not impact the computation of retention rates, but largely worsens the progression rates if they are computed over a time window that starts after the students’ admission to the higher education institution, regardless of the student being subject to a foundation year or being partly or fully exempted from it. Our proposed adjustment here for proper benchmarking (when the available reference progression rates correspond to a system not having a foundation year, where students get admitted directly to the degree program) is scaling down these reference progression rates through a multiplicative “penalty” factor. We propose that this penalty factor starts at 0.5 (selected here as the midway between the extreme limits of 0 and 1) in the first-year progression rate, which means that if the foundation-free (unadjusted) benchmarking value or target for the first-year progression rate is 80% for example, the higher education institution may expect to achieve only half of this as a result of having students spending their first year in the non-credit foundation year, which is not considered when the progress in the degree program is quantified. We further suggest that this penalty factor (progression rate adjustment factor) is relaxed if the first-year progression rates are extrapolated to obtain multi-year estimates, with a relaxation factor of ($\Lambda$=1/0.9=1.11111). Thus, the two-year progression rate adjustment factor is 0.5/0.9 = 0.55556; the three-year progression rate adjustment factor is 0.5/0.9² = 0.61728; and the four-year progression rate adjustment factor is 0.5/0.9³ = 0.68587. The reason for this suggested relaxation is the decay of the interruption caused by the initial foundation year as students exit it and advance through the for-credit degree program.

Designating the progression rate adjustment factor by the symbol ($\mu$), and the adjusted progression rate for the effect of a foundation year by the symbol (${\widehat{\mathrm{P}\mathrm{R}}}_{\mathrm{F}\mathrm{Y}}$), then the following expression describes mathematically the suggested correction to incorporate the effect of a foundation year:

$${\widehat{\mathrm{P}\mathrm{R}}}_{\mathrm{F}\mathrm{Y}}\left(\mathrm{o}\mathrm{n}\mathrm{e} \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\right)=\mu \widehat{\mathrm{P}\mathrm{R}}\left(\mathrm{o}\mathrm{n}\mathrm{e} \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\right);\mu =0.5$$

(21)

$${\widehat{\mathrm{P}\mathrm{R}}}_{\mathrm{F}\mathrm{Y}}\left(\mathrm{t}\mathrm{w}\mathrm{o} \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{s}\right)=\mu \widehat{\mathrm{P}\mathrm{R}}\left(\mathrm{t}\mathrm{w}\mathrm{o} \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{s}\right);\mu =0.5\Lambda =0.5/0.9=0.55556$$

(22)

$${\widehat{\mathrm{P}\mathrm{R}}}_{\mathrm{F}\mathrm{Y}}\left(\mathrm{t}\mathrm{h}\mathrm{r}\mathrm{e}\mathrm{e} \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{s}\right)=\mu \widehat{\mathrm{P}\mathrm{R}}\left(\mathrm{t}\mathrm{h}\mathrm{r}\mathrm{e}\mathrm{e} \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{s}\right);\mu =0.5{\Lambda }^2=0.5/{0.9}^2=0.61728$$

(23)

$${\widehat{\mathrm{P}\mathrm{R}}}_{\mathrm{F}\mathrm{Y}}\left(\mathrm{f}\mathrm{o}\mathrm{u}\mathrm{r} \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{s}\right)=\mu \widehat{\mathrm{P}\mathrm{R}}\left(\mathrm{f}\mathrm{o}\mathrm{u}\mathrm{r} \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{s}\right);\mu =0.5{\Lambda }^3=0.5/{0.9}^3=0.68587$$

(24)

Figure 1 visualizes the variation of the adjustment factor ($\mu$) and the duration to which the progression rate corresponds. The gradual increase in the value of that penalty factor is the result of the relaxation parameter ($\Lambda$). Although the variation appears linear (represented by a straight line), it is actually nonlinear (represented by a concave-up curve in the figure), but the nonlinearity is not pronounced because the relaxation parameter ($\Lambda$) is close to 1.0.

In all the progression figures presented in the subsequent “Results” section, two sets of progression rates are presented; the smaller progression rate is the one after applying the aforementioned adjustment model for approximating the influence of a foundation year, and it is more suitable for higher education institutions that employ such a preparatory non-credit bridging scheme and also define the progression rate according to the “within-institution/program study advancement” type. Although the raw progression (persistence) data curated here are based on the “expanded retention rate” type, where the aforementioned adjustment is irrelevant; we still apply it for numerical demonstration purposes, and the reader should pay attention to this.

4. Results

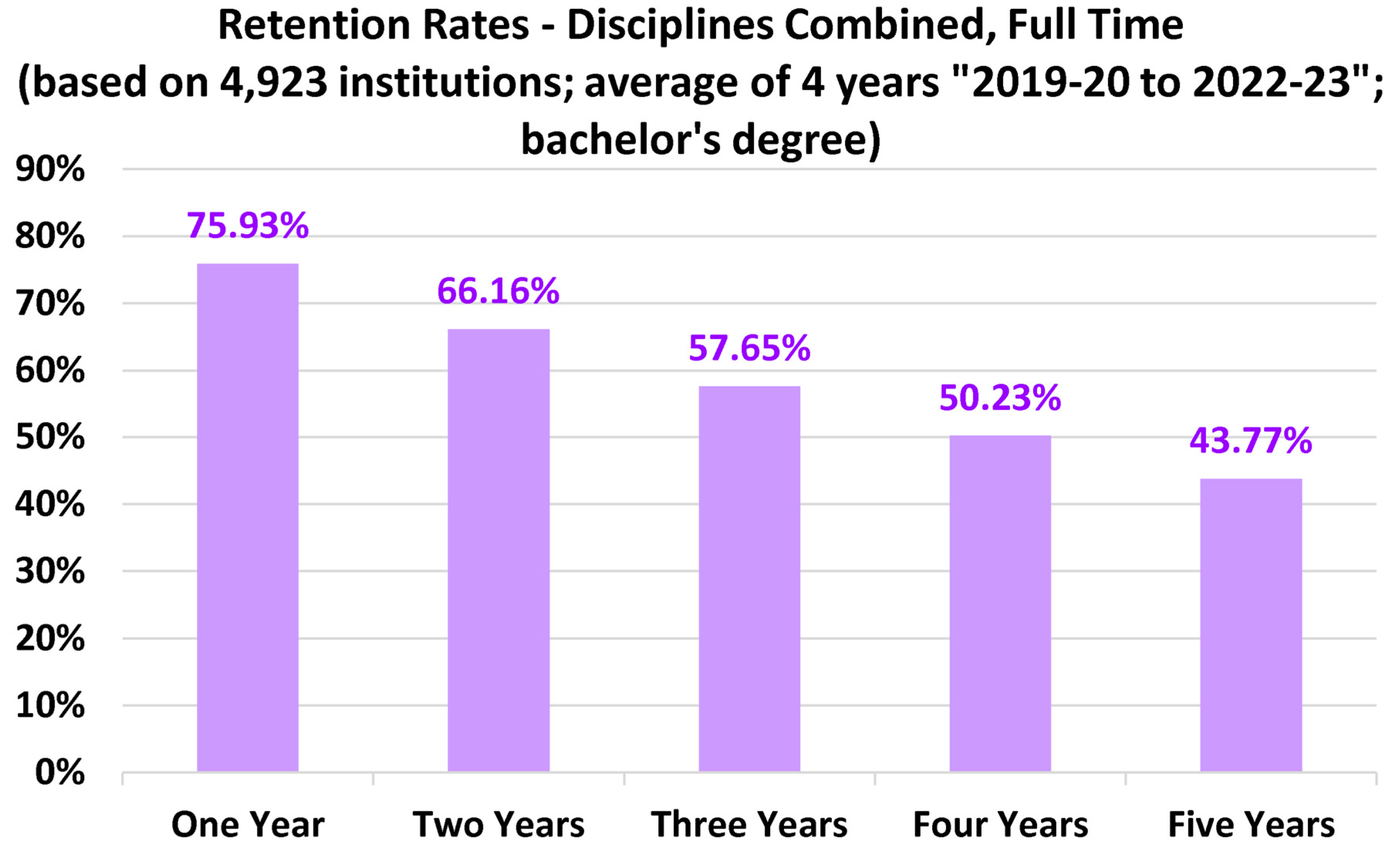
4.1. Overall Full-Time Bachelor’s Degree Retention Rates

Our results start with the overall (not the discipline-specific) retention rates. Figure 1 shows the estimated retention rates for bachelor’s degree students. These estimates are based on raw data from NCES (National Center for Education Statistics) covering a large number of higher education institutions (4,923), and raw retention rates reported over four consecutive years (from Fall 2019-20 to Fall 2022-23). The average first-year retention rate (this corresponds to $\overline{\mathrm{R}\mathrm{R}}$ in our mathematical expressions) is 75.93%. Thus, about three-quarters of the bachelor’s degree students are retained; which gives an average first-year attrition rate of 24.07%. For higher education institutions or academic programs that report their retention rates over an entire nominal undergraduate study period of four years, the extrapolated benchmarking retention rate drops to 50.23%. If an additional fifth year of a foundation bridging phase also exists after admission, our suggested benchmarking retention rate is the five-year extrapolated value of 43.77%.

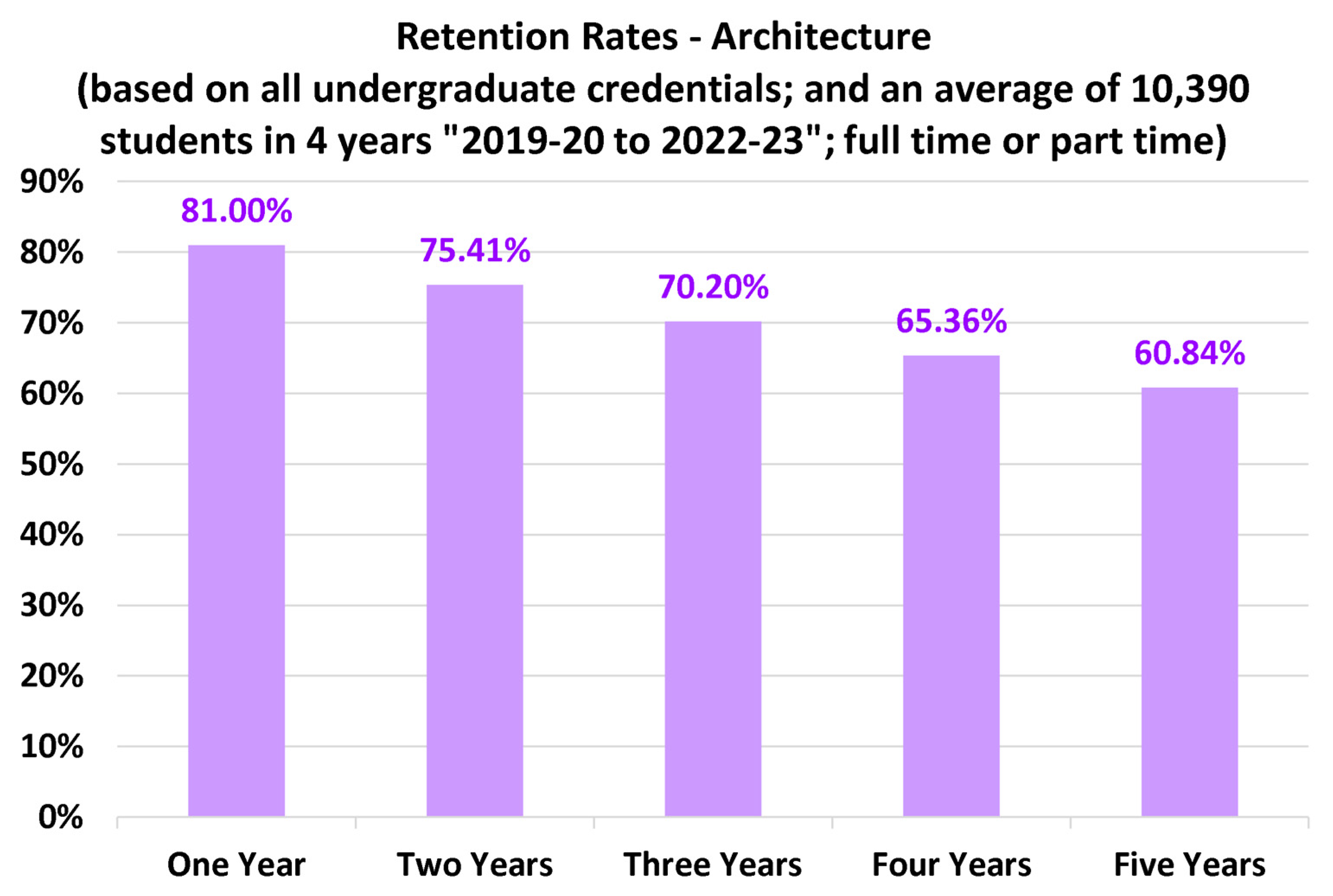
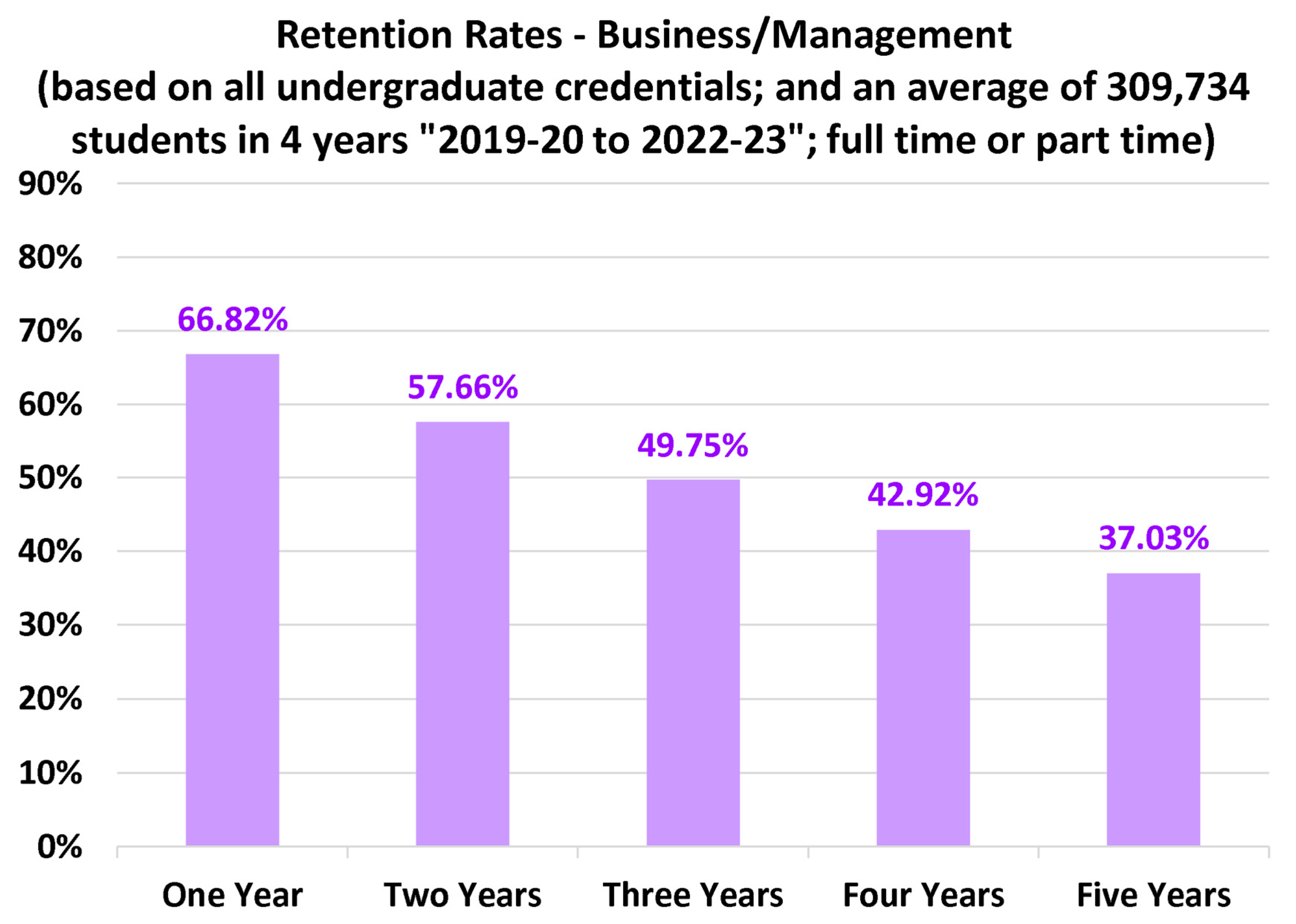
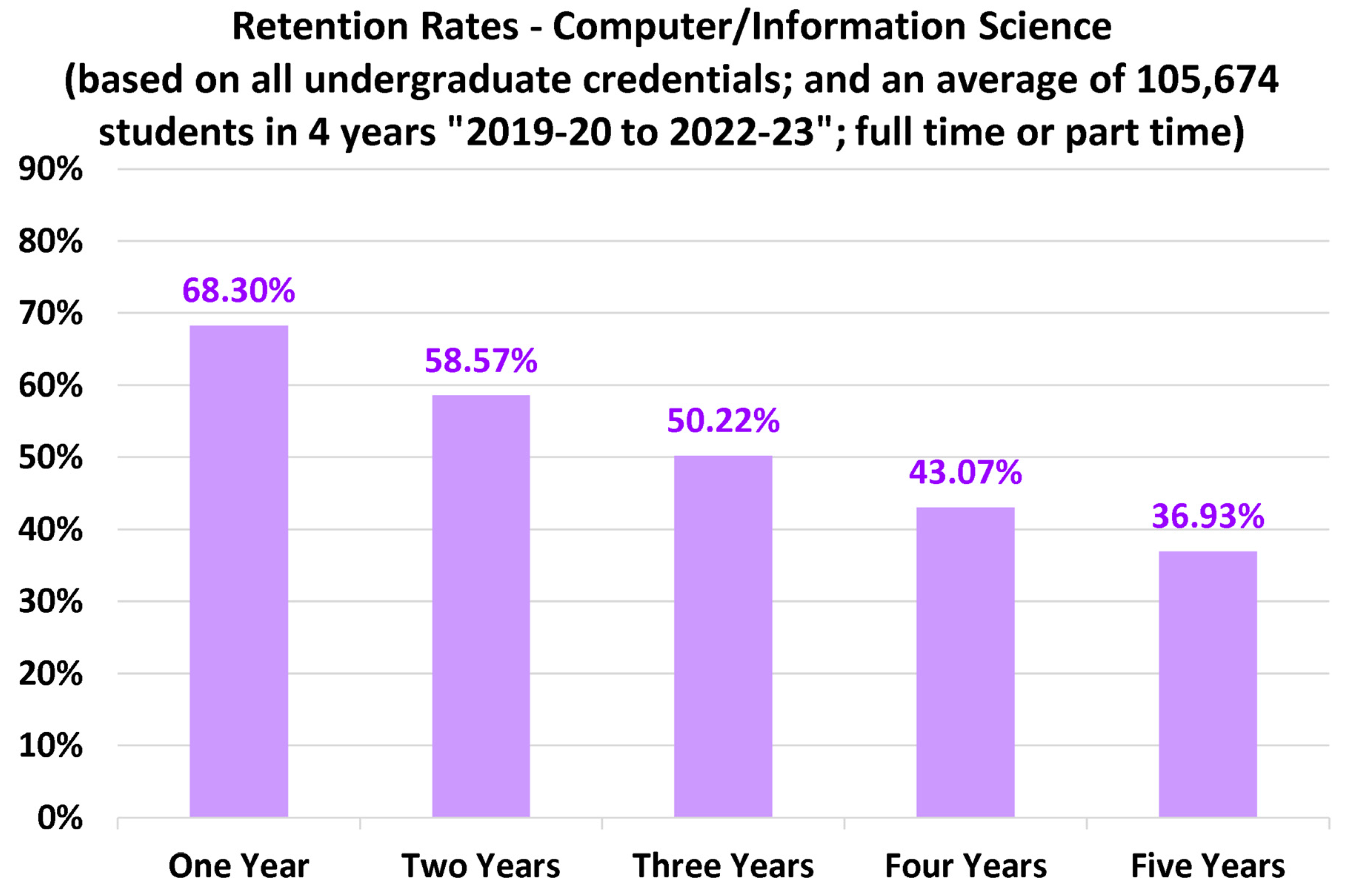
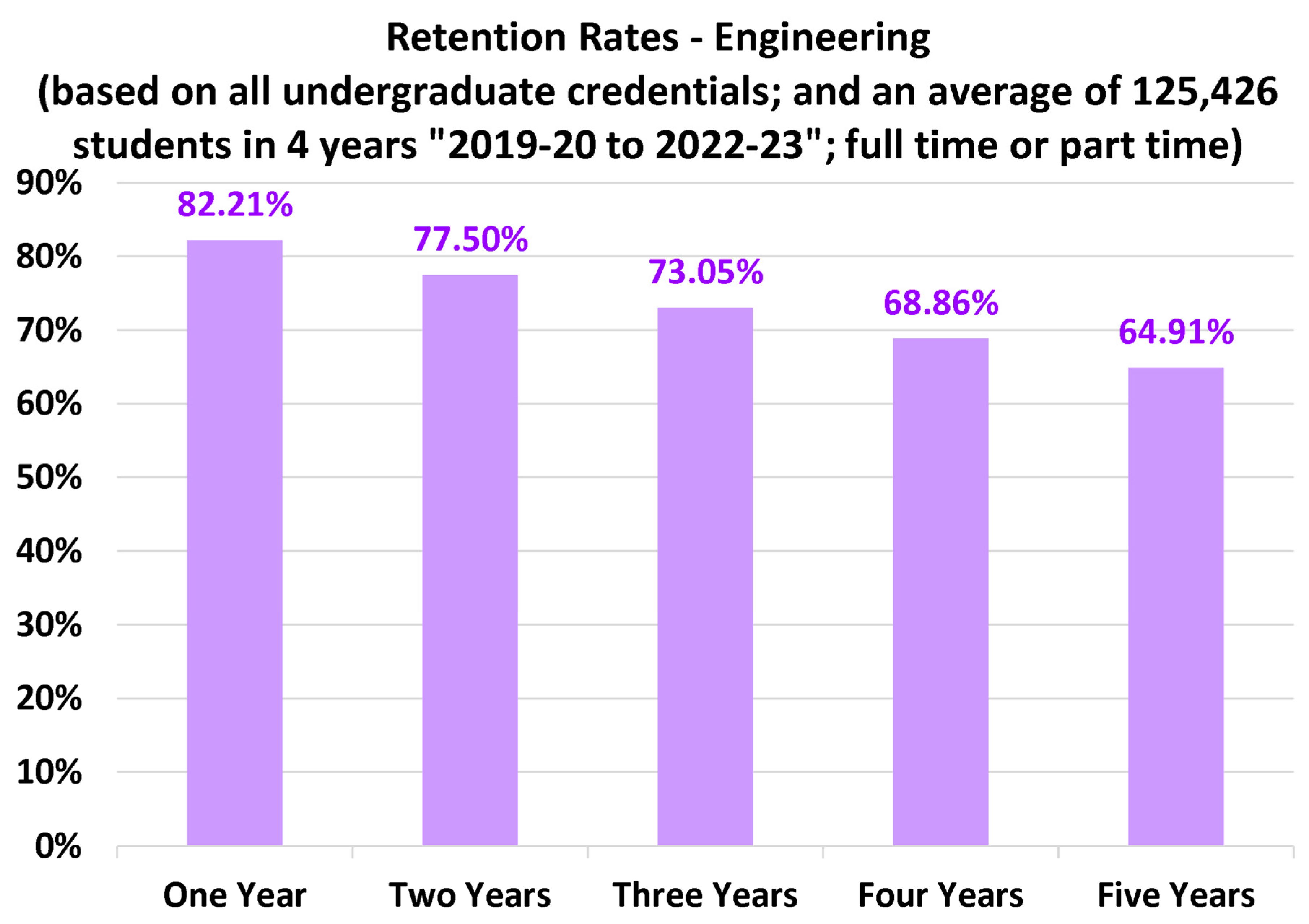
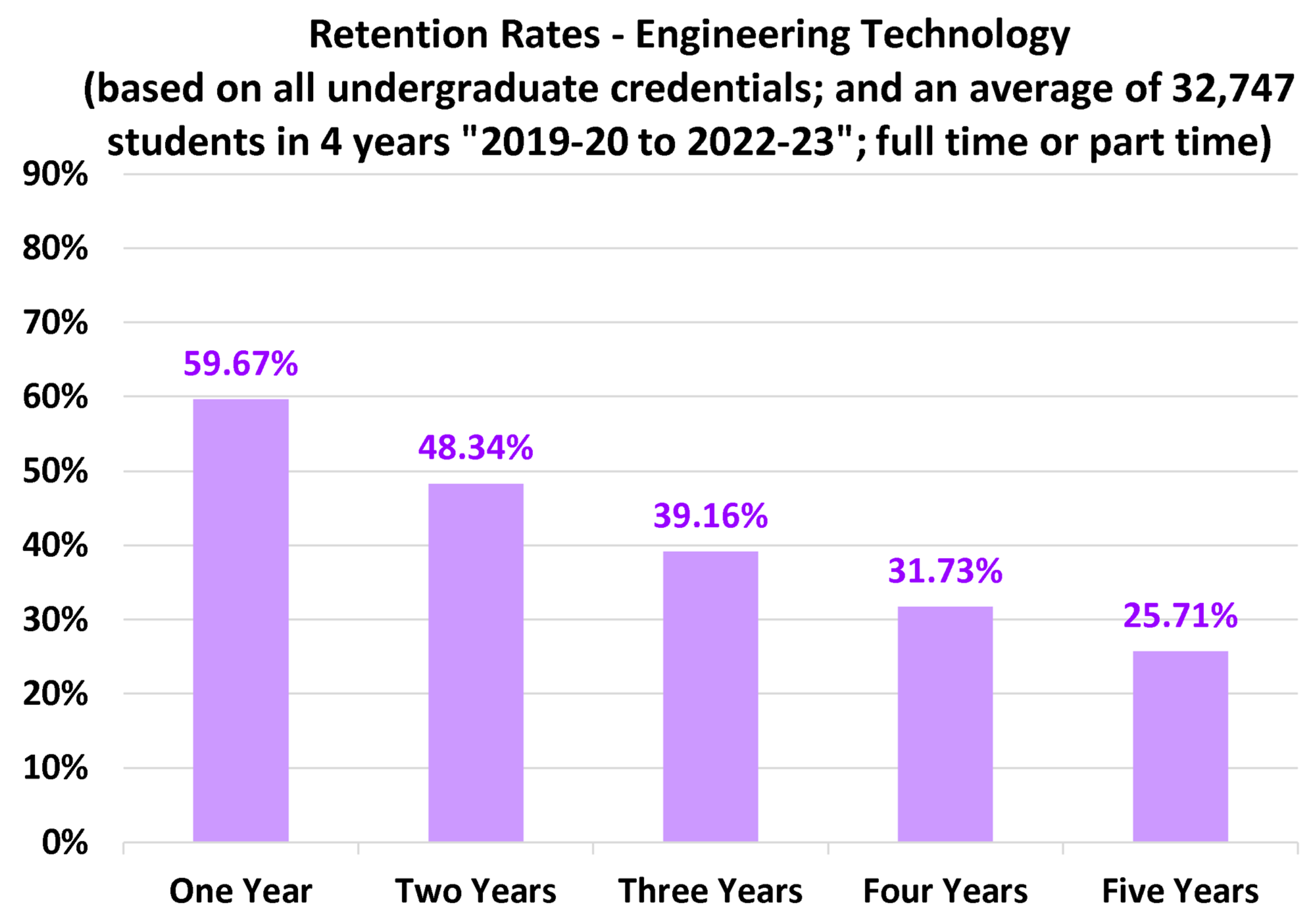
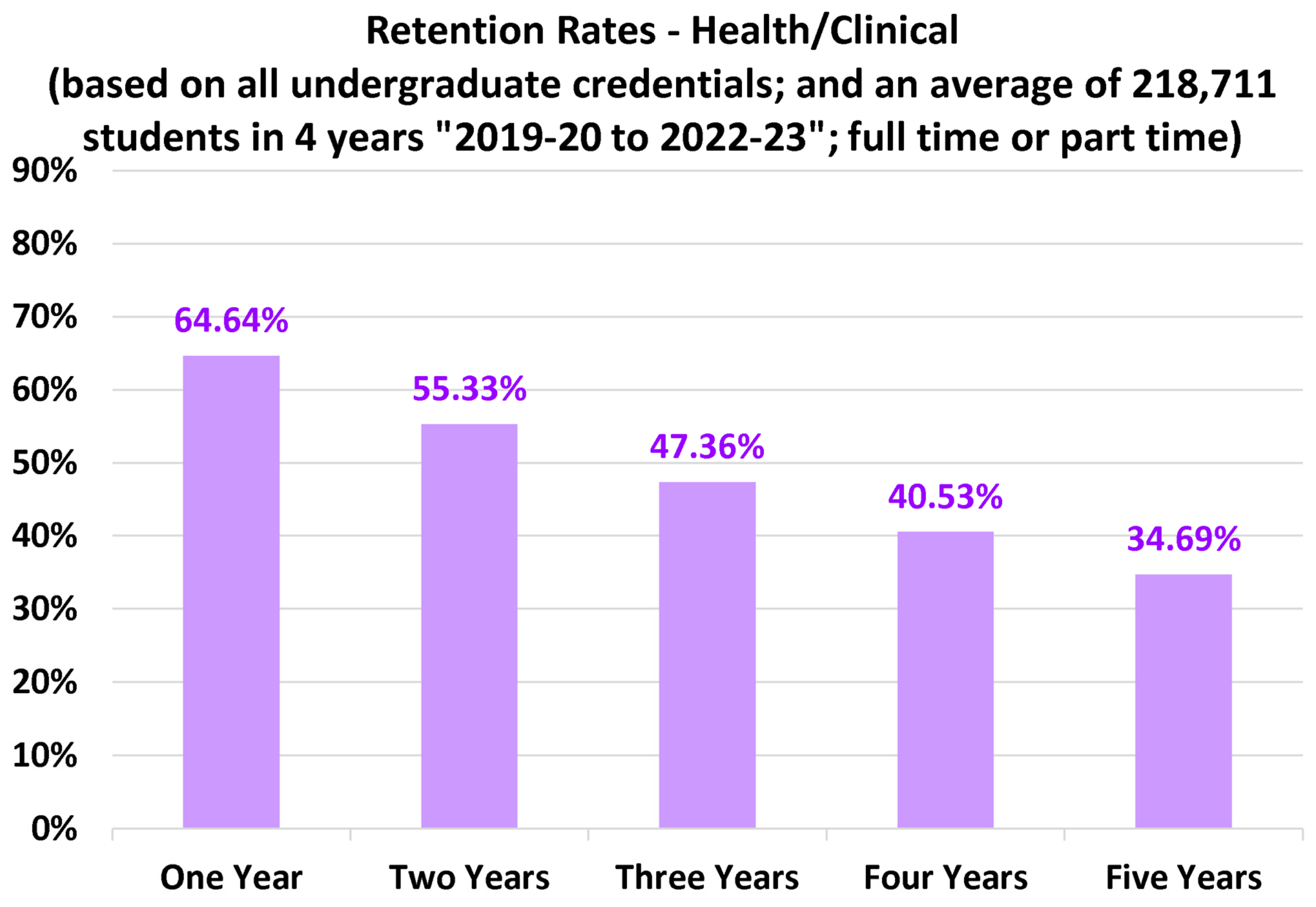
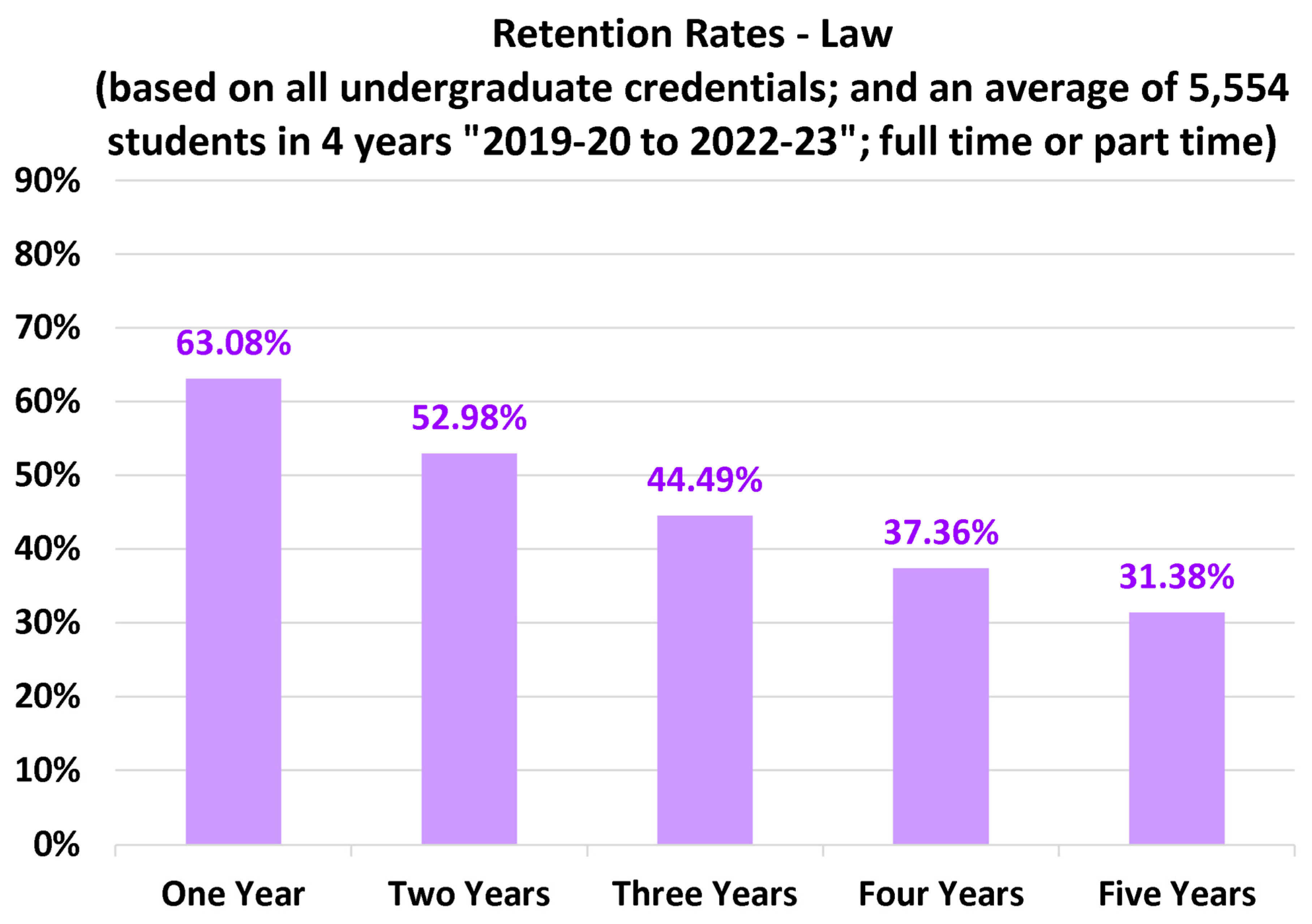
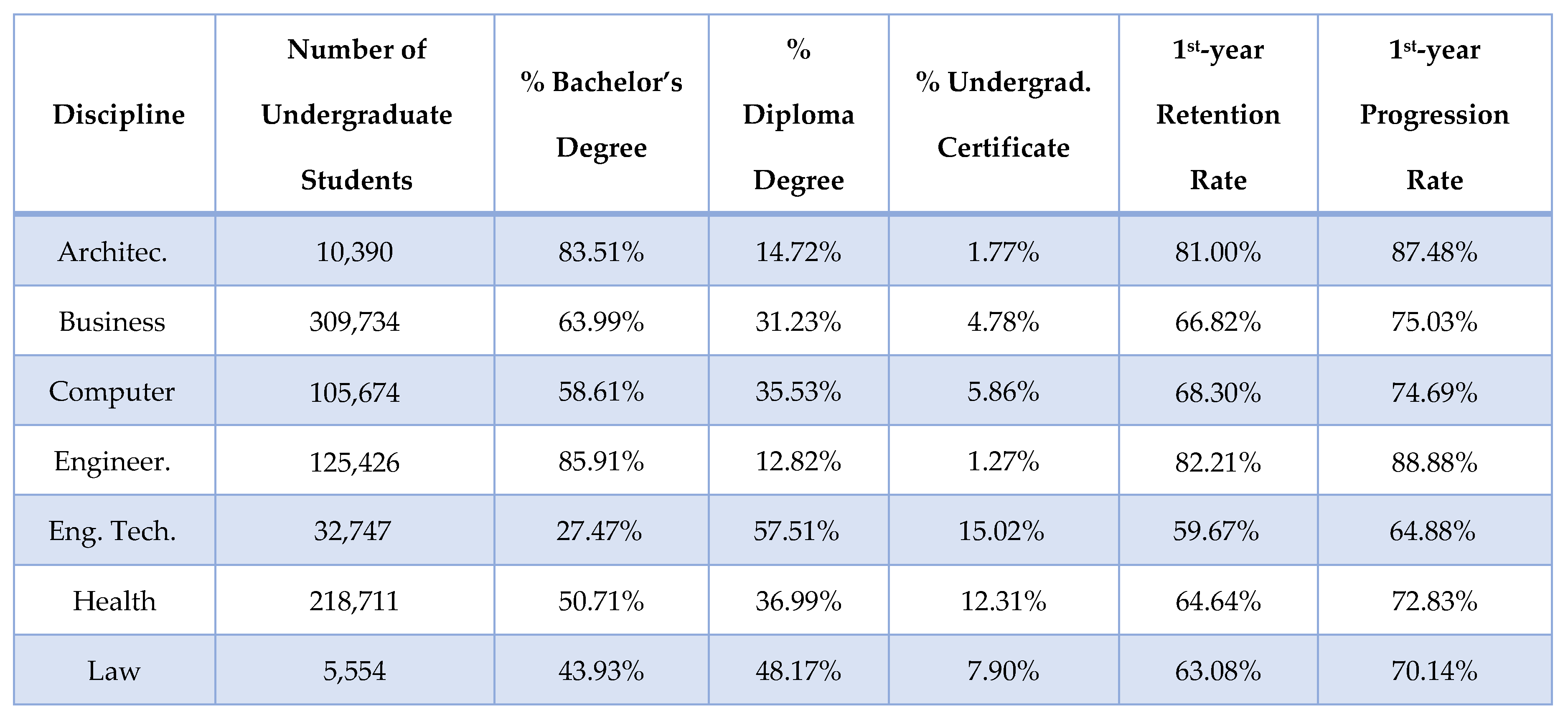
4.2. Discipline-Specific Retention Rates

For the selected seven broad disciplines, and based on our proposed analysis of the raw data of NSC-RC (National Student Clearinghouse – Research Center), we provide here estimated discipline-specific undergraduate retention rates for benchmarking purposes.

Figure 3 shows the retention rates (with five time windows, from one year to five years) for the architecture discipline, based on an average number of 10,390 undergraduate students (average of four consecutive years, representing the admission cohorts of Fall 2019-20, Fall 2020-21, Fall 2021-22, and Fall 2022-23); who are mostly bachelor’s degree students (83.51%), with a small fraction of 14.72% at the associate degree (diploma) level, and only 1.77% at the level of undergraduate certificate. These retention rates correspond to the precise classification category “Architecture and Related Services”. Relative to the overall average first-year retention rate of 75.93%, the architecture-specific average first-year retention rate is higher by about six percentage points (6 pp), with a value of 81.00%; which is the second highest among the seven disciplines covered in this study, and it is close to the highest (being 82.21%) for engineering.

Figure 4 shows the retention rates for the business/management discipline, based on an average number of 309,734 undergraduate students, with the distribution by degree being 63.99% at the bachelor’s level, 31.23% at the diploma’s level, and 4.78% at the certificate’s level. These retention rates correspond to the precise classification category “Business, Management, Marketing, and Related Support”. Relative to the overall average first-year retention rate of 75.93%, this discipline has a lower average first-year retention rate of 66.82%.

Figure 5 shows the retention rates for the computer/information science discipline, based on an average number of 105,674 undergraduate students, with the distribution by degree being 58.61% at the bachelor’s level, 35.53% at the diploma’s level, and 5.86% at the certificate’s level. These retention rates correspond to the precise classification category “Computer and Information Sciences and Support Services”. Relative to the overall average first-year retention rate of 75.93%, this discipline has a lower average first-year retention rate of 68.30%.

Figure 6 shows the retention rates for the engineering discipline, based on an average number of 125,426 undergraduate students, with the distribution by degree being 85.91% at the bachelor’s level, 12.82% at the diploma’s level, and 1.27% at the certificate’s level. These retention rates correspond to the precise classification category “Engineering”. Relative to the overall average first-year retention rate of 75.93%, this discipline has a higher average first-year retention rate of 82.21%; which is in fact the highest among the seven disciplines covered in this study.

Figure 7 shows the retention rates for the engineering technology discipline, based on an average number of 32,747 undergraduate students, with the distribution by degree being 27.47% at the bachelor’s level, 57.51% at the diploma’s level, and 15.02% at the certificate’s level. These retention rates correspond to the precise classification category “Engineering Technologies/Technicians”. Relative to the overall average first-year retention rate of 75.93%, this discipline has a lower average first-year retention rate of 59.67%; which is in fact the lowest among the seven disciplines covered in this study.

Figure 8 shows the retention rates for the health/clinical discipline, based on an average number of 218,711 undergraduate students, with the distribution by degree being 50.71% at the bachelor’s level, 36.99% at the diploma’s level, and 12.31% at the certificate’s level. These retention rates correspond to the precise classification category “Health Professions and Related Clinical Sciences”. Relative to the overall average first-year retention rate of 75.93%, this discipline has a lower average first-year retention rate of 64.64%.

Figure 9 shows the retention rates for the law discipline, based on an average number of 5,554 undergraduate students, with the distribution by degree being 43.93% at the bachelor’s level, 48.17% at the diploma’s level, and 7.90% at the certificate’s level. These retention rates correspond to the precise classification category “Legal Professions and Studies”. Relative to the overall average first-year retention rate of 75.93%, this discipline has a lower average first-year retention rate of 63.08%.

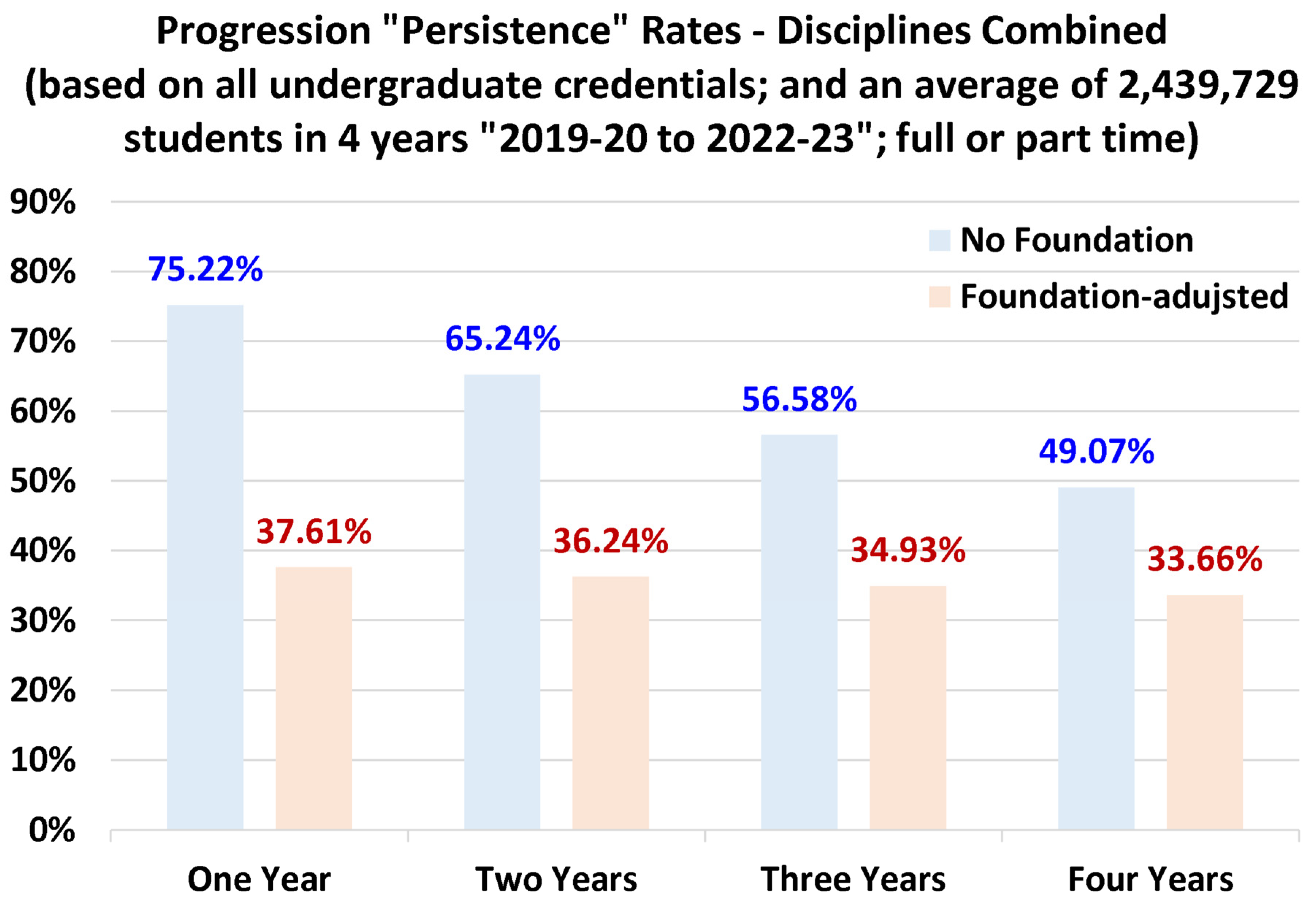
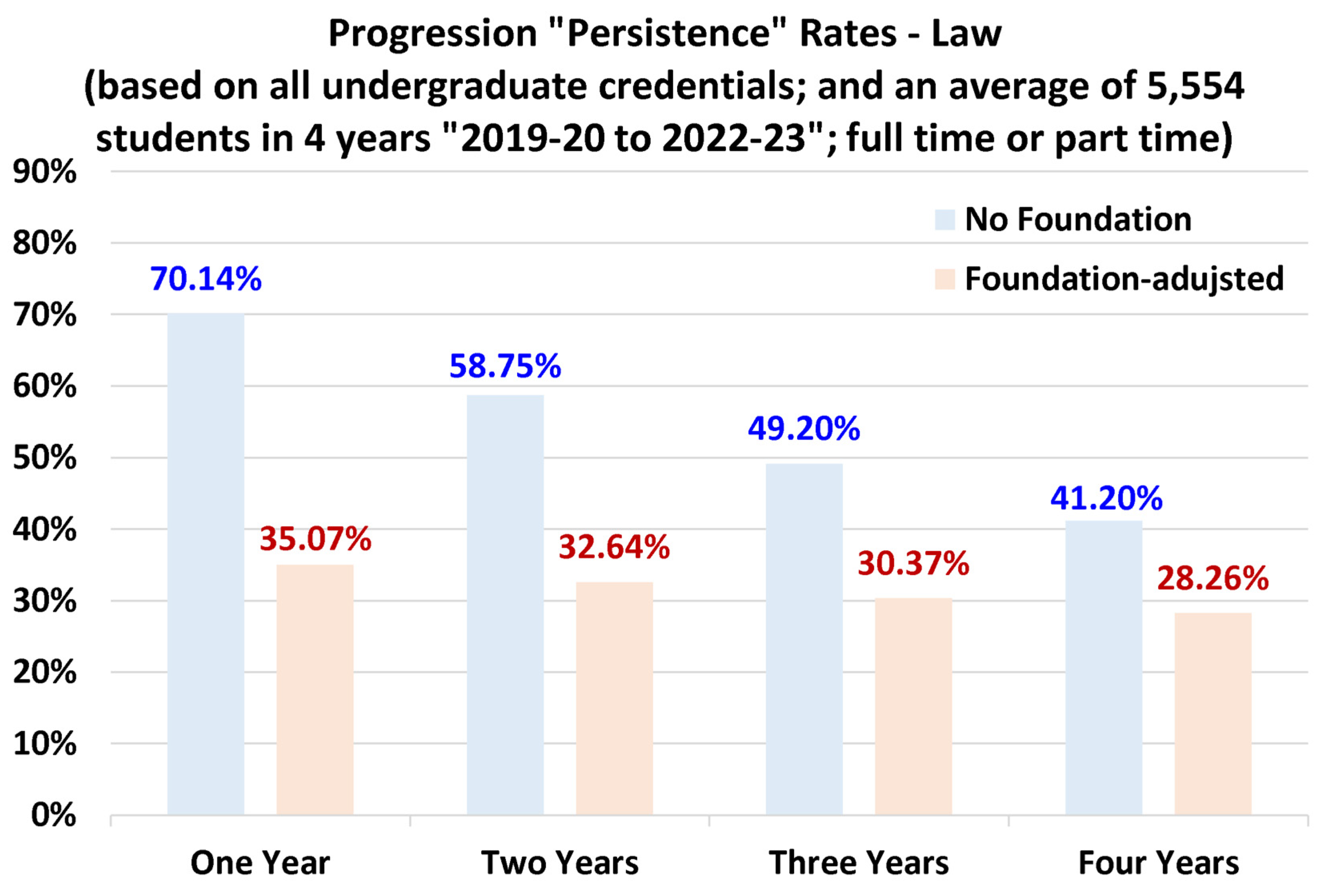
4.3. Overall Progression Rates

Going back to overall (not discipline-specific) results, Figure 10 shows the estimated undergraduate graduation rates. These estimates are based on raw data from NSC-RC, covering a large number of students (2,439,729) averaged over four consecutive Fall-entry cohorts from 2019-20 to 2022-23. After averaging over these four years, we found that these undergraduate students were distributed as 79.34% full-time students, 16.35% part-time students, 1.50% non-credential students, and 2.81% students with unspecified "unknown" programs. The average first-year progression rate is 75.22% (this is $\overline{\mathrm{P}\mathrm{R}}$); which is close to the average first-year overall bachelor’s degree full-time retention rate previously obtained as 75.93% (this is $\overline{\mathrm{R}\mathrm{R}}$ or $\mathrm{P}\mathrm{R}(\mathrm{o}\mathrm{n}\mathrm{e} \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r})$). For higher education institutions or academic programs that adopt a non-credit bridging foundation, if this progression rate is of the “within-institution/program study advancement” type (this is $\widehat{\mathrm{P}\mathrm{R}}\left(\mathrm{o}\mathrm{n}\mathrm{e} \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\right)$), then its adjusted average first-year value is 37.61% (this is ${\widehat{\mathrm{P}\mathrm{R}}}_{\mathrm{F}\mathrm{Y}}\left(\mathrm{o}\mathrm{n}\mathrm{e} \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\right)$, which in our model is approximated as $\widehat{\mathrm{P}\mathrm{R}}\left(\mathrm{o}\mathrm{n}\mathrm{e} \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\right)/2$). If our extrapolation model is applied, the obtained four-year progression rates become either 49.07% (without a foundation year; this is $\mathrm{P}\mathrm{R}(\mathrm{f}\mathrm{o}\mathrm{u}\mathrm{r} \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{s})$) or 33.66% (with a foundation year “hypothetical situation in this work”; this is ${\widehat{\mathrm{P}\mathrm{R}}}_{\mathrm{F}\mathrm{Y}}\left(\mathrm{f}\mathrm{o}\mathrm{u}\mathrm{r} \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{s}\right)$). This means that about one-half of the students who are admitted to a four-year undergraduate degree program are expected to remain progressing (persistent) four years after they start the program; whereas in the case that the students are typically admitted to a one-year foundation studies, then about one-third of them is expected to graduate within four years after admission (roughly three years after transitioning from the non-credit foundational component and starting their for-credit college component). The influence of the foundation year is reflected by having a lower benchmarking level for graduation, which makes the comparison fairer by taking into account the influence of the foundation year into statistical progression data that do not originally reflect the presence of such an additional study load.

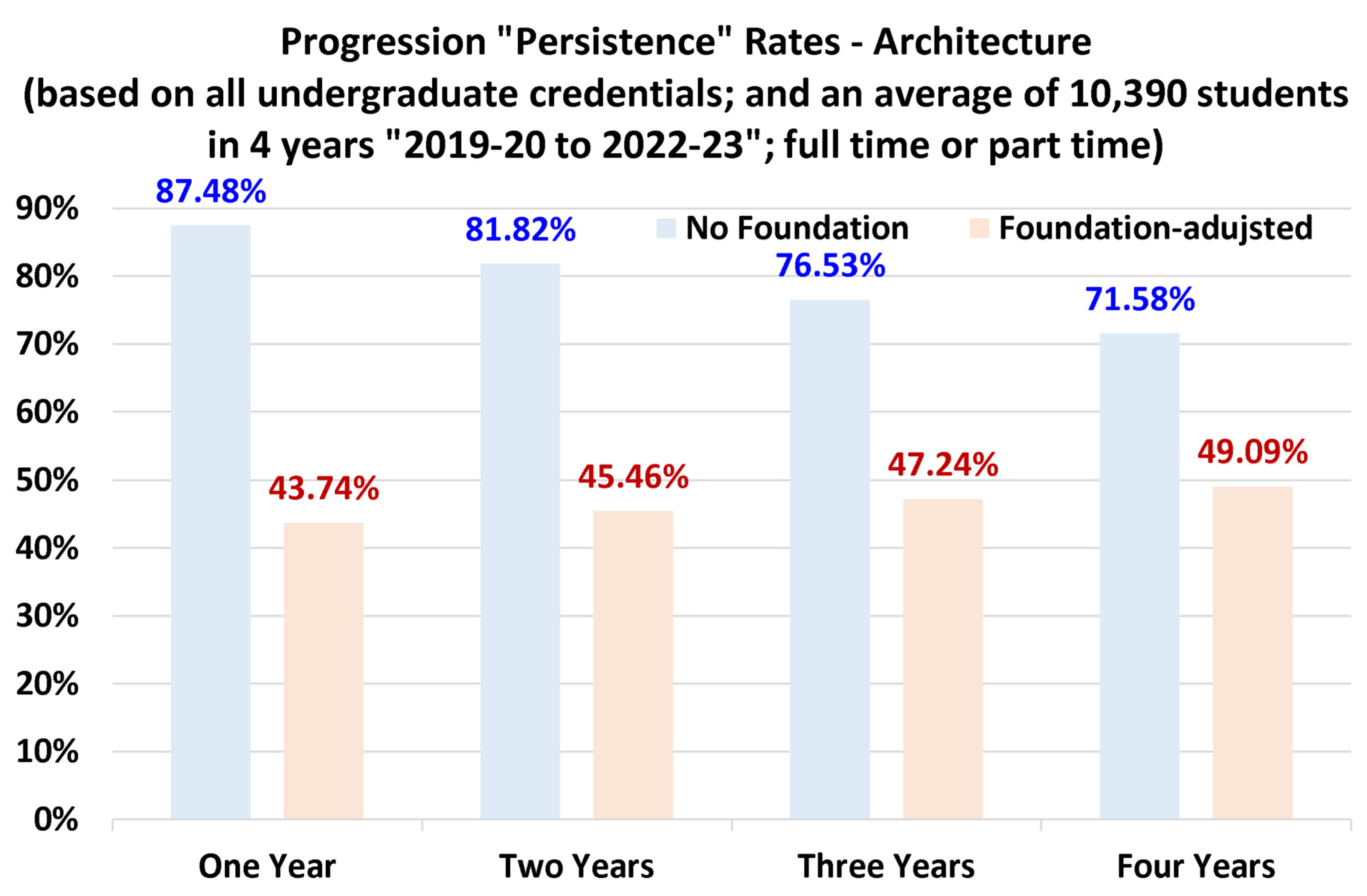
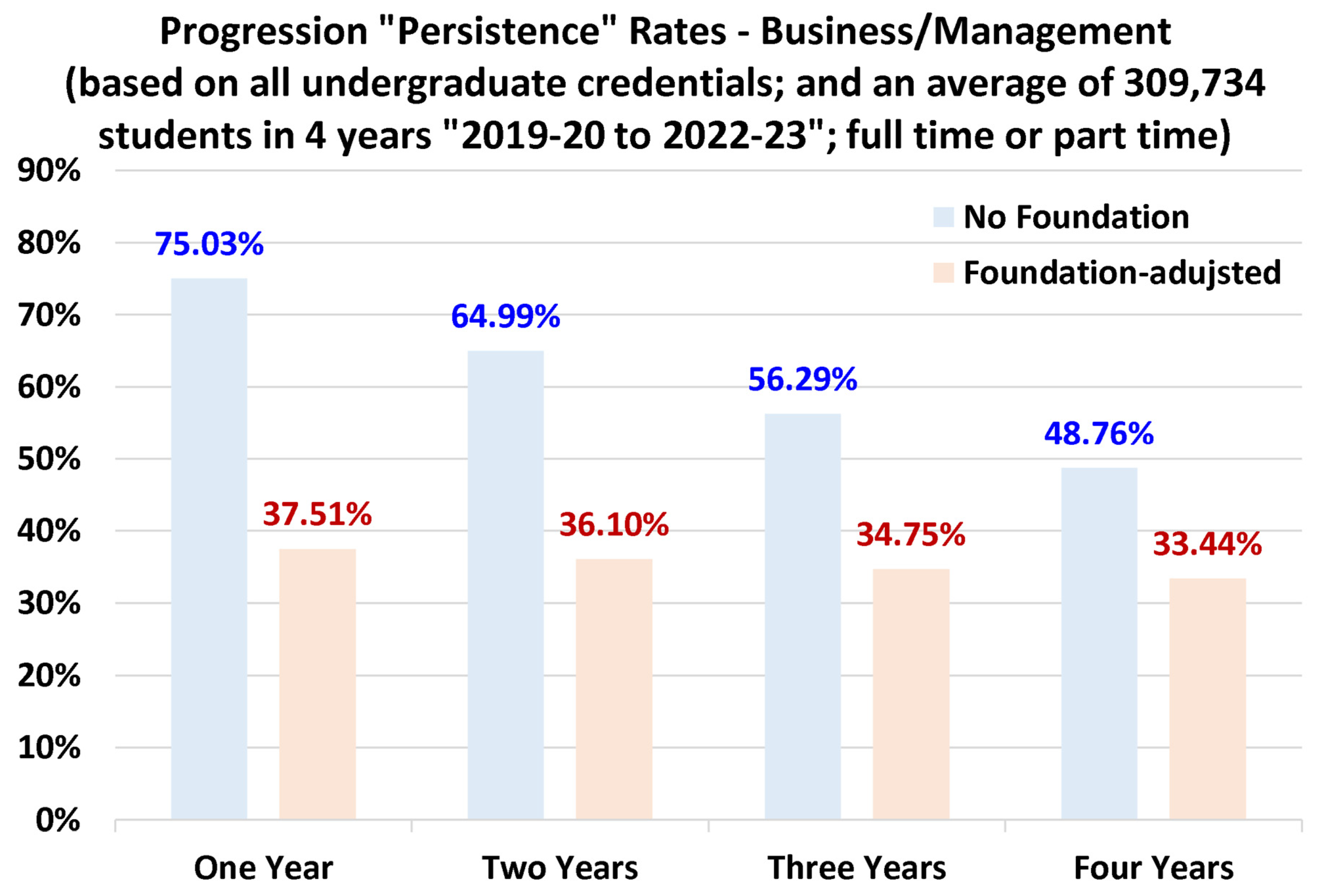
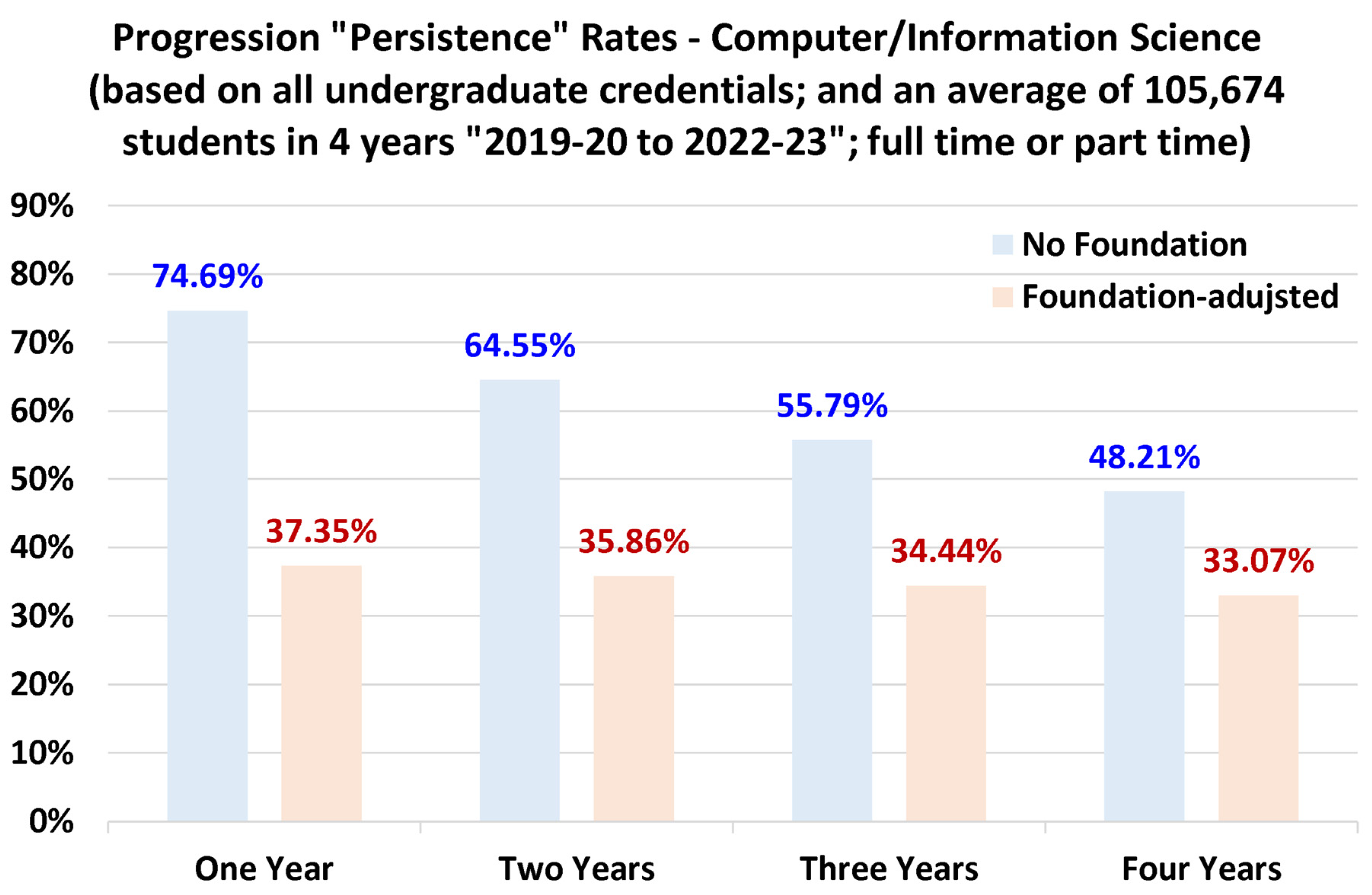
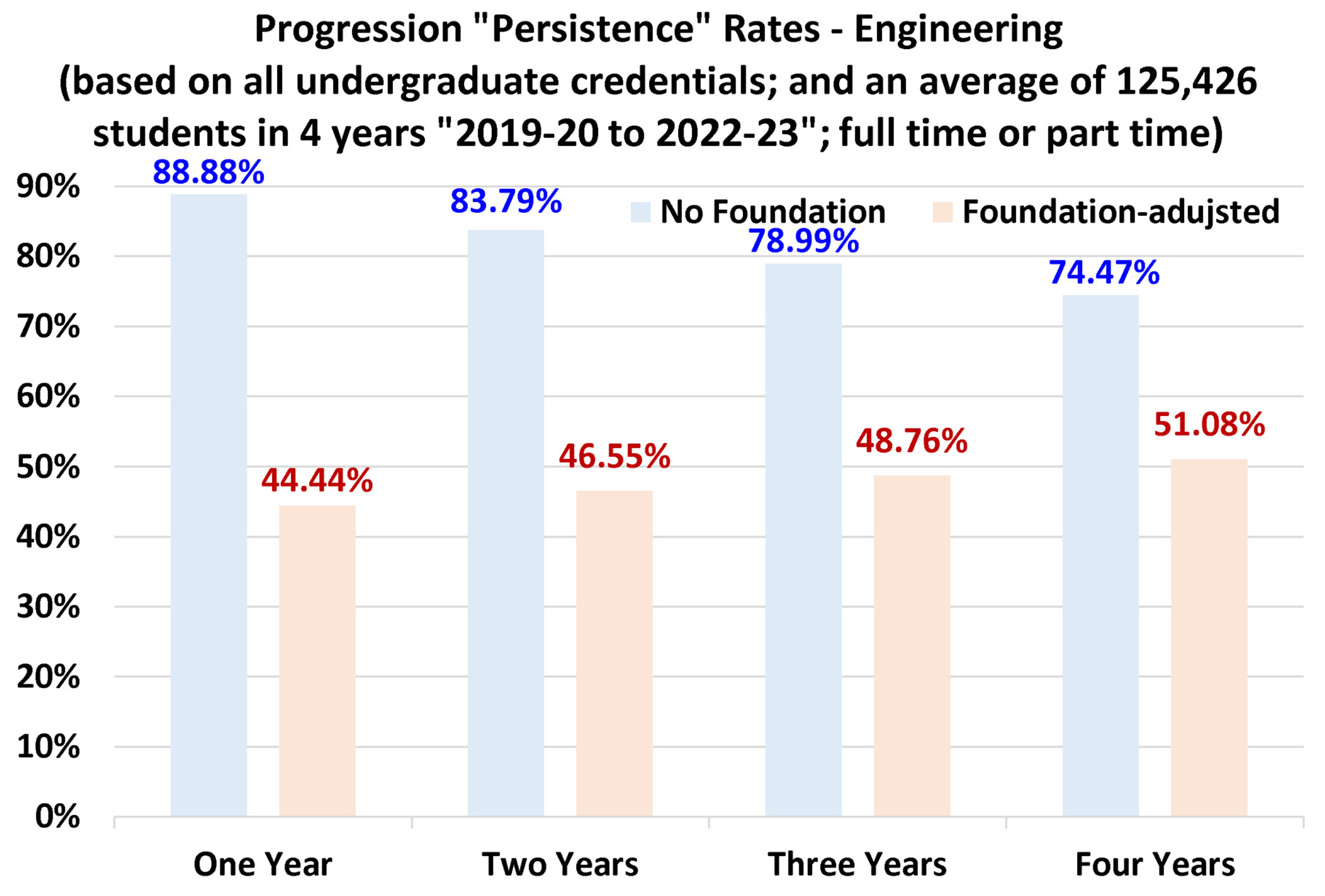
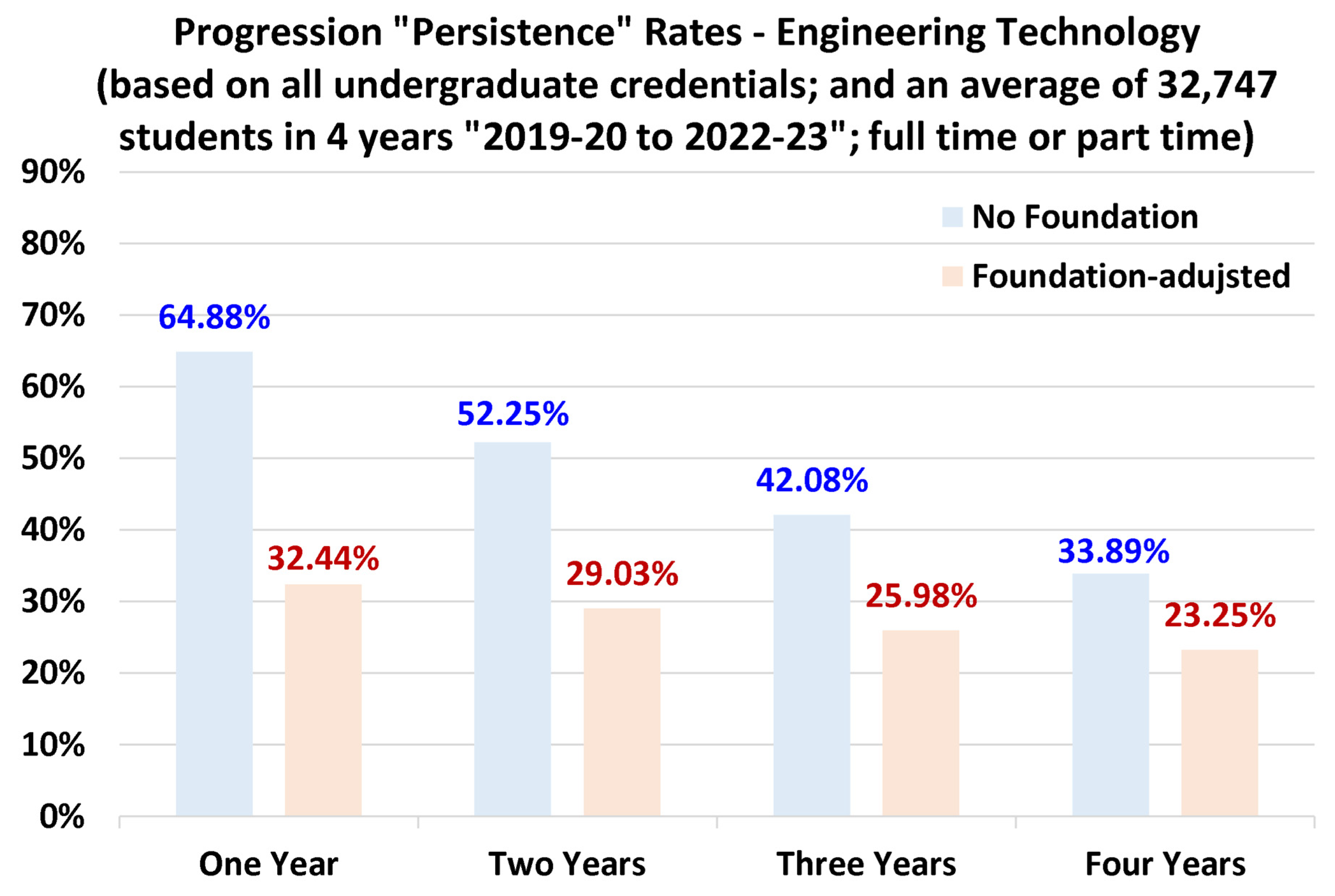
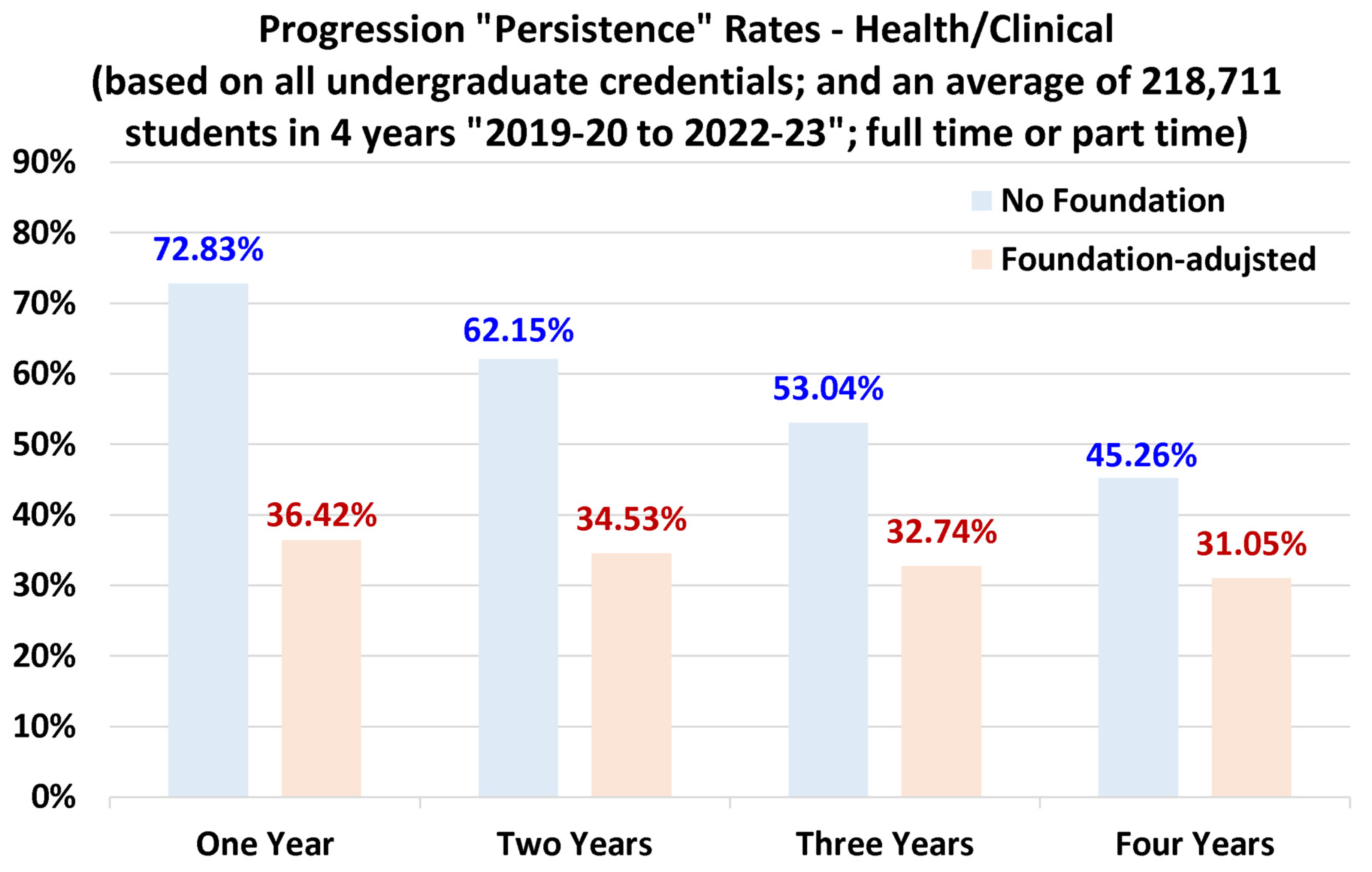
4.4. Discipline-Specific Progression Rates

For the selected seven disciplines, and based on our proposed analysis of the raw data of NSC-RC, we provide here estimated discipline-specific undergraduate progression rates for benchmarking purposes; in a similar manner that was followed for the discipline-specific retention rates. The number of undergraduate students in each discipline, their distribution by degree level, and the precise classification category title are the same as those mentioned earlier when presenting the discipline-specific retention rates; and thus are not repeated here.

Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17 show the progression rates (with four time windows, from one year to four years) for the architecture, business/management, computer/information science, engineering, engineering technology, health, and law disciplines; respectively. The overall average first-year progression rates for these disciplines are 87.48%, 75.03%, 74.69%, 88.88%, 64.88%, 72.83%, and 70.14%; respectively. Relative to the overall average first-year progression rate of 75.22%, the engineering progression rate is the highest among the seven disciplines covered in this study, exceeding the overall progression rate by about twelve percentage points (12 pp); then comes the architecture progression rate with a small difference. The lowest (worst) discipline-specific progression rate among the examined seven disciplines is for engineering technology, lying more than ten percentage points (10 pp) below the overall average. These three relative positions of the progression rates match those observed earlier in the case of the discipline-specific retention rates.

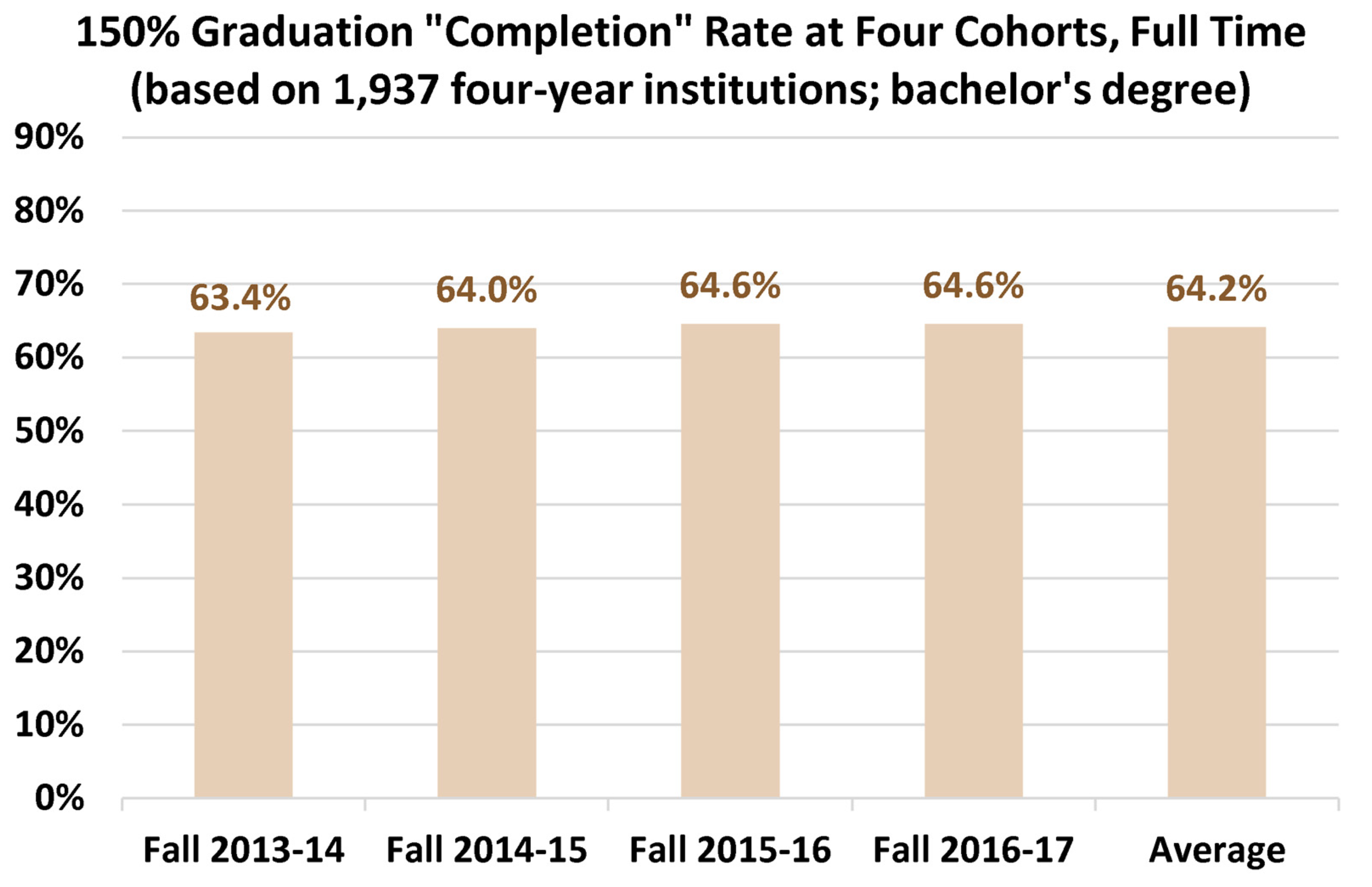
4.5. General Full-Time Bachelor’s Degree Graduation Rates

After presenting the retention rates and the progression rates, we present our estimation for the benchmarking graduation rates. Figure 18 shows the 150% graduation rates (graduation over 150% of the nominal study period) for four consecutive cohorts (from Fall 2013-14 to Fall 2016-17), based on raw data from NCES, covering full-time bachelor’s degree study in 1,937 four-year higher education institutions. The graduation rate was consistently increasing in the first three cohorts, rising from 63.4% to 64.6%, which remained at the same level for the fourth cohort. The four-cohort average rate is 64.2%, and this is our suggested benchmarking graduation (or completion) rate.

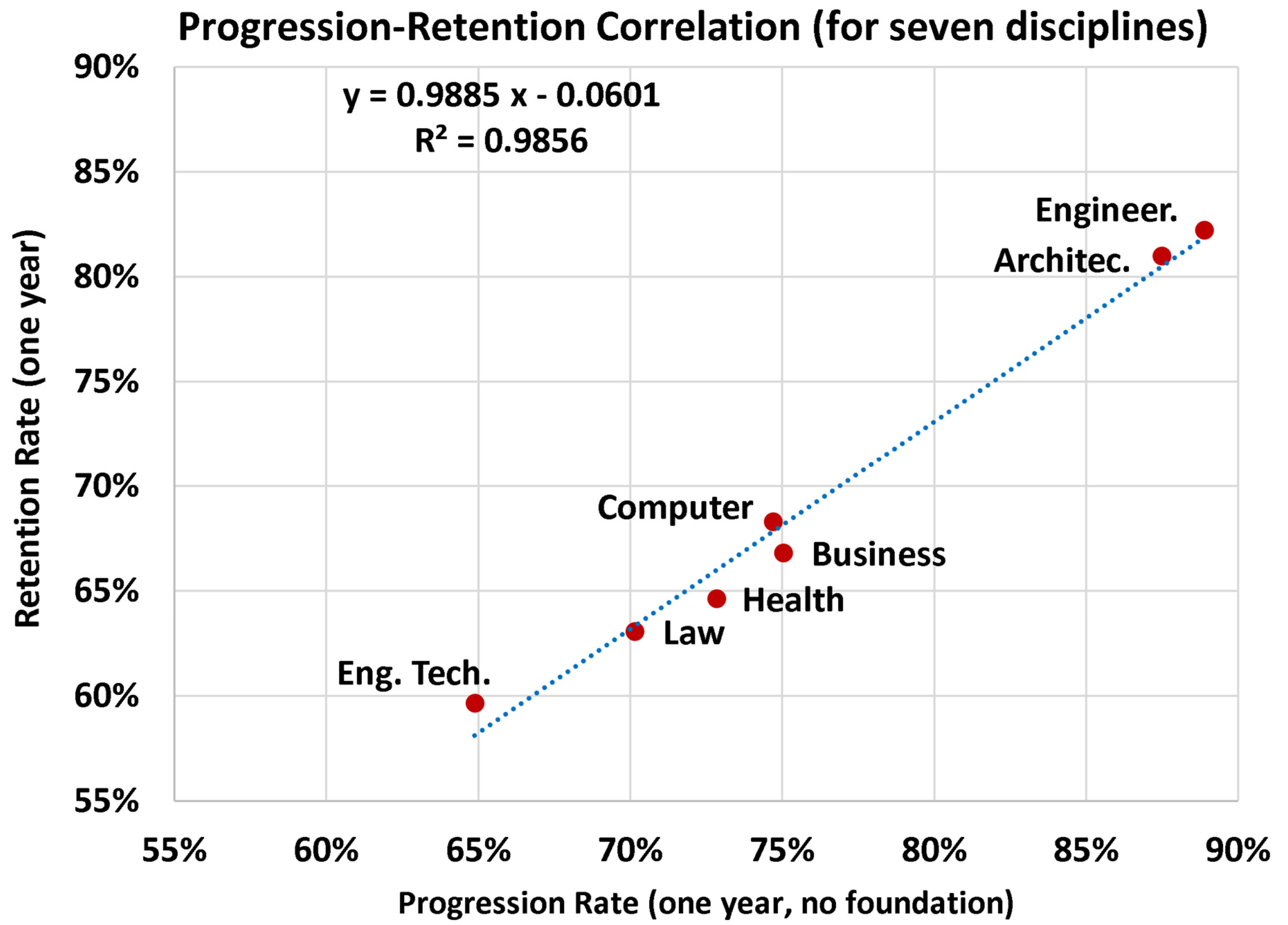
4.6. Retention-Progression Correlation

The observed matching of the disciplines having extremum retention rates and progression rates stimulates further investigation of the correlation between the retention rates and progression rates for the seven disciplines covered here. Through Figure 19, we show that there is nearly a linear correlation between the two tracking rates (the figure is based on the rates with a one-year time window, without extrapolation); where we obtained the following reduced-order model, with the coefficient of determination (or R-squared) being 0.9856, and its adjusted R-squared value being 0.9827; and both values are favorably close to one, suggesting string linear dependence [166,167,168,169,170,171,172,173,174,175]:

RR(one year) = 0.9885 PR(one year) − 6.01%

(25)

Further statistical analysis (hypothesis testing) shows that this linear dependence is statistically significant, with a p-value of only 8.50×10^–6, which is much less than the typical threshold significance level of 0.05 [176,177,178,179,180,181,182,183]. Furthermore, the 95% confidence interval for the regression coefficient (0.9885) is (0.8511-1.1259), and the 99% confidence interval for it is (0.7730-1.2040); and both intervals are relatively far from the trivial zero value; therefore, that the null hypothesis that retention rates are not dependent on the progression rates can be rejected.

It should be noted that the linear correlation obtained here is partly attributed to the inherent coupling mentioned earlier between the retention rate and progression rate, according to the way both are defined.

5. Discussion

In this section, we make five supplementary comments.

First, it should be noted that according to the defining expression in Equation (4) for the “within-institution/program” progression rate ($\widehat{\mathrm{P}\mathrm{R}}$), this progression rate is actually influenced by the retention rate, where $\widehat{\mathrm{P}\mathrm{R}}$ cannot reach 100% if RR is below 100%. This feature mandates that $\widehat{\mathrm{P}\mathrm{R}}$ should not be interpreted independently of RR, due to the coupling between them. A preferred expression for a scaled “within-institution/program” progression rate ($\widehat{\mathrm{P}\mathrm{R}}$′) that is magnified for properly becoming an efficiency-like figure normalized to lie exactly between 0 and 100% or 1.0 is [184,185,186,187,188,189,190,191]

$$\widehat{\mathrm{P}\mathrm{R}}\mathrm{\text{'}}={\displaystyle \frac{\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{s}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s} \mathrm{m}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{n}\mathrm{g} \mathrm{a} \mathrm{s}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{s}\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{r}\mathrm{y} \mathrm{p}\mathrm{a}\mathrm{c}\mathrm{e}}{\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{r}\mathrm{e}\mathrm{t}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{d} \mathrm{s}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s}}}=\widehat{\mathrm{P}\mathrm{R}}/\mathrm{R}\mathrm{R}$$

(26)

Similarly, according to the defining expression in Equation (7) for the graduation rate (GR) or completion rate (CR), this graduation rate is actually influenced by the retention rate, where GR cannot reach 100% if RR is below 100%. This feature mandates that GR should not be interpreted independently of RR, due to the coupling between them. A preferred expression for a scaled graduation rate (GR′) or a scaled completion rate (CR′) that is magnified for properly becoming an efficiency figure (exactly bounded between 0% and 100% or 1.0) is

$${\mathrm{G}\mathrm{R}}^{\mathrm{\text{'}}}\left(\mathrm{o}\mathrm{r} {\mathrm{C}\mathrm{R}}^{\mathrm{\text{'}}}\right)={\displaystyle \frac{\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{s}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s} \mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{u}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d} \mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{i}\mathrm{n} \mathrm{a}\mathrm{n} \mathrm{e}\mathrm{x}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{d} \mathrm{p}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{d}}{\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{r}\mathrm{e}\mathrm{t}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{d} \mathrm{s}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s}}}=\mathrm{G}\mathrm{R}/\mathrm{R}\mathrm{R}(\mathrm{o}\mathrm{r} \mathrm{C}\mathrm{R}/\mathrm{R}\mathrm{R})$$

(27)

Second, all the students’ tracking rates analyzed in the current study (retention, progression, and graduation) are not affected by the grades of the students. While this might not be a problem for the retention rate and the graduation rate; it can be viewed as a shortcoming in the progression rate, because it does not allow distinguishing between students who advance toward graduation while maintaining higher grades and those also advancing at the same rate while receiving only the passing marks. Thus, an additional metric may be devised for monitoring this aspect, such as the portion of students with a cumulative grade point average (CGPA) above a set threshold. Alternatively, a performance-based “within-institution/program” progression rate ($\widehat{\mathrm{P}\mathrm{R}}$′′) may be introduced, rather than being merely based on passing courses regardless of the level of academic performance. Such a performance-based progression rate may be expressed as

$$\widehat{\mathrm{P}\mathrm{R}}\mathrm{\text{'}}\mathrm{\text{'}}={\displaystyle \frac{\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{s}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s} \mathrm{m}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{n}\mathrm{g} \mathrm{a} \mathrm{s}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{s}\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{r}\mathrm{y} \mathrm{p}\mathrm{a}\mathrm{c}\mathrm{e} \mathrm{a}\mathrm{n}\mathrm{d} \mathrm{s}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{s}\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{r}\mathrm{y} \mathrm{C}\mathrm{G}\mathrm{P}\mathrm{A}}{\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{r}\mathrm{e}\mathrm{t}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{d} \mathrm{s}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s}}}$$

(28)

Third, for programs that may have ambiguity in terms of their classification into one of the seven broad disciplines covered in this study, such as being possibly considered an “engineering” program but also possibly viewed as a “computer/information science” program; we propose that the official title of the program is used a criterion for the classification [192,193,194,195,196,197]. If the program title has the word “Engineering”, then our suggested engineering retention and progression benchmarking rates can be used for that program. This proposed method for resolving any classification conflict is aligned with the program eligibility requirement for accreditation by ABET (Accreditation Board for Engineering and Technology), where the word “engineering” in the program's name is necessary to be accredited according to the Engineering criteria of ABET, whereas the phrase “engineering technology” in the program's name is necessary to be accredited according to the Engineering Technology criteria of ABET [198,199,200,201,202,203]. For example, we prefer that a “Computer Engineering” undergraduate program utilizes our suggested benchmarking rates for the (engineering) discipline, whereas we prefer that a “Computer Science” program utilizes our suggested benchmarking rates for the (computer/information science) discipline. Similarly, we prefer that an “Architectural Engineering” undergraduate program utilizes our suggested benchmarking rates for the (engineering) discipline, whereas we prefer that an “Interior Architecture” program utilizes our suggested benchmarking rates for the (architecture) discipline.

Fourth, the way how the raw progression (persistence) rates were obtained explains why the progression rate here is always larger than the retention rate for the same discipline; because each retained student is automatically progressing (persistent), while not each progressing (persistent) student is necessarily retained. If these raw progression (persistence) rates were obtained based on the study advancement within the same institution or program, then the progression rate is always less than or equal to the retention rate; because each progressing (persistent) student is automatically retained in this case, while not each retained student is necessarily progressing (persistent).

Fifth, by summarizing some of the previously listed discipline-specific characteristics of the seven disciplines covered here, some insights can be made regarding how these disciplines compare to each other. Such a summary is given in Table 2. In terms of the number of students, the business/management discipline is the largest while the law discipline is the smallest. In terms of the potion of students studying for a bachelor’s degree, the engineering discipline is the largest (and closely comes the architecture discipline after it). In terms of the portion of students studying for a diploma degree (associate degree), engineering technology is the largest (and then comes the law discipline).

6. Conclusions

In the current empirical study, various benchmarking rates for tracking the performance of undergraduate students and their academic programs or higher education institutions were developed under different settings, such that a wide range of institutions and programs select and adopt rates that suit their own condition, with less chance of wrong decision and interpretation due to setting a benchmarking target that belongs to an irrelevant education structure. In addition to the general rates, seven broad disciplines were selected for obtaining additional discipline-specific rates, which are architecture, business/management, computer/information science, engineering, engineering technology, health/clinical, and law. Although the data are US-based, their large size makes them representative of a wide spectrum of students and institutions. The following findings can be stated:

• Overall, the recommended benchmarking first-year retention rate for bachelor’s degree students is 76%.
• Overall, the recommended benchmarking first-year progression rate for undergraduate students admitted directly to the degree program is 75%.
• Overall, the recommended benchmarking graduation rate for bachelor’s degree students within 150% of the nominal study period is 64%.
• Among the seven disciplines examined here, engineering and architecture have similarly high retention rates, progression rates, as well as portions of bachelor’s degree students (as compared to diploma/associate degree students).
• Among the seven disciplines examined here, engineering technology has the lowest retention rates, progression rates, as well as the portion of bachelor’s degree students (as compared to diploma/associate degree students).
• The progression (or persistence) rate is more ambiguous compared to the retention rate and the graduation rate, with multiple definitions existing in the literature for it. Thus, one should be more cautious when dealing with reported progression (persistence) rates. The other two rates can also be defined differently by different sources, but their overall purpose seems to be less scattered.