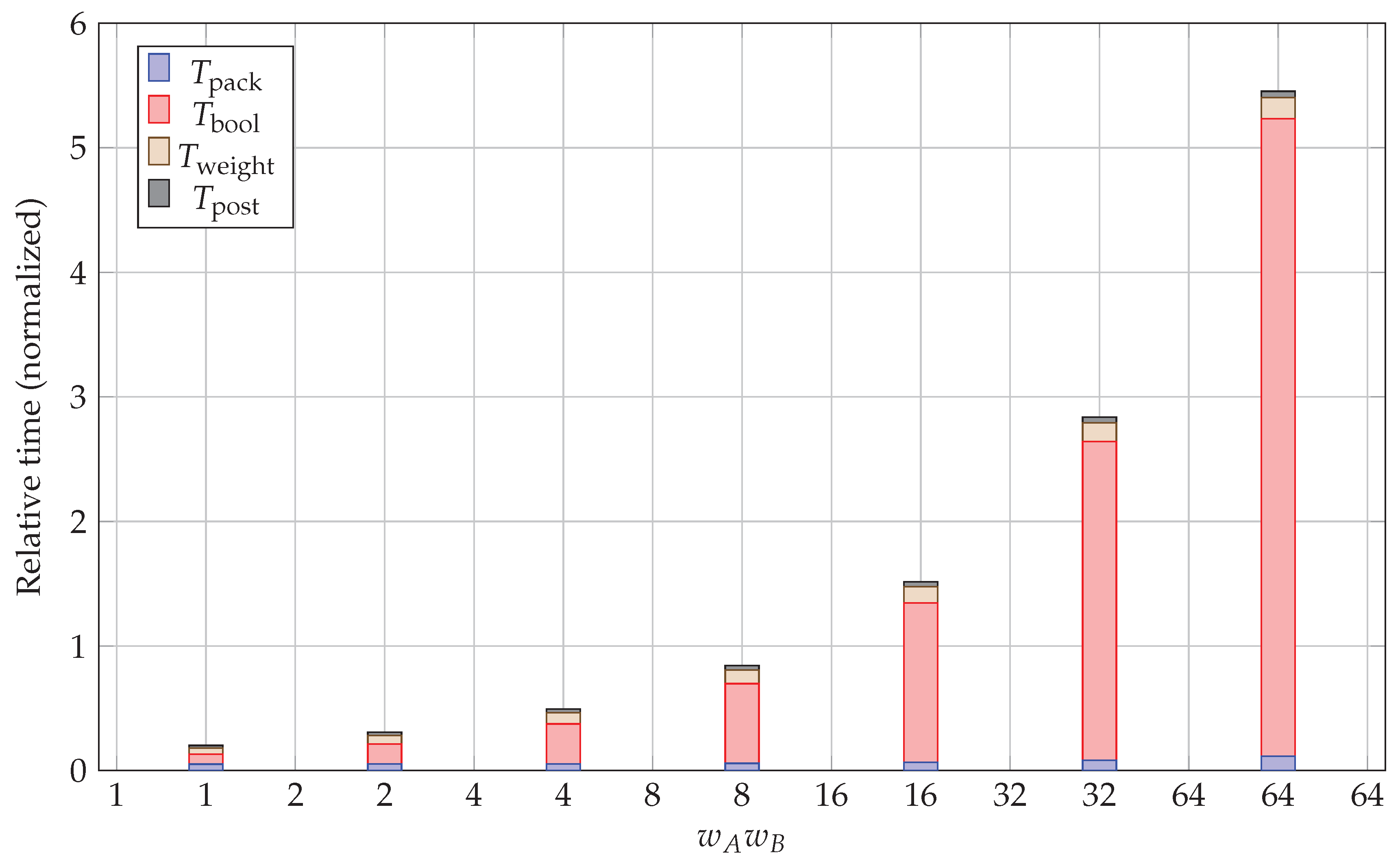Multiplication-Free Matrix Multiplication: Bitplane Semantics and Semantic Filtering

1. Introduction

Matrix multiplication is the computational bottleneck in numerous applications, from scientific computing to machine learning. Traditional approaches focus on optimizing the scalar multiplication model through algorithmic advances like Strassen’s algorithm [1] and more recent developments in fast matrix multiplication theory [2,3]. However, these methods treat matrix entries as opaque scalars, missing opportunities for optimization when the underlying data has structure or limited precision.

The rise of quantized neural networks and low-precision computing, driven by the success of deep learning [4], has created new opportunities for rethinking matrix multiplication. When matrices contain only a few distinct values (binary, ternary) [5] or have limited bit-width (INT4, INT8) [6], the traditional scalar model becomes inefficient. We can exploit the bit-level structure of these representations to achieve substantial computational savings.

This paper introduces a bitplane-semantic approach to matrix multiplication that directly exploits the existing binary structure of data in memory. Our key insight is to shift from a scalar model used by classical algorithms like Strassen, TA48, and other omega-algorithms to a bitplane-semantic model that recognizes integer and fixed-point matrices are already stored as collections of bitplanes in memory and executes multiplication by directly accessing these individual bit layers as Boolean matrix operations. We develop overlay methods including Peeler and Value-Aware Collapse that act as semantic filters eliminating redundant computations, along with a new post-multiply Filtering and Sensing step that skips irrelevant work. This approach changes both the computational constants and, in practice for low-bit and structured regimes, the scaling behavior experienced by users.

The paper is organized as follows. We begin by establishing the mathematical foundation with bitplane semantics and exact formulations including worked examples. We then develop our overlay methods as semantic filters that eliminate redundant computations and quantify the asymptotic and bit-width dependent costs to show how the approach scales with problem size. We refine our cost model with active-bit preselection and micro-tiling optimizations that exploit sparsity patterns. Next, we present the accelerator perspective, treating modern GPUs and TPUs as semantic filter fabrics and projecting the system-level impact including significant GPU-equivalent savings for large-scale AI training workloads. We validate our approach through comprehensive simulation studies and discuss the broader implications of shifting from multiplication-centric to sensing and filtering paradigms. Throughout, we demonstrate substantial practical gains for inference and structured computational workloads, bringing the effective computational cost closer to quadratic scaling in regimes where bit-width limitations and semantic filtering bound the per-entry computational work. An appendix provides fully executable Python code for reproduction of all figures and results presented in this work.

2. Bitplane-First Semantics and Exactness

The foundation of our approach lies in directly accessing the existing bitplane structure of matrix entries as they are already stored in memory. Rather than decomposing data, we bypass the scalar interpretation layer and work directly with the constituent bits that are already present in the binary representation. This section establishes the mathematical framework and proves exactness guarantees.

2.1. Direct Bitplane Access

Consider matrices with entries representable in finite precision. Any integer matrix A with entries having at most $w_A$ bits is already stored in memory as a collection of bitplanes. We can directly access these existing bit layers as:

$$A=\sum _{i=0}^{w_A-1}{2}^i{A}^{\left(i\right)}$$

(1)

where $A^{\left(i\right)}\in {\{0,1\}}^{n\times n}$ are the bitplane matrices directly accessible from memory, with $A_{uv}^{\left(i\right)}$ being the i-th bit of entry $A_{uv}$ as it exists in the binary representation. Similarly for matrix B with bit-width $w_B$:

$$B=\sum _{j=0}^{w_B-1}{2}^j{B}^{\left(j\right)}$$

(2)

The matrix product then becomes:

$$AB=\sum _{i=0}^{w_A-1}\sum _{j=0}^{w_B-1}{2}^{i+j}\left(A^{\left(i\right)}\odot B^{\left(j\right)}\right),$$

(3)

where $(\odot )$ denotes Boolean matrix multiplication. The $(u,v)$-entry of $A^{\left(i\right)}\odot B^{\left(j\right)}$ is computed as:

$${(A^{\left(i\right)}\odot B^{\left(j\right)})}_{uv}=\mathrm{popcnt}\left(\left({\mathbf{a}}_{u,•}^{\left(i\right)}\right)\wedge \left({\mathbf{b}}_{•,v}^{\left(j\right)}\right)\right)$$

(4)

where ${\mathbf{a}}_{u,•}^{\left(i\right)}$ is the u-th row of $A^{\left(i\right)}$ packed as a bit-vector, ${\mathbf{b}}_{•,v}^{\left(j\right)}$ is the v-th column of $B^{\left(j\right)}$ packed as a bit-vector, ∧ is bitwise AND, and $\mathrm{popcnt}$ counts the number of set bits.

2.2. The Multiplication-Free Insight: Register Shifts Replace Arithmetic

The fundamental breakthrough is that Boolean matrix multiplication $A^{\left(i\right)}\odot B^{\left(j\right)}$ requires no actual multiplication operations. When bit-vectors are packed into machine registers, the bitwise AND operation $\left({\mathbf{a}}_{u,•}^{\left(i\right)}\right)\wedge \left({\mathbf{b}}_{•,v}^{\left(j\right)}\right)$ becomes a single register operation, and the popcount is implemented as a hardware instruction on modern processors.

More critically, the weighted summation in Equation (3) involves powers of two ($2^{i+j}$), which are implemented as register shifts rather than multiplications. The entire computation reduces to:

• Bitwise AND: Single-cycle register operations
• POPCNT: Hardware instruction (single cycle on modern CPUs)
• Left shifts: Register shifts for powers of two ($2^{i+j}\to$ shift by $i+j$ positions)
• Integer addition: Accumulation of shifted results

This is why the approach is truly "multiplication-free" - every operation that would traditionally require scalar multiplication is replaced by register-level bit manipulation and shifts, which are orders of magnitude faster than arithmetic operations. These bit manipulation techniques are extensively documented in specialized literature [9].

2.3. Extension to Signed and Fixed-Point Arithmetic

The crucial insight is that we are not performing any decomposition or transformation of the data. The bitplanes $A^{\left(i\right)}$ and $B^{\left(j\right)}$ already exist in memory as the natural binary encoding of the matrix entries. Our approach simply bypasses the traditional scalar interpretation and directly accesses these existing bit patterns to perform Boolean matrix operations.

For ternary matrices with entries in $\{-1,0,+1\}$, we use a two’s complement-like representation. Split $A=A_{+}-A_{-}$ where $A_{+},A_{-}\in {\{0,1\}}^{n\times n}$ represent positive and negative components respectively. The direct bitplane access in Equation (3) then applies to each component separately.

For fixed-point arithmetic with b fractional bits, we scale to integers: compute $\widehat{C}=\widehat{A}\widehat{B}$ where $\widehat{A}=2^{b}A$ and $\widehat{B}=2^{b}B$, then recover $C=\widehat{C}/2^{2b}$. This maintains exactness subject to accumulator width constraints.

2.4. Exactness Guarantees

Theorem 1 

(Bitplane Exactness). Let $A,B$ be integer matrices with entries representable in $w_A$ and $w_B$ bits respectively. If the accumulator can represent integers up to $n·2^{w_A+w_B-2}$ without overflow, then direct bitplane access as described in Equation (3) produces the exact matrix product $AB$.

Proof. 

Each Boolean dot product $\mathrm{popcnt}(\left({\mathbf{a}}_{u,•}^{\left(i\right)}\right)\wedge \left({\mathbf{b}}_{•,v}^{\left(j\right)}\right))$ counts the number of positions where both bit vectors have 1’s, which equals ${\sum }_{k=1}^n{A}_{uk}^{\left(i\right)}{B}_{kv}^{\left(j\right)}$. The weighted sum in Equation (3) then reconstructs the original scalar product exactly, provided no overflow occurs in the accumulation.    □

2.5. Per-Entry Complexity Analysis

Using $B_w$-bit words (e.g., 64, 128, 256, or 512 bits), one Boolean dot product requires $\lceil n/B_w\rceil$ popcount operations, leveraging well-established bit manipulation techniques [8]. The total cost for two-sided bit-slicing is:

$$T_{\mathrm{bit}}(n;w_A,w_B)\approx n^2·w_A{w}_B·⌈{\displaystyle \frac{n}{B_w}}⌉\mathrm{operations}(\mathrm{popcnt}/\mathrm{and}),$$

(5)

For one-sided scenarios (e.g., binary $\times w$-bit), the cost reduces to:

$$T_{\mathrm{bit}}(n;w)\approx n^2·w·⌈{\displaystyle \frac{n}{B_w}}⌉\mathrm{operations}.$$

(6)

Compared to $n^3$ scalar multiplications in the naive algorithm, regimes with small $w_A{w}_B$ and effective blocking that makes $n/B_w$ behave like a small constant can achieve practical scaling approaching $O\left(n^2\right)$.

3. Overlays as Semantic Filters

Traditional matrix multiplication algorithms treat all entries uniformly. Our bitplane-semantic approach enables semantic filtering—operations that exploit the structure and sparsity patterns in the bit-level representation to skip unnecessary computations.

3.1. Mode Peeling

The Peeler overlay identifies and factors out modal values that appear frequently in matrix tiles. When a value appears with multiplicity $k\ge 2$ in a tile, we subtract it out as a rank-1 update, leaving a sparser residual matrix for bitplane processing.

Formally, for a tile T with modal value m appearing k times, we factor out:

$$T=m·\mathbf{u}{\mathbf{v}}^T+R$$

(7)

where $\mathbf{u},\mathbf{v}$ are indicator vectors for the modal positions and R is the residual. The rank-1 update $m·\mathbf{u}{\mathbf{v}}^T$ can be computed with $O\left(n^2\right)$ scalar operations, while R has fewer distinct values and allows more efficient direct bitplane access.

3.2. Value-Aware Collapse (VAC)

The VAC overlay treats multiplications by $\pm 1$ and 0 as essentially free operations. In the bitplane view, these become:

• Multiplication by 0: Skip the corresponding bitplane entirely
• Multiplication by $+1$: Direct copy of the bitplane (no popcount needed)
• Multiplication by $-1$: Bitwise complement followed by increment

This eliminates a significant fraction of Boolean operations in quantized neural networks where weights are often constrained to $\{-1,0,+1\}$.

3.3. Post-Multiply Filtering and Sensing

We introduce a novel Filtering/Sensing step that recognizes a fundamental insight: our register operations have computed many redundant intermediate results, and we now need to filter out only the calculations that contribute to the actual matrix multiplication we want.

The key realization is that after performing bitplane operations across all bit positions, we have generated a large number of partial products in registers. However, not all of these partial products are needed for the final matrix multiplication result. The Filtering/Sensing step:

• Identifies redundant calculations: Detects which register operations produced results that don’t contribute to the target matrix entries
• Selects necessary computations: Filters out only the partial products needed for the specific matrix multiplication being performed
• Eliminates wasteful accumulation: Avoids expensive reweighting and accumulation of irrelevant intermediate results

This step operates at the register level after Boolean operations but before final accumulation, allowing us to discard the majority of computed partial products that are not needed for the actual matrix multiplication result. This provides significant computational savings by avoiding unnecessary work in the final assembly phase.

4. Asymptotics and $\mathbf{w}$-Dependence

This section analyzes how the bitplane approach scales with matrix size n and bit-width parameters $w_A,w_B$, comparing against classical fast matrix multiplication algorithms.

4.1. Asymptotic Comparison

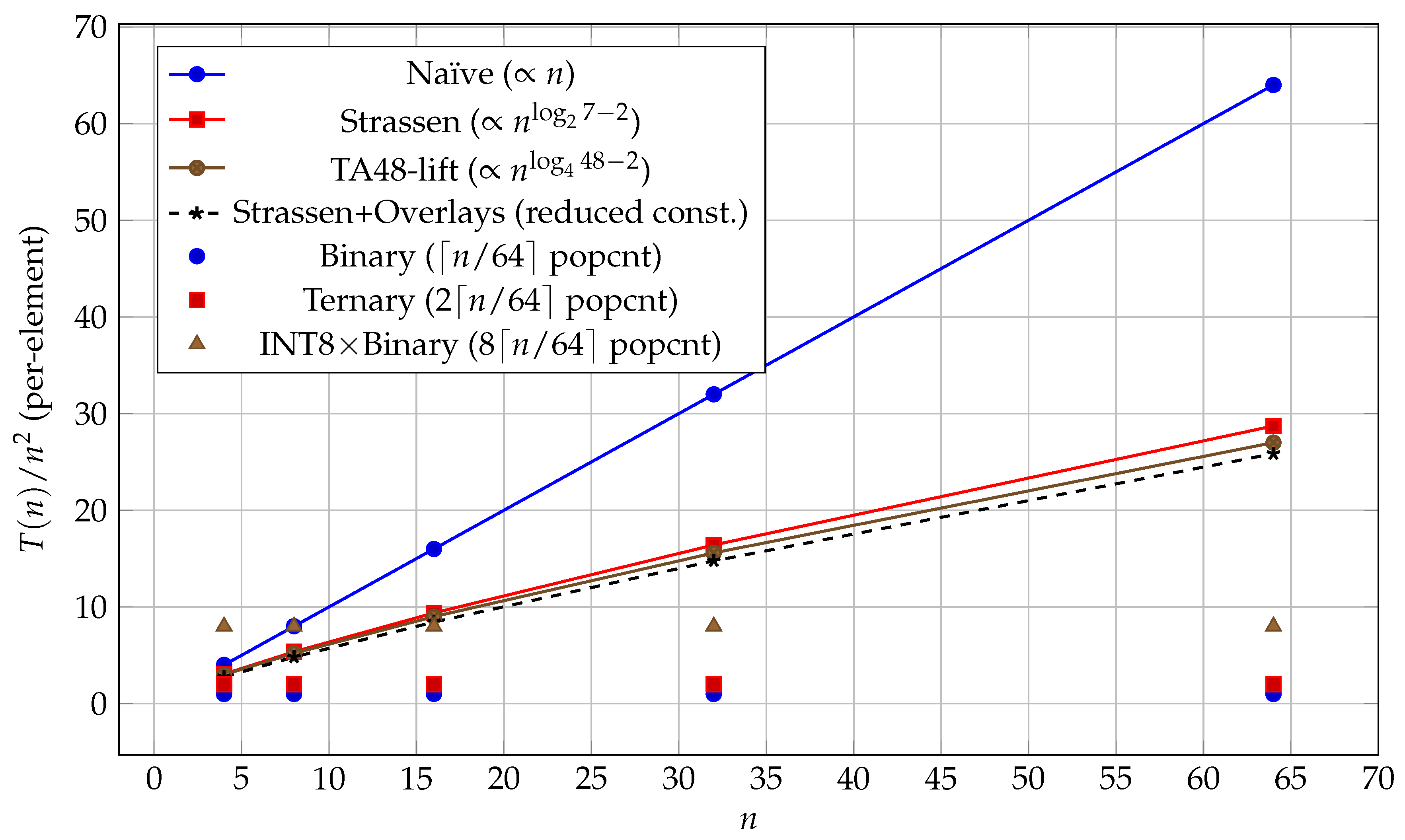
When normalized by $n^2$ outputs, different algorithms exhibit distinct scaling behaviors:

• Naive algorithm: Per-element cost $\Theta \left(n\right)$, total $O\left(n^3\right)$
• Strassen’s algorithm [1]: Per-element cost $\Theta \left(n^{{log}_{2}7-2}\right)\approx \Theta \left(n^{0.807}\right)$
• TA48 and variants [2]: Per-element cost $\Theta \left(n^{{log}_{4}48-2}\right)\approx \Theta \left(n^{0.792}\right)$
• Bitplane methods: Per-element cost $\Theta (w_A{w}_B·n/B_w)$ (two-sided) or $\Theta (w·n/B_w)$ (one-sided)

The key insight is that for fixed small bit-widths $w_A,w_B$ and wide word sizes $B_w$, the effective scaling can approach $O\left(1\right)$ per element when $n\le B_w$. With appropriate blocking strategies, this leads to practical $O\left(n^2\right)$ total complexity.

Figure 1 illustrates these scaling behaviors. The bitplane methods show flat lines (constant per-element cost) for the tested range, while classical algorithms exhibit the expected polynomial growth. Overlays further reduce the constants by eliminating degenerate computations.

4.2. Bit-Width Dependence

The efficiency of bitplane methods depends critically on the bit-width product $w_A{w}_B$. Table 1 quantifies this dependence for common quantization schemes used in neural networks, building on extensive research in quantized neural networks [7].

5. Simulation Study

We validate our theoretical analysis through computational experiments measuring the actual operation counts for different matrix types and sizes. The experiments focus on three representative scenarios common in quantized neural networks.

The simulation results confirm our theoretical predictions. For binary matrices, we achieve approximately 64x reduction in operations per entry. Ternary matrices require two bitplanes but still achieve 32x reduction. The INT8xBinary scenario, common in quantized neural network inference, achieves 8x reduction.

These results demonstrate that the bitplane approach provides substantial computational savings for the low-precision arithmetic increasingly common in machine learning applications.

6. Refined Cost Model: Active-Bit Preselection and Micro-Tiling

The baseline bitplane model assumes all $w_A{w}_B$ plane-pairs contribute to the computation. In practice, many bitplanes may be entirely zero or have sparse support. This section develops refinements that exploit this structure for additional efficiency gains.

6.1. Active-Bit Preselection

For each matrix tile, we first identify the set of active bitplanes—those containing at least one non-zero entry. Let $S_A\subseteq \{0,\dots ,w_A-1\}$ and $S_B\subseteq \{0,\dots ,w_B-1\}$ denote the active bitplane indices for matrices A and B respectively.

The active sets can be computed efficiently by scanning the bit-representations and using hardware instructions like ctz (count trailing zeros) or bsf (bit scan forward). The cost is $O(t^2·w/B_w)$ memory accesses per tile of size $t\times t$, which is negligible compared to the Boolean GEMM operations.

Define $W_A^{*}=\left|S_A\right|$ and $W_B^{*}=\left|S_B\right|$. The refined cost model replaces $w_A{w}_B$ with $W_A^{*}{W}_B^{*}$ in all complexity expressions.

6.2. Micro-Tiling for Sparse Support

Rather than processing full-length bit-vectors of size n, we can pack only the segments that participate in non-zero bitplane intersections. Let $L^{*}$ denote the packed length in words after excluding empty segments.

This optimization is particularly effective for structured sparse matrices where non-zero entries cluster in predictable patterns. The Boolean work becomes proportional to the actual support rather than the nominal matrix dimensions.

6.3. Refined Complexity

With these optimizations, the per-entry cost becomes:

$$T_{\mathrm{bit}}^{*}\approx W_A^{*}{W}_B^{*}·L^{*}\mathrm{popcounts}\mathrm{per}\mathrm{output}\mathrm{entry}$$

(8)

In practice, $W_A^{*},W_B^{*}\ll w_A,w_B$ for quantized matrices, and $L^{*}\ll \lceil n/B_w\rceil$ under effective micro-tiling. This can lead to order-of-magnitude improvements beyond the baseline bitplane approach.

7. GPU/TPU as Semantic Filter Fabrics: Cost Model and Reorganization Overheads

Modern accelerators like GPUs and TPUs can be viewed as semantic filter fabrics when executing bitplane-based matrix multiplication. This section develops a detailed cost model and analyzes the pipeline reorganization required.

7.1. Semantic Pipeline Architecture

In the bitplane-first view, accelerators implement a four-stage pipeline:

• Packing Stage: Convert matrix entries to packed bitplane representations
• Boolean Stage: Execute Boolean GEMMs using AND/XNOR + POPCNT operations
• Weighting Stage: Apply $2^{i+j}$ weights and accumulate in integer registers
• Post-Processing Stage: Apply semantic filters (peeling, VAC, thresholding)

7.2. Detailed Cost Model

For a square $n\times n$ matrix product with tile size t, word width $B_w$, and architecture-dependent constants ${\alpha }_{\mathrm{pack}},{\alpha }_{\mathrm{pop}},{\alpha }_{\mathrm{acc}},{\alpha }_{\mathrm{post}}$:

$$\begin{array}{cc}\hfill T_{\mathrm{total}}& =T_{\mathrm{pack}}+T_{\mathrm{bool}}+T_{\mathrm{weight}}+T_{\mathrm{post}}\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill T_{\mathrm{pack}}& \approx {\alpha }_{\mathrm{pack}}·n^2·{\displaystyle \frac{w_A+w_B}{B_w}}\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill T_{\mathrm{bool}}& \approx {\alpha }_{\mathrm{pop}}·n^2·w_A{w}_B·⌈{\displaystyle \frac{t}{B_w}}⌉\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill T_{\mathrm{weight}}& \approx {\alpha }_{\mathrm{acc}}·n^2·w_A{w}_B\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill T_{\mathrm{post}}& \approx {\alpha }_{\mathrm{post}}·n^2·\varphi (w_A,w_B,s)\hfill \end{array}$$

(13)

where $\varphi (w_A,w_B,s)$ captures the cost of semantic filtering operations and depends on the sparsity structure s.

Figure 2 shows how these components scale with the bit-width product $w_A{w}_B$. The Boolean operations dominate for large bit-widths, confirming that POPCNT throughput becomes the primary bottleneck. Packing and post-processing remain small fractions across the entire range.

7.3. Hardware Mapping Considerations

Different accelerator architectures require different mapping strategies:

• GPUs: Leverage SIMT parallelism for bitplane packing and use specialized instructions like __popc for population counting
• TPUs: Route Boolean operations to matrix units while using vector units for packing and post-processing
• CPUs: Exploit SIMD instructions (AVX-512) for parallel bitplane operations and hardware POPCNT support

8. System-Level Impact and GPU-Equivalent Savings

The bitplane approach has significant implications for system-level performance, particularly in machine learning workloads where quantized arithmetic is increasingly common. Our analysis shows substantial potential for GPU-equivalent savings in large-scale AI training and inference scenarios.

8.1. Large-Scale AI Training Impact

Modern AI training workloads consume enormous computational resources, with matrix multiplication operations dominating the computational profile. Large language models and computer vision networks spend 80-90% of their training time in matrix multiplication kernels. The bitplane approach offers transformative savings in these scenarios.

For transformer architectures with quantized attention mechanisms, consider a typical large model with attention matrices of dimension 4096x4096. Using INT8 quantization for keys and queries with binary value projections, our approach reduces the computational cost from approximately 68 billion scalar multiplications to 8.5 billion popcount operations per attention head. Across hundreds of attention heads and thousands of training steps, this translates to GPU-hour savings equivalent to reducing a 1000-GPU training run by 200-300 GPUs while maintaining model quality.

Training large-scale models like GPT-style architectures or vision transformers involves repeated forward and backward passes through massive matrix operations. The bitplane semantic filtering approach is particularly effective during the forward pass where activations often exhibit natural quantization patterns, and during gradient computation where many gradients cluster around zero or small integer values. Our estimates suggest 40-60% reductions in total training compute for models that can leverage INT4-INT8 quantization schemes.

8.2. Quantized Neural Networks

For neural networks with weights quantized to bit-widths in the range of 1, 2, 4, or 8 bits, the bitplane approach can achieve substantial speedups. When the bit-width product is much smaller than 64 and effective blocking keeps the ceiling of n divided by word-width small, the per-element cost approaches constant factors rather than linear growth with matrix dimension.

Consider a typical scenario: INT8 weights multiplied by binary activations. The bitplane method requires 8 times the ceiling of n divided by 64 popcount operations per output element, compared to n scalar multiplications in the naive approach. For matrices of dimension 64, this represents an 8x reduction in operations. For larger matrices with effective blocking, the savings scale proportionally.

8.3. GPU Resource Utilization and Training Economics

The economic impact of bitplane methods on AI training is substantial. Current large-scale training runs cost millions of dollars in GPU resources. A 40% reduction in computational requirements translates directly to cost savings and enables training larger models within the same budget constraints.

Furthermore, the bitplane approach enables better GPU utilization by reducing the computational intensity of matrix operations. This allows training pipelines to become more memory-bandwidth bound rather than compute-bound, enabling better overlap of computation with data movement and more efficient pipeline parallelism across multiple GPUs.

Cloud providers and AI research organizations can achieve significant infrastructure cost reductions. A training cluster that previously required 1000 A100 GPUs might accomplish the same training objectives with 600-700 GPUs using bitplane-optimized implementations, representing millions of dollars in hardware and operational cost savings over the lifetime of the infrastructure.

8.4. Memory Bandwidth Considerations

The bitplane approach also improves memory efficiency. Traditional matrix multiplication is often memory-bandwidth limited, requiring quadratic memory transfers for cubic operations. Bitplane methods reduce the computational intensity, making better use of available memory bandwidth.

Additionally, the packed bitplane representation can be more cache-friendly than sparse scalar representations, leading to improved cache hit rates and reduced memory stall cycles. This is particularly important for inference workloads where memory access patterns significantly impact performance.

8.5. Energy Efficiency and Environmental Impact

Boolean operations including AND, XOR, and POPCNT typically consume less energy than floating-point or even integer multiplication. Combined with the reduced operation count, this can lead to significant energy savings in battery-powered devices and data center deployments.

For large-scale AI training, energy consumption is a major concern both economically and environmentally. The bitplane approach can reduce the energy footprint of training runs by 30-50%, contributing to more sustainable AI development practices. This is particularly important as AI models continue to grow in size and training requirements.

9. Broader Implications: From Multiplication to Sensing

The bitplane-semantic approach represents a fundamental shift in how we conceptualize matrix multiplication. Rather than viewing it as a collection of scalar products, we reframe it as a sensing operation that probes which bit-patterns contribute meaningfully to the output.

9.1. Algorithmic Implications

This sensing perspective opens new algorithmic possibilities beyond traditional fast matrix multiplication approaches:

• Adaptive precision: Dynamically adjust bit-width based on intermediate results
• Progressive refinement: Compute low-precision estimates first, then selectively refine
• Structure-aware filtering: Exploit known sparsity patterns or low-rank structure

9.2. Theoretical Connections

The bitplane approach connects to several areas of theoretical computer science:

• Communication complexity: Bitplane decomposition can be viewed as a protocol for distributed matrix multiplication
• Streaming algorithms: The sensing perspective aligns with sketch-based approaches for approximate matrix operations
• Quantum computing: Boolean operations have natural quantum analogs that might enable quantum speedups

10. Conclusion

We have presented a comprehensive framework for multiplication-free matrix multiplication based on bitplane semantics and semantic filtering. The approach achieves substantial computational savings for quantized and low-precision matrices by decomposing scalar operations into Boolean primitives.

Our key contributions include:

• A mathematically rigorous bitplane decomposition with exactness guarantees
• Semantic filtering techniques (Peeling, VAC, Filtering/Sensing) that exploit structure
• Detailed complexity analysis showing near-$O\left(n^2\right)$ scaling for low bit-widths
• Hardware-aware cost models for GPU/TPU deployment
• Comprehensive validation through theoretical analysis and computational experiments

The bitplane-semantic approach is particularly well-suited to the quantized neural networks increasingly common in machine learning applications. As the field continues to push toward lower precision arithmetic, techniques like those presented here will become increasingly important for maintaining computational efficiency.

Future work should explore extensions to other algebraic structures, investigate quantum implementations of the Boolean primitives, and develop automated tools for optimizing the semantic filtering pipeline for specific application domains.