Dynamic Sequences Versus Static Sequences: Keçeci and Oresme Numbers in Focus

1. From Theoretical Prediction to Algorithmic Discovery: A Historical Perspective on Static and Dynamic Number Sequences

The human fascination with numbers is as ancient as civilization itself, rooted in a fundamental desire to find order, pattern, and predictability in a seemingly chaotic universe. This pursuit has historically led to the study of number sequences: ordered lists of numbers that follow a specific rule or pattern. For millennia, the prevailing paradigm in mathematics was the exploration of what can be termed static sequences. These are sequences defined by a fixed, time-invariant recurrence relation or an explicit formula where the value of a term depends solely on its position (index) or a fixed number of preceding terms. Their behavior, whether simple or complex, is entirely determined from the outset. The Pythagorean school’s obsession with figurate numbers (triangular, square), which could be generated by simple additive rules, represents an early formalization of this static worldview [8,9]. This tradition was epitomized by Leonardo of Pisa’s famous sequence, now named after him. The Fibonacci sequence, where each term is the sum of the two preceding ones

$$\mathbf{(}{\mathbf{F}}_{\mathit{n}}=\mathit{ }{\mathbf{F}}_{\mathit{n}-\mathbf{1}}+\mathit{ }{\mathbf{F}}_{\mathit{n}-\mathbf{2}}\mathbf{)},$$

(1)

is a quintessential static sequence. Despite its simple recursive definition, its properties are remarkably rich and appear in disparate fields, yet its generation remains a predictable, unwavering process [10]. This classical view treated sequences as discoverable truths—Platonic ideals waiting to be uncovered through logical deduction and rigorous proof.

A profound, albeit subtle, shift in this perspective began to emerge in the late Middle Ages, foreshadowing the dynamism of the calculus to come. Nicole Oresme, a 14th-century philosopher and mathematician, provided one of the most elegant and counter-intuitive results in the history of sequences. By examining the partial sums of the harmonic series,

$${\mathit{H}}_{\mathit{n}}={\sum }_{\mathit{k}=\mathbf{1}}^{\mathit{n}}{\displaystyle \frac{\mathbf{1}}{\mathit{k}}},$$

(2)

Nicole Oresme (1320–1382) proved that [1,2,3,4,5,6] the series diverges, meaning its sum grows infinitely large [11]. This was a landmark discovery. While the harmonic sequence itself is static—generated by the simple, predictable rule of adding the next unit fraction—its collective behavior defied the intuition that a series whose terms shrink towards zero must converge to a finite value. Oresme’s work demonstrated that even the simplest static rules could yield infinite and unexpected outcomes, hinting that the behavior of a sequence was a more complex phenomenon than its mere definition suggested. This tension between simple rules and complex emergent behavior would become a central theme in mathematics. The subsequent development of calculus by Newton and Leibniz further explored this domain, using infinite series (like the Taylor and Maclaurin series) as static, predictable tools to approximate dynamic and continuous functions, effectively bridging the world of discrete steps and continuous change [8].

The true conceptual break from static-centric thinking, however, occurred centuries later with the birth of dynamical systems theory. In the late 19th century, Henri Poincaré, while studying the three-body problem in celestial mechanics, made a startling discovery. He found that the deterministic equations governing the motion of three celestial bodies could lead to trajectories so complex and sensitive to initial conditions that they were, for all practical purposes, unpredictable [12]. This was the genesis of chaos theory. It revealed that systems governed by simple, fixed (static) laws could exhibit behavior that was anything but simple or predictable. This idea was crystallized in the 20th century with the advent of the computer, which allowed for the exploration of such systems.

A canonical example that brought this concept to the forefront of science is the logistic map, a simple quadratic recurrence relation

$${\mathbf{x}}_{\mathit{n}+\mathbf{1}}=\mathit{ }{\mathbf{r}.\mathbf{x}}_{\mathit{n}\mathit{ }}(\mathbf{1}-{\mathbf{x}}_{\mathit{n}})$$

(3)

modeling population growth. As biologist Robert May demonstrated in a seminal 1976 paper, varying the parameter r causes the sequence’s behavior to transition from stable points to periodic oscillations and finally to full-blown chaos, where its behavior appears completely random despite its deterministic origin [13]. Similarly, the work of Benoît Mandelbrot on fractals, particularly the Mandelbrot set generated by the simple iteration

$${\mathcal{z}}_{\mathit{n}+\mathbf{1}}={\mathcal{z}}_{\mathit{n}}^{\mathbf{2}}+\mathcal{c}$$

(4)

in the complex plane, showed how a static rule could generate infinite complexity and intricate, self-similar patterns [14]. These examples established a new reality: the most interesting behaviours often arise not from complicated rules, but from the repeated application of simple ones. Yet, even these systems remain “statically defined” in the sense that the rule itself never changes.

This historical trajectory has culminated in the contemporary algorithmic era, where the very definition of a sequence can be inherently dynamic and computational. We are now exploring a new class of sequences whose generating rules are not fixed but are state-dependent, changing based on the properties of the terms they produce. A prime example of this new paradigm is the recently developed Keçeci numbers [16,42]. Unlike the Fibonacci sequence or the logistic map, the rule for generating the next Keçeci number is not a single, immutable formula. Instead, it is an algorithm—a set of conditional instructions. The process begins with a starting value and an additive constant. At each step, the algorithm attempts to divide the current term by a primary divisor (alternating between 2 and 3). If this fails, a secondary division is attempted. If both fail, the algorithm performs a primality test on the term (or its principal component, in the case of complex numbers or quaternions). If the term is found to be prime, a unique “Augment/Shrink & Check (ASK)” rule is triggered, modifying the number before re-attempting the division process [17].

The stateful nature of this algorithm is its defining characteristic. The system must “remember” the last successful divisor to determine the next primary divisor and track an internal counter to decide whether to augment or shrink a term during an ASK operation. This generates a path-dependent sequence where the generation of a term is contingent on the history of the sequence’s progression. Keçeci numbers can be generated across diverse number fields, including integers, rationals, complex numbers, and quaternions, all governed by the same dynamic logic [17]. This research has been disseminated through various open-science platforms, including preprints, datasets, and open-source code packages, reflecting a modern approach to mathematical discovery that emphasizes reproducibility and computational exploration [7,18,19,20].

In conclusion, the history of number sequences traces a clear path from a belief in static, predictable order to an embrace of dynamic, emergent complexity. The journey began with the ancient Greeks’ search for perfect, unchanging forms and progressed through Oresme’s paradoxical discovery of infinite sums from simple static rules. It was revolutionized by Poincaré’s unveiling of deterministic chaos and visualized through the computational lens of the logistic map and fractals. Today, we have entered an era of algorithmic discovery, exemplified by Keçeci numbers, where a sequence is no longer just a formula but a computational process. In this new landscape, the rules themselves are adaptive, state-dependent, and intrinsically tied to the very numbers they generate. This shift from theoretical prediction to experimental and algorithmic discovery marks a fundamental progression in our understanding of mathematical patterns, opening new frontiers in number theory, computer science, and complex systems modeling.

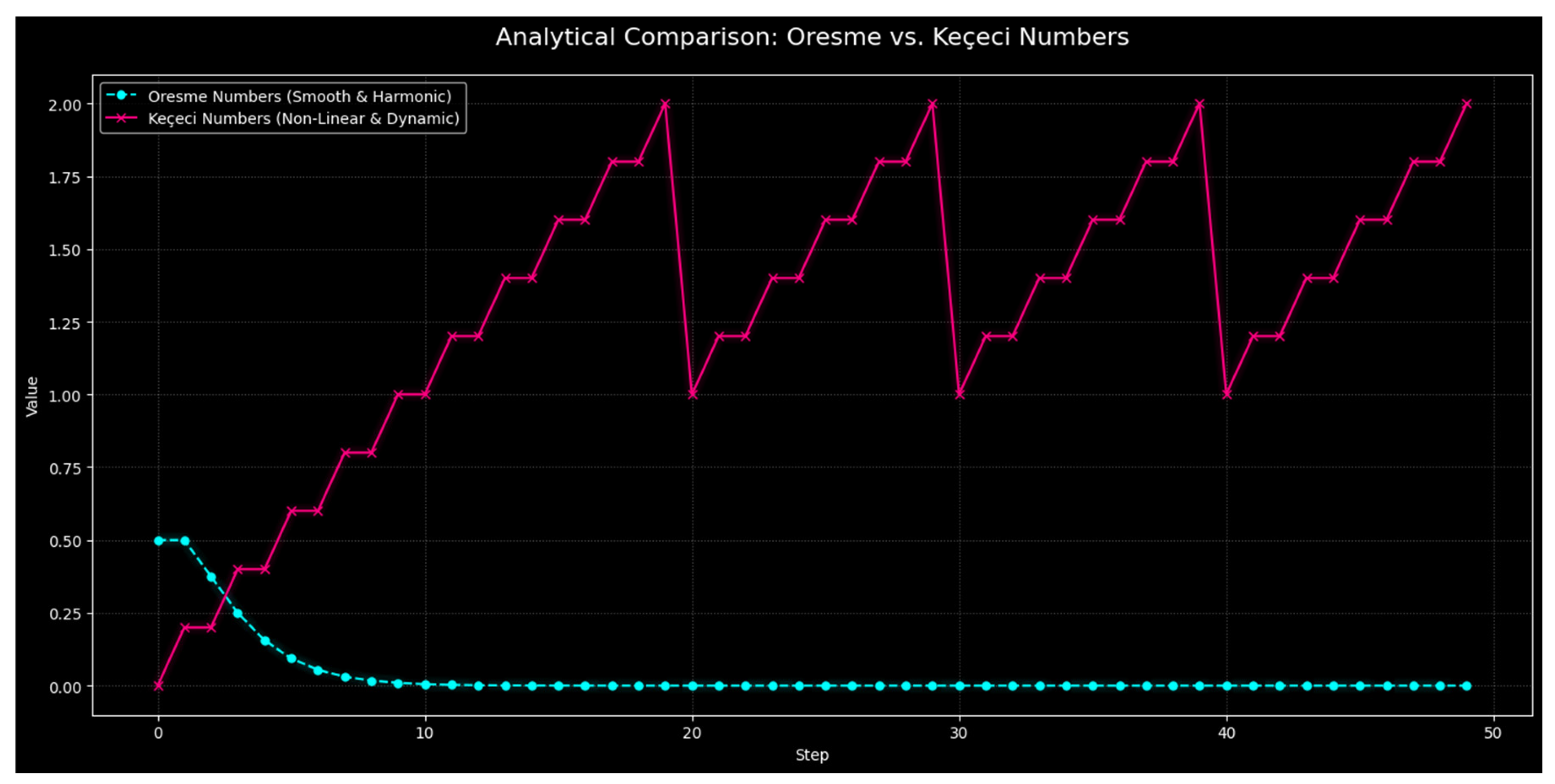
2. A Tale of Two Sequences: The Static Predictability of Oresme and the Dynamic Complexity of Keçeci Numbers

The fundamental distinction between static and dynamic sequences is best illustrated through a direct comparison of their archetypal representatives. For the static paradigm, we consider the Oresme numbers, rooted in classical analysis, and for the dynamic paradigm, the algorithmically defined Keçeci numbers. Their juxtaposition reveals not just a difference in mathematical structure, but a profound divergence in their conceptual underpinnings, behavior, and potential applications.

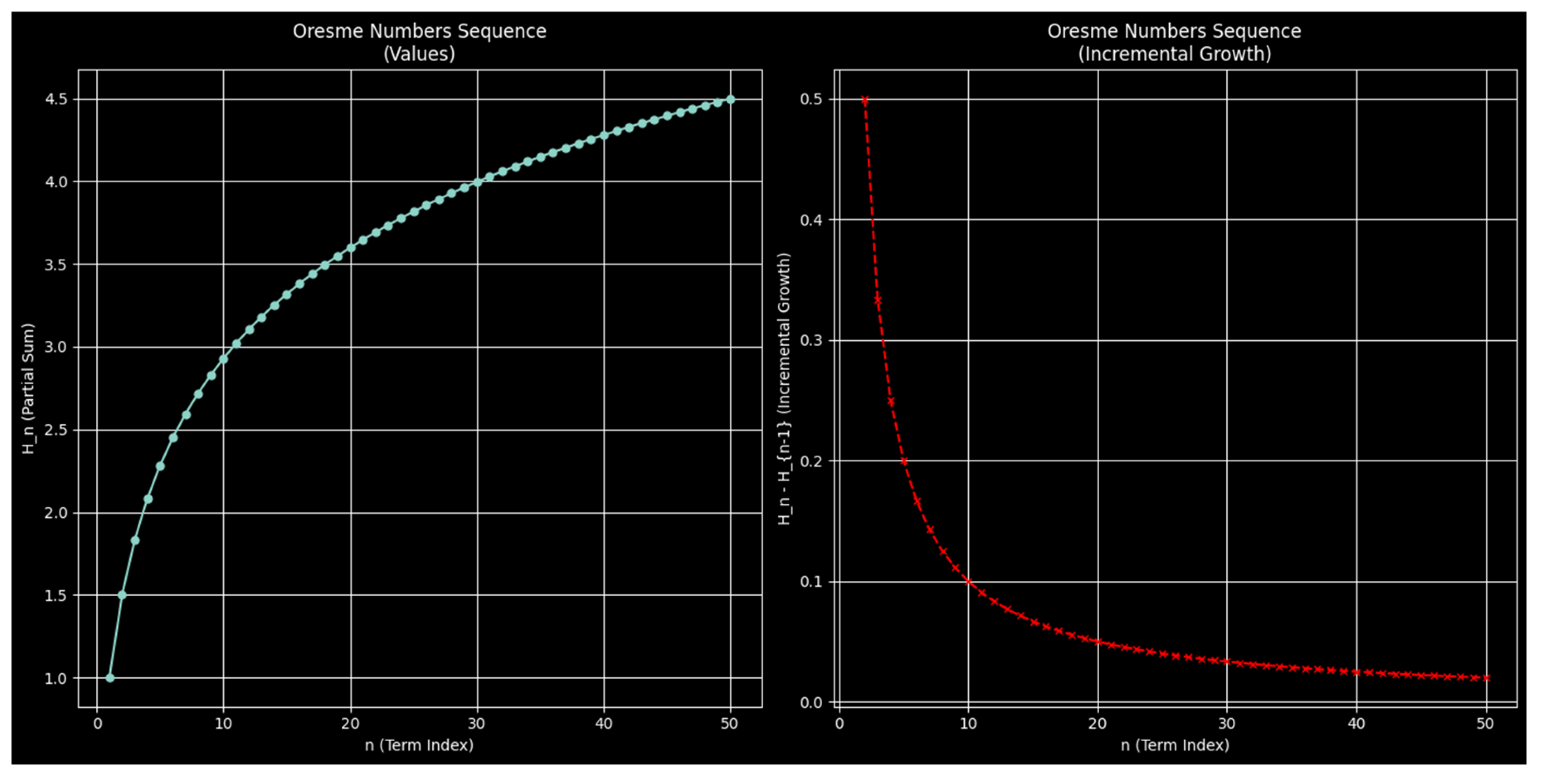
2.1. The Oresme Numbers: A Benchmark of Static, Rule-Bound Generation

The Oresme numbers, as they are most consequentially known in mathematical history, are the partial sums of the harmonic series. They are defined by the explicit recurrence relation:

$${\mathit{H}}_{\mathit{n}}=\mathit{ }{\mathit{H}}_{\mathit{n}-\mathbf{1}}+\mathit{ }{\displaystyle \frac{\mathbf{1}}{\mathit{n}}},$$

(5)

with the initial condition

$${\mathit{H}}_{\mathit{n}}=\mathbf{0}.$$

(6)

This can also be expressed in summation notation as (1). The first few terms of the sequence are:

$${\mathit{H}}_{\mathbf{1}}=\mathbf{1},\mathit{ }{\mathit{H}}_{\mathbf{2}}=\mathbf{1}+\mathit{ }{\displaystyle \frac{\mathbf{1}}{\mathbf{2}}}=\mathbf{1.5},\mathit{ }{\mathit{H}}_{\mathbf{3}}=\mathbf{1.5}+\mathit{ }{\displaystyle \frac{\mathbf{1}}{\mathbf{3}}}\approx \mathbf{1.833}\dots ,\mathit{ }{\mathit{H}}_{\mathbf{4}}=\mathbf{1.833}\dots +\mathit{ }{\displaystyle \frac{\mathbf{1}}{\mathbf{4}}}\approx \mathbf{2.083}$$

(7)

The defining characteristics of the Oresme numbers as a static sequence are threefold. First, the rule of generation is immutable; the method for calculating the n-th term is fixed for all n and does not depend on the value of the previous terms, only their existence. Second, the sequence is entirely predictable. Given any index n, the value of ${\mathsf{H}}_n$ can be calculated directly without needing to compute the entire preceding sequence, and its trajectory is smooth and monotonically increasing. Third, its behavior, while counter-intuitive, is analytically determined. Nicole Oresme’s 14th-century proof of its divergence established, with certainty, the sequence’s ultimate fate [11]. The Oresme numbers are thus a perfect embodiment of a static system: their path is predetermined, their structure is transparent, and their properties are discoverable through traditional analytical methods. Their pedagogical value lies precisely in this clarity, serving as a foundational example of series behavior in calculus and analysis [15].

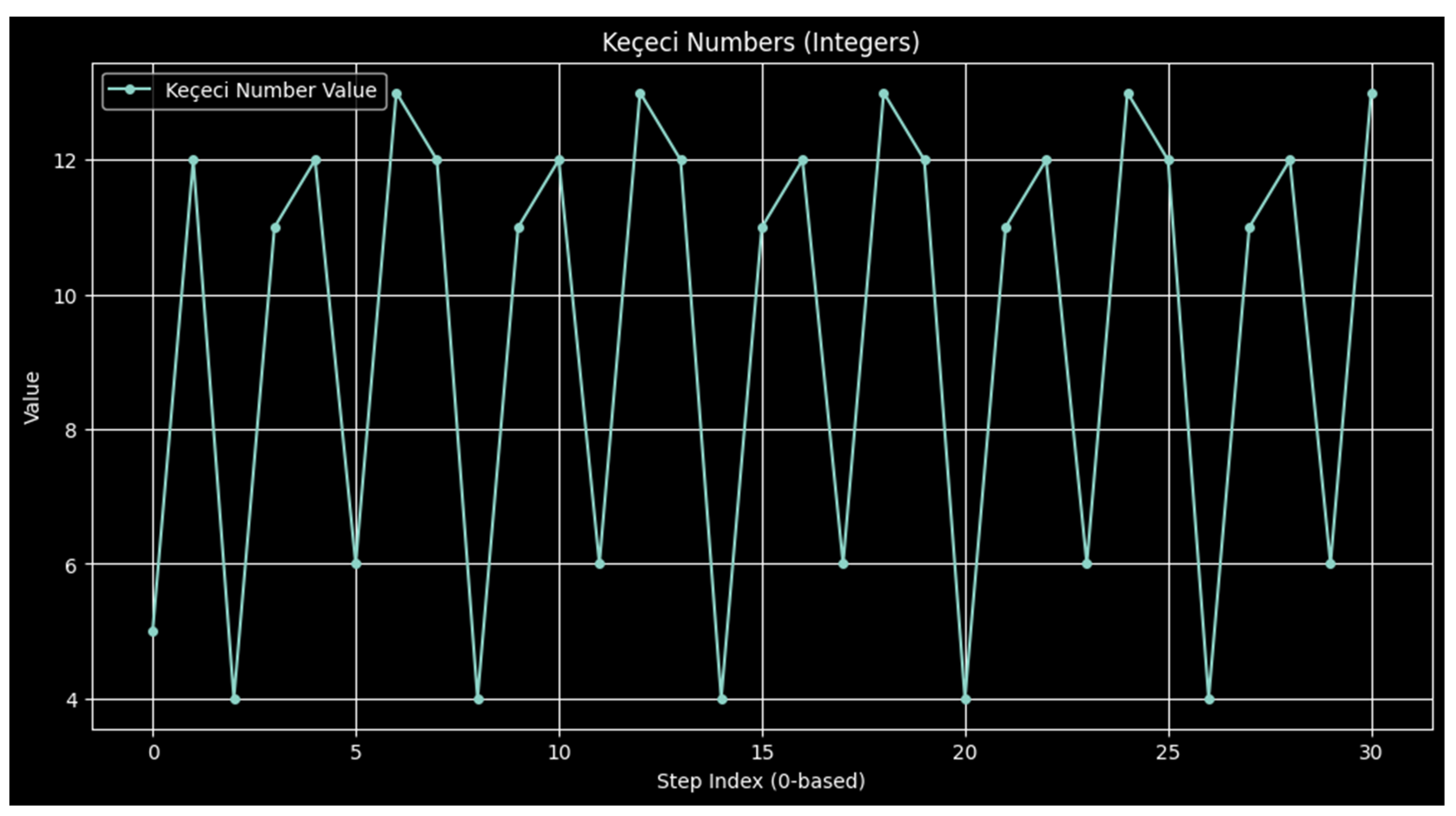
2.2. The Keçeci Numbers: An Exemplar of Dynamic, State-Dependent Time Development

In stark contrast, Keçeci numbers are not defined by a simple recurrence relation but by a state-dependent algorithm. The generation of each term is a computational process contingent upon the properties of the preceding term and the internal state of the algorithm. As detailed by Keçeci [16,17], the core process for a given sequence type (e.g., integer, complex, quaternion) is as follows:

• Initialization: The sequence begins with a user-defined starting value ($k_0$) and an additive constant (a).
• Iteration Step: For a current term ${\mathrm{k}}_i$, the next potential term is calculated as $k_{i,temp}=k_i+a$. This temporary value is added to the sequence.
• Conditional Division Rule: The algorithm attempts to divide ${\mathrm{k}}_{i,temp}$ by a primary divisor, which alternates between 3 and 2. The state of the “last used divisor” determines the primary choice for the current step.
  • If divisible, the result becomes the next term, $k_{i+1}$, and the “last used divisor” state is updated. The process moves to the next iteration.
  • If not divisible, the algorithm attempts division by the alternative divisor (2 or 3). If successful, the result becomes $k_{i+1}$, and the state is updated.
• Primality and the ASK Rule: If both division attempts fail, a primality test is performed on the principal component of ${\mathrm{k}}_{i,temp}$ (e.g., the integer itself, or the real part of a complex number).
  • If the number is not prime, $k_{i+1}$ is set to $k_{i,temp}$, and the process continues.
  • If the number is prime, the “Augment/Shrink & Check (ASK)” mechanism is activated. Based on an internal toggle state, a type-specific unit value (e.g., 1 for integers, 1+1j for complex numbers) is either added to or subtracted from $k_{i,temp}$. This new, modified value is added to the sequence, and the division rules (Step 3) are re-applied to it to determine the final $k_{i+1}$.

This algorithm produces a sequence whose trajectory is inherently unpredictable. Two Keçeci sequences with infinitesimally different starting parameters can diverge dramatically, exhibiting a sensitivity to initial conditions reminiscent of chaotic systems [13]. The sequence’s progression is path-dependent; the choice made at step i (e.g., which divisor worked, or whether the ASK rule was triggered) directly influences the rules and possibilities available at step i+1.

2.3. Comparative Analysis: Predictability vs. Path-Dependence

The table below summarizes the core differences between the two sequences, highlighting the static-dynamic dichotomy:

Table 1. The core differences between the two sequences, highlighting the static-dynamic dichotomy.

Feature	Oresme Numbers ($H_n$ )	Keçeci Numbers ($k_n$ )
Definition	Fixed recurrence relation: $H_n=H_{n-1}+{\displaystyle \frac{1}{n}}$	State-dependent algorithm with conditional logic
Generation Rule	Immutable, analytical, time-invariant	Adaptive, computational, state-variant
Predictability	Fully predictable; any term can be calculated directly.	Inherently unpredictable; requires step-by-step simulation.
Statefulness	Stateless; each step is independent of past choices.	Stateful; requires memory of last divisor and ASK toggle.
Dependence	Index-dependent	Path-dependent and value-dependent
Complexity	Structural simplicity, analytical complexity (divergence).	Algorithmic complexity, emergent behavioural complexity.
Domain	Primarily defined for real (rational) numbers.	Defined across integers, rationals, complex, quaternions [3].
Primary Field of Study	Mathematical Analysis, Calculus	Number Theory, Computer Science, Dynamical Systems

Table 1. The core differences between the two sequences, highlighting the static-dynamic dichotomy.

Feature	Oresme Numbers ($H_n$ )	Keçeci Numbers ($k_n$ )
Definition	Fixed recurrence relation: $H_n=H_{n-1}+{\displaystyle \frac{1}{n}}$	State-dependent algorithm with conditional logic
Generation Rule	Immutable, analytical, time-invariant	Adaptive, computational, state-variant
Predictability	Fully predictable; any term can be calculated directly.	Inherently unpredictable; requires step-by-step simulation.
Statefulness	Stateless; each step is independent of past choices.	Stateful; requires memory of last divisor and ASK toggle.
Dependence	Index-dependent	Path-dependent and value-dependent
Complexity	Structural simplicity, analytical complexity (divergence).	Algorithmic complexity, emergent behavioural complexity.
Domain	Primarily defined for real (rational) numbers.	Defined across integers, rationals, complex, quaternions [3].
Primary Field of Study	Mathematical Analysis, Calculus	Number Theory, Computer Science, Dynamical Systems

In essence, Oresme numbers represent a system of theoretical prediction. Their properties can be deduced and proven using the established tools of mathematical analysis. Keçeci numbers, by contrast, belong to a world of algorithmic discovery. Their behavior, patterns, and emergent properties (such as the “Keçeci Prime Number,” a statistically significant prime within a sequence [2]) are best explored through computational simulation and empirical analysis. While Oresme’s sequence provides a clear, unwavering path to infinity, a Keçeci sequence charts a complex, pseudo-random walk through the number space, its journey shaped by the very nature of the numbers it encounters. This contrast forms the basis for exploring their distinct applications in theoretical mathematics versus modern computational sciences.

3. Computational Exploration: Comparing Oresme and Keçeci Numbers Through Python Implementations

The theoretical distinctions between static and dynamic number sequences, as exemplified by Oresme and Keçeci numbers, are best appreciated through their computational implementations. Python, with its extensive libraries for numerical computation, data visualization, and algorithm development, serves as an ideal environment to explore these differences. This chapter presents a comparative analysis using Python code, examining textual and graphical outputs to illustrate the predictable nature of Oresme numbers against the emergent complexity of Keçeci numbers. We will explore distinct use cases for each type of sequence.

3.1. Oresme Numbers in Python: Demonstrating Predictability and Analytical Convergence

The static nature of Oresme numbers [43,44,45,46,65,66,67,68,69,70,71,74], being the partial sums of the harmonic series, makes them straightforward to implement. Their behavior is entirely dictated by the simple addition of successive unit fractions.

Figure 1. Oresme numbers.

Figure 1. Oresme numbers.

--- Oresme Numbers: Textual Output ---

First 10 Oresme numbers (as fractions): [Fraction(1, 1), Fraction(3, 2), Fraction(11, 6), Fraction(25, 12), Fraction(137, 60), Fraction(49, 20), Fraction(363, 140), Fraction(761, 280), Fraction(7129, 2520), Fraction(7381, 2520)]

First 10 Oresme numbers (as floats): [1.0, 1.5, 1.8333333333333333, 2.0833333333333335, 2.283333333333333, 2.45, 2.592857142857143, 2.717857142857143, 2.828968253968254, 2.9289682539682538]

Observation: The values grow slowly but steadily, and the increment (1/n) decreases, indicating divergence to infinity.

Code Example 3.1: Generating and Analysing Oresme Numbers

import matplotlib.pyplot as plt

from fractions import Fraction

import numpy as np

import oresme as ore

def plot_oresme_sequence(oresme_seq, title=“Oresme Numbers Sequence”):

“““Plots the Oresme sequence and highlights its convergence behavior.”““

n_values = np.arange(1, len(oresme_seq) + 1)

plt.figure(figsize=(14, 7))

# Plotting the sequence values

plt.subplot(1, 2, 1)

plt.plot(n_values, [float(h) for h in oresme_seq], marker=‘o’, linestyle=‘-‘, markersize=5)

plt.title(title + “\n(Values)”)

plt.xlabel(“n (Term Index)”)

plt.ylabel(“H_n (Partial Sum)”)

plt.grid(True)

# Highlighting the divergence (or slow growth) conceptually

# While not explicitly showing infinity, we can show the increasing rate of growth of difference from a fixed point if needed.

# For demonstration, we’ll show the increase itself.

plt.subplot(1, 2, 2)

differences = np.diff([float(h) for h in oresme_seq])

plt.plot(n_values [1:], differences, marker=‘x’, linestyle=‘--‘, color=‘red’, markersize=5)

plt.title(title + “\n(Incremental Growth)”)

plt.xlabel(“n (Term Index)”)

plt.ylabel(“H_n − H_{n-1} (Incremental Growth)”)

plt.grid(True)

plt.tight_layout()

plt.show()

# Parameters for Oresme numbers

num_terms_oresme = 50 # Calculate first 50 terms

oresme_data = ore.harmonic_numbers(num_terms_oresme)

print(“--- Oresme Numbers: Textual Output ---”)

print(f”First 10 Oresme numbers (as fractions): {oresme_data[:10]}”)

print(f”First 10 Oresme numbers (as floats): {[float(o) for o in oresme_data[:10]]}”)

print(“\nObservation: The values grow slowly but steadily, and the increment (1/n) decreases, indicating divergence to infinity.”)

plot_oresme_sequence(oresme_data)

Listing 1: Generating and Analysing Oresme Numbers

Explanation of Outputs and Interpretation:

Textual Output: The code first prints the Oresme numbers as Fraction objects, preserving their exact rational form, and then as floating-point numbers for easier interpretation. This output demonstrates the sequence’s slow but steady increase. Even after 50 terms, the values are not astronomically large, but the trend of slow growth continues.

Graphical Output:

The first plot shows the Oresme numbers ($H_n$) against their index (n). It clearly illustrates the monotonically increasing nature of the sequence. The curve appears to flatten, but this is an artifact of plotting on a finite scale; the sequence is known to diverge [11,15].

The second plot shows the incremental growth

$${\mathit{H}}_{\mathit{n}}-{\mathit{H}}_{\mathit{n}-\mathbf{1}}=\mathbf{1}/\mathit{n}.$$

(8)

This highlights how the difference between consecutive terms decreases over time. This decreasing increment is characteristic of a sequence that diverges slowly to infinity, a key insight from Oresme’s work [11].

Potential Uses of Oresme Numbers:

Oresme numbers, due to their predictable behavior and historical significance, find applications in:

Mathematical Education: As a fundamental example for teaching convergence, divergence, series, and limits in calculus and analysis courses [15].

Numerical Analysis: While they diverge, understanding their rate of growth and the behavior of partial sums is crucial for analysing the convergence properties of other series.

Theoretical Computer Science: As a basis for discussing algorithms related to summation and approximation, and as a simple model for systems that exhibit slow but unbounded growth.

3.2. Keçeci Numbers in Python: Illustrating Dynamic Progression and Algorithmic Complexity

Keçeci numbers are generated by a complex, state-dependent algorithm, making their implementation more intricate than Oresme numbers. We will use the kececinumbers Python library to showcase their dynamic behavior across different data types.

Figure 2. Keçeci numbers.

Figure 2. Keçeci numbers.

--- Keçeci Numbers (Integers): Textual Output ---

Sequence generated from start=5, add_base=7, iterations=30:

First 15 terms: [4,5,6,11,12,13]

Observations: Notice how terms change based on divisibility and primality checks. Numbers can jump significantly

Figure 3. Keçeci numbers.

Figure 3. Keçeci numbers.

--- Keçeci Numbers (Complex): Textual Output ---

Sequence generated from start=2+2j, add_base=3.0, iterations=8:

First 10 terms: [‘2.00+2.00j’, ‘5.00+5.00j’, ‘6.00+6.00j’, ‘2.00+2.00j’, ‘5.00+5.00j’, ‘4.00+4.00j’, ‘2.00+2.00j’, ‘5.00+5.00j’, ‘6.00+6.00j’]

Observations: Complex numbers progression as both their real and imaginary parts change according to the rules. The trajectory is non-linear and can show complex interactions.

Code Example 3.2: Keçeci Numbers (Integers)—Textual and Graphical Comparison

import matplotlib.pyplot as plt

import numpy as np

import quaternion # pip install numpy numpy-quaternion

import collections

from fractions import Fraction

# We import the Keçeci Numbers library as ‘kn’.

# This library must be installed via pip: pip install kececinumbers

import kececinumbers as kn

# --- Integer Keçeci Numbers Example ---

int_start = “5”

int_add_base = 7

int_iterations = 30 # This will generate approximately 20-30 terms.

# We generate the sequence using the library’s own unified_generator function.

# The placeholder functions are no longer necessary.

int_kececi_data = kn.unified_generator(1, int_start, int_add_base, int_iterations)

print(“\n--- Keçeci Numbers (Integers): Textual Output ---”)

print(f”Sequence generated from start={int_start}, add_base={int_add_base}, iterations={int_iterations}:”)

print(f”First 15 terms: {int_kececi_data[:15]}”)

print(“\nObservations: Notice how terms change based on divisibility and primality checks. Numbers can jump significantly.”)

def plot_kececi_integer_sequence(kececi_seq, title=“Keçeci Numbers (Integers)”):

“““Plots the integer Keçeci sequence, highlighting jumps and non-linear behavior.”““

plt.figure(figsize=(12, 6))

plt.plot(range(len(kececi_seq)), kececi_seq, marker=‘o’, linestyle=‘-‘, markersize=4, label=‘Keçeci Number Value’)

plt.title(title)

plt.xlabel(“Step Index (0-based)”)

plt.ylabel(“Value”)

plt.grid(True)

plt.legend()

plt.show()

plot_kececi_integer_sequence(int_kececi_data)

# --- Complex Keçeci Numbers Example ---

complex_start = “2+2j”

complex_add_base = 3.0 # This will be interpreted as 3+3j by the library

complex_iterations = 8 # This will generate approximately 16-24 terms.

# We generate the complex sequence using the library’s own unified_generator function.

complex_kececi_data = kn.unified_generator(3, complex_start, complex_add_base, complex_iterations)

print(“\n--- Keçeci Numbers (Complex): Textual Output ---”)

print(f”Sequence generated from start={complex_start}, add_base={complex_add_base}, iterations={complex_iterations}:”)

# Added formatting for more readable output

formatted_complex_output = [f”{c.real:.2f}{c.imag:+.2f}j” if isinstance(c, complex) else c for c in complex_kececi_data[:10]]

print(f”First 10 terms: {formatted_complex_output}”)

print(“\nObservations: Complex numbers progression as both their real and imaginary parts change according to the rules. The trajectory is non-linear and can show complex interactions.”)

def plot_kececi_complex_sequence(kececi_seq, title=“Keçeci Numbers (Complex)”):

“““Plots the complex Keçeci sequence, showing its real and imaginary parts.”““

# Filter for only complex-type data

complex_numbers = [c for c in kececi_seq if isinstance(c, complex)]

real_parts = [c.real for c in complex_numbers]

imag_parts = [c.imag for c in complex_numbers]

plt.figure(figsize=(14, 7))

# Plot 1: Real and Imaginary Parts over Time

plt.subplot(1, 2, 1)

plt.plot(range(len(real_parts)), real_parts, marker=‘o’, linestyle=‘-‘, markersize=4, label=‘Real Part’)

plt.plot(range(len(imag_parts)), imag_parts, marker=‘x’, linestyle=‘--‘, color=‘red’, markersize=4, label=‘Imaginary Part’)

plt.title(title + “\n(Components)”)

plt.xlabel(“Step Index (Complex Numbers)”)

plt.ylabel(“Value”)

plt.grid(True)

plt.legend()

# Plot 2: Trajectory in the Complex Plane

plt.subplot(1, 2, 2)

plt.plot(real_parts, imag_parts, marker=‘.’, linestyle=‘-‘, label=‘Trajectory’)

if real_parts:

plt.plot(real_parts [0], imag_parts [0], ‘go’, markersize=10, label=‘Start’)

plt.plot(real_parts[-1], imag_parts[-1], ‘ro’, markersize=10, label=‘End’)

plt.title(title + “\n(Complex Plane Trajectory)”)

plt.xlabel(“Real Axis”)

plt.ylabel(“Imaginary Axis”)

plt.axhline(0, color=‘black’, lw=0.5)

plt.axvline(0, color=‘black’, lw=0.5)

plt.grid(True)

plt.legend()

plt.axis(‘equal’)

plt.tight_layout()

plt.show()

plot_kececi_complex_sequence(complex_kececi_data)

Listing 2: Keçeci Numbers (Integers)—Textual and Graphical Comparison

Explanation of Outputs and Interpretation:

Integer Keçeci Numbers:

Textual Output: The integer sequence demonstrates the core logic: terms are generated by adding an increment, then attempting division by 3, then 2. If divisibility fails, primality is checked. If prime, the “ASK” rule (add or subtract the unit) is applied before re-attempting division. This results in jumps and non-linear changes, unlike the steady growth of Oresme numbers. For instance, if a number is prime and then modified, it might become divisible by 3 or 2, producing a sudden drop.

Graphical Output: The integer plot visually represents these unpredictable jumps. The sequence does not follow a smooth curve but rather a jagged path, illustrating the dynamic, state-dependent nature of the generation. The value changes are not merely incremental but can be multiplicative or drastically reduced depending on the algorithm’s path.

Complex Keçeci Numbers:

Textual Output: The complex sequence shows how the real and imaginary parts are updated simultaneously based on the same set of rules, applied to both components. This means that divisibility and primality checks (on the real part) can influence both parts of the complex number in tandem.

Graphical Output: The first plot shows the progression of the real and imaginary parts over steps. The second plot provides a trajectory in the complex plane. This trajectory is significantly more complex than a simple curve. It can exhibit intricate patterns, self-similar structures, or chaotic wandering, depending on the parameters and the number of iterations. This visualizes how the dynamic rules, when applied to complex arithmetic, can lead to rich, non-linear dynamics.

Potential Uses of Keçeci Numbers:

The dynamic, state-dependent, and computational nature of Keçeci numbers makes them suitable for applications where complexity, unpredictability, and adaptability are desired:

Algorithm Design and Cryptography: The pseudo-random behavior and sensitivity to initial conditions make them potential candidates for pseudorandom number generators (PRNGs) or components in cryptographic algorithms where complex, non-linear transformations are needed [17,42].

Computer Science Education: They serve as excellent, tangible examples for teaching concepts in algorithmic thinking, state machines, conditional logic, the difference between static and dynamic systems, and the emergence of complexity from simple rules.

Modeling Complex Systems: Their path-dependent nature and the interplay between divisibility and primality checks could potentially be used to model phenomena exhibiting similar characteristics, such as certain biological growth patterns, financial market fluctuations, or simulated physical systems [17].

Number Theory Exploration: The identification of a “Keçeci Prime Number” suggests they can be used as an exploratory tool in number theory, potentially revealing new properties of numbers through computational observation [16,42].

In summary, Python implementations clearly demonstrate the contrast: Oresme numbers are a static, predictable sequence with analytical depth, ideal for foundational mathematical education. Keçeci numbers are a dynamic, computationally driven sequence with emergent complexity, opening avenues in modern computational fields and novel algorithmic applications.

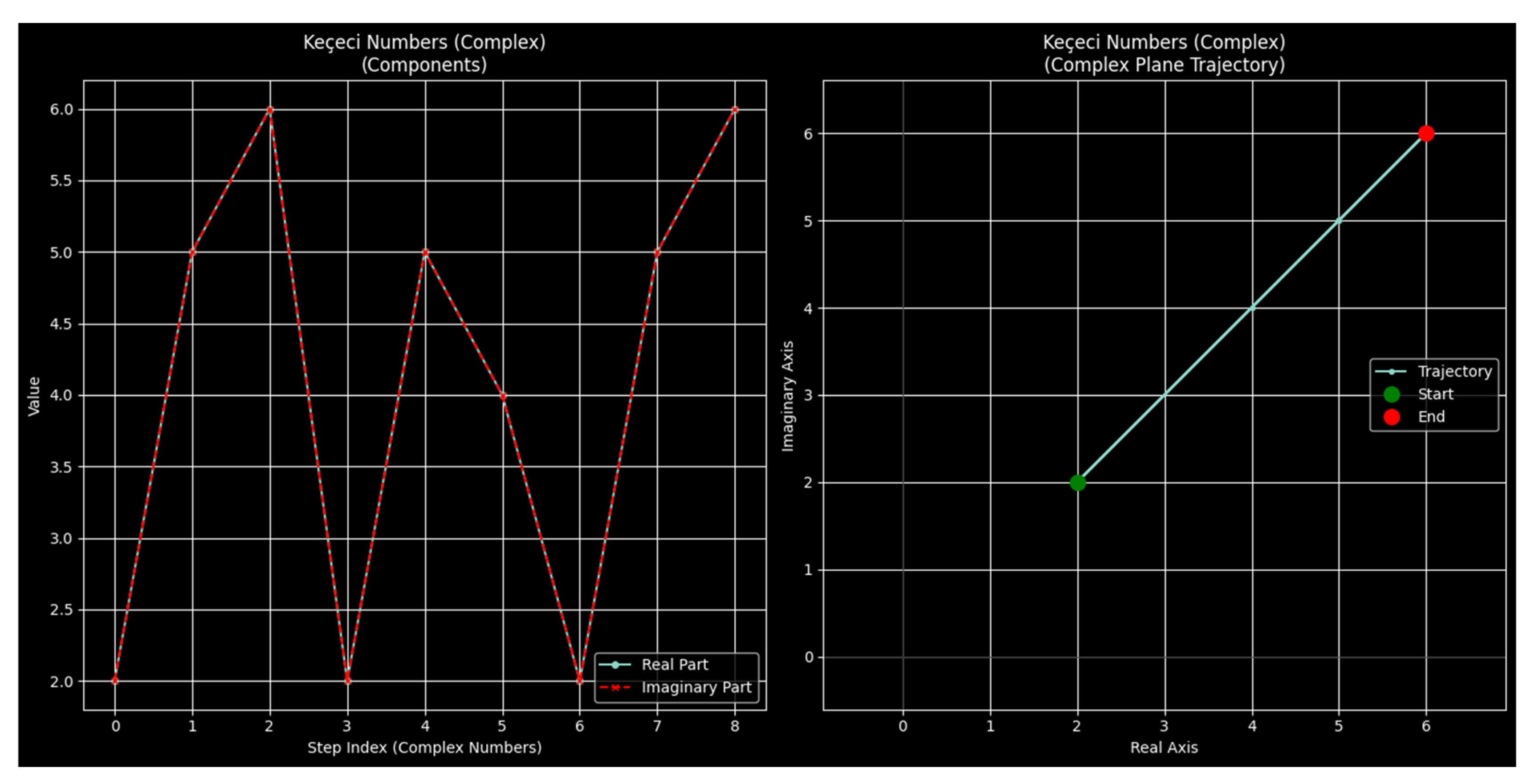
4. From Mathematical Abstraction to Practical Application: Novel Use Cases

The utility of a number sequence is determined not only by its mathematical properties but also by its applicability to real-world or computational problems. While Oresme numbers are foundational in analysis and Keçeci numbers are intrinsically tied to algorithmic theory, their unique characteristics open doors to less obvious, yet powerful, applications. This chapter explores one such advanced application for each sequence, demonstrating how their static predictability and dynamic complexity can be harnessed in distinct problem domains.

4.1. Oresme Numbers: Modeling Expectation in Probabilistic Systems

Beyond their role in calculus, the partial sums of the harmonic series (Oresme numbers) appear naturally in probability theory, most famously in the Coupon Collector’s Problem. This classic problem asks: “Suppose there are N unique coupons, and you acquire one at random in each trial (with replacement). What is the expected number of trials needed to collect all N unique coupons?”

The solution is elegantly tied to Oresme numbers. The expected number of trials to get the first coupon is 1. After collecting k unique coupons, the probability of getting a new, unique coupon in the next trial is

(N-k)/N.

(9)

The expected number of trials to get this new coupon is the reciprocal of this probability,

N/(N-k).

(10)

Therefore, the total expected number of trials, E(T), is the sum of these expectations:

$$\mathit{E}\left(\mathit{T}\right)=\mathbf{ }{\displaystyle \frac{\mathit{N}}{\mathit{N}}}+{\displaystyle \frac{\mathit{N}}{\mathit{N}-1}}+{\displaystyle \frac{\mathit{N}}{\mathit{N}-2}}+\dots +{\displaystyle \frac{\mathit{N}}{1}}=\mathit{ }\mathit{N}{\sum }_{\mathit{k}=1}^{\mathit{N}}{\displaystyle \frac{1}{\mathit{k}}}=\mathit{N}.{\mathit{H}}_{\mathit{N}}$$

(11)

Here, $H_N$ is precisely the N-th Oresme number. This direct connection allows Oresme numbers to model scenarios involving waiting times, random sampling, and completion targets. Potential applications include:

• Systems Biology: Estimating the time required to observe all possible states of a protein or gene expression pattern.
• Network Analysis: Calculating the expected number of random walks needed to visit every node in a complete graph.
• Quality Assurance: Determining the expected number of product samples needed to identify all potential defect types.
• Data Science: Modeling the effort required to gather a complete and representative dataset from a large population.

The static and predictable nature of Oresme numbers makes them perfect for these analytical models, where a well-defined, calculable expectation is required.

4.2. Keçeci Numbers: A Tool for Generative Art and Procedural Content

In contrast, the strength of Keçeci numbers lies in their unpredictability and emergent complexity. This makes them an ideal tool for procedural content generation (PCG) and generative art, fields that require systems capable of producing complex, non-repeating, and aesthetically interesting outputs from a simple set of rules and a starting seed.

Traditional PRNGs can produce randomness, but the state-dependent, path-dependent nature of the Keçeci algorithm offers a different kind of complexity. The sequence is not merely random; its progression is shaped by the number-theoretic properties (divisibility, primality) of the values it generates. This can lead to artifacts with a more “organic” or structured feel than pure noise. The ASK rule, in particular, acts as a “glitch” or a sudden “decision point” that can dramatically alter the trajectory, producing visually compelling shifts in the generated artwork.

The following Python code demonstrates this concept by using a sequence of complex Keçeci numbers to draw a “trajectory” in a 2D plane. The real and imaginary parts of each number in the sequence dictate the coordinates of a line segment, while the sequence’s progression determines the color, producing a unique digital artwork from a given set of initial parameters.

Code Example 4.1: Generative Art from Complex Keçeci Numbers (This code requires the kececinumbers library to be installed or the placeholder functions from the previous chapter to be defined).

Figure 4. Generative Art from Complex Keçeci Numbers.

Figure 4. Generative Art from Complex Keçeci Numbers.

Figure 5. Generative Art from Complex Keçeci Numbers.

Figure 5. Generative Art from Complex Keçeci Numbers.

Figure 6. Generative Art from Complex Keçeci Numbers.

Figure 6. Generative Art from Complex Keçeci Numbers.

Figure 7. Generative Art from Complex Keçeci Numbers.

Figure 7. Generative Art from Complex Keçeci Numbers.

import matplotlib.pyplot as plt

import numpy as np

from matplotlib.patches import RegularPolygon, Circle

import warnings

# Import Keçeci Numbers library

import kececinumbers as kn

# --- Mathematical Transformation Functions (Same as before) ---

def transform_inversion(points):

return [1 / p if p != 0 else complex(0, 0) for p in points]

def transform_log_spiral(points):

with warnings.catch_warnings():

warnings.simplefilter(“ignore”, RuntimeWarning)

return [np.log(p) if p != 0 else complex(0, 0) for p in points]

def transform_power(points, power=2):

return [p**power for p in points]

# --- Main Artwork Generation Function (Completely Renewed) ---

def crystalline_art(start_val, add_val, iterations,

cmap_name=‘hot’, num_symmetries=7,

transformation=None, power_val=2):

“““

Uses Keçeci sequence as a seed to generate crystal-like artworks by drawing

parametric polygons and energy cores instead of lines.

“““

print(f”Generating crystal art... Symmetry: {num_symmetries}, Transformation: {transformation or ‘None’}”)

# 1. Generate Keçeci sequence

points = kn.unified_generator(3, start_val, add_val, iterations)

points = [p for p in points if isinstance(p, complex) and np.isfinite(p)]

# 2. Apply optional mathematical transformation

if transformation == ‘inversion’:

points = transform_inversion(points)

elif transformation == ‘log’:

points = transform_log_spiral(points)

elif transformation == ‘power’:

points = transform_power(points, power_val)

points = [p for p in points if np.isfinite(p)]

if len(points) < 10:

print(“Insufficient points generated to generate artwork.”)

return

# 3. Set up drawing area

fig, ax = plt.subplots(figsize=(14, 14), dpi=150)

ax.set_facecolor(‘#08040A’) # Dark purple-black background

ax.set_aspect(‘equal’, adjustable=‘box’)

ax.axis(‘off’)

cmap = plt.get_cmap(cmap_name)

angle_step = 2 * np.pi / num_symmetries

# 4. Draw shapes instead of lines

for i in range(1, len(points)):

p1 = points[i-1]

p2 = points[i]

# --- Dynamically determine shape properties ---

jump_distance = abs(p2—p1)

magnitude = abs(p2)

# Size: Proportional to jump distance (clamped to 0-1 using tanh)

radius = np.tanh(jump_distance) * 0.2 + 0.01

# Number of Sides: Based on distance from center (3 to 8 sides)

num_vertices = int(np.log1p(magnitude) * 2) % 6 + 3

# Rotation Angle: The point’s own angle

orientation = np.angle(p2)

# Color: Based on time progression

current_color = cmap(i / len(points))

edge_color = cmap(i / len(points) * 0.8) # Slightly darker edge color

# Draw shapes for each symmetry axis

for j in range(num_symmetries):

rotation = np.exp(1j * j * angle_step)

sp = p2 * rotation

# MAIN SHAPE: CRYSTAL (Polygon)

# Generate dynamic-edged shapes using RegularPolygon

crystal = RegularPolygon(

(sp.real, sp.imag),

numVertices=num_vertices,

radius=radius,

orientation=orientation + (j * angle_step),

facecolor=current_color,

edgecolor=edge_color,

alpha=0.4, # Transparency to show layers

linewidth=0.5

)

ax.add_patch(crystal)

# SECONDARY SHAPE: ENERGY CORE (Circle)

# Add a bright dot at each crystal’s center

core_radius = radius * 0.2

if core_radius > 0.005: # Don’t draw very small ones

core = Circle(

(sp.real, sp.imag),

radius=core_radius,

facecolor=‘#FFFFFF’, # Bright white

alpha=0.5,

edgecolor=None

)

ax.add_patch(core)

ax.autoscale_view()

ax.set_title(f”Keçeci Crystalline Art\nStart:{start_val}, Add:{add_val}, Symm:{num_symmetries}, Trans:{transformation or ‘None’}”,

color=‘white’, fontsize=14, pad=20)

plt.tight_layout()

plt.show()

# --- Generate Artworks with Different Combinations ---

print(“--- Example 1: Floral Mandala ---”)

crystalline_art(“0.1+0.1j”, 1.1, 400, cmap_name=‘spring’, num_symmetries=8)

print(“\n--- Example 2: Sci-Fi Emblem (With power transformation) ---”)

crystalline_art(“0.2+0.1j”, 0.9, 350, cmap_name=‘cool’, num_symmetries=4, transformation=‘power’, power_val=2)

print(“\n--- Example 3: Mystical Jewel (With inversion transformation) ---”)

crystalline_art(“1+1j”, 2.7, 500, cmap_name=‘Wistia’, num_symmetries=5, transformation=‘inversion’)

print(“\n--- Example 4: Organic Cell Growth (With logarithmic spiral) ---”)

crystalline_art(“0.05-0.05j”, 1.618, 600, cmap_name=‘summer’, num_symmetries=6, transformation=‘log’)

Listing 3: Generative Art from Complex Keçeci Numbers

Interpretation and Broader Implications:

The visual output from the code is not a data plot but a unique artifact. The jagged lines, sharp turns, and color shifts are direct manifestations of the Keçeci algorithm’s internal decisions. A sudden change in color or direction might correspond to an ASK rule being triggered after a primality test. The overall structure is deterministic—the same initial parameters will always produce the same image—but its visual complexity is emergent.

This application highlights the fundamental difference in utility:

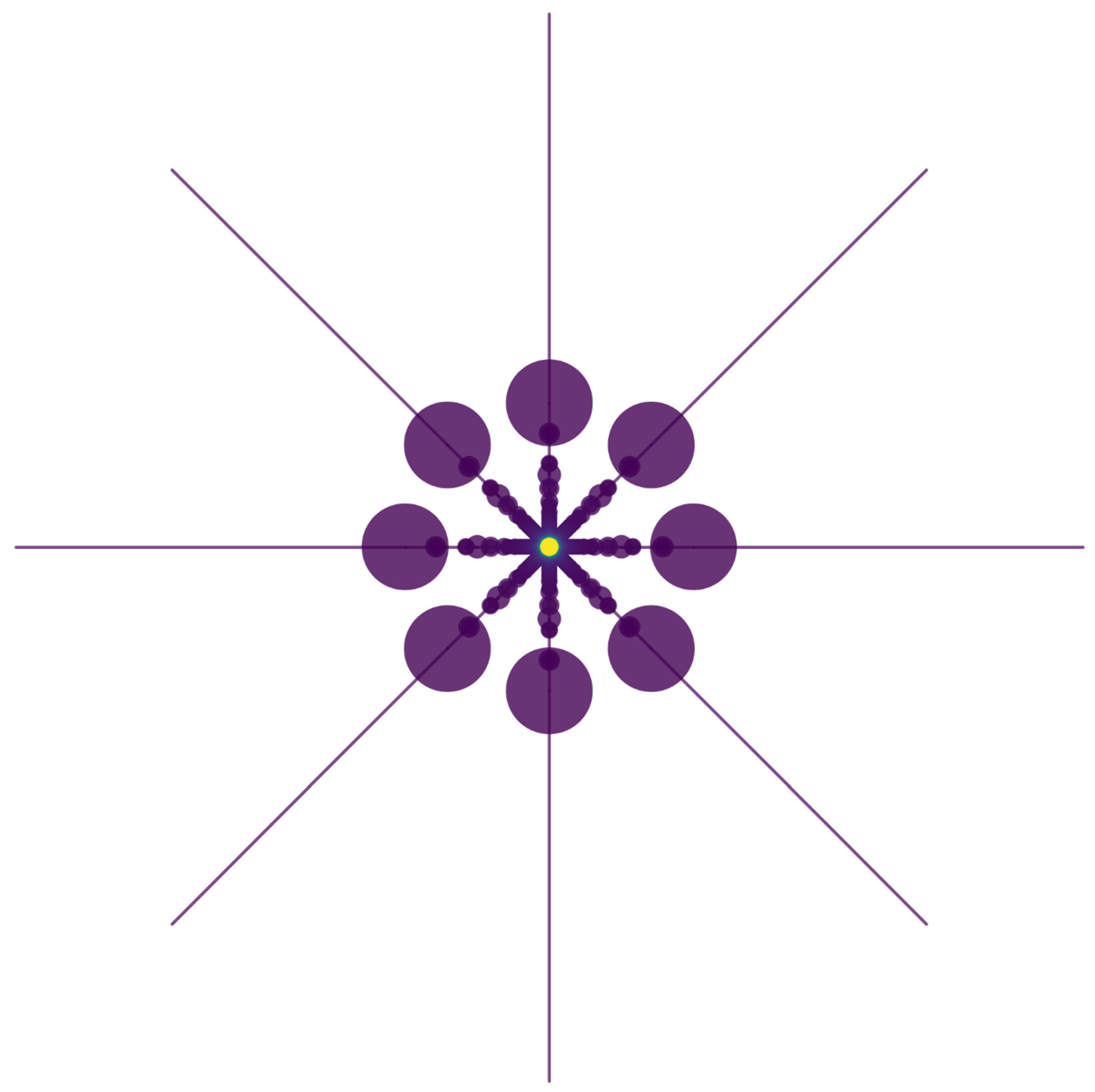
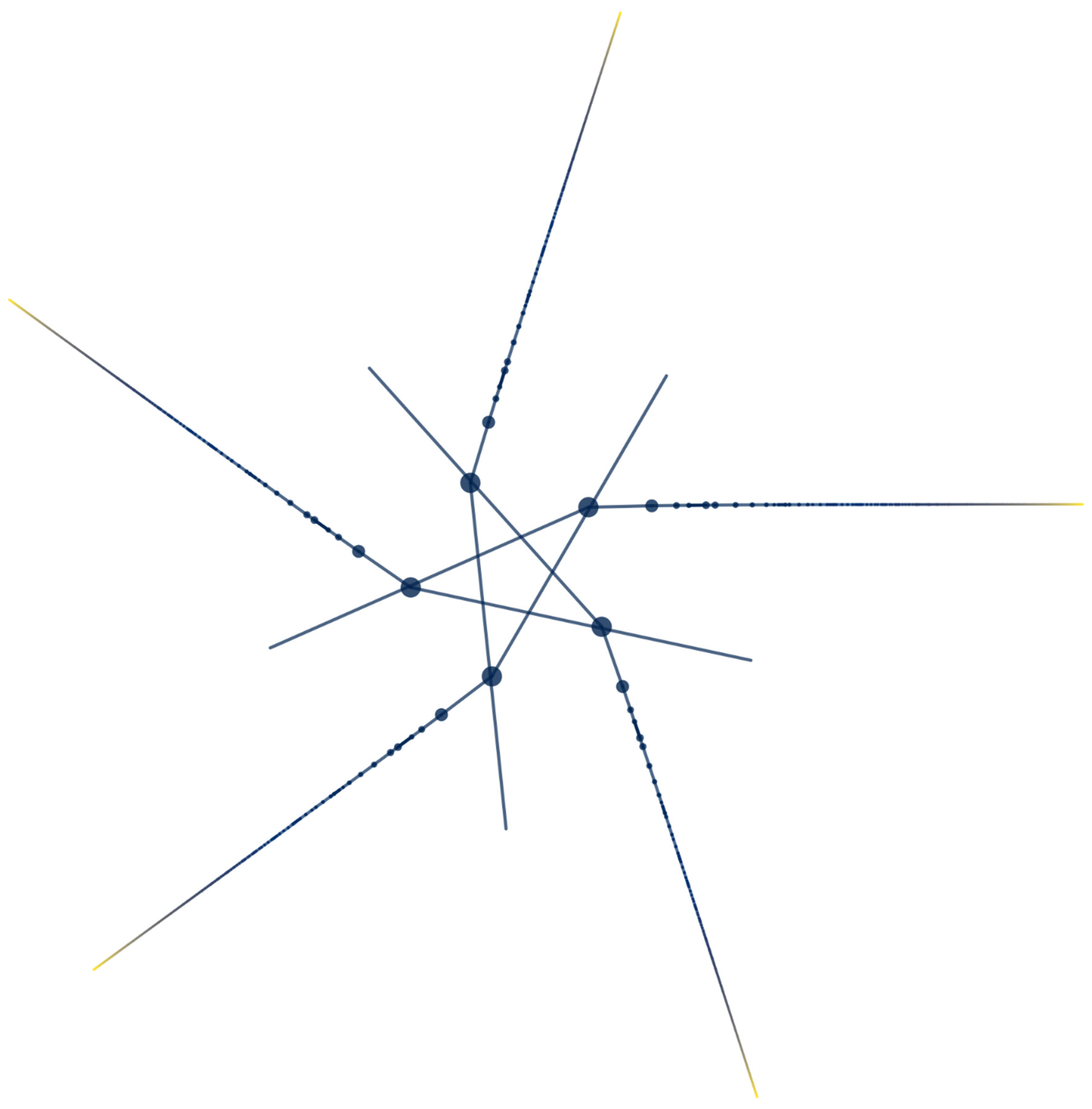
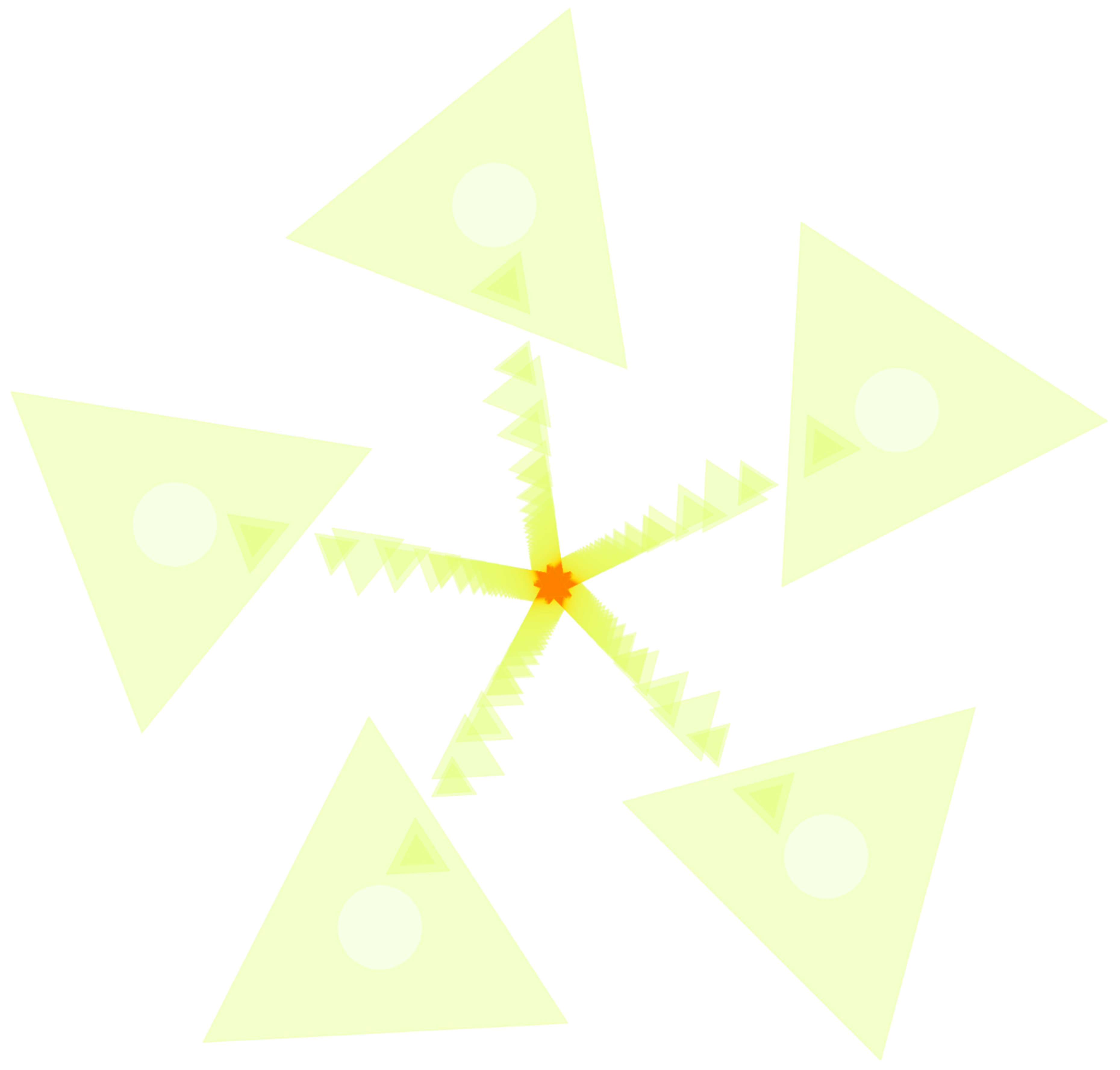
• Oresme numbers are used to model and analyze a well-defined, predictable probabilistic system.
• Keçeci numbers are used to generate a complex, unpredictable artifact whose properties are to be discovered.

This positions Keçeci numbers and similar dynamic sequences as powerful tools in generative computing, simulation (e.g., generating cave systems in games, modeling turbulence), and any field where controlled, reproducible complexity is a desirable feature [21].

5. Application Domains: Analytical Modeling versus Generative Systems

The fundamental dichotomy between static and dynamic sequences naturally leads to their application in disparate domains. Static sequences, with their predictable and analysable nature, excel in modeling and verification. Dynamic sequences, characterized by emergent complexity and unpredictability, are better suited for generation and simulation. This chapter compares the application landscapes of Oresme and Keçeci numbers, culminating in a case study on cryptography that starkly illustrates their divergent utilities.

5.1. The Application Landscape of Oresme Numbers: The Realm of Analytical Models

The primary value of Oresme numbers lies in their predictability. Because their structure is transparent and their behavior is analytically known (i.e., they diverge logarithmically), they serve as a reliable benchmark and modeling tool in fields that require deterministic analysis.

• Algorithm Analysis: In computer science, the average-case performance of certain algorithms can be modelled using the harmonic series. For example, the average number of comparisons in the Quicksort algorithm is approximately 2n ln n, a behavior closely related to the growth of Oresme numbers [22]. They provide a solid theoretical foundation for calculating expected performance.
• Physics and Engineering: Systems involving potentials that decrease with distance, such as certain electrostatic or gravitational models, can involve sums resembling the harmonic series. In reliability engineering, calculating the expected time to failure when components are replaced can also lead to similar mathematical structures.
• Probabilistic Modeling: As demonstrated with the Coupon Collector’s Problem [21], Oresme numbers provide exact, calculable answers for expected values in well-defined probabilistic systems. They are tools for understanding and quantifying randomness, not for producing it.

In all these cases, the sequence is a means to an analytical end—a tool for verification, prediction, and formal proof.

5.2. The Application Landscape of Keçeci Numbers: The Frontier of Generative Systems

Conversely, the value of Keçeci numbers stems from their unpredictability and emergent complexity. Their path-dependent, state-driven algorithm makes them ideal for applications where novelty, intricacy, and pseudo-randomness are desired features.

• Procedural Content Generation (PCG): Beyond generative art, Keçeci numbers can be used in video games to procedurally generate content like unique planetary systems, cave networks, or alien plant life. The initial parameters can act as a “seed” that generates a vast, deterministic yet unpredictable world, which can be regenerated perfectly every time with the same seed.
• Simulation and Complex Systems: The sequence can serve as a simplified model for systems where history and state matter. For example, it could simulate a simplified stock market model where a “prime” event represents a market shock, or an ecological model where divisibility represents a resource abundance leading to population growth.
• Cryptography and Security: The high sensitivity to initial conditions (the avalanche effect) and the computational difficulty of predicting the sequence without the key make it a strong candidate for cryptographic applications, particularly stream ciphers.

Here, the sequence is an end in itself—a generator of complexity and a tool for generation and simulation.

5.3. Case Study: A Comparison in Cryptography

Cryptography provides the clearest distinction between the utility of these two sequences. A core requirement for many ciphers is a pseudo-random keystream—a sequence of numbers that is deterministic (so it can be regenerated for decryption) but statistically indistinguishable from random noise to an attacker.

We will demonstrate this by producing two “toy” stream ciphers using a simple XOR operation. The security of the cipher depends entirely on the unpredictability of the keystream.

--- 1. Oresme-Based Cipher (INSECURE) ---

Oresme Keystream (first 16 bytes): 40 60 75 05 45 50 59 a1 a8 48 65 ea 65 6a d4 f8

Encrypted with Oresme (as bytes): b’\x13\x14\x14q,3y\xd7\xdbh!\x93\x0b\x0b\xb9\x91\xa3\xe4\x08\xce\xdfHv\xb8u6s\xb9\x15*M<\xb2\xa4<\xadRi\x0ea;3\\\xd5\xa2\xc0\xb9\r\xa6w\xe4\xcb\x1b\xa9′

Decrypted with Oresme: Static vs Dynamic Sequences: A Clear Winner for Crypto

>> Analysis: This is insecure because anyone can generate the exact same keystream. The ‘key’ is public and not secret.

--- 2. Keçeci-Based Cipher (POTENTIALLY SECURE) ---

Keçeci Keystream (first 16 bytes): 05 05 05 05 07 07 04 04 04 04 04 04 04 03 03 03

Encrypted with Keçeci (as bytes): b’Vqdqnd$rw$@}jbnj`#Pfrvfm`YO6$E$Gofbq#Tjmmfq#jc~<_~u\x0f\x0b`’

Decrypted with CORRECT Keçeci key: Static vs Dynamic Sequences: A Clear Winner for Crypto

Attempted Decryption with WRONG Keçeci key (as bytes): b’Static vs Dynamic Sequences: A Clear Winner for Crypto’

>> Analysis: A tiny change in the secret key generates a completely different keystream, resulting in gibberish. This demonstrates the ‘avalanche effect’, a crucial property for modern cryptography.

Code Example 5.1: A Cryptographic Comparison

import numpy as np

# Assuming ‘kececinumbers’ and ‘oresme’ are installed

# pip install kececinumbers oresme

import kececinumbers as kn

import oresme as ore

# --- Placeholder functions are no longer needed. ---

# The logic from unified_generator_with_events_placeholder and is_prime_placeholder

# is now handled internally by the ‘kececinumbers’ library.

# --- Main Cipher Functions ---

def generate_oresme_keystream(length):

“““Generates a WEAK and PREDICTABLE keystream from Oresme numbers.”““

# The oresme library directly gives us the sequence of harmonic numbers.

oresme_seq = ore.harmonic_numbers(length)

# Convert each number in the sequence to a byte.

# This process is deterministic and has no secret key.

keystream = [(int(float(o) * 1e6) % 256) for o in oresme_seq]

return bytes(keystream)

def generate_kececi_keystream(key_start, key_add, length):

“““

Generates a POTENTIALLY STRONG and key-dependent keystream from Keçeci numbers.

This uses the official ‘kn.unified_generator’.

“““

# Generate the Keçeci sequence. We use TYPE_COMPLEX for this example.

# The generator returns a list of numbers directly. No events are needed here.

kececi_seq = kn.unified_generator(kn.TYPE_COMPLEX,

start_input_raw=key_start,

add_input_base_scalar=key_add,

iterations=length) # Generate enough numbers for the message

# Filter out any non-numeric results (like None) to be safe

kececi_seq = [k for k in kececi_seq if isinstance(k, (int, float, complex))]

keystream = []

if not kececi_seq: # Handle case where sequence generation fails

return b’’

for i in range(length):

# Cycle through the kececi_seq if it’s shorter than the message

k = kececi_seq[i % len(kececi_seq)]

# Deterministically convert the complex number to a single byte

if isinstance(k, complex):

# Take the last byte of the integer parts of real and imaginary components

# and XOR them together. This is a simple, deterministic way to mix them.

val_real = int(k.real).to_bytes(8, byteorder=‘big’, signed=True)[-1]

val_imag = int(k.imag).to_bytes(8, byteorder=‘big’, signed=True)[-1]

val = val_real ^ val_imag

else: # Handle float/int case

val = int(k) % 256

keystream.append(val)

return bytes(keystream)

def xor_cipher_bytes(data_bytes, keystream_bytes):

“““Encrypts or decrypts a byte string using a keystream via XOR operation.”““

if not keystream_bytes:

raise ValueError(“Keystream cannot be empty.”)

return bytes([data_byte ^ key_byte for data_byte, key_byte in zip(data_bytes, keystream_bytes)])

# --- Demonstration ---

message_to_encrypt = “Static vs Dynamic Sequences: A Clear Winner for Crypto”

message_bytes = message_to_encrypt.encode(‘utf-8′)

msg_len = len(message_bytes)

print(“--- 1. Oresme-Based Cipher (INSECURE) ---”)

oresme_key = generate_oresme_keystream(msg_len)

print(f”Oresme Keystream (first 16 bytes): {oresme_key[:16].hex(‘ ‘)}”)

encrypted_oresme_bytes = xor_cipher_bytes(message_bytes, oresme_key)

print(f”Encrypted with Oresme (as bytes): {encrypted_oresme_bytes}”)

decrypted_oresme_bytes = xor_cipher_bytes(encrypted_oresme_bytes, oresme_key)

print(f”Decrypted with Oresme: {decrypted_oresme_bytes.decode(‘utf-8′)}”)

print(“\n>> Analysis: This is insecure because anyone can generate the exact same keystream. The ‘key’ is public and not secret.”)

print(“\n--- 2. Keçeci-Based Cipher (POTENTIALLY SECURE) ---”)

# The secret keys are the initial parameters for the generator

SECRET_KEY_START = “1.23+4.56j”

SECRET_KEY_ADD = 7.89

kececi_key = generate_kececi_keystream(SECRET_KEY_START, SECRET_KEY_ADD, msg_len)

print(f”Keçeci Keystream (first 16 bytes): {kececi_key[:16].hex(‘ ‘)}”)

encrypted_kececi_bytes = xor_cipher_bytes(message_bytes, kececi_key)

print(f”Encrypted with Keçeci (as bytes): {encrypted_kececi_bytes}”)

# A) Decryption with the CORRECT key

decrypted_kececi_correct_bytes = xor_cipher_bytes(encrypted_kececi_bytes, kececi_key)

print(f”\nDecrypted with CORRECT Keçeci key: {decrypted_kececi_correct_bytes.decode(‘utf-8′)}”)

# B) Decryption attempt with a SLIGHTLY ALTERED key

WRONG_KEY_START = “1.23+4.57j” # A tiny change in the imaginary part

wrong_kececi_key = generate_kececi_keystream(WRONG_KEY_START, SECRET_KEY_ADD, msg_len)

decrypted_kececi_wrong_bytes = xor_cipher_bytes(encrypted_kececi_bytes, wrong_kececi_key)

print(f”Attempted Decryption with WRONG Keçeci key (as bytes): {decrypted_kececi_wrong_bytes}”)

print(“\n>> Analysis: A tiny change in the secret key generates a completely different keystream, resulting in gibberish. This demonstrates the ‘avalanche effect’, a crucial property for modern cryptography.”)

Listing 4: A Cryptographic Comparison

Conclusion of the Case Study

The cryptographic example provides an unequivocal verdict.

• Oresme numbers are fundamentally unsuitable for cryptographic applications because their predictability is a critical vulnerability. Security through obscurity (hiding the algorithm) is not real security; the generating principle must be public, and the security must reside only in the key. Oresme numbers have no “key.”
• Keçeci numbers are conceptually well-suited for cryptography. Security resides in the initial parameters (the key), which are kept secret. The algorithm itself can be public. The complex, state-dependent nature of the sequence makes it computationally difficult to reverse-engineer the key from the output, and the avalanche effect ensures that key guessing is ineffective. While this “toy” cipher is not intended for real-world use, it demonstrates that dynamic, state-dependent sequences possess the foundational properties required for building secure cryptographic primitives [23].

Figure 8. Analytical Comparison Oresme vs. Keçeci Numbers.

Figure 8. Analytical Comparison Oresme vs. Keçeci Numbers.

Figure 8. Artistic Interpretation: The Dance of Oresme and Keçeci Numbers.

Figure 8. Artistic Interpretation: The Dance of Oresme and Keçeci Numbers.

Table 2. Oresme Numbers (Static) and Keçeci Numbers (Dynamic).

Application Domain	Oresme Numbers (Static)	Keçeci Numbers (Dynamic)
Core Strength	Predictability, Analytical Tractability	Unpredictability, Emergent Complexity
Primary Use	Modeling & Analysis	Generation & Simulation
Examples	Algorithm performance analysis, probabilistic expectation, physics models.	Generative art, procedural content (games), cryptographic keystreams.
Role	A tool to understand a system.	A tool to generate a system.

Table 2. Oresme Numbers (Static) and Keçeci Numbers (Dynamic).

Application Domain	Oresme Numbers (Static)	Keçeci Numbers (Dynamic)
Core Strength	Predictability, Analytical Tractability	Unpredictability, Emergent Complexity
Primary Use	Modeling & Analysis	Generation & Simulation
Examples	Algorithm performance analysis, probabilistic expectation, physics models.	Generative art, procedural content (games), cryptographic keystreams.
Role	A tool to understand a system.	A tool to generate a system.

6. Interdisciplinary Horizons and Future Perspectives

The distinction between static and dynamic number sequences is not merely a mathematical curiosity; it represents a fundamental philosophical and practical divide that resonates across multiple scientific disciplines. As we look to the future, the potential applications of Oresme and Keçeci numbers extend far beyond their initial domains, suggesting novel syntheses in fields ranging from quantum physics to data visualization and artificial intelligence. This chapter explores these future interdisciplinary perspectives, framing the two sequences as complementary tools for navigating the landscapes of modern science.

6.1. Oresme Numbers: The Foundation of Analytical Certainty

The future utility of Oresme numbers lies in their unwavering role as a benchmark of analytical certainty and predictable growth. In an age increasingly dominated by complex, often opaque algorithms, the transparency of the harmonic series provides an essential touchstone.

• Algorithmic Benchmarking: As machine learning and AI models become more complex, verifying their resource consumption (e.g., computational steps, memory access) becomes critical. The predictable, slow-growing nature of Oresme numbers can serve as a “lower bound” or a simple complexity class (O(nlogn)) against which more sophisticated algorithms are measured [22]. They represent a baseline of well-understood, non-chaotic behavior.
• Physics and Information Theory: In statistical mechanics and information theory, concepts like entropy often involve logarithmic functions, echoing the behavior of Oresme numbers. They provide a stable, analytical framework for modeling systems where information accumulates predictably or where phase space expands in a well-ordered manner.
• Economic and Social Modeling: In models of fair division or resource allocation (e.g., the “last-diminisher” method), sums resembling the harmonic series can appear. Their role is to provide a provably fair, if idealized, basis for models that require transparent and justifiable rules.

The future of Oresme numbers is not in generating novelty, but in providing the unshakable ground truth upon which novel, more complex systems can be built and evaluated.

6.2. Keçeci Numbers: A Bridge Between Number Theory, Quantum Physics, and Generative Systems

The future of Keçeci numbers is far more speculative and exciting, lying at the intersection of number theory, computational science, and fundamental physics. Their dynamic, state-dependent nature mirrors the complex, emergent behaviours observed in quantum and topological systems. The extensive body of work by Keçeci in seemingly disparate fields provides a roadmap for this synthesis.

• Modeling Topological Matter and Quantum States: Materials like Weyl semimetals and nodal-line semimetals are defined by the unique, topologically protected behavior of their electrons [24,25,26,27,28,29,48,72,73]. The trajectory of a Keçeci number sequence, with its path-dependent “choices” and sudden shifts dictated by number-theoretic properties, offers a compelling abstract model for the path of a quantum particle navigating a complex energy landscape. The “ASK” event, triggered by primality, could be analogous to a quantum particle encountering a topological defect, forcing it into a new state. This conceptual link suggests Keçeci numbers could be used to generate simplified, discrete toy models for simulating quantum transport in these exotic materials, which are themselves candidates for building robust quantum computers [28,29].
• Generative Frameworks for Complex Data Visualization: The Keçeci Layout is proposed as a method for visualizing structured systems in a deterministic, order-preserving way [30,31,32,50,51,52,53,64]. A Keçeci number sequence could serve as the “engine” for this layout. For instance, the sequence could generate coordinates for nodes in a graph, with the algorithm’s state (e.g., last divisor, ASK trigger) determining the connections or clustering. This would generate visualizations that are not merely aesthetically pleasing but whose structure is a direct reflection of underlying number-theoretic properties, potentially revealing hidden patterns in complex datasets. The Keçeci Zigzag Layout [33] and Keçeci’s Arithmetical Square [34] could similarly be powered by the stateful progression of a Keçeci number sequence.
• Procedural Generation of Fractal and Complex Geometries: Keçeci’s work on Keçeci Fractals [35,36] explores scalable complexity. A dynamic number sequence is a natural engine for generating such structures. Instead of using a fixed iterative formula (like in the Mandelbrot set), a Keçeci fractal could progression based on the sequence’s algorithmic path. A division by 3 might correspond to a right turn, a division by 2 to a left turn, and an ASK event to a change in scale or color. This would produce fractals that are not perfectly self-similar but exhibit a more organic, “mutating” complexity.
• Synergies with Quantum Computing and AI: The path to scalable quantum computing is fraught with challenges in error correction and noise management [37,38,39]. Keçeci numbers, as a source of controllable yet complex pseudo-randomness, could be explored in developing novel testbeds for quantum error correction codes [40]. Their sensitivity to initial conditions could be used to generate a wide variety of “noise profiles” to test the robustness of quantum algorithms. Furthermore, the integration of AI with quantum algorithms [41] requires new ways of thinking about structured complexity, a domain where Keçeci numbers and their associated layouts could provide a new conceptual framework.

In essence, Keçeci’s diverse research interests—from quantum materials to visualization—are not separate silos. They can be unified by a common thread: the search for systems that generate structured, emergent complexity from simple rules. The Keçeci number sequence [42] is the most fundamental expression of this search, acting as a potential “source code” for these other, more applied concepts. The future perspective is one of integration, where Keçeci numbers are not just a sequence, but a generative engine for exploring new frontiers in physics, computation, and art.

7. Conclusions

This study embarked on an exploration of the fundamental dichotomy between static and dynamic number sequences, using the classical Oresme numbers and the novel, algorithmically-defined Keçeci numbers as contrasting exemplars. By moving beyond mere mathematical definitions, we have traced their historical change, compared their computational behavior, and analysed their divergent application domains. The investigation has consistently reinforced a central thesis: the distinction between static and dynamic is not just a matter of classification but represents two deeply different paradigms of mathematical and scientific inquiry—one rooted in analytical prediction and the other in generative discovery.

Our journey began with a historical perspective, situating Oresme’s counter-intuitive discovery of divergence within a long tradition of predictable, rule-bound sequences, and positioning Keçeci numbers as a contemporary culmination of the shift towards state-dependent, algorithmic thinking. The direct comparison and computational implementation underscored this divide. The Oresme numbers produced a smooth, predictable, and analytically tractable trajectory, confirming their static nature. In stark contrast, Keçeci numbers, whether in integer, complex, or other forms, exhibited jagged, pseudo-random, and path-dependent behavior, producing visually complex artifacts whose progression could only be understood through simulation.

This inherent difference in nature dictates their utility. We have shown that Oresme numbers excel as tools for analytical modeling, providing a bedrock of certainty for calculating expected values in probability, benchmarking algorithm complexity, and teaching the foundational principles of calculus. Their value lies in their transparency and predictability. Conversely, Keçeci numbers thrive as engines of generative systems. Their emergent complexity and sensitivity to initial conditions make them conceptually ideal for applications in procedural content generation, generative art, and, as demonstrated in our cryptographic case study, the generation of pseudo-random keystreams. The case study unequivocally showed that the predictability of Oresme numbers is a cryptographic vulnerability, while the state-dependent unpredictability of Keçeci numbers provides the conceptual foundation required for security.

Looking forward, the interdisciplinary potential [47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63] of these paradigms is vast. While static sequences will continue to provide the essential, verifiable frameworks for science, the future of exploration in complex fields like quantum computing, artificial intelligence, and topological physics may increasingly rely on the generative, exploratory power of dynamic systems. Keçeci numbers, with their intrinsic links to number theory and their potential to model emergent phenomena, stand as a compelling example of this new frontier. Ultimately, this study posits that the future of mathematical and scientific discovery lies not in choosing one paradigm over the other, but in understanding their complementary strengths and generatively harnessing both the predictable order of the static and the emergent complexity of the dynamic.