Submitted:
25 March 2025
Posted:
26 March 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
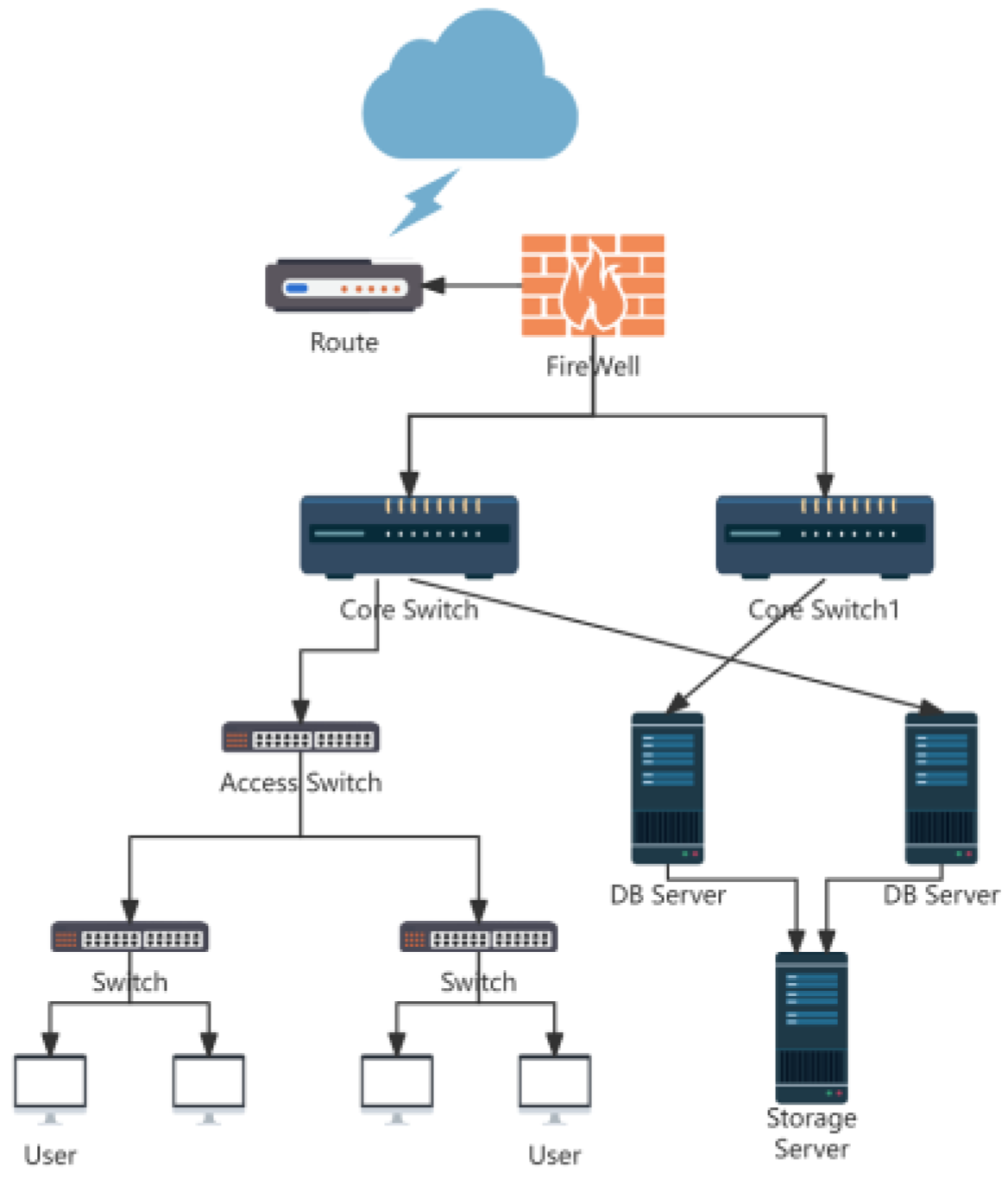
2. Materials and Methods
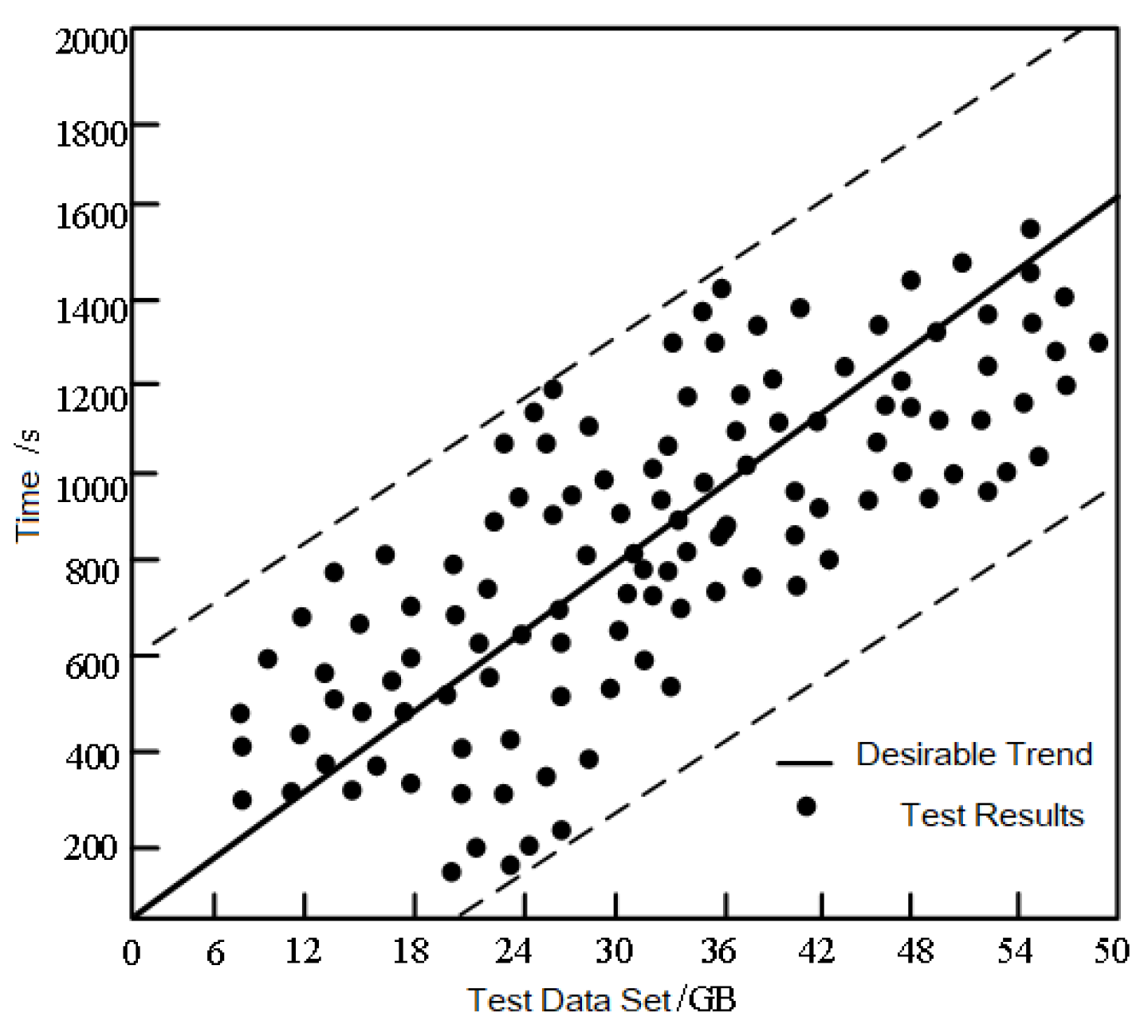
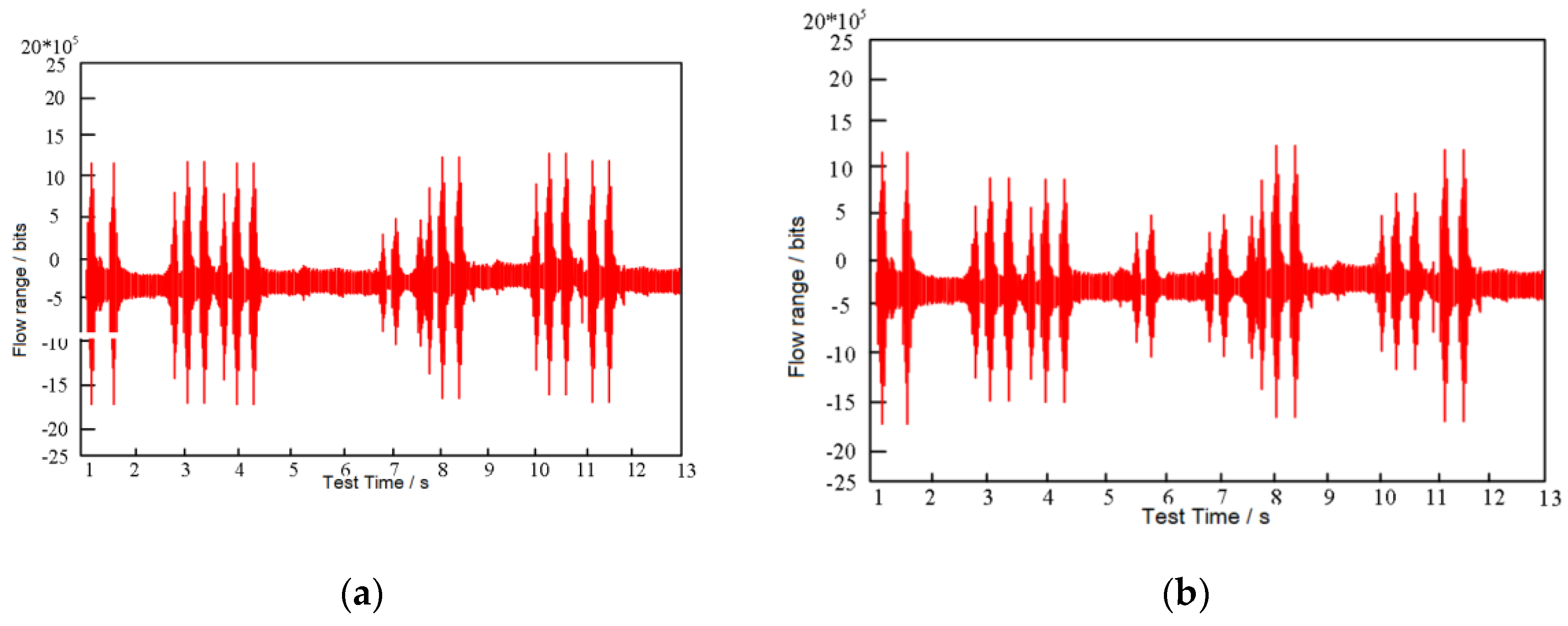
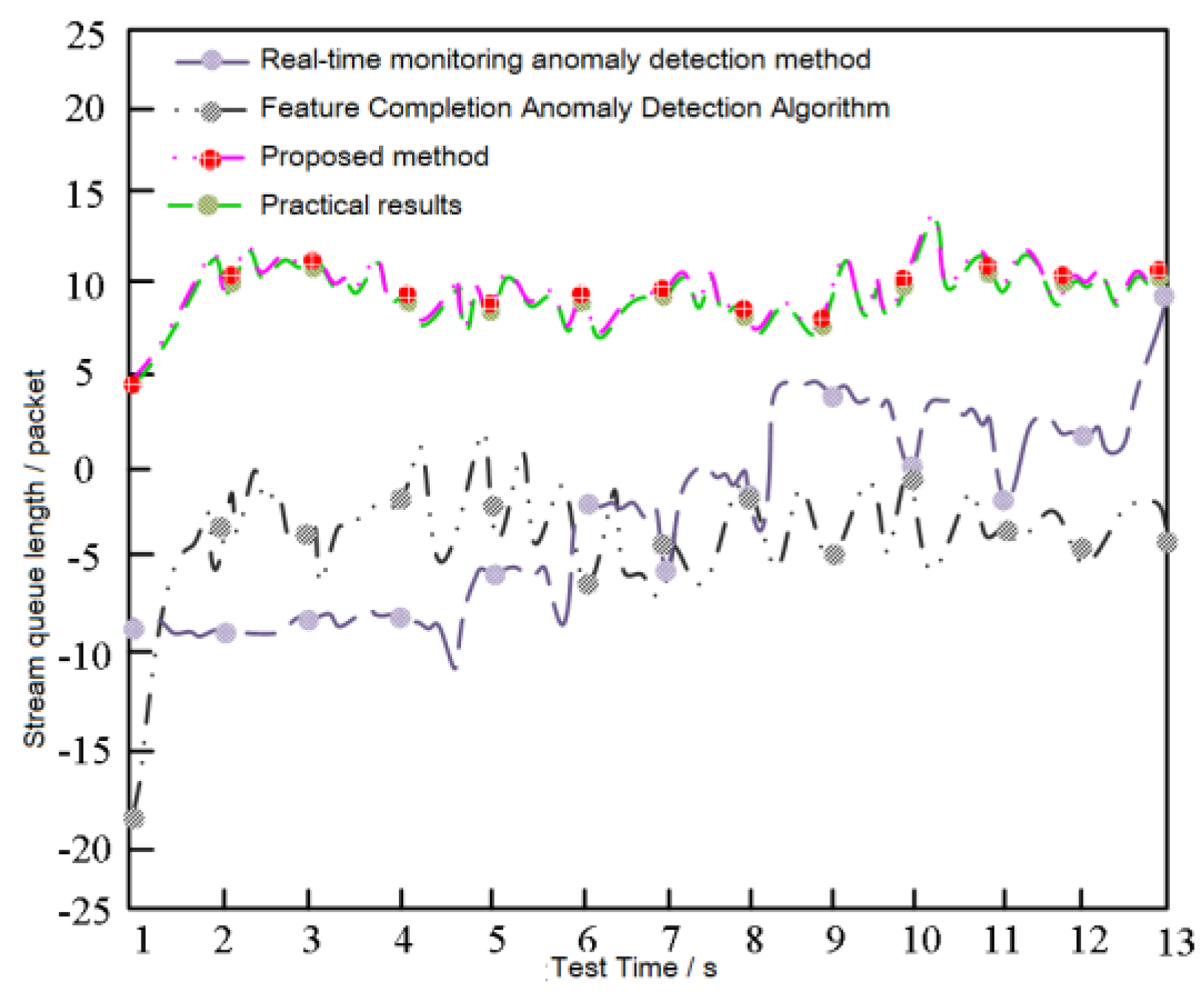
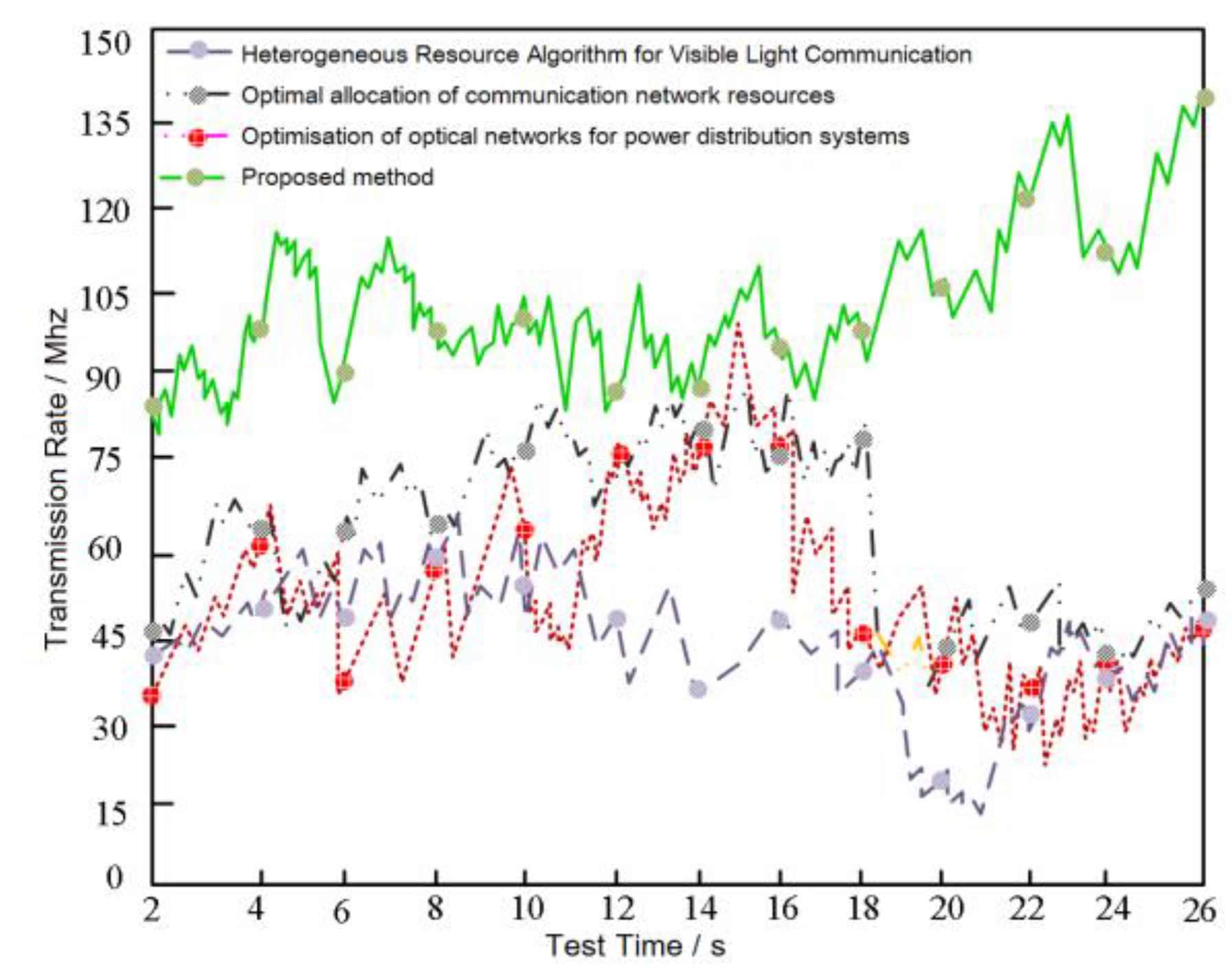
3. Results
3.1. Experimental Environment
4. Discussion
5. Conclusions
6. Patents
- (1)
- Natural Science Foundation of Fujian Province, grant number 2023J011807
- (2)
- Natural Science Foundation of Fujian Province, grant number 2023J011800
- (3)
- Educational Research Programme for Young and Middle-aged Teachers in Fujian Province,grant number:JAT210557
References
- Maged, A.; Zwetsloot, I. Anomaly Detection via Real-Time Monitoring of High-Dimensional Event Data. IEEE Trans. Ind. Informatics 2023, 20, 2856–2864. [CrossRef]
- Zheng Junhua, Wei JinHong. Anomaly Data Flow Detection in Wireless Sensor Networks Based on Feature Completion [J]. Chinese Journal of Sensors and Actuators, 2024, 37 (06): 1061-1066.
- Zhang Lei, Peng Fei, Cao Zining, et al. Data Flow Soft Error Detection Algorithm Based on SIMD Vectorization [J]. Journal of Chinese Computer Systems, 2023, 44 (05): 1114-1120.
- Gao R , Wei X S , Chen A D W .Leveraging DNA-Based Nanostructures for Advanced Error Detection and Correction in Data Communication[J].ACS nano, 2023, 17(18):18055-18061.
- Wei Debin, Pan Chengsheng, Yang Li, et al. Adaptive Random Early Detection Algorithm Based on Network Traffic Level Prediction [J]. Journal of Communications, 2023, 44 (06): 154-166.
- Yin Xiaokang, Lu Bin, Cai Ruijie, et al. Memory Copy Function Identification Technique with Control Flow and Data Flow Analysis [J]. Journal of Computer Research and Development, 2023, 60 (02): 326-340.
- Huang Fenglan, Ni Feng, Liu Jiang, et al. Data flow modeling and verification of complex BPMN collaboration models based on HCPN [J]. Computer Integrated Manufacturing Systems, 2024, 30 (05): 1754-1769.
- Gong Xiaoxing, Dong Peixin. A Traffic Flow Anomaly Data Detection Model Based on Improved Isolation Forest Algorithm [J]. Journal of Chongqing Jiaotong University (Natural Science Edition), 2024, 43 (05): 61-69+90.
- An T , Yan P , Zuo J ,et al. Enhancing Cross-Lingual Sarcasm Detection by a Prompt Learning Framework with Data Augmentation and Contrastive Learning[J].electronics,2024,13(11):2163.
- Schultz V , Hedderich D M , Schmitz-Koep B ,et al. Removing outliers from the normative database improves regional atrophy detection in single-subject voxel-based morphometry[J].Neuroradiology,2024,66(4):507-519.
- Su Xiangjing, Deng Chao, Li Fengyong, et al. Interpretable Detection Method for False Data Injection Attack on Power Grid Based on Multi-head Graph Attention Network and Time Convolution Network Model [J]. Automation of Electric Power Systems, 2024, 48 (02): 118-127.
- Chen M , Hu Y . An image-based runway detection method for fixed-wing aircraft based on deep neural network[J].IET image processing,2024,18(8):1939-1949.
- Wang Dewen, Pan Xiaofei, Zhao Hongbo. Temporal Data Anomaly Detection Based on Improved Generative Adversarial Networks [J]. Computer Engineering and Design, 2024, 45 (03): 762-768.
- Jiang Z , Zhou C . Age detection by optimizing the structure of layers and neurons in the neural network[J].Journal of optics,2024,53(2):1186-1202.
- Wang Shaorong, Huang Weichun, Zong Bo. Defect Dynamic Feature Classification Algorithm Based on Manifold Learning Dimensionality Reduction[J]. Computer Simulation,2023,40(11):475-479.
- Chen Weitong, Xu Xin, Zhu Changqing, et al. Copyright protection algorithm for remote sensing object detection dataset based on backdoor watermarking and region of interest encryption [J]. Acta Geodaetica et Cartographica Sinica, 2024, 53 (11): 2086-2098.
- Miyazaki, K.; Ida, M. Performance evaluation of character-level CNNs using tweet data and analysis for weight perturbations. Artif. Life Robot. 2024, 29, 266–273. [CrossRef]
- Liu Y , Xu J , Yee A L . The analysis of Iris image acquisition and real-time detection system using convolutional neural network[J].Journal of supercomputing,2024,80(4):4500-4532.
- Xu Tianhui, Guo Qiang, Zhang Caiming. A serial autoencoders based method for detecting time series anomalies [J]. Control and Decision, 2023, 38 (12): 3507-3515.
- Drner S , Clausius J , Brink C S T .Learning Joint Detection, Equalization and Decoding for Short-Packet Communications[J].IEEE Transactions on Communications, 2023, 71(2):837-850.
- Guan, S.; He, Z.; Ma, S.; Gao, M. Multivariate time series anomaly detection with variational autoencoder and spatial–temporal graph network. Comput. Secur. 2024, 142. [CrossRef]
- Gensler, A.; Sick, B. Performing event detection in time series with SwiftEvent: an algorithm with supervised learning of detection criteria. Pattern Anal. Appl. 2017, 21, 543–562. [CrossRef]
- Zhang S, Zhou C, Zhang P, et al. Multiple hypothesis testing for anomaly detection in multi-type event sequences[C]//2023 IEEE International Conference on Data Mining (ICDM). IEEE, 2023: 808-817.
- Yang G, Kulkarni N, Dua P, et al. Anomaly detection for spatiotemporal data in action[C]//Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining. 2022: 4844-4845.
- Hassan E, Shroff G, Agarwal P. Multi-sensor event detection using shape histograms[C]//Proceedings of the 2nd ACM IKDD Conference on Data Sciences. 2015: 20-29.
- Nguyen H V, Vreeken J. Linear-time detection of non-linear changes in massively high dimensional time series[C]//Proceedings of the 2016 SIAM International Conference on Data Mining. Society for Industrial and Applied Mathematics, 2016: 828-836.
- Xiao, X.; Chen, P.; Ye, Z.; Tsui, K.-L. On computing multiple change points for the gamma distribution. J. Qual. Technol. 2020, 53, 267–288. [CrossRef]
- Yamin K, Wang H, Montreuil B, Xie Y. Online detection of supply chain network disruptions using sequential change-point detection for Hawkes processes. arXiv preprint arXiv:2211.12091. 2022 Nov 22.
- Cao, Y.; Xie, L.; Xie, Y.; Xu, H. Sequential Change-Point Detection via Online Convex Optimization. Entropy 2018, 20, 108. [CrossRef]
- Leland WE, Taqqu MS, Willinger W, Wilson DV. On the self-similar nature of Ethernet traffic. InConference proceedings on Communications architectures, protocols and applications 1993 Oct 1 (pp. 183-193).
- Roquer T, Arancibia G, Crempien JG, Mery D, Rowland J, Sepúlveda J, Veloso EE, Nehler M, Bracke R, Morata D. Multi-scale flow structure of a strike-slip tectonic setting: A self-similar model for the Liquiñe-Ofqui Fault System and the Andean Transverse Faults, Southern Andes (39–40° S). Geothermics. 2022 Jul 1;103:102424.
- Uritsky, V.M.; Karpen, J.T.; Raouafi, N.E.; Kumar, P.; DeVore, C.R.; Deforest, C.E. Self-similar Outflows at the Source of the Fast Solar Wind: A Smoking Gun of Multiscale Impulsive Reconnection?. Astrophys. J. 2023, 955, L38. [CrossRef]
- Coluccio, M.L.; Gentile, F.; Das, G.; Nicastri, A.; Perri, A.M.; Candeloro, P.; Perozziello, G.; Zaccaria, R.P.; Gongora, J.S.T.; Alrasheed, S.; et al. Detection of single amino acid mutation in human breast cancer by disordered plasmonic self-similar chain. Sci. Adv. 2015, 1, e1500487. [CrossRef]
- Karimov, A.; Babkin, I.; Rybin, V.; Butusov, D. Matryoshka multistability: Coexistence of an infinite number of exactly self-similar nested attractors in a fractal phase space. Chaos, Solitons Fractals 2024, 187. [CrossRef]
- Anjos, P.H.A.; Zhao, M.; Lowengrub, J.; Li, S. Electrically controlled self-similar evolution of viscous fingering patterns. Phys. Rev. Fluids 2022, 7, 053903. [CrossRef]
- Sadegh, S.; Higgins, J.L.; Mannion, P.C.; Tamkun, M.M.; Krapf, D. Plasma Membrane is Compartmentalized by a Self-Similar Cortical Actin Meshwork. Phys. Rev. X 2017, 7, 011031. [CrossRef]
- Han, C.; Xiong, W.; Yu, R. A Hybrid Forecasting Model for Self-Similar Traffic in LEO Mega-Constellation Networks. Aerospace 2024, 11, 191. [CrossRef]
- Trabes, E.; Jordan, M.A. A Node-Based Method for SLAM Navigation in Self-Similar Underwater Environments: A Case Study. Robotics 2017, 6, 29. [CrossRef]
- Expert, P.; Lambiotte, R.; Chialvo, D.R.; Christensen, K.; Jensen, H.J.; Sharp, D.J.; Turkheimer, F. Self-similar correlation function in brain resting-state functional magnetic resonance imaging. J. R. Soc. Interface 2010, 8, 472–479. [CrossRef]
- Mahdavi, H.; Poulios, K.; Niordson, C.F. A Pragmatic Approach for the Evaluation of Depth-Sensing Indentation in the Self-Similar Regime. J. Appl. Mech. 2021, 89, 1–24. [CrossRef]
| Item | Parameter |
| Transmission Rate | 1000Mbps |
| Frequency bandwidth | 100MHz |
| Attenuation Coefficient | 22dB |
| Frequency Response | ±300dB |
| Baud rate | 0*0001 words |
| Communication channel byte number | 2316bytes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





