Empirical Verification of Goldbach’s Conjecture Beyond Four Quintillion

1. Introduction

Goldbach’s Conjecture, stated by the mathematician Christian Goldbach in 1742, states that every even integer greater than two can be expressed as a sum of prime numbers. While computational efforts have been made to verify the conjecture up to 4 × 10¹⁸, extending this boundary further will be of immense help to provide empirical support of its being true. With the ranges being increased further, there are fewer chances that a counterexample exists and would further instill confidence in the conjecture’s validity. By testing these ranges, we contribute empirical insights into the conjecture’s robustness and behaviour of primes in these extreme numerical ranges.

2. Historical Background

There have been several attempts to try and show that Goldbach’s conjecture holds for all even integers less than 4 × 10¹⁸. Primality testing is done to determine whether a number is prime or not. Initially, a brute force method was used in the late 19th century and early 20th century. In 1973, the Chinese mathematician Chen Jingrun came up with Chen’s theorem, which states that every sufficiently large even prime number can be written as the sum of either two primes or a prime and a semiprime (a number that is the product of two primes). Chen's theorem was even regarded as the weakened form of Goldbach's conjecture. In the early 2000s, developments led to computing being introduced to help prove it, which led to the use of the segmented Sieve of Eratosthenes. The segmented sieve is a modified version of the original sieve, which can’t be implemented due to the memory constraints of computers, which proposes that we compute prime numbers within a specified range. These approaches used parallel computing, and first, it was proven until 4 × 10¹⁴ and then further computational calculations advanced it to 4 × 10¹⁸. This paper extends the previous computational studies by verifying the Goldbach Conjecture for even integers beyond 4 × 10¹⁸ and explores the behaviour of prime sums in this range.

3. Material and Methods

3.1. Research Question

Does the Goldbach Conjecture hold for even numbers between 4 × 10¹⁸ and 5 × 10¹⁸ using probabilistic primality testing and trial division?

3.2. Computational Techniques

Our work is based on various existing and verified computational techniques:

1. 

Trial Division

Trial division up to √n was used for the smaller range of primes.

2. 

Miller-Rabin Test

A probabilistic primality test with five iterations to minimise false positives.

3. 

Cross Verification

All primes were cross-verified using Factordb.

3.3. Experimentation and Further Exploration

While experimenting on different even numbers after 4 × 10¹⁸, we tried to find two prime numbers which would add up to even integers which are slightly higher than 4 × 10¹⁸. We found that

4,000,000,000,000,000,002 = 211 + 3,999,999,999,999,999,791

4,000,000,000,000,000,004 = 313 + 3,999,999,999,999,999,691

4,000,000,000,000,000,008 = 317+ 3,999,999,999,999,999,691

4,000,000,000,000,000,012 = 251 + 3,999,999,999,999,999,761

4,000,000,000,000,000,016 = 1213 +3,999,999,999,999,998,803

4,000,000,000,000,000,020 = 137 + 3,999,999,999,999,999,883

4,000,000,000,000,000,024 = 137 + 3,999,999,999,999,999,887

4,000,000,000,000,000,028 = 337 + 3,999,999,999,999,999,691

4,000,000,000,000,000,032 = 149 + 3,999,999,999,999,999,883

4,000,000,000,000,000,036 = 149 + 3,999,999,999,999,999,887

4,000,000,000,000,000,040 = 3 + 4,000,000,000,000,000,037

We further tried testing for a few numbers in the 5 × 10¹⁸ range and found some similar results, just like the previous range.

50000000000000000004 = 41 + 4,999,999,999,999,999,963

50000000000000000008 = 5 + 5,000,000,000,000,000,003

50000000000000000012 = 229 + 4,999,999,999,999,999,783

50000000000000000016 = 13 + 5,000,000,000,000,000,003

50000000000000000020 = 17 + 5,000,000,000,000,000,003

50000000000000000024 = 61 + 4,999,999,999,999,999,963

50000000000000000028 = 139 + 4,999,999,999,999,999,889

50000000000000000032 = 29 + 5,000,000,000,000,000,003

50000000000000000036 = 73 + 4,999,999,999,999,999,963

50000000000000000040 = 37 + 5,000,000,000,000,000,003

Lastly, we even verified it for the 6 x 10¹⁸ range and found that the conjecture does hold true for this range too.

6000000000000000000 = 23 + 5999999999999999977

6000000000000000004 = 41 + 5999999999999999963

6000000000000000008 = 31 + 5999999999999999977

6000000000000000012 = 199 + 5999999999999999813

6000000000000000016 = 53 + 5999999999999999963

6000000000000000020 = 43 + 5999999999999999977

6000000000000000024 = 47 + 5999999999999999977

6000000000000000028 = 5 + 6000000000000000023

6000000000000000032 = 349 + 5999999999999999683

6000000000000000036 = 13 + 6000000000000000023

6000000000000000040 = 3 + 6000000000000000037

To ensure consistency, we compared the outputs with known datasets (factordb).

3.4. Formal Proof for a Particular Number

Let N = 4,000,000,000,000,000,002 so there exists some prime numbers p₁ + p₂which equals N here p₁= 3,999,999,999,999,999,791 and p₂= 211.

We further tested the primality of 211 by a few methods:

Trial division up to √211, and no factors were found.

6k + 1 form: 211 satisfies this condition where k=35

Using Miller-rabin and Fermat Tests also showed that this number is prime

Primality of 3,999,999,999,999,999,791

It can be expressed in the form of 6k + 1, where k= 666,666,666,666,632

Trial division also confirms the absence of small divisors.

4. Connection with Cramer’s Conjecture

4.1. Cramer’s Conjecture

The cramer’s conjecture states that the difference between the nth and (n+1)-th prime numbers, denoted as p_n+1−p_n, is asymptotically bounded by the square of the logarithm of p_n​:

This bound helps give an upper limit on the gaps between consecutive prime numbers and serves as a theoretical framework to analyse these gaps at large scales.

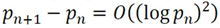
4.2. Prime Gaps Analysis

We analysed a dataset containing prime gaps in extremely large numerical ranges, ranging from primes near the range of 4 × 10¹⁸ and beyond. The data included actual prime gaps, expected gaps and the deviation.

4.3. Findings

4.3.1. General consistency

The majority of the prime gaps lie within the expected bound $(logp{)}^2$ according to Cramer's conjecture. This is also following the previous studies done regarding this.

4.3.2. Local Clustering

Some gaps are significantly smaller than expected, showing local clustering of primes. This might indicate that there is a possibility that primes don’t always spread out evenly but tend to form denser regions.

4.3.3. Lack of Extreme Deviations

No instances were found where prime gaps drastically exceeded the bound suggested by Cramer’s conjecture. This also shows that Cramer's conjecture is valid at such extreme numerical ranges.

5. Results

Our results prove that this conjecture holds even after 4 × 10¹⁸ numbers, which are slightly bigger than this. Furthermore, we even show that this holds for the initial set of even integers in the range 5 × 10¹⁸. The prime gaps observed are consistent with expected distributions at such scales. The smaller primes ranged between 3 and 1,213, while the larger primes fell within N-10⁶.

6. Discussion

While our experiment results support that Goldbach’s conjecture is valid beyond 4 × 10¹⁸, we had several limitations:

Computational Constraints: Due to the limitation of computer resources, exhaustive techniques like the segmented Sieve of Eratosthenes or Monte Carlo simulation or other exhaustive approaches, including ones carried out using parallel computing by previous works, weren’t possible.

Theoretical Insights: This study primarily focuses on empirical verification rather than theoretical advancement. However, these findings may inspire new mathematical insights regarding prime distributions in such high numerical ranges.

Novelty: It is an extension of the empirical verification rather than a theoretical insight. Our work doesn't propose a new algorithm or a breakthrough in the existing approaches. However, this can be considered as an additional piece of evidence in support of Goldbach's conjecture.

7. Future Work

We propose to extend the verification to 10¹⁸ using parallel computing and reaching to potential researchers and organisations which might have such computing power. Furthermore, we want to highlight that there is a need to explore the correlation between prime pairs and the density of valid Goldbach partitions.