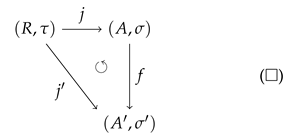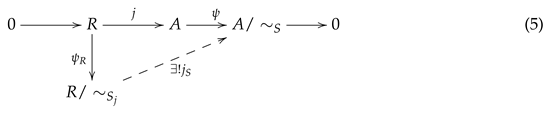On Non Commutative Multirings with Involutions

1. Introduction

Multialgebraic structures are ”algebraic-like” structures endowed with multiple valued operations. The definition and the study of the concept of multigroup started in the 1930s; in the 1950s, the commutative hyperrings were introduced. Since then, research on these (multi)structures and a broad amount of applications have been developed.

There are many instances of (multi-)algebraic structures codifying the nature of mathematical objects using operations, we remember some basic examples and provide others considering the non-commutative case.

Also, the exploration of this subject remains open compared to the classical case. The natural maturity of the subject provided us with polynomials [3], linear algebra [4], and orderings [5].

The main purpose of the present work is to provide the fundamental steps to expand Marshall’s seminal paper [2] to the context of non-commutative multirings with involutions: this concerns mainly in provide and study the expansion of the notion of “Mashall’s quotient” (see [1]), since it is a fundamental construction in abstract notions of real algebra and real algebraic geometry (space of signs [6]; abstract real spectra [7]; real semigroups [8]; real reduced multirings [2]). Building over this basis, a future work will be devoted to developing a “real spectra” for non-commutative rings with involutions, a preparation to establish an abstract theory of hermitian forms ([9]).

Considering this context, we introduce the notion of Marshall’s quotient available for involutive (non-commutative) multirings and discuss some applications to quaternion algebras over formally real fields. The main technical results obtained are Theorems 4.11, 4.14, and 4.16. To illustrate an application, in Section 5 we provide the:

Theorem 1.1

(5.4). Let R be a commutative ring and A be a R-algebra with involution σ. Denote

$$Orth\left(A\right):=\{a\in A:a\sigma (a)=\sigma (a)a=1\}.$$

If $Orth\left(A\right)\subseteq Z\left(A\right)$, then $A{/}_{m}Orth\left(A\right)$ is a (non-commutative) hyperring.

Outline:

In Section 2, we provide a brief introduction to multi/super-structures relevant to this work. We offer a non-standard example that extends Krasner’s hyperfield and the signal hyperfield in Example 2.5. In Section 3, the basic objects of the theory of (non-commutative) multirings with Involution are introduced and, the reader is invited to compare this subject theory with the classical theory. Besides, we treat various constructions and examples such as multigroups, products, and matrices. In Section 4, we define Marshall’s quotient on involutive multialgebras and analyze conditions for their existence using some ”coherent” approach. Theorem 4.11 presents two types of quotients characterized by certain multiplicative subsets. Nevertheless, many relations can be considered in taking classes in the quotient, we deal with four different possibilities and show how they are similar (Lemma 4.6). Moreover, in developing some particular examples, we verify the independence between the conditions in 4.11. Besides, the available quotient accommodates a ”concrete” path encoding several types. We finish the work in Section 5, which deals with some applications and connects examples of quotients that generate well-known multi-structures.

2. Multi-Structures

We reserve this section to bring a brief background on multi-structures for the reader and establish notations.

Definition 2.1

(Adapted from Definition 1.1 in [2]). A multigroup is a first-order structure $(G,·,r,1)$ where G is a non-empty set, $r:G\to G$ is a function, 1 is an element of G, $·\subseteq G\times G\times G$ is a ternary relation (that will play the role of binary multioperation, we denote $d\in a·b$ for $(a,b,d)\in ·$) such that for all $a,b,c,d\in G$:

M1 -

If $c\in a·b$ then $a\in c·\left(r\right(b\left)\right)\wedge b\in \left(r\right(a\left)\right)·c$. We write $a·b^{-1}$ to simplify $a·\left(r\right(b\left)\right)$.

M2 -

$b\in a·1$ iff $a=b$.

M3 -

If $\exists x(x\in a·b\wedge t\in x·c)$ then $\exists y(y\in b·c\wedge t\in a·y)$.

The structure $(G,·,r,1)$ is said to be commutative (or abelian) if satisfy for all $a,b,c\in G$ the condition

M4 -

$c\in a·b$ iff $c\in b·a$.

The structure $(G,·,1)$ is a commutative multimonoid (with unity) if satisfy M3, M4 and the condition $a\in 1·a$ for all $a\in G$.

Definition 2.2

(Definition 5 in [3]). A (commutative) superring is a sextuple $(R,+,·,-,0,1)$ satisfying:

• $(R,+,-,0)$ is a commutative multigroup and $(R,·,1)$ is a (commutative) multimonoid;
• (Null element) $a·0=0$ and $0·a=0$ for all $a\in R$;
• (Weak distributive) If $x\in b+c$, then $a·x\in a·b+a·c$ and $x·a\in b·a+c·a$. Or equivalently, $(b+c)·a\subseteq b·a+c·a$ and $a·(b+c)\subseteq a·b+a·c$.
• The rule of signals holds: $-\left(ab\right)=(-a)b=a(-b)$, for all $a,b\in R$.

Note that if $a\in R$, then $0=0·a\in (1+(-1\left)\right)·a\subseteq 1·a+(-1)·a$, thus $(-1)·a=-a$.

R is said to be a multiring if $(R,·,1)$ is a monoid. An hyperring R is a multiring such that if for $a,b,c\in R$, $a(b+c)=ab+ac$ and $(b+c)a=ba+ca$. A multiring (respectively, an hyperring) R is said to be a multidomain (hyperdomain) if it does not have zero divisors. A commutative multiring R will be a multifield if every non-zero element of R has a multiplicative inverse;

If $a=0$, then $a(b+c)=ab+ac$ and $(b+c)a=ba+ca$. Observe that hyperfields and multifields coincide. Indeed, by definition, every hyperfield is multifield, and, for a given multifield R, if $a\ne 0$ then

$$a^{-1}(ab+ac)\subseteq b+cimpliesa{a}^{-1}(ab+ac)\subseteq a(b+c),$$

whenever $b,c\in R$. Therefore, $a(b+c)=ab+ac$.

Definition 2.3.

Let A and B superrings. A map $f:A\to B$ is a morphism if for all $a,b,c\in A$: 2

• $f\left(1\right)=1$ and $f\left(0\right)=0$;
• $f(-a)=-f\left(a\right)$;
• $f\left(ab\right)=f\left(a\right)f\left(b\right)$;
• if $c\in a+b$ then $f\left(c\right)\in f\left(a\right)+f\left(b\right)$.

A morphism f is a full morphism if for all $a,b\in A$,

$$f(a+b)=f\left(a\right)+f\left(b\right)andf(a·b)=f\left(a\right)·f\left(b\right).$$

In this text, we provide some examples and treat about (noncommutative) multirings. For more details, we recommend the reader to check [3,10,11,12,13,14,15], and [16] for advances and results in multiring/hyperring (commutative) theory.

Example 2.4.

• Suppose that $(G,·,1)$ is a group. Defining $a\ast b=\{a·b\}$, and $r\left(g\right)=g^{-1}$, we have that $(G,\ast ,r,1)$ is a multigroup. In this way, every ring, domain, and field is a multiring, multidomain and hyperfield, respectively.
• Let $K=\{0,1\}$ with the usual product and the sum defined by relations $x+0=0+x=x$, $x\in K$ and $1+1=\{0,1\}$. This is a hyperfield called Krasner’s hyperfield [17].
• $Q_2=\{-1,0,1\}$ is the “signal” hyperfield with the usual product (in $\mathbb{Z}$) and the multivalued sum defined by relations

  $$\left\{\begin{array}{c}0+x=x+0=x,foreveryx\in Q_2\hfill \\ 1+1=1,(-1)+(-1)=-1\hfill \\ 1+(-1)=(-1)+1=\{-1,0,1\}\hfill \end{array}\right.$$
• For every multiring R, we can define the opposite multiring $R^{op}$ which has the same structure unless $(R^{op},{·}^{op},1^{op})$ is the opposite monoid of $(R,·,1)$, i.e., ${·}^{op}$ is the reverse multiplication. The null element and the weak distributive properties are both sides satisfied in $R^{op}$ since they are satisfied at (both) opposite sides in R.

The next example codifies the structure of ranks of square matrices.

Example 2.5

(Superrings of Signed Ranks). Consider $n\in \mathbb{N}$ and

$$K_n^{\pm }=\{0,1,2,...,n-1,n_{-},n_{+}\}$$

the superring endowed with addition ⊕ and multiplication ⊙ defined by:

($n=0,1$)

$K_0^{\pm }=K_0=\left\{0\right\}$, $K_1^{\pm }=Q_2$ and $K_1=\{0,1\}=K$.

(K1)

0 is an identity with respect to the addition ⊕;

(K2)

• $m\oplus m^{\prime }=\left\{\begin{array}{c}\left[\right|m-m^{\prime }|,m+m^{\prime }];m,m^{\prime }\in \{1,...,n-1\},m+m^{\prime }<n;\hfill \\ \prime |,m+m^{\prime }]\cup \left\{n_{\pm }\right\};m,m^{\prime }\in \{1,...,n-1\},m+m^{\prime }\ge n;\hfill \end{array}\right.$
• $m\oplus n_{\pm }=[n-m,n-1]\cup \left\{n_{\pm }\right\}$ whenever $m\le n-1$;
• (n is even) $n_{+}\oplus n_{+}=n_{-}\oplus n_{-}=K_n^{\pm }$ ;
  $n_{+}\oplus n_{-}=K_n^{\pm }\setminus \left\{0\right\}$.
• (n is odd) $n_{+}\oplus n_{+}=n_{-}\oplus n_{-}=K_n^{\pm }\setminus \left\{0\right\}$;
  $n_{+}\oplus n_{-}=K_n^{\pm }$.

(K3)

$n_{+}$ is an identity with respect to the multiplication ⊙ and $n_{-}\odot n_{-}=n_{+}$;

(K4)

For $m,m^{\prime }<n$,

$$m\odot m^{\prime }=\left\{\begin{array}{c}[m+m^{\prime }-n,min(m,m^{\prime })],\mathrm{whenever}m+m^{\prime }>n;\hfill \\ \prime \left)\right],\mathrm{otherwise}.\hfill \end{array}\right.$$

We denote the Superrings of ranks by $K_n=\{0,1,2,...,n-1,n\}$, whose axioms are identical except that $n_{+}=n_{-}=n$.

Example 2.6

(Kaleidoscope, Example 2.7 in [1]). Let $n\in \mathbb{N}$ and define

$$X_n=\{-n,...,0,...,n\}\subseteq \mathbb{Z}.$$

We define then-kaleidoscope multiring by $(X_n,+,·,-,0,1)$, where $-:X_n\to X_n$ is the restriction of the opposite map in $\mathbb{Z}$, $+:X_n\times X_n\to \mathcal{P}\left(X_n\right)\setminus \{\varnothing \}$ is given by the rules:

$$a+b=\left\{\begin{array}{c}\left\{a\right\},ifb\ne -aand\left|b\right|\le \left|a\right|\hfill \\ \left\{b\right\},ifb\ne -aand\left|a\right|\le \left|b\right|\hfill \\ \{-a,...,0,...,a\}ifb=-a\hfill \end{array}\right.,$$

and $·:X_n\times X_n\to X_n$ is given by the rules:

$$a·b=\left\{\begin{array}{c}sgn\left(ab\right)max\left\{\right|a|,|b\left|\right\}ifa,b\ne 0\hfill \\ 0ifa=0orb=0\hfill \end{array}\right..$$

With the above rules we have that $(X_n,+,·,-,0,1)$ is a multiring which is not an hyperring for $n\ge 2$ because

$$n(1-1)=b·\{-1,0,1\}=\{-n,0,n\}$$

and $n-n=X_n$. Note that $X_0=\left\{0\right\}$ and $X_1=\{-1,0,1\}=Q_2$.

Example 2.7

(Triangle Hyperfield [18]). Let ${\mathbb{R}}_{+}$ be the set of non-negative real numbers endowed with the following (multi)operations:

$$\left\{\begin{array}{c}a▿b=\{c\in {\mathbb{R}}_{+}\left|\right|a-b|\le c\le |a+b|\},foralla,b\in {\mathbb{R}}_{+},\hfill \\ a·b=ab,theusualmultiplicationin{\mathbb{R}}_{+},\hfill \\ -a=a.\hfill \end{array}\right.$$

Actually, this is an hyperfield that does not satisfies the double distributive property (see 5.1 in [18] for more details).

Example 2.8.

• The prime ideals of a commutative ring (its Zariski spectrum) are classified by equivalence classes of morphisms into algebraically closed fields, however, they can beuniformly classifiedby a multiring morphism into the Krasner hyperfield $K=\{0,1\}$.
• The orderings of a commutative ring (its real spectrum) are classified by classes of equivalence of ring homomorphisms into real closed fields. Although, they can be uniformly classified by a multiring morphism into the signal hyperfield $Q_2=\{-1,0,1\}$.
• A Krull valuation on a commutative ring with a group of values $(G,+,-,0,\le )$ is just a morphism into the hyperfield $T_G=G\cup \{\infty \}$.

3. Multialgebras with Involution

For a multiring A, we denote

$$Z\left(A\right):=\{a\in A:forallb\in A,ab=ba\},$$

the center of A. Of course, if A is commutative, $Z\left(A\right)=A$. The classical theory of central algebras with involution suggests a development of this subject in a very similar way.

Definition 3.1.

• Let R be a commutative multiring, A be a (non necessarily commutative) multiring, and $j:R\to A$ a homomorphism of multirings such that $j\left[R\right]\subseteq Z\left(A\right)$, then $(A,j)$ is a R-multialgebra.
• A morphism of R-multialgebras $f:(A,j)\to (A^{\prime },j^{\prime })$ is a morphism of multirings $f:A\to A^{\prime }$ such that $f\circ j=j^{\prime }$.
• An involution σ over the R-multialgebra $(A,j)$ is an (anti)isomorphism of R-multialgebras $\sigma :(A,j)\to (A^{op},j^{op})$ where $A^{op}$ is the opposite multiring, $j^{op}:R^{op}\to A^{op}$ is a homomorphism and ${\sigma }^{op}={\sigma }^{-1}$. Thus, for all $a,b\in A$, $\sigma \left(ab\right)=\sigma \left(b\right)\sigma \left(a\right)$.
• A multialgebra with involution is just a $(R,\tau )-$multialgebra endowed with an involution where $(R,\tau )$ is a multiring with involution. A morphism of $R-$ multialgebras with involution is a morphism of $R-$ multialgebras $f:(A,j,\sigma )⟶(A^{\prime },j^{\prime },{\sigma }^{\prime })$ satisfying $f\circ \sigma ={\sigma }^{\prime }\circ f$.
• For each commutative multiring with involution $(\mathcal{R},\tau )$ is the category of $(R,\tau )-$ multialgebras with involution, whose objects are $(R,\tau )-$ multialgebras with involution and morphisms are morphisms of $R-$multialgebras with involution.

Whenever the involution $\tau$ is clear we will omit it and write only $\mathcal{R}$. Note that item 1 implies that $(R,\tau )$ is an initial object in $\mathcal{R}$. Item 2 provides us that every morphism $f:(A,j,\sigma )⟶(A^{\prime },j^{\prime },{\sigma }^{\prime })$ is represented by a commutative triangle.

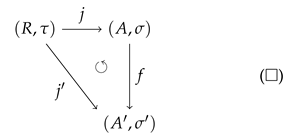
We call $(A,\sigma )$ a subalgebra of $(A^{\prime },{\sigma }^{\prime })$ if the diagram (□) is satisfied by the restricted identity morphism $f=i{d}_{A^{\prime }}{|}_A$. An ideal $J\subseteq A$ is a $\sigma -$invariant ($\sigma \left(J\right)\subseteq J$) non-empty subset satisfying $J·A\subseteq J$ and $x+y\subseteq J$ for all $x,y\in J$. Once J is $\sigma -$invariant and $\sigma$ is an isomorphism, $A·J=\sigma \left(\sigma \right(J)·\sigma (A\left)\right)\subseteq \sigma \left(J\right)\subseteq J$, and thence J is a two-sided ideal. A proper ideal is an ideal $J\ne A$. We call J a prime ideal if J is an ideal such that $ab\in J$ implies $a\in J$ or $b\in J$ for any pair $a,b\in A$. The smallest ideal generated by $a_1,...,a_k\in A$ is

$${\displaystyle J(a_1,...,a_k)=\sum _{i=1}^{k}A{a}_{i}A+A\sigma \left(a_i\right)A.}$$

We define the quotient $A/J$ as usual (see for instance, [1,3,19], or [20]). We have many standard and effusive constructions that raise various examples in category $\mathcal{R}$.

Let I be a non-empty set. For a given family ${(A_i,j_i,{\sigma }_i)}_{i\in I}$ of $R-$multialgebras with involution, the direct product$\prod A_i=({\prod }_{i\in I}(A_i,{\pi }_i),\stackrel{`}{j},\stackrel{`}{\sigma })$ is an $R-$multialgebra with involution such that ${\pi }_{i_0}:\prod A_i⟶A_{i_0}$ are projection morphisms for each $i_0\in I$. Indeed, $\stackrel{`}{\sigma }{\left(a_i\right)}_{i\in I}={\left({\sigma }_i\left(a_i\right)\right)}_{i\in I}$ is an involution over $\prod A_i$, and $\stackrel{`}{j}\left(r\right)={\left(j_i\left(r\right)\right)}_{i\in I}\in Z\left(\prod A_i\right)$ is a well-defined map satisfying the necessary conditions above.

Matrices over a given commutative multiring are natural constructions. Denote by $M_n\left(A\right)$ the set of square matrices of order n with coefficients in $(A,j,\sigma )$ and set the sum and product of matrices as follows:

For all matrices $C={\left(c_{ij}\right)}_{n\times n},B={\left(b_{ij}\right)}_{n\times n}\in M_n\left(A\right)$, we define the function $\overline{\sigma }:M_n\left(A\right)⟶M_n\left(A\right)$ by $\overline{\sigma }\left(B\right)={\left(\sigma \left(b_{ji}\right)\right)}_{n\times n}$ and (multi)operations

$$\begin{array}{cc}\hfill C+B& :=\{\left(d_{ij}\right):d_{ij}\in c_{ij}+b_{ij}foralli,j\}\ne \varnothing \hfill \\ \hfill CB& :=\{\left(d_{ij}\right):d_{ij}\in \sum _{k=1}^n{c}_{ik}{b}_{kj}=c_{i1}{b}_{1j}+c_{i2}{b}_{2j}+...+c_{in}{b}_{nk}foralli,j\}\ne \varnothing \hfill \\ \hfill \lambda C& :={\left(\lambda c_{ij}\right)}_{n\times n},\mathrm{for}\mathrm{all}\lambda \in R.\hfill \end{array}$$

Since $\sigma$ is an involution and A is a commutative multiring, it follows that $\overline{\sigma }$ is also an involution. Finally, let $f:(A,\sigma )⟶(M_n\left(A\right),\overline{\sigma })$ the diagonal morphism $f\left(a\right)=\mathrm{diag}(a,a,...,a)\in M_n\left(A\right)$, which associates each $a\in A$ with a diagonal matrix in $M_n\left(A\right)$ and $\overline{j}:=f\circ j$ is the injective morphism such that $\overline{j}\left(R\right)\subseteq Z\left(M_n\left(A\right)\right)$. We will avoid the verification that $(M_n\left(A\right),\overline{j},\overline{\sigma })$ is a $R-$multialgebra with involution, but the reader can check Section 2 of [4], Theorem 2.3, and Lemma 2.5. However, we give an example to illustrate this construction.

Example 3.2.

Consider the $2-$kaleidoscope multiring $(X_2,+,·,-,0,1)$ as defined in 2.6 and ${\left(\right)}^t$ the matrix transposition. Then, $(M_2\left(X_2\right),{\left(\right)}^t)$ is a $X_2-$multialgebra with involution.

Let $A=\left[\begin{array}{cc}1& 2\\ -1& 0\end{array}\right]$ and $B=\left[\begin{array}{cc}0& 1\\ -1& 1\end{array}\right]$ matrices over $X_2$. Thus,

$$AB=\left[\begin{array}{cc}1·0+2·(-1)& 1·1+2·1\\ -1·0+0·(-1)& -1·1+0·1\end{array}\right],A^t=\left[\begin{array}{cc}1& -1\\ 2& 0\end{array}\right],B^t=\left[\begin{array}{cc}0& -1\\ 1& 1\end{array}\right].$$

Therefore, ${\left(AB\right)}^t=B^t{A}^t=\left[\begin{array}{cc}-2& 0\\ 2& -1\end{array}\right]$.

Example 3.3.

(Adapted from [21]) Let $G^0=G\cup \left\{0\right\}$ be a group with 0 and define + the multioperation satisfying

$$\begin{array}{c}\hfill x+0=0+x=x,\forall x\in G^0;\\ \hfill x+x=G^0\setminus \left\{x\right\},\forall x\in G^0;\\ \hfill x+y=\{x,y\},\forall x,y\in G^0\mathrm{with}x\ne y.\end{array}$$

We can define an involution σ over this structure by setting $\sigma \left(x\right)=x^{-1}$ for all $x\in G$ and $\sigma \left(0\right)=0$. In fact, σ is additive and it is easy to verify that $(G^0,0,1,+,·,\sigma )$ is a multiring with involution.

4. Marshall’S Quotient of Multialgebras with Involution

Throughout this section, we fix a R-multialgebra with involution $(A,j,\sigma )$. We are interested in Marshall coherent subsets satisfying at least one of the conditions in Theorem 4.11, i.e., normality or convexity. These conditions interact in many ways with the relations below (4.2) compared to the commutative case. First of all, we explore basic properties due to definitions.

Definition 4.1.

A subset (without zero divisors) $S\subseteq A$ is called a Marshall coherent subset whenever

• S is a multiplicative submonoid of $(A,·,1)$
• $\sigma \left[S\right]\subseteq S$ (or, equivalently $\sigma \left[S\right]=S$)

We call S standard if $s\sigma \left(s\right)\in Z{\left(A\right)}^{\times }$, for all $s\in S$. We said that S is convex if $xS\sigma \left(x\right)\subseteq S$ for all $x\in A_0$ in the subset of nonzero divisors of A. If $x\sigma \left(x\right)\in S$ for all $x\in A_0$, we said that S is $1-$convex.

Immediately, convexity implies $1-$convexity. One can check Lemma 4.7 and Proposition 4.12 for a reciprocal result. From now on, we fix a Marshall coherent subset $S\subseteq A$.

Definition 4.2.

Let $a,b\in A$ and $s_1,s_2,t_1,t_2\in S$. We define:

• $a{\sim }_{1}b$ iff $a=s_{1}b{s}_2$ and $b=t_{1}a{t}_2$;
• $a{\sim }_{2}b$ iff $s_{1}a{s}_2=t_{1}b{t}_2$;
• $a{\sim }_{3}b$ iff $a{s}_1=t_{1}b$ and $s_{2}a=b{t}_2$;
• $a{\sim }_{4}b$ iff there is $s\in S$ such that $as\sigma \left(b\right)\in S$.

Of course, $a{\sim }_{1}b$ implies $a{\sim }_{2}b$. Further, ${\sim }_4$ is an equivalence relation when S is $1-$convex. Indeed, this relation concurs with ${\sim }_3$ (see Lemma 4.6). We start exploring these relations and related properties of Marshall coherent subsets.

Lemma 4.3.

For $\sim ={\sim }_1$, as defined above, ∼ is an equivalence relation and satisfies:

• For all $a\in A$ and all $s\in S$, $\sigma \left(s\right)as\sim a$, $sa\sigma \left(s\right)\sim a$, and $abs\sim ab$, $sab\sim ab$.
• For all $a,b\in A$ if $a\sim b$ then $\sigma \left(a\right)\sim \sigma \left(b\right)$.

Proof. 

Of course ∼ is reflexive (since S has 1) and symmetric. Now let $a\sim b$ and $b\sim c$, with $a=s_{1}b{s}_2$, $b=t_{1}a{t}_2$ and $b=r_{1}c{r}_2$, $c=w_{1}b{w}_2$, $s_1,s_2,t_1,t_2,r_1,r_2,w_1,w_2\in S$. Then

$$a=s_{1}b{s}_2=s_1\left(r_{1}c{r}_2\right)s_2=\left(s_1{r}_1\right)c\left(r_2{s}_2\right)$$

and

$$c=w_{1}b{w}_2=w_1\left(t_{1}a{t}_2\right)w_2=\left(w_1{t}_1\right)a\left(t_2{w}_2\right).$$

Since S is multiplicative, we have $s_1{r}_1,r_2{s}_2,w_1{t}_1,t_2{w}_2\in S$, which implies $a\sim c$. Hence, $\sim ={\sim }_1$ is an equivalence relation. Items 1 and 2 follow straightforward once S is multiplicative and $\sigma -$invariant.

□

Lemma 4.4.

If S is standard, then $\sim ={\sim }_2$ is an equivalence relation and satisfies:

• For all $a\in A$ and all $s\in S$, $\sigma \left(s\right)as\sim a$, $sa\sigma \left(s\right)\sim a$, and $abs\sim ab$, $sab\sim ab$.
• For all $a,b\in A$ if $a\sim b$ then $\sigma \left(a\right)\sim \sigma \left(b\right)$.

Proof. 

Reflexivity and symmetry follow immediately. Note that $s\sigma \left(s\right)\in Z\left(A\right)$, enable us to rewrite the definition of $\sim ={\sim }_2$ as follows:

$$a{\sim }_{2}biff{s}_{1}a{s}_2=t_{1}b{t}_{2}iff\sigma \left(s_1\right)s_{1}a{s}_2\sigma \left(t_2\right)=\sigma \left(s_1\right)t_{1}b{t}_2\sigma \left(t_2\right)iffa{s}_1^{\prime }=t_1^{\prime }b,$$

for $s_1^{\prime },t_1^{\prime }\in S$.

Consider $a\sim b$ and $b\sim c$ which means that there exist $s_1,t_1,s_2,t_2\in S$ such that $a{s}_1=t_{1}b$ and $b{s}_2=t_{2}c$. Scaling the previous equation on the right by $s_2$, and the later, on the left by $t_1$, we conclude that $a\left(s_1{s}_2\right)=\left(t_1{t}_2\right)c$. Thus, ∼ is transitive, that is, an equivalence relation.

For Item 1, observe that $w\left(\sigma \left(s\right)as\right)w^{\prime }=\left(w\sigma \left(s\right)\right)a\left(s{w}^{\prime }\right)$, and $w\left(abs\right)w^{\prime }=w\left(ab\right)s{w}^{\prime }$ for all $s,w,w^{\prime }\in S$. Item 2 follows by applying $\sigma$ both sides of $as=bt$. □

Lemma 4.5.

Suppose that $x·S=S·x$ for each $x\in A$. Let $a,a^{\prime }\in A$, the following statements are equivalent:

• $\exists s,t,s^{\prime },t^{\prime }\in S$ such that $sat=s^{\prime }{a}^{\prime }{t}^{\prime }$
• $\exists u,u^{\prime }\in S$ such that $ua=u^{\prime }{a}^{\prime }$
• $\exists v,v^{\prime }\in S$ such that $av=a^{\prime }{v}^{\prime }$

That is, $a{\sim }_2{a}^{\prime }$ if, and only if, $a{\sim }_3{a}^{\prime }$. Furthermore, ${\sim }_S={\sim }_2={\sim }_3$ is an equivalence relation.

Proof. 

$\left(1\right)\iff \left(2\right)\iff \left(3\right)$ follows immediately from the hypothesis. Thus, ${\sim }_i={\sim }_j$ for each pair $(i,j)$, $i,j\in \{2,3\}$. For simplicity, denote ${\sim }_S={\sim }_i$, for each $i\in \{2,3\}$.

${\sim }_S$ is an equivalence relation: suppose that $ua=u^{\prime }{a}^{\prime }$ and $r^{\prime }{a}^{\prime }=r^{\prime \prime }{a}^{\prime \prime }$ for $u,u^{\prime },r^{\prime },r^{\prime \prime }\in S$. Observe that

$$\begin{array}{c}\hfill ua=u^{\prime }{a}^{\prime }\Rightarrow r^{\prime }ua=r^{\prime }\left(u^{\prime }{a}^{\prime }\right)\therefore r^{\prime }ua=r^{\prime }\left(a^{\prime }{v}^{\prime }\right),\mathrm{for}\mathrm{some}{v}^{\prime }\in S.\end{array}$$

Also,

$$\begin{array}{c}\hfill \left(r^{\prime }u\right)a=\left(r^{\prime }{a}^{\prime }\right)v^{\prime }=\left(r^{\prime \prime }{a}^{\prime \prime }\right)v^{\prime }\Rightarrow \exists r^{\prime }u=v,v^{\prime \prime }\in S,\mathrm{such}\mathrm{that}\left(r^{\prime }u\right)a=v^{\prime \prime }{a}^{\prime \prime }.\end{array}$$

It follows that $a{\sim }_S{a}^{\prime },a^{\prime }{\sim }_S{a}^{\prime \prime }$ implies $a{\sim }_S{a}^{\prime \prime }$. We already prove that ${\sim }_S$ is transitive. Reflexivity and symmetry follow from $1\in S$ and the equivalence of the statements 1, 2, and 3. □

We observe that, for a given Marshall’s coherent subset S, convexity is the reflexivity property of ${\sim }_4$ by definition. Indeed, there is a suitable relationship between the upward-selected set of relations and Marshall’s coherent convex subsets.

Lemma 4.6.

Suppose that S is convex. Let $a,a^{\prime }\in A$, the following statements are equivalent:

• $a{\sim }_2{a}^{\prime }$;
• $a{\sim }_3{a}^{\prime }$;
• $a{\sim }_4{a}^{\prime }$.

Furthermore, ${\sim }_S={\sim }_2={\sim }_3={\sim }_4$ is an equivalence relation. Additionally, for every $1-$convex $S^{\prime }$, ${\sim }_4={\sim }_3\subseteq {\sim }_2$.

Proof. 

$1\Rightarrow 2:$ There are $s_1,s_2,t_1,t_2\in S$ such that

$$\begin{array}{ccc}\hfill s_{1}a{s}_2=t_1{a}^{\prime }{t}_2\Rightarrow & \underset{\in S}{\underbrace{s_{1}a{s}_2(\sigma \left(a\right)}}a)=t_1{a}^{\prime }\underset{\in S}{\underbrace{t_2\left(\sigma \left(a\right)a\right)}}\hfill & \hfill \left(S\mathrm{is}\mathrm{Marshall}\mathrm{convex}\right)\\ \hfill \therefore \underset{\in S}{\underbrace{\left(a^{\prime }\sigma \left(a^{\prime }\right)\right)s_3}}a=(a^{\prime }\underset{\in S}{\underbrace{\sigma \left(a^{\prime }\right))t_1{a}^{\prime }{t}_2^{\prime }}}\Rightarrow & sa=a^{\prime }t.\hfill \end{array}$$

(1)

$2\Rightarrow 3:$ Suppose that $a{\sim }_3{a}^{\prime }$. Then, there exist $s_1,t_1\in S$ satisfying

$$\begin{array}{cc}\hfill a{s}_1=t_1{a}^{\prime }\Rightarrow & a{s}_1\sigma \left(a^{\prime }\right)=t_1{a}^{\prime }\sigma \left(a^{\prime }\right)\in S.\hfill \end{array}$$

(2)

$3\Rightarrow 1:$ Finally, if $a{\sim }_4{a}^{\prime }$, then $\exists s,t_1\in S$ such that

$$\begin{array}{ccc}\hfill as\sigma \left(a^{\prime }\right)=t_1\Rightarrow & a\underset{\in S}{\underbrace{s\sigma \left(a^{\prime }\right)a^{\prime }}}=t_1{a}^{\prime }\therefore \hfill & \hfill 1·a{s}_2=t_1{a}^{\prime }·1.\end{array}$$

(3)

To prove the final assertion, consider $a{\sim }_{S}b=a{\sim }_{4}b$, for all $a,b\in A$. Since $1\in S$ and S is convex, $a\sigma \left(a\right)\in S$ for all $a\in A$. Moreover, as long as S is $\sigma -$invariant, $as\sigma \left(b\right)\in S$ if, and only if, $b\sigma \left(s\right)\sigma \left(a\right)\in S$. It turns out that $a{\sim }_{S}b$ if, and only if, $b{\sim }_{S}a$. Thus, ${\sim }_S$ is reflexive and symmetric.

Finally, we prove the transitivity property. Put $a{\sim }_{S}b$ and $b{\sim }_{S}c$. Thus, by definition, it follows that

$$\exists r,s,s^{\prime },s"\in S;\left\{\begin{array}{c}as\sigma \left(b\right)=s^{\prime }\mathbf{1}\hfill \\ br\sigma \left(c\right)=s"\mathbf{2}\hfill \end{array}\right.\stackrel{\mathbf{1}·\mathbf{2}}{\Rightarrow }a\underset{\in S}{\underbrace{s\sigma \left(b\right)br}}\sigma \left(c\right)=s^{\prime }s"\in S.$$

Remember that S is closed under multiplication and $1-$convex. As follows, we have already proved the transitivity holds. We conclude that ${\sim }_S$ is an equivalence relation. The final assertion follows straightforward. □

The next lemma summarizes and proves many results concerning the properties of Marshall coherent subsets and the above relations.

Lemma 4.7.

Let S be a Marshall coherent set in $(A,\sigma )$. The succeeding statements hold:

• If $y·S=S·y$ for all $y\in A$ and S is $1-$convex, then S is convex;
• If S is convex and $x\sigma \left(x\right)\in Z{\left(A\right)}^{\times }$ for all non-zero divisor $x\in A$, then $x·S=S·x$ (S is normal);
• If $S\subseteq A^{\times }$ and S is $1-$convex, then $A_0=A^{\times }$ is the set of non-zero divisors, i.e. every non-zero divisor has an inverse in A;
• If S is standard, then $S\subseteq A^{\times }$;
• If S is standard then $a{\sim }_1{a}^{\prime }$ if, and only if, $a{\sim }_2{a}^{\prime }$;

Proof. 

• Let $x\in A$ a non-zero divisor and $s\in S$. Thus, $\sigma \left(x\right)sx=z$ for some $z\in A$. Commuting s with x, it follows that $\sigma \left(x\right)x{s}^{\prime }=y$ for a suitable $s^{\prime }\in S$. Hence, $1-$convexity and closure of multiplication implies $y\in S$. Therefore, $\sigma \left(x\right)Sx\subseteq S$.
• Let $x\in A^{\ast }$ a non-zero divisor. For any $s_1\in S$, $\sigma \left(x\right)s_{1}x=s_2$ for some $s_2$. Therefore $\left(x\sigma \left(x\right)\right)s_{1}x=x{s}_2$, which implies $s_{1}x=x{s}_2{\left(x\sigma \left(x\right)\right)}^{-1}$. Since $x\sigma \left(x\right)\in S^{\times }$ has inverse in S, $s_{1}x=x{s}_1^{\prime }$ for a suitable choice of $s_1^{\prime }$. Hence, $S·x\subseteq x·S$. The reverse inclusive follows from symmetry.
• By definition, $A^{\times }\subseteq A_0$. For the inverse inclusion, note that $A_0$ is a Marshall coherent set and, let $y\in A_0$ and $1\in S$. Thus, $\sigma \left(y\right)y=s^{\prime }\ne 0$.

  $$\begin{array}{cc}\hfill \sigma \left(y\right)y=s^{\prime }\Rightarrow s^{\prime -1}\sigma \left(y\right)y=1\therefore & y_l^{-1}=s^{\prime -1}\sigma \left(y\right)isaleftinversefory.\hfill \end{array}$$

  (4)
  The same argument shows that y has the right inverse $y_r^{-1}$. Note that $y{y}_l^{-1}=s_1\in S$. Thus, $y{y}_l^{-1}y=s_{1}y$, implies $y=s_{1}y$, for some $s_1\in S$. Scaling by $y_r^{-1}$ both right sides of equation, we obtain $1=s_1$. Hence $y^{-1}=y_l^{-1}=y_r^{-1}$.
• By hypothesis, $s\sigma \left(s\right)\in Z{\left(A\right)}^{\times }(\cap S)$. Hence, $\exists x\in A$ such that $\left(x\sigma \right(s\left)\right)s=1$. Direct calculations show it is a both-side unique inverse.
• The statement has straightforward proof by scaling and dividing.

□

For each $\sim \in \{{\sim }_1,{\sim }_2,{\sim }_3,{\sim }_4\}$, denote an element in $A/\sim$ (whenever it exists) by $\left[a\right]$. We have well-defined rules

$$\begin{array}{cc}\hfill \left[a\right]+\left[b\right]& :=\{\left[c\right]:c=s_{1}a{s}_2+t_{1}b{t}_{2}forsome{s}_1,s_2,t_1,t_2\in S\}and,\hfill \\ \hfill \left[b\right]& :=\left\{\right[c]:c=rasbtforsomer,s,t\in S\}.\hfill \end{array}$$

Observe the involutory structure can be defined in the very same way for superrings.

Definition 4.8.

A superring with involution $(A,\sigma )$ is a superring satisfying (mutatis mutandis) the axioms for multialgebras with involution.

Theorem 4.9.

The structure $(A/{\sim }_2,+,·,\left[0\right],\left[1\right])$ is a superring with involution $\sigma \left(\right[a\left]\right):=\left[\sigma \right(a\left)\right]$. If S is standard, then $(A/{\sim }_1,+,·,\left[0\right],\left[1\right])$ is a superring with involution $\sigma \left(\right[a\left]\right):=\left[\sigma \right(a\left)\right]$.

Proof. 

Just proceed with a very similar argument to the one used in Theorem 5.2. □

We define existing quotients for general Marshall coherent subsets. In the sequence, we deal in particular with normality and convexity.

Definition 4.10.

We define the superring $(A/\sim ,+,·,[0],[1\left]\right)$ as the Marshall’s Quotient of A by S, and denote it by $A{/}_{m}S:=A/\sim$.

Whenever ∼ is chosen, we might indicate the Marshall subset S by adding it to the index, i.e., writing ${\sim }_S$.

Theorem 4.11.

Let $S\subseteq A$ be a Marshall coherent subset of a multiring A satisfying one of the additional conditions below

• (Normal) $xS=Sx$, for all $x\in A$.
• (Convex) For all $x\in A$, a nonzero divisor in A, $xS\sigma \left(x\right)\subseteq S$.

If $(A,\sigma )$ is a $(R,\tau )-$multialgebra with involution, the set $S_j:=j^{-1}\left[S\right]\subseteq R$ is a multiplicative submonoid of $(R,·,1)$. Moreover, $j_S:R/{\sim }_{S_j}\to A/{\sim }_S,\left[r\right]\mapsto \left[j\left(r\right)\right]$ defines a $R/{\sim }_{S_j}$-multialgebra structure over $A/{\sim }_S$, and ${\sigma }_S:A/{\sim }_S\to A/{\sim }_S,\left[a\right]\mapsto \left[\sigma \left(a\right)\right]$ is an involution over the $R/{\sim }_{S_j}$-multialgebra $(A/{\sim }_S,j_S)$. In both cases, $A/{\sim }_S$ is a multiring.

Proof. 

Once $j:(R,\tau )⟶(A,\sigma )$ is a homomorphism, if $s_{1}r{s}_2=t_1{r}^{\prime }{t}_2$ in R, then $j\left(\left[r\right]\right)=\left[j\left(r\right)\right]=\left[j\left(r^{\prime }\right)\right]=j\left(\left[r^{\prime }\right]\right)$. It is easy to check that $S_j$ is a multiplicative submonoid of R and, due to S being Marshall coherent, $\sigma \left(j\right(r\left)\right)=j\left(\tau \right(r\left)\right)\in S$ for all $r\in S_j$. Thus, $\tau \left(r\right)\in S_j$ whenever $r\in S_j$. We conclude that $S_j$ is Marshall coherent,i.e. $R/{\sim }_{S_j}$ is a multiring with involution $\tau \left(\right[r\left]\right):=\left[\tau \right(r\left)\right]$.

Now, consider the following diagram:

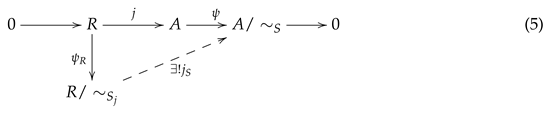
(1) If $xS=Sx$, then $\sim ={\sim }_2$ can be read as $a\sim b$ if, and only if, $as=tb$ for some $s,t\in S$. Previous constructions (see 4.9) and demonstrations show that $(A/{\sim }_S)$ is a superring. Let $\left[c\right]$ and $\left[c^{\prime }\right]$ be elements in $\left[a\right]·\left[b\right]$, thus $c=abs$ and $c^{\prime }=s^{\prime }ab$ for some $s,s^{\prime }\in S$. Scaling equations and comparing gives us $s^{\prime }c=c^{\prime }s=s^{\prime }abs$. Which means that $c\sim c^{\prime }$. Therefore, $\left[a\right]·\left[b\right]=\left\{\right[ab\left]\right\}$ and, $A/\sim$ is a multiring.

By the universal property of the quotient $R/{\sim }_{S_j}$, $j_s$ is unique. Since all arrows are homomorphisms, $(A/{\sim }_S,j_S)$ is $R/{\sim }_{S_j}-$multialgebra. Furthermore, S is $\sigma$ invariant, which means $\sigma \left(aS\right)=\sigma \left(a\right)S$. Consequently, the induced antihomomorphism ${\sigma }_S:A/{\sim }_S⟶A/{\sim }_S$ such that $\sigma \left(\right[a\left]\right)=\left[\sigma \right(a\left)\right]$ is well-defined and an involution over $A/{\sim }_S$.

(2) Let $\sim ={\sim }_2$. In this case, 4.6 and the preceding case show that $A/\sim$ is a multiring. The proof is the same as before since 4.9 still holds.

□

The above theorem provides us with two kinds of quotients lying in the class of multrings. One can wonder if the quotient can give some information about the Marshall coherent subset.

Proposition 4.12.

Let $A/{\sim }_S$ be a multiring, S be a Marshall coherent subset, such that $1\in S$ and $\sim ={\sim }_2$. Then, $\left[1\right]$ is $1-$convex if, and only if, $\left[1\right]$ is convex.

Proof. 

Sketch of the proof: Note that $\left[S\right]=\left[1\right]$ is Marshall coherent. The converse is immediate. To prove the reciprocal statement, use $\left[x\right]·\left[s\right]·\left[\sigma \right(x\left)\right]=\left[xs\sigma \right(x\left)\right]=\left[1\right]$ (since the quotient is a multiring, · is actually a usual operation) for all $s\in \left[1\right]$. □

According to the above results, some immediate examples follow below.

Example 4.13.

For a given $(A,\sigma )$, a $(R,{\sigma }^{\prime })$-multialgebra with involution, the next sets are Marshall coherent:

a)

The set of all non-zero divisors $A_0$;

b)

The set of all invertible elements $A^{\times }$;

c)

The set of all symmetric elements (in $A_0$) $Sym(A,\sigma )=\{a\in A_0|a=\sigma \left(a\right)\}$;

d)

If $x\sigma \left(x\right)\in Z\left(A\right)$ for all $x\in A$, then $A_0\sigma \left(A_0\right)=\left\{a\sigma \left(a\right)\right|a\in A_0\}$ is Marshall coherent and convex.

In the next section, we provide more examples minutely. For now, we treat about another kind of operations in the quotient. For $a,a^{\prime }\in A$, let $a{\sim }_S{a}^{\prime }$ if, and only if, there exist $s,t,s^{\prime },t^{\prime }\in S$ such that $sat=s^{\prime }{a}^{\prime }{t}^{\prime }$. This can be replaced in terms of the equivalent statements in 4.5 or 4.6, whether $x·S=S·x$ or S is convex, respectively. Hence ${\sim }_S$ is an equivalence relation. Moreover, each $\left[a\right]$ is invariant under S action, $\left[a\right]=\left[sa\right]$ for all $s\in S$.

In $A/{\sim }_S$ define $\left[a\right]+\left[b\right]:=\{\left[c\right]:\exists r_i,s_i,t_i\in S,r_{0}c{r}_1\in s_{0}a{s}_1+t_{0}b{t}_1\}$, $-\left[a\right]:=[-a]$ and $\left[a\right]·\left[b\right]:=\left[ab\right]$.

Theorem 4.14.

Suppose that $x·S=S·x$. Then,

• $A/{\sim }_S$ is a (non-commutative) multiring.
• If A is a hyperring, then $A/{\sim }_S$ is a hyperring. In particular, if A is a ring, then $A/{\sim }_S$ is a hyperring.
• It holds the universal property of Marshall’s quotient for homomorphisms $f:A\to M$ and anti-homomorphisms (= homomorphism $f:A\to M^{op}$) such that $f\left[S\right]=\left\{1\right\}$.

Proof. 

To demonstrate 1, we note that $+,·$, and − are well-defined as multigroup operations, and $0=\left[0\right]=\left\{0\right\}$ is the null element because A is a multiring.

Suppose that $\left[c\right]\in \left[a\right]+\left[b\right]$. Thus, there exists $r,s,t\in S$ satisfying $rc\in sa+tb$ in A. Therefore, $sa\in rc+t(-b)$ (in A). Similarly, $tb\in s(-a)+rc$. Consequently, $\left[a\right]\in \left[c\right]-\left[b\right]$ and $\left[b\right]\in -\left[a\right]+\left[c\right]$.

Let $\left[b\right]\in \left[a\right]+\left[0\right]$. By definition, exists $r\in S$ such that $rb\in sa+t0$ for some $s,t\in S$. However, it implies $\left[a\right]=\left[b\right]$. The reciprocal is obvious.

If $\left[x\right]\in \left[a\right]+\left[b\right]$ and $\left[t\right]\in \left[x\right]+\left[c\right]$, then $vt\in wx+zc$ and $r^{\prime }wx\in s^{\prime }a+p^{\prime }b$ for $r^{\prime },s^{\prime },p^{\prime },v,w,z\in S$. Afterward,

$$\begin{array}{cc}\hfill vt\in wx+zc& \Rightarrow r^{\prime }vt\in r^{\prime }wx+r^{\prime }zc\hfill \\ \hfill \exists r^{\prime }wx(r^{\prime }wx\in s^{\prime }a+p^{\prime }b\wedge r^{\prime }vt\in r^{\prime }wx+r^{\prime }zc)& \Rightarrow \exists y(y\in p^{\prime }b+r^{\prime }zc\wedge r^{\prime }vt\in s^{\prime }a+y)\hfill \end{array}$$

The last implication means $\exists \left[y\right]\left(\right[y]\in [b]+[c]\wedge [t]\in [a]+[y\left]\right)$. Once A is a multiring, $\left[c\right]\in \left[a\right]+\left[b\right]$ if, and only if, $\left[c\right]\in \left[b\right]+\left[a\right]$ follows.

We have already proved that $(A/{\sim }_S,+,-,0)$ is a multigroup. Note that exists $1=\left[1\right]=S\in A/{\sim }_S$ such that $\left[a\right]·\left[1\right]=\left[a\right]$ for all $\left[a\right]\in A/{\sim }_S$. Thus, $(A/{\sim }_S,·,1)$ is a monoid. Moreover, $\left[a\right]·0=0$. Finally, let $\left[c\right]\in \left[a\right]+\left[b\right]$ and $pd\in \left[d\right]\in A/{\sim }_S$. By definition, exists $r,s,t\in S$ such that $rc\in sa+tb$. Since A is a multiring, $rcpd\in sapd+tbpd$. Using the ’normality property’ of S, we rewrite it as follows:

$$\begin{array}{c}\hfill r^{\prime }cd\in s^{\prime }ad+t^{\prime }bd\therefore \left[c\right]\left[d\right]\in \left[a\right]\left[d\right]+\left[b\right]\left[d\right].\end{array}$$

Similarly, $\left[d\right]\left[c\right]\in \left[d\right]\left[a\right]+\left[d\right]\left[b\right]$ holds. It follows that $A/{\sim }_S$ is a multiring.

For the second assertion, suppose that A is a hyperring. Let $\left[e\right]\in \left[a\right]\left[d\right]+\left[b\right]\left[d\right]$. Thus,

$$\begin{array}{ccc}\hfill \exists s,r,t\in S,se\in rad+tbd& \Rightarrow se\in (ra+tb)d\hfill & \hfill \left(A\mathrm{is}\mathrm{hyperring}\right)\\ \hfill & \Rightarrow \left[e\right]\in \left(\right[a]+[b\left]\right)\left[d\right]\hfill & \hfill (\mathrm{by}\mathrm{definition}\mathrm{of}+).\end{array}$$

Therefore, $\left[a\right]\left[d\right]+\left[b\right]\left[d\right]=\left(\right[a]+[b\left]\right)\left[d\right]$. By symmetry, $\left[d\right]\left[a\right]+\left[d\right]\left[b\right]=\left[d\right]\left(\right[a]+[b\left]\right)$ also follows.

To demonstrate the third statement, consider $f:A⟶M$ a homomorphism such that $f\left(\right[S\left]\right)=1$. Let $a\in A$ and $s\in S$. Thus, $f\left(sa\right)=f\left(s\right)f\left(a\right)=f\left(a\right)$. Define the homomorphism $\overline{f}:A/{\sim }_S⟶M$ with $\overline{f}\left(\left[a\right]\right)=f\left(a\right)$. Hence, $\overline{f}$ is well-defined, and $f=\overline{f}\circ \psi$, with $\psi \left(a\right)=\left[a\right]$ the canonical projection. It is immediate that another homomorphism $\overline{g}:A/{\sim }_S⟶M$ satisfying $f=\overline{g}\circ \psi$ must coincide with $\overline{f}$. □

Remark 4.15.

The Theorem 4.14 is valid if S is convex. Since both conditions normality and convexity imply ${\sim }_2={\sim }_3$, we are capable of proving the distributive laws hold and the entire rest of the proof follows as above.

The next theorem distinguishes Marshall coherent subsets that lie in the center $Z\left(A\right)$ from an ordinary one.

Theorem 4.16.

Let A be a multialgebra with involution and $S\subseteq A$ be a Marshall coherent subset such that $S\subseteq Z\left(A\right)$ (thus, in particular $xS=Sx$, for all $x\in A$). Then $A{/}_{m}S$ is a (non commutative) hyperring with induced involution.

Proof. 

From previous considerations and 4.9, we prove that $A{/}_{m}S$ is a multiring instead of a superring, and the hyperring property still holds.

In fact, if $\left[c\right]\in \left[a\right]\left[b\right]$ then $cr=asbt$ for some $r,s,t\in S\subseteq Z\left(A\right)$, which means $cr=\left(ab\right)\left(st\right)$ and $c\sim ab$. Then $\left[a\right]\left[b\right]=\left\{\right[ab\left]\right\}$, proving that $A{/}_{m}S$ is a multiring.

Now, let $\left[y\right]\in \left[c\right]\left[a\right]+\left[c\right]\left[b\right]$. Then $\left[y\right]=\left[d_1\right]+\left[d_2\right]$ for some $\left[d_1\right]\in \left[c\right]\left[a\right]$, $\left[d_2\right]\in \left[c\right]\left[b\right]$, providing equations

$$\begin{array}{cc}\hfill y& =r_1{d}_1{s}_1+r_2{d}_2{s}_2,\hfill \\ \hfill d_1& =t_{1}c{v}_{1}a{w}_{1}and\hfill \\ \hfill d_2& =t_{2}c{v}_{2}a{w}_2\hfill \end{array}$$

for some $r_1,r_2,s_1,s_2,t_1,t_2,v_1,v_2,w_1,w_2\in S$. Then

$$\begin{array}{cc}\hfill y& =r_1{d}_1{s}_1+r_2{d}_2{s}_2\hfill \\ \hfill & =r_1\left[t_{1}c{v}_{1}a{w}_1\right]s_1+r_2\left[t_{2}c{v}_{2}a{w}_2\right]s_2\hfill \\ \hfill & =c\left(r_1{t}_1{v}_1\right)a\left(w_1{s}_1\right)+c\left(r_2{t}_2{v}_2\right)a\left(w_2{s}_2\right)\hfill \\ \hfill & =c[\left(r_1{t}_1{v}_1\right)a\left(w_1{s}_1\right)+\left(r_2{t}_2{v}_2\right)a\left(w_2{s}_2\right)]\hfill \end{array}$$

which imply $\left[y\right]\in \left[c\right]\left(\right[a]+[b\left]\right)$. The same reasoning provides $\left[ac\right]+\left[bc\right]\subseteq \left(\right[a]+[b\left]\right)\left[c\right]$. □

5. Applications

This last section is reserved for results surrounding particular examples. We verify some quotients associated with typical multi-structures, a few of them presented in Section 2. Throughout the subsections below, we deal with technical results and interpret elements in the Marshall quotient as classes of isometric elements.

5.1. Orthogonal

Let R be a commutative ring and A be a R-algebra with involution $\sigma$. Denote

$$Orth\left(A\right):=\{a\in A:a\sigma (a)=\sigma (a)a=1\}.$$

Once we prove that $Orth\left(A\right)$ is a Marshall coherent subset then, by definition, the standard property also holds.

Lemma 5.1.

The set $Orth\left(A\right)$ is non-empty and if $a,b\in Orth\left(A\right)$ then $\sigma \left(a\right),ab\in Orth\left(A\right)$.

Proof. 

The set $Orth\left(A\right)$ is non-empty because $1\in Orth\left(A\right)$. For the rest, note that $\sigma \left(a\right)\sigma \left(\sigma \right(a\left)\right)=\sigma \left(a\right)a$ and $\left(ab\right)\sigma \left(ab\right)=ab\left[\sigma \right(b\left)\sigma \right(a\left)\right]$ for all $a,b\in A$. If $a,b\in Orth\left(A\right)$ these imply $\sigma \left(a\right)a=a\sigma \left(a\right)=1$ and

$$\left(ab\right)\sigma \left(ab\right)=ab\left[\sigma \right(b\left)\sigma \right(a\left)\right]=a\left[b\sigma \right(b\left)\right]\sigma \left(a\right)=a\sigma \left(a\right)=1.$$

□

Now let $a,b\in A$. We define

$$a\sim bif,andonlyif,as=tbforsomeb,t\in Orth\left(A\right).$$

Note that $a\sim b$ if, and only if, $a=sbt$ for some $s,t\in Orth\left(A\right)$, because S is Marshall coherent standard subset.

Theorem 5.2.

The structure $(A/\sim ,+,·,[0],[1\left]\right)$ is a superring with involution $\sigma \left(\right[a\left]\right):=\left[\sigma \right(a\left)\right]$.

Proof. 

Note that $a\sim 0$ if, and only if, $a=0$. Moreover, from the very definitions of the sum and the product we have for all $a,b\in A$,

$$\begin{array}{cc}\hfill \left[a\right]+\left[0\right]& =\left[0\right]+\left[a\right]=\left\{\right[a\left]\right\},\left[a\right]\left[1\right]=\left[1\right]\left[a\right]=\left\{\right[a\left]\right\},\hfill \\ \hfill +\left[b\right]& =\left[b\right]+\left[a\right],\hfill \\ \hfill \sigma \left(\right[a\left]\right[b\left]\right)& =\left[\sigma \right(b\left)\right]\left[\sigma \right(a\left)\right],\hfill \\ \hfill \in & \left[a\right]+\left[b\right]\iff \left[b\right]=-\left[a\right].\hfill \end{array}$$

Now, let $a,b,c\in A$ and $\left[e\right]\in \left(\right[a]+[b\left]\right)+\left[c\right]$. As a result, $\left[e\right]$ also belongs to $\left[x\right]+\left[c\right]$ for some $\left[x\right]\in \left[a\right]+\left[b\right]$. Consequently, we can express e as $s_{1}x{s}_2+t_{1}c{t}_2$ and x as $v_{1}a{v}_2+w_{1}b{w}_2$ where $s_1,s_2,t_1,t_2,v_1,v_2,w_1,w_2\in Orth\left(A\right)$. Then,

$$\begin{array}{cc}\hfill e& =s_{1}x{s}_2+t_{1}c{t}_2\hfill \\ \hfill & =s_1(v_{1}a{v}_2+w_{1}b{w}_2)s_2+t_{1}c{t}_2\hfill \\ \hfill & =\left(s_1{v}_1\right)a\left(v_2{s}_2\right)+\left(s_1{w}_1\right)b\left(w_2{s}_2\right)+t_{1}c{t}_2\hfill \\ \hfill & =\left(s_1{v}_1\right)a\left(v_2{s}_2\right)+[\left(s_1{w}_1\right)b\left(w_2{s}_2\right)+t_{1}c{t}_2]\hfill \end{array}$$

Let $y=\left(s_1{w}_1\right)b\left(w_2{s}_2\right)+t_{1}c{t}_2$. Then $\left[e\right]\in \left[a\right]+\left[y\right]$ with $\left[y\right]\in \left[b\right]+\left[c\right]$, implying $\left[e\right]\in \left[a\right]+\left(\right[b]+[c\left]\right)$. The same reasoning provides $\left[a\right]\left(\right[b\left]\right[c\left]\right)=\left(\right[a\left]\right[b\left]\right)\left[c\right]$.

Finally, let $\left[x\right]\in \left[c\right]\left(\right[a]+[b\left]\right)$. Therefore, $\left[x\right]\in \left[c\right]\left[d\right]$ for some $\left[d\right]\in \left[a\right]+\left[b\right]$. These provide equations $x=rcsdt$ and $d=s_{1}a{s}_2+t_{1}b{t}_2$. Thus,

$$\begin{array}{cc}\hfill x& =rcsdt\hfill \\ \hfill & =rcs[s_{1}a{s}_2+t_{1}b{t}_2]t\hfill \\ \hfill & =rcs{s}_{1}a{s}_{2}t+rcs{t}_{1}b{t}_{2}t\hfill \\ \hfill & =rc\left(s{s}_1\right)a\left(s_{2}t\right)+rc\left(s{t}_1\right)b\left(t_{2}t\right)\hfill \end{array}$$

with $r,s{s}_1,s_{2}t,s{t}_1,t_{2}t\in Orth\left(A\right)$, concluding that $\left[x\right]\in \left[c\right]\left[a\right]+\left[c\right]\left[b\right]$. Similarly, $\left(\right[a]+[b\left]\right)\left[c\right]\subseteq \left[a\right]\left[c\right]+\left[b\right]\left[c\right]$. □

Observe that S is not necessarily convex, and neither satisfies $xS=Sx$ (see 4.9). Thus, $A/\sim$ may not be a multiring.

Definition 5.3.

We define the superring $(A/\sim ,+,·,[0],[1\left]\right)$ as the orthogonal fragment of A, and denote by $A{/}_{m}Orth\left(A\right):=A/\sim$.

Theorem 5.4.

If $Orth\left(A\right)\subseteq Z\left(A\right)$, then $A{/}_{m}Orth\left(A\right)$ is a (non-commutative) hyperring.

Proof. 

This is a particular case of 4.16. □

Theorem 5.5.

Let F be a field and $A=M_2\left(F\right)$. Then $A{/}_{m}Orth\left(A\right)$ consists of rotation $2\times 2$ matrices over F.

Proof. 

Note that $a\in Orth\left(A\right)$ if, and only if, $a{a}^t=i{d}_2$, with $\sigma \left(a\right)=a^t$ the transpose matrix of $a={\left(a_{ij}\right)}_{2\times 2}$. Applying the definition of matrix product we have to solve the following system:

$$\left\{\begin{array}{c}{a}_{11}^2+a_{12}^2=1\hfill \\ a_{21}^2+a_{22}^2=1\hfill \\ a_{11}{a}_{21}+a_{12}{a}_{22}=0\hfill \\ det{\left(a\right)}^2=1\hfill \end{array}\right..$$

We conclude that

$$Orth\left(A\right)=\left\{\left(\begin{array}{cc}x& y\\ y& -x\end{array}\right)|x^2+y^2=1,x,y\in F\right\}\cup \left\{\left(\begin{array}{cc}x& -y\\ y& x\end{array}\right)|x^2+y^2=1,x,y\in F\right\}.$$

(6)

□

If $F=\mathbb{R}$, in (6), the second subset (with positive determinant equal to 1) is the set of orthonormal matrices or the set of linear transformations in ${\mathbb{R}}^2$ that are rotations by some angle $\theta \in [0,2\pi )$ with $x=cos\left(\theta \right)$ and $y=sin\left(\theta \right)$. Moreover, consider the inner product

$${\displaystyle \langle a,b\rangle =\sum _{i,j=1}^2{a}_{ij}{b}_{ij},\mathrm{for}a,b\in A.}$$

One may check the action of elements in $Orth\left(A\right)$ works as a set of isometries. In fact, solving a very similar system of equations as above, we can prove that these actions constitute a subset of isometries such that the related matrix, say $T=\left(t_{ij}\right)$, has determinant different from $\pm (t_{11}-t_{12})$. Thus, this quotient describes the behavior concerning certain kinds of isometry classes considering the underlined inner product.

5.2. Quaternions over Real Closed Fields

Now we explore the diversity of quotients in quaternions. Although it includes a lot of calculations, this provides quick verification of independence regarding normal and convex quotients.

Example 5.6.

Let R be a real closed field and $H=R\{x,y\}/(x^2+1,y^2+1,xy+yx)$ the corresponding quaternion algebra ${(1,1)}_R$: it is a R-division algebra of dimension 4. Put $S=R_{>0}·1\subseteq H$. Note that S satisfies the second condition of the 4.11 (it is a convex set) in the previous section and $S=\left\{\sigma \right(a)·a:a\in H\setminus \{0\left\}\right\}$.

Then $H{/}_{m}S\cong {\mathbb{S}}^3$ as a monoid. And, in this quotient $\overline{x·\sigma \left(x\right)·x}=\overline{x}$, since $\overline{x·\sigma \left(x\right)}=1$.

We observe that, in this case, S is also standard, "normal" and $1-$convex (see 4.7).

Example 5.7.

Let $\mathbb{H}$ the quaternions real algebra endowed with the standard involution $\sigma \left(a\right)=\overline{a}$, for all $a\in \mathbb{H}$. Set $S=\mathbb{R}\setminus \left\{0\right\}$ and define $a/\sim b$ iff $a=\sigma \left(x\right)by$ for some $x,y\in S$. Thus, $\left[0\right]=\left\{0\right\}$, and for a nonzero element a, $\left[a\right]$ is the line determined by the origin and the quaternion a(without $\left\{0\right\}$), i. e. $\mathbb{H}{/}_{m}S\cong R{P}^3$.

Once $S\subseteq Z\left(\mathbb{H}\right)$ (actually, S has the first "normality" property of the 4.11), it is easy to check that $S=\left[1\right]=[-1]$, and $[\pm a]=Sa$, for a a pure quaternion as well. If $a=a_0+a_{1}i+a_{2}j+a_{3}k$ and $b=b_0+b_{1}i+b_{2}j+b_{3}k$ are quaternion numbers, then

$$\left[a\right]+\left[b\right]=\bigcup [x_0+x_{1}i+x_{2}j+x_{3}k],$$

(7)

for $x_i\in \mathbb{R}$, $x_i\in S$, or $x_i=0$, depending on $a_i,b_i\ne 0$, or $a_i\ne 0$ and $b_i=0$ (and vice-versa), or both $a_i=b_i=0$, respectively, for each $i\in \{0,1,2,3\}$. Hence, $\left[a\right]+\left[b\right]$ is the plane determined by $\left[a\right]$ and $\left[b\right]$, containing (or not) the origin.

Example 5.8.

The orthogonal fragment $Orth\left(\mathbb{H}\right)$: Consider $S={\mathbb{S}}^3\subseteq \mathbb{H}$ the sphere of radius equal 1 centered at the origin.

Clearly, $1\in S$ and S is a multiplicative set satisfying $x^{-1}\in S$ whenever $x\in S$. Once $\left|x\right|=x\sigma \left(x\right)$, it is immediate that S is $\sigma -$invariant. It remains to verify that the sphere is also "a normal set" in $\mathbb{H}$ (item 1 of 4.11), and thus the quotient is a multiring. In fact, let $a\in \mathbb{H}$ and $x\in S$, the norm is multiplicative, thus

$$\begin{array}{cc}\hfill \left|ax\right|=\left|a\right|& \Rightarrow a\sigma \left(a\right)x\sigma \left(x\right)=\sigma \left(a\right)a\Rightarrow a\sigma \left(a\right)x=\sigma {\left(x\right)}^{-1}\sigma \left(a\right)a\hfill \\ & \Rightarrow \sigma \left(a\right)ax=\sigma {\left(x\right)}^{-1}\sigma \left(a\right)a\Rightarrow ax=\left(\sigma {\left(a\right)}^{-1}\sigma {\left(x\right)}^{-1}\sigma \left(a\right)\right)a.\hfill \end{array}$$

(8)

Yet, we have ${|\sigma \left(a\right)}^{-1}\sigma {\left(x\right)}^{-1}{\sigma \left(a\right)|=|\sigma \left(a\right)}^{-1}{\left|\right|\sigma \left(x\right)}^{-1}{\left|\right|\sigma \left(a\right)|=|\sigma \left(a\right)}^{-1}\left|\right|\sigma \left(a\right)|=1$, therefore

$$y=\sigma {\left(a\right)}^{-1}\sigma {\left(x\right)}^{-1}\sigma \left(a\right)\in S.$$

We conclude that $ax=ya$ for some $y\in S$, i.e., $aS\subseteq Sa$. The reverse inclusion follows by symmetry. Actually, in a general division algebra with standard involution, this property holds since $S=Orth\left(\mathbb{H}\right)$.

Let $a\sim b$ iff $a=\sigma \left(x\right)by$, with $x,y\in S$. Hence, $a\sim b$ iff $\left|a\right|=\left|b\right|$. It is obvious that $\left[0\right]=\left\{0\right\}$ and $\left[1\right]={\mathbb{S}}^3=S$. The elements $\left[a\right]$ are spheres centered at the origin with radius $\sqrt{\left|a\right|}$. In fact, $\sqrt{\left|a\right|}=a·{\displaystyle \frac{\sigma \left(a\right)}{\sqrt{\left|a\right|}}}$, with $x={\displaystyle \frac{\sigma \left(a\right)}{\sqrt{\left|a\right|}}}\in S$. Therefore, $\sqrt{\left|a\right|}\sim a$. For $a\in \left[b\right]$, $\left[a\right]+\left[b\right]$ is the fulfilled sphere with radius $2\sqrt{\left|a\right|}$. If $\left|a\right|>\left|b\right|$, both triangular inequalities $|a+b|\le \left|a\right|+\left|b\right|$ and $\left|\left|a\right|-\left|b\right|\right|\le |a-b|$ provide that $\left[a\right]+\left[b\right]$ is the ’hollow’ surface determined by the two spheres with coincident centers at the origin and radius $\sqrt{\left|a\right|}+\sqrt{\left|b\right|}$ and $\sqrt{\left|a\right|}-\sqrt{\left|b\right|}$. Moreover, $\mathbb{H}{/}_{m}S\cong {\mathbb{R}}_{+}$ as a multimonoid with multiaddition satisfying:

$$\left[a\right]+\left[b\right]=\left\{\begin{array}{c}[a-b,a+b] if a\ge b;\hfill \\ [b-a,a+b] if b\ge a.\hfill \end{array}\right.$$

Thus, this is the Triangle Hyperfield 2.7. In the last example, S does not satisfy the convexity property. At the same time, 5.6 shows Marshall coherent sets satisfying many properties simultaneously. These examples suggest the definitions in the last section provide elements of different types of structures and independence between statements in Theorem 4.11.