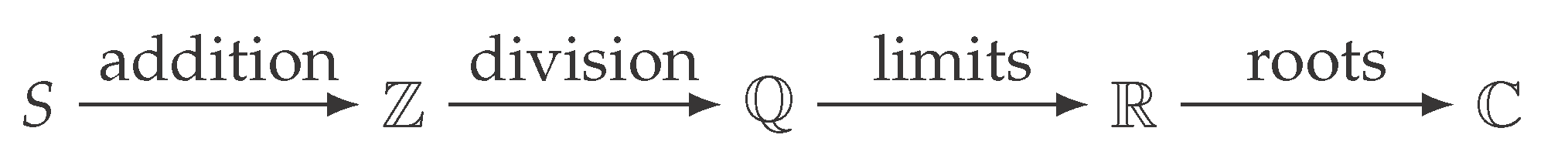1. Introduction
The integers
appear throughout mathematics as a distinguished set: the digits of balanced ternary [
5], the truth values of three-valued logic [
4], and the eigenvalues of fundamental physical operators [
8]. This ubiquity is not coincidental. We demonstrate that this set is not merely useful but necessary—it is the unique finite algebra satisfying the minimal requirements for a self-consistent generative system.
Our approach begins not with numbers but with states: conditions of being that precede quantification. From three primordial states and the demand that their interactions be closed, total, and stable, exactly one algebra emerges, aligning with broader mathematical structures [
6,
7].
2. The Primordial States
2.1. Before Number
Prior to arithmetic and quantity, there exist three fundamental conditions of being:
Definition 2.1 (Primordial States). The three primordial states are:
-
1
(Creation): The condition of arising.
-
2
(Destruction): The condition of passing.
-
3
(Potential): The condition of poise, neither arising nor passing.
These are modes of becoming, describing the fundamental relations to existence.
2.2. The Interaction Constraints
When two states interact, a state must result. We impose three constraints:
Axiom 1 (Closure).
For any two states , their interaction produces a state in the set:
Axiom 2 (Totality). Every interaction is defined, with no undefined combinations.
Axiom 3 (Stability). The system neither collapses to a single state nor proliferates without bound.
Lemma 2.2 (Cancellation is Forced).
Under Axioms 1–3, there must exist a pair of distinct non-neutral elements whose interaction yields the neutral state . Specifically, stability forces
Proof. Suppose, for contradiction, that no interaction of two distinct non-neutral states yields . Consider the possible outputs of :
Case 1: . Then by closure, iterating produces unbounded “positive” accumulation, violating stability.
Case 2: . By symmetry with Case 1, this leads to unbounded “negative” accumulation.
Case 3: and with . Then the non-neutral states form a closed subsystem excluding , and iterative self-composition proliferates without returning to neutral—violating stability.
In all cases, the absence of cancellation produces either unbounded growth or permanent exclusion of the neutral state. Therefore, stability requires . □
2.3. The Critical Property: Cancellation
The interaction is therefore derived, not postulated. Cancellation preserves information conservation (no net gain or loss of “being”) and maintains symmetry under inversion. Lemma 2.2 establishes that any algebra satisfying closure, totality, and stability must exhibit this property.
3. The Emergence of Number
3.1. The Mapping to Algebra
We map states to symbols for manipulation:
This preserves interactions:
3.2. The Algebraic Axioms
The primordial constraints translate to algebraic requirements:
Axiom 4 (Additive Identity). S contains such that , . Thus .
Axiom 5 (Multiplicative Identity). S contains such that , . Thus .
Axiom 6 (Additive Inverse of Multiplicative Identity). S contains such that . Thus .
Lemma 3.1 (Two Elements are Insufficient). No two-element set satisfies Axioms 4–6.
Proof. Any two-element set drawn from lacks at least one required element:
: Missing ; fails Axiom 6 (no additive inverse of 1).
: Missing 1; fails Axiom 5 (no multiplicative identity).
: Missing 0; fails Axiom 4 (no additive identity).
□
Lemma 3.2 (Four Elements Overdetermine the System). No four-element algebra satisfies Axioms 1–6 while maintaining closure and stability.
Proof. Suppose with . By totality, x must interact with all elements of T. Consider the required interactions:
Case 1: If (identity), (identity), and (inverse), then we require . If , then , so , implying —contradiction. If , then , so —contradiction.
Case 2: If x acts as an absorbing element ( for some operations), then repeated application collapses the algebra toward , violating stability.
Case 3: If x interacts to produce only elements of , then x is algebraically redundant—it adds no new structure and can be removed without loss.
No consistent role for a fourth element exists. □
Theorem 3.3 (Uniqueness of the Minimal Set). The unique finite set satisfying Axioms 4–6 is .
Proof. Axioms 4–6 require exactly three distinct elements: 0 (additive identity), 1 (multiplicative identity), and (additive inverse of 1). Lemma 3.1 excludes smaller sets. Lemma 3.2 excludes larger sets. Therefore is unique. □
3.3. Self-Regeneration
Definition 3.4 (Self-Regenerating Algebra). A finite algebra A is self-regenerating if every element of A is the output of some binary operation on two distinct elements of A.
Theorem 3.5 (Self-Regeneration of S). is self-regenerating. No proper subset of S is self-regenerating under addition.
Proof. Under addition of distinct pairs:
Each element is produced exactly once. For
: only
and
are available; 0 is never produced by addition of distinct elements. Similarly,
fails. Only
S regenerates all its elements through distinct-pair operations. □
4. The Completion Sequence
4.1. Non-Closure as Generative Mechanism
S is closed under multiplication but not under addition: . This additive non-closure is not a defect but the engine of generation.
4.2. The Extension Chain
Theorem 4.1 (The Completion Sequence).
The unique chain of field extensions forced by successive closure demands is:
Proof. Each extension addresses a specific non-closure:
: Iterated addition generates all integers.
: Demanding multiplicative inverses (division) generates rationals.
: Demanding metric completeness (Cauchy sequence convergence) generates reals.
: Demanding algebraic closure (roots of all polynomials) forces .
□
Figure 1.
The Completion Sequence.
Figure 1.
The Completion Sequence.
4.3. Termination
Theorem 4.2 (Termination at ). The extension sequence halts at .
Proof. By the Fundamental Theorem of Algebra, is algebraically closed: every non-constant polynomial with complex coefficients has a root in . Thus , and no further algebraic extension is required. □
5. The Termination Certificate
Definition 5.1 (Termination Certificate). A termination certificate for the completion sequence is a minimal non-trivial identity in that:
-
1
Connects the algebraic forcing element (i) with the analytic forcing elements (e, π);
-
2
Resolves entirely to elements of the generating set S.
Theorem 5.2 (Euler’s Identity as Termination Certificate).
The identity
is the termination certificate for the completion sequence.
Proof. The identity connects:
e: forced by analytic completeness as ;
: forced as the period of the complex exponential ;
i: forced by algebraic closure as .
Resolution to
S: We have
,
, and thus:
The completed system expresses its fundamental relation using only the primordial alphabet. □
Corollary 5.3 (The Ouroboros Property). The completion sequence begins with S containing 0 and terminates with an identity resolving to 0. The algebra returns to its origin.
6. The Central Theorem
Definition 6.1 (Complete and Generative). A finite algebra A is complete before extension if it contains all required identity and inverse elements. It is generative after extension if its radical closure produces a strictly larger algebraically closed field.
Theorem 6.2 (The Primordial Algebra Theorem). is the unique finite algebra that is complete before extension and generative after extension.
Proof. Completeness :
S contains 0 (additive identity), 1 (multiplicative identity), and (additive inverse of 1, and the unique non-trivial involution satisfying ).
Generativity: Under radical closure:
Exclusion of alternatives:
: Closed under radicals (, ). Never escapes. Not generative.
: Generates i via , but then forces inclusion of 1. Not complete before extension.
Only S satisfies both properties. □
7. Structural Correspondences
The primordial algebra exhibits isomorphism with several established structures:
8. Conclusion
We have established that:
Three primordial states and the demand for closure, totality, and stability force a unique algebra (Lemmas 2.2, 3.1, 3.2; Theorem 3.3).
This algebra is self-regenerating: every element is produced by operations on distinct elements (Theorem 3.5).
The completion sequence is forced by successive closure demands and terminates at (Theorems 4.1, 4.2).
Euler’s Identity serves as the termination certificate, resolving the completed system to the primordial alphabet (Theorem 5.2).
is the unique algebra that is complete before extension and generative after it (Theorem 6.2).
The primordial algebra is not constructed but derived. From states to numbers to fields to closure, the path is forced at every step.
References
- Euler, L. Introductio in analysin infinitorum; Lausanne, 1748. [Google Scholar]
- Peano, G. Arithmetices principia, nova methodo exposita; Turin, 1889. [Google Scholar]
- Peirce, C.S. The Categories Defended. Harvard Lectures on Pragmatism, 1903. [Google Scholar]
- Łukasiewicz, J. On Three-Valued Logic. Ruch Filozoficzny 1920, 5, 170–171. [Google Scholar]
- Knuth, D.E. The Art of Computer Programming. Seminumerical Algorithms; Addison-Wesley, 1981; Vol. 2. [Google Scholar]
- Baez, J.C. The Octonions. Bull. Amer. Math. Soc. 2002, 39, 145–205. [Google Scholar] [CrossRef]
- Tegmark, M. The Mathematical Universe. Found. Phys. 2008, 38, 101–150. [Google Scholar] [CrossRef]
- Yang, C.N. The Law of Parity Conservation and Other Symmetry Laws of Physics. In Nobel Lecture; 1957. [Google Scholar]
- Macedonia, C.J. Principia Kosmoplex: Mathematical Principles of Computational Physics with Emphasis on Derivations of Constants and Falsifiable Experimentation (Version 4); Zenodo, 2025. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).