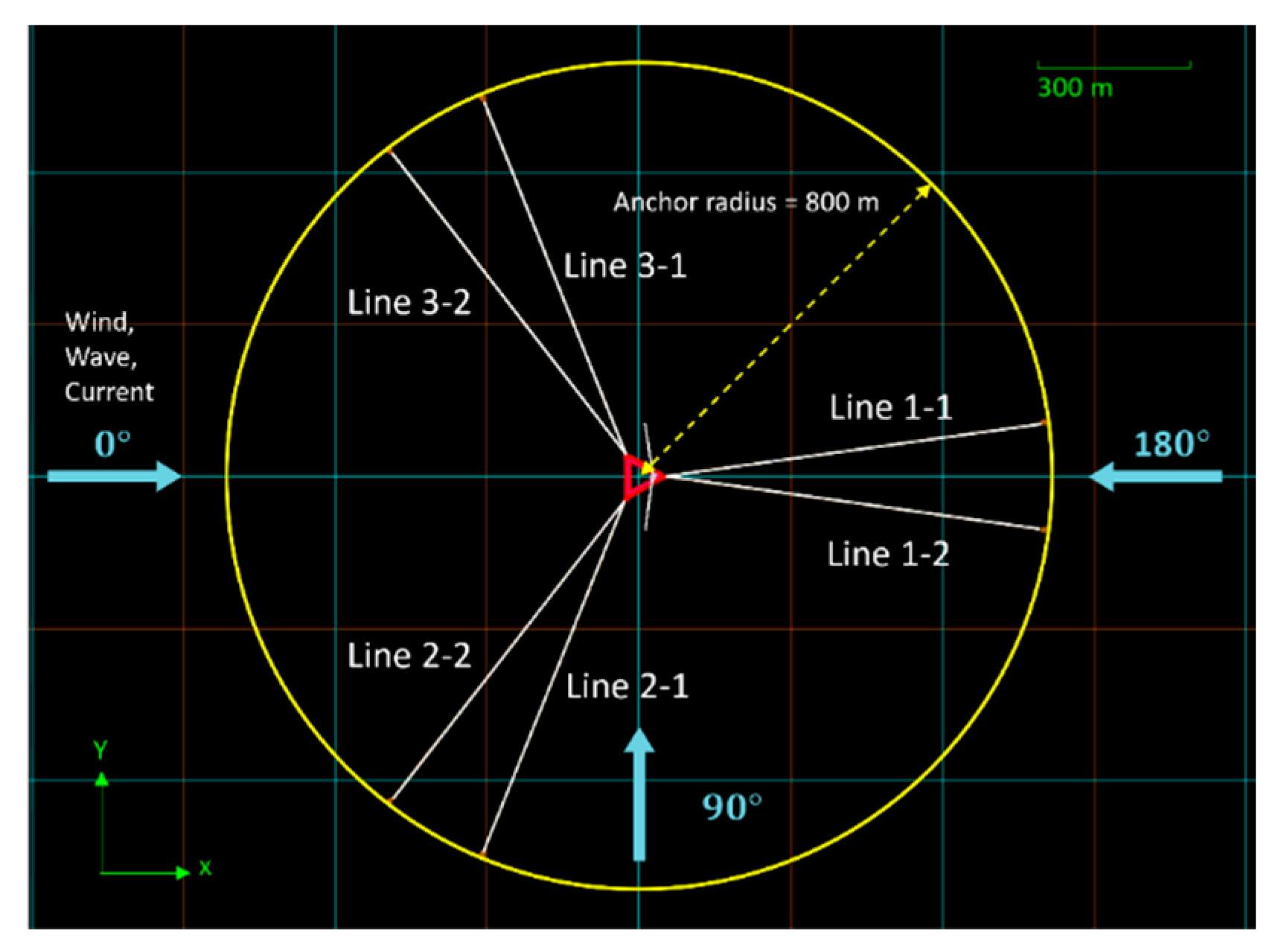
1. Introduction
Wind energy is one of the fastest-growing sources of renewable and sustainable energy. The global offshore wind pipeline, including both operational and planned projects, has reached 453.6 GW, with Europe leading the way. While Europe and China currently dominate the more advanced stages of offshore wind development, the United States and Oceania are also making significant progress (McCoy et al., 2024). In the first half of 2024, Europe added 6.4 GW of new wind power capacity, with 5.7 GW contributed by the EU-27 countries. According to industry forecasts, global offshore wind capacity is projected to reach 486 GW (Bloomberg New Energy Finance, BNEF) or 421 GW (4C Offshore) by 2035. As more offshore wind resources are in deeper waters, accelerating the development of floating wind technology has become increasingly important. Floating wind systems allow turbines to operate in water depths greater than 60 meters, unlocking new opportunities in high-wind-speed regions located farther offshore. By 2030, the European Union is expected to achieve around 350 GW of total wind energy capacity, comprising 296 GW from onshore and 54 GW from offshore wind falling short of its 425 GW target as shown in
Figure 1. (GWEC, 2024). Achieving this target and advancing toward net-zero carbon emissions will require accelerating the design and deployment of offshore wind technologies, including floating wind, to rapidly scale up clean energy production.
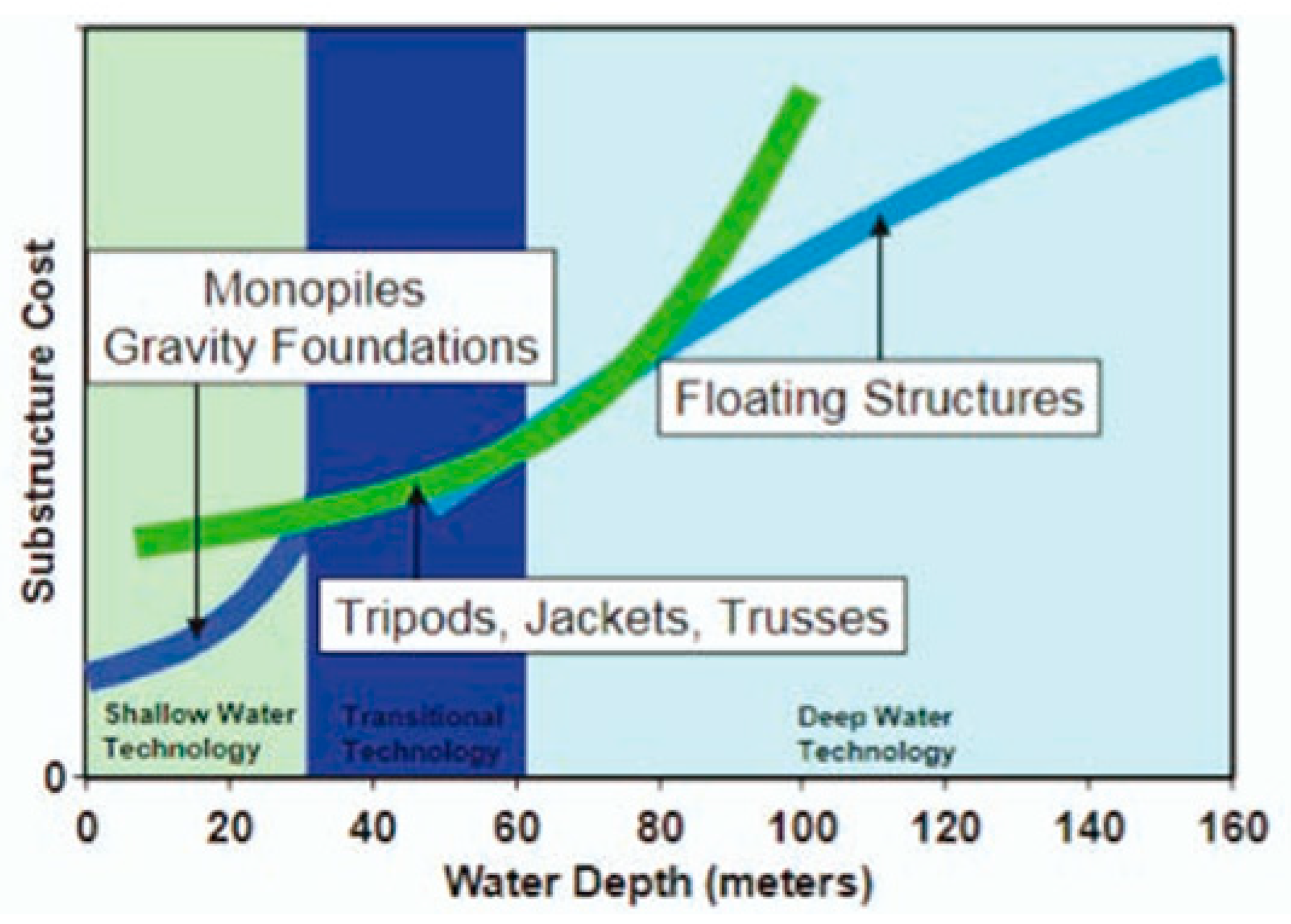
In Taiwan, offshore wind development has primarily focused on nearshore shallow waters using fixed-bottom foundations. However, as these areas become increasingly saturated, attention is shifting toward floating wind technology for deeper waters. According to the Global Wind Energy Council, more than 80% of the world’s offshore wind potential lies in waters deeper than 60 meters. In Taiwan, offshore areas exceeding this depth are estimated to have the potential to support up to 9 GW of installed capacity (Lu et al., 2015). However, the cost of installing traditional fixed-bottom wind turbines rises sharply beyond this depth (Hywind Kincardine Windfloat Atlantic Fukushima Forward, 2023). As a result, floating wind turbines are increasingly recognized as the most viable solution for wind energy development in deep-water regions, as illustrated in
Figure 2.
Taiwan’s challenging environmental conditions particularly typhoons and earthquakes require mooring systems proven overseas to undergo rigorous re-evaluation to ensure adequate load-bearing capacity and navigational safety. This is vital for maintaining structural integrity and long-term reliability.
Floating platforms are continuously exposed to wind, waves, and currents that induce drift, which must be controlled within safe operating limits. Excessive motion can cause deviation from optimal wind zones, risk of collision, and increased maintenance costs, especially under extreme conditions (McMillan et al., 2024). Therefore, an effective mooring system is essential to ensure platform stability and reliable turbine operation.
To ensure a comprehensive assessment during the initial design phase, external environmental conditions are categorized into four limit states, as defined by DNV-OS-E301 (DNV-OS-E301, 2021):
ULS (Ultimate Limit State): Evaluates the maximum tension in mooring lines under extreme environmental conditions.
FLS (Fatigue Limit State): Assesses the fatigue life of mooring lines subjected to long-term waves and wind loading.
ALS (Accidental Limit State): Considers the impact of mooring line failure, vessel collisions, or other accidental events.
SLS (Serviceability Limit State): Examines platform performance and stability under normal operating conditions.
This study will first assess whether the mooring line tensions and platform motion responses under ULS conditions provide sufficient safety margins to ensure the overall stability of the system. Based on these results, further evaluations under SLS, FLS, and ALS conditions will be progressively carried out to complete the overall design assessment.
Based on the preceding discussion, this study selects the catenary mooring system as a widely used solution for shallow-water offshore engineering as the target design. Among various mooring line configurations, pure chain mooring lines without additional modifications exhibit the steepest restoring force curve. Therefore, this study does not incorporate any additional modifications, such as clump weights or buoys. Instead, the mooring system will be designed using unmodified chain material, following catenary theory. This approach simplifies the design parameters and allows for a clearer comparison of mooring line behavior across different configurations.
Shallow water depth constraints cause significant variation in the touchdown point (TDP) of mooring lines. When the touchdown section is lifted off the seabed, it can generate high instantaneous tension. If the mooring system is poorly designed, this can accelerate chain fatigue and increase the risk of system failure. The horizontal restoring force curve of mooring lines shows that excessive pre-tension may amplify platform motion, leading to a sharp rise in restoring forces. Additionally, under depth-limited conditions (Huang & Yang, 2021), mooring tension fluctuations tend to become more severe in shallow waters.
Therefore, in addition to meeting the basic safety requirements of floating wind turbine platforms such as limiting drift and controlling platform inclination mooring system design must also optimize tension distribution to reduce the risk of failure caused by excessive loads. As the deployment of large-scale wind turbines expands, cost-effective mooring system design becomes increasingly critical. This study focuses on eliminating unnecessary redundancy and reinforcing key load-bearing components to improve design efficiency, lower the LCOE, and enhance overall project feasibility.
Building on the findings of (Yue et al., 2023), this study examines how mooring layout parameters affect platform motions and mooring dynamics based on the system’s dynamic response. By optimizing these parameters and using algorithmic methods, we aim to enhance wind-farm stability, lower collision risk, and reduce economic losses. Focusing on asymmetric mooring, the study targets reduced drift and improved overall stability. Results show that asymmetric layouts can enhance stability while cutting material redundancy and unnecessary motions. Prior work by (Formosa & Sant, 2022) indicates that asymmetric systems strongly influence pitch, roll, and line tensions. (Yu et al., 2024) f further show that directional environmental loads can make symmetric layouts suboptimal under some conditions.
According to (Mulyadi et al., 2024) a fourteen-line asymmetric system for offshore aquaculture that maintained integrity and stability while limiting environmental impact. The results demonstrate that this asymmetric configuration provides excellent structural integrity and stability, effectively withstanding environmental loads while minimizing the system’s impact on coastal ecosystems.
Overall, mooring optimization effectively reduces platform motions. Under relatively uniform conditions, a well-designed asymmetric configuration achieved by tuning parameters such as line length and line can improve stability, balance tension distribution, and lower costs.
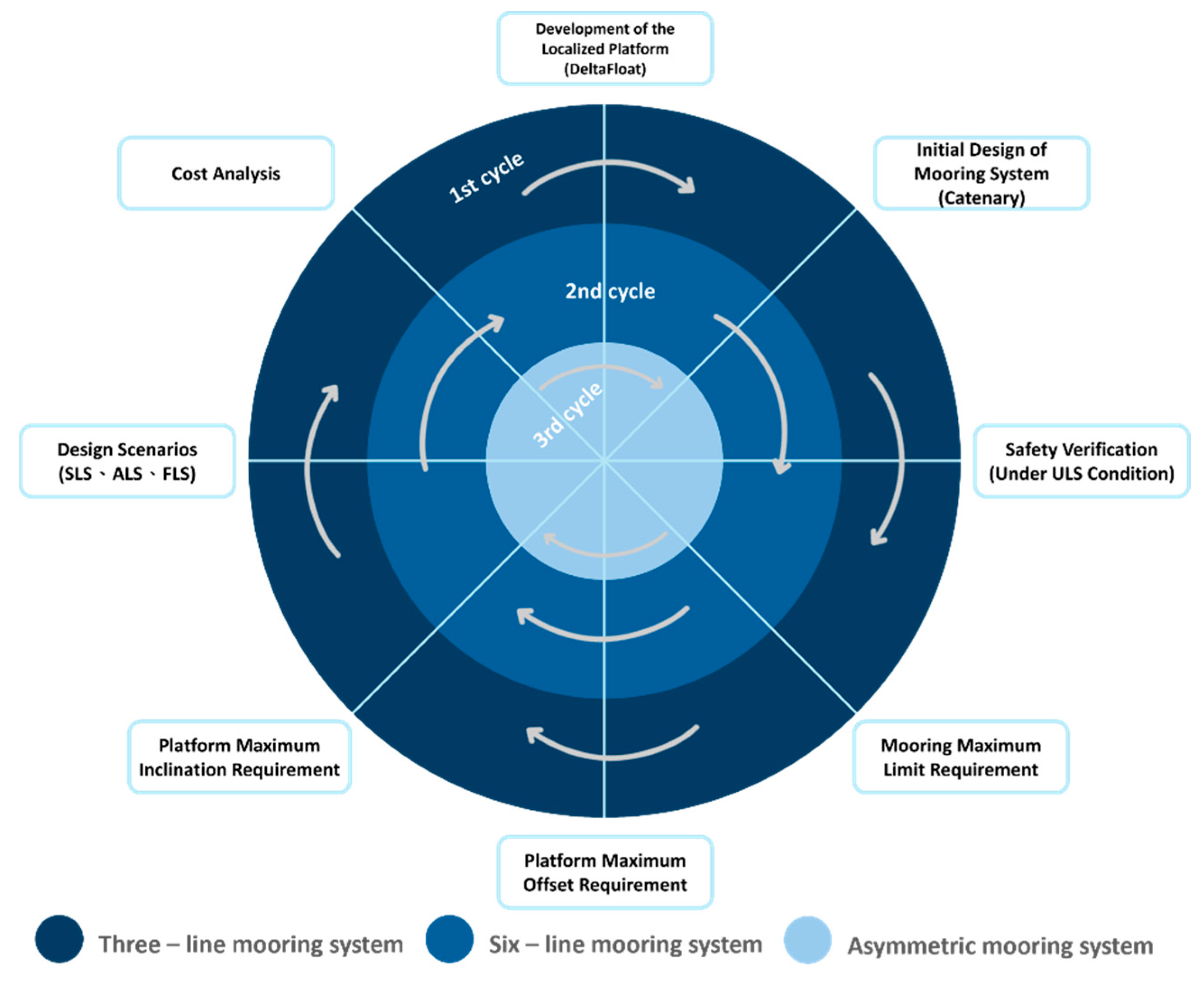
In this study, a three-stage design spiral approach is adopted to systematically refine and optimize the mooring system configuration for floating wind platforms in the Taiwan Strait. The first stage involves the development of a three-line mooring system, primarily aimed at identifying fundamental design trends and understanding the relationship between mooring parameters and platform motion responses. Based on these insights, the second stage introduces a six-line mooring configuration. Statistical analysis, specifically Analysis of Variance (ANOVA), is applied to determine the key design parameters that significantly influence system performance, with an emphasis on minimizing failure risk and ensuring cost-effectiveness. In the final stage, an asymmetric mooring layout is proposed and optimized. This configuration aims to achieve a balance between structural safety and economic feasibility, ultimately providing a more practical solution tailored to Taiwan’s unique offshore environmental conditions, as shown in
Figure 3.
5. Numerical Model Result and Discussions
5.1. Free Decay Test
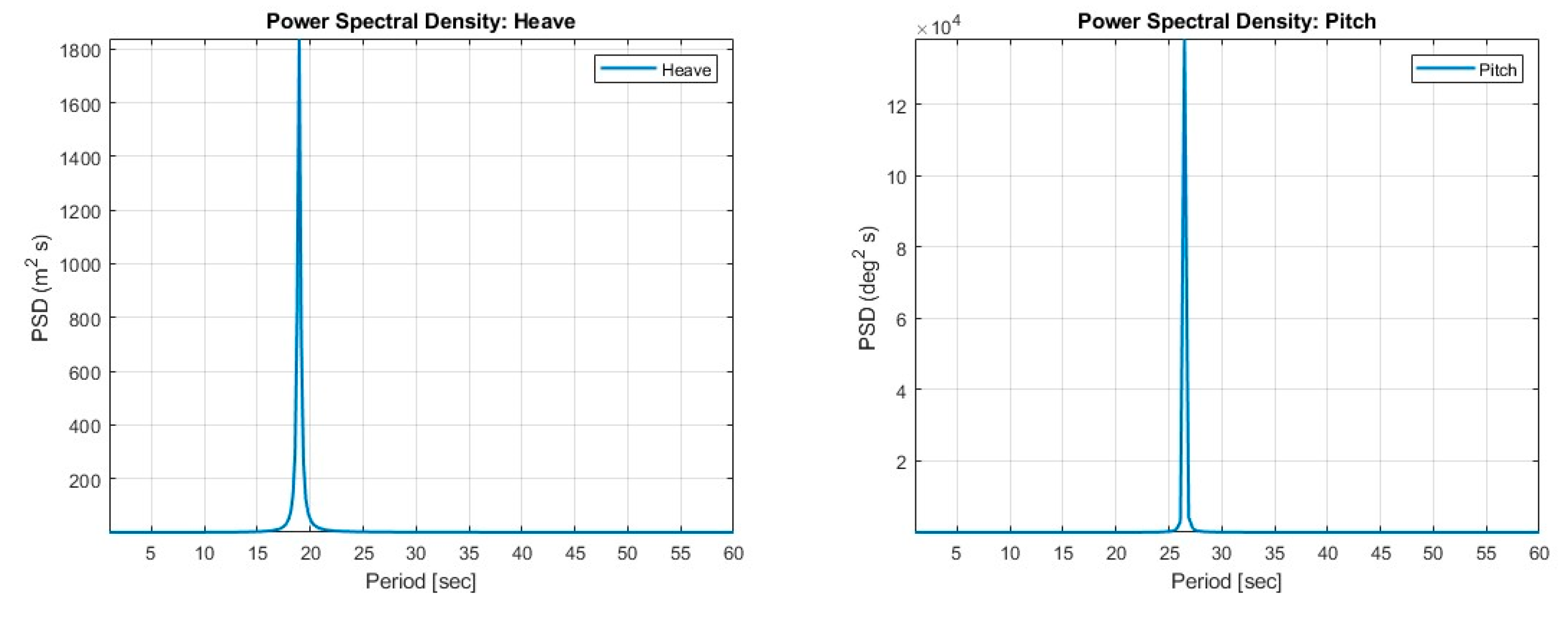
In this section, all free decay tests are performed without mooring lines installed, focusing on the degrees of freedom among the six DOFs that are primarily governed by the platform’s inherent restoring forces specifically, Heave and Pitch. These motions are less influenced by mooring effects and more representative of the platform’s natural behavior. The objective of these tests is to identify the platform’s natural periods and validate the accuracy of the numerical model, thereby ensuring sufficient confidence in the model’s reliability for subsequent simulation analyses. At the same time, the natural periods will be verified to ensure they are well separated from the typical wave periods in the target sea area, reducing the risk of resonance and enhancing structural safety, as shown in
Figure 8.
5.2. Three-Line Mooring System Optimization
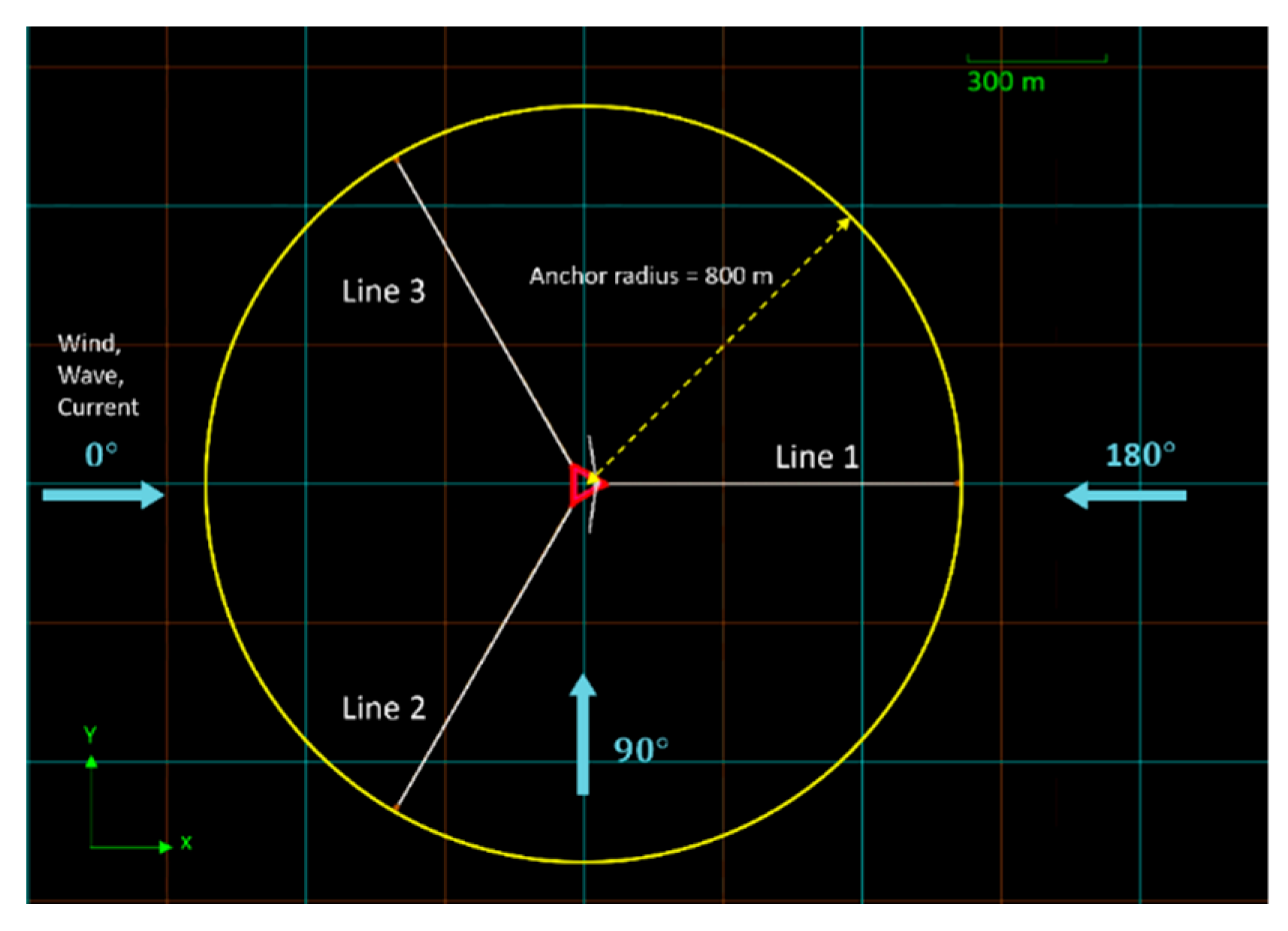
The study begins with the design of a three-line baseline mooring system. To efficiently evaluate and optimize mooring configuration parameters, the environmental incident angle is initially fixed at 0 degrees as shown in
Figure 9. This simplification allows for a focused screening and optimization of key design parameters, including mooring line length and line diameter, before proceeding to more complex multi-directional environmental analyses.
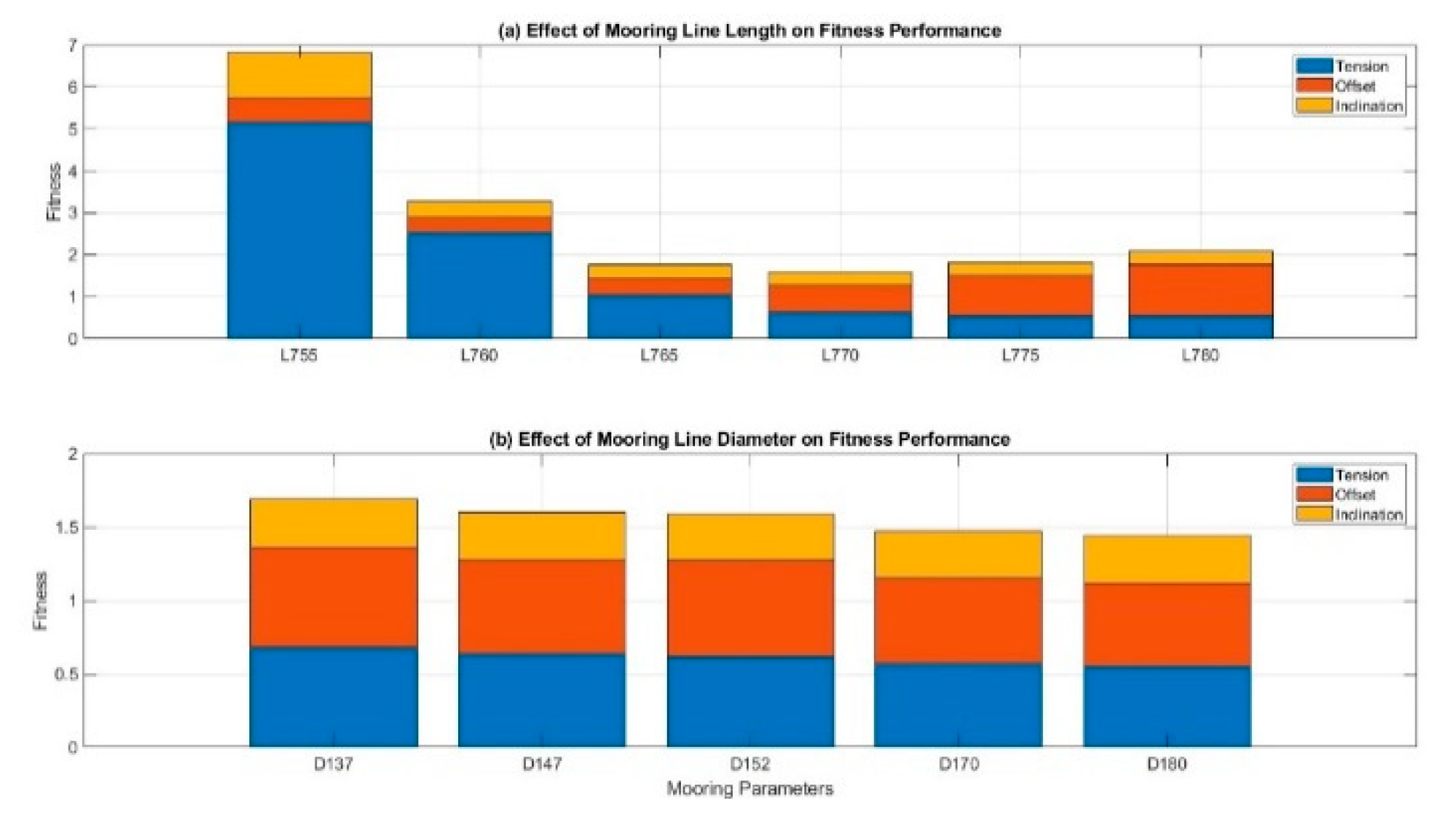
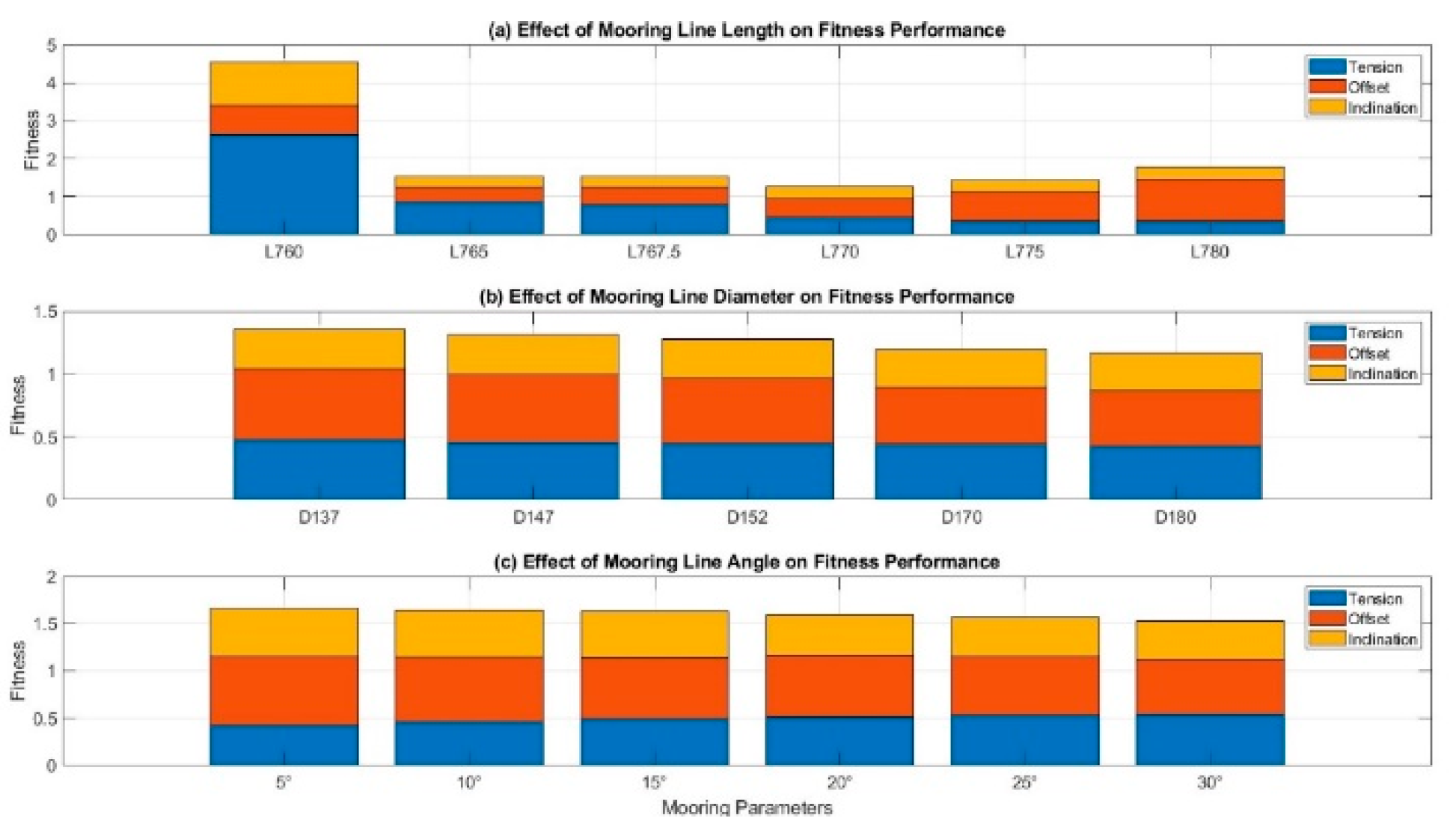
According to the fitness comparison results for the three-line mooring system, illustrating the effects of mooring line length and diameter on overall performance. When the line diameter is fixed at 152 mm, the total fitness decreases markedly by increasing line length, reaching a minimum at L770, which achieves the most balanced response among tension, offset, and inclination. When the mooring line length is fixed at 770 m, varying the line diameter shows that the D180 mm configuration achieves the lowest total fitness value, making it the preferred choice for design optimization, as shown in
Figure 10.
Overall, the three-line mooring system converges to an optimal configuration of L770 m line length and D180 mm diameter, providing a stable balance between tension control and platform motion performance under the 800 m anchor radius constraint.
To determine whether mooring line diameter and length are the dominant design parameters for this mooring system, we performed a combined sensitivity analysis. In this analysis, both parameters were varied simultaneously to observe their coupled effects on system performance. The goal is to validate whether the currently selected configuration represents the optimal setup for the three-line mooring system under the specified design conditions, and to provide a basis for further optimization if necessary.
In this analysis, the environmental incident angle is fixed at 0 degrees, and Line 1, which is aligned with the incident direction, is selected as the reference for tension analysis. However, based on the results of previous calculations, it was observed that variations in mooring line length or diameter have a minimal impact on platform inclination. Therefore, this parameter study will primarily focus on the comparison of mooring line tension and platform offset as the key performance indicators, as shown in
Figure 11.
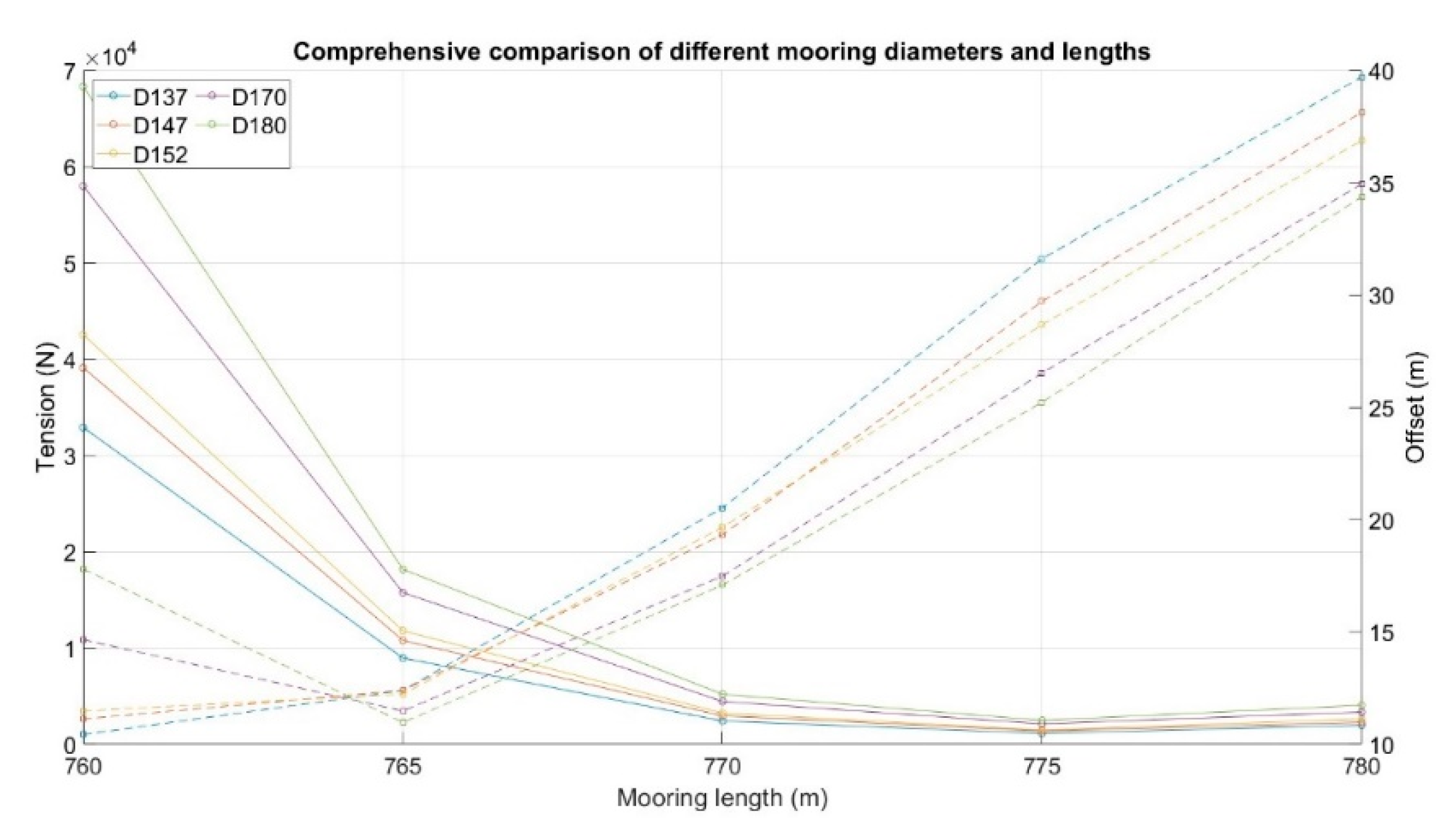
According to the results, increasing the mooring line length effectively reduces the maximum tension by relieving the system’s overall tension load. Nevertheless, this reduction comes with a corresponding increase in platform offset, which is consistent with the trends observed in previous analyses.
The results also reveal that mooring line length significantly influences the shape of the catenary segment. When the line length is relatively short (e.g., L760 case), the tension differences among various diameters (D137, D147, D152, D170, D180) are more pronounced. In contrast, when the line length increases to 780 m, these tension differences diminish, indicating a reduced sensitivity to diameter variations.
This suggests that in longer mooring configurations, the tension response is governed more by the shape of the catenary segment provided by the increased line length, rather than by the unit weight differences associated with varying line diameters. Therefore, it can be concluded that mooring line length is the dominant design parameter for catenary mooring systems in shallow-water applications.
It is worth noting that when the mooring line length is 760 meters, the platform offset appears to be greater than that of the 765-meter configuration when the mooring line diameter is increased (e.g., to D170 or D180). Upon further investigation, it was found that larger mooring line diameter enhances the restoring force during platform oscillation. However, with a shorter line length of 760 meters, the catenary segment becomes relatively stiff and limited in flexibility, causing the swinging forces to be transmitted more directly and rapidly to the platform. This results in excessive oscillation, leading to an unexpected increase in platform offset that deviates from the general trend.
These findings highlight the importance of carefully balancing both mooring line length and diameter in the design of catenary mooring systems, particularly in shallow-water or space-constrained environments, to ensure optimal system performance and avoid undesirable motion amplification.
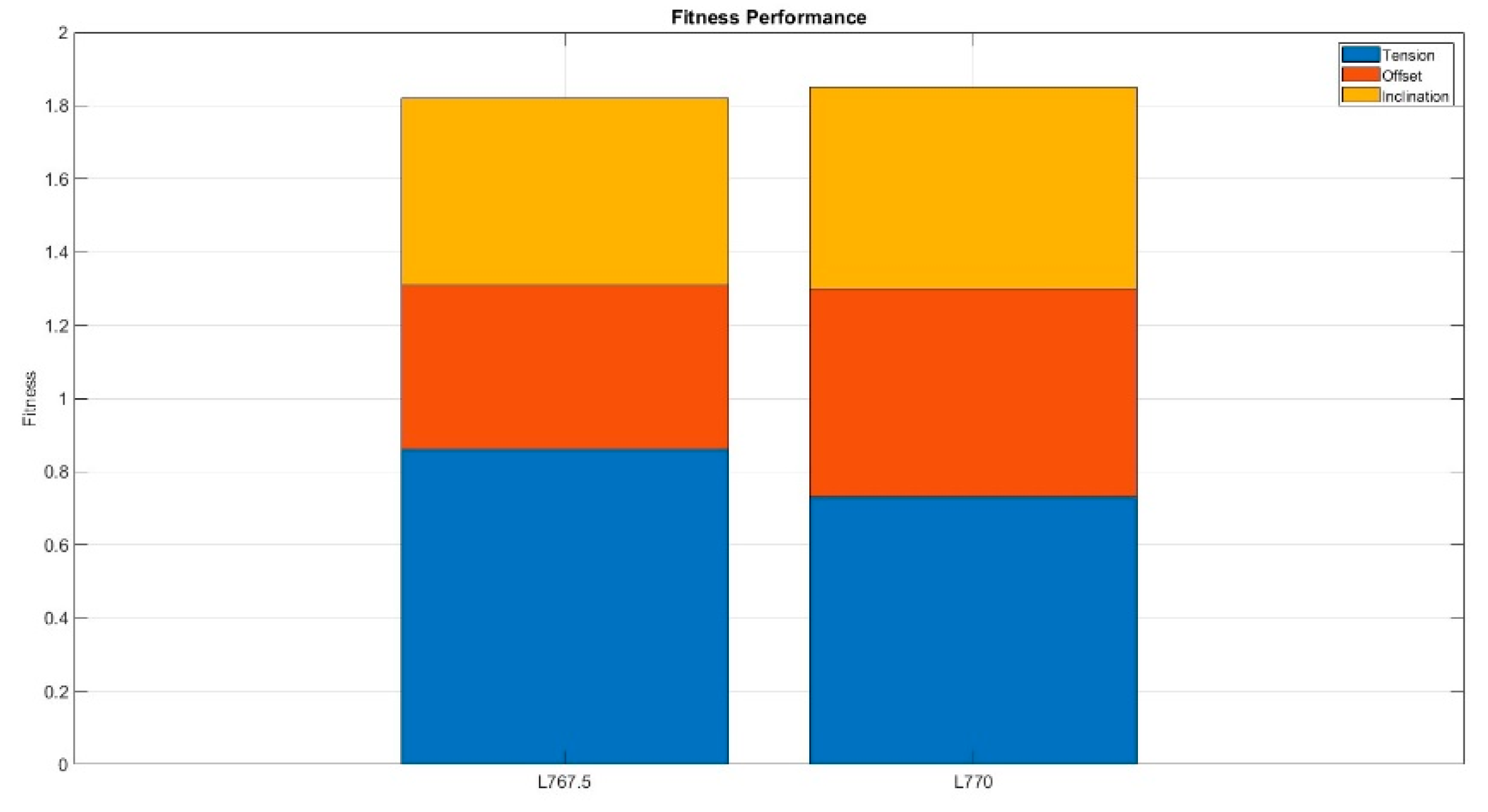
Additionally, the results reveal that the intersection points of the overall trend lines for tension and offset occur at a mooring line length of approximately 767.5 meters, showing a slight deviation from the initially selected 770 meters. Based on this observation, L767.5 and L770 are selected for further comparison in the next phase of the analysis to determine the optimal mooring line length configuration.
Following this, a quantitative comparison will be conducted using the Fitness parameter, focusing on the maximum values of each performance indicator such as tension and platform motion under the evaluated environmental load directions (from 0 to 180°), as shown in
Figure 12.
5.3. Six-Line Mooring System Optimization
Based on the optimization results of the three-line mooring system presented in
Section 5.2, although the configuration meets international standards, it still exhibits limited tension redundancy under certain incident angles. Additionally, both the study (Mooring Systems for Floating Offshore Wind: Integrity Management Concepts, Risks and Mitigation, 2023) and (Castillo et al., 2023) have highlighted that three-line mooring systems generally lack sufficient safety redundancy in extreme or accidental scenarios.
In response to these concerns, this section proposes the development of a six-line mooring configuration. The objective is to reduce tension concentration and improve safety redundancy by increasing the number of mooring lines, thereby enhancing the overall reliability and robustness of the mooring system, as shown in
Figure 13.
In a six-line mooring system, the environmental incident angle is fixed at 0 degrees, and analysis of a composite performance metric (combining mooring line tension, platform offset, and inclination) shows that mooring line length and diameter significantly influence overall system performance. Among the lengths examined, a 770 m mooring line (L770) achieves the lowest total fitness value (1.27), indicating the best balance of reduced tension, moderate offset, and limited inclination. In contrast, a shorter 760 m line (L760) produces excessive tension and deviates from the design trend and is therefore excluded from consideration. For line diameter, although the largest tested diameter of 180 mm (D180) yields the best performance (total fitness = 1.17), a 152 mm diameter (D152) is selected as the preferred option due to its nearly optimal fitness (1.28) combined with a more moderate cost.
Mooring line angles also play a crucial role in performance. Increasing the line deployment angle improves the system’s resistance to offset and inclination at the expense of slightly higher tension. Among the angles evaluated, a 30° line angle produces the lowest overall fitness value, representing the optimal trade-off, as shown in
Figure 14.
Building on the completed optimization process described above, the Fitness values of all mooring line design parameters will now be integrated to support the next stage of analysis. Recognizing that the previous configurations may have been inconsistent or not fully comprehensive, this section will expand the exploration to include a broader range of parameter combinations. The goal is to identify the final optimal configuration for the six-line mooring system, ensuring a well-balanced design that meets performance and safety requirements. The combination selection in this section will follow the approach of previous studies (Xie et al., 2024), utilizing the Design of Experiments (DOE) method to systematically recombine different parameters and revalidate the reliability of earlier results.
Mooring line length will be selected based on the trend of decreasing tension, focusing on the 765, 770 and 775 meters, where a significant tension reduction was observed.
Mooring line diameter will be categorized into thin, medium, and thick specifically 137 mm, 152 mm, and 180 mm to comprehensively cover the design space.
Mooring line angle will be selected as 15°, 20°, and 30°, based on the Fitness-integrated evaluation discussed earlier.
Environmental conditions will continue to be evaluated through a full environmental sensitivity analysis (Incident angle from 0 to 180°) to support a comprehensive assessment as shown in
Table 6,
Table 7 and
Table 8.
After combining various mooring line diameters, angles between mooring lines, and line lengths, the results indicate that mooring line length has the greatest influence on the system’s overall performance. Configurations with a line length of L765 generally exhibited higher Fitness values, suggesting less favorable performance compared to other configurations.
The results also show that if the line is too short (e.g., 760 m), increasing the diameter can lead to a substantial rise in tension, resulting in a worse Fitness score than smaller-diameter configurations. As a result, tension limitations are no longer critical when the line length is properly proportioned.
Moreover, increasing the mooring line diameter further reduces platform motions, leading to better overall Fitness performance. Therefore, although the D152 was initially favored for cost-effectiveness, the D180 offers a comprehensively superior design in terms of structural reliability and system stability.
Among all the evaluated configurations, the D180A15L770 configuration demonstrates the best overall performance and is selected as the optimal six-line mooring system configuration for further analysis and design validation.
5.4. ANOVA Analysis
In
Section 5.3, the optimal configuration for the six-line mooring system was identified, and the overall design trends were analyzed. Although the system’s performance has already been objectively evaluated using the quantitative Fitness assessment, it is important to note that, as demonstrated in
Section 5.2, the three-line mooring system also meets the relevant regulatory requirements under the same evaluation criteria, despite showing a lower Fitness performance compared to the six-line configuration.
This observation suggests that the current six-line system may include overdesign redundancies that could be further optimized or simplified without compromising regulatory compliance or essential performance requirements.
To further clarify how different parameter combinations such as mooring line length, diameter, and angle between mooring lines influence Fitness performance within the six-line mooring system configuration, this section applies the ANOVA method. The objective is to quantify the influence of each parameter, verify its impact on system performance, and identify a mooring system configuration that achieves the best balance between performance and practicality. This analysis provides a solid foundation for the initial design and helps define key optimization directions for future mooring system development as shown in
Table 9.
Based on the results of the ANOVA analysis, it can be concluded that a larger sum of squares (sum_sq) value indicates a greater influence of the corresponding parameter on the variation in the Fitness value of the mooring system. Among the single-parameter effects, mooring line length is identified as the most dominant factor, followed by the angle between mooring lines, with mooring line diameter having the least impact. Importantly, the influence of line length is found to be significantly greater than that of the other two parameters, confirming its critical role in mooring system performance.
In the two-parameter interaction analysis, the results further confirm that combinations involving mooring line length exhibit significantly higher sum_sq values compared to interactions involving only diameter and angle. This finding reinforces the conclusion that mooring line length plays a dominant role in driving system performance variations, making it the most critical parameter to prioritize in mooring system design and optimization.
Furthermore, according to the P-value criteria referenced from (Cowles & Davis, 1982), when the P-value is less than 0.05, the effect is considered statistically significant, allowing the rejection of the null hypothesis that the observed effect is due to random chance. The results show that both mooring line angle and line length have statistically significant effects on Fitness performance, whether considered individually or through their interaction.
Therefore, based on the ANOVA analysis, this study further conducted main effect and interaction effect analyses to correct for biases introduced by other factors, while also accounting for interaction effects and addressing design imbalance through result normalization. The objective is to identify the Global Stable Optimal Configuration, representing the overall best-performing trend across various parameter combinations. This configuration will serve as the foundation for subsequent design refinements, with the goal of further reducing redundancy in the six-line mooring system as shown in
Figure 15 and
Figure 16.
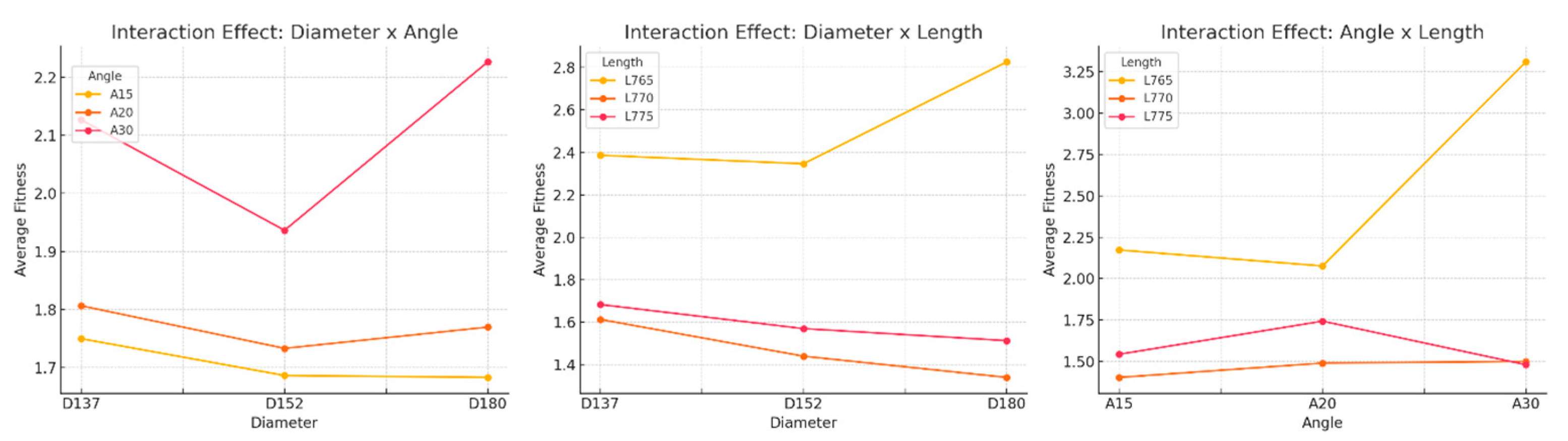
The purpose of the main effects plots is to examine the average influence of each individual parameter such as mooring line diameter, angle, and length on the Fitness value.
From the diameter main effect plot, it is evident that diameter variations have a significant impact on the Fitness value, with D152 identified as the optimal design choice. The angle main effect plot shows a clear upward slope from A15 to A30, indicating a strong main effect and suggesting that angle variations have a considerable influence on overall system performance.
Meanwhile, the length main effect plot identifies L770 a medium line length as the most suitable design point, balancing system stability and tension performance.
The purpose of the interaction plot is to explore whether two parameters interact in their influence on the Fitness value. In the diameter–angle interaction plot, the A30 trend line shows a significant increase under D180, indicating that the impact of angle varies depending on diameter. In the diameter–length interaction plot, the L765 trend line rises notably, while the L770 trend line remains relatively flat or shows a slight decrease, suggesting that the effect of diameter is not consistent across different line lengths. This finding reinforces the earlier observation in the three-line mooring system, confirming that diameter and length exhibit strong interaction effects and must be carefully balanced in the design process.
Lastly, in the angle–length interaction plot, the L765 trend line shows a sharp increase, indicating that shorter line lengths are more sensitive to angle variations. Based on these results, a slightly longer line length is recommended to enhance system robustness and reduce sensitivity to angle changes.
Based on the above analysis and the observed trends in the main and interaction plots, D152A15L770 is identified as the Global Stable Optimal Configuration. However, as noted in Section5.4, the configuration with the lowest single-point Fitness value among all parameter combinations is D180A15L770, representing the single-point optimal configuration.
This distinction highlights an important insight from the main effects analysis: while D180 achieves the best Fitness performance under specific conditions (e.g., A15 and L770), it performs poorly under other conditions (such as A20 or L765). This suggests that D180-based designs are more sensitive and less stable when subjected to broader parameter variations.
In contrast, D152 demonstrates a lower average Fitness across all parameter combinations, indicating more consistent and reliable performance. This makes D152A15L770 the preferred choice for establishing a robust starting point for further tuning and optimization.
Therefore, considering both design reliability and tolerance to environmental variability, this study recommends D152A15L770 as the initial design configuration. This selection aims to achieve a balanced outcome between system performance and operational stability, providing a robust foundation for subsequent design refinement and optimization.
5.5. Asymmetric Mooring Design
Building on the ANOVA analysis presented in
Section 5.4, this study concludes that mooring line length is the key design parameter for catenary mooring systems in shallow-water applications. Furthermore, the main effects and interaction effects plots have identified an optimal balanced configuration that can serve as a foundation for further design development.
By reinforcing the mooring lines on the windward side, corresponding to the predominant environmental directions at the target site, and reducing the number of mooring lines on the leeward side, as proposed in previous studies such as (Yu et al., 2024) and (Mulyadi et al., 2024), this approach seeks to eliminate unnecessary design redundancy and further reduce mooring system costs, while maintaining system stability and operational performance.
Considering Taiwan Strait as the target deployment area, the prevailing environmental conditions from October to the following March are dominated by the northeast monsoon, which represents the most severe normal operating conditions. Under these conditions, abundant wind energy is available to drive wind turbine operation, making this period a key reference scenario for establishing the primary design basis of the mooring system.
Furthermore, typhoons are frequent in Taiwan. According to statistical data from 1911 to 2024 (Central Meteorological Administration, 2025), typhoons are categorized into nine and seven types based on their track classifications, with approximately 14% passing directly through the Taiwan Strait.
To ensure a comprehensive assessment of the structural strength and safety of the asymmetric mooring design, the analysis will continue to be conducted under co-directional wind–wave–current conditions. A full environmental direction sensitivity analysis will be carried out, covering incident angles from 0° to 180°, based on the geometric symmetry of the platform. This approach ensures robust design validation and supports the identification of optimal configuration using the Fitness indicator as the key evaluation metric.
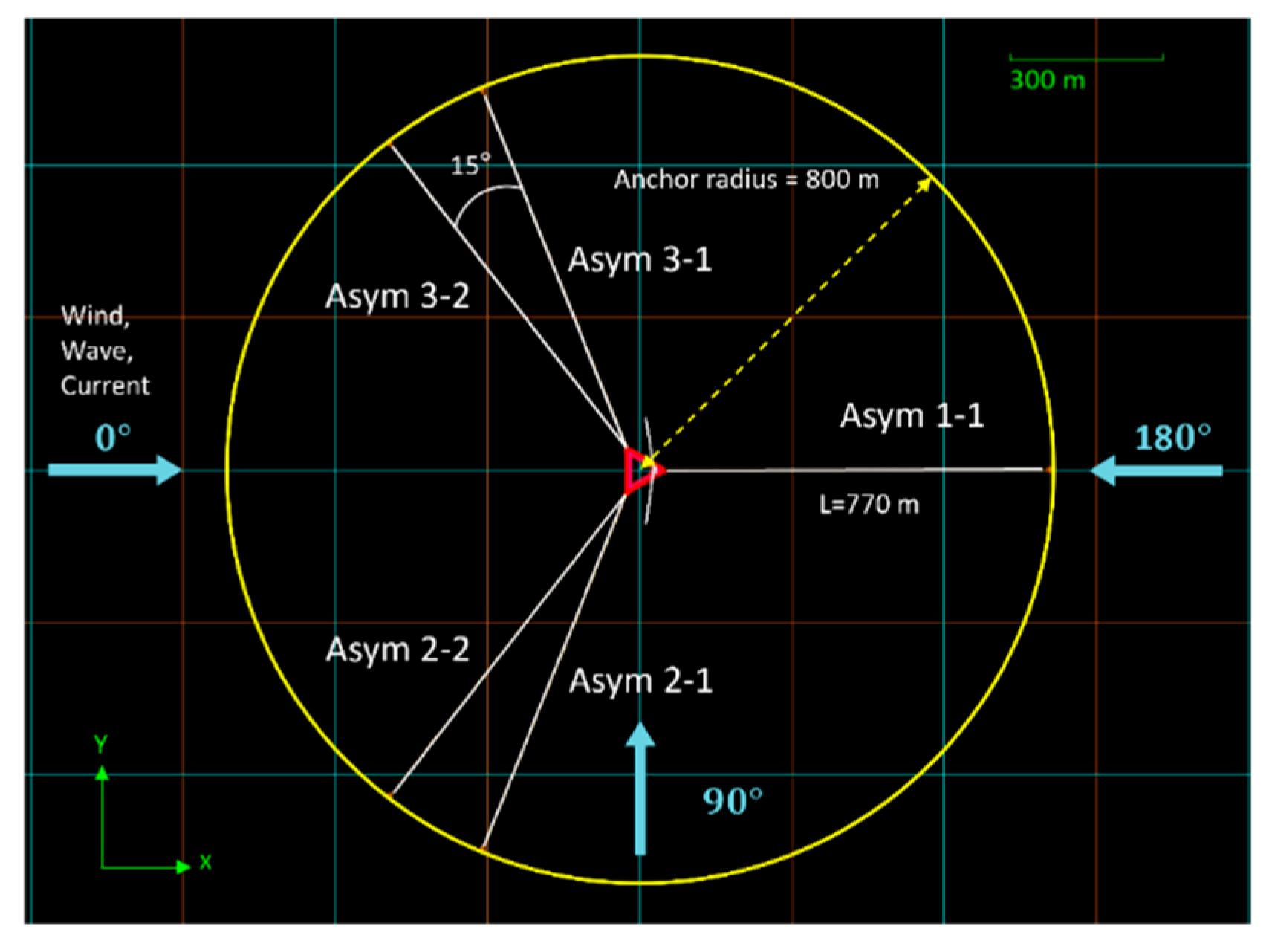
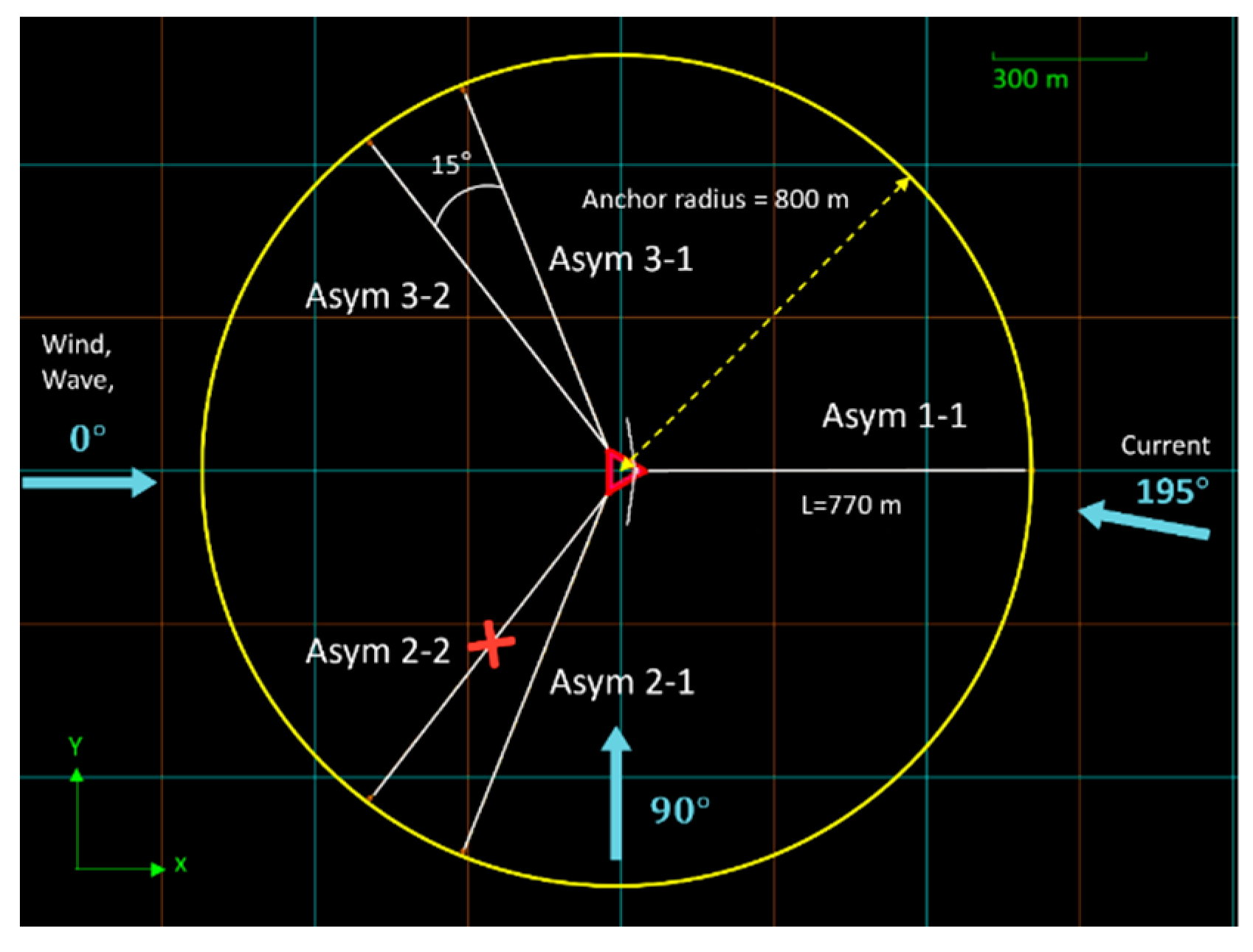
Therefore, based on the environmental characteristics of the deployment location under normal operating conditions, this study proposes a 2-2-1 asymmetric mooring system, hereafter referred to as the Asym system. In this configuration, the number of mooring lines is increased on the windward and wave-facing sides to enhance system resilience under the northeast monsoon conditions.
Both the windward and leeward mooring lines adopt the mooring line length previously identified as providing the best Fitness performance, serving as the initial design. This approach ensures stable system behavior not only during normal operating conditions but also during typhoon events approaching from the south. It helps to prevent excessive tension or displacement in any individual mooring line, thereby reducing the risk of unexpected failures and supporting reliable long-term performance, as shown in
Figure 17.
After establishing the initial Asym mooring system design, this study will proceed with further optimization to identify the best-performing asymmetric configuration. Building on the ANOVA analysis results, which highlighted mooring line length as the key parameter influencing mooring strength performance, this phase focuses on evaluating the effects of varying mooring line lengths. The objective is to refine the asymmetric layout and achieve improved system performance under site-specific environmental conditions.
Three design categories are defined based on different length arrangements:
Type A: Equal line lengths on both the wave-facing and back-wave-facing sides
Type B: Longer wave-facing lines and shorter back-wave-facing lines
Type C: Shorter wave-facing lines and longer back-wave-facing lines
The range of mooring line lengths will follow the six-line mooring system design scope, i.e., from 765 to 780 meters. Each test condition will be named using the format: Asym (Asymmetric mooring system) - Wave-facing line length (L) - Back-wave-facing line length (L), e.g., Asym-L770-L770 as shown in
Table 10.
Based on the evaluation of various mooring line length combinations across Types A, B, and C, it can be concluded that moderate adjustments to line length can further optimize overall system performance compared to uniform line length configurations. Among the three design strategies, the Type B asymmetric mooring system offers the greatest safety redundancy by balancing tension distribution and platform motion control.
Of all the configurations evaluated, Asym-L775-L770 achieved the best overall Fitness performance and is therefore identified as the optimal configuration for the asymmetric mooring system.
To further compare the performance of this optimal asymmetric configuration with the three-line and six-line mooring systems, the mooring line diameter in the Asym-L775-L770 configuration will be increased to D180, aligning with the benchmark diameter used in the previous evaluations. This adjustment aims to address tension-related concerns and validate whether the Fitness performance of this configuration better satisfies the design requirements when compared to the other mooring system alternatives, as shown in
Table 11 and
Table 12.
The design redundancy of this benchmark-adjusted configuration performs as expected, with its Fitness value falling close to that of the three-line mooring system. However, whether performance discrepancies may arise under other design scenarios remains uncertain and requires further evaluation.
To address this, the subsequent analysis will compare the optimal configurations of the three-line, six-line, and asymmetric mooring systems under different design conditions, including normal operating conditions and accidental line failure scenarios, to provide a more comprehensive performance assessment.
5.6. Regular Wave Test
The RAO is a commonly used dynamic response indicator for ships and offshore platforms. It characterizes the response behavior of a structure when subjected to external wave forces at different wave frequencies. The RAO quantifies the sensitivity of the platform to wave excitation across a range of frequencies, providing critical insights for marine structure design and dynamic performance analysis. Here, Z_a represents the motion amplitude at the center of gravity, and δ_a represents the amplitude of the incident wave, as defined by the following equation:
In this section, RAO analysis is conducted for different mooring system configurations. The analysis uses regular waves as the external loading condition, covering a wave period range from 2 seconds to 50 seconds, with simulations performed at 2-second intervals, resulting in a total of 25 wave period cases. In each simulation scenario, the wave height is set to 2 meters with a fixed incident angle of 0 degrees, aiming to assess whether different mooring configurations cause the platform’s motion response to deviate from its original natural periods.
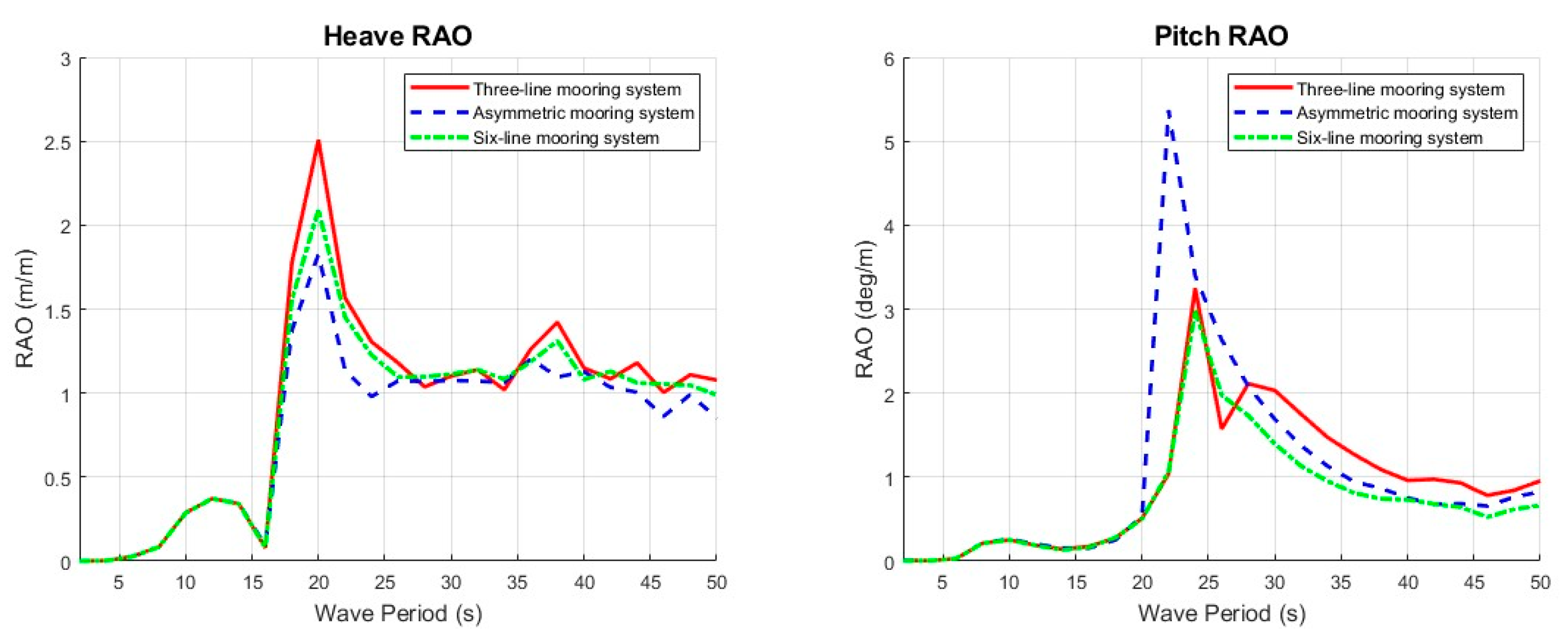
This analysis focuses primarily on the Heave and Pitch degrees of freedom, which are critical to power generation efficiency and generator safety. The platform’s motion characteristics are recorded across a full range of wave periods, providing essential data for mooring system design and dynamic performance assessment, as shown in
Figure 18.
The RAO analysis results indicate that the heave motion response is generally not significantly influenced by the mooring system, although variations in the number of mooring lines do provide different levels of vertical motion restraint on the platform.
In contrast, the pitch motion response shows notable variations among the evaluated configurations. Since the restoring forces provided by the mooring system play a critical role in controlling platform pitch motions, different mooring layouts exhibit varying degrees of influence on pitch response behavior.
Additionally, the peak pitch response is observed to occur at shorter wave periods, with the peak location shifting depending on the mooring configuration. Notably, the symmetric three-line and six-line mooring systems provide better pitch restraint, reflected in lower peak response values, compared to the five-line asymmetric mooring system. Their balanced force characteristics also make them less likely to shift the platform’s natural period, contributing to greater dynamic stability.
5.7. Normal Sea State (SLS & FLS)
Based on the normal environmental conditions summarized in
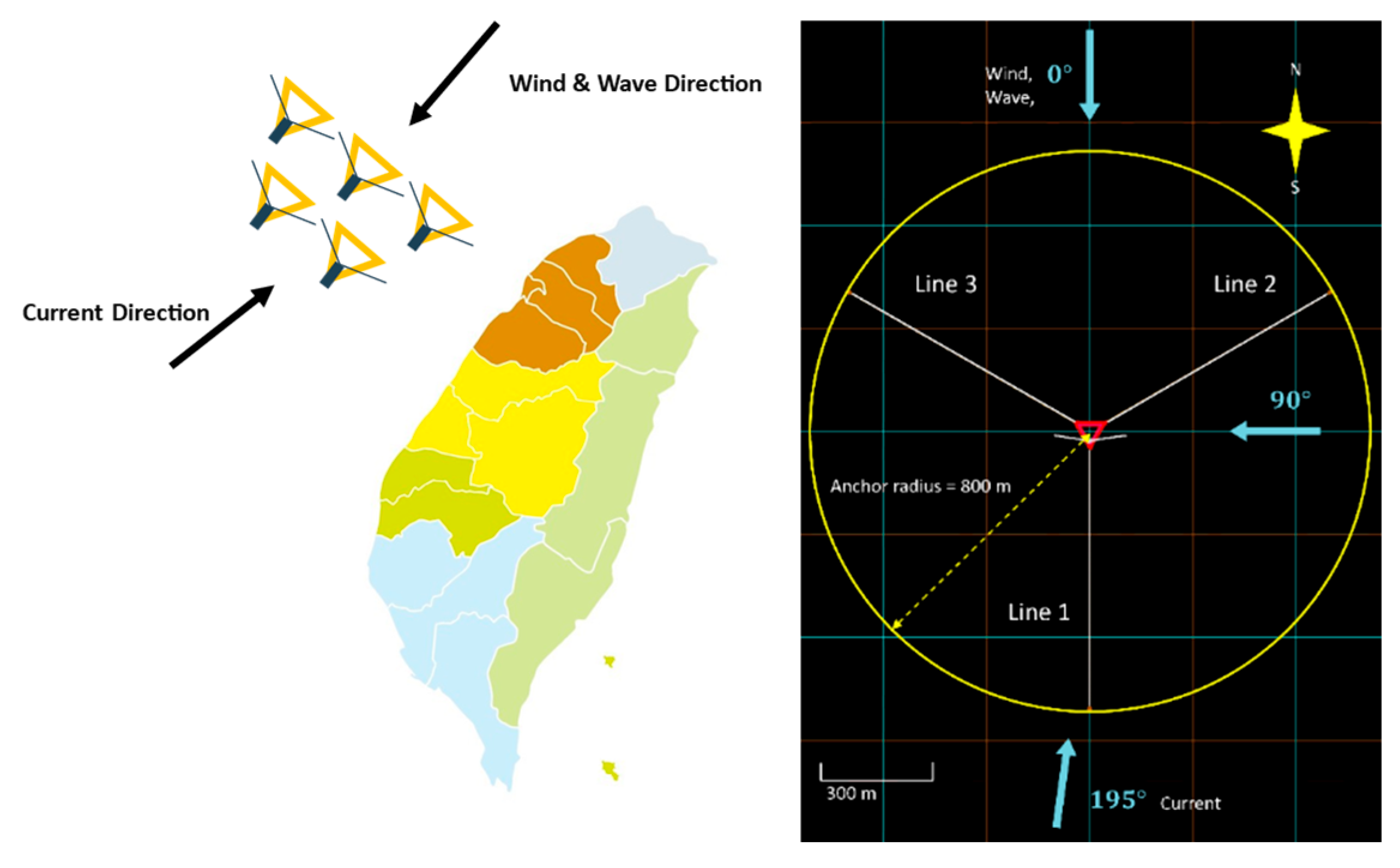
Section 3.2, it was observed that during the northeast monsoon season, the wind and wave directions are nearly co-directional, while the current flows from the opposite (leeward) direction. To better reflect real-world operational conditions, the environmental condition analysis in this chapter will adopt this specific wind–wave–current directional setup as the basis for performance evaluation as shown in
Figure 19.
5.7.1. SLS Design Scenario
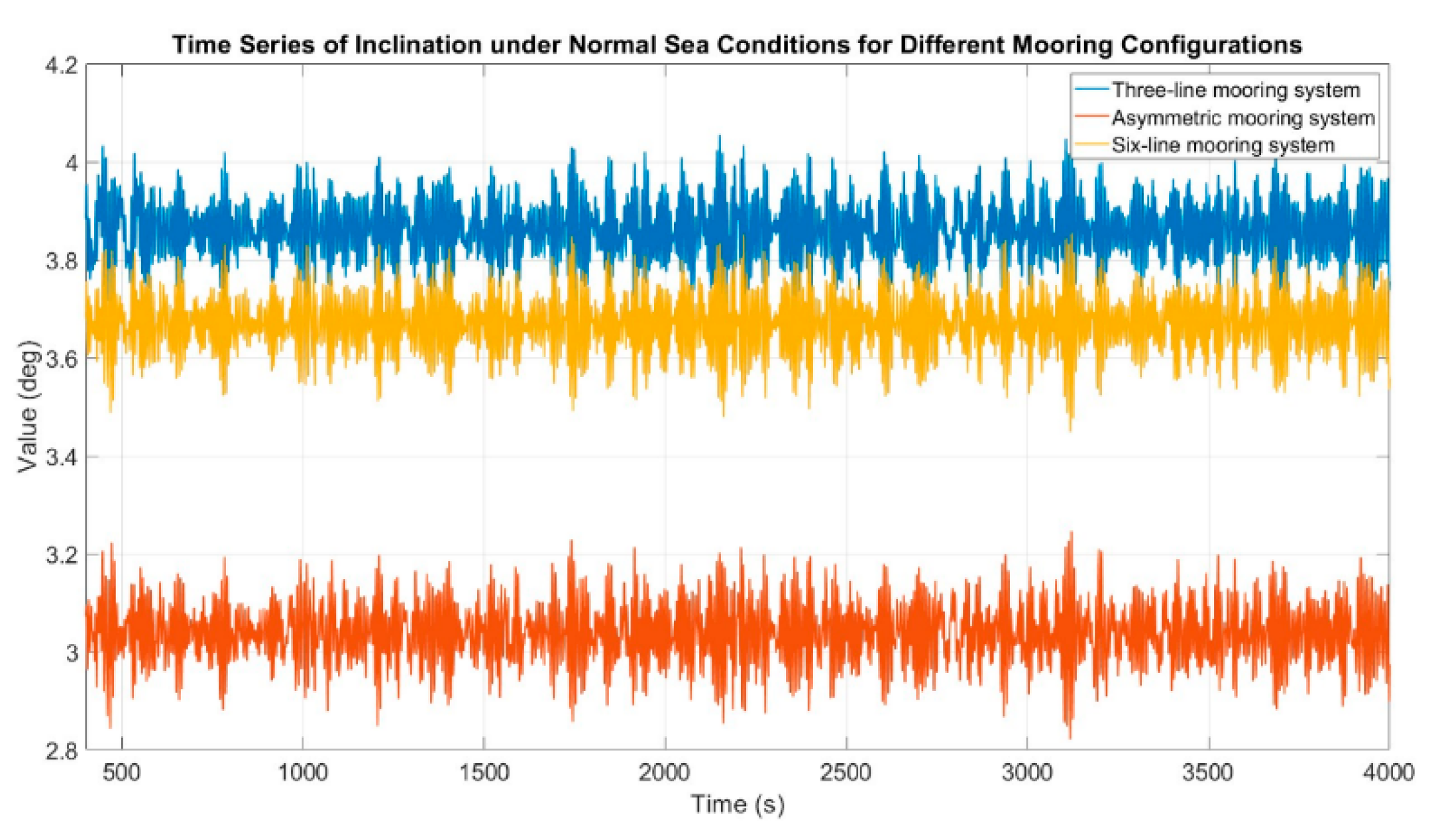
For the SLS design assessment, the three-line, six-line, and asymmetric mooring system configurations will be evaluated using the deployment layout illustrated in
Figure 20. The analysis will be conducted based on the normal environmental conditions defined in
Section 3.2. Finally, the platform inclination response will be examined and verified to ensure compliance with operational safety and performance requirements, as shown in
Figure 20 and
Figure 21.
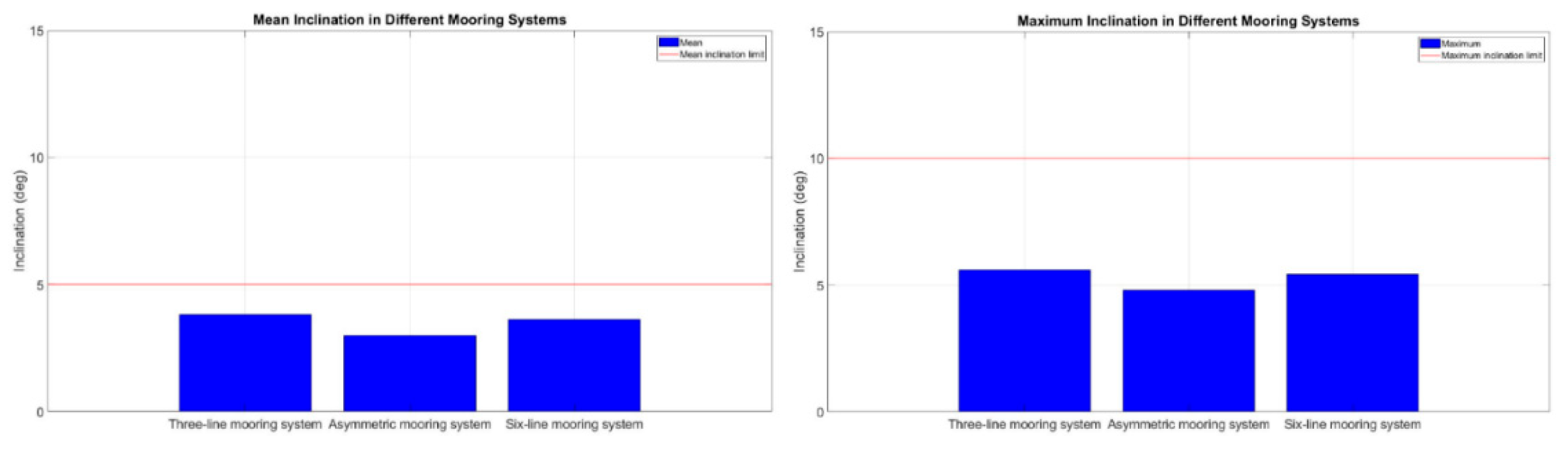
Based on the design evaluation under normal environmental conditions, all three mooring configurations three-line, six-line, and asymmetric are confirmed to meet international regulatory standards. Notably, the asymmetric mooring system demonstrates superior performance in terms of both mean and maximum platform inclination when compared to the traditional three-line and six-line symmetric systems.
The analysis indicates that this enhanced performance is attributed to the four mooring lines on the windward side of the asymmetric system, which matches the restraint capacity of the six-line symmetric system in that direction, providing sufficient resistance against environmental forces. At the same time, the reduced number of mooring lines on the leeward side, compared to the six-line configuration, helps to minimize unnecessary mooring force, improving system efficiency.
As a result, the asymmetric mooring system maintains high strength on the windward side to counteract wind-induced platform motions, while the reduction of leeward mooring resistance enhances overall system performance, making it more efficient than the traditional six-line mooring system.
5.7.2. FLS Design Scenario
To assess the impact of different mooring systems on mooring line fatigue under normal environmental conditions, this study conducted numerical simulations with varying wind speeds, which represent the primary driver of fatigue. Wave and current conditions were kept constant, based on the normal scenario defined earlier. Fatigue damage is expressed as fatigue per unit hour, allowing for direct comparison of fatigue accumulation across different mooring configurations and wind speed conditions.
The analysis focuses on the maximum cumulative fatigue observed on each side of the mooring system. Based on the symmetry of the mooring layouts, a representative line from each side is selected for evaluation for example, Line1-2, Line2-2, and Line3-2 in the six-line mooring system. This approach enables the efficient identification of the highest fatigue accumulation zones and provides a comprehensive understanding of the overall fatigue response trends under varying wind speeds and different mooring configurations as shown in
Table 13.
The asymmetric mooring system shows the highest average fatigue damage across all mooring lines. Due to the imbalanced force distribution resulting from the asymmetric line arrangement, the single mooring line on one side (Asym 1-1) bears a disproportionately higher load. This line records the highest fatigue damage among all configurations, identifying it as a critical design vulnerability that requires careful attention in the asymmetric mooring system. Nevertheless, aside from this weaker-side segment, the overall fatigue performance of the asymmetric mooring system remains comparable to that of the six-line mooring system, demonstrating that the proposed layout maintains acceptable structural reliability while reducing material usage.
5.8. ALS Design Scenario
For the evaluation of accidental scenarios, this study references the failure considerations proposed by (J. Huang et al., 2024), which highlights the risk of unexpected mooring line failure. Two high-probability scenarios are considered: (a) Accidental line breakage during normal operation, caused by fatigue damage or external impacts such as vessel collisions. (b) Mooring failure under extreme environmental conditions, when the system lacks sufficient safety redundancy.
This section will further evaluate the mooring system’s performance based on relevant industry standards, with a focus on windward-side line failure, which represents the primary load-bearing direction. The objective is to verify whether the system can maintain sufficient structural integrity in the event of a line break, thereby preventing cascading failures, excessive platform offset, and potential collisions with navigation routes or other secondary hazards, as shown in
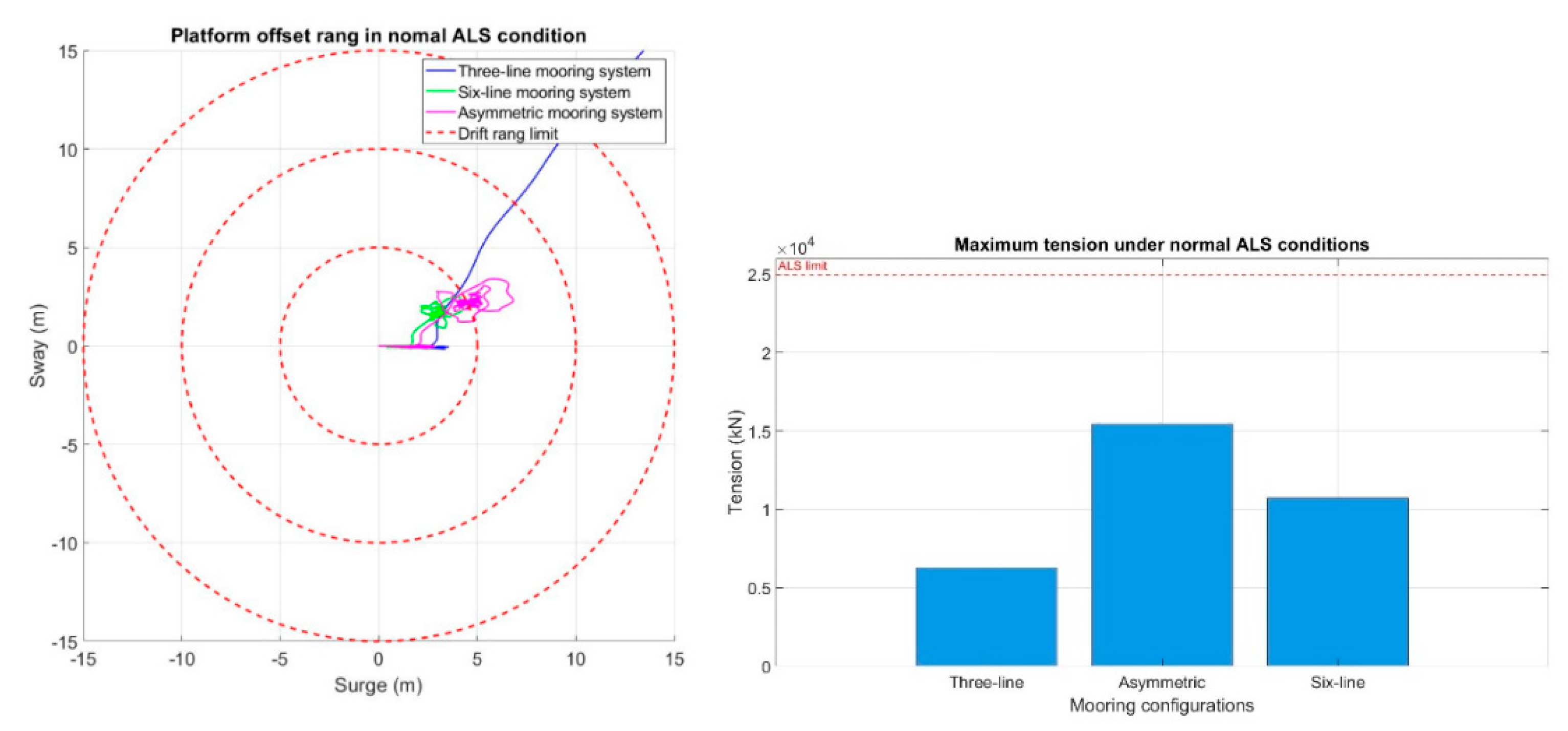
Figure 22.
5.8.1. Normal Operation Conditions
The design scenario under normal environmental conditions assumes that the wind turbine remains operational when an unexpected mooring line failure occurs, either due to external impacts or long-term fatigue damage. The primary objective of this evaluation is to determine whether the remaining mooring system can retain sufficient strength to resist the wind thrust generated by the turbine and the existing environmental loads prior to turbine shutdown. Successfully maintaining this balance is essential to prevent cascading mooring failures and excessive platform drift, which could compromise structural safety and operational continuity, as shown in
Figure 23.
Under the normal accidental line failure conditions, it is assumed that after environmental forces have stabilized, a mooring line failure occurs at 400 seconds. The results indicate that when a line fails in the three-line mooring system, the mooring restraint capacity is effectively lost, resulting in minimal remaining tension and the largest platform offset an undesirable outcome from a safety and operational perspective.
As a result, the ALS analysis focuses on comparing the asymmetric mooring system with the six-line mooring system. While the surge motion results show only minimal differences between the two configurations, a closer examination of the overall platform offset reveals that the six-line mooring system provides better restraining performance, maintaining a post-failure equilibrium position that is closer to the original operating location.
Upon further inspection, it was found that when line failure occurs in the asymmetric mooring system, the remaining configuration becomes 1-2-1, leaving one mooring line on both the failed side and the leeward side, while the opposite side retains two mooring lines. This imbalance in mooring line distribution causes the platform to shift further toward the upper right, resulting in slightly reduced restraining performance compared to the six-line mooring system, which maintains a more balanced post-failure configuration.
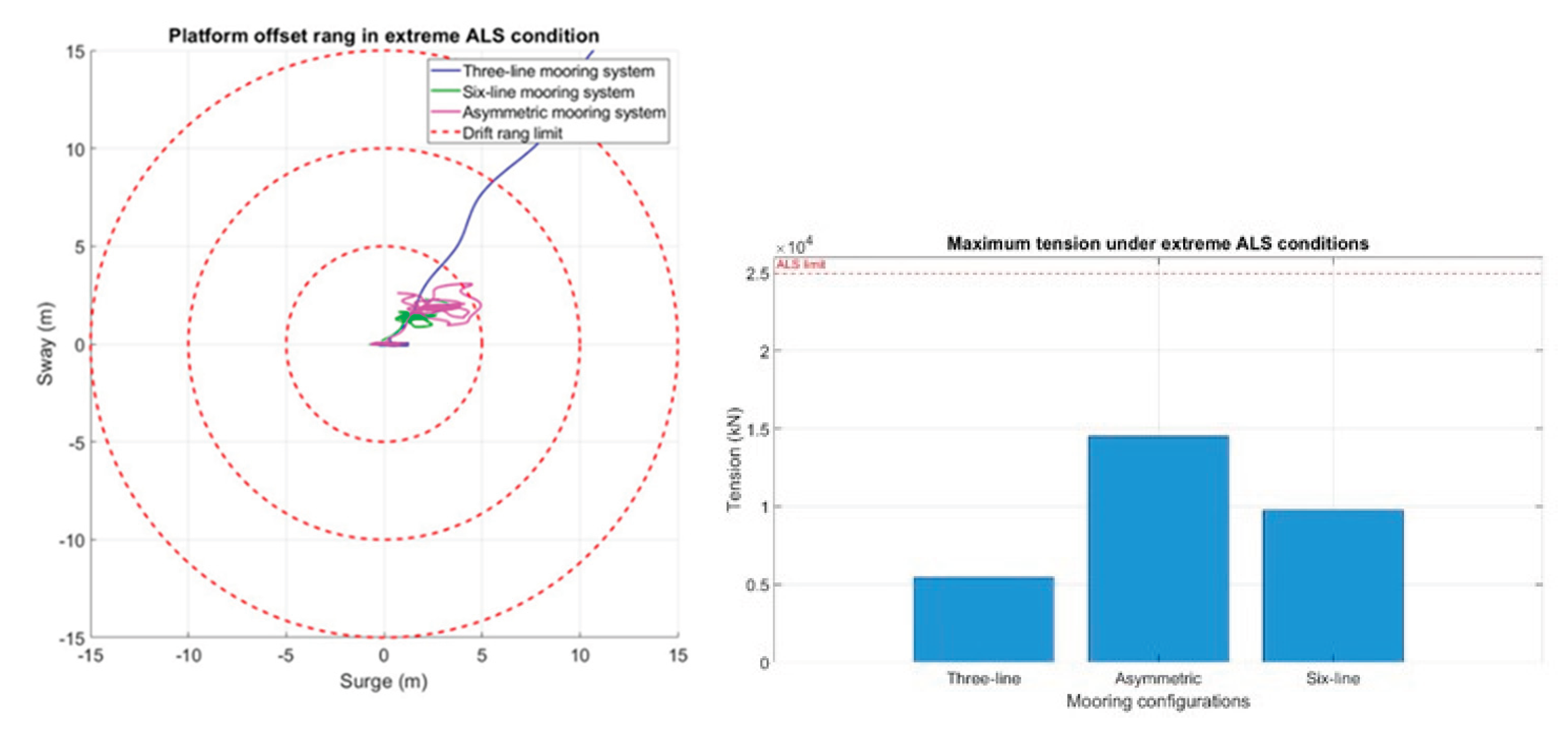
5.8.2. Extreme Environmental Conditions
According to the extreme conditions defined by DLC 7.1, the accidental mooring line failure scenario under turbine shutdown conditions will adopt the 1-year return period as the basis for environmental loading. The inflow directions will follow those defined for normal operating conditions, with co-directional wind and waves, and the current flowing in the opposite direction.
However, compared to normal operating conditions, the wind, wave, and current intensities in this scenario are significantly more severe. The objective of this design assessment is to evaluate whether the mooring system retains sufficient structural capacity to withstand these extreme and unexpected loads, ensuring the integrity and safety of the platform even under failure conditions, as shown in
Figure 24.
Under the extreme shutdown mooring line failure scenario, it was observed that both the maximum mooring tension and platform offset were lower than those recorded under normal operating conditions (with the turbine running). This outcome is likely attributed to the coupled effect of environmental loads and rotor thrust during operation, which imposes greater stress on the damaged mooring system compared to shutdown conditions.
In this scenario, the six-line mooring system once again demonstrated the best performance among the three configurations, providing superior platform restraint and tension control following mooring line failure. The asymmetric mooring system followed, showing acceptable but slightly reduced performance in comparison.
5.9. Cost Analysis and Comprehensive Comparison
In the cost analysis, the mooring system cost estimation is based on the installed capacity of BlueFloat’s 1 GW floating wind farm project in the Taiwan Strait (EIA for BlueFloat’s 1 GW Taiwanese Floating Offshore Wind Project Gets Green Light | Offshore Wind, 2023). For estimating mooring line costs, this study adopts the cost calculation methodology for R4-grade mooring lines as outlined in (Corewind D2.1 Review of the State of the Art of Mooring and Anchoring Designs 2, 2020) as shown in
Table 14. The formula is as follows:
Based on the cost calculations for the evaluated mooring configurations, using the three-line mooring system as the baseline representing the most cost-effective but highest-risk design it was found that the asymmetric mooring system, while offering slightly lower overall stability compared to the six-line system, can achieve a cost reduction of approximately 33%, significantly lowering overall project costs.
This study conducted a comprehensive evaluation of all three mooring configurations, starting from the initial optimized design under ULS conditions, through the normal operational scenarios of SLS and FLS, and including the accidental line failure assessment under ALS conditions. The evaluation concluded with a cost-based ranking applied to a 1 GW floating wind farm scenario.
Based on the ranking results, the proposed asymmetric mooring system demonstrates a well-balanced performance between safety and installation cost efficiency across various design conditions. This system may serve as a valuable reference for future mooring system design strategies, particularly in cost-sensitive floating wind developments as shown in
Table 15.
Figure 1.
Wind power installation in the EU (GWEC, 2024).
Figure 1.
Wind power installation in the EU (GWEC, 2024).
Figure 2.
Cost of offshore and floating wind turbine with water depth (Hywind Kincardine Windfloat Atlantic Fukushima Forward, 2023).
Figure 2.
Cost of offshore and floating wind turbine with water depth (Hywind Kincardine Windfloat Atlantic Fukushima Forward, 2023).
Figure 3.
Design spiral of mooring system.
Figure 3.
Design spiral of mooring system.
Figure 4.
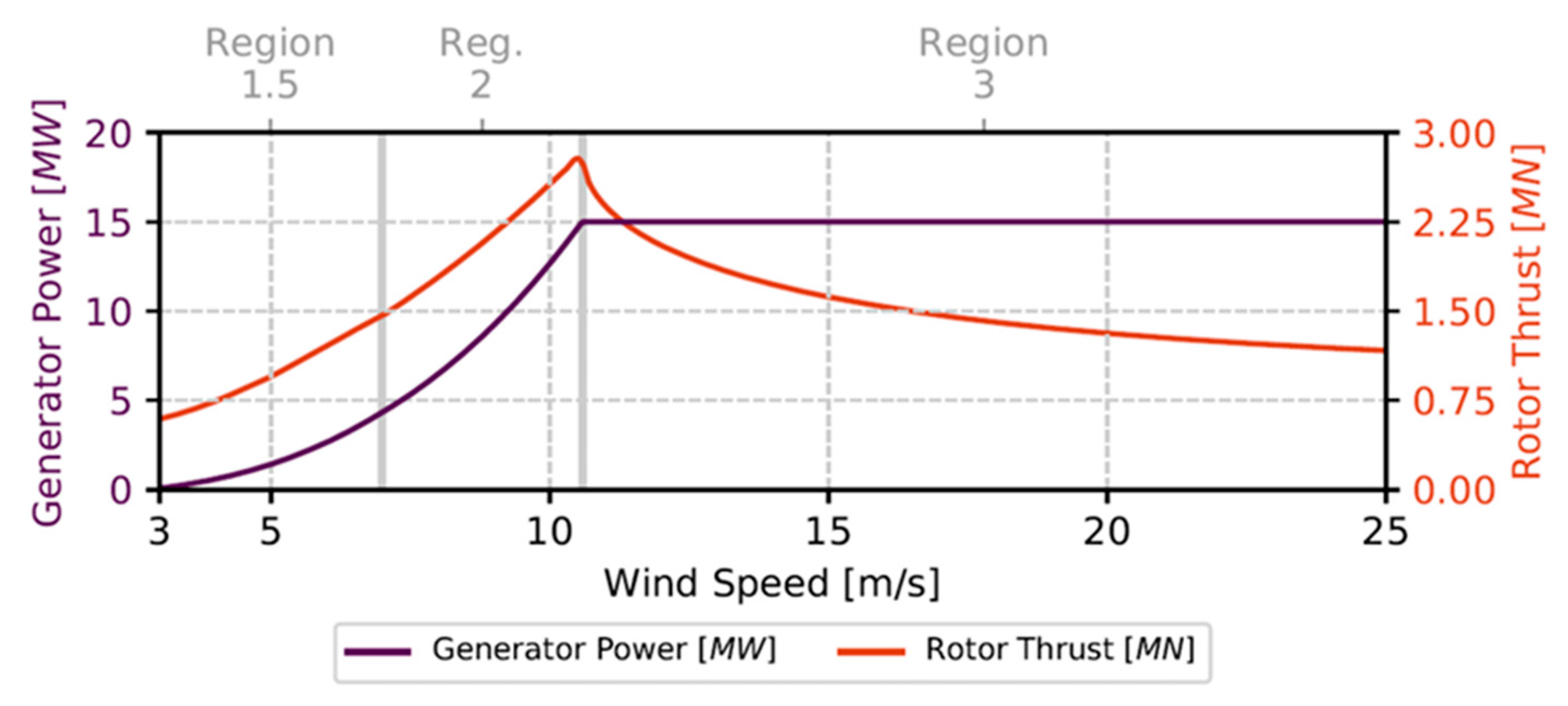
Power and rotor thrust curves of IEA-15MW wind turbine.
Figure 4.
Power and rotor thrust curves of IEA-15MW wind turbine.
Figure 5.
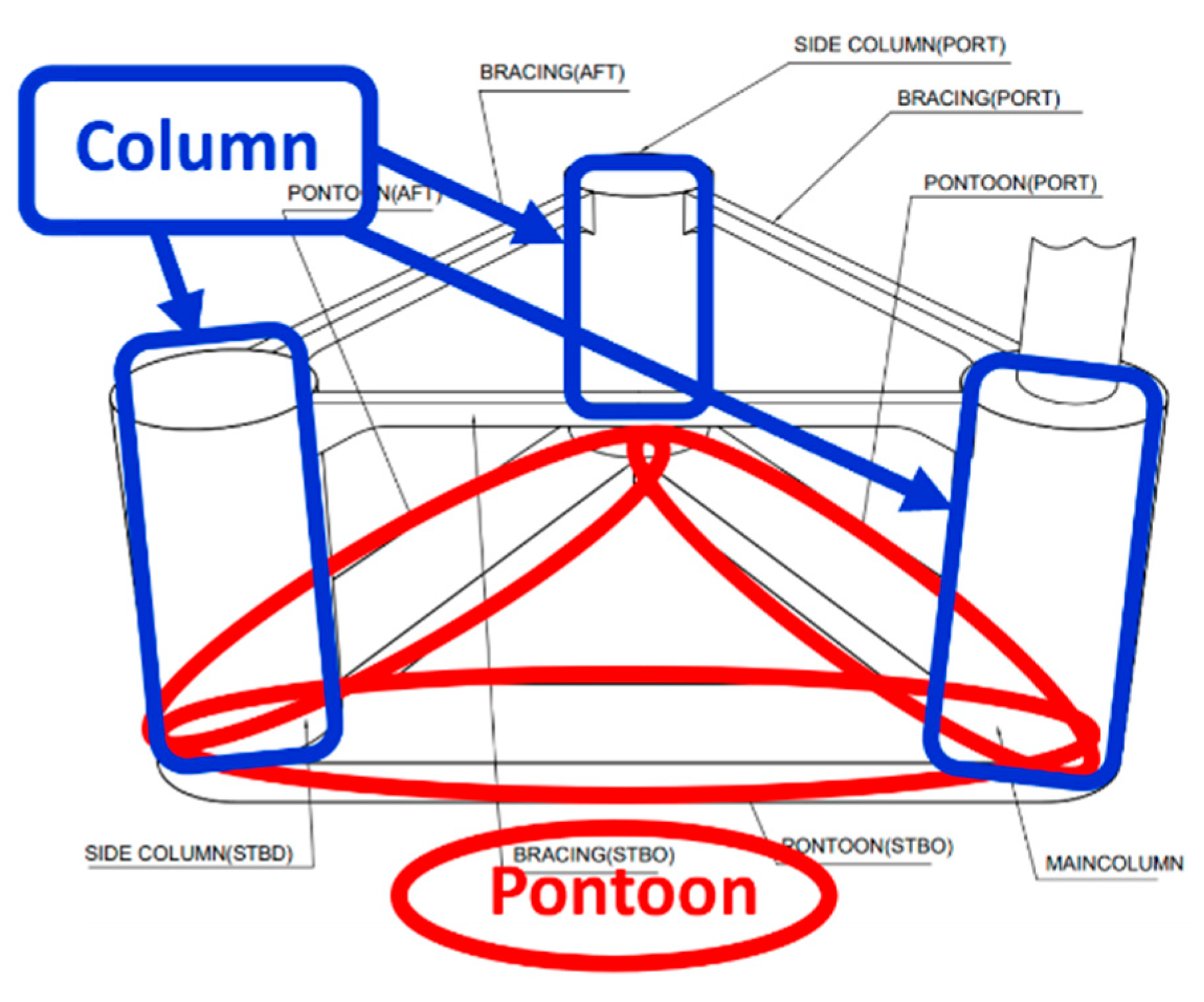
Positions of DeltaFloat components.
Figure 5.
Positions of DeltaFloat components.
Figure 6.
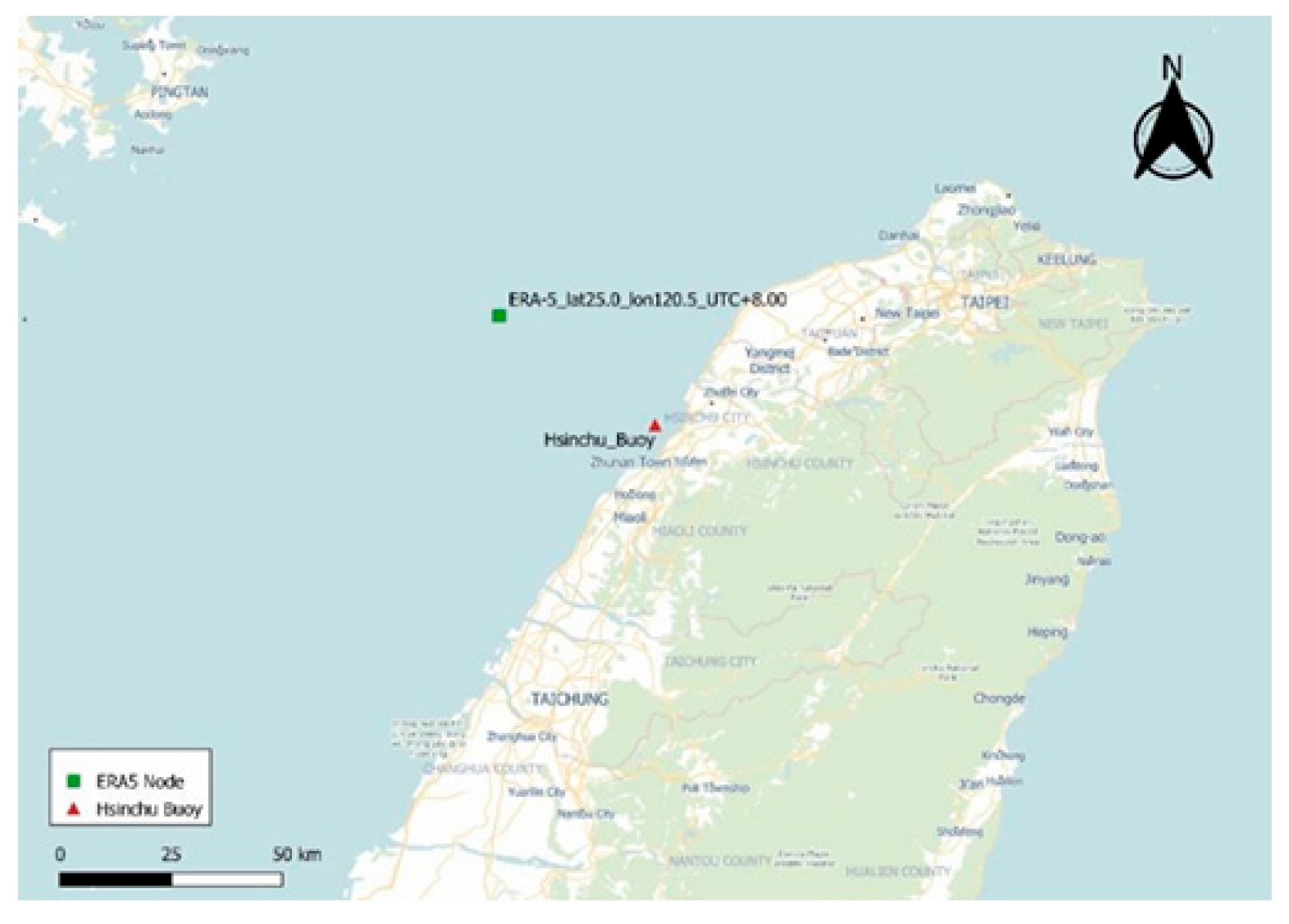
Diagram of ERA-5 node and Hsinchu Buoy (Su, 2024).
Figure 6.
Diagram of ERA-5 node and Hsinchu Buoy (Su, 2024).
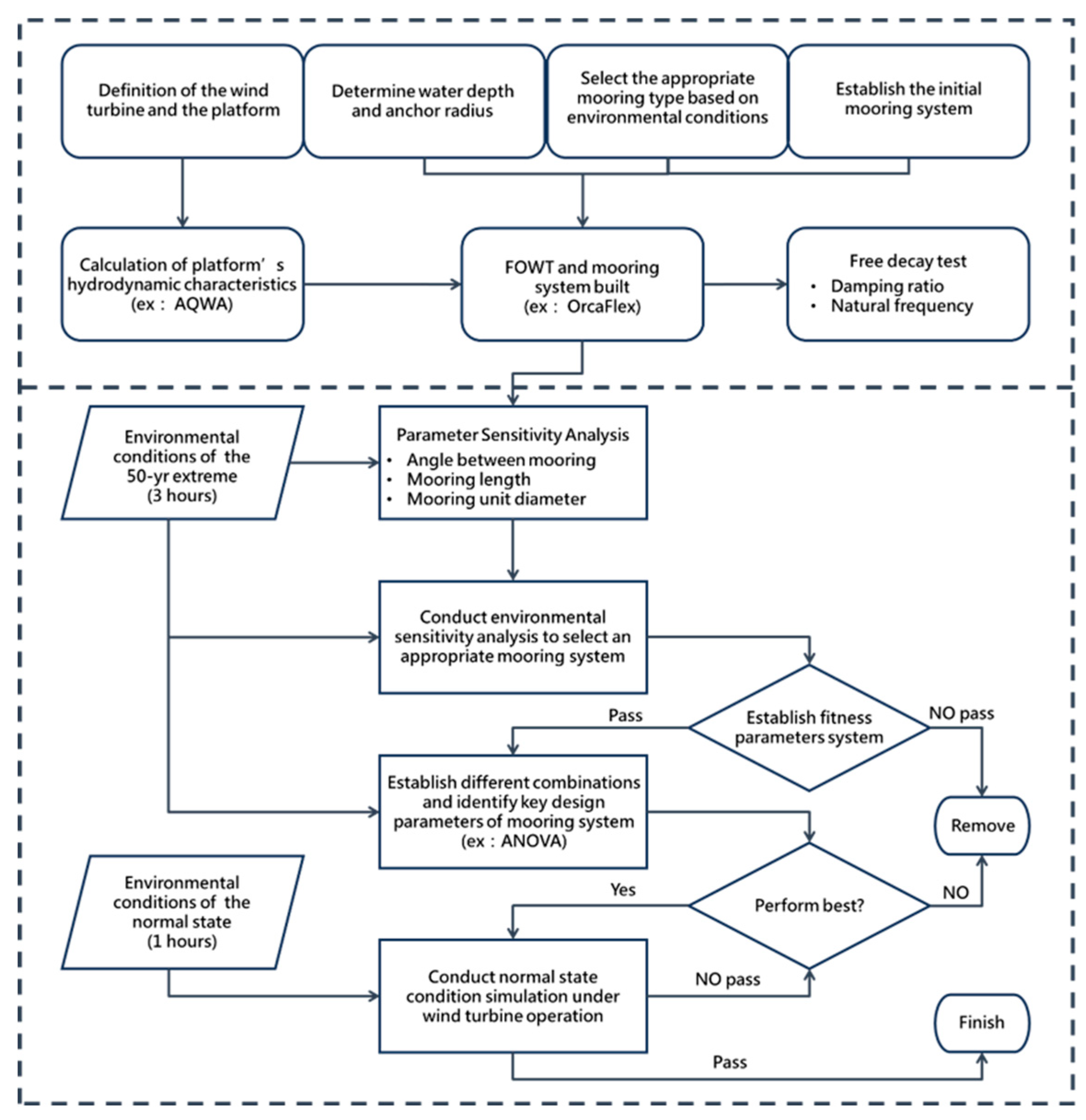
Figure 7.
Flow chart of methodology in this study.
Figure 7.
Flow chart of methodology in this study.
Figure 8.
Power Spectral Density result for Heave and Pitch (19.0 & 25.7 sec).
Figure 8.
Power Spectral Density result for Heave and Pitch (19.0 & 25.7 sec).
Figure 9.
Top view of the three-line mooring system configuration.
Figure 9.
Top view of the three-line mooring system configuration.
Figure 10.
Fitness performance comparison of mooring parameters in three-line system.
Figure 10.
Fitness performance comparison of mooring parameters in three-line system.
Figure 11.
Interaction effects between different mooring line lengths and diameters.
Figure 11.
Interaction effects between different mooring line lengths and diameters.
Figure 12.
Compare with L767.5 and L770 Fitness values.
Figure 12.
Compare with L767.5 and L770 Fitness values.
Figure 13.
Top view of the six-line mooring system configuration.
Figure 13.
Top view of the six-line mooring system configuration.
Figure 14.
Fitness performance comparison of mooring parameters in six-line system.
Figure 14.
Fitness performance comparison of mooring parameters in six-line system.
Figure 15.
Main effects plot of mooring parameters.
Figure 15.
Main effects plot of mooring parameters.
Figure 16.
Interaction effects plot of mooring parameters.
Figure 16.
Interaction effects plot of mooring parameters.
Figure 17.
Top View of asymmetric mooring system.
Figure 17.
Top View of asymmetric mooring system.
Figure 18.
Heave and Pitch RAO in different mooring configurations.
Figure 18.
Heave and Pitch RAO in different mooring configurations.
Figure 19.
Normal environmental layout diagram: the left Fig illustrates the actual environmental direction, while the right Fig shows the simulation setup configuration.
Figure 19.
Normal environmental layout diagram: the left Fig illustrates the actual environmental direction, while the right Fig shows the simulation setup configuration.
Figure 20.
Time series of inclination responses under normal environmental conditions.
Figure 20.
Time series of inclination responses under normal environmental conditions.
Figure 21.
Max and mean inclination statistics for different mooring configurations.
Figure 21.
Max and mean inclination statistics for different mooring configurations.
Figure 22.
Top view of the ALS mooring line failure scenario design.
Figure 22.
Top view of the ALS mooring line failure scenario design.
Figure 23.
Maximum offset and tension value under normal ALS design scenarios.
Figure 23.
Maximum offset and tension value under normal ALS design scenarios.
Figure 24.
Maximum offset and tension value under extreme ALS design scenarios.
Figure 24.
Maximum offset and tension value under extreme ALS design scenarios.
Table 1.
IEA-15MW wind turbine parameter in OrcaFlex.
Table 1.
IEA-15MW wind turbine parameter in OrcaFlex.
| Parameter (Unit) |
Value |
| Hub height (m) |
150 |
| Blade mass (ton) |
65.7 |
| RNA mass (ton) |
911 |
| Tower mass (ton) |
1,263 |
| Cut-in wind speed (m/s) |
3 |
| Rated wind speed (m/s) |
10.59 |
| Cut-out wind speed (m/s) |
25 |
Table 2.
Platform parameter with different capacity of DeltaFloat.
Table 2.
Platform parameter with different capacity of DeltaFloat.
| Parameter (Unit) |
Value |
| Equipped wind turbine (MW) |
10 |
15 |
| Displacement (ton) |
19,400 |
21,587 |
| Column diameter (m) |
12.5 |
16.5 |
| Pontoon height (m) |
7 |
4 |
| Draft (m) |
20 |
20 |
| Freeboard (m) |
15 |
15 |
| Hull steel weight (ton) |
3,800 |
4,231 |
Table 3.
Key parameters of mooring system.
Table 3.
Key parameters of mooring system.
| Parameters (Unit) |
Value |
| Mooring material |
Studless Chain |
| Mooring grade |
R4 |
| Number of moorings |
6 |
| Anchor radius (m) |
800 |
| Initial mooring length (m) |
770 |
| Nominal diameter (mm) |
137 |
147 |
152 |
170 |
180 |
| Mass per unit length (te/m) |
0.37 |
0.43 |
0.46 |
0.58 |
0.65 |
| Minimum breaking loads (kN) |
16,990 |
19,090 |
20,160 |
24,070 |
26,280 |
Table 4.
Summary of different return periods for environmental conditions.
Table 4.
Summary of different return periods for environmental conditions.
| Parameters |
Unit |
Value |
| Water depth |
m |
70 |
| Wave spectrum |
- |
JONSWAP |
| Wind profile |
- |
ETM |
| Peak Enhancement Factor (γ) |
- |
2.08 |
| Significant Wave Height () |
m |
11.8(ULS) / 4.1(ALS) |
| Significant Wave Period () |
s |
13.8(ULS) / 8.2(ALS) |
| Current speed ( |
m/s |
2.12(ULS) / 1.39(ALS) |
| Wind speed (at hub height) |
m/s |
57(ULS) / 38.6(ALS) |
Table 5.
Summary of Normal Conditions.
Table 5.
Summary of Normal Conditions.
| Parameters (Unit) |
Value |
| Wave direction (°) |
30 |
| Significant wave height (m) |
2.12 |
| Peak wave period (s) |
6.78 |
| Current direction (°) |
225 |
| Current speed (m/s) |
0.3 |
| Wind profile |
NTM |
| Wind direction (°) |
30 |
| Wind speed (m/s) |
10 /11(SLS) /12 /13 /14 |
Table 6.
Results of each configuration with a diameter of 137 mm.
Table 6.
Results of each configuration with a diameter of 137 mm.
| Diameter(mm) |
Angle(°) |
Length(m) |
Tension(kN) |
Offset(m) |
Inclination(°) |
Fitness |
| D137 |
A15 |
L765 |
1.22 |
0.39 |
0.37 |
1.98 |
| D137 |
A15 |
L770 |
0.65 |
0.5 |
0.38 |
1.53 |
| D137 |
A15 |
L775 |
0.57 |
0.7 |
0.47 |
1.74 |
| D137 |
A20 |
L765 |
1.30 |
0.4 |
0.38 |
2.08 |
| D137 |
A20 |
L770 |
0.68 |
0.5 |
0.37 |
1.55 |
| D137 |
A20 |
L775 |
0.59 |
0.66 |
0.46 |
1.71 |
| D137 |
A30 |
L765 |
2.04 |
0.56 |
0.53 |
3.13 |
| D137 |
A30 |
L770 |
0.84 |
0.4 |
0.36 |
1.60 |
| D137 |
A30 |
L775 |
0.61 |
0.62 |
0.42 |
1.65 |
Table 7.
Results of each configuration with a diameter of 152 mm.
Table 7.
Results of each configuration with a diameter of 152 mm.
| Diameter(mm) |
Angle(°) |
Length(m) |
Tension(kN) |
Offset(m) |
Inclination(°) |
Fitness |
| D152 |
A15 |
L765 |
1.23 |
0.44 |
0.38 |
2.05 |
| D152 |
A15 |
L770 |
0.60 |
0.47 |
0.36 |
1.43 |
| D152 |
A15 |
L775 |
0.49 |
0.65 |
0.44 |
1.58 |
| D152 |
A20 |
L765 |
1.33 |
0.46 |
0.39 |
2.18 |
| D152 |
A20 |
L770 |
0.63 |
0.43 |
0.36 |
1.42 |
| D152 |
A20 |
L775 |
0.51 |
0.66 |
0.43 |
1.60 |
| D152 |
A30 |
L765 |
1.72 |
0.56 |
0.53 |
2.81 |
| D152 |
A30 |
L770 |
0.71 |
0.4 |
0.36 |
1.47 |
| D152 |
A30 |
L775 |
0.54 |
0.59 |
0.4 |
1.53 |
Table 8.
Results of each configuration with a diameter of 180 mm.
Table 8.
Results of each configuration with a diameter of 180 mm.
| Diameter(mm) |
Angle(°) |
Length(m) |
Tension(kN) |
Offset(m) |
Inclination(°) |
Fitness |
| D180 |
A15 |
L765 |
1.33 |
0.63 |
0.53 |
2.49 |
| D180 |
A15 |
L770 |
0.56 |
0.41 |
0.28 |
1.25 |
| D180 |
A15 |
L775 |
0.41 |
0.64 |
0.4 |
1.45 |
| D180 |
A20 |
L765 |
1.5 |
0.67 |
0.69 |
2.86 |
| D180 |
A20 |
L770 |
0.58 |
0.39 |
0.34 |
1.31 |
| D180 |
A20 |
L775 |
0.42 |
0.58 |
0.39 |
1.39 |
| D180 |
A30 |
L765 |
2.08 |
0.71 |
1.2 |
3.99 |
| D180 |
A30 |
L770 |
0.67 |
0.35 |
0.34 |
1.36 |
| D180 |
A30 |
L775 |
0.45 |
0.5 |
0.36 |
1.31 |
Table 9.
ANOVA results for main effects and interaction effects.
Table 9.
ANOVA results for main effects and interaction effects.
| |
sum_sq |
df |
F |
P-value |
| C(Diameter) |
0.07 |
2 |
0.5 |
0.63 |
| C(Angle) |
0.79 |
2 |
5.55 |
0.003 |
| C(Length) |
5.99 |
2 |
42.16 |
5.6 E-05 |
| C(Diameter) : C(Angle) |
0.08 |
4 |
0.27 |
0.89 |
| C(Diameter) : C(Length) |
0.52 |
4 |
1.81 |
0.22 |
| C(Angle) : C(Length) |
2.16 |
4 |
7.62 |
0.008 |
| Residual |
0.57 |
8 |
|
|
Table 10.
Classification combinations and test naming of asym mooring system.
Table 10.
Classification combinations and test naming of asym mooring system.
| Type |
Wave-facing Line (L) |
Back-wave-facing Line (L) |
Naming Format |
| A |
765 |
765 |
Asym-L765-L765 |
| A |
770 |
770 |
Asym-L770-L770 |
| A |
775 |
775 |
Asym-L775-L775 |
| A |
780 |
780 |
Asym-L780-L780 |
| B |
770 |
765 |
Asym-L770-L765 |
| B |
775 |
765 |
Asym-L775-L765 |
| B |
775 |
770 |
Asym-L775-L770 |
| B |
780 |
765 |
Asym-L780-L765 |
| B |
780 |
770 |
Asym-L780-L770 |
| B |
780 |
775 |
Asym-L780-L775 |
| C |
765 |
770 |
Asym-L765-L770 |
| C |
765 |
775 |
Asym-L765-L775 |
| C |
765 |
780 |
Asym-L765-L780 |
| C |
770 |
775 |
Asym-L770-L775 |
| C |
770 |
780 |
Asym-L770-L780 |
| C |
775 |
780 |
Asym-L775-L780 |
Table 11.
Comparison of Fitness between D152 and D180 asym mooring configurations.
Table 11.
Comparison of Fitness between D152 and D180 asym mooring configurations.
| Case name |
Tension(kN) |
Offset(m) |
Inclination(°) |
Fitness |
| Asym-L775-L770-D152 |
0.77 |
0.64 |
0.54 |
1.95 |
| Asym-L775-L770-D180 |
0.7 |
0.58 |
0.55 |
1.83 |
Table 12.
Comparison of Fitness for different mooring configurations in ULS.
Table 12.
Comparison of Fitness for different mooring configurations in ULS.
| Mooring configuration |
Tension(kN) |
Offset(m) |
Inclination(°) |
Fitness |
| Three-line mooring system |
0.86 |
0.45 |
0.51 |
1.82 |
| Six-line mooring system |
0.56 |
0.41 |
0.28 |
1.25 |
| Asymmetric mooring system |
0.7 |
0.58 |
0.55 |
1.83 |
Table 13.
Maximum fatigue damage per hour on different mooring configurations.
Table 13.
Maximum fatigue damage per hour on different mooring configurations.
| Three-line mooring system |
| Line 1 |
6.28E-07 |
| Line 2 |
1.61E-06 |
| Line 3 |
1.64E-06 |
| Asymmetric mooring system |
| Asym 1-1 |
1.33E-05 |
| Asym 2-2 |
2.86E-07 |
| Asym 3-2 |
2.71E-07 |
| Six-line mooring system |
| Line 1-2 |
1.28E-07 |
| Line 2-2 |
2.78E-07 |
| Line 3-2 |
2.27E-07 |
Table 14.
Cost estimation for different mooring configurations in a 1GW wind farm.
Table 14.
Cost estimation for different mooring configurations in a 1GW wind farm.
| Mooring system |
Total mooring cost (€) |
Cost of a 1 GW offshore wind farm (€) |
| Three-line mooring system |
3,741,563 |
250,684,721 |
| Asymmetric mooring system |
6,256,250 |
419,168,750 |
| Six-line mooring system |
7,507,500 |
503,002,500 |
Table 15.
Ranking of the different configurations under different design scenarios.
Table 15.
Ranking of the different configurations under different design scenarios.
| Mooring system |
ULS |
SLS |
FLS |
ALS |
Cost |
SUM |
Rank |
| Three-line |
2 |
3 |
3 |
3 |
1 |
12 |
3rd |
| Asymmetric |
3 |
1 |
2 |
2 |
2 |
10 |
2nd |
| Six-line |
1 |
2 |
1 |
1 |
3 |
8 |
1st |