Reviewing the Mathematical Physics of General Relativity: Is Contraction of Radial Space from the Gravitational Radius as Valid a Solution as Radial Curvature?

1. Introduction

A theory claiming to match or replace general relativity must have general equivalence. It should reproduce in some useful form the results of Einstein’s field equations and all field effects, including the Lorentzian increase in mass, dilation of time and contraction of space with velocity, the gravitational red shift near massive bodies, the effect on rates of clocks on satellites, the time delay of light signals deflected near the sun and gravitational radiation from the slowing down of pulsars or from fusion of black hole horizons. Furthermore, it should offer some new advantages such as reconciling gravitation and quantum theory. These consequences of general relativity for different inertial coordinate systems have entertained or frustrated generations ever since its complex algorithms were presented on a formal mathematical basis by Albert Einstein more than a century ago [1,2]. An initial requirement to correct mass, length and time for relative velocity using the Lorentz transformation (1 – v²/c²)^1/2 was extended using Gaussian tensor calculus in a Riemannian manifold as algorithms for description of general relativity. Einstein required that “the general laws of nature are to be expressed by equations that hold good for all systems of coordinates, that is, are co-variant with respect to any substitutions whatever”. These included a set of field equations summarized in the following Ricci tensor algorithm [2] that we will not examine here in detail − except where necessary for comparisons with radial relativity.

R_μν – ½g_μνR = −κT_μν = 8πGT_μν/c⁴ (1)

Here R_μν was regarded as the contracted Riemann tensor of curvature, R the scalar of curvature formed by contraction and T_μν the-tensor of matter-energy. This implies that the constant κ = 8πG/c² where G is Newton’s constant of gravitation and c the speed of light. The mathematical tensor requirements needed for calculations and the predictions in general relativity have placed understanding of the theory beyond the ambition of most scientists.

But does this challenge in developing satisfactory space-time algorithms need to remain so out of reach? Using a 4-dimensional approach to coordinates relying on vectors described by tensors, Einstein was able predict accurately the known precession of the plane of orbit of the planet Mercury and the unknown deflection of star light passing the Sun, his predictions confirmed five years later in the field led by the British physicist, Eddington.

In this article we will propose an alternative mathematical theory of radial relativity, based on the principle of least or stationary action that we claim matches Einstein’s general relativity, perhaps is more convenient, neither using Ricci coordinates nor requiring curving of space. Radial action relativity provides mathematical physics achieved in a Euclidean framework. This is achieved by shortening space near matter, still providing algorithms that match general relativity in all the ways outlined above.

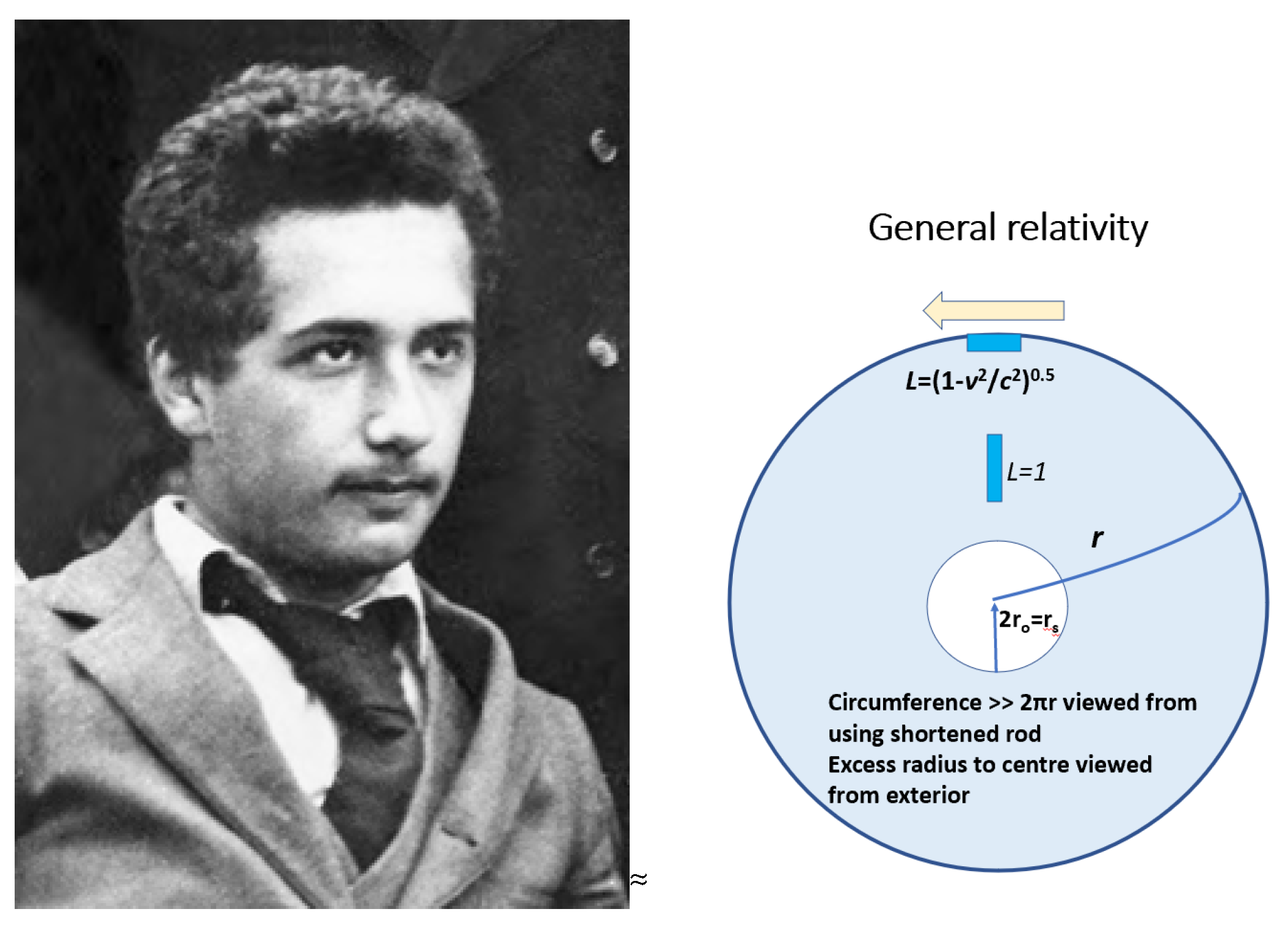
2. On General Relativity

2.1. Einstein’s Choice of Coordinates for Field Equations of General Relativity

In 1915 Einstein employed approximations rather than exact solutions for the field equations. He claimed that if we define Minkowski space-time coordinates (x₁, x₂, x₃, x₄) using relativistic equivalents as g^στ values (g_11, g_22, g_33, g₄₄) the latter will no longer be constants but definable functions of space and time. From his analysis he defined (g₄₄ = 1 – α/r) subject to variation of 1 or 0 and r = $\sqrt{x_1^2+ x_2^2+ x_3^2}$. Further, the constant α = κM/4π was defined using κ from Equation (1), given that a Poisson function of density ∇²g₄₄ was given by the same constant.

Einstein then examined “the influence exerted by the field of the mass M upon the metrical properties of space”. The relationship he called the covariant fundamental tensor shown in Equation (2), with ds taken as the geodesic for the mass point, with the variation in the path integral from point to point $\delta \int ds=0$ indicating it stationary property [2]. Then the square of ds in Riemannian function shown in Equation (2) “always hold between the locally measured lengths and times ds on the one hand, and the differences of coordinates dx_ν, on the other hand” ${ds}^2=g_{\mathrm{\mu }\mathsf{\nu }}{dx}_{\mathrm{\mu }}{d\mathrm{x}}_{\nu }$ (2)

Einstein’s tensor theory selected an expression for field equations requiring a squared gradient of the gravitational potential with a factor of κ equal to 8πG/c². Then κM/4π giving α as a function of mass M, twice the gravitational radius r_o where the only material in gravitational orbit must be at the speed of light. If κ was chosen as 4πG/c² then α would have been the gravitational radius from which a material particle cannot escape, judged unsuitable for his minimum radius.

Einstein succeeded in his mathematical description of general relativity by late 1915 using multidimensional Ricci tensors [2]. This mathematical treatment was also given by Einstein in differentials of Cartesian coordinates although there was a requirement for spherical symmetry of a field-producing point mass at the origin of coordinates. He found “for a unit-measure of length laid parallel to the axis of x, for example, we should have to set ds² = -1; dx₂ = dx₃ = dx₄ =0.

Therefore, he states, $-1=g_{{11}^2}{dx}_1^2$$g_{11}=-(1+\alpha /r)$ (3)

It followed that, correct to a first order of small quantities by taking the square root, $dx=1-\alpha /2r$ (4)

The unit measuring rod thus appears a little shortened in relation to the system of coordinates by the presence of the gravitational field”, so radial distance is slightly longer as a relativistic effect. We will return to this equation later for the extension of radial length viewed from far distance.

In an analogous fashion he concludes the length of the coordinates in tangential direction setting, ${ds}_2$ to -1; dx₁ = dx₃ = dx₄ = 0; x₁ = r₁, x₂ = x₃ = 0 gives the following result.

$-1=g_{22}^2{dx}_2^2$= - ${dx}_2^2$

So the gravitational field of the point of mass has no influence on the length of the measuring rod. Given that the circumference of an orbit should not change between differential and tensor coordinates, 2πr nevertheless in a gravitational field will be longer according to Ricci tensor coordinates, providing the reason for the rotation of the planet Mercury’s perihelion in each orbit because of the excess radius affecting the observed rotation of the plane of orbit.

As stated above, Einstein had defined the constant α = kM/4π, where k = 8πG/c² or 8πr_o/M, given MG = r_oc². Here, r_o is the gravitational radius proportional to a central mass M with α (= 2r_o) named later the Schwarzschild radius, with an escape velocity for a particle of matter equal to the speed of light. Therefore, Equation (3) for the differential coordinate compared to the tensor version could be rendered as in Equation (5).

${dx}_1=1-r_0/r$ (5)

Consequently, according to Einstein, the radial tensor g₁₁ is made (1 + r_o/r) longer, as an approximation when r is much greater than r_o. In all the above cases, using a differential dx = -dr/r², Einstein had obtained the radially symmetrical solution for spatial components of the gravitational field designated g_μν, “quantities describing the gravitational field in relation to the chosen system of reference”.

Turning to relativistic time, he concluded [2] from theory that the tensor equivalent to dx₄ holds good.

$g_{44}=1-\alpha /r (=1-2r_0/r)$ (6)

His solution for “the rate of a unit clock, which is arranged to be at rest in a static gravitational field. Here we have for a clock period ds = 1; ${dx}_1= {dx}_2= {dx}_3=0".$

Therefore, $1=g_{44}{dx}_4^2$ (7)

The Cartesian coordinate dx₄ is therefore the inversion of the square root of g₄₄.

${dx}_4=1/\surd g_{44}=1/\surd (1+(g_{44}-1\left)\right)=1-\mathrm{½}(g_{44}-1)\approx (1+r\mathrm{o}/r)$ (7)

The relativistic correction for the clock for dx₄ needed to be greater than 1 towards the center. Given that his constant α is 2r_o, later called the Schwarzschild radius, his unit of space dx is transformed by r_o/r. He takes this as a lengthening of space by (1 + r_o/r by inversion), towards at origin at r = 0. In radial action relativity we must show it as lengthening too, but only of the radius just outside r_o. The differential correction for time was thus set approximately to (1 + a/2r) or (1 + r_o/r), shown in Equation (7). This differential for dx₄ is equivalent to (1 + r₀/r) increasing the measure of time as a time equivalent. So general relativity corrects time by increasing the mathematical duration between ticks on a unit clock in the gravitational field (dx₄).

Radial action relativity to be introduced in Section 3 is proposed to dilate time by the gravitational field reducing the frequency of quantum radiation directly. Einstein’s result is a mathematical measure of the effect of the field on the measure of time, although both are descriptive of field conditions and both effects can be taken as real effects on clocks. It is noteworthy that Einstein’s differential approximation for adjustment of time is effectively the inverse of the radial action correction for frequency.

In Einstein’s terse mathematical physics the constant factor α was set equal to κM/4π or 8πGM/4πc² = 2r₀, twice the gravitational radius of the central mass. Einstein’s reason for the choice of the 8π magnitude was explained simply by Feynman [3] as “8π serves to eliminate irrelevant factors from the most useful formulae”, hardly a robust reason, but perhaps needed for consistency with the expressions of Schwarzschild and Droste for correction of time in their geodesics, as shown in Equation (6). In most modern versions of the Schwarzschild metric, α is replaced by 2M.

(ds)² = (1 - α/R)(dt)² = (1 – 2r_o/R) (dt)² (9)

(ds)² = g₄₄(dt)² (10)

By applying the Lorentzian correction [1] of (1-V²/c²)^-1/2, Einstein could generate approximate correction terms for g₄₄ from Equation () of (1 – r₀), or (1 + r₀) if inverted. This choice was critical in determining an event horizon at the Schwarzschild radius, where the escape velocity for material objects is the speed of light. Obviously, while matter cannot escape to infinity at that radius, we suggest it might still achieve A set of higher orbits if accelerated to less than light speed at each stage.

In a critical prediction for verification of his theory, Einstein gives the relativistic velocity of light past the Sun ($\gamma$) defined in the sense of Euclidean geometry as in Equation (11).

$\gamma =\surd$ ((${\displaystyle \frac{{dx}_1}{{dx}_4}}{)}^2+$ (${\displaystyle \frac{{dx}_2}{{dx}_4}}{)}^2+ ({\displaystyle \frac{{dx}_3}{{dx}_4}}{)}^2$ (11)

“We easily recognize that the course of the light-rays must be bent with regard to the system of coordinates, if the $g_{\mathrm{\mu }\mathsf{\nu }}$ associated with Equation (2) are not constant”. In this way, Einstein introduced the idea of the gravitational curvature of space. Choosing the velocity in tensors, at a radius of Δ, the tensor velocity (γ) is shown in Equation (12).

γ = √(-${\displaystyle \frac{g_{44}}{g_{22}}})=1- {\displaystyle \frac{\alpha }{2r}}\left(1+{\displaystyle \frac{{x_2}^2}{r^2}}\right)$ (12)

This calculation for the velocity of the light beam gives κM/2πΔ or 2α/Δ as the solution, so that a ray of light going past the sun undergoes a total deflection of 1.7 degrees. Incidentally, this variation of path, according to the Huygens principle for refraction of 4r_o/r, differs at the variable radius at each point of observation. The experimental confirmation of this prediction by observations during a solar eclipse by a British team of researchers led by Eddington led to the widespread acceptance of Einstein’s theory of general relativity.

Einstein’s major paper on general relativity [2] concludes with an estimation of the orbital motion of the ellipse of a planet undergoes a slow rotation in the direction of motion, of the following amount per revolution.

ε = 24π³${\displaystyle \frac{a^2}{T^2{c}^2(1- e^2)}}$ (13)

In this formula, a denotes the major semi-axis, c the velocity of light and T the time of revolution in seconds. For the planet Mercury a rotation of 43” per century was well known beforehand, now possible to explain with the g_µν coefficients shown above. Gravity altered the differential scales of measure for both space and time. In 1913 when working with his friend Grossman, Einstein [4] had thought that a law of gravitation, invariant in relation to any transformation of co-ordinates whatever, was inconsistent with the principle of causation. “These errors of thought cost me two years of excessively hard work, until I recognized them as such at the end of 1915 and succeeded in linking the question up with the facts of astronomical experience, after which I ruefully returned to the Riemannian curvature”.

2.2. The Schwarzschild Metric

In a letter to Einstein from the Russian warfront in early 1916, Schwarzschild [5] reinterpreted Einstein’s conclusions his masterly polar metric using α equal to 2r_o as a singularity, guided by Einstein’s 2015 paper in Berlin.

${ds}^2=(1-{\displaystyle \frac{\alpha }{R}}){dt}^2$ - ${\displaystyle \frac{{dR}^2}{1-\frac{\alpha }{R}}}- R^2\left({d\vartheta }^2+ {sin}^2\vartheta {d\varphi }^2\right), R=(r^3+ {\alpha }^3{)}^{1/3}$ (14)

This metric or similar derivatives have been the basis of many future analyses of Einstein’s relativistic geodesic, including adding spin by Kerr in New Zealand [6]. K. Schwarzschild’s contribution surprised Einstein at the ease of his solution but it was based firmly on Einstein’s principle of zero variation.

$\delta \int ds=0 where ds=\sqrt{\Sigma g_{\mu \nu }}{dx}_{\mu }{dx}_{\nu }$ (15)

In short, the point shall move along a geodesic line in the manifold characterized by the line element ds. Schwarzschild pointed out that the volume element in polar co-ordinates is equal to r²sinϑdrdϑdϕ and that “an easy trick to circumvent difficulties” was to put the following.

$x_1={\displaystyle \frac{r^3}{3}}, x_2=-cos\vartheta , x_3=\varphi$ (16)

Then the polar volume element r²drsinϑdrdϑdϕ is equal to ${dx}_1{dx}_2{dx}_3$. When one includes t = $x_4$ the field equations and the determinant equation of Einstein remain in unaltered form. If one restricts motion to the equatorial plane (ϑ= 90^o, dϑ = 0) intermediate integrals read as follows.

$(1-{\displaystyle \raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$R$}\right.})({\displaystyle \frac{dt}{ds}}{)}^2-{\displaystyle \frac{1}{1-\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$R$}\right.}}({\displaystyle \frac{dR}{ds}}{)}^2-R^2({\displaystyle \frac{d\varphi }{ds}}{)}^2=h, a constant$ (17)

Unlike more recent versions of this metric, R was taken equal to (ρ + r³)^1/3 rather the r as the distance to the centre of mass, discussed Schwarzschild then confirmed that this stationary value gives Einstein’s observed anomaly in the perihelion of Mercury.

2.3. Droste’s Variational Metric

Another contributor to developing general relativity in this era guided by direct reading of Einstein’s developing 1915 research included J. Droste, a PhD student of H.A. Lorentz based in Leiden University. Indeed, so impressed was Einstein by the Droste and Lorentz treatment [7,8] using the principle of variation that he published an article in 1916 [9] in response on Hamilton’s principle and the general theory of relativity drawing attention to Droste’s use of Lagrange’s principle to give clarity. Einstein criticized D. Hilbert’s treatment from Göttingen for making too many assumptions, emphasizing the need for complete liberty in the choice of the system of coordinates. In this article Einstein also expressed the principle of variation as follows, where G is a function of gravitational field.

$\mathsf{\delta }\int G\mathrm{d}\mathsf{\tau }$= 0 (18)

This gives as many differential equations as there are functions g_µv and q_(p) of momentum and energy to be defined, varying independently of each other, in such a way that the limits of integration all vanish because of their covariance. We will analyse further Droste’s strategy in applying the action principle and its application to Einstein’s general relativity. Droste’s solution derived separately using the principle of variation from his thesis research, though with prior knowledge of Schwarzschild’s work was rendered by Droste as follows, with α equal to 2r_o consistent with Einstein’s selection using 8π to modify the κ constant.

ds² = (1 – α/r)dt² – dr²/(1 – α/r) – r²dϕ² (19)

Later, this was expressed by Hilbert for an orbital plane as Equation (20).

ds² = (1 – 2M/R)c²dt² – (1 – 2M/R)^-1dr² – r²dϕ² (20)

essentially both the same equations, but including c² seems incorrect, unless c = 1.

Droste in his thesis solution pointed out [7] that a moving particle outside the sphere given by α/r equal to 1.0 can never pass inside that sphere so that in studying its motion, we can disregard the space where r is less than α. Einstein has introduced one form of principle in the covariant fundamental tensor shown above in Equation (2). He also defined the four-dimensional continuum by ∫ds as stationary, between any two points p, calling this a geodetic line in space-time.

δ∫ds = 0 (21)

Unlike Schwarzschild’s brief analysis, Droste, and presumably Lorentz in Leiden were impressed by this Lagrangian or least action approach. Defining ds/dt equal to L, “then ∫Ldt will be zero, if the varied positions for t at t₁ and t₂ are the same as the actual ones, with L representing the following quantity.

L = ds/dt = √[(1 – α/r – r^.2/(1 – α/r) – r²dϑ² + sin²ϑdϕ2)] (22)

The equations of motion are ${d(}_{\partial \vartheta }^{\partial L})/dt=0, d{(}_{\partial r}^{\partial L})/dt-\partial L/\partial r=0$ (23)

From these it follows that ${\displaystyle \frac{d}{dt}}\left({\displaystyle \frac{\left(1-\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$r$}\right.\right)}{L}}\right)=0$ (24)

We now obtain ${\displaystyle \frac{1-\alpha /r}{L}}=const; {\displaystyle \frac{r^2\omega }{L}}=constant$ (25)

In 1916, Einstein was so impressed by the Leiden laboratory’s development of variation, referring to four papers by Lorentz in 1915 and 1916. He published his response in a paper on Hamilton’s principle and the general theory of relativity [9] in the Prussian Academy of Wissenschaften, stressing that there is complete liberty in the choice of the stem of coordinates. Later, he was offered a chair in physics in Leiden, requiring Queen Wilhelmina’s signature in 1920, so strong was the mutual admiration. Later, Einstein in an essay on science reflected that “since the gravitational field is determined by the configuration of masses and charges with it, the geometric structure of this space is also dependent on physical factors. ….. The problem of gravitation was thus reduced to a mathematical problem: it was required to find the simplest fundamental equations which are covariant in relation to any transformation of coordinates whatever”. There is no doubt that his use of Riemannian geometry had achieved this.

In the radial relativity theory following, we accept Droste’s conclusion regarding restricted interior space with no central singularity, but only at α/₂. This assumes that the space inside the gravitational radius (r₀) must be void and that quantized energy cannot cross into that space except by instantaneous displacement of momentum. We recognize α as the Schwarzschild radius where r equals 2MG/c₂ or 2r_o, defining a location where complete escape from orbiting a gravitational body theoretically requires the speed of light. However, that does not mean that orbit is impossible.

2.4. An Alternative Metric

In radial action, the cumulative gravitational radius is r₀, defining a virtual spherical surface populated very densely by quanta, preventing all access to the internal void. In any case, once the choice of horizon was made in Einstein’s equation [2] it was necessary to curve space to the origin of coordinates because the g₁₁ radius extended r₀/3 beyond the Euclidean center [Feynman 3]. By contrast, the shortened radius (1 – r₀/r) viewed from the exterior used in the algorithms of radial action relativity does not require such curvature since there is radial lengthening of the Euclidean coordinate but only up to this surface. All radial action gravitational effects lie outside the gravitational radius, a surface encircling a Euclidean void inside r₀ up the Euclidean zero of coordinates.

Another way of expressing the Schwarzschild-Droste metric is as follows.

(ds)² = (1 – r_o/r)²(dt)² – (dr)²/(1 – r_o/r)² – r²dϕ² (26)

(ds)² = (1 – 2r_o/r + (r_o/r)²)(dt)² – (dr)²/(1 – 2r_o/r + (r_o/r)²) – r²dϕ² (27)

Using (ds)² here instead of ds² emphasizes that this term is the square of ds, not a differential of the function s². Discarding the square term (r_o/r)² as irrelevant in scale, this reproduces the Schwarzschild metric in close approximation, but the logical expression for ds/dt now as (1 – r_o/r) for time and dr/dt as dr/(1 - r_o/r) for space then becomes a matter of accuracy. Incidentally, the use of dτ as the differential in place of ds as a measure of proper time in the absence of gravity [Brown, 12] gives the measure of dilated time dt/dτ viewing processes from a distance, taken as dx₄ approximately equal to (1 + r_o/r) derived in Equation (7) by Einstein as a correction factor for time dilation. This inversion applies to both time and space regarded as static in the abbreviated Equation (28).

ds = (1 - r_o/r)dt – dr/(1 - r_o/r) (28)

The possible implications of this mathematical revision will be explored in the following sections.

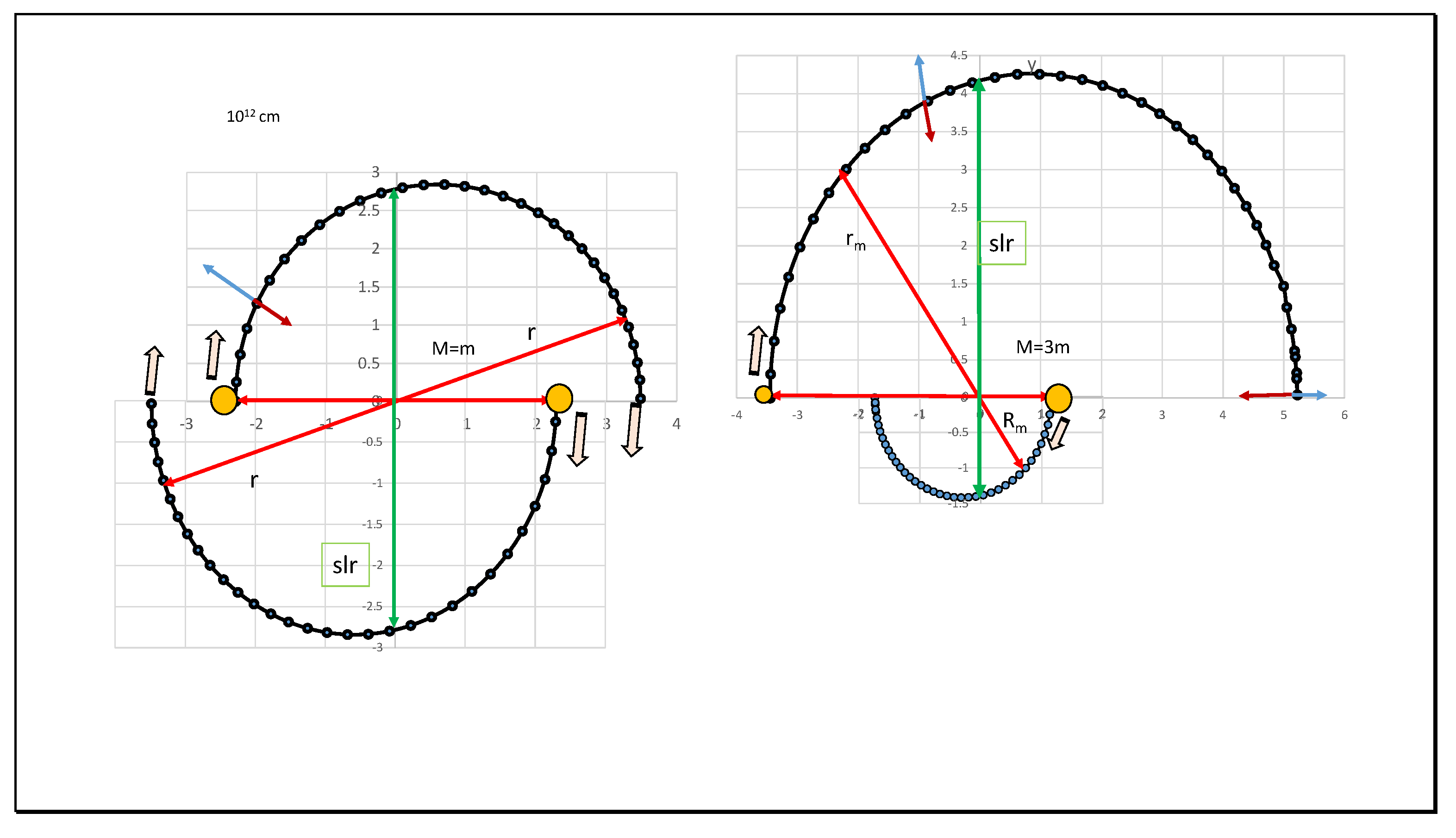
3. Radial Action Relativity

A different viewpoint on relativity using Euclidean coordinates is proposed, expressing the inertial motion of matter sustained by field energy, consistent with Lagrangian least action [3].

(i)

Radial action relativity employs polar coordinates ranging from zero gravity at infinity to a radial surface on a sphere at the gravitational radius (r_o = MG/c²) defining the curvature for motion of the speed of light (1/r₀).

(ii)

Matter considered to be at the origin of coordinates shortens the radial dimension (to r – r_o). This shortening is caused by pressure excluding all physical interactions in the interior space occupied by the ultimate particles of matter. Yet the energy required by processes with diminished inertia (mr) may allow higher frequencies of orbital motion. This exclusive central surface for gravitational objects is a result of the speed of transmission having a maximum speed of c, quite unknown to Newtonian gravity (MG = RV² = r_oc²) that assumed that gravity acted without a time delay.

(iii)

The gravitational radius is directly proportional to the collective mass, implying a material inertia mr₀ distributed on a surface area of 4πr₀² surrounding a void. We will show how this revision of radial action gives rational algorithms for both the Lorentz transformation [10] and the conclusions of general relativity, retaining a Euclidean framework consistent with the invariance of least action.

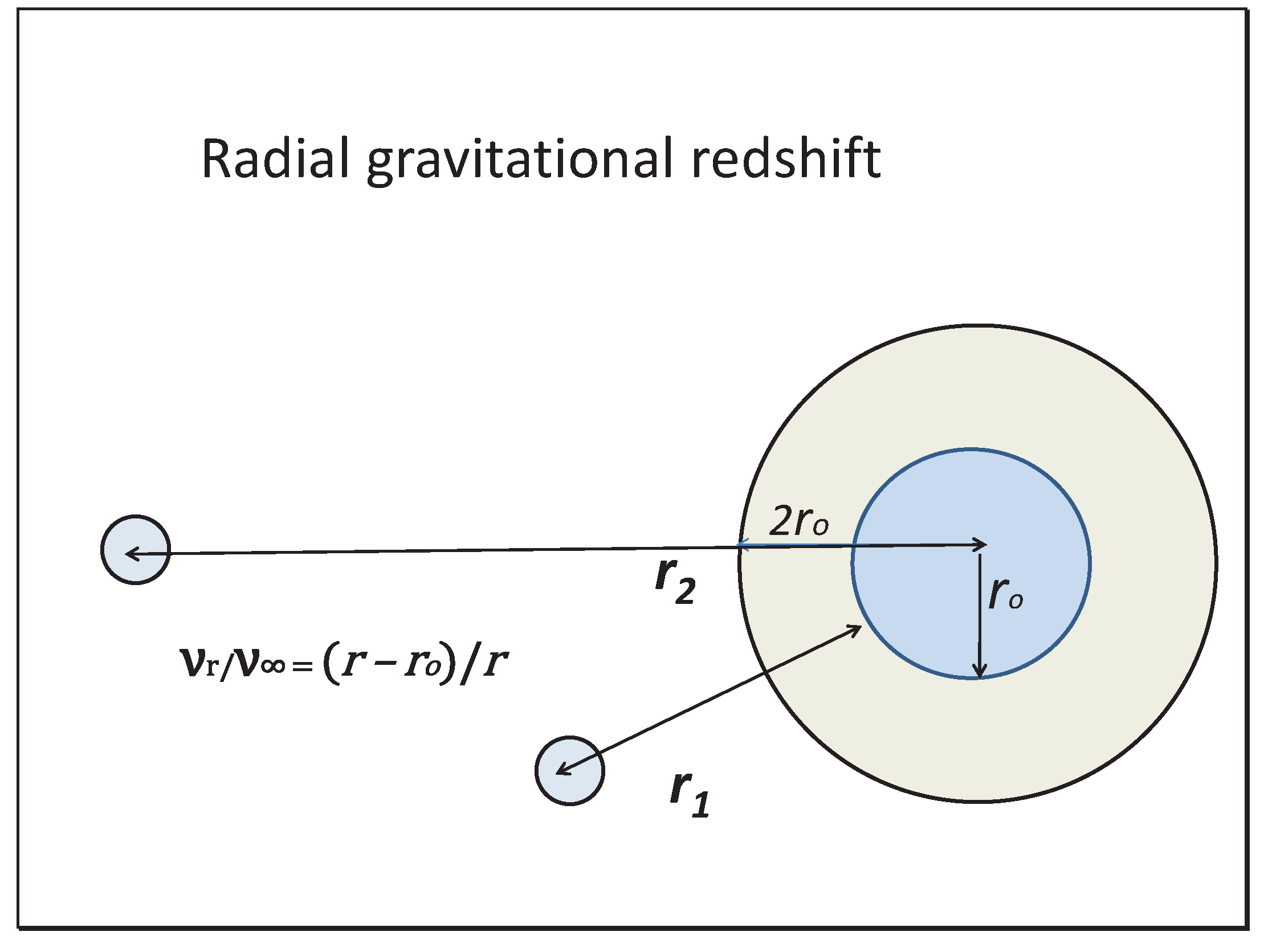
3.1. The Radial Gravitational Algorithm for Stationary Clocks

Our hypothesis for relativity termed radial action dilates time and contracts space near gravitational bodies viewed from a radial coordinate towards infinity. The theory employs a simple radial inertial coordinate (r - r_o), excluding the space from the gravitational radius to the origin of spherical Euclidean coordinates. The area of surface determined by the quantity of gravitating matter in the central body (Fig. 1) is equivalent to 4πr_o². This revision can accommodate effects of both special and general relativity with the proposition that velocity greater than orbital speed requires decreased curvature of motion, increasing inertial action with respect to the fixed stars. Thus, to the far distant observer, clock time is dilated at a radius r from the Euclidean center compared to that at infinity, or free of gravitational influence; the perceived change in the ratio of the same clock frequency ratio (ν_r/ν_∞) is exactly equal to the relative magnitude of the reduced radius (1 – r_o/r).

ν_r = ν_⧝(1 – r_o/r) (29)

Given that the quantum clock at r is perceived from r_⧝as running slower or red shifted to a lower frequency it is logical to assume that its conjugate quantum wavelength is longer, preserving the speed of light at r viewed from infinity as c. However, using frequency to indicate dilation of time in radial action is in direct contrast to general relativity, given the latter indicates dilation of time perceived as larger values of the differential dt between ticks. To be consistent with Equation (29), adjustment of wavelength at r perceived at infinity should be given as in Equation (30), its inverse.

λ_⧝ = λ_r(1 – r_o/r) (30)

λ_r = λ_⧝/(1 – r_o/r) (31)

The values in Equations (29) to (30) are from a distance, not local clocks or rulers of space. We also predict that at a radius of r, a light beam travelling radially to a centre of inertial mass will be viewed from a distance with a reduced velocity c_r involving identical corrections for both time and space.

Applying a shorter wavelength at r and a higher frequency will mean that its measure of space is shortened so that v_∞λ_∞ = v_rλ_r = c. The observer located at r will not agree with either of the distant observer’s perceptions. No dilation of time, lower ticking rate for the same clock or wavelength dilation or contraction of space is perceived at r, because r_o is now the local origin of coordinates and not the Euclidean point at r zero. The tumbling rate of caesium atoms however affected by local gravity will be taken as the physical standard of time by the local clock observer. The effect in Equation (31) cannot be perceived locally since it sets its own standard. If clocks run slower locally because of gravity, so will all physical processes of inertia, including human thought. The laws of physics remain the same in all frames of reference as required by Einstein’s principle of relativity. Thus, a shorter local wavelength than perceived from infinity must be regarded as the standard measure of space at r, lengthening the radial distance to r_o to match that of the Euclidean center. This distinction is a result of an effect on material inertia, not a distortion of space like a Ricci tensor but a correction lengthening space to the gravitational radius surface.

A measurement of light speed at r using a gravitationally slower clock, also reducing radial distance because of a shorter wavelength ruler, will still measure its radial velocity as c. However, an observer effectively at infinity (or far distance) needs to make corrections to explain their view of the radial light beam at r. Both use a similar quantum clock and thus wavelength ruler at infinity to measure time and space. The observer at r need make no such adjustments. However, a double correction for the radial light beam viewed from infinity where there is no gravitational influence is shown accurately in Equation (32) below. An approximation when r remains at least 100 times greater than r_o, is given in Equation (33). There is a resemblance to Schwarzschild’s solution of Einstein’s field equation for general relativity, a similarity to be revisited in Section 4.

(λ_rν_r) / (λ_⧝ν_⧝) = (1 – r_o/r)²

= (1 - 2r_o/r + r_o²/r² (32)

≈ (1 - 2r_o/r) (33)

Both local measures and products of wavelength and frequency (λ_⧝ν_⧝=λ_rν_r=c) will give the correct proper speed for light, but the perceptions of the different observers will be false for both comparisons of the speed of light, a diminished speed in the interior nearer r_o viewed from infinity and sped up viewed towards the exterior to the approximation of Equation (33). When r is near the event horizon less than 10 times greater than r₀, Equation (32) with the squared ratio should be used for radial action relativity. Note that Equation (33) gives a similar correction to that made by Schwarzschild in Equations (14) for ds²/dt² so that ds/dt ≈ (1 – ro/r). On the geodesic equation a correction for (ds/dt)² is needed for coordinate space with time.

An essential feature of relativity as defined by Einstein was the local constancy of the speed of light or gravity, assumed here to always be equal to the product of wavelength and frequency (c = λν). We emphasize that a fundamental approach to relativity would be to conclude that observers more distant from a gravitational center will consider frequencies (ν) to be reduced or red-shifted when closer to the center and thus wavelength lengthened. Yet life systems operating closer to the center will retain certainty that no such shifts occur or are needed. All physical and biological processes including clocks operating at a shorter radius are assumed to be equally affected by the more intense gravity. At any distance the same result occurs but observers examining the other system will set redshifts in the interior or blue shifts to the exterior. Not only are frequencies disparate, but relative wavelengths observed must also vary, with a red shift wrongly implying a longer wavelength and a blue shift wrongly implying a shorter wavelength. Such corrections are not needed for local observers. The equations for corrections operate purely for the benefit of the distant observers to correct their information. The key fact to consider is that local shorter wavelength consistent with the frequency of the process is the proper measure of space and time, not the lengthened wavelength perceived by an observer at distance.

Taking these effects locally, the speed of light as a product remains constant, as required by covariant relativity. However, if these local measures of space and time are not considered jointly, false conclusions will be made. An interior wavelength used as a ruler for local space shortens for a clock running slower making all interior velocities invariant, not only for light. Viewed from the exterior, interior space will be falsely shortened radially but it is lengthened locally, though unconsciously. The radial relativistic correction needed is to always subtract the gravitational radius from the actual radius to the center. When the radius of observation nears zero gravity or infinity, no local correction is needed. For all intermediate radii, as r approaches r_o the correction becomes more significant. The key point for this correction is the shortened radial distance (r–r_o), real in physical terms but not for Euclidean geometry as a product of reason.

By contrast, in general relativity corrections to space and time (Fig. 4) involve an extended radius of r₀/3 [3] to a point or singularity, requiring the intervening space to be curved as non-Euclidean. In a lecture given to the Prussian Academy of Sciences in 1921, Einstein was in no doubt that Euclidean geometry could be retained, but only as “purely axiomatic geometry”, compared to the “practical geometry” of curved space if supported by experience. An ether might also be retained provided that “the idea of motion may not be applied to it” disqualifying it as a reference system.

3.2. Using Natural Radial Coordinates

Einstein’s relativistic corrections g_µν to rectilinear inertial reference systems discussed in Section 2.1 led to recognition of the significance of spatial curvature. General relativity had major successes such as predicting the extent of bending of starlight near the sun, in modelling the excess precession of the planet Mercury and the theory of black holes, largely by virtue of the Schwarzschild solution to Einstein’s field equations, satisfying most needs of physicists (e.g. the photoelectric Compton effect, nuclear reactions, quantum theory) have been met by use of special relativity. The use of Cartesian coordinates, while having local value, may be of limited application universally. Instead, radial coordinates with an emphasis on the curvature of transverse motion and the nature of the inertial radius as a key factor in impacts will be explained.

In Einstein’s book of 1916 [11] published by Three Rivers explaining relativity to a general audience Einstein explained the behavior of clocks and measuring rods in a rotating frame of reference. According to the Lorentzian correction of (1 - v²/c²)^1/2 an observer at rest at the origin of coordinates K in Figure 1 will consider a standard unit rod as of length less than 1.0 when in motion on the circumference (Fig. 1). To maintain velocity constant, time as measured by a clock on the extended circumference must be dilated. By contrast the rod will not experience a shortening as judged from K at the center if it is applied in the direction of the radius. A number larger than π (3.1416..) will be obtained if the diameter is divided into the circumference. However, for a disc not in motion the ratio circumference to diameter will be precisely equal to π. Judged from the circumference where an observer will experience an inertial force indistinguishable from gravity the radius can no longer be depicted in Euclidean geometry given that, judged by the circumference an excess radius will extend beyond the origin. The idea in general relativity of a radial straight line from the rotating circumference fails and it follows that the space to the Euclidean origin must be curved. In 1915, Einstein was able to introduce curved Gaussian coordinates to calculate the results of general relatively regarding the motion of particles near central masses.

Can an equivalent solution be found using radial action?

This question is answered here in the affirmative, partly illustrated in Figure 2 and Figure 3, though not disputing that Einstein’s mathematical Riemannian tensors remain legitimate for physics. However, the need to recognize spatial curvature using tensor analysis in general relativity may be lessened by using natural or radial coordinates with a role for variable curvature in the primary description of inertia m(r-r_o) itself. Thus, in the action resonance theory [12], inertia was proposed to involve not only the quantity of matter designated by m but also its product with the action radius, the inertia mr. We recognize this inertial effect as direct sense data whenever we employ a lever to raise a body as weight, or make use of a wheeled barrow. Indeed, we can control the inertia of the weight – that is its resistance to being accelerated and set in motion in the gravitational field – by varying the position of the fulcrum.

Thus, for central bodies and their satellites in orbit in the radial action frame, inertia involves not only the quantity of matter m but also the distance to the center of mass r_m of a coupled gravitational system such as the Sun and each of its planets. The key equality of radial inertia for both bodies in gravitational couples (mr_m = Mr_M) as well as of balancing gravitational forces (mMG/r² = mr_mω²r/l = Mr_Mω²r/l) and of opposing inertial forces (mr_mω² = Mr_Mω²) [13]. We also have equality of radial inertia in orbital rotational motion (mr_m = Mr_M), although not of energy itself since mr_m² is not equal to Mr_M².

For radial action relativity in Figure 2, the formula for gravitational red shift viewed from a distant exterior is given as ν_r/ν_∞ equal to (r – r_o/r). This provides an elementary model generating dilation of time, contraction of space and other features required for equivalence with general relativity, to be fully explained in following sections.

3.4. Comparing Mathematical Relativistic Corrections

At large distances, radial action produces almost the same gravitational red and blue shifts as general relativity, according to the relative position of observers in different radial inertial systems. It should be noted that effects on relative time of stationary clocks is purely radial and not tangential (see Section 2.1); this depends on the relative size of the radius and the gravitational radius, according to the factor [r_o/(r-r_o)]. In addition, there is also an apparent shrinkage of space near massive bodies, consistent with maintaining constancy of the speed of light in each inertial system. One of Einstein’s invariant rods placed there might be found to be shorter using the longer wavelength standard seen from afar. Yet the local observer sees the opposite radially, using the correct standard wavelength for the frequency observed locally, always the same for the same clock.

Table 1 compares the estimated correction factors based on the gravitational radius (r_o) and Schwarzschild metric that must be applied locally for radial spatial observations at r using both models including general relativity. Clock shifts involving frequency behave similarly in both relativity models, although a zero event horizon occurs at the gravitational radius (r_o) in radial action and at the Schwarzschild radius (2r_o) in general relativity using the Schwarzschild solution. Spatial corrections for radial action relativity involve shortening of r matching time shifts whereas those for general relativity involve lengthening, leading to the need for additional curvature because of central mass. These differences in relativistic factors could be used to determine if the radial action theory is more consistent with cosmological observations than general relativity.

Event horizons may occur at the Schwarzschild radius (2r_o) and at the gravitational radius (r_o) in general relativity and in radial action respectively. Data for the Schwarzschild metric is shown both for ds² and its square root, ds.

Both models give similar results at r greater than 50r_o and almost identical results at much greater distances such as on Earth (1,438,136,866r_o) or the Sun (470,548r_o); radial action and general relativity differ significantly only below 10r_o, allowing tests to distinguish between them only in the case of black holes or neutron stars such as pulsars. Such observations cannot currently be made. However, they could allow either one or both current models to be falsified according to recommendations of Karl Popper.

3.5. Comparisons of Schwarzschild and Radial Action Metrics

The observer-clock at the Sun will still consider it observes the same time as the proper time dτ_∞ observed at zero gravity or infinity, given the same clock is used to set time in both localities. So dt_Sun/dτ_Sun for the ratio of times observed on the Sun and at infinity must equal, at least as an approximation, 1 - M/R. This is the proper time at the Sun, equivalent to a lower frequency (ν_Sun) and a longer wavelength (λ_Sun) viewed from infinity. However, relative to the constant speed of light (c) in a vacuum, all stationary observers will consider their proper time dτ to be the same/ The radial action metric is generated directly from the proposal that the nuclear and electronic centers of extreme high density (>10¹⁴ g cm^-3) comprising any mass M represent excluded space for normal physical interactions. Thus, space is shortened by the magnitude of the gravitational radius (r_o), in proportion to the ratio (r-r_o)/r cm cm^-1, where MG = r_oc². As a result, viewed from the distance r, the frequencies of molecular clocks near M such as the Sun are significantly reduced, showing a red shift

ν_Sun/ν_∞ = (r-r_o)/r = λ_∞/λ_Sun = dt_∞/dt_Sun (34)

To the far distant observer, the wavelength of light for photons associated with a particular electronic quantum state transition in a stronger gravitational field appears lengthened compared to the local wavelength for the same quantum transition. Given that [1 – M/R) factor from the Schwarzschild metric is formally the same as the (r-r_o)/r of radial action, these factors appear at first sight to be identical for adjusting relativistic frequencies. However, this may not be the case. The differential clock intervals (dt) of the Schwarzschild metric play a role like wavelength (λ) in radial action theory, their ratios being inverted with respect to frequency (ν). So dt may not indicate the beating or ticking rate from afar of the clock near a massive body, like frequency, but rather the duration of the intervals. In statistical mechanics, momentum and position compete in phase space with frequency likely to be the primary effect, more closely aligned with momentum than wavelength, In that sense, its appearance as a differential for time can be misleading mathematically and needs careful interpretation.

Thus λ_∞.dt_Sun = λ_Sun. dt_∞

λ_Sun/dt_Sun = λ_∞/dt_∞ = c

Equally, ν_Sun/ν_∞ = λ_∞/λ_Sun

Thus, ν_Sunλ_Sun = ν_∞λ_∞ = c (35)

This analysis requirees the invariance of the speed of light c at both locations for all observers. It also shows that even though time near the Sun appears to run slower from a distance as shown by the lower observed frequency, light has less far to travel locally when travelling radially, so it will still travel at c, irrespective of whether viewed from a distance or using local proper time. Given the longer wavelength of light near the Sun, Einstein’s invariant rods will be measured as shorter using the wavelength as ruler, so space is contracted when viewed from afar. In radial action, the contraction of space at locations near massive objects viewed from afar (r-r_o)/r cm cm^-1 is expressed in Equation (36).

λ_∞/λ_Sun= dr_Sun/dr_∞ = (r-r_o)/r = dt_∞/dt_Sun (36)

Thus, shortening of Euclidean space may be real but not realized by the local observer who lengthens space measured by the lengthened wavelength. There is an actual contraction of space for physical interactions caused by the presence of the central mass of magnitude (r-r_o)/r. To the distant observer, the number of local wavelengths required to reach the physical center will seem to be reduced and the distance thus shorter, according to the radial metric (r-r_o)/r cm cm^-1. However, to the local observer near the massive center, wavelength must be unaffected since it provides the local standard of length. To the distant observer, space must be lengthened or stretched near the massive object to match physics to geometry.

For light travelling radially, we can compute its apparent radial velocity dr_Sun/dt_Sun viewed near the Sun from afar where dr_∞/dt_∞ equals c, using the equations above.

(r-r_o)/r = dr_Sun/dr_∞ = dt_∞/dt_Sun (37)

We can then deduce the following Equation (38) for the apparent speed of light passing the Sun.

dt_∞/dt_Sun. dr_Sun/dr_∞ = (r-r_o)/r_. (r-r_o)/r

Thus

dt_∞/dr_∞. dr_Sun/dt_Sun = [(r-r_o)/r]²

v^r_Sun = c(1 - 2r_o/r + r_o²/r²) (38)

The higher order term r_o²/r² in the expression (9) for the apparent radial velocity of light can be ignored for a far distant observer (r >>> r_o), so the apparent velocity is given by Equation (57).

V^r_Sun= c(1 - 2r_o/r) (39)

Once again, according to this interpretation, dt_∞/dt_Sun as dτ/dt must be considered as indicating the ratio of the universal proper time over the observed time interval on the clock near the Sun, given that the clock near the Sun runs slower, consistent with [1 – 2M/R) being less than one and dt being greater than dτ, indicating time dilation. The impression that these limiting differential values may be a relativistic variable is a challenge to calculus.

Nonetheless, taking the square root,

dτ² = [1 – 2M/R]dt²

dτ = [1 – M/R]dt (40)

The basis for the choice of [1 – 2M/R] rather than [1 – 2M/R + M²/R²] is presumably to be consistent with Einstein’s choice in 1915 [2] of the Schwarzschild radius as the event horizon, required by his preference for 8πG equal to _K in the tensor equation of Section 2.1 G_μν equals KTμν so that Einstein’s metrical law of general relativity would reduce to Newtonian gravity in the weak field limit. However, no rigorous case for the solution of [1 – 2M/R] as exact was provided by either Einstein, Schwarzschild or Droste [7,8]. In any case, Einstein regarded his solutions of 1915-1916 in general relativity as approximations and might not have been concerned about an omission in the metric of the scale of M²/R². He did consider his derivation of the gravitational field component g₄₄ required for the first approximation in Newtonian theory as equal to 1 – α/r, yielding exactly 2r_o for α, with the square root of the metric ds² clearly as an approximate solution (see p. 161 in Einstein [2]). Here, we suggest the reverse could be true in choosing the square root of [1 – 2M/R + M²/R²] rather than [1 – 2M/R] to solve ds as the correct solution. In any case, the difference is negligible, unless r is close to r_o, as shown in Table 1.

It is important to recognize that expressing dt_∞/dt_Sun as dτ/dt refers not to lower ticking rates at distance, but higher rates (i.e. dt_∞ is shorter than dt_Sun), consistent with ν_Sun being less than ν_∞, viewed from far distance. Considering the spatial term in the Schwarzschild metric, ds can require an imaginary form (i) in Equation (41).

ds²/dt² = – [1 – 2M/R]^-1dr²/dt²

ds/dt = i [1 + M/R]dr/dt

ds = i [1 + M/R]dr (41)

3.6. The Lorentzian Transform in General Relativity

In 1905, recounted in 1916, Einstein [11] pointed out that the mass m in this equation varied with relative velocity elsewhere according to the equation, required to explain the increase in inertia and impulse.

m = m_o/(1-v²/c²)^1/2 (42)

Furthermore, a contraction of distance where x was the direction of motion was also found necessary.

x = x_o(1-v²/c²)^1/2 (43)

Since this shortening of length was accompanied by an equivalent slowing of time on clocks, this ensured that the speed of light would be measured as constant (and the maximum speed achievable) in all rectilinear inertial systems. Since we have already shown that r₀c² ≈ rV² it is possible to replace (1-v²/c²)^1/2 by (1 - r₀/2r), a relativistic correction one half that given by centripetal or gravitational effects. In the case of rotational work with dimensions of mr²ω² differences in potential are proportional to - mr²ω²/2 (=hv) rather than -mr³ω²/l. Expanding the mass Equation (49) using the binomial theorem, Einstein [12] proposed mass increased as follows.

m = m_o(1 + ½v²/c² + ³/₈v⁴/c⁴ + …) (44)

This applied equally to energy, equating the increase in mass and energy to the increase in inertia.

E = mc² = m_oc²+ ½m_ov² + ³/₈m_ov⁴/c² +.....(45)

Thus, as the velocity increases the mass appears to increase without limit. The increase in mass was associated with increased energy content and this energy itself was considered as the source of its increased inertia [14]. While discussing this aspect of general relativity in his book on the Special and the General Theory, Einstein [11] considered a system K’ which is in rotation about a Galilean system K at rest. “Clocks of identical construction and which are considered at rest with respect to the rotating reference body go at rates which are dependent on the position of the clocks. So, a clock at a distance r from the center of a disc has a velocity relative to K which is given by v = ωr where ω represents the angular velocity of rotation of the disc K’.” Then while v is small compared to c,

ν = ν_o(1 – v²/c²)^1/2

ν ≈ ν_o(1 – v²/2c² (46)

“If we represent the difference of potential of the centrifugal force between the position of the clock and of the disk by φ, i.e. the work considered negatively which must be performed on the unit of mass against the centrifugal force in order to transport it from the position of the clock on the rotating disc to the center of the disk, then we have.

Φ = – ω²r ²/2 (47)

From this it follows that the inertial or centrifugal relativistic correction for frequency is given by Equation (48).

ν = ν_o (1 - V²/2c²) (48)

We will see later how this inertial effect must be combined with the gravitational effect if clocks are compared at different inertial and gravitational potential. This is consistent with the virial theorem that determines the potential energy of quantum systems, involving absorption of a quantum of energy exactly equal to the decline in kinetic energy, an increase in potential of the sum of both.

3.7. The Inertial Radial Relativity Correction

However, if we consider the relativistic energy mc² comprises the rest mass m_o and the field energy sustaining increased action radii, then we can recast the energy equation as follows.

E = mc² = m_oc²+ ½m_ov² + ³/₈m_ov⁴/c² +......

mc² = m_oc²√(1- v²/ c²) = m_oc²√(r/r- r_o) = m_oc²(1 + r_o/2r + 3r_o²/8r² + ....) (49)

Thus, (m - m_o )/m_o = (r_o/2r + 3r_o²/8r² + .....), with the apparent mass increasing as both r_o and r increase, if r_o increases at a greater rate than r. This suggests that the increase in total energy with increasing velocity reflects an increased radial inertia from an increasing gravitational baseline, discussed in more detail below. The relativistic inertial ratio √r/(r- r_o) is a parameter for the curvature of motion and its radial inertia – the straighter the path the greater is the field energy included within the orbital trajectory. As r_o approaches r, the ratio approaches infinity. This explanation for the increase in mass with velocity attributes the greater inertia not to increased mass m but to an increased inertial mass because of an increasing radius of action, where r and r_o can increase limited only by the total mass of the universe.

For a stationary free electron of mass m_e, m_ec² represents the total potential energy available as kinetic and radiant field energy in binding to a proton. As the electron binds in forming the hydrogen atom, radiant energy equivalent to the increase in kinetic energy ½m_ev² = hν = mc² is emitted to the external field, so that the change in potential energy to a bound state is functionally equal to m_ec²- m_ev² [5]. The electron can ultimately be annihilated by fusion with other electrons and protons to yield a helium atom and two gamma rays, each of radiant energy equivalent to the mass of an electron or m_ec², the total potential or rest energy.

By contrast, the additional energy acquired by an electron implied by E = mc² in an electron synchrotron in great excess to its rest energy m_ec² is the increased inertial energy of the unbound state when accelerated to more linear motion in an electric field. The apparent relativistic increase in mass (m–m_e), in radial action theory, is simply m_ev²/2 +Σhν/c² = 2Σhν/c². Therefore, no relativistic change in mass is required. By then decelerating this linear motion with increased curvature in a magnetic field, some of the field energy supporting this linear inertia in the accelerator must be emitted as a tangential beam of x-rays and ultraviolet radiation.

There has been much speculation as to the source of inertia, a subject of major interest to Einstein. According to Mach, inertia resulted from an interaction of local matter with the distant universe. But the content of radial inertia theory is more suggestive of a primary interaction of the moving body with the nearby energy field, sustained by local interaction with other matter both within and outside the curvature of the action radius. Einstein concluded [14] that the mass-inertia of a body simply increased with its energy content, according to the Lorentz transformation [2,10]. Thus, radiation by matter corresponded to a loss of mass according to the equation Δm=ΔE/c² = hν/c², where ν is the frequency of the radiated photon. In 1905, Einstein [14] estimated that a relativistic change in energy for two states of a body at zero velocity and then V would differ in energy according to the following Equation (50).

K₀ - K₁ = L[1/(1 – V²/c²)^1/2 - 1]

≈ L(V²/2c²) (50)

Thus “if a body gives off energy L in the form of radiation, its mass decreases by L/c².”

In action resonance theory [12], it was concluded that this quantum loss of inertial mass as photons is a simple result of the release of the field energy no longer needed to sustain the mass of the electron at a higher speed and lower radial inertia. The sharper the curve, the greater will be the energy release. This emission is from the energy field needed for lower radial action that Einstein attributes to loss of relativistic inertial mass. This analysis for the synchrotron applies to an unbound electron in curvilinear, not rectilinear motion, proceeding on ever straighter trajectories with greater radial inertia as its speed increases in the electric field.

For changes in radial action, the radius of motion of a particle changes as the quantum is absorbed in the field. This means that the ratio r₀/r changes so that the inertia mr will change, becoming greater when energy is absorbed or less when energy is emitted. For absorption of a quantum by a system with variable action the potential energy (-mv² = -mr²ω²) increases at twice the size of the quantum, given that kinetic energy decreases equally to the quantum absorbed in the field, according to the virial theorem.

hν = (mr₁²ω₁^{2 --} mr₂²ω₂²)/2 = mr₀c²(1/r₁ – 1/r₂)/2

= mr₀c²(r₁ – r₂)/2

hν/c² = mr_o(1/r₁ – 1/r₂)/2

m_photon = m(r_o/2r₁ – r_o/2r₂)

= m(V₁²/2c² – V₂²/2c²) (51)

In radial action, the relativistic mass of the quantum is absorbed into the field of the molecule, moving with less curved motion indicated by the factor r_o/r. This result in Equation (26) is the same as in (24), where Einstein uses the Lorentz transform. So, an important difference between general relativity and radial action relativity is the different method used to show inertia, one for translational motion always in a straight line and the other using natural coordinates where the translational motion is of variable curvature.

3.7. The Gravitational Radius and the Gravity Effect on Time and Space

Clocks based on the frequency of the emission of a photon released from an electronic transition will differ in radial inertial systems at different gravitational potential. This is a simple result of the photon emitted or absorbed including the fine structure of the gravitational field in its magnitude. Because the magnitude of the gravitational quantum decreases as the radial coordinate shortens by the radial geometric factor (r-r_o)/r, a relativistic effect will exist for all transitional frequencies, as given in Equation (16).

ν_r = ν_∞(1 – r_o/r)

In radial coordinates we can write for two observers at systems with differing radial inertias defined by r₁ and r₂, where the latter is greater.

ν₁ = ν_∞(1 – r_o/r₁)

ν₂ = ν_∞(1 – r_o/r₂)

(ν₁ - ν₂)/ν_∞ = r_o(r₂ – r₁)/r₂r₁ (52)

From this simple formula, the relativity red-shift for an observation of a surface emission made at a height 22.6 meters above the Earth’s surface would be 2.4593396101290x10^-15 lower frequency than that emitted at the surface (i.e. ν_{1 =} ν₂ (1 - 2.4593396101290x10^-15), a negligible difference, but consistent with the results announced by Pound and Rebka in 1960 [15], widely regarded as the first firm confirmation of Einstein’s theory regarding relativistic clocks. Further, when viewed from the Earth a photon emitted in an electronic transition on the Sun will be red shifted, where r₁ is the Sun’s radius and r₂ is the Earth’s orbital radius around the Sun. The residual gravitational effect at r₂ from the Sun must be distinguished from that resulting from the frequency shift due to the Earth’s gravitational potential, also causing a red shift to observers viewing the Earth from elsewhere although only one ten-thousandth the magnitude of that caused at the Sun’s surface.

Nevertheless, a global positioning satellite (GPS) of slight mass orbiting at 26,600 km from the Earth’s center will still see a measurable gravitational red shift at the Earth’s surface using its local clock or color camera, equivalent to the satellite’s clock running about 45.55 µsec per sidereal day fast. Incidentally, this time contraction estimated from radial action strictly refers to that between clocks in orbit at r₁ = 26,600 km and just above the Earth’s surface. The relatively slower motion of the GPS receiver on the Earth’s surface as inertial motion relative to the stars would also need to be considered to calculate the true difference in time of the clocks. A motionless clock on the surface at the Poles would experience the full gravitational acceleration towards the Earth’s center but reduced inertial acceleration away from the center because of its lack of radial action, compared to being in orbit.

So, in a system with a more negative gravitational potential, there is a real physical effect on time and space, reaching extreme values near black holes, where r²ω² approaches c². Under these conditions the red shift is so intense that ν_r/ν_∞ for such clocks must approach zero, and wavelengths infinity, consistent with radiation from bodies near absolute zero, as gravitational quanta. Thus, the space-time effects apparent to outside observers have a genuine basis, even though they are not obvious to the local observers experiencing the more negative potential, who will trust their clocks. Indeed, their own bodily processes including the speed of thought are affected in the same way. We must conclude with Einstein that the passage of time in the Universe is physically relative depending on the clocks’ environment, lacking absolute status.

Some values of these gravitational red shifts, predicted from action theory for some radial inertial systems, are shown in Table 2. The blue shift refers to the extent to which molecular clocks will appear to run faster to observers viewing clocks at higher gravitational potential (i.e. less negative), responding to the surface gravity and hence the mass of central bodies, as pointed out by Einstein [2]. Incidentally, the red shift factor viewed from far distant stars from the Sun’s gravity at the orbital radius of the Earth is about 9.8739x10^-9, greater than that from the Earth’s gravity of 6.9535x10^-10. But the gradient for the Earth’s field is three orders of magnitude greater than that for the Sun (or the Moon) at the Earth’s surface, so that the height above the Earth’s surface predominated in the Pound-Rebka experiment that employed the Mossbauer effect to allow the gravitational shift to be displayed. The time-of-day effect of the Sun would vary over a range of 2.9832x10^-18, between mid-day and mid-night. The Moon’s effect would be several times greater, like its relative effect on Earth tides.

4. Equivalences in Application Between Radial Action and General Relativity

In this section we will show where radial action relativity can emulate general relativity. Einstein completed his field equations for general relativity in the final months of 1915, more than a century ago. His remarkable theory provided answers to outstanding questions in physics but its main contributions were (i) the establishment of the principles of relativity ruling frames of reference for space and time and (ii) the principle of equivalence of the property of mass for both gravity and inertia. Radial action includes both these principles in its postulates. We have no intention of reviewing general relativity in detail. However, aspects of the theory must be discussed.

4.1. Lagrangian Variations of Action and Central Force Orbital Equations

The principle of least action is also defined with action as the time integral of the Lagrangian (L) defined as the difference between the kinetic energy and the potential energy (V) ($L=T-V).$ Action (S) is obtained by integrating the Lagrangian with respect to time ($S=\int Ldt)$. The motion of the conservative system is to minimize the variation of the action and deviations from geodesics of predicted paths.

We can express the Lagrangian per unit mass as a gravitational system, assuming similar forms of equations apply to all bound particles.

${\displaystyle \frac{L}{m}}= {\displaystyle \frac{1}{2}}\left({\dot{r}}^{2 }+r^2{\dot{\theta }}^2\right)+{\displaystyle \frac{G\left(M+m\right)}{r}}={\displaystyle \frac{T-V}{m}} ;$ $\left({\dot{r}}^{2 }+r^2{\dot{\theta }}^2\right)=v^2$ (53)

In our unpublished work with the late Barrie Fraser [16] using generalized coordinates and velocities $(\dot{r},\dot{\theta })$ and ($r,\theta )$(the vertical dot indicates differentiation with respect to time, $\dot{r}$=dr/dt, $\dot{\theta }=d\theta /dt= \mathsf{\omega })$ to minimize the action we have obtained two equations in the form of Euler-Lagrange calculus of variations, for unit mass. For the first set of coordinates we have ${\displaystyle \frac{d}{dt}}\left({\displaystyle \frac{\partial L}{\partial \dot{r}}}\right)= \ddot{r}$ and ${\displaystyle \frac{\partial L}{\partial r}}= r\dot{{\dot{\theta }}^2- {\displaystyle \frac{G\left(M+m\right)}{r^2}} }$we obtain equation (2) from differentiation of (1).

${\displaystyle \frac{d}{dt}}\left({\displaystyle \frac{\partial L}{\partial \dot{r}}}\right)- {\displaystyle \frac{\partial L}{\partial r}}= \ddot{r}-r\dot{{\dot{\theta }}^2+ {\displaystyle \frac{G\left(M+m\right)}{r^2}} =0}$ (54)

So, the first Euler-Lagrangian expresses an equation of motion as a balance between accelerations (force per unit mass), one like Newton’s second law and the second an inertial acceleration. Applying the second set of coordinates ($r,\theta )$ produces Equation (55), given the absence of a theta term affecting the Lagrangian in (1).

${\displaystyle \frac{d}{dt}}\left({\displaystyle \frac{\partial L}{\partial \dot{\theta }}}\right)- {\displaystyle \frac{\partial L}{\partial \theta }}$ = ${\displaystyle \frac{d}{dt}}(r^2\dot{\dot{\theta })= 0}$ (55)

The angular momentum per unit mass $r^2\dot{\theta }$is constant in this conservative system. Thus, the Euler-Lagrangian calculus of variations gives the same orbital equations as derived by Newton based on his definition of forces. Using an approach conserving force (energy) Leibniz equated a reversible variation between vis viva (2T) with gravitational work, governed by an equation in which an inertial term was proportional to the inverse cube of radial separation and gravitation to the inverse square of radius; this was equivalent to $\ddot{r}=r\dot{{\dot{\theta }}^2- {\displaystyle \frac{C}{r^2}} or d^{2}r/d{t}^2}= r{\omega }^2- {\displaystyle \frac{C}{r^2}}$for elliptical motion, the same solution as in (2). Leibniz’s approach Kennedy at al. 2023, [7] foreshadowed least action, as a counterplay between inertial action and central attraction.

4.2. Radial Action Relativity and Precession of Ellipses

Equation (6) like Leibniz’s equation expresses radial acceleration as the difference of the centrifugal and centripetal terms. These are not equal, despite such claims in many textbooks.

d²r/dt² = h²/r³ - h²/lr² = rω² - r²ω²/l (56)

It can be observed that this equation for the radial acceleration given by Leibniz is usually written, for Newtonian orbits, as follows.

d²r/dt² - h²/r³ = -C/r² (57)

The second term (h²/r³ = rω²) is sometimes referred to as the centripetal acceleration, although it is clearly directed outwards and the third term (-C/r²) as the gravitational acceleration inwards. Newton’s followers vehemently opposed Leibniz’s proposal [17] that the net radial acceleration could be obtained from the difference between Newton’s inward-acting gravitational force and an outward-acting inertial or centrifugal force, arguing that the gravitational and centripetal forces should always balance one another. On the contrary, Leibniz concluded that it was possible to describe an elliptical orbit defined using factors proportional to the inverse of radius cubed minus the radius squared, like Equation (8), using the equation as he originally expressed.

ddr/ddt = a/r³ - b/r²(58)

For the natural coordinates of radial action, Leibniz is considered correct, and the gravitational acceleration is -C/r² or -r²ω²/l as discussed in Section 1.2. Another point worth noting for the sake of future revision is that the equation is only valid for the full radius r separating the centers of the gravitating bodies, m and M. Therefore, for ultimate accuracy, the quickness or swiftness of action (celerity) must be obtained as the product of the total sum of the masses and G (C=(m+M)G). For the sake of convention, this discussion will continue here for gravitational orbits calculated with the total radial separation r. However, orbits for dual stars are better calculated using center of mass coordinates r_m and r_M that together equal r, separating the accelerations caused by each star. The gravitational equation of elliptical motion provides inertial and centripetal accelerations, critical in determining the position of perihelion.

d²r/dt² = rω² - (m+M)G/r² = h²/r³ - h²/lr² (59)

We can make appropriate relativistic adjustment to the centripetal or gravitational acceleration as follows, ignoring second order corrections.

d²r/dt² = rω² - h²/(l -r_o)(r - r_o)² (60)

= rω² - h²/(l -r_o)(r - r_o)²

≈ rω² - h²/lr²(1- 3r_o/l)

≈ rω² - h²(1+ 3r_o)/lr²

≈ rω² - r²ω²/l - 3r_oω² (61)

We claim no correction is required to the inertial term h²/r³ in Equation (42) as the radius r has no strict causal role in the centrifugal acceleration, only being a result of the centripetal acceleration.

d²r/dt² = rω²(1 – r/l – 3r_o/r) 62)

The final term in the equation of motion is the same as Einstein’s relativistic correction.

d²r/dt² = -m/r² + h²/r³ - 3h²m/r⁴ (63)

= -m/r² + ω²(r – 3m) (64)

Here m = MG/c² = r_o, achieved by assuming G and c defined to be unity, so that mass as the only variable is made clear. So, Equation (62) above is the same expression as Einstein’s result in Equation (46), obtained more simply with radial action coordinates. In this expression m is equal to (r_m²ω)²/lc², where the center of mass coordinate r_m approximates r when M is at least several orders of magnitude greater in mass than m, the mass of the satellite.At 3r_o, the relative acceleration is -3r_oω², with equal inertial and centripetal accelerations, so the precession is extreme at 2π radians.

Explained by Feynman [3, feynman], one remarkable result of Einstein’s general relativity is the concept of the excess radius, requiring spatial curvature because physical length towards the interior exceeds Euclidean length. This can be contrasted with the inherent curvature of radial inertia discussed above, which is strictly Euclidean. Compared to Newtonian gravitation, general relativity requires recognition that Euclidean geometry appears to underestimate the orbital radius for Newton’s Law. Proportional to the mass of a central body, the radius is suggested to slightly exceed that expected from the area of a spherical surface measured as (A/4π)^1/2 to provide the precession observed in Mercury’s orbit. The extent to which it does this [3] is given by r_measured - (A/4π)^1/2 = MG/3c², equal to r_o/3, where r_o is the gravitational radius for a central mass (1.477 km for the Sun). So, the radial distance between the Sun and Mercury is apparently 0.4923857 km further than expected and space is said to be curved to this extent.

According to Einstein [2] because of general relativity the “orbital ellipse of a planet undergoes a slow rotation in the direction of motion, of amount 24π³a²/T²c(1 - e²). In this formula a denotes the major semiaxis, c the velocity of light, e the eccentricity, T the time of revolution”. This may be written in radial coordinates simply as 6πr_o/l radians per planet’s orbital year, or 3r_o/l radians per radian of orbit. Using this relative radial action approach to estimate more realistic values, some planetary precessions for the solar system are given in Table 3.

We can explain this in the context of the radial action discussion given above for special relativity. For the minimal mass-inertia mr_o occurs for orbits near the Schwarzschild radius r_s. As V=rω for an object with increased inertial speed increases above local orbital speed, so do r and r_o for the object. No longer in a local orbit, the greater inertial speed will now relate to a new orbit requiring greater central mass, less curvature and an increased Schwarzschild radius (see Figure 5).

Thus, radial action recognizes space shortened by the voids for material particles, cumulatively a void between r₀ and the Euclidean center. This explains why Newton was able to consider the mass of central bodies as at a central point. decreasing the numerator in gravitational acceleration [-(m + M)G/r²l] as the square of the radial action per unit length of the semilatus rectum. Given that the value of the mass of the central body M and the constant for universal gravitation G was estimated by observation (MG = C = rV² or h²/l) for this orbital motion, their product MG must be a slight overestimate of the celerity h²/l.

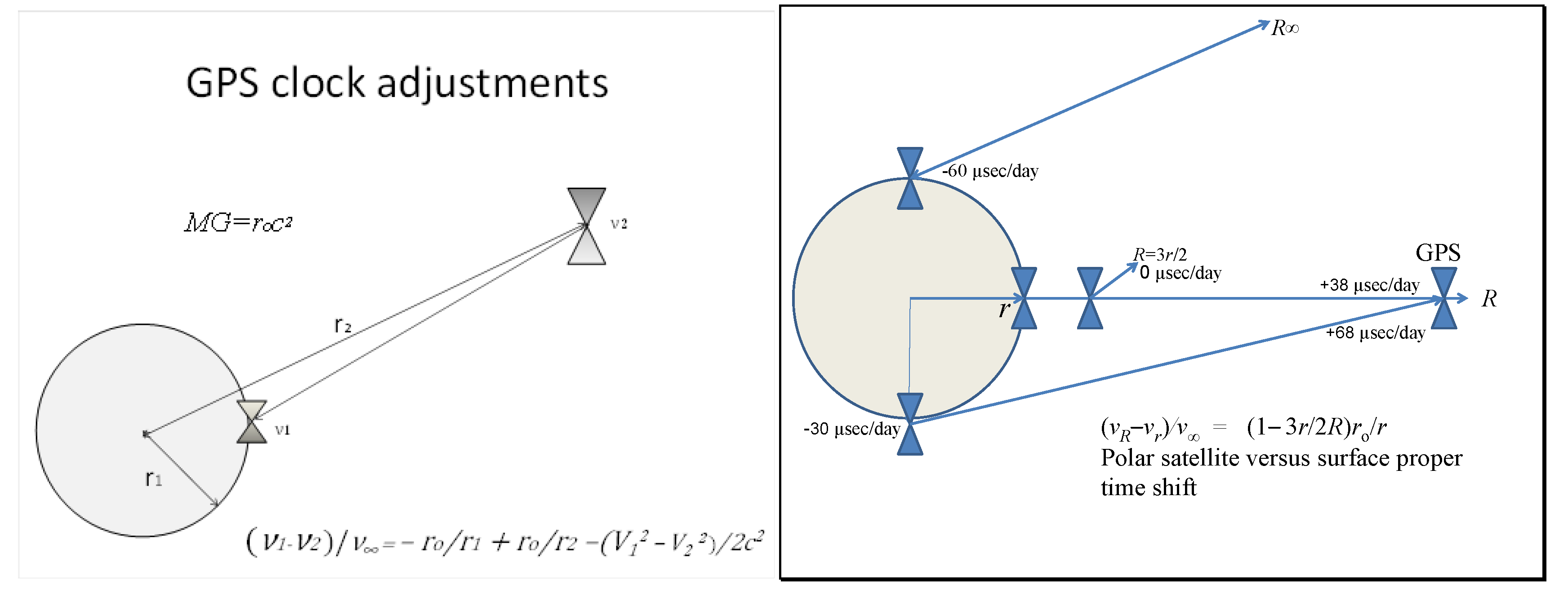
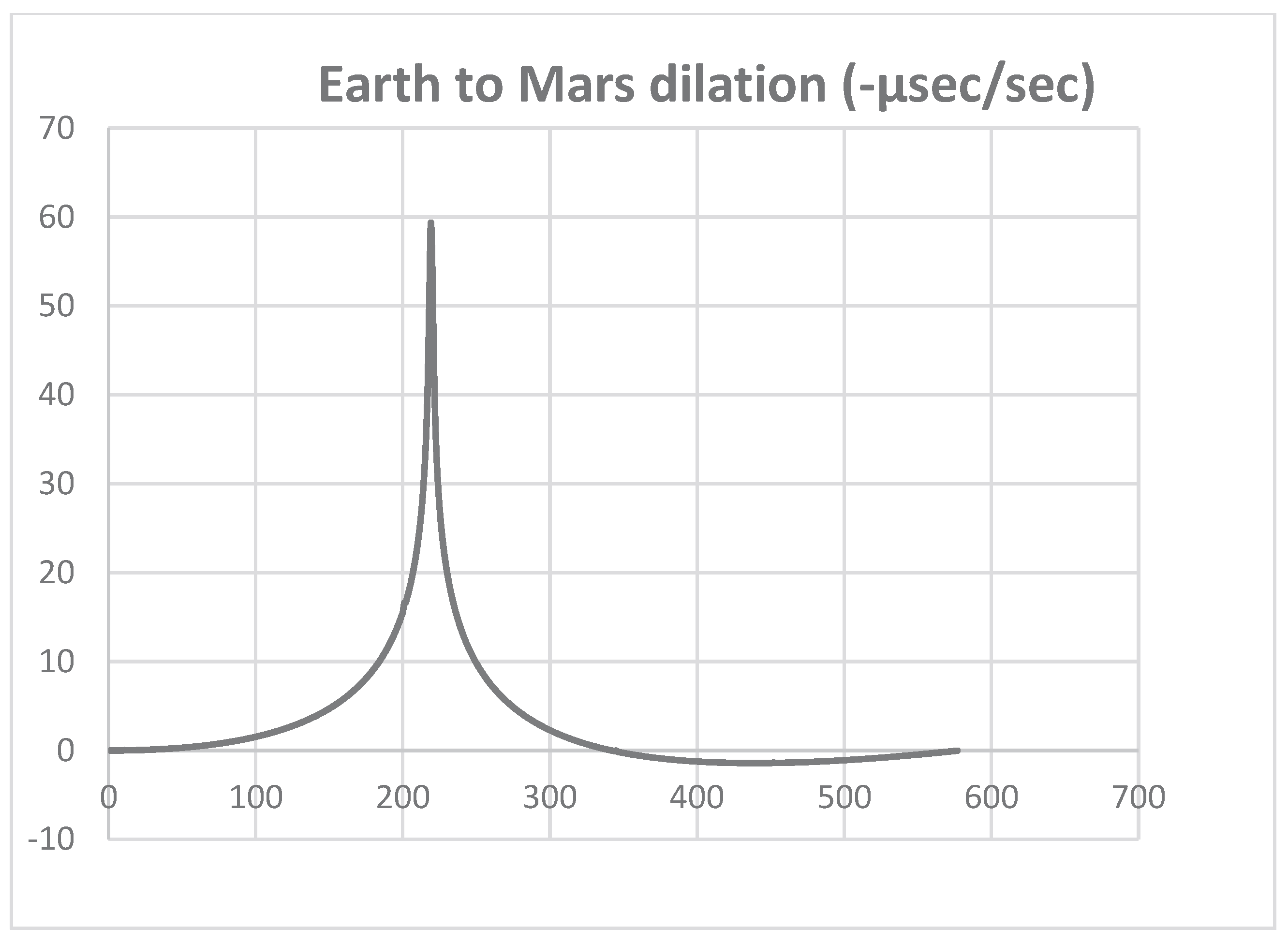
4.3. Corrections for Clocks in Motion

In addition to gravitational effects on clocks, there are also inertial effects on clocks in motion. These can be considered as functions of circular velocities with respect to the stars. The effect on clock frequencies therefore pertains to the centrifugal acceleration (h²/r³) in the Leibniz Equation (6) whereas the radial gravitational effect on clocks in Equation (23) pertains to the centripetal acceleration (h²/lr²), also the source of the precession of orbits to be discussed following.

In 1916, while discussing this aspect of general relativity in his book on the Special and the General Theory, Einstein [14] considered a system K’ which is in rotation about a Galilean system K at rest. “Clocks of identical construction and which are considered at rest with respect to the rotating reference body go at rates which are dependent on the position of the clocks. Then a clock at a distance r from the center of a disc has a velocity relative to K which is given by v = ωr where ω represents the angular velocity of rotation of the disc K’.” Then while v is small compared to c.

ν = ν_o(1 – v²/c²)^1/2

ν ≈ ν_o(1 – v²/2c²)

ν ≈ ν_o(1 – ω²r ²/2c²) = ν_o(1 – φ/c²) (65)

“If we represent the difference of potential of the centrifugal force between the position of the clock and of the disk by φ, i.e. the work considered negatively which must be performed on the unit of mass against the centrifugal force in order to transport it from the position of the clock on the rotating disc to the center of the disk, then we have in terms of potential.

Φ = – ω²r ²/2 (66)

Einstein says further, “an atom absorbs or emits light of frequency which is dependent on the potential of the gravitational field in which it is situated. …. Thus, the amount of displacement viewing spectral lines of the same element at the surface of stars compared the same element at the surface of the Earth will be”

(ν_o - ν)/ν_o = GM/r’c² (67)

This prediction has been considered earlier using radial action and is rendered differently for gravitation, using the observer at infinity as reference.

GM/rc² ≈ r_o/r

(ν₁ -ν₂)/ν_∞ = r_o(1/r₂ - 1/r₁) (68)

To be consistent, any inertial correction must be based on the transverse velocity with respect to far distant stars. The faster the relative normal motion, the greater the inertial correction required. This need applies automatically whenever clocks are in orbit but also applies to clocks travelling on the surface of planets, such as on the Earth. In such cases of non-orbital motion, the transverse motion on the planet’s surface is treated as though it was at a radius r where such a velocity would be orbital. Therefore, a clock on a vehicle travelling in the same direction as the Earth is rotating will have a greater red shift compared to infinity than when travelling in the opposite direction. In effect, the behavior is like a Coriolis effect as clocks at the poles are not affected. Given that clocks on Earth satellites orbit the Sun as well as the Earth, appropriate corrections may be required for perfect accuracy.

In an earlier section the change in inertial mass for photons emitted or absorbed in molecules at different gravitational potential was discussed. Changes of orbital gravitational potential energy involve the virial theorem, so that half the potential change is decreased or increased kinetic energy and half the change is absorption or emission of a quantum of energy. The change in mass involved in an energy exchange shown as hν(r₁ – r_1a)/r₁r_1a or mc²(r₁ – r_1a)/r₁r_1a, where the relativistic mass change m is hν/c². However, this change in the total field of energy represents just half the change in potential energy. So, the inertial relativistic correction involves just half the change in the velocity squared, as shown in Equation (30). In general relativity, a very similar correction given in Equation (26) involves an inertial or centrifugal work function of the same magnitude. In the case of Einstein’s rotating coherent disc discussed above, the centrifugal work function of Φ = –ω²r ²/2 (25) involves energy changes of the same magnitude.

We employ Equations (68) and the radial action version of (27) to provide an algorithm for corrections of GPS positioning clocks in orbit at r₂ or on the Earth’s surface at r₁, with the radius r_o providing the gravitational potential needed and with the squared velocity with respect to the stars providing the inertial potential (Fig. 6). There is no requirement that clocks be in orbit to make comparisons.

(ν₁ - ν₂)/ν_∞ = r_o/r₂ - r_o /r₁ + v₂²/2c² - v₁²/2c² (69)

Below, we suggest that these corrections are accurate and that their use jointly provides greater ease of application, dispensing with some of the other corrections currently employed.

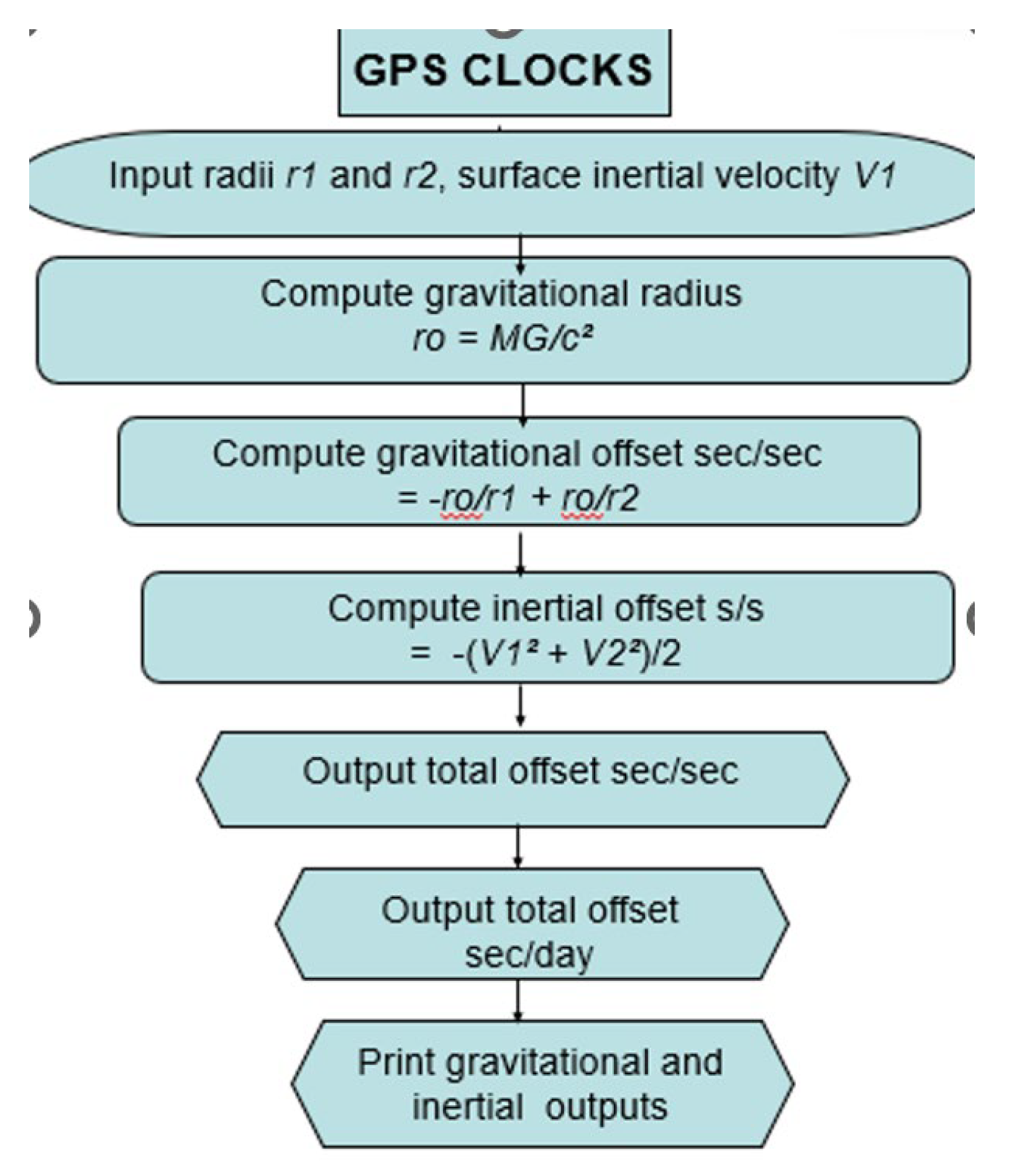
4.4. Radial GPS Clock Adjustments Involving Both Gravitational (r₀/r) and Inertial (r₀/2r) Corrections

Continuing the discussion above regarding relativistic corrections by relative shortening of radial distances, in the case of comparing clocks in different gravitational fields there are two corrections applicable. The first of these is gravitation with respect to the gravitational radius. We will find the gravitational difference between clocks located at two different radii will be as given in Equation [34].

ν_r1 = ν_⧝(1 – r_o/r₁)

ν_r2 = ν_⧝(1 – r_o/r₂)

(ν_{r1 -} ν_r2)/ν_⧝ = (r_o/r₂ - r_o/r₁₎ = r_o(δr)/r₁r₂ (70)

The second correction needed is inertial, just as we separated gravitational orbits as the net effect of gravitational and inertial accelerations as favored by Leibniz, discussed by Aiton [18]. This is a function of the curvature of the orbit, as discussed above with respect to the equivalence of the absorption of quanta and an apparent increase in mass. The more curved the motion, the greater the inertial correction. Then the variation in frequency of observations made between the orbits are as in Equation (35).

(ν_{r1 -} ν_r2) = (V₂² – V₁²)/2c² (71)

Overall, combining the two causes of clock variation we have Equation (72), also shown in Figure 6.

(ν_{r1 -} ν_r2)/ν_⧝ = [r_o/r₂ - r_o/r₁ - (V₁² – V₂²)/2c²] (72)

This radial action model for GPS corrections is tested with cases shown in Table 4. The data shown agree well with published results. It must be appreciated that the values calculated using Equation (40) are relative. For a satellite orbiting the Earth, there is no need to calculate an absolute correction for both with respect to zero gravity at infinity as in Equation (25).

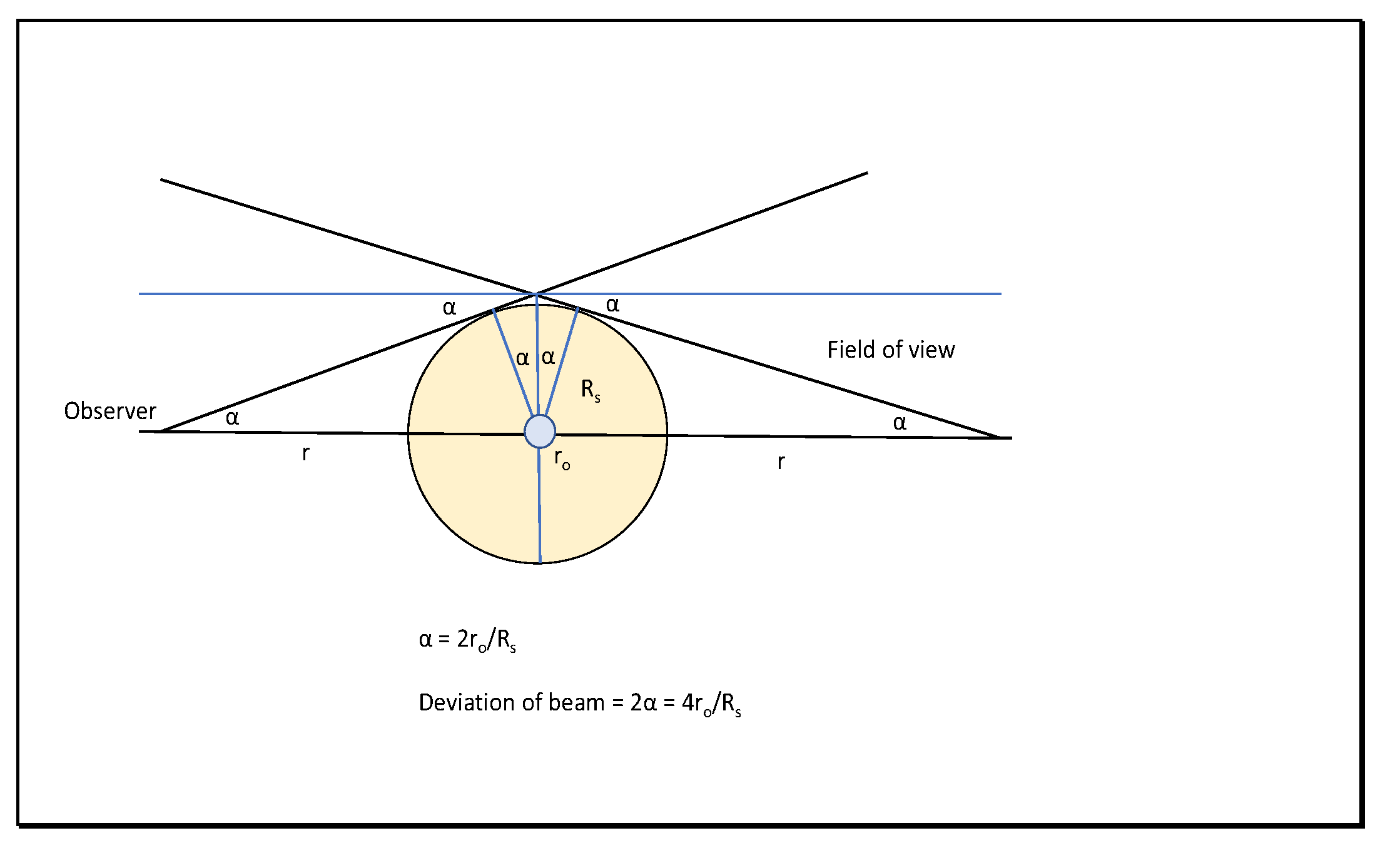
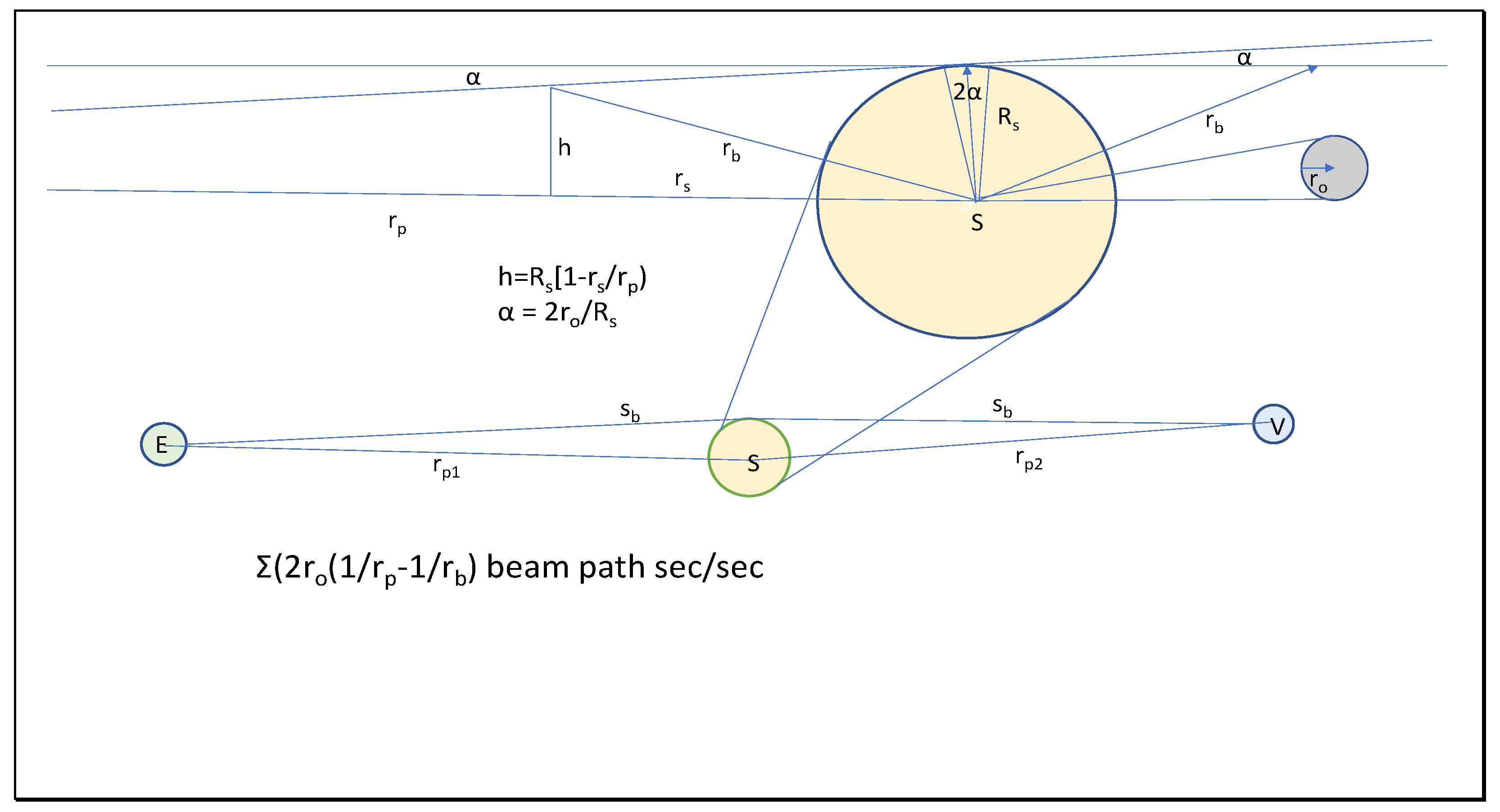
4.5. Bending and Time Delay of Light Beams Near Masses

Compelling evidence for the predictions of general relativity was the bending of the pathway of light and its slowing down near the Sun. Einstein’s general theory in 1916 [2] predicted that the total angle of deflection for radial motion would be 4M/R (4r_o/R), twice as great as he predicted in 1911, where R was the Sun’s radius and M the gravitational radius (r_o). For the Sun, this angular deflection amounts to 1.75392 arc seconds, an exceedingly small angle. Despite uncertainty regarding observations made during eclipses of the Sun when nearby stars are more visible, more recent measurements using radar reflected from Mercury and Venus have confirmed to a high degree of accuracy the increase in the time taken during a transit past the Sun, although his was not predicted in 1916.

We consider the trajectory of light from a star appearing close to the Sun using radial action theory. As indicated above, the apparent speed of light according to an observer more distant to the central body is affected twice as much during radial motion as during tangential motion, a result of combining both temporal dilation (ν_Sun<ν_r so clocks tick slower near the Sun) and spatial contraction (λ_r< λ_Sun), defining the distance cdt light is considered to travel near the Sun. The velocity of a beam of light travelling past the Sun is mainly radial. However, only light from objects in a narrow annulus occulted by the Sun, depending on the viewpoint of an observer, can be subject to maximum visible bending. This is illustrated in an exaggerated fashion in Figure 7.

Light experiencing the gravitational effect at the periphery of the Sun is effectively at the Schwarzschild radius exceeding the orbital velocity of c/2^1/2 can continue at the escape velocity of c at r, showing that objects closer than r will still be obscured by the Sun but those at r or more distant will become visible from light bending. In the case of the Sun (R=695,000 km; r_o=1.4771 km), from an observation point of r 163,504,500,002.1 km distant, an occulted star lying on an extension of the radial axis r at the same distance (63.297 light days) would become visible as an annulus by light bending of α radians, as shown in Figure 7 (α=4r_o/R; 2r_or=R²). The trajectory of light just grazing the surface will be tangential to the surface at R deflected by an angle of 2r₀/R_s on both sides of the Sun’s radius. This was discussed in section 3.4 consistent with Equation (29) regarding the apparent dual effect of gravity on the perceived speed of light from r.

V_r = V_∞(1 - r_o/r)² = (1 – 2r₀/r + r_o²/r²) (73)

However, at such a large distance, corrections would be required to account for relative motion during the 126.6 light days that a light beam takes to travel the distance between an occulted star and the observer. It is of interest that a star of the same mass and density as the Sun at about ten times the breadth of the solar system from the Earth could no longer obscure the light from any objects lying behind it. In the case of a black hole of 3.0 km diameter of similar mass to the Sun, such an effect would occur for objects as close as 4.5 km distant, deflecting light by 1.3^. radians, half of the deviation occurring in the approach to the black hole and half when receding to the point of observation (Fig. 6). Numerical methods provide an effective means to integrate the space-time trajectory of the light beam and to estimate its time of flight.

Not considered to by Einstein, Shapiro [19] and colleagues pointed out that general relativity also predicted a time delay for electromagnetic signals sent past gravitational bodies such as the Sun. Our computer program used to compute the delay time is given in Figure 8, based on the model shown in Figure 9, with computed data showing the extent of delay given in Figure 10. The algorithm obtained of 2r₀[1/r_p -1/r_b] applying at each point on the trajectory of the light beam estimates the effect of the Sun on the light beam (r_b) and on the stationary earth clock at r_p. We estimated the round radio beam trip to Mars Lander to be delayed about 230 μsec by the Sun, as viewed from Earth, with most of the delay occurring within 10 diameters of the Sun.

As shown in Figure 10, there is a small blueshift of about 2.832 μsec total while the light path to Mars exceeds the Earth’s distance from the Sun with a delay only between that distance and the Sun and the Earth. Nearly all the dilation is generated up to ten times the Sun’s diameter each side of glancing surface, where the trajectory is expected to follow the Sun’s surface for a short distance. The reason for the blue-shift in light speed lies in the fact that the delay is always measured from a point of observation with a clock based on the surface of the Earth. Once the distance to the Earth is exceeded on the path towards Mars and returning, the light frequency exceeds that of the Earth clock and the relativistic effect is reversed.

We consider that estimating the delay in the beam’s trajectory determined by this radial action algorithm is simpler in conception than others which have been published [20].

The time delay estimated from Earth near the Sun has been amply confirmed by others [21,22].

4.6. Radial Action Algorithms for Black Holes or Void Horizons

4.6.1. Hawking Black Holes at the Schwartzschild Radius (α = 2r_o)

Based on a concept introduced by Bekenstein [23], Hawking [24,25] showed that the entropy of a black hole is proportional to its surface area (A) at the Schwarzschild radius (2r_o= 2GM/c²). At 2r_o, the escape velocity for matter from the gravitational field is the speed of light (c); matter contained inside the Schwarzschild radius is therefore unable to directly escape from the gravitational centre as one action. Hawking’s celebrated expression of S = Akc³/4ћG relates entropy (S) to one-fourth of the Schwarzschild horizon area (A) of a black hole, as a function of Boltzmann’s constant (k), the speed of light (c), Planck’s quantum of action (ћ) and Newton’s universal gravitational constant (G). It is relevant to discussion in this paper that A/4 is equal to the area of the surface horizon at of the gravitational radius r_o. The divisor for area of 4 at the Schwarzschild radius was Hawking’s correction for Bekenstein’s original conjecture.

To calculate entropy of black holes, Hawking proposed that this was a simple function of quantizing one quarter of the surface area of the Schwarzschild horizon (A_s) as a simple function of the Planck length (L=1.61622837x10^-33 cm) and the Boltzmann constant (k).

A_s/4L² = N_H (74)

Consistent with the Schwarzschild metric given in Equations (17) and (19) Hawking [29] using this dimensional analysis defined the entropy (S) of a black hole is proportional to its surface area (A), with a singularity at the Schwarzschild radius 2r_o. In fact, Hawking’s expression for entropy can be reduced to a simpler mechanistic form, given that A at this radius is 16πr_o², four times the spherical area of the horizon at the gravitational radius (r_o).

S/k = Ac³/4ћG = 4πMr_oc/ћ = N_H (75)

The product of the black hole mass with the Newton’s constant of MG is equal to r_oc² at this radius. This is consistent with Newton’s conclusion with gravitational orbits that MG ≈ R_sV², stated for orbit in relativistic terms {17]. Then from Hawking’s entropy (S) can be written as S/k equal to 4πMr_oc/ћ. This analysis shows the ratio of the entropy (S) to Boltzmann’s constant (k) is also a simple ratio of the black hole’s radial action at r_o, Mr_oc divided by Planck’s [10] reduced quantum of action ћ, excepting the extra factor. He defined temperature of a black hole as a function of mass (M).

T = ћc³/8πkGM (76)

We can infer that this value for T, written more simply, equals ћc/8πkr_o. Then by multiplication we can conclude that for all black holes, based on Hawking’s results that ST is given by Equation (77).

ST = 4πkMr_oc/ћ x ћc/8πkr_o = Mc²/2 (77)

An inverse relationship exists between the mass of a black hole and its temperature. Given that the dynamic substance of a black hole must all have a speed of c, adding energy to a black hole cannot increase its temperature. On the contrary, by increasing its inertial mass extra energy must cool a black hole because of a larger radius and surface area. In Table 5, the number of quanta on the surface is estimated as equal N as Mr_oc/ћk.

The use of Planck’s quantum of action (h) as a reference value for entropy also occurs in statistical mechanics and our theory of action mechanics [11] in the partition functions for translational and rotational energy, invented by Willard Gibbs. Normally, the reduced quantum of action ħ applied to molecular action and h to radiation. However, unlike the case of matter-energy in motion at the ultimate speed of c where entropy is simply the total number of quanta, the relationship between entropy, action by material particles and the configurational Gibbs field energy [Kennedy et al., 2025,] sustaining chemical systems is logarithmic [3]. The absolute requirement discovered by Carnot that a system’s configurational energy denoted by ST cannot be used to do work except with a heat sink at lower temperature must also apply to black holes and similar objects like neutron stars. The feature of disorder characterizing Boltzmann entropy indicates that action in the event horizon too must be disordered or random in nature, not allowing additional work lacking a temperature gradient. However, a spinning black hole must have work potential for a stationary structure.

4.6.2. A Radial Action Black Hole Surface at r_o

Hawking’s model of a black hole is challenged here in Table 5 with the radial action black void surface at the gravitational radius (r_o), consistent with the relativity given previously in this article. In radial action Hawking’s equation could be recast using the gravitational radius as the event horizon and removing the factor of 4π from the expression for temperature allowing the action ratio Mr_oc/h to equal to the number of particles orbiting statistically like Brownian particles on the surface of the black hole, all unable to penetrate the void to the center. Then the black hole temperature could be obtained in a similar way using the Wien displacement formula, relating temperature and peak wavelength of radiation from black bodies as described by Planck [33]. As explained below, we will use a purer form of black hole temperature because it gives more credible results.

The radial approach uses the same form for action (Mr_oc), but Hawking’s use of the reduced quantum ħ elevates the Hawking number of quantum bits by a factor of 4π. Hawking entropy is therefore 4π larger than that from radial action relativity whereas Hawking’s estimate of temperature is 8π lower. Consequently, ST is only half as large in the Hawking model, equal to Mc²/2, a matter poorly explained.

Is it appropriate to use the Planck black body theory for vibrating molecules to estimate surface temperature of a dense event horizon of quanta in Brownian motion? From Wien’s displacement law, Planck [33] calculated the relation between temperature and the maximum wavelength for rate of molecular vibration by the following Equation (78), showing the factor β for matter equal to 4.9651. The latter factor of β is derived from its equality with the relationship hc/kλ_mT, because differentiation of the equation for (dE_λ/ dλ) = 0 yields the maximum at λ_m.

b = hc/βk = 0.28979 cm degree (78)

However, the surface at r₀ is not a black body with vibrating molecules. It consists of pure quanta

Possibly from transitioned matter with a circular local velocity at light speed r₀ω₀ and an invariant inertia of (mr₀) of the same value as quanta with longitudinal velocity(mλ). All quanta have the same action (h=mλc). Then the temperature for quantum black hole radiation at its wavelength of 1.47702x10⁵ cm might be given by Equation (79), assuming no such correction factor (β) is needed.

T_B = hc/r_ok =mr₀c²/r_ok= mc²/k (79)

T = 1.4398/λ_m (80)

For λ equal to 1.477015 km, this gives a mean black temperature for a Sun mass of 1.5144x10^-6 K.

Einstein’s selection of the 8π factor in Equation (1) defined twice the gravitational radius as the internal limit of gravitation, rather than the gravitational radius. Was this necessary? Einstein thought so as it validated the Riemannian tensor mathematical physics he was applying, curving radial space. This system of coordinate conversion also satisfied his principle of covariance. Both Schwarzschild and Droste thought so too, thus promoting the same metric.

In this article we have shown that a different system of coordinates shrinking space rather than bending based on using the frequency and conjugate wavelengths of radiation also gives the same results in terms of relativistic principles. Table 5 also illustrates how Hawking’s results proposing black holes can also be reinterpreted, possibly with more satisfactory results. The quantum nature of entropy is well accepted in physics, such as in Boltzmann’s definition as a function of his constant. That entropy is proportional to the area of the black hole is also logical, though with one-quarter the area having a metric half the size. Logically, kT for a quantum should then equal mc² shown in Equation (77) with the Boltzmann constant a dimensionless factor increasing the scale of temperature 1/1.3806x10^-16 times. This temperature is 16π² times the value found by Hawking for black hole surface shown in Table 5. The wavelength λ for black body radiation is taken as 2πr for a helical quantum. However, the quanta on the horizon surface lack the longitudinal velocity required for emission of radiation; instead, their speed of light c is equal to r₀ω₀ using the frequency notation for a constrained particle (ω). We estimate a gravitational radius or pseudo-black void of 0.4435 cm for Earth (r₀=MG/c²), suggesting a surface temperature for quanta of 0.51672 K (Table 5) on Earth.

The cosmic radiation said to be a remnant of the big bang in the standard theory of physics has a maximum frequency of 160.4 GHz, corresponding to a Planck black body temperature of 2.726 K. However, according to Equation (79), this colder temperature also requires a longer radius (r₀) or wavelength of 0.5278 cm, 1.19 times longer than 0.4434 cm, with frequency 56.7 GHz. For black body radiation, a maximum radiation at a wavelength of 0.2514 cm (119.3 GHz) on a wavelength axis rather than a wavelength of 0.1869 cm for radiation of frequency 160 GHz. Is it possible that a statistically small proportion of the black void radiation with a mean temperature of 3.25 K could stochastically acquire through Brownian collisions on the horizon a slightly lower temperature just below 3 K and be radiated longitudinally to space? This coincidence is striking, but it could be fortuitous.

Thus, if we assume voids inside a surface at the gravitational radius r₀ can exist, we can substitute revised values for entropy and temperature at Hawking’s event horizon (see Table 5). The temperature of our action revision predicts gravitational temperatures for the virtual horizons for the Sun and Earth of ca. 1.55x10^-6 K and 0.5 K respectively, with radiation maxima near 22.3 kHz and 10 GHz, with r_o values of 1.4771 km and 0.4435 cm respectively. Then viewpoints with modified radial curvature to virtual centers of gravity [(m+M)G/c² ≈ r_o] might provide a cause for all effects of general relativity. Radial action mechanics allows simpler computations from a quantized event horizon at the gravitational radius, justifying new algorithms for relativistic corrections of gravitational red shift near massive bodies, dilation of time, contraction of space caused by increasing velocity, clocks on satellites and the angular deflection and time delay of radial light signals near the Sun and the Lorentzian increase in mass [4].

Given that these gravitating bodies are not black holes, the calculated gravitational radii from each celerity can only be virtual, but still represent the voids in primary particles making up the Earth. Newton considered the mass to be concentrated at a point but was well aware the mass was spherically distributed, behaving as though it was concentrated. Nonetheless, the gravitational radius is representative of the cumulative gravitational effects of matter subject to increasing pressure, towards each center containing voids with mass-inertia distributed on surfaces. Since all matter may contain completely empty voids at its center, protected by oscillating yet non-longitudinal quanta travelling at c in their most minute elements, we may assume that the centripetal acceleration (-r²ω²/l) in Equation (6) may actually be caused by a gravid, attractive response to these voids, varying in elliptical orbits by radius (r/l), equal to a ratio of 1.0 on the semi-latus rectum (l). By comparison, the inertial acceleration (rω² ) in the Leibniz equation is a function of the resonant Gibbs quantum field that defines the action. In the case of the Earth the total area of surface implied by this gravitational radius is only 2.4714 square cm, with an equivalent void volume of 0.36534 cubic cm. This implies that the weak force known as gravity is caused passively by a natural abhorrence of an absolute vacuum devoid of matter or energy, also causing the expansion of the universe.

4.6.2. Gravitational Radiation 

Equation (56) giving center of mass coordinates would be suitable to model gravitational wave energy as a product of Einstein’s general relativity in 2016. Following the We follow the approach of Hill and Norowski [24], considering Einstein his field equations as in Equation (1), for the relativistic variance for the geodesics,${ds}^2=g_{\mathrm{\mu }\mathsf{\nu }}{dx}_{\mathrm{\mu }}{d\mathrm{x}}_{\nu }$.

R_μν – ½g_μνR = −κT_μν = 8πGT_μν/c⁴ (1)

By linearizing curved space at far distance, Einstein concluded that general relativity theory that solutions in which perturbations to the Minkowski space-time would admit plane waves travelling at the speed of light. Then the tensor slightly perturbed Minkowski metric g_µν = η_µν + εh_µν is evaluated for 0 < ε< 1, neglecting all powers of ε^k with κ > 1. Einstein also explained how the wave would have unique feature of progressive compression then extension of receptors. Confirmation of gravitational radiation in 2015 by the LIGO/Virgo team used this approach to detection of the merging of two black holes in the LIGO antennae on the Earth’s surface.

This equation provides a Lagrangian equation of motion that can govern gravitational and inertial accelerations, only the gravitational attractive term being affected radially, as in Equation (62), effectively with an additional attractive term of – 3r_oω².

d²r/dt² = h²/r³ - h²/lr² = rω² - r²ω²/l (56)

The gradual collapse of one black hole orbiting another despite relative size can be modelled as given in Kennedy et al. [13], as shown in Figure 11.

Employing a form of the Schwarzschild metric as shown in Equation (81) and adjustment can be made to be compatible with a metric compatible with a gravitational metric, with ρ² = x² + y² + z² and h = dx² + dy² + dz².

$g=c^2{\displaystyle \frac{(1-\frac{r_s}{4\rho }{)}^2}{(1+\frac{r_s}{4\rho }{)}^2}}{dt}^2+ (1-{\displaystyle \frac{r_s}{4\rho }}{)}^{4}h$ (81)

$g=$-c²dt² + a²(t)g_x (82)

The second term in (82) is a Doppler correction for expansion of the universe.

Then the alternative form of (81) in radial relativity is given in Equation (83).

$g=c^2{\displaystyle \frac{(1-\frac{r_o}{\rho }{)}^2}{(1+\frac{r_o}{\rho }{)}^2}}{dt}^2+ (1-{\displaystyle \frac{r_o}{\rho }}{)}^{4}h$ (83)

As an approximate, Equation (83) could ignore the square terms expanding to yield (1 2ro/ρ) factors Using radial action relativity, the frequency of virtual gravitational quanta in the gravitational wave near the merging process will appear reduced viewed from distance but for a similar process locally if possible they would be appropriate and not lengthened. It could be of interest to researchers in this area to consider the gravitational relativity correction, where there would be no need to include curvature since it involves shortening rather than curving space.

5. General discussion

We stated in the introduction that a theory claiming to match or replace general relativity must have general equivalence. We have shown that radial relativity reproduces in a useful form the results of Einstein’s field equations and all field effects, including the Lorentzian increase in mass, dilation of time and contraction of space with velocity, the gravitational red shift near massive bodies, the effect on rates of clocks on satellites, the time delay of light signals deflected near the sun and gravitational radiation from the slowing down of pulsars or from fusion of black hole horizons. Furthermore, it does offer new advantages, such as reconciling gravitation and quantum theory.

Nothing proposed in this paper questions the validity of the conclusions of Einstein’s theories of special and general relativity, using algorithms based on local tensor analysis. These remain correct in terms of their basic propositions as shown by experiment. In a strict sense a mathematical description of a physical system can only be proved in terms of its assumptions, a form of Godel’s theorem. Incidentally, Godel and Droste cooperated in art work.

Later in the 1930s Einstein was still dissatisfied [6]. “What are the simplest conditions to which a space-structure of kind described can be subjected?” His satisfactory answer was obviously the equations of Riemannian geometry given in Section 2. Then “the chief question which still remains to be investigated is this:- To what extent can physical fields and primary entities be represented by solutions, free of singularities, of the equations which answer the former question? In this article radial action relativity with polar coordinates set in a Euclidean metaphysical framework provides another answer to the first question.

This new choice a century later enables similar spatial and temporal coordinates for both special and general relativity. Furthermore, by excluding the void, surrounded by dense energy apparently travelling at c, within the gravitational radius r_o, equal to (m+M)G/c², interior to the Schwarzschild radius, it allows a radial viewpoint that retains flat Euclidean space with no need for a singularity at the origin. All masses are contained ultimately in fundamental surfaces at light speed, ptreventing access. There is still a preeminent role for variable curvature of space in orbital motion but allowing radial separation to contract closer to the gravitational radius surface still allows covariant fundamental equations that can successfully transformed. Importantly, elliptical motion combines variations in linear radii with varying curvature (1 - r_o/r).

As explained in this account, unique features of relativity as radial action include:

(i) The invariant speed of gravity or light in all frames of reference is more than a postulate, it is a physical requirement. Using a caesium clock of standard frequency for time that is also invariant simultaneously sets the local standard of space-time, with an invariant product (c=νλ). Our choice of standard references being the same as the SI system is fortuitous but also removes the need for all other standards since these would be equally affected by the gravitational environment. This speed is required as the speed of functional communication and flow of information has a general effect on all local processes, including brain speed. This natural law for space and time is the cause of Einstein’s principle of equivalence. It would be welcomed by Leibniz.

(ii) The internal center of coordinate for physical processes is chosen at the gravitational radius (r_o), half as distant from the Euclidean origin as the Schwarzschild radius (2r_o). This is an event horizon where even light cannot escape, unlike the Schwarzschild horizon, where light speed allows matter to escape. However, escape may still be possible at 2r_o by arranging gradual increases in orbital energy.

(iii) The ultimate external coordinate is taken at infinity, a region devoid of material gravity. Here, clocks will tick unimpeded by gravity and space measured by the wavelength of light will be maximal. Then differences at interior sites can be corrected using the radial (r-r_o)/r ratio. Obviously, at infinity this ratio is exactly 1.0. Corrections at separate interior locations for viewpoints are obtained simply by difference.

(iv) The radial action corrections based on clock frequency and wavelength are simpler in execution, the theory claiming exactness using the radial ratio rather than approximations. In general, the radial action theory provides the same relativistic corrections given that the simplification used by Einstein and others of (1 – 2M/R)^1/2 as given in the Schwarzschild metric is effectively the same as (1-M/R), equal to (1 - r_o/r). Only when the event horizons are approached in the order of views will significant differences in predictions be observed (Table 4).

These differences from general relativity might provide a test of which theory should be favored. The corrections of general relativity required to preserve rectilinear inertial systems are said to result from length being underestimated, varying by a function of the radius to gravitational centers in the Schwarzschild metric; but adjustments in curvature are rationally just as well achieved by the inverse operation of using the ratios of the Euclidean radius to the shortened physical radius indicated by the limit of r_oc².

The consequences of such a change of view may be considerable. The radial action theory arose from recognition of the nature of gravitational orbits as a physical contest between gravitational and inertial accelerations [16], using a similar equation as proposed in the 1690s by Leibniz, discussed by Aiton in 1997 [17]. The Newtonian vectorial method for plotting orbits using rectilinear inertial coordinates then becomes a good approximation in naturally curved space, provided sufficiently small increments of radial motion are used in integration of the vectors. The stepwise quantized radial action approach is exact, requiring no such approximation.

In practice, the problem of relativity becomes a contest between one set of mathematical algorithms and another set. Radial action relativity has unique features. Mathematically, it relies on simpler algebra and geometry. Conceptually it is easier to imagine how to apply its algorithms. However, is it more correct than general relativity? In part that could be determined by testing its predictions under extreme conditions such as in the proximity of black holes or voids. Philosophically, radial action mechanics proposes wider revisions based on applying the principle of minimum action that can include chemistry, biology and environmental science in its fields of enquiry as an action revision [5]. However, Einstein’s major contributions to physics firmly establishing the principles of relativity regarding equivalence of all inertial coordinate systems remain. Indeed, radial action relativity extends these principles with mass never appearing except when attached to a coordinate mr defining inertia by curvature.

A young Jean Nicod’s philosophical geometric analysis [35], honed by working with Bernard Russell, in his book on the geometry of the sensible world emphasized that the space of views is more relevant to human perception than the space of objects and their location [17, Kennedy] that can never be observed simultaneously. We can assume simultaneity of events in the space of objects, but humanity is committed to the geometry of its current space of views, wherever this exists. Furthermore, Nicod strongly rejected [35] the conclusion made by Poincaré that “the relation of geometry to experience includes action, particularly”, even calling this a surprising delusion by the famous scholar. In fact Leibnizian=Lagrangian action as stationary for much of the world is an illusion, despite its reliability in many areas like planetary orbits or statistical mechanics. Frequently the flow of energy and work processes through systems are dissipative, one system supporting another. Yet nature as we know it must be a geometrically sensible world still be physically consistent with local action and inertia invariant, as are all forms of velocity including that of light.

Nicod’s conclusion that we can only make intellectual progress working from the order of views rather than that of objects seems prescient. Before we extend our view of good action to a general viewpoint, we need to be fully aware of the great differences in perspective of the world of views and the world of objects. Fortunately, physics is known to be consistent in all views shown by both general and radial relativity. To Nicod’s analysis of the sensible reality we also need to be aware of the metaphysical significance of Karl Popper’s [27] three metaphysical worlds, World 1 – the realm of the physical and biological beings and environmental objects that Nicod parses by viewpoint; World 2 – the realm of human (and other) consciousness, thoughts and all other subjective states requiring objective testing; World 3 – the realm of the objective products of the human knowledge that we must work to ensure have enduring value for human civilization and evolution. The question that remains for humans must be how to decide the evolutionary value are our current viewpoints, guided where possible by reliable tests.