A Masi-Entropy Image Thresholding Based on Long-Range Correlation

1. Introduction

Image segmentation is a mid-level processing technique used for image analysis. Such a method consists of splitting an image into several disjoint parts by grouping the pixels to form homogeneous regions regarding pixel features like intensities, textures, heat signatures, among other characteristics. The regions formed should be visually distinct and their homogeneity based on a correlation between the pixels in the image. Errors in the segmentation could be caused by effects of illumination, shadowing, noise, partial occlusion, and subtle object-to-background changes.

One of the most basic and well-known ways to segment grayscale images is thresholding that works by selecting one or more gray levels of the image, called thresholds, to separate objects from their background. When the objective is to separate the object region (foreground) from the background through only one gray level, the method is called bi-level thresholding [1,2,3,4,5,6,7,8]. This form of region segmentation results in a binary image, in which each region is either white or black. Otherwise, if the separation of the regions of interest from the background depends on different gray tones, the process is called multilevel thresholding [9,10,11,12,13,14,15,16].

The focus of this work is bi-level image thresholding. Entropy-based approaches constitute the most common techniques in this area. Basically, thresholding is implemented through an optimization technique that consists of selecting a threshold that maximizes the entropy of the segmented image. For instance, Kapur et al. maximize the Shannon entropy of segmented classes to obtain the optimal threshold values [17]. Suboptimal results of image thresholding can also be considered to deal with the time-consuming computation involved. In this line, the work [8] proposed to segment infrared (IR) images based on maximum entropy of $2D$ histograms and PSO algorithm. Other works on the maximum entropy method proposed over the years have been based on Rényi’s [18], Tsallis [3], and Kaniadakis entropies [19].

IR images have a lot of low-frequency information, and the experimental tests have shown that some classical thresholding methods [5,6,7] are not efficient in this case. IR imaging is very useful in the military field for detecting objects with strong heat signatures, such as equipment and troop motions [20,21,22]. In addition, we can mention medical image applications [23], power equipment fault detection [24], and pedestrian detection on a scene [25].

Pixel intensities maintain a local long-range correlation in the neighborhood of the pixels in regions of an image. This fact is explored in [5], which is based on the long-range correlation between gray levels of an IR image and Tsallis entropy. In this case, the long-range interactions between the pixels are captured by the entropic parameter q inherent to the Tsallis entropy formula.

Another entropy from the context of the thermodynamic science tested on IR images is the Masi one [6] that arises from the analysis between Rényi and Tsallis entropies [26]. These entropies cannot simultaneously manipulate long-range correlation, long-term memory, and fractal behavior [6]. Like Tsallis, Masi entropy is nonextensive, with a degree of nonextensivity measured by a parameter r.

An image histogram is a fundamental source of information for entropy-based methods [27,28]. In general, the appearance of a histogram is not that of two symmetrical portions with respect to an axis (threshold), which imposes difficulties on the thresholding techniques. To address this issue, [29] presented a model that incorporates the Gumbel distribution to improve thresholding via cross-entropy in skewed histograms. In the same line, [30] presents a method for automatic thresholding that allows selecting reasonable thresholds for images with unimodal, bimodal, multimodal, and peakless histograms.

The basic hypothesis for entropy-based bi-level thresholding methods is that the object and background regions are independent of each other. Recently, a method based on breaking this paradigm was proposed in [31], through the Tsallis entropy correlation.

In this work, we propose a new thresholding method based on long-range correlation and Masi entropy. Specifically, inspired by the methodology presented in [5], the novel technique computes the threshold through a $max-min$ optimization problem that involves the Masi and Shannon entropies.

The parameters selection of nonextensive entropies requires a little effort on the part of the user. Optimization techniques and empirical methods have been extensively researched on the subject [4,32,33]. However, nothing good enough to obtain an optimal parameter that provides better thresholding has yet emerged in the literature. In our case the parameters are selected by the user himself.

The experiments are concentrated to IR and nondestructive testing (NDT) images to allow the comparison with related works [3,5,6]. However, our segmentation approach can be applied to other types of images. The results proved to be very competitive in relation to those of [3,5,6], with very low error measures. The former is the baseline for our proposal while [6] applies only Masi and [3] uses only Tsallis entropy. These facts have motivated the comparison between these state-of-the-art approaches and our proposal.

The organization of this paper is as follows: Section 2 discusses works related with our proposal. Section 3 presents the entropy functions investigated here. In Section 4, our method is presented. Section 5 shows the obtained results. Finally, Section 6 reports conclusions.

2. Related Work

Nowadays, image segmentation approaches can be divided into two classes: traditional and deep learning methods. The former is composed by techniques based on edge extraction, fuzzy and morphological concepts, region representation, partial differential equations (PDEs), graph formulations, stochastic and thresholding approaches [34]. On the other hand, deep learning methods rely on the universality of neural network computing, large annotated databases, theoretical and hardware developments that allow the training of deep architectures in feasible times [35]. Hence, despite of outstanding results obtained by deep neural networks in segmentation tasks, such performance is only possible if there is sufficient data for training, with proper diversity and representativeness, or if we can design appropriate architectures and/or methodologies for transfer learning, data augmentation, and data imbalance, which are tasks with their own issues (see [36,37,38], section 2.2).

Thresholding methodologies achieve competitive results even if a small dataset is accessible for test [1]. These methods do not depend on time consuming training stages, like deep learning and some stochastic approaches. The parameter setting is simpler than edge extraction (like active contour models) and graph formulations (like graph cuts). Its formulation is simple and intuitive allowing the development of algorithms with complexity lower than PDE-based methods, specially in the bi-level case. Those observations support the research in thresholding methods nowadays, as we have noticed in recent works for segmentation of thermograms [39], medical imaging [40], satellite images [41], color images [42], among others [43,44].

In [1] thresholding methods are separated into six groups depending on whether they are based on features related to the histogram shape, object attributes, stochastic correlation between pixels, local image characteristics, clustering algorithms, or entropy concepts. The latter class is derived inside information theory methodologies that are grounded on statistical mechanics elements [45]. This viewpoint started in [2] , by applying the Shannon entropy and the concept of anisotropy coefficient. On the other hand, if we consider the entropy as the measure of the information contained in the image then the best threshold is the one that maximizes the entropy of the result. This line is followed by [46] that seeks for a threshold t that partitions the histogram into two regions that maximize the Shannon entropy of the corresponding joint probability distribution. However, such proposal may fail if applied to distinct images with identical histograms, as pointed out in [47]. One direction to address this issue is the application of more general entropic concepts that include new parameters that can be customized to fit the application requirements.

That is the case of Renyi’s entropy used in [47] for bi-level thresholding which uses an approach analogous to the one presented in [46] but replacing Shannon entropy to the Renyi one. Shannon and Renyi entropies characterize systems known as extensive ones [48]. On the other hand, some nonextensive systems follow another entropy formula proposed by Tsallis in [49].

Tsallis entropy includes the entropic parameter $q\in \mathbb{R}$ and we can show that in the limit $q\to 1$ it equals the Shannon information measure. Tsallis entropy is the foundation of a new formalism in statistical mechanics where the level of nonextensivity of a physical system is quantified by the parameter q [50]. The work [3] was the first one to use the Tsallis entropy formalism for bi-level thresholding. Then, multilevel segmentation [51] approaches have been developed using Tsallis entropy with applications in medical imaging [40], multispectral image analysis [52], among others.

In this scenario, an important point is the distinction between long-range and short-range correlations. Specifically, image fields characterized by long-range correlations are more efficiently represented using Tsallis entropy while Shannon entropy models short-range correlations [3,5].

Such distinction raised the issue about the utilization of another entropy measure that is more flexible with respect to the long-range correlation events but preserves the Shannon entropy characteristics. The Masi entropy, used in [6], is a choice in this direction which is dependent of the entropic parameter r such that the limit $r\to 1$ recovers the Shannon measure. These facts have motivated our proposal that puts together Masi and Shannon entropies in a new thresholding approach. Our work is inspired in [5] that applies a $max-min$ optimization problem that involves Tsallis and Shannon information measures.

3. Entropy Functions

Entropy is the measure of disorder in physical systems or the measure of the amount of information that may be needed to specify the full microstates of the system. In 1948, Shannon added entropy to information theory, and his approach measures the uncertainty associated with a random variable or the amount of information produced by a process [53] as:

$$S\left(X\right)=-\sum _{i=1}^n{p}_{i}log{p}_i,$$

(1)

where X is a random variable that can take values $\{x_1,\dots ,x_n\}$ and $p_i=p\left(x_i\right)$ is the corresponding probability of $x_i$. Eq. (1) is the Shannon entropy that describes systems that obey the following additive property: Let A and B be two random variables associated to independent statistical subsystems of a physical system. Then

$$S(A+B)=S\left(A\right)+S\left(B\right).$$

(2)

Systems of this kind are called extensive systems. A certain class of physical systems, which entail long-range interactions, long-time memory, and fractal-type structures, indicated the need for an extension. Tsallis entropy [54] extends its applications to so-called nonextensive systems using an adjustable parameter q. Tsallis entropy can explain a complex system class such as long-range and long-memory interactions. It can be expressed as

$$S_q\left(X\right)={\displaystyle \frac{1}{1-q}}\left(\sum _{i=1}^n{p}_i^q-1\right),$$

(3)

where X is a random variable, $q\in \mathbb{R}$ and $S_q\left(X\right)$ converges to $S\left(X\right)$ in the limit $q\to 1$. The function $S_q\left(X\right)$ has the following pseudo-additivity property for $q\ne 1$:

$$S_q(A+B)=S_q\left(A\right)+S_q\left(B\right)+(1-q)S_q\left(A\right)S_q\left(B\right),$$

(4)

where A and B are independent subsystems of a physical system. In 2005, Masi proposed a new entropy that combines the nonextensivity of Tsallis entropy and the additivity of Rényi’s entropy [26], namely:

$$S_r\left(X\right)={\displaystyle \frac{1}{1-r}}log\left[1-(1-r)\sum _{i=1}^n{p}_{i}log{p}_i\right],$$

(5)

where $r\in \mathbb{R}$$(r>0$ and $r\ne 1)$. Moreover, $S_r$ satisfies

$$S_r(A+B)=S_r\left(A\right)+S_r\left(B\right),$$

(6)

with A and B as before. The parameters q and r can be viewed as measures for the degree of nonextensivity that exists in the system for the Tsallis and Masi entropies, respectively.

3.1. Entropy Functions and Image Thresholding

For the image thresholding context, we will consider an image with n gray levels, and $p_1,p_2,\dots ,p_n$ be the probability distribution of the levels. Here, two probability distributions can be derived from the original distribution, one for the background (class A) and the other for the object (class B). Their probabilities can be given by

$$A:{\displaystyle \frac{p_1}{P_A}},{\displaystyle \frac{p_2}{P_A}},\dots ,{\displaystyle \frac{p_t}{P_A}},B:{\displaystyle \frac{p_{t+1}}{P_B}},{\displaystyle \frac{p_{t+2}}{P_B}},\dots ,{\displaystyle \frac{p_n}{P_B}},$$

(7)

where $P_A={\sum }_{i=1}^t{p}_i$ and $P_B={\sum }_{i=t+1}^n{p}_i$.

In this case, Albuquerque’s method obtains an optimal threshold by maximizing the information measure between the two classes, where the objective function $S_q^{A+B}=S_q^A+S_q^B+(1-q)S_q^A{S}_q^B$ is parametrically dependent upon the threshold value t that separates foreground and background. Hence, Albuquerque’s solution is given by $t_{opt}=argmax\left[S_q^{A+B}\left(t\right)\right]$. The nonextensive parameter q represents the strength of the long-range correlation. Eq. (4) indicates that there is a global correlation not only in the areas of foreground and background but also between them. Moreover, the strength of the global correlation is described by the same value q.

Regarding Masi entropy applied in Nie et al. method [6], although this entropy is nonextensive, it is also additive. The parameter r establishes the degree of nonextensivity and the strength of the long-range correlation property. The long-range correlation could be indicated by the Eq. (6) whose optimum $t_{opt}=argmax\left[S_r^{A+B}\left(t\right)\right]$ gives the threshold value in [6].

In practice, the global long-range correlation indicated by Eq (4) does not apply for IR images since the thresholding results only show local long-range correlation [5] in this case. Thus, the optimal value found by the maximization process is not sensitive to small variations of the nonextensive parameter q, as reported in [5]. In that reference, the authors argue that it would be inappropriate for these types of images to say that there is a global long-range correlation. The long-range correlation would be weaker in the background of some images, in the context of Tsallis entropy. Thus, instead of simply maximizing the sum of the entropies of object and background, they decided to maximize both the Shannon entropy on the background of the image and Tsallis on the object. But, it is hard to obtain the absolute maxima of them by a single threshold unless their thresholds happen to be equal. For this reason, the solution involved a trade-off that is addressed in [5] as the optimization problem:

$$t_{opt}=argmax\left\{min\left[S^A\left(t\right),S_q^B\left(t\right)\right]\right\},$$

(8)

where $S^A$ is the Shannon entropy calculated on the background of the image and $S_q^B$ is the Tsallis entropy calculated on the object. Some tested images apparently had a stronger long-range correlation on the background of the image. To mitigate this effect, Lin & Ou [5] also proposed an alternative way for the trade-off, interleaving the entropies:

$$t_{opt}=argmax\left\{min\left[S_q^A\left(t\right),S^B\left(t\right)\right]\right\}$$

(9)

where $S_q^A$ is the Tsallis entropy calculated on the background of the image and $S^B$ is the Shannon entropy calculated on the object.

4. Proposed Method

Our proposal is to combine the Masi and Shannon entropies in a trade-off similar to that used by Lin & Ou in Eqs. (8)-(9). Two facts motivated the current proposal involving Masi entropy. First, its image thresholding results do not present a weak correlation in the background of images for the appropriate parameter r. Therefore, Masi entropy could be thought of as a method based on global long-range correlation. Second, the optimal value found in the maximization process of Masi entropy is very sensitive to the variation of the nonextensive parameter r. Thus, we propose a trade-off as follows:

$$t_{opt}=argmax\left\{min\left[S^A\left(t\right),S_r^B\left(t\right)\right]\right\}$$

(10)

where $S^A$ is the Shannon entropy calculated on the background of the image and $S_r^B$ is the Masi entropy calculated on the object. When there are distributions of different gray levels in the image, we can propose an alternative way as in Eq. (9).

$$t_{opt}=argmax\left\{min\left[S_r^A\left(t\right),S^B\left(t\right)\right]\right\}$$

(11)

where $S_r^A$ is the Masi entropy calculated on the background of the image and $S^B$ is the Shannon entropy calculated on the object. This would be the case of having a weaker long-range correlation in the background of the image, for example. We execute trial-and-error tests to set the value of the parameter r. The same procedure is used to define q and r in [3,5,6]. Although some works have being developed to automatically set entropic parameters [55,56,57], this subject remains an open issue in image processing. In our case, we uniformly sample a set of values and take the one that approximate the target segmentation using the Masi entropy methodology [6]. The alternative form is used when a thresholding result close to the optimal value is not achieved by Eq. (10). Then, we seek for another r value and we execute the optimization process given by Eq. (11), instead of Eq. (10). Experimentally, in all cases, it was possible to obtain a near optimal solution through the ability to capture the long-range correlation properties among the pixels due to Masi entropy. In the following section, we report the results and offer quantitative comparisons with the other methods.

5. Experimental Results

Eq. (10) was tested on several IR and some NDT images. To infer the performance of our method, we adopted four quantitative measures. One of them is the misclassification error (ME) measure [1]. It can be written as

$$ME=1-{\displaystyle \frac{|B_{GT}\cap B_T|+|F_{GT}\cap F_T|}{\left|B_{GT}\right|+\left|F_{GT}\right|}}$$

(12)

where $B_{GT}$ and $B_T$ are the pixels of background in ground-truth image and thresholded image, $F_{GT}$ and $F_T$ are the pixels of foreground in the ground-truth image and thresholded image, and $|\circ |$ is the cardinality of a set. The ME varies from 0 for a perfectly segmented image to 1 for a totally wrong binarized image. Another measure is the Jaccard similarity (JS), used in [20,58], which can be written as

$$JS(F_{GT},F_T)={\displaystyle \frac{|F_{GT}\cap F_T|}{|F_{GT}\cup F_T|}}.$$

(13)

Differently from Eq. (12), the correct segmentation gets $JS=100\%$. The third measure is the relative foreground area error (RAE) [59] that represents the accuracy and completeness of segmented foreground. It can be expressed as

$$RAE={\displaystyle \frac{|\left|F_{GT}\right|-\left|F_T\right||}{max(\left|F_{GT}\right|,\left|F_T\right|)}}.$$

(14)

The lower the RAE value the better the segmentation result. The fourth measure is F-measure [60,61] that is defined as the harmonic mean of precision and recall rate with weight $\alpha$, which represents a compromise between under-segmentation and over-segmentation. Its value is provided by the expression

$$F_{\alpha }={\displaystyle \frac{(1+\alpha )·P·R}{(\alpha ·P)+R}},$$

(15)

where P and R are the precision and recall rate given by

$$P={\displaystyle \frac{|F_{GT}\cap F_T|}{\left|F_T\right|}}andR={\displaystyle \frac{|F_{GT}\cap F_T|}{\left|F_{GT}\right|}}.$$

Generally, larger values for P and R indicate better segmentation results. ${\mathbf{F}}_{\alpha }$ could be a balanced measure for segmentation results through a good choice of harmonic coefficient $\alpha$. Usually, $\alpha$ is set to $0.5$ for segmentation algorithms [60,61]. However, a segmentation that matches the ground truth obtains $F_{\alpha }=1$ whatever the value of $\alpha$.

Table 1 shows thresholding values, as well as number of misclassified pixels, ME, JS, RAE, and _Fα values, for the images. Also, the results with lower ME and RAE values and higher JS and F_α values are marked in bold. Our proposal proved to be the most efficient among the experiments carried out. The Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 show the results generated with the reported image thresholding methods:

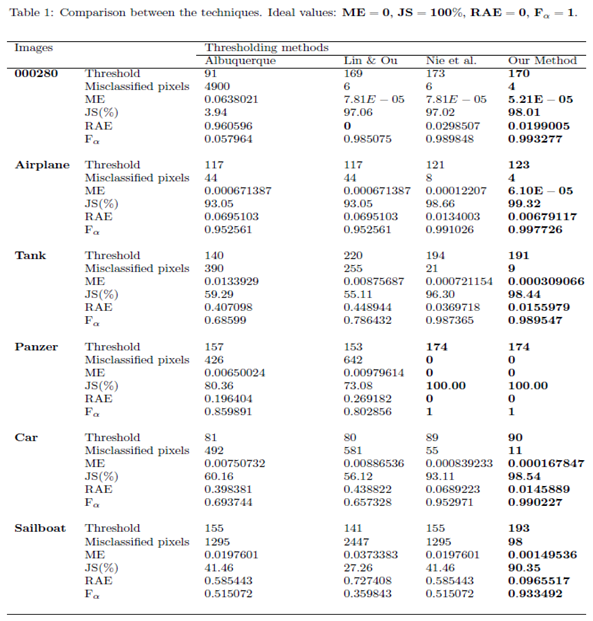
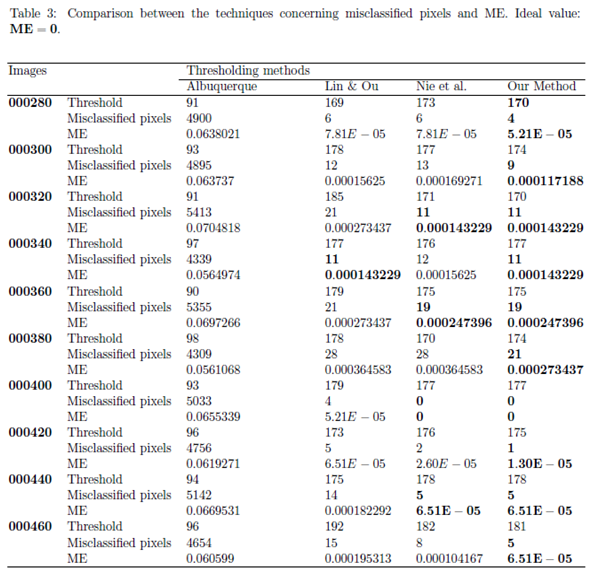
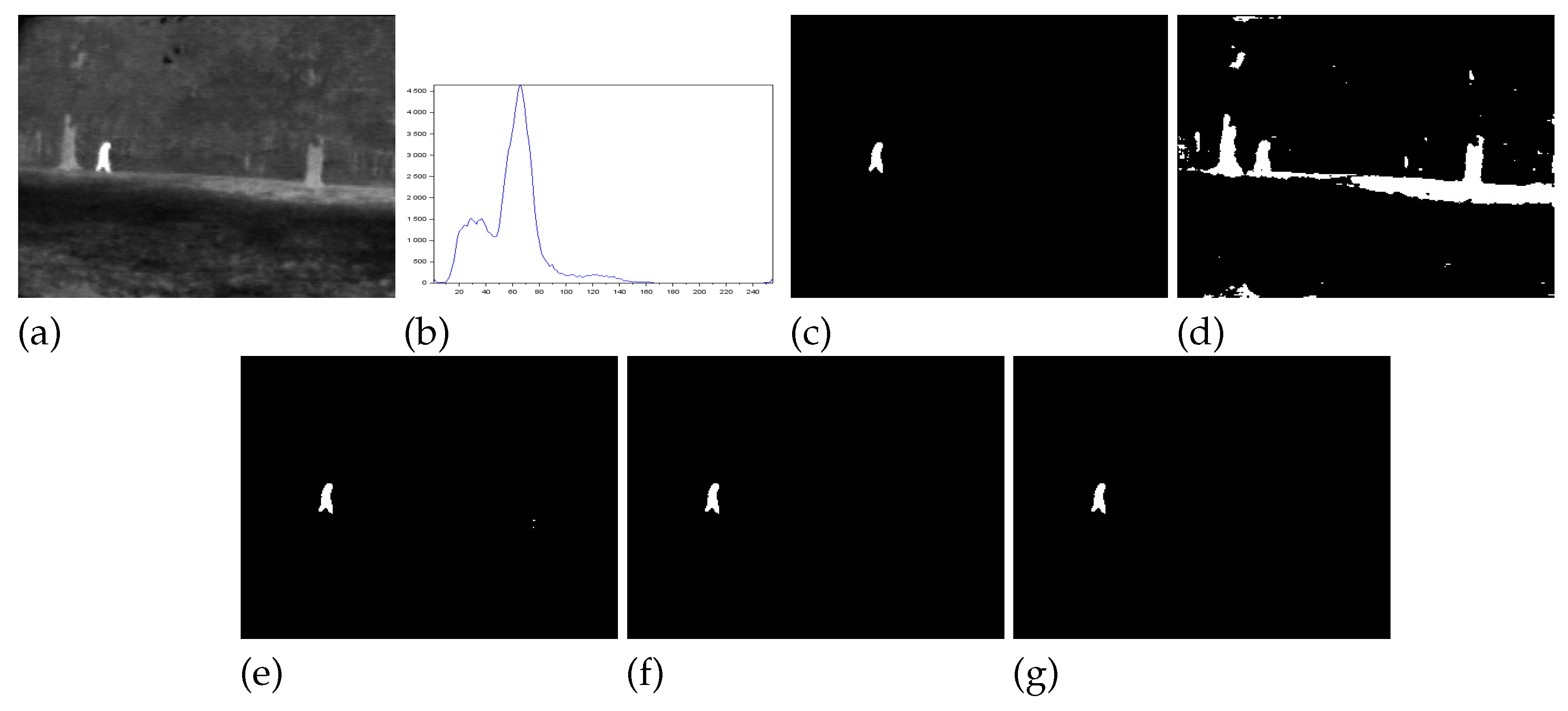
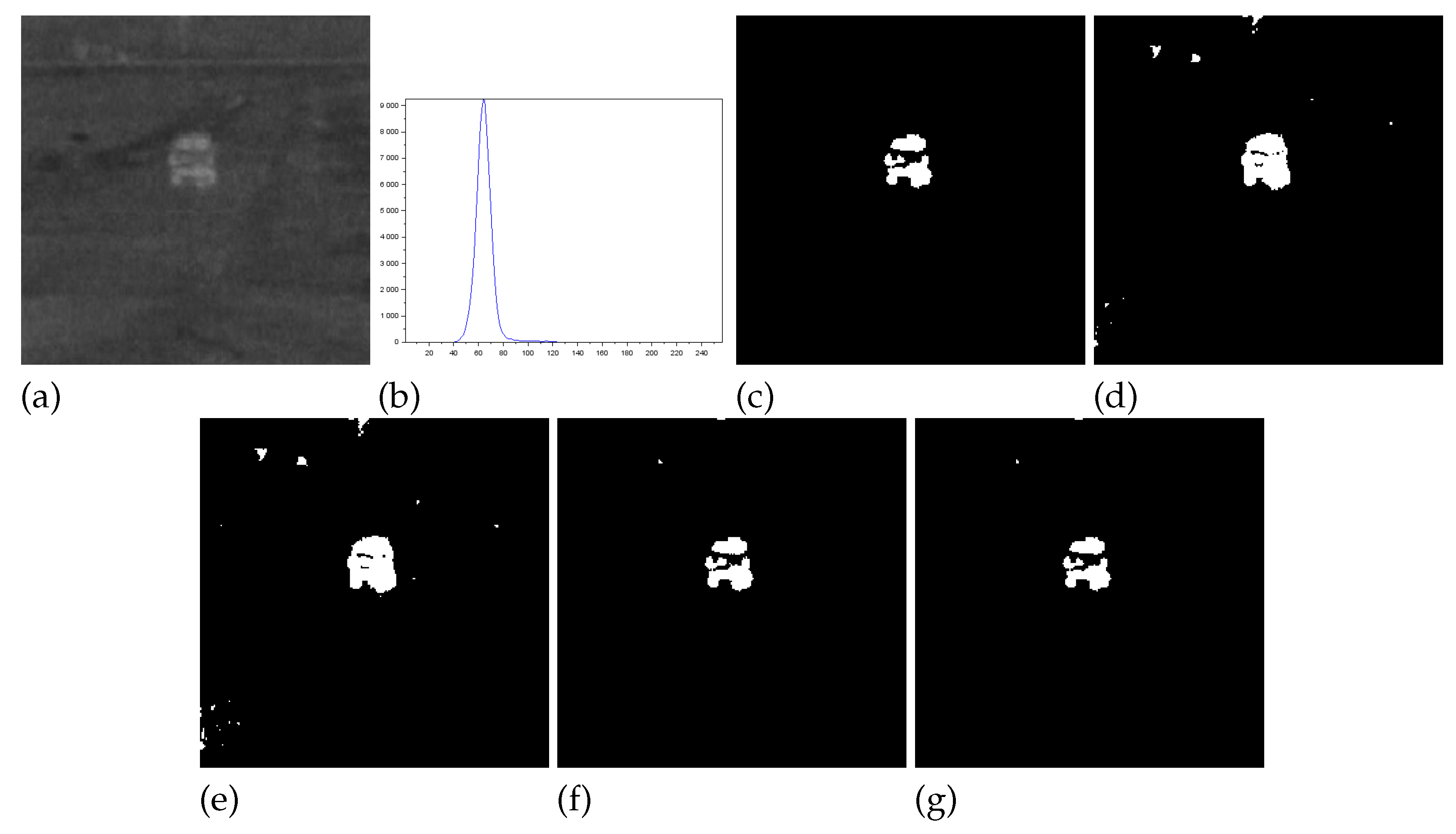
• Figure 1 - 000280 image: We notice that Lin & Ou’s method had an RAE equal to zero which implies that the number of pixels in the foreground of ground truth matched the number of pixels in the foreground of the thresholded image. However, visually we can notice differences between the ground truth and the segmented image by the Lin & Ou’s method. The other measures corroborate this observation showing that the behavior of our method was slightly better than the Lin & Ou’s and the Nie et al. methods, whose results were similar. The proposed method exhibited the highest JS value for that image.
  
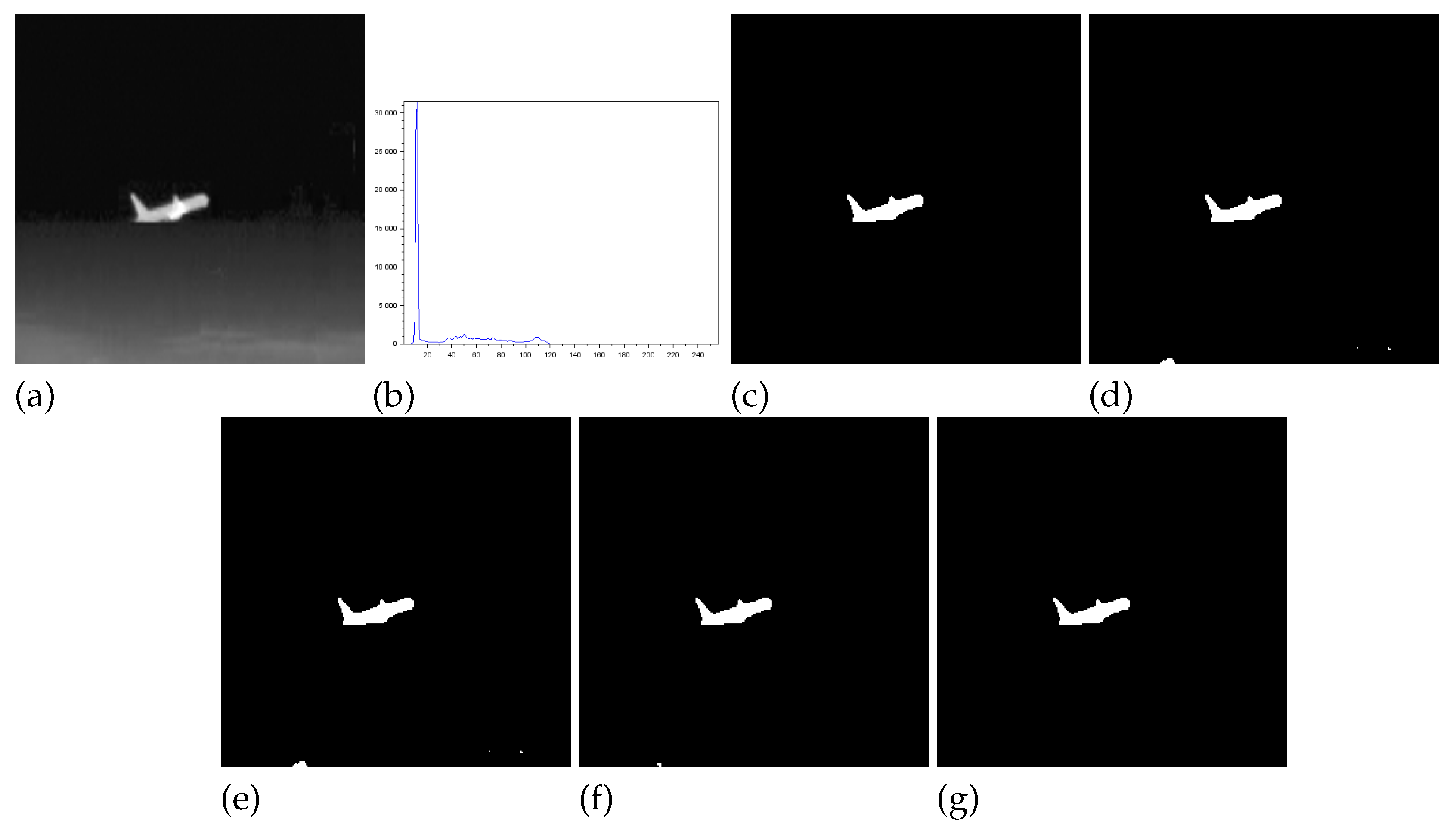
• Figure 2 - Airplane image: Our proposal surpasses all the others obtaining JS (Eq. (13)) greater than $99\%$ and a _Fα value close to 1. Albuquerque’s and Lin & Ou’s methods match up and show inferior results if compared to the second best approach that is the Nie et al. in this case. The image obtained with the Lin & Ou’s method was generated with the alternative form given by Eq. (9). This should be an indication that the correlation in the region of background is most strongly captured by Tsallis entropy (see the sharp peak in the histogram in Figure 2(b)).
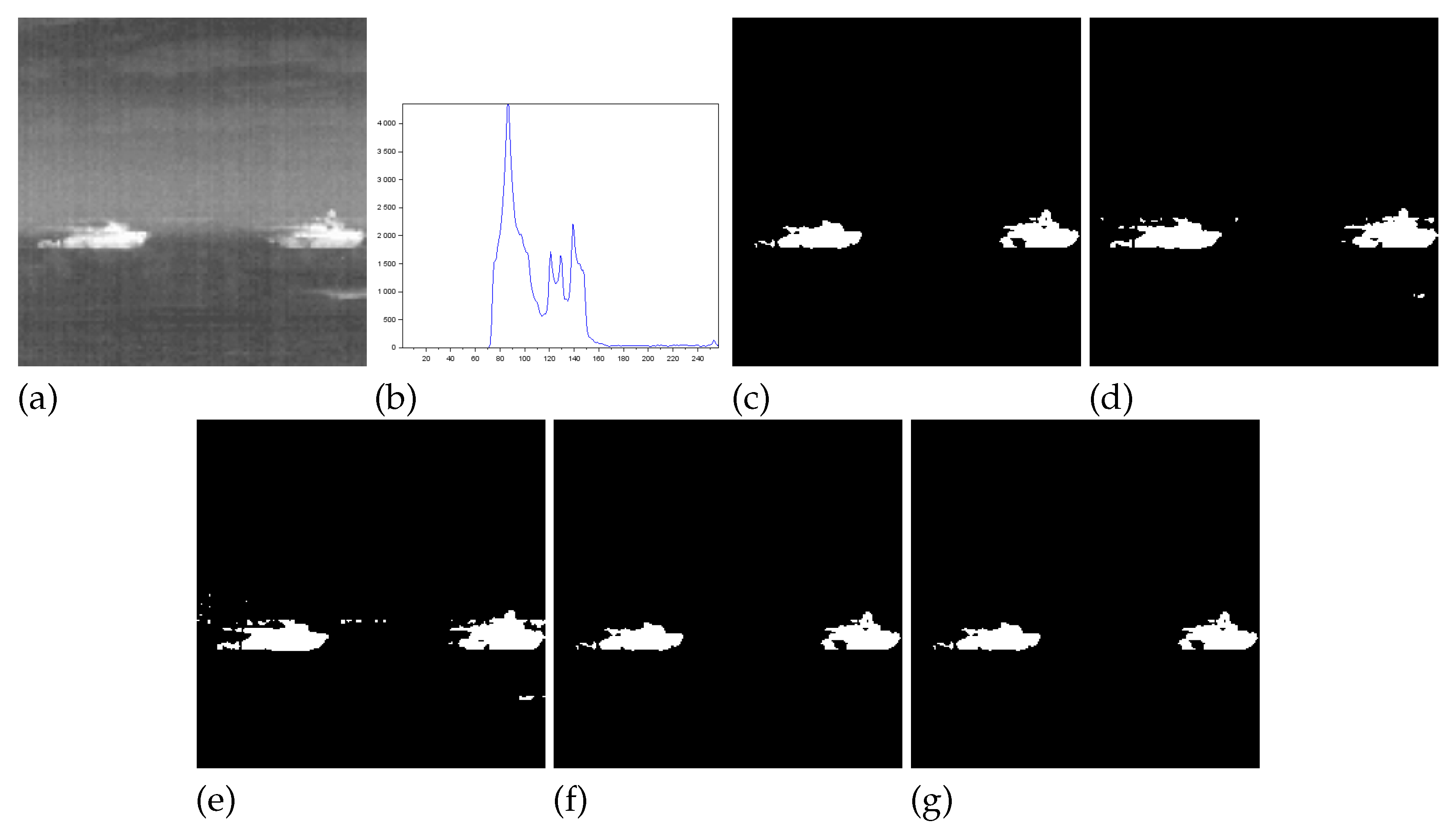
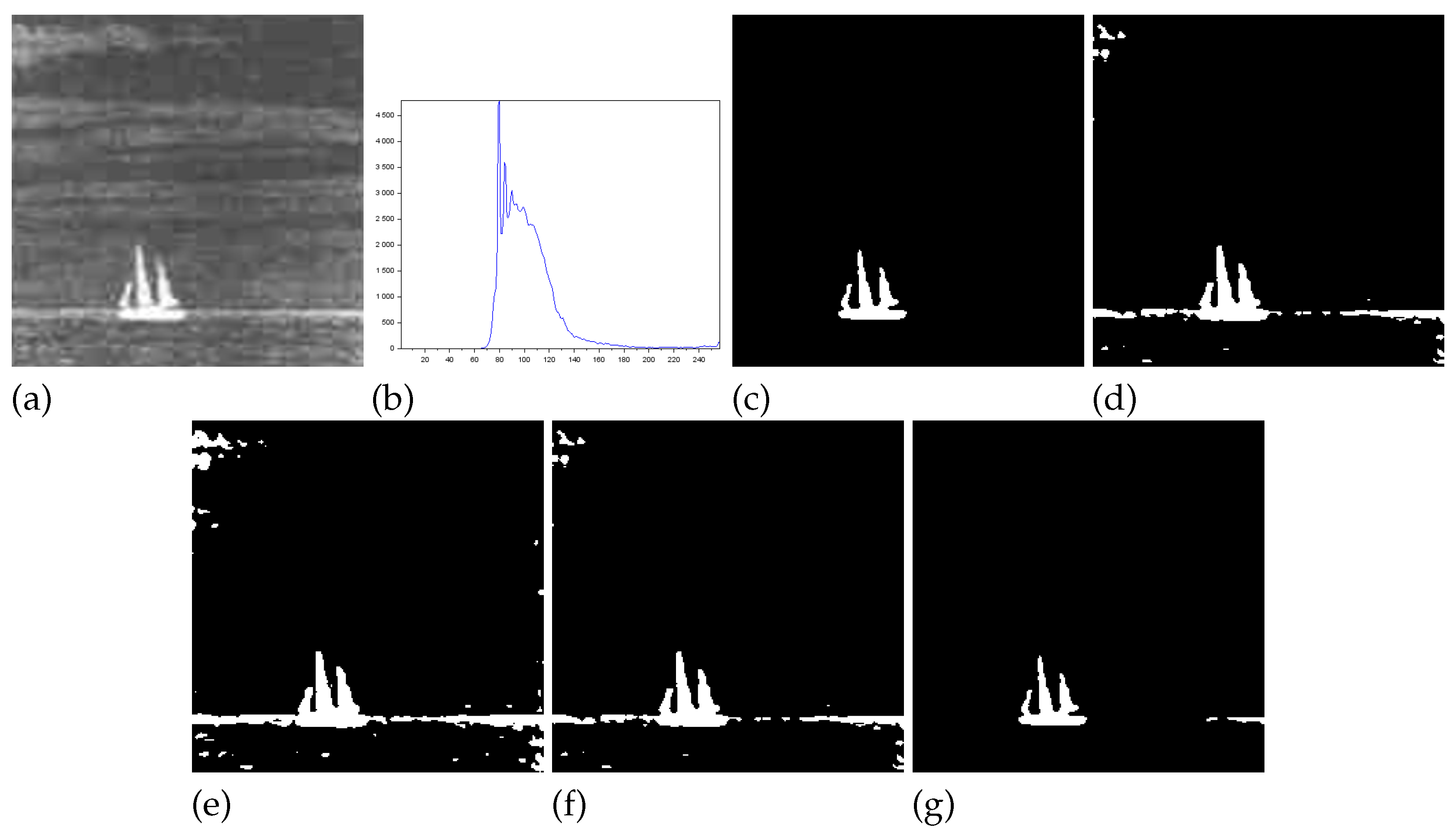
• Figure 3 - Tank image: Our method overcomes all other techniques and provides more than $98\%$ of Jaccard similarity (Eq. (13)). This example shows a significant difference with respect to the misclassified pixeis and JS value in relation to the second-best result, that of Nie et al. Albuquerque and Lin & Ou’s methods performs far from our technique for all the considered measures.
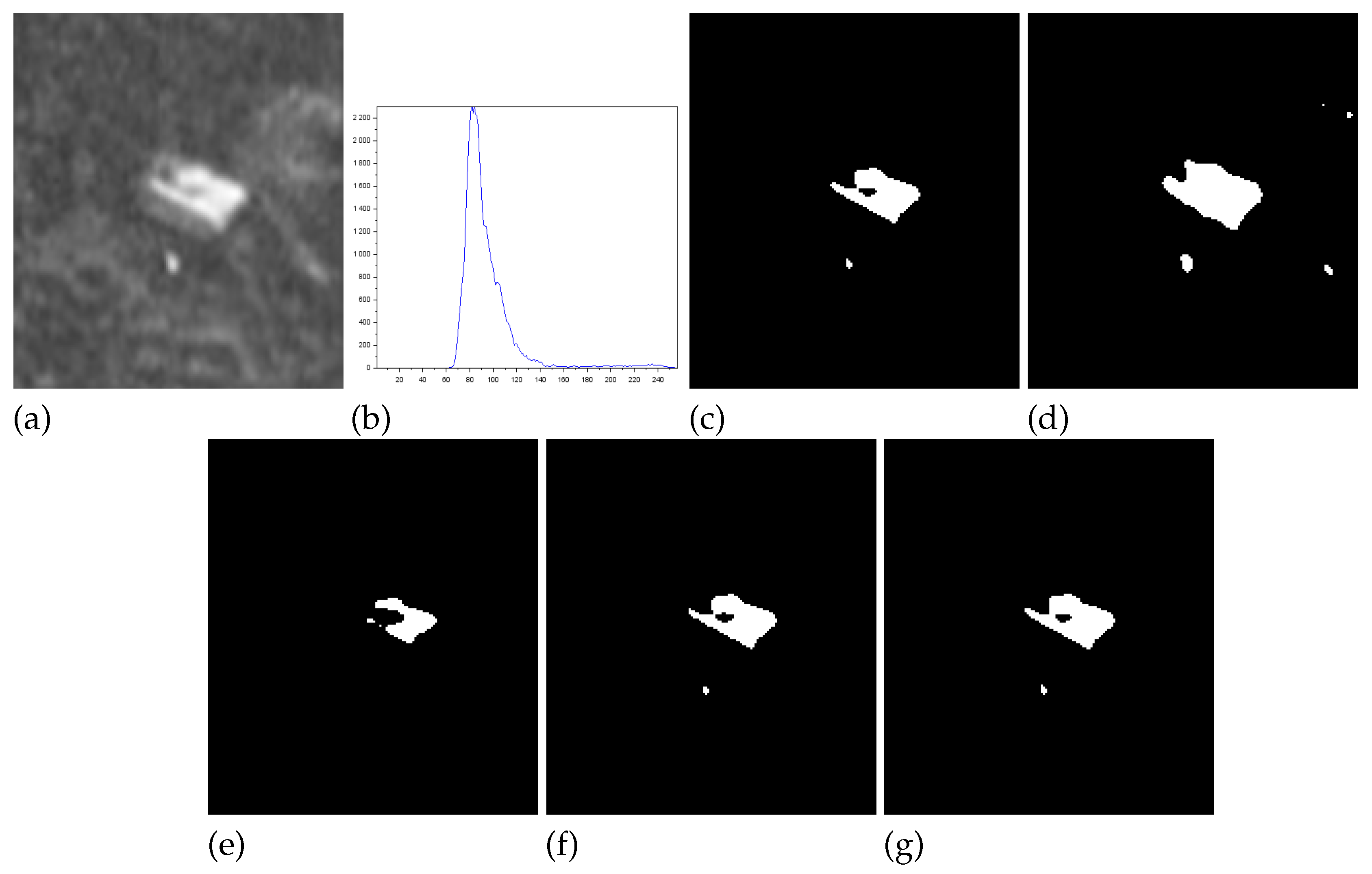
• Figure 4 - Panzer image: Our method and Nie et al. approach achieve perfect segmentation. The number of misclassified pixels, ME, and RAE values are zero. The image obtained with the Lin & Ou’s method was generated with the alternative form (9). However, both Albuquerque and Lin & Ou’s methods obtain segmentations far from the ground truth, as indicated by the values of the considered measures.
• Figure 5 - Car image: Our result was far superior to that shown by everyone else. Again the alternative form (9) for the Lin & Ou’s method was used to generate the corresponding image.
• Figure 6 - Sailboat image: Our results are much superior to other methods for all the measures considered. The image obtained with the Lin & Ou’s method was generated with the alternative form (9).

The error measures reported in Table 1 show that our proposal is more efficient than competing techniques. The second best technique, the Nie et al. method, performs as our approach only in the Panzer image, being inferior in the other cases. In addition, our proposal for image thresholding based on local long-range correlation and Masi entropy provides much better results than those based on Tsallis entropy. A range of q values used to generate images of the Albuquerque’s and Lin & Ou’s methods was $0.1\le q\le 0.9$.

The ranges of r values used for Nie et al method and ours were $0.9\le r<1.4$ and $0.7<r<1.3$ ($r\ne 1$), respectively. As observed in [5], the optimal value found by the Tsallis entropy maximization process is not sensitive to the small variations of q. Differently, Masi entropy maximization process is quite sensitive to variations of r, even the small ones. This fact is relevant for establishing the step for sampling the above interval to set r in Eqs. (10)-(11).

Figure 7 shows a test performed with an image sequence. Such images contain an object (a person) moving on the same background. As in Lin & Ou’s work [5], we assume that the strength of the long-range correlation of the images should be similar for Tsallis entropy. The authors judged that the correlation strength would be the same for that object on the images, which yields the same optimal q value. Thus, we kept q fixed at $0.8$, the same value for image 000280 from the Figure 1. For the Nie et al method and ours, the ranges of r values found were $1.3\le r<1.4$ and $1.1\le r<1.3$, respectively.

Table 2 shows the JS obtained for this experiment. Our approach achieves the best results or performs equally the best methods. Lin & Ou’s method ties with our approach in only one of the listed cases (000340 image). The Nie et al. method ties with our method in three of the images in the sequence (000360, 000400 and 000440 images).

Table 3 shows the threshold values, misclassified pixels, and misclassification error (ME) for the segmentation of the infrared images (IR) in Figure 7. Data in Table 3 corroborate our approach as the best among those analyzed since it outperforms the competing methods or ties with the best one. Specifically, Table 3 shows a tie between the proposed method and the results of Lin & Ou’s technique (000340 image) and four ties with the Nie et al. approach (000320, 000360, 000400 and 000440 images). This highlights the competitive potential of the proposed approach against Lin & Ou and Nie et al. methods, which are based on nonextensive entropies. In the 000320 image, the ME and misclassified pixel values for our method and the one of Nie et al. are the same, given by $0.000143229$ and 11, respectively. Despite this, Table 2 reports that our approach obtained a JS value of $94.93\%$, while Nie et al. obtained $94.91\%$. Hence, we notice that the difference between their JS values is 2 hundredths. This shows a slight advantage of our approach in comparison with the Nie et al. method in this case.

Finally, Figure 8, Figure 9 and Figure 10 form a set of three nondestructive testing (NDT) images, further tested. Table 4 shows the quantitative measures of the performance of the methods for these images.

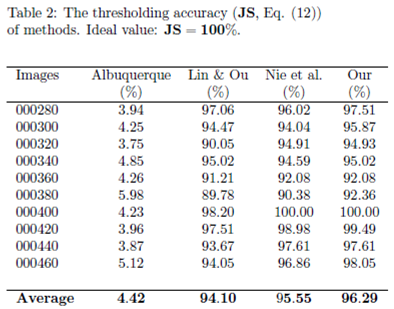
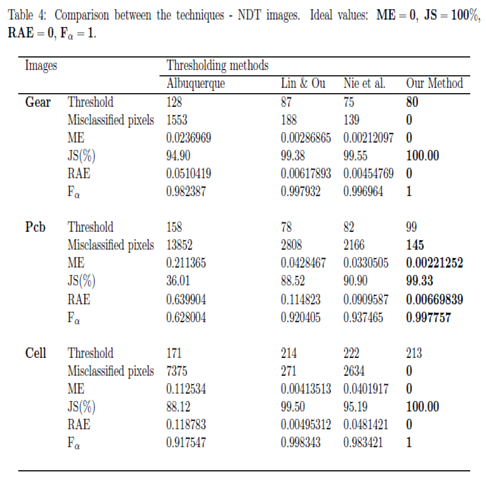
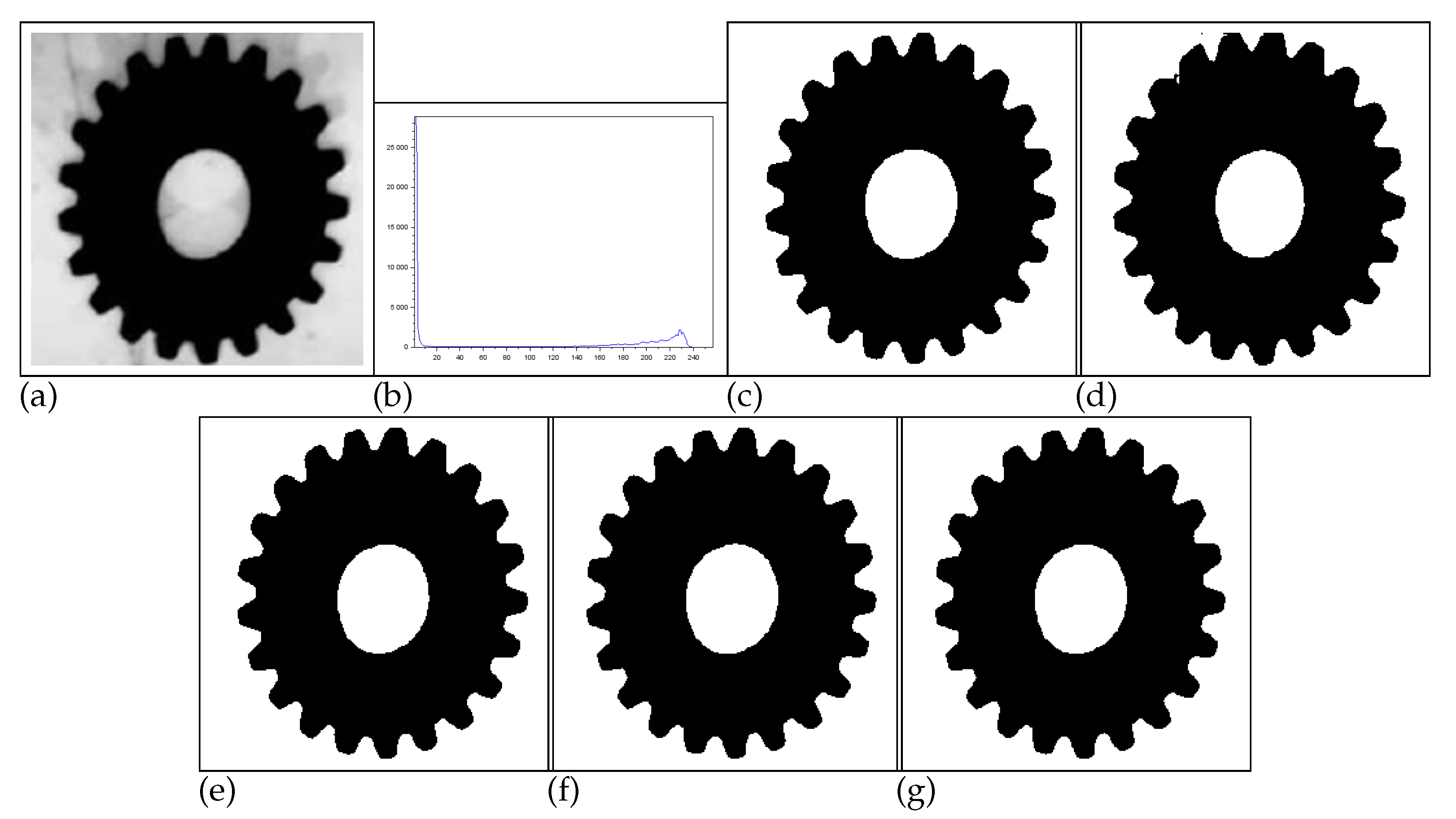
• Figure 8 - Gear image: Although the Lin & Ou’s and the Nie et al. methods have obtained a good visual approximation of the ground truth, the result of our technique matches the ground truth image with $\mathbf{JS}=\mathbf{100}\%$, according to Table 4. For this image, the computational experiments have shown that Albuquerque’s method is very sensitive to the variation of parameter q. Since this image was not applied in Lin & Ou’s paper, the q values were determined by trial-and-error to optimize the performance. This allowed Albuquerque’s result to be more than $94\%$ accurate according to JS. The image histogram itself suggests how easy it would be for the method to separate the regions of the image. As it is shown in Figure 8(b) below, there is a sharp peak in the begining histogram. It can be considered as the strong correlations of the pixels in the foreground. Thus, as performed in Lin & Ou’s experiments, the alternative form, (9), was necessary for this image. The same occurred for our method in which we used an alternative form to Eq. (10) given by Eq. (11). This happens due to a weaker long-range correlation in the background composed by the lightest area of the image.
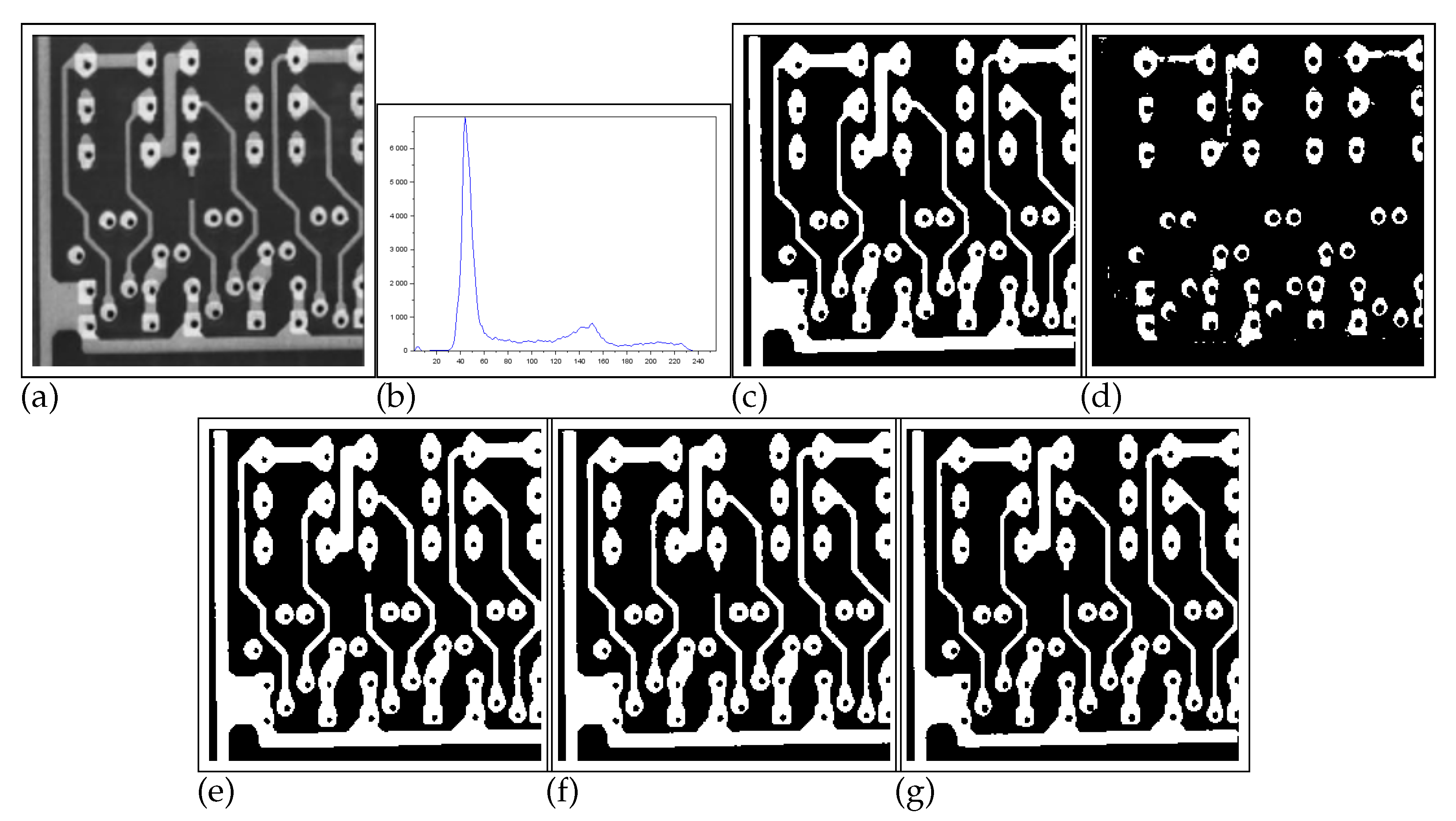
• Figure 9 - Pcb image: In this example, the Nie et al. technique surpasses the one of Lin & Ou’s, having more than $90\%$ of similarity with the ground truth image. The image obtained with the Lin & Ou’s method was generated with the alternative form (9). Even so, our method is more efficient than the others, making the accuracy of $99.33\%$, as shown in Table 4.
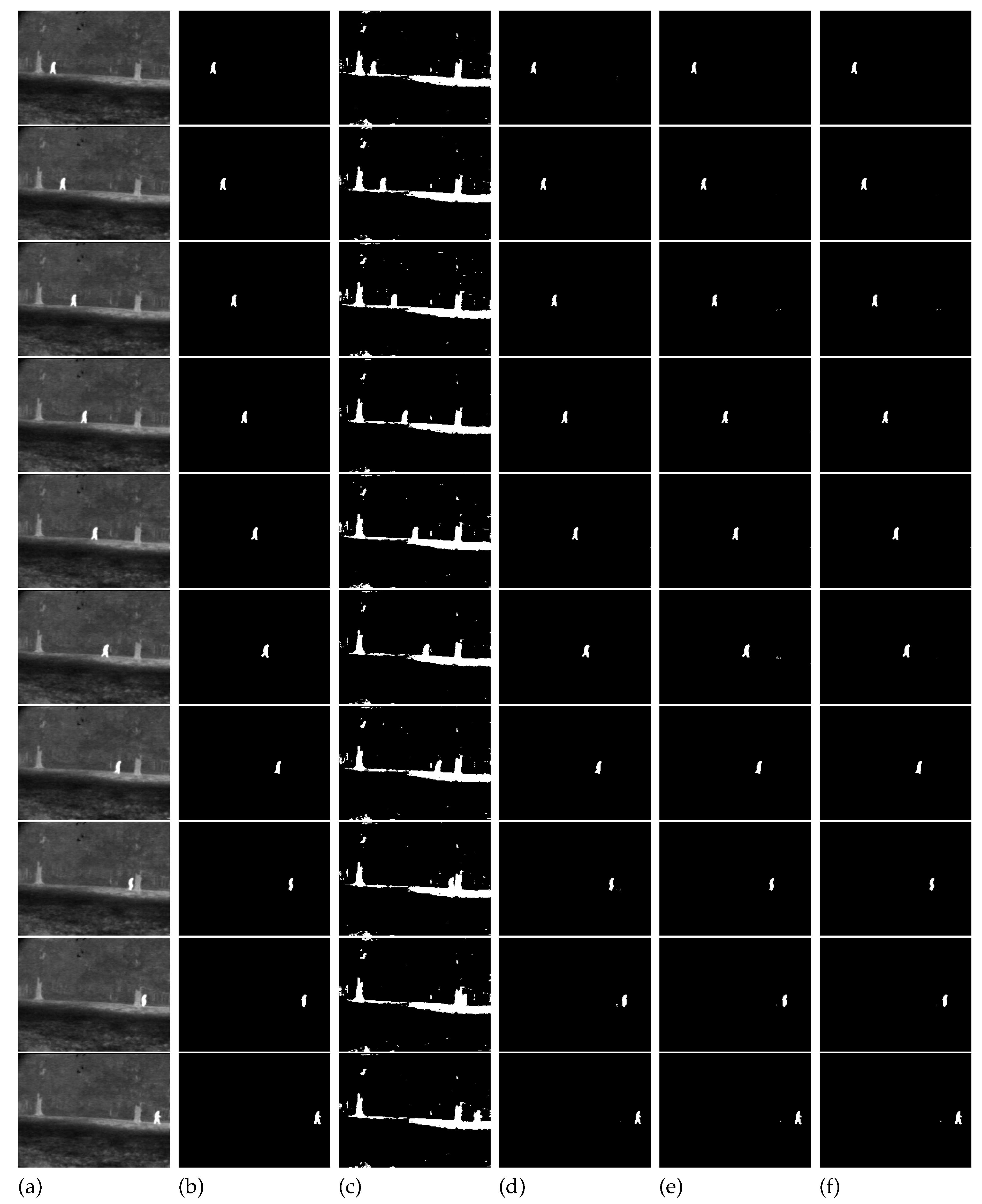
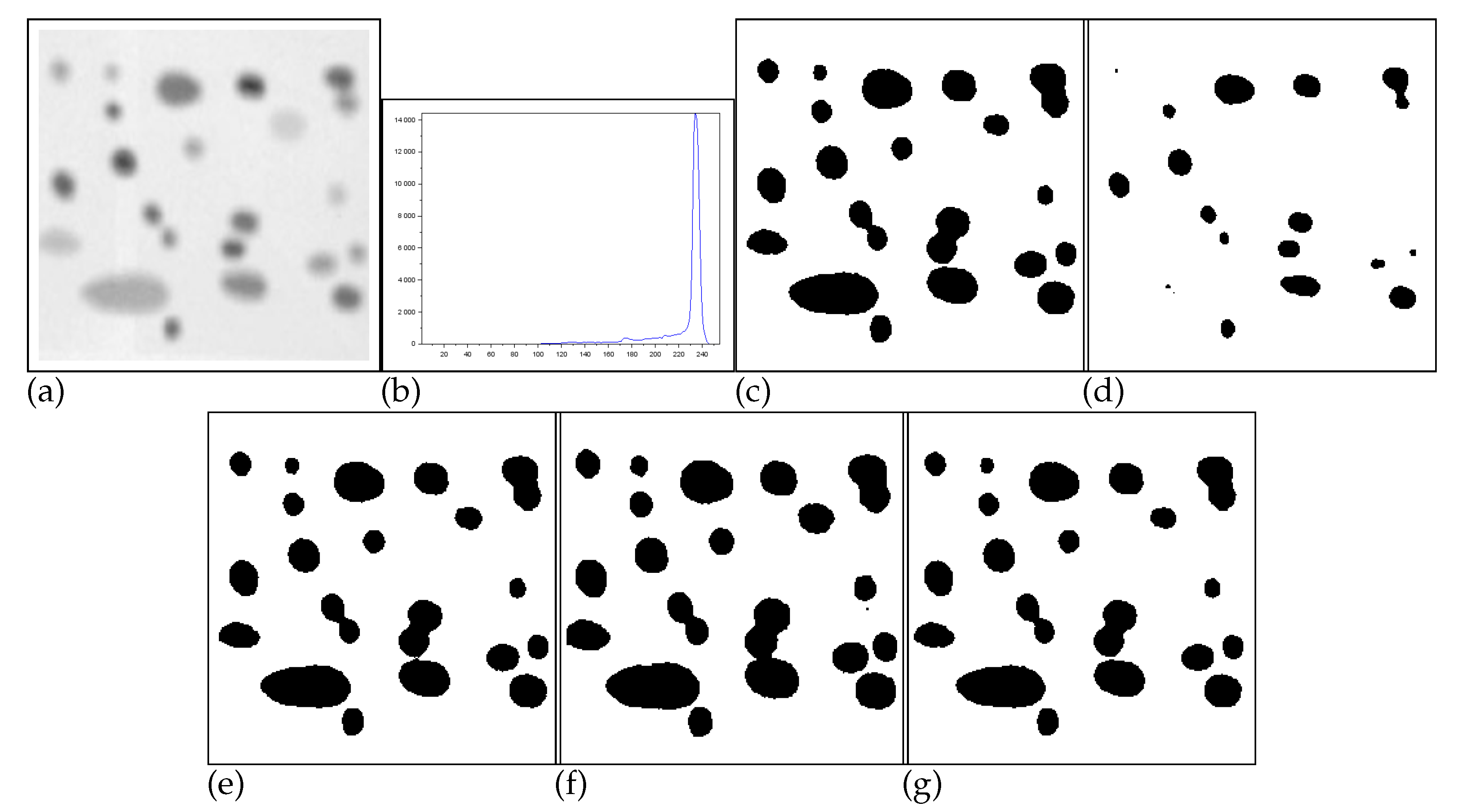
• Figure 10 - Cell image: Lin & Ou’s method is more effective than the Nie et al. method, in this case. However, it is still not possible to overcome our result, which is $100\%$ accurate (see Table 4).

The set of results proves the superiority of our method against counterparts in the application on IR and NDT images.

6. Discussion

The long-range correlation of an image can be captured by the Tsallis and Masi entropies. In particular, IR and NDT images show local long-range correlation instead of global long-range correlation. In this work, the image segmentation technique based on Tsallis entropy and long-range correlation proposed by Lin & Ou was improved. The combination of Masi and Shannon entropies not only outperforms that method but has also shown itself to be competitive against works that apply only Masi or only Tsallis models. Misclassification error, Jaccard similarity, misclassified pixels, relative foreground area error, and $F-$measure have proven the effectiveness of our method.