Fractional-Order Modeling of a Multistable Erbium-Doped Fiber Laser

1. Introduction

Erbium-doped fiber lasers (EDFLs) have been the subject of extensive research over the past three decades due to their wide range of applications in optical communications, sensing, biomedical imaging, and ultrafast photonics [1,2,3]. Their ability to generate stable continuous-wave, Q-switched, or mode-locked outputs makes them indispensable tools in both applied and fundamental studies. An important property of EDFLs is their inherent nonlinear dynamics, which often manifest as bistability, self-pulsing, or chaotic regimes depending on pump power, cavity losses, and saturable absorption [4]. Understanding and controlling such multistable behaviors are critical for optimizing EDFL performance in advanced photonic systems [5,6,7].

The EDFL dynamics is usually analyzed using two complementary approaches: experimental and theoretical. The experimental approach allows the observation of time series and power spectra which demonstrate complex dynamical behavior such as bifurcations, chaos, and multistability under real operating conditions [6,8,9]. On the other hand, the theoretical approach seeks to develop mathematical models capable of simulate dynamics of these lasers using tools such as stability analysis, Lyapunov exponent, bifurcation diagrams, and approximate numerical methods, with the aim of reproducing experimental results as faithfully as possible [8,9,10].

Conventional modeling of EDFLs has primarily relied on integer-order rate equations or delay-differential equations that describe the population inversion dynamics and field evolution. For example, Lacot et al. [10] described the EDFL dynamics using a theoretical model of two coherently pumped coupled lasers. The study reports the presence of a Hopf bifurcation at low pumping parameter values. Additionally, in the stationary regime, a transition was observed from continuous-wave operation to deterministic chaos, passing through various self-pulsing modes. In contrast, other researchers [8,9,11] investigated an EDFL subjected to pump modulation of a diode laser. They developed a mathematical model that fitted the experimental data with high precision demonstrating complex dynamics which included subharmonic and higher harmonic oscillations and chaos, as well as the coexistence of different periodic and chaotic regimes for the same parameter values. These behaviors are explored through bifurcation diagrams as a function of one or two control parameters: modulation amplitude and frequency. While these models successfully reproduce many qualitative features of laser operation, they often fail to capture memory effects, anomalous relaxation, and long-term correlations observed experimentally in rare-earth–doped fiber systems [12]. Such discrepancies indicate the need for more generalized mathematical frameworks capable of describing the nonlocal and hereditary properties inherent to complex laser media.

Recent years have seen a growing interest in exploring laser systems from the perspective of fractional-order calculus. Fractional-order differential equations extend the classical formalism by introducing derivatives of non-integer order, thereby providing an additional degree of flexibility in capturing long-range temporal correlations [13,14,15]. Fractional calculus has recently emerged as a powerful tool for modeling physical systems with memory and anomalous dynamics. This mathematical extension allows for more accurate modeling of systems with memory, an especially useful feature for optical devices where cumulative effects are relevant [16].

In photonics, fractional-order models have been successfully applied to describe nonlinear oscillators, optical solitons, and chaotic lasers [17,18,19]. For example, Alzaid et al.[20] investigated the dynamics of a chaotic laser modeled by the Lorenz–Haken equations within the fractional-order framework using the Caputo derivative. Their method, based on the Laplace transform and its inverse, enabled the construction of an iterative solution whose existence and uniqueness were rigorously established; numerical simulations were then carried out using the Atangana–Seda iterative method[21]. Similarly, Liu [22] proposed a fractional-order delayed single-mode laser model, while more recently Khalaf et al. [23] introduced a distributed-order hyperchaotic detuned laser model that exhibits multistability for certain parameter regimes. Together, these contributions demonstrate the power of fractional calculus in capturing and predicting complex dynamical behaviors in photonic systems.

Nevertheless, despite these advances, fractional-order modeling has not yet been applied to EDFLs, to the best of our knowledge. Given the inherent memory effects and nonlocal dynamics in such laser systems, fractional analysis offers a promising advantageous for more accurately reproducing their experimental behavior. In this work, we propose and analyze a fractional-order model of an EDFL operating in a multistable regime. Specifically, we extend the standard rate equations to fractional order and investigate how memory effects influence stability boundaries and dynamic transitions. For numerical integration, we employ the two-stage fractional Runge–Kutta method [24], which enables us to construct detailed bifurcation diagrams as functions of key control parameters, including modulation amplitude, modulation frequency, and the fractional order itself.

The remainder of this paper is organized as follows. Section 2 introduces the conventional EDFL model. Section 3 presents the fractional-order extension based on the Caputo derivative and develops both local and global stability analyses. In Section 4, we discuss the numerical results and compare them with experimentally observed EDFL dynamics. Finally, Section 5 summarizes the main findings and outlines future directions.

2. Mathematical Model of the Erbium-Doped Fiber Laser

The mathematical model of the EDFL is based on a power balance approach that incorporates excited-state absorption (ESA) at the lasing 1550-nm wavelength and assumes an averaged population inversion along the pumped active fiber [9]. This model accounts for key physical effects, including the depletion of the pump wave as it propagates through the gain medium. These mechanisms give rise to intrinsic undamped oscillations in the laser output, phenomena that have been experimentally observed even in the absence of external modulation [8].

2.1. General Model and Parameters

The rate equations governing the EDFL dynamics describe the intracavity laser power P, defined as the sum of the forward- and backward-propagating wave powers, expressed in photons per second (${\mathrm{s}}^{-1}$), and the average population inversion y over the length of the active fiber L. The resulting system of equations is given by:

$$\left[\begin{array}{c}{\displaystyle \frac{dP}{dt}}\\ {\displaystyle \frac{dy}{dt}}\end{array}\right]=\left[\begin{array}{c}{\displaystyle \frac{2L}{T_r}}P\{r_{\omega }{\alpha }_0[y(\xi -\eta )-1]-{\alpha }_{th}\}+P_{sp}\\ -{\displaystyle \frac{{\sigma }_{12}{r}_{\omega }P}{\pi r_0^2}}(y\xi -1)-{\displaystyle \frac{y}{\tau }}+P_{pump}\end{array}\right],$$

(1)

where ${\sigma }_{12}$ is the absorption cross-section from the ground state (“1”) to the excited state (“2”). We assume that the stimulated emission cross-section ${\sigma }_{21}$ is approximately equal to ${\sigma }_{12}$, leading to $\xi =({\sigma }_{12}+{\sigma }_{21})/{\sigma }_{12}=2$. The parameter $\eta ={\sigma }_{23}/{\sigma }_{12}$ represents the ratio of the excited-state absorption cross-section to the ground-state absorption cross-section. The photon lifetime in the cavity is given by $T_r=2n_0(L+l_0)/c$, where $l_0$ is the effective length of the cavity ends formed by the Bragg gratings, $n_0$ is the refractive index of the erbium-doped fiber core in the ground state, and c is the speed of light in vacuum. The small-signal absorption of erbium at the lasing wavelength is ${\alpha }_0=N_0{\sigma }_{12}$, with $N_0=N_1+N_2$ being the total erbium ion concentration. Cavity losses are described by ${\alpha }_{\mathrm{th}}={\gamma }_0+nL(1/R)/\left(2L\right)$, where ${\gamma }_0$ accounts for intrinsic losses and R is the mirror reflectivity. The parameter $\tau$ denotes the lifetime of the excited state (“2”). Additionally, $r_0$ and ${\omega }_0$ are the core radius of the fiber and the mode field radius of the fundamental mode, respectively. The overlap factor $r_{\omega }=1+exp[-2{(r_0/{\omega }_0)}^2]$ quantifies the coupling efficiency between the optical mode and the doped region.

The average population inversion of level “2” is defined as

$$y={\displaystyle \frac{1}{n_{0}L}}{\int }_0^L{N}_2\left(z\right)dz,$$

where $N_2\left(z\right)$ is the local population density of the excited state at position z along the fiber. Spontaneous emission coupled into the fundamental lasing mode is modeled as

$$P_{\mathrm{sp}}={\displaystyle \frac{{10}^{-3}y}{\tau T_r}}{\left({\displaystyle \frac{{\lambda }_g}{{\omega }_0}}\right)}^2{\displaystyle \frac{r_0^2{\alpha }_{0}L}{4{\pi }^2{\sigma }_{12}}},$$

and the effective pump power is expressed as

$$P_{\mathrm{pump}}=P_p{\displaystyle \frac{1-exp[-\beta {\alpha }_{0}L(1-y)]}{N_0\pi r_0^{2}L}},$$

where $P_p$ is the input pump power at the entrance of the fiber, $\beta ={\alpha }_p/{\alpha }_0$ is the ratio of the absorption coefficients of the erbium-doped fiber at the pump wavelength ${\lambda }_p$ and the lasing wavelength ${\lambda }_g$, with ${\alpha }_p$ being the pump absorption coefficient.

2.2. Inclusion of Pump Modulation and Simulation Parameters

We assume that the laser spectral linewidth is ${10}^{-3}$ times the full spectral width of the erbium fluorescence bandwidth, consistent with typical experimental conditions of the EDFL [8].

It is important to note that the system in Eq. (1) describes the EDFL dynamics in the absence of external modulation, and thus its long-term solution corresponds to a stable equilibrium. To obtain periodic and chaotic oscillations and coexisting dynamical regimes (multistability) an external harmonic modulation is introduced in the pump power as

$$P_p=P_p^0\left[1+A_{m}sin\left(2\pi f_{0}t\right)\right],$$

where $P_p^0$ is the pump power without modulation, $A_m$ is the modulation amplitude, and $f_0$ is the modulation frequency.

The parameters used in the numerical simulations are derived from the experimentally measured parameters of the real EDFL with an active fiber of length $L=70$ cm. Specifically: $n_0=1.45$, $l_0=20$ cm, $T_r=8.7$ ns, $r_0=1.5\times {10}^{-4}$ cm, and ${\omega }_0=3.5\times {10}^{-4}$ cm. Although this last value, obtained experimentally, is slightly larger than the analytically estimated mode field radius of $2.5\times {10}^{-4}$ cm, it leads to a mode-overlap factor $r_{\omega }=1+exp[-2{(r_0/{\omega }_0)}^2]=0.308$.

The absorption characteristics of the erbium-doped fiber at the lasing and pump wavelengths are defined by ${\alpha }_0=0.4{\mathrm{cm}}^{-1}$ and $\beta ={\alpha }_p/{\alpha }_0=0.5$, respectively, consistent with direct measurements on a heavily doped fiber with an erbium concentration of $2300\mathrm{ppm}$. The cross-sections are set to ${\sigma }_{12}={\sigma }_{21}=3\times {10}^{-21}{\mathrm{cm}}^2$, ${\sigma }_{23}=0.6\times {10}^{-21}{\mathrm{cm}}^2$, yielding $\xi =({\sigma }_{12}+{\sigma }_{21})/{\sigma }_{12}=2$ and $\eta ={\sigma }_{23}/{\sigma }_{12}=0.2$. Other key parameters are $\tau ={10}^{-2}\mathrm{s}$ (upper-state lifetime), ${\gamma }_0=0.038$ (intrinsic cavity loss), $R=0.8$ (mirror reflectivity), resulting in a total cavity loss ${\alpha }_{\mathrm{th}}=3.92\times {10}^{-2}$. The lasing wavelength is ${\lambda }_g=1.56\times {10}^{-4}\mathrm{cm}$ ($1560\mathrm{nm}$).

The pump power is expressed in terms of the normalized pump rate above threshold $ϵ$, defined as $P_p^0=ϵP_{\mathrm{th}}$, where the lasing threshold pump power $P_{\mathrm{th}}$ and the threshold population inversion $y_{\mathrm{th}}$ are given as follows:

$$P_{\mathrm{th}}={\displaystyle \frac{y_{\mathrm{th}}}{\tau }}·{\displaystyle \frac{n_{0}L\pi {\omega }_p^2}{1-exp\left[-\beta {\alpha }_{0}L(1-y_{\mathrm{th}})\right]}},$$

$$y_{\mathrm{th}}={\displaystyle \frac{1}{\xi }}\left(1+{\displaystyle \frac{{\alpha }_{\mathrm{th}}}{r_{\omega }{\alpha }_0}}\right).$$

In the simulations, we assume that the pump beam radius ${\omega }_p$ matches the lasing mode radius ${\omega }_0$, i.e., ${\omega }_p={\omega }_0$.

2.3. Nondimensionalization of the Erbium-Doped Fiber Laser Model

To transform the system in Eq. (1) into a dimensionless form, the following procedure is applied [11]. For the first equation, the following variable transformations are introduced:

$$\begin{array}{cc}\hfill N_1& =r_{\omega }(y{\xi }_1-1),y={\displaystyle \frac{N_1+r_{\omega }}{{\xi }_1{r}_{\omega }}},{\displaystyle \frac{dy}{dt}}={\displaystyle \frac{1}{{\xi }_1{r}_{\omega }}}{\displaystyle \frac{d{N}_1}{dt}},\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\displaystyle \frac{dP}{dt}}& ={\displaystyle \frac{2L}{T_r}}{\alpha }_{0}P{N}_1-{\displaystyle \frac{2L}{T_r}}{\alpha }_{th}P+{\displaystyle \frac{N_1+r_{\omega }}{{\xi }_1{r}_{\omega }}}\gamma ,I={\displaystyle \frac{P}{\gamma }},\theta ={\displaystyle \frac{t}{{\tau }_{sp}}},\hfill \end{array}$$

where I is the normalized intracavity intensity, $\theta$ is the dimensionless time, and ${\tau }_{sp}$ is the spontaneous emission lifetime. Substituting these values into the first equation, we obtain:

$${\displaystyle \frac{dI}{d\theta }}=2L{\displaystyle \frac{{\tau }_{sp}}{T_r}}{\alpha }_{0}I{N}_1-2L{\displaystyle \frac{{\tau }_{sp}}{T_r}}{\alpha }_{\mathrm{th}}I+{\displaystyle \frac{{\tau }_{sp}}{{\xi }_1{r}_{\omega }}}(N_1+r_{\omega }),$$

(2)

where $N_1$ is the population on the lower laser level.

For the second equation in Eq. (1), we use the conservation relation:

$$\begin{array}{c}\hfill {\displaystyle \frac{N_1+r_{\omega }}{{\xi }_1{r}_{\omega }}}={\displaystyle \frac{N_2+r_{\omega }}{{\xi }_2{r}_{\omega }}}\Rightarrow N_1={\displaystyle \frac{{\xi }_1{N}_2+({\xi }_1-{\xi }_2)r_{\omega }}{{\xi }_2}},\end{array}$$

where $N_2$ is the population on the upper laser level. Applying this transformation and using the same scaling for time and intensity, the rate equation for $N_2$ becomes:

$${\displaystyle \frac{d{N}_2}{d\theta }}=-{\displaystyle \frac{{\tau }_{sp}{\xi }_2{r}_{\omega }{\sigma }_{12}}{\pi r_0^2}}\gamma I{N}_2-(N_2+r_{\omega })+P_p{\displaystyle \frac{{\tau }_{sp}{\xi }_2{r}_{\omega }}{N_0\pi r_0^{2}L}}\left\{1-exp\left[-\beta {\alpha }_{0}L\left(1-{\displaystyle \frac{N_2+r_{\omega }}{{\xi }_2{r}_{\omega }}}\right)\right]\right\}.$$

(3)

Substituting the expression for $N_1$ into Eq. (2), we rewrite the intensity equation in terms of $N_2$, we obtain:

$${\displaystyle \frac{dI}{d\theta }}=2L{\displaystyle \frac{{\tau }_{sp}}{T_r}}{\displaystyle \frac{{\xi }_1}{{\xi }_2}}{\alpha }_{0}I{N}_2-2L{\displaystyle \frac{{\tau }_{sp}}{T_r}}\left[{\alpha }_{\mathrm{th}}-{\displaystyle \frac{{\alpha }_0({\xi }_1-{\xi }_2)}{{\xi }_2}}{r}_{\omega }\right]I+{\displaystyle \frac{{\tau }_{sp}}{{\xi }_2{r}_{\omega }}}(N_2+r_{\omega }).$$

(4)

Now, the system of dimensionless differential equations becomes:

$$\left[\begin{array}{c}{\displaystyle \frac{dI}{d\theta }}\\ {\displaystyle \frac{d{N}_2}{d\theta }}\end{array}\right]=\left[\begin{array}{c}2L{\displaystyle \frac{{\tau }_{sp}}{T_r}}{\displaystyle \frac{{\xi }_1}{{\xi }_2}}{\alpha }_{0}I{N}_2-2L{\displaystyle \frac{{\tau }_{sp}}{T_r}}\left[{\alpha }_{\mathrm{th}}-{\displaystyle \frac{{\alpha }_0({\xi }_1-{\xi }_2)}{{\xi }_2}}{r}_{\omega }\right]I+{\displaystyle \frac{{\tau }_{sp}}{{\xi }_2{r}_{\omega }}}(N_2+r_{\omega })\\ -{\displaystyle \frac{{\tau }_{sp}{\xi }_2{r}_{\omega }{\sigma }_{12}}{\pi r_0^2}}\gamma I{N}_2-(N_2+r_{\omega })+P_p{\displaystyle \frac{{\tau }_{sp}{\xi }_2{r}_{\omega }}{N_0\pi r_0^{2}L}}\left\{1-exp\left[-\beta {\alpha }_{0}L\left(1-{\displaystyle \frac{N_2+r_{\omega }}{{\xi }_2{r}_{\omega }}}\right)\right]\right\}\end{array}\right].$$

(5)

To simplify notations, we define the following dimensionless parameters:

Using the parameters listed in Table 1, Eq. (5) simplifies to:

$$\left[\begin{array}{c}{\displaystyle \frac{dI}{d\theta }}\\ {\displaystyle \frac{d{N}_2}{d\theta }}\end{array}\right]=\left[\begin{array}{c}aI{N}_2-bI+c(N_2+r_{\omega })\\ -dI{N}_2-(N_2+r_{\omega })+e\left\{1-exp\left[-\beta {\alpha }_{0}L\left(1-{\displaystyle \frac{N_2+r_{\omega }}{{\xi }_2{r}_{\omega }}}\right)\right]\right\}\end{array}\right].$$

(6)

Finally, we perform a change of variables to adopt standard dynamical system notation:

$$\begin{array}{c}\hfill x=I,y=N_2,t=\theta ,\varrho =r_{\omega }=0.3075,\rho ={\xi }_2{r}_{\omega }=0.6150.\end{array}$$

Additionally, we use the experimentally justified approximation $\beta {\alpha }_{0}L=18$. Substituting these values into Eq. (6), we obtain the final dimensionless system:

$$\left[\begin{array}{c}{\displaystyle \frac{dx}{dt}}\\ {\displaystyle \frac{dy}{dt}}\end{array}\right]=\left[\begin{array}{c}axy-bx+c(y+\varrho )\\ -dxy-(y+\varrho )+e\left\{1-exp\left[-18\left(1-{\displaystyle \frac{y+\varrho }{\rho }}\right)\right]\right\}\end{array}\right],$$

(7)

where x represents the normalized laser intensity and y the population inversion. In the absence of external modulation, this system exhibits only one stable fixed point.

To enable complex dynamics such as periodic and chaotic oscillations, chaos, and multistability, we introduce harmonic modulation of the pump power by adding a time-dependent term to the second equation:

$${\displaystyle \frac{dy}{dt}}=-dxy-(y+\varrho )+e\left[1+A_{m}sin\left(2\pi f_{0}t\right)\right]\left\{1-exp\left[-18\left(1-{\displaystyle \frac{y+\varrho }{\rho }}\right)\right]\right\},$$

where $A_m$ and $f_0$ are the modulation amplitude and frequency.

Thus, the final modulated system is given by:

$$\left[\begin{array}{c}{\displaystyle \frac{dx}{dt}}\\ {\displaystyle \frac{dy}{dt}}\end{array}\right]=\left[\begin{array}{c}axy-bx+c(y+\varrho )\\ -dxy-(y+\varrho )+e\left[1+A_{m}sin\left(2\pi f_{0}t\right)\right]\left\{1-exp\left[-18\left(1-{\displaystyle \frac{y+\varrho }{\rho }}\right)\right]\right\}\end{array}\right].$$

(8)

2.4. Rescaling the Erbium-Doped Fiber Laser Model

For computational efficiency in the MATLAB implementation, it was necessary to rescale Eq. (8). We introduce the time rescaling $t=k\tau$, where k is a scaling parameter and $dt=kd\tau$. Under this transformation, Eq. (8) becomes:

$$\left[\begin{array}{c}{\displaystyle \frac{dx}{kd\tau }}\\ {\displaystyle \frac{dy}{kd\tau }}\end{array}\right]=\left[\begin{array}{c}axy-bx+c(y+\varrho )\\ -dxy-(y+\varrho )+e\left[1+A_{m}sin\left(2\pi f_{0}k\tau \right)\right]\left\{1-exp\left[-18\left(1-{\displaystyle \frac{y+\varrho }{\rho }}\right)\right]\right\}\end{array}\right].$$

(9)

Solving Eq. (9) for the derivatives with respect to $\tau$, we obtain:

$$\left[\begin{array}{c}{\displaystyle \frac{dx}{d\tau }}\\ {\displaystyle \frac{dy}{d\tau }}\end{array}\right]=\left[\begin{array}{c}k\left(axy-bx+c(y+\varrho )\right)\\ k\left(-dxy-(y+\varrho )+e\left[1+A_{m}sin\left(2\pi f_{0}k\tau \right)\right]\left\{1-exp\left[-18\left(1-{\displaystyle \frac{y+\varrho }{\rho }}\right)\right]\right\}\right)\end{array}\right].$$

(10)

3. Fractional Derivative Laser Model

Let us now extend the model in Eq. (10) to incorporate fractional-order dynamics. To this end, we employ the two-stage fractional Runge–Kutta method [24], implemented in MATLAB, to compute time series and phase-space trajectories for different values of the control parameters, namely the modulation frequency, modulation amplitude, and the fractional order $\alpha$. These simulations enable the construction of bifurcation diagrams of the local maxima of the laser intensity, $x^{\max }$, as functions of both the modulation frequency and the fractional order. To validate the approach, we first perform simulations with $\alpha =1$, confirming that the method accurately reproduces the classical dynamics. This benchmark demonstrates both the robustness of the numerical scheme and the reliability of the results obtained.

3.1. Two-Stage Fractional Runge–Kutta Method

According to Ghoreish et al. [24], the Caputo fractional derivative of order $\alpha >0$ with $a\ge 0$ is given by:

$$\begin{array}{cc}\hfill {\phantom{,}}_a^C{D}_x^{\alpha }f\left(x\right)& =J_a^{n-\alpha }{D}^{n}f\left(x\right)\hfill \\ \hfill {\phantom{,}}_a^C{D}_x^{\alpha }f\left(x\right)& =\left\{\begin{array}{cc}{\displaystyle {\displaystyle \frac{1}{\Gamma (n-\alpha )}}{\int }_a^x{(x-t)}^{n-\alpha -1}{D}^{n}f\left(t\right)dt,}\hfill & n-1<\alpha <n,n\in \mathbb{N},\hfill \\ D^{n}f\left(x\right),\hfill & \alpha =n,\hfill \end{array}\right.\hfill \end{array}$$

(11)

where $\Gamma$ is the Euler gamma function and $J_a^{\alpha }$ denotes the Riemann–Liouville fractional integral operator of order $\alpha >0$, defined as:

$$J_a^{\alpha }f\left(x\right)={\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}{\int }_a^x{(x-t)}^{\alpha -1}f\left(t\right)dt.$$

The two-stage explicit fractional Runge–Kutta method is formulated as follows [24]:

$$\begin{array}{cc}\hfill K_{1,1}& =h^{\alpha }f(t_n,x_n,y_n),\hfill \\ \hfill K_{1,2}& =h^{\alpha }g(t_n,x_n,y_n),\hfill \\ \hfill K_{2,1}& =h^{\alpha }f(t_n+c_2^{\alpha }h,x_n+a_{21}{K}_{1,1},y_n+a_{21}{K}_{1,2}),\hfill \\ \hfill K_{2,2}& =h^{\alpha }g(t_n+c_2^{\alpha }h,x_n+a_{21}{K}_{1,1},y_n+a_{21}{K}_{1,2}),\hfill \\ \hfill x_{n+1}& =x_n+{\omega }_1{K}_{1,1}+{\omega }_2{K}_{2,1},\hfill \\ \hfill y_{n+1}& =y_n+{\omega }_1{K}_{1,2}+{\omega }_2{K}_{2,2},\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill c_2^{\alpha }& ={\displaystyle \frac{{(\Gamma (2\alpha +1))}^2}{\Gamma (3\alpha +1)\Gamma (\alpha +1)}},a_{21}={\displaystyle \frac{c_2^{\alpha }}{\Gamma (\alpha +1)}},{\omega }_2={\displaystyle \frac{\Gamma (\alpha +1)}{c_2^{\alpha }\Gamma (2\alpha +1)}},{\omega }_1={\displaystyle \frac{1}{\Gamma (\alpha +1)}}-{\omega }_2.\hfill \end{array}$$

Here, we extend the method developed by Ghoreishi et al. [24] for a single fractional differential equation to the more complex and computationally challenging case of a $2\times 2$ system.

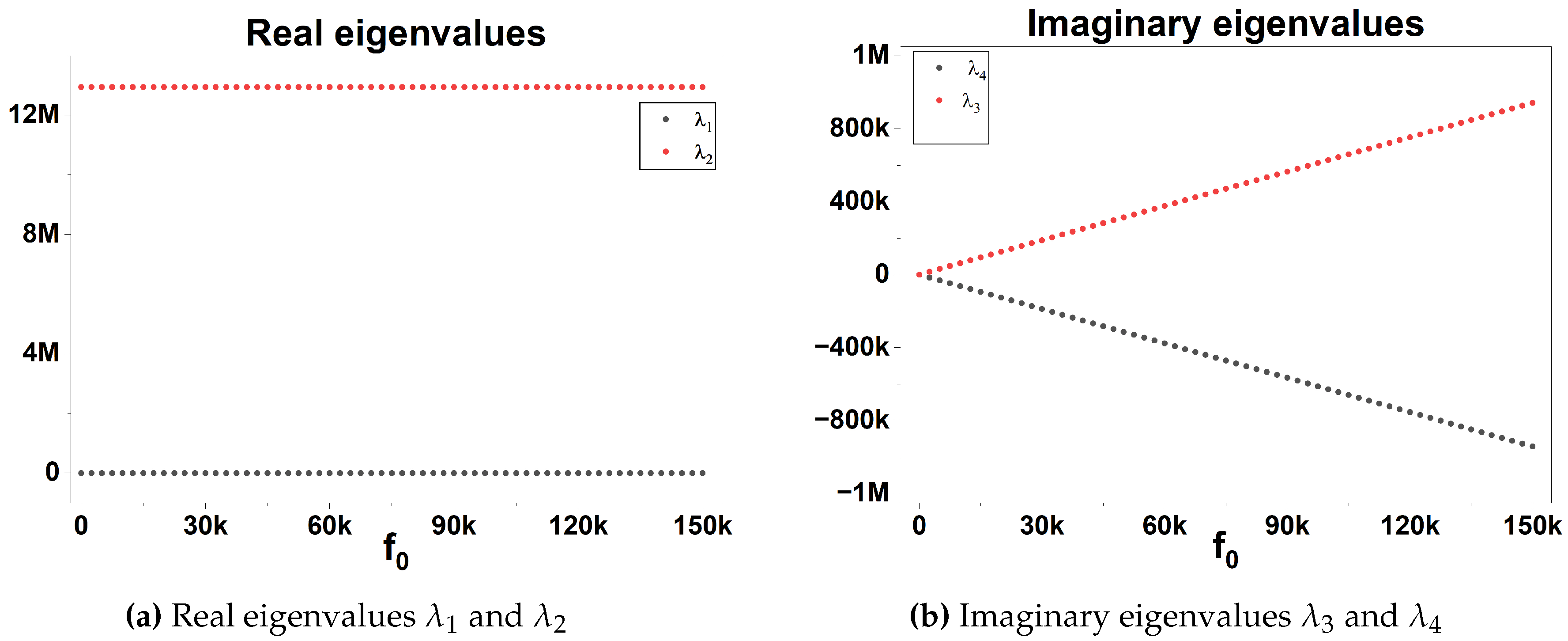
3.2. Local Stability Analysis

We analyze the local stability of the EDFL model, governed by the non-autonomous fractional-order system in Eq. (10). To enable the use of equilibrium point analysis, we first convert the system to an autonomous form [25] by introducing an auxiliary variable:

$$z=1+A_{m}sin\left(\omega \tau \right),$$

(12)

where $\omega =2\pi f_{0}k$.

Differentiating Eq. (12) twice with respect to $\tau$, we obtain:

$${\displaystyle \frac{d^{2}z}{d{\tau }^2}}=-A_m{\omega }^{2}sin\left(\omega \tau \right).$$

(13)

From Eq. (12), we isolate $A_{m}sin\left(\omega \tau \right)$:

$$A_{m}sin\left(\omega \tau \right)=z-1.$$

(14)

Substituting into Eq. (13) yields:

$${\displaystyle \frac{d^{2}z}{d{\tau }^2}}=-{\omega }^2(z-1)={\omega }^2-{\omega }^{2}z.$$

(15)

Rewriting this second-order equation as:

$${\displaystyle \frac{d^{2}z}{d{\tau }^2}}+{\omega }^{2}z={\omega }^2,$$

(16)

we transform it into a system of first-order differential equations by introducing an additional variable u, defined as:

$${\displaystyle \frac{dz}{d\tau }}=-{\omega }^{2}u.$$

(17)

Differentiating Eq. (17) with respect to $\tau$ gives:

$${\displaystyle \frac{d^{2}z}{d{\tau }^2}}=-{\omega }^2{\displaystyle \frac{du}{d\tau }}.$$

(18)

Substituting into Eq. (16):

$$-{\omega }^2{\displaystyle \frac{du}{d\tau }}+{\omega }^{2}z={\omega }^2,$$

and solving for $du/d\tau$, we obtain:

$${\displaystyle \frac{du}{d\tau }}=z-1.$$

(19)

Thus, Eq. (16) is equivalent to the first-order system formed by Eqs. (17) and (19).

Accordingly, the original system in Eq. (10) is extended to the following autonomous four-dimensional system:

$$\left[\begin{array}{c}{\displaystyle \frac{dx}{d\tau }}\\ {\displaystyle \frac{dy}{d\tau }}\\ {\displaystyle \frac{dz}{d\tau }}\\ {\displaystyle \frac{du}{d\tau }}\end{array}\right]=\left[\begin{array}{c}k\left(axy-bx+c(y+\varrho )\right)\\ k\left(-dxy-(y+\varrho )+ez\left\{1-exp\left[-18\left(1-{\displaystyle \frac{y+\varrho }{\rho }}\right)\right]\right\}\right)\\ -{\omega }^{2}u\\ z-1\end{array}\right].$$

(20)

At this stage, we generalize Eq. (20) to the fractional-order regime by introducing a new control parameter $\alpha \in (0,1]$, representing the fractional order of differentiation. Using the Caputo definition, the fractional-order autonomous system becomes:

$$\left[\begin{array}{c}{\displaystyle \frac{d^{\alpha }x}{d{\tau }^{\alpha }}}\\ {\displaystyle \frac{d^{\alpha }y}{d{\tau }^{\alpha }}}\\ {\displaystyle \frac{d^{\alpha }z}{d{\tau }^{\alpha }}}\\ {\displaystyle \frac{d^{\alpha }u}{d{\tau }^{\alpha }}}\end{array}\right]=\left[\begin{array}{c}k\left(axy-bx+c(y+\varrho )\right)\\ k\left(-dxy-(y+\varrho )+ez\left\{1-exp\left[-18\left(1-{\displaystyle \frac{y+\varrho }{\rho }}\right)\right]\right\}\right)\\ -{\omega }^{2}u\\ z-1\end{array}\right].$$

(21)

To analyze the local stability, we first determine the fixed points $(x^{*},y^{*},z^{*},u^{*})$ of the integer-order Eq. (20) by setting the right-hand side of the system to zero:

$$\left[\begin{array}{c}k\left(a{x}^{*}{y}^{*}-b{x}^{*}+c(y^{*}+\varrho )\right)\\ k\left(-d{x}^{*}{y}^{*}-(y^{*}+\varrho )+e{z}^{*}\left\{1-exp\left[-18\left(1-{\displaystyle \frac{y^{*}+\varrho }{\rho }}\right)\right]\right\}\right)\\ -{\omega }^2{u}^{*}\\ z^{*}-1\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right].$$

(22)

Solving Eq. (22) row-wise, we obtain the following equilibrium conditions. From the third and fourth rows:

$$\begin{array}{cc}\hfill u^{*}& =0,z^{*}=1.\hfill \end{array}$$

From the first row, we find a relation for $x^{*}$:

$$x^{*}={\displaystyle \frac{c{y}^{*}+c\varrho }{b-a{y}^{*}}},$$

(23)

which is valid provided $b\ne a{y}^{*}$.

Substituting Eq. (23) into the second equation of the system in Eq. (22) with $z^{*}=1$, yields:

$$-d\left({\displaystyle \frac{c{y}^{*}+c\varrho }{b-a{y}^{*}}}\right)y^{*}-(y^{*}+\varrho )+e\left\{1-exp\left[-18\left(1-{\displaystyle \frac{y^{*}+\varrho }{\rho }}\right)\right]\right\}=0.$$

(24)

Given that Eq. (24) is nonlinear in $y^{*}$, an analytical solution is intractable. Consequently, we employ the Newton–Raphson method [26] to obtain the numerical solution:

$$y^{*}=0.30745845.$$

(25)

Substituting this value into Eq. (23) gives:

$$x^{*}=-7.74592\times {10}^{-10}.$$

Thus, the fixed point of the system in Eq. (21) is:

$$(x^{*},y^{*},z^{*},u^{*})=(-7.74592\times {10}^{-10},0.30745845,1,0).$$

It is important to note that this is the only fixed point of the autonomous system in Eq. (20), and it is independent of all control parameters, including modulation amplitude $A_m$, modulation frequency $f_0$, and the fractional order $\alpha$. Regardless of variations in these parameters, the fixed point remains unchanged and no other equilibria exist.

Following the procedure detailed in [25], we compute the Jacobian matrix of Eq. (20):

$$J(x,y,z,u)=\left[\begin{array}{cccc}ay-b& ax+c& 0& 0\\ -dy& -dx-1-ez{\displaystyle \frac{18}{\rho }}{e}_c& e(1-e_c)& 0\\ 0& 0& 0& -{\omega }^2\\ 0& 0& 1& 0\end{array}\right],$$

(26)

where

$$e_c=exp\left[-18\left(1-{\displaystyle \frac{y+\varrho }{\rho }}\right)\right].$$

Evaluating the Jacobian at the fixed point $(x^{*},y^{*},z^{*},u^{*})$, we derive the characteristic equation of the system:

$${\lambda }^4+\chi {\lambda }^3+({\omega }^2+\zeta ){\lambda }^2+\chi {\omega }^2\lambda +\zeta {\omega }^2=0,$$

(27)

where the coefficients are defined as:

$$\begin{array}{cc}\hfill \chi & =-a{y}^{*}+b+d{x}^{*}+1+e{\displaystyle \frac{18}{\rho }}{z}^{*}{e}_c,\hfill \\ \hfill \zeta & =-a{y}^{*}-e(a{y}^{*}-b){\displaystyle \frac{18}{\rho }}{z}^{*}{e}_c+bd{x}^{*}+b-cd{y}^{*}.\hfill \end{array}$$

Solving the characteristic Eq. (27), we find the eigenvalues:

$$\begin{array}{cc}\hfill {\lambda }_1& =-{\displaystyle \frac{1}{2}}\left(\chi +\sqrt{{\chi }^2-4\zeta }\right),{\lambda }_2=-{\displaystyle \frac{1}{2}}\left(\chi -\sqrt{{\chi }^2-4\zeta }\right),{\lambda }_3=\omega i,{\lambda }_4=-\omega i.\hfill \end{array}$$

(28)

Recall that $\omega =2\pi f_{0}k$, where k is the time rescaling factor introduced earlier for numerical efficiency. For consistency in the following analysis, we set $k=1$, so that $\omega =2\pi f_0$. The imaginary eigenvalues then become: ${\lambda }_3=2\pi f_{0}i$ and ${\lambda }_4=-2\pi f_{0}i$. The parameter values used are: $A_m=1$, $f_0\in [0,150]\mathrm{kHz}$, $a=6.6207\times {10}^7$, $b=7.4151\times {10}^6$, $c=0.0163$, $d=4.0763\times {10}^3$, $e=506$, $\varrho =0.3075$, and $\rho =0.6150$.

Figure 1 illustrates how the eigenvalues vary with the modulation frequency $f_0$. In Figure 1(a), the real eigenvalues ${\lambda }_1$ and ${\lambda }_2$ remain nearly constant over the frequency range. It is expected since they do not depend directly on $f_0$. In contrast, the imaginary eigenvalues ${\lambda }_3$ and ${\lambda }_4$ shown in Figure 1(b) increase linearly with $f_0$, consistent with their dependence on $\omega =2\pi f_0$.

As seen from Eq. (28) and Figure 1, the real eigenvalues do not depend on the modulation frequency;. Specifically, one eigenvalue is positive (${\lambda }_1>0$) while another is zero (${\lambda }_2=0$). Together with the pair of purely imaginary eigenvalues ($\pm 2\pi f_{0}i$), this configuration implies, following nonlinear dynamics theory [25] and recent studies on EDFLs [11], that the fixed point is a saddle-node with a center manifold. Such a structure is typically associated with complex dynamical behavior, including the emergence of periodic orbits and bifurcations, particularly under parameter variations or in the presence of fractional-order dynamics.

This analysis for the integer-order case can be extended to the fractional-order system, enabling classification of local stability as a function of the fractional order $\alpha$. According to the established results in [27,28], the following stability criteria apply to fractional-order systems:

- The system is stable if and only if $|arg\left({\lambda }_j\right)|\ge {\displaystyle \frac{\alpha \pi }{2}}$ for all eigenvalues ${\lambda }_j$.

- The system is asymptotically stable if and only if $|arg\left({\lambda }_j\right)|>{\displaystyle \frac{\alpha \pi }{2}}$ for all eigenvalues ${\lambda }_j$.

- The system is unstable if $|arg\left({\lambda }_j\right)|<{\displaystyle \frac{\alpha \pi }{2}}$ for at least one eigenvalue ${\lambda }_j$.

In our case, for all $\alpha \in (0,1)$, the arguments of the eigenvalues are:

- $|arg({\lambda }_1\left)\right|=\pi$,       - $|arg\left({\lambda }_3\right)|={\displaystyle \frac{\pi }{2}}$,

- $|arg({\lambda }_2\left)\right|=0$,        - $|arg\left({\lambda }_4\right)|={\displaystyle \frac{3\pi }{2}}$.

As can be seen, and in accordance with [27,28], for all $\alpha \in (0,1)$, the fractional-order system Eq. (21) is unstable. This is due to the presence of at least one eigenvalue, specifically ${\lambda }_2$, with $|arg({\lambda }_2\left)\right|=0$, whose argument lies strictly within the instability region, since $0<\alpha \pi /2$ for any $\alpha >0$.

This situation is illustrated in Figure 2, where the complex plane is divided into stability and instability regions based on the critical angle $\alpha \pi /2$. While three of the eigenvalue arguments (${\lambda }_1$, ${\lambda }_3$, and ${\lambda }_4$) lie within the stable sectors, the eigenvalue ${\lambda }_2$ lies on the positive real axis, where $|arg({\lambda }_2\left)\right|=0<\alpha \pi /2$, placing it in the unstable region for any $\alpha \in (0,1)$.

Since the system possesses a single fixed point, it follows that the dynamics are inherently unstable in the neighborhood of this equilibrium for all $\alpha \in (0,1)$. Therefore, any sustained behavior, such as periodic oscillations, multistability, or chaos, must originate from nonlocal mechanisms, driven by the combined effects of external modulation and the memory properties intrinsic to fractional-order derivatives.

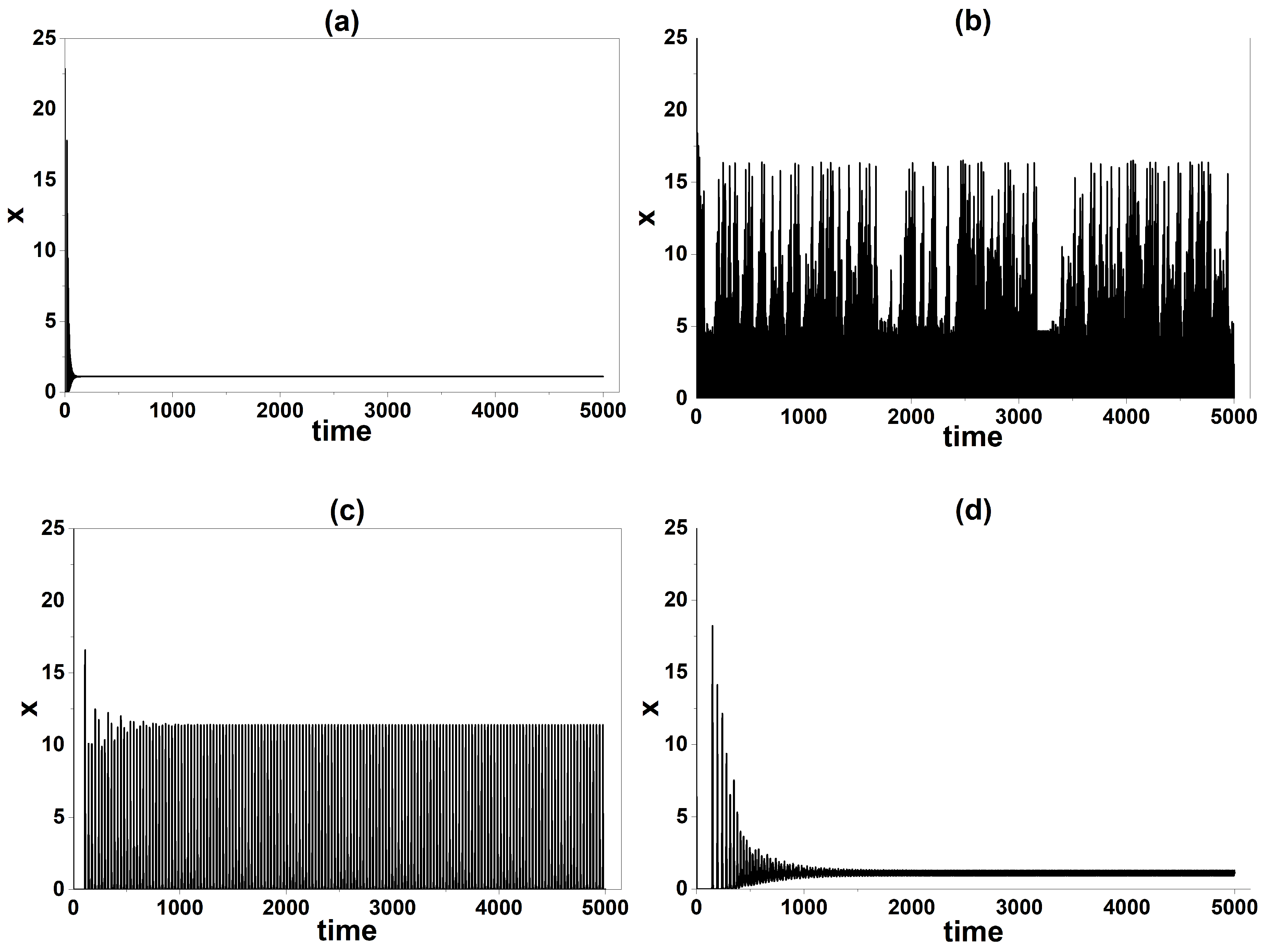
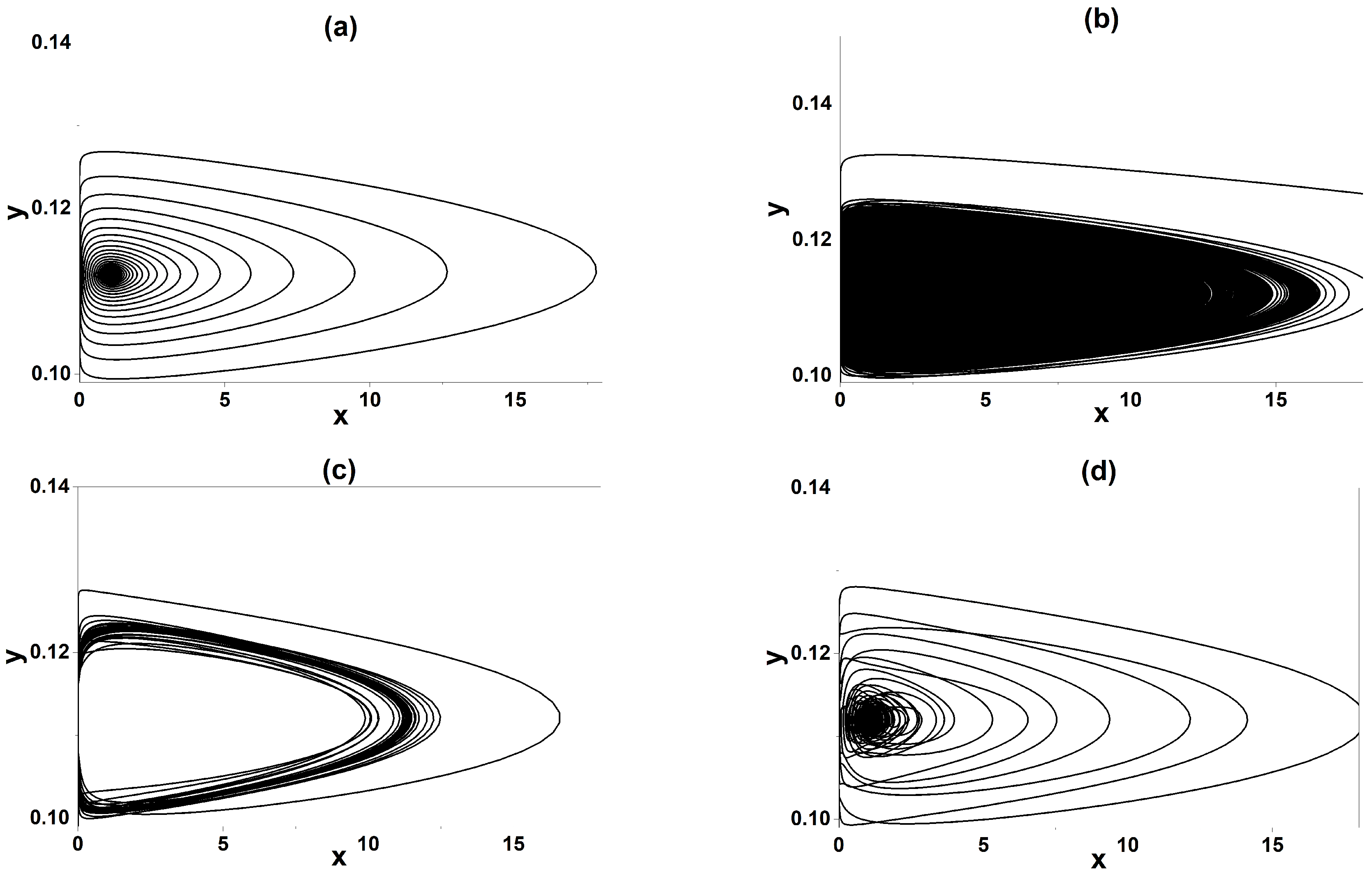
3.3. Global Stability Analysis

The global dynamical behavior of the fractional-order laser model is investigated by generalizing Eq. (10) by introducing control parameter $\alpha$, representing the fractional order of differentiation:

$$\left[\begin{array}{c}{\displaystyle \frac{d^{\alpha }x}{d{\tau }^{\alpha }}}\\ {\displaystyle \frac{d^{\alpha }y}{d{\tau }^{\alpha }}}\end{array}\right]=\left[\begin{array}{c}k\left(axy-bx+c(y+\varrho )\right)\\ k\left(-dxy-(y+\varrho )+e\left[1+A_{m}sin\left(2\pi f_{0}k\tau \right)\right]\left\{1-exp\left[-18\left(1-{\displaystyle \frac{y+\varrho }{\rho }}\right)\right]\right\}\right)\end{array}\right].$$

(29)

The fractional-order system is solved numerically using the two-stage fractional Runge–Kutta method [24]. The resulting dynamics of Eq. (29) are analyzed through time series, phase-space trajectories, and bifurcation diagrams.

Figure 3 displays the time series of $x\left(t\right)$ for modulation frequency $f_0=100$ kHz and difference fractional order $\alpha$ for random initial conditions.

As seen in Figure 3(a), for very low fractional order ($\alpha =0.1$), the laser system converges to a fixed point. At $\alpha =0.49$, the dynamics become chaotic (Figure 3(b)), while for $\alpha =0.8$ and $\alpha =0.9$, the system displays multistability (Figure 3(c)–(d)). These observations are consistent with, and will be further clarified by, the bifurcation diagrams presented below.

The corresponding state-space trajectories in Figure 4 illustrate the relationship between the population inversion y and the laser intensity x.

Figure 5 presents the bifurcation diagrams of the local maxima of the laser intensity, $x^{\max }$, plotted as a function of the modulation frequency $f_0$ for different values of the fractional order $\alpha$.

As shown in Figure 5, the laser exhibits a wide range of dynamical behaviors, including a chaotic regime at low modulation frequencies and the coexistence of multiple periodic states at higher frequencies. Notably, the extent of the chaotic region decreases with increasing $\alpha$. In parallel, the range of multistability (coexisting branches) systematically shifts toward lower frequencies as $\alpha$ increases. Specifically, multistability occurs for $f_0\in (125,380)$ kHz at $\alpha =0.7$ (Figure 5(a)), $f_0\in (50,150)$ kHz at $\alpha =0.8$ (Figure 5(b)), $f_0\in (40,120)$ kHz at $\alpha =0.9$ (Figure 5(c)), and $f_0\in (30,100)$ kHz in the classical integer-order case $\alpha =1$ (Figure 5(d)).

These results demonstrate that the fractional order $\alpha$ directly influences both the location and the shape of the multistability region. This sensitivity underscores the potential of fractional-order modeling for the design and control of optical devices, as it provides a more refined description of memory and hereditary effects in the gain medium.

To further explore the role of $\alpha$, Figure 6 presents bifurcation diagrams of $x^{\max }$ with $\alpha$ as the control parameter for different fixed values of the modulation frequency $f_0$. This representation highlights how bifurcation structures evolve as a function of the fractional order.

As shown in Figure 6, the laser system exhibits multistable behavior over a broad range of the fractional order, $\alpha \in (0.7,1)$. This result confirms that multistability is not only preserved but can also be effectively tuned through variations in $\alpha$, thereby providing an additional degree of freedom for system control.

4. Comparison with Experimental Results

The results obtained in this study demonstrate that the fractional-order model of the pump-modulated EDFL provides a consistent description of its complex dynamical behavior. This naturally raises two key questions: (i) does the fractional-order model capture the laser dynamics more accurately than the traditional integer-order formulation, and (ii) if so, what is the optimal fractional order that best reproduces the experimental observations?

Our findings indicate that the fractional-order framework offers clear advantages for modeling EDFL dynamics. By allowing the system to evolve under non-integer differentiation, the model captures memory effects and long-range correlations that are intrinsic to the physical processes of the laser but are not well represented in integer-order models. This improved flexibility helps reproduce dynamical transitions such as bifurcations, chaos, and multistability with higher fidelity.

To further validate these results, we compared the numerical simulations obtained with the fractional-order model to experimental data [7,8].

The dynamics of the pump-modulated EDFL was investigated experimentally using the setup shown in Figure 7. The laser cavity, 6.5 m in length, consists of a 1.5 m heavily erbium-doped fiber (core diameter 2.7 $\mu$m, single-mode) spliced with two fiber Bragg gratings (FBG1 and FBG2) and a wavelength-division multiplexing coupler (WDM-WD9850FD). FBG1 and FBG2 have bandwidths of 0.288 nm and 0.544 nm, with reflectivities of 100% and 96%, respectively, at 1550 nm. All components are interconnected with single-mode SMF-28 fiber (cladding diameter 200 $\mu$m).

The EDF is pumped by a 977-nm diode laser (LD-BL976PAG500), with current supplied and stabilized by a laser diode controller (LDC-ITC510). In our experiments, the pump current was fixed at 145.5 mA (corresponding to 20 mW pump power), above the lasing threshold of 110 mA. A harmonic modulation signal, $Asin\left(2\pi f_{0}t\right)$, generated by a waveform generator (WFG-AFG3102), was applied to the pump current. A polarization controller (PC) was inserted to optimize cavity alignment and polarization state. The output signal is passed through an optical attenuator (OA-PW410), which scales the transmitted power by factor k ($k=0\%$ corresponding to zero transmittance, $k=100\%$ to full transmission). The attenuated signal is detected by a photodiode (PD1) and digitized using a data acquisition card (DAC) for dynamical analysis.

Under modulation, the EDFL exhibits the coexistence of up to four periodic attractors: period-1 (P1), period-3 (P3), period-4 (P4), and period-5 (P5). The bifurcations are clearly visible in the bifurcation diagram of the laser peak intensity $I_p$ shown in Figure 8. The diagrams were constructed from time series by varying the modulation frequency $f_0$ as a control parameter, while exploring different initial conditions obtained by switching the driving signal on and off 10 times. The periodic regimes P3, P4, and P5 emerge in saddle-node bifurcations as $f_0$ is increased [29,30,31].

A detailed analysis of Figure 8 for fixed modulation amplitude $A=1$ V reveals the regions of the coexistence of different attractions. Specifically, stable periodic orbits P1, P3, and P4 coexist for $f_0\in (87,100)$ kHz; P1 and P4 coexist for $f_0\in (100,107)$ kHz; and P1, P4, and P5 coexist for $f_0\in (107,115)$ kHz. Examples of the corresponding laser intensity time series can be found in [31].

The integer-order model of the EDFL predicts regions of multistability within the interval $f_0\in (80,100)$ kHz (see Figure 5(d)), which is consistent with earlier numerical studies [8,9,30]. However, this interval does not fully coincide with the experimentally observed region (Figure 8). Previous works have attributed such discrepancies to experimental factors, including electrical and optical noise, uncertainties in the parameters of the active medium, and simplifications in the experimental setup. These effects likely cause shifts in the bifurcation diagrams, leading to broader intervals, less sharply defined boundaries, and more irregular chaotic windows. Our results, however, demonstrate that incorporating fractional-order derivatives significantly improves the agreement between simulations and experiments.

A direct comparison of numerical (Figure 5) and experimental (Figure 8) bifurcation diagrams shows that the experimental results are best reproduced by the fractional-order model with $\alpha =0.9$ (see Figure 5(c)), whereas the integer-order case (Figure 5(d)) is shifted toward higher modulation frequencies. This highlights the role of fractional calculus in enhancing the fidelity of the model with respect to experimental data.

Importantly, the fractional framework ($\alpha <1$) does not alter the fundamental physics of the system. As illustrated in Figure 5(a–c), the same qualitative dynamical features—periodic, chaotic, and multistable behaviors—are preserved as in the integer-order model. Instead, the fractional index $\alpha$ serves as a fine-tuning parameter, effectively shifting the localization of multistable regions along the modulation frequency axis. In particular, for $f_0>100$ kHz, the experimentally observed coexistence regions (Figure 8) are well captured by the fractional-order model with $\alpha =0.9$.

Thus, the fractional analysis of the erbium-doped fiber laser provides a new degree of freedom for system characterization, with the fractional index $\alpha$ acting as a control parameter. While the nature of the dynamical regimes remains unchanged, their positions in parameter space can be adjusted systematically. For $\alpha <1$, the multistability regions shift toward higher or lower modulation frequencies depending on the chosen value of $\alpha$, whereas the case $\alpha =1$ recovers the classical dynamics. This confirms both the robustness of the fractional modeling approach and its utility in reconciling numerical predictions with experimental observations. Beyond improving model accuracy, this tunability has broader implications for the design and control of nonlinear photonic systems.

5. Conclusions

In this work, the mathematical model of the pump-modulated EDFL was extended into the fractional domain and analyzed using a two-stage Runge–Kutta method. The study reveals the direct influence of the fractional index $\alpha$ on laser dynamics, particularly on the position and morphology of multistability regions. While the fundamental dynamical regimes remain unchanged, the control parameter (modulation frequency) and the fractional index jointly determine the precise location of these regions, offering a new degree of freedom for system characterization and control.

The results demonstrate that fractional-order modeling not only reproduces the well-established integer-order case ($\alpha =1$) but also provides a closer agreement with experimental observations for $\alpha =0.9$. This suggests that non-integer derivatives capture essential physical mechanisms neglected in conventional models. Importantly, the fractional index $\alpha$ acts as an effective control parameter, enabling the systematic tuning of dynamical regimes, an insight with clear implications for the design of EDFLs in applications requiring robust and precise control of nonlinear behaviors.

Numerical simulations further show that fractional calculus advances the understanding of critical transitions in EDFL dynamics, identifying shifts in multistability regions both in location and structure compared to the integer-order framework. These findings underscore the value of fractional-order models as a unifying theoretical tool for describing complex laser dynamics. The existence of an optimal fractional order that minimizes discrepancies with experiment emerges as an open question and a promising direction for future research. In addition, the proposed electronic implementation of the model may facilitate experimental validation and broaden practical applications.

Overall, this study highlights fractional calculus as a powerful extension of conventional laser theory. Beyond EDFLs, the framework may prove valuable for a wider class of nonlinear photonic systems, particularly those where memory effects and long-range temporal correlations govern the dynamics. By bridging numerical models and experimental observations, the fractional-order approach opens new perspectives for the development of next-generation photonic devices.