1. Introduction
As critical national transportation infrastructure in China, high-speed railways (HSR) feature a remarkably high proportion of bridges within the domestic network to ensure track levelness [
1,
2]. With HSR lines extending into regions traversing active fault zones, the track-bridge systems of HSR in near-fault seismic belts face significant seismic challenges. Relevant research indicates that near-fault ground motions exhibit distinct characteristics, including pronounced long-period velocity pulse and intense vertical ground motion (VGM) [
3,
4,
5], which result in structural responses distinctly different from those induced by far-field ground motions [
6,
7] and cause particularly severe damage to engineering structures [
8,
9,
10,
11]. Although seismic isolation techniques have proven effective in mitigating seismic damage to buildings and highway bridges [
12,
13,
14], existing research predominantly focuses on horizontal seismic responses, with insufficient attention paid to the significant vertical ground motions in near-fault regions. Increased seismic observation records reveal that the peak vertical ground accelerations in some strong motions exceed their horizontal counterparts, constituting a major contributor to structural damage [
15]. Consequently, investigating the response patterns and damage mechanisms of seismically isolated HSR track-bridge systems subjected to near-fault vertical ground motions holds important theoretical value and engineering guiding significance.
Domestic and international scholars have conducted extensive research on the characteristics of near-fault ground motions. Studies by Tao et al. [
16], and Jiang et al. [
17] demonstrate that the pulse effects inherent in near-fault ground motions exert a significant influence on structural responses. Jiang et al. [
18] investigated the impact of near-fault pulse-like ground motions and pulse parameters on the long-span arch bridge-track system of HSRs. Their findings indicate that ground motion records exhibiting fling-step pulses induce more pronounced seismic responses, with structural responses intensifying as pulse amplitude increases. Furthermore, the studies [
19,
20] found that pulse effects may also amplify the displacements of seismic isolation bearings. The VGM component also has a notable impact on the seismic responses of bridge structures, Guo et al. [
21] demonstrated that the VGM in near-fault regions plays a crucial role and can potentially cause running trains to derail from bridge tracks. Ryan et al. [
22] demonstrated that considering the vertical seismic component leads to significant amplification of base shear in structures isolated with spherical sliding bearings. Shao et al. [
23] proposed a novel model of bridge seismic fragility surface conditioned on the horizontal peak ground velocity and the ratio of vertical to horizontal ground motion, and analyzed the influence and mechanism of VGM on damage probability. Wei et al. [
24] further corroborated that VGMs can affect the seismic fragility of bridge structures. In general, fruitful achievements have been made in the research on the pulse effect of near-fault ground motions, but the research on strong VGMs remains incomplete.
Seismic isolation bearings are widely recognized for their effectiveness in reducing seismic forces transmitted to engineering structures [
25]. Currently, some scholars have conducted research on the seismic isolation design of HSR bridges under near-fault earthquakes. Chen et al. [
26] demonstrated that under near-fault ground motions with various peak characteristics, the optimally-tuned seismic isolation system for HSR bridges can simultaneously reduce both deck displacements and internal forces, achieving high-efficiency seismic mitigation. Based on the functional separation design principle, Liu et al. [
27] developed a new type of isolation bearing that can achieve multi-level control objectives to meet the strict requirements of HSRs for track smoothness. Friction pendulum bearings (FPB) are widely used in bridge structures due to their advantages of simple design, large deformation, easily adjustable period, and excellent seismic isolation performance [
28,
29,
30]. Compared with ductile bridges, the vulnerable location of isolated bridges shifts from piers to bearings, and under near-fault ground motions, bearing failure becomes one of the primary damage modes [
31]. Scholars have also conducted research on the influence of VGM on FPB. Loghman et al.’s study shows that considering the vertical component of earthquakes has no significant effect on determining the peak bearing displacement, and the maximum average error reaches 29.5% when calculating the base shear of the structure while ignoring this component [
32]. Through statistical analysis, Zhong et al. [
33] found that the VGM component should be reasonably considered in evaluating the seismic performance of friction-isolated bridges in near-fault regions, which is particularly critical for accurately calculating the response of friction pendulum bearings. Xiao et al. [
34] examined the influence of FPB isolation parameters on component damage and operational safety performance within the HSR bridge-track system subjected to near-fault earthquakes. Despite the progress made in existing research, significant limitations persist: the understanding of the displacement responses and damage degree of components of HSR isolated track-bridge systems caused by near-fault VGMs, and targeted research is urgently required to address these gaps.
Consequently, this study focuses on investigating the influence of near-fault VGMs on HSR isolated track-bridge systems, with the following research contents: Chapter 2 develops and validates a refined FEM incorporating the track structure, bridge, and seismic isolation bearings. Chapter 3 performs nonlinear time-history analysis to compare the structural displacements under isolated and common working conditions, considering different ratios αVH of vertical peak ground acceleration (PGAV) to horizontal peak ground acceleration (PGAH) (where αVH = PGAV/ PGAH), as well as different earthquake intensities. Chapter 4, based on a defined damage index system, quantifies the damage degree and progression patterns of critical components under different αVH ratios and seismic intensities, evaluates the seismic control effect of the isolation technology, and puts forward suggestions on the selection of αVH values. Chapter 5 draws the research findings and conclusions, providing a scientific basis for the seismic design of HSR infrastructure in near-fault regions.
2. The Structural Dynamic Analysis Model
2.1. Simulation of HSR Track-Bridge System
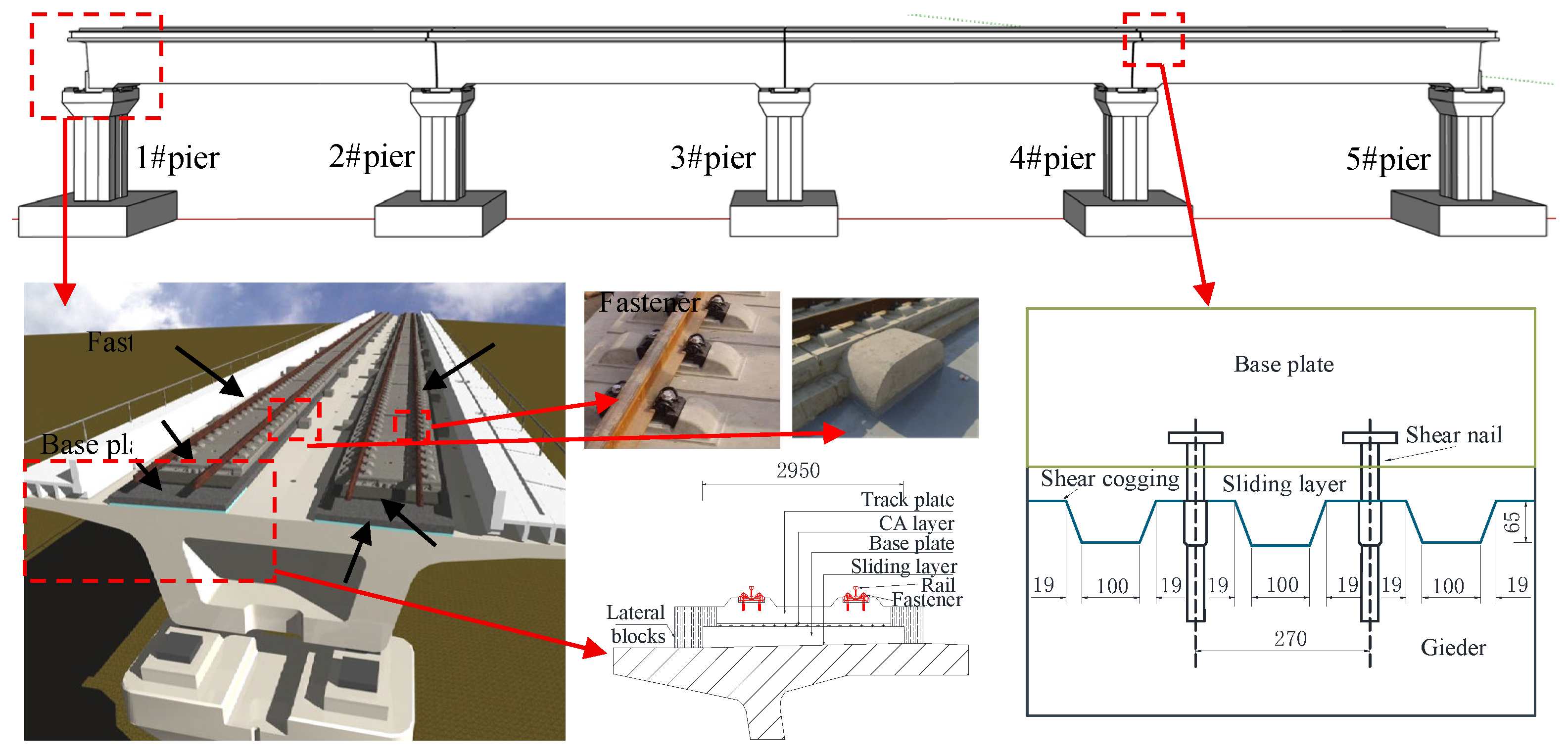
In this study, a typical high-speed railway simply supported beam bridge located in a near-fault area with 8-degree seismic fortification on type II site is taken as the analysis object. The bridge structure comprises four equal spans of 32 meters each as shown in
Figure 1. The main girders of the bridge adopt equal-section single-box single-chamber box girders, and the piers are solid piers with rectangular sections, all with a height of 13.5 m. The track system employs a typical CRTS II slab ballastless track system as shown in
Figure 1, whose material selection, dimensional parameters, and component layout are consistent with those in existing studies [
28,
29].
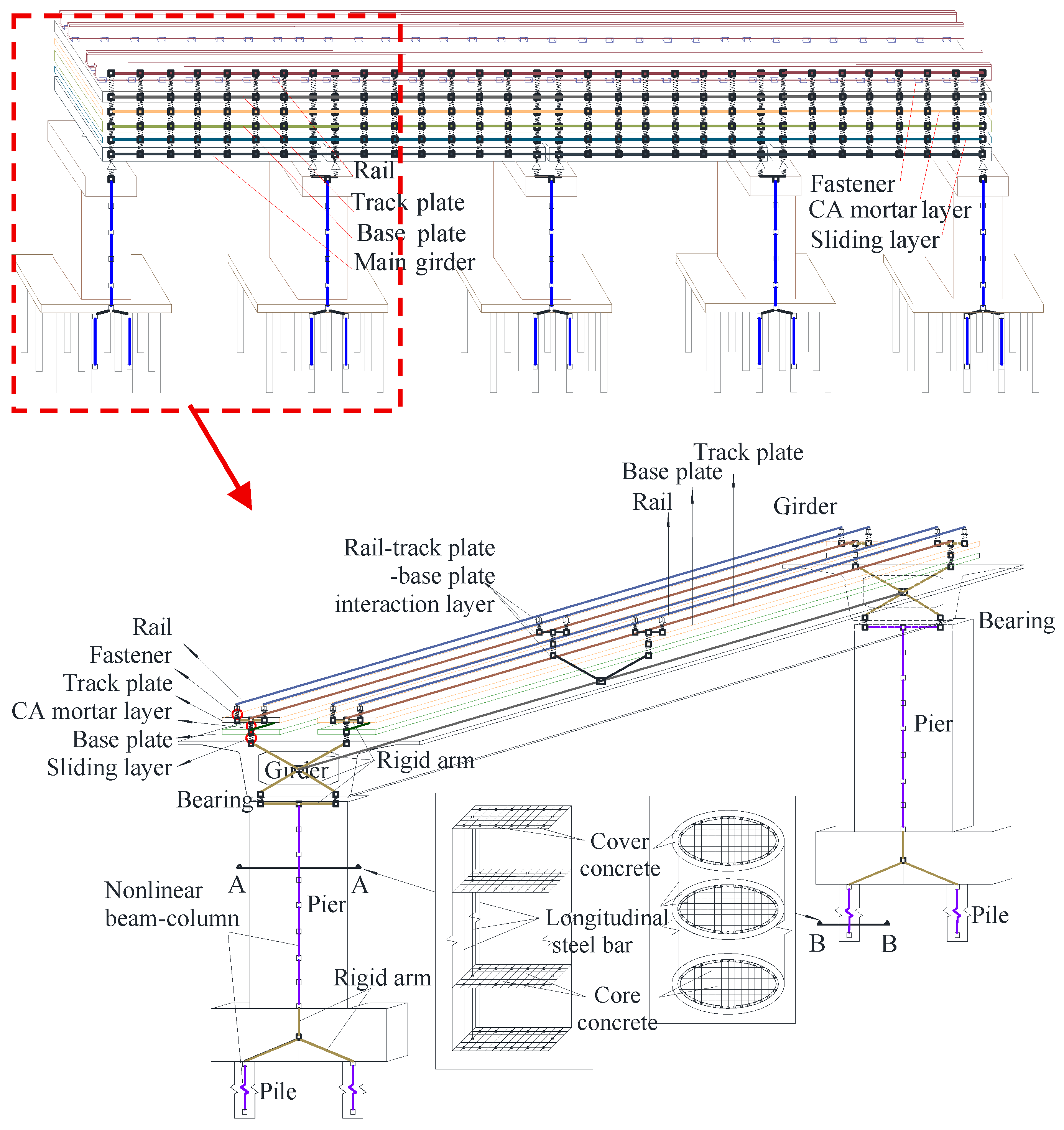
A dynamic analysis model of the HSR track-bridge system is established in this study utilizing the OpenSEES platform, as shown in
Figure 2 Based on the bearings types employed in the HSR track-bridge system, the system is divided into two categories: the common system and the isolated system. The dynamic calculation models of these two systems are identical in all aspects except for the simulation method of the bearings.
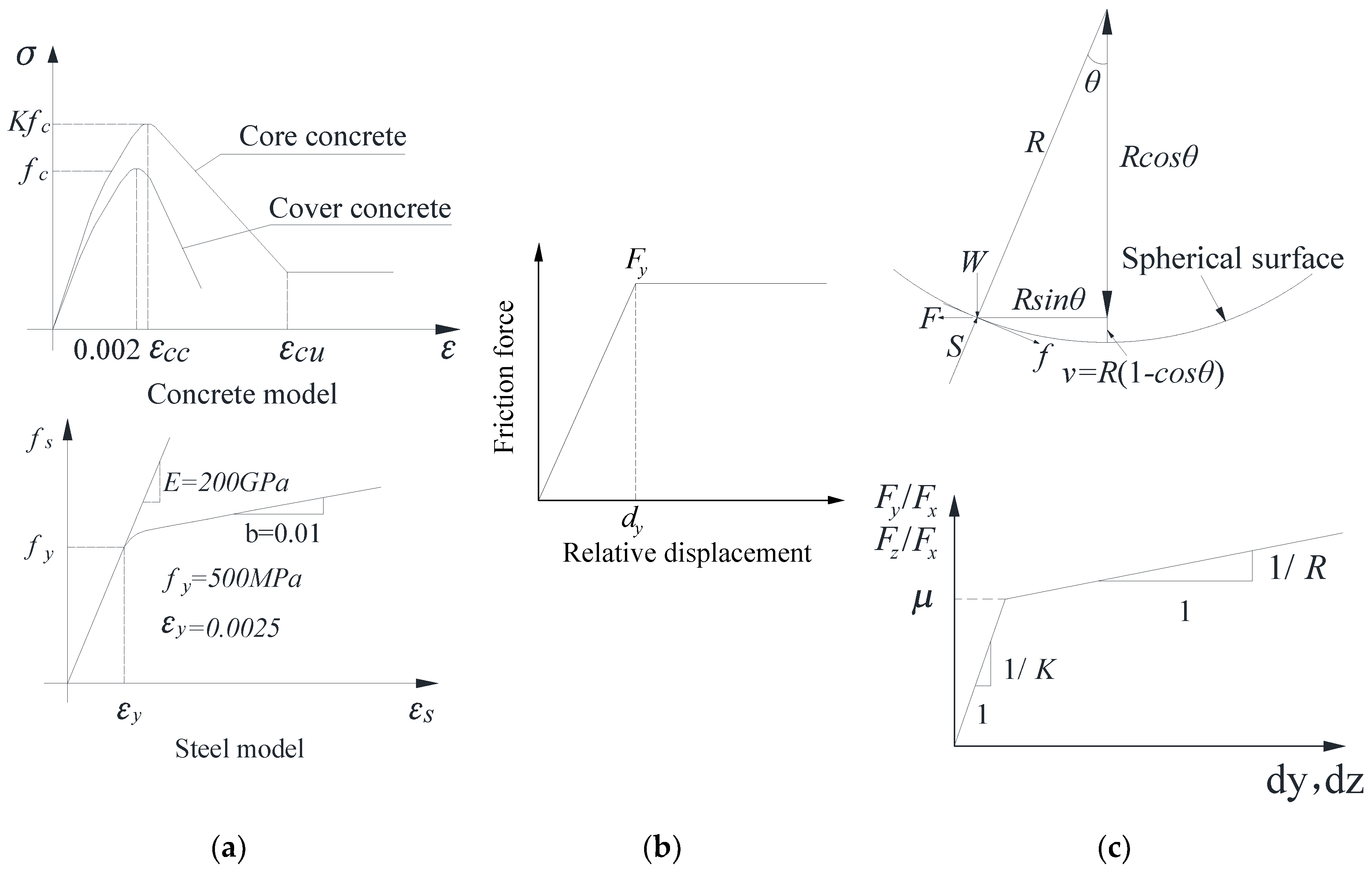
Specifically, the modeling approaches are maintained identically for the main girders, piers, and track system components in the two models. Based on evidence from existing seismic damage investigations [
35], the rail, track plate, base plate, and girders are generally observed to remain elastic under seismic excitation. Consequently, these elastic components are simulated using elastic beam elements in this study, with the corresponding parameters for each element type provided in
Table 1. Piers are simulated using fiber elements in OpenSEES to analyze their nonlinear behavior under seismic action [
34]. The cover concrete and core concrete are represented by the Concrete 01 material model, albeit with distinct parameter sets. The ultimate compressive strength of the core concrete is calculated according to the Kent-Scott-Park model, incorporating the confinement effect of reinforcement. Longitudinal reinforcement is modeled using the Steel 02 material in OpenSEES, with specific parameters shown in
Figure 3a. The interlayer components of the CRTS II slab ballastless track are all simulated using zero-length elements. The force-displacement relationships for these nonlinear zero-length elements are presented in
Figure 3b, and their corresponding parameters are tabulated in
Table 2. Furthermore, the vertical constitutive behavior of the aforementioned components is modeled employing large stiffness values.
Figure 2.
Schematic of the FEM of the HSR track-bridge system.
Figure 2.
Schematic of the FEM of the HSR track-bridge system.
The distinction between the two systems is manifested primarily in the simulation of the bearings. Spherical steel bearings are employed in the common system. For the isolated system, friction pendulum bearings (FPBs) are selected and modeled using the SingleFPB element in OpenSEES. The specific parameters for this element are presented in
Figure 3c. The design parameters include the friction coefficient and the radius of curvature of the sliding surface, which are assigned values of 0.02 and 3.5 m, respectively.
Figure 3.
The constitutive models of different elements: (a) Concrete and steel bar element; (b) Force-displacement curve of the zero-length element; (c) Single friction pendulum bearing.
Figure 3.
The constitutive models of different elements: (a) Concrete and steel bar element; (b) Force-displacement curve of the zero-length element; (c) Single friction pendulum bearing.
2.2. Near-Fault Ground Motions and Distribution of αVH
A total of 100 near-fault ground motion records are selected from the PEER ground motion database, characterized by rupture distances ranging from 0.07 km to 28.04 km and moment magnitudes between 5.4 and 7.9. To investigate the response of the HSR track-bridge system under various combinations of vertical and horizontal seismic excitations, the ratio of the peak vertical ground acceleration (PGA
V) to the peak horizontal ground acceleration (PGA
H), denoted herein as α
VH and assumed to be an independent variable, is employed to quantify VGMs [
23,
24]. Systematic statistical analyses are performed on these 100 near-fault ground motion records to establish the distribution relationships between the α
VH values and the rupture distance, moment magnitude, and faulting mechanism, as illustrated in
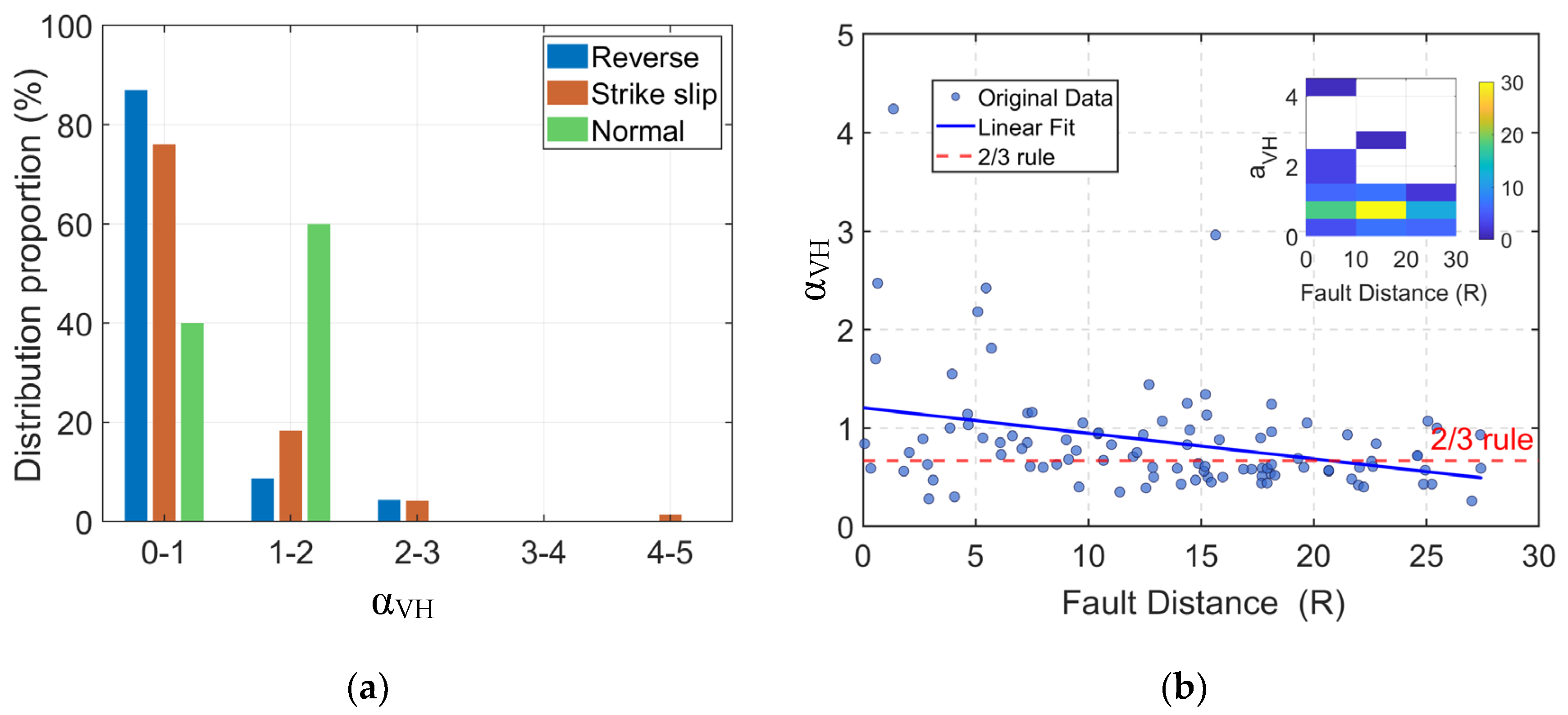
Figure 4.
The distribution proportions of α
VH in each interval (0-1, 1-2, 2-3, 3-4, 4-5) under three fault mechanisms (reverse, strike-slip faults, and normal) of near-fault earthquakes is presented in the bar chart in
Figure 4a. The specific distribution characteristics are as follows: Under reverse faults, α
VH is accounted for the highest proportion (over 85%) in the 0-1 interval, then drops significantly to within 10% in the 1-2 interval, and remains at an extremely low level (<5%) in the 2-3 and higher intervals. For strike-slip faults, α
VH is made up nearly 75% in the 0-1 interval, decreases to approximately 20% in the 1-2 interval, and negligible proportions (<5%) are maintained in higher intervals (≥2–3). In normal fault regimes, α
VH is occupied about 40% in the 0-1 interval, rises to around 60% in the 1-2 interval to become dominant, and maintains an extremely low proportion in the 2-3 and higher intervals. Collectively, distinct mechanistic partitioning of α
VH distributions across fault mechanisms is conclusively demonstrated.
Figure 4b shows the distribution and density of the original α
VH data with varying fault distances. It can be observed that the original α
VH data generally exhibit a decreasing trend with the increase of fault distance, as quantitatively confirmed by the blue linear fitting line. Significant deviations are observed between actual α
VH scatter points and the normative reference (“2/3 rule”, red dashed line), with most data points positioned above this benchmark. The data density histogram in the upper right corner (with a color scale of 0-30, where values are positively correlated with density) objectively reveals the spatial distribution characteristics of α
VH values with fault distances. Within the fault distance range of 10–20 km, α
VH values exhibit significant spatial aggregation, mainly densely distributed in the interval of 0.5–1.5. The practice of uniformly setting α
VH to 2/3 in current codes may lead to a systematic underestimation of the vertical ground motions, which in turn causes negative deviations in the prediction of structural dynamic responses and ultimately results in inaccurate assessment of vertical seismic performance. Therefore, it is necessary to conduct refined research on the selection of α
VH values in combination with the distribution characteristics of actual seismic data.
To quantify the effects of near-fault vertical ground motions on the response and damage of HSR isolated track-bridge systems, three levels of horizontal seismic intensities are employed in this study (corresponding to the 8-degree seismic fortification zone: 0.1g for frequent earthquakes, 0.3g for design earthquakes, and 0.57g for rare earthquakes). Based on the distribution patterns revealed in
Figure 4 that α
VH is densely distributed within the range of 0.5~1.5, the scaling factor α
VH is set as {0, 0.3, 0.6, 0.9, 1.2, 1.5} to characterize the variation of vertical ground motions. A representative near-fault ground motion record, IMPVALL.H_H-CPE237 (fault distance: 15.19 km, positioned within the 10-20 km high-density interval exhibiting α
VH clustering) is selected as seismic input to systematically analyze the influence of α
VH on component responses and damage evolution.
3. Influence of Near-Fault VGM on the Longitudinal Responses of Components
It has been empirically established that component damage induced by longitudinal seismic actions significantly exceeds that caused by transverse scenarios [
35]. Consequently, nonlinear time-history analyses were conducted to compute structural responses of the high-speed railway track-bridge system under longitudinal excitations, with the influence mechanism of different α
VH on component damage revealed.
3.1. Impact on the Seismic Performance of Bearings and Piers
In seismic research of HSR track-bridge structures, the seismic responses of bearings and piers are recognized as key safety indicators. Based on three levels of seismic intensity, namely frequent earthquake (FE), design earthquake (DE), and rare earthquake (RE), the influence patterns of common and isolated cases on the responses of bearings and piers under different αVH ratios are systematically evaluated in this paper, and theoretical basis is provided for the optimization of seismic design of HSR track-bridge structures.
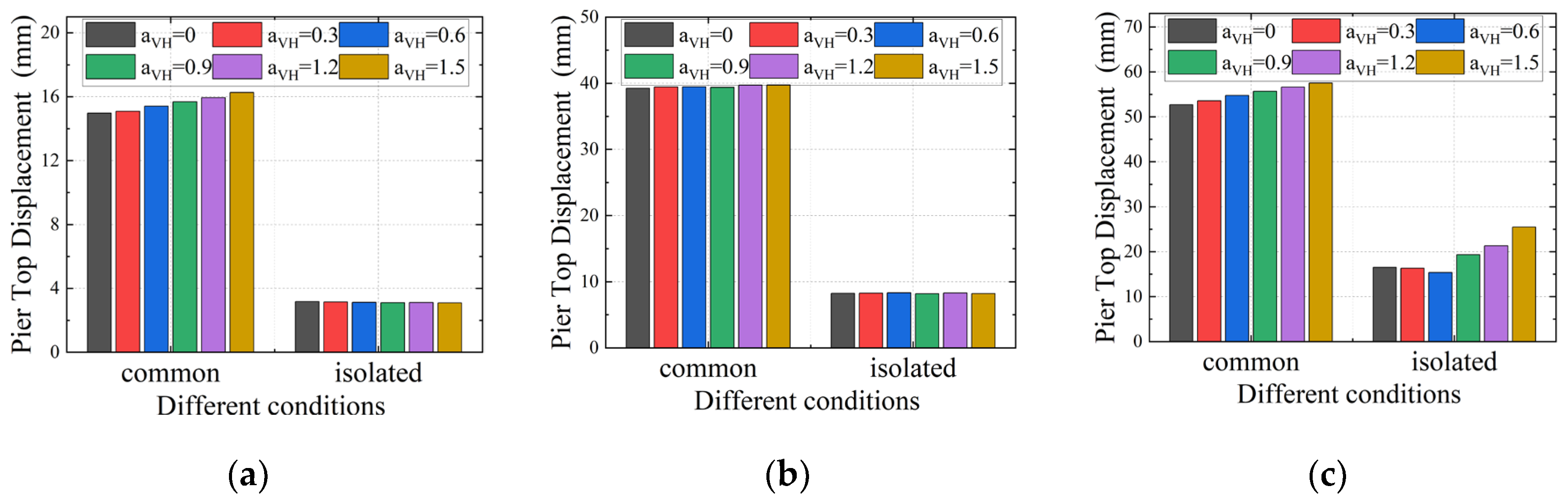
Figure 5 depicts the 3# pier top displacement responses under three seismic intensity levels (FE, DE, RE). The following key findings are observed: In common cases, pier top displacements exhibit a monotonic increase with rising α
VH ratios (indicating enhanced vertical seismic components), with more pronounced amplification of growth rates as seismic intensity increases (from FE to DE to RE); and under high α
VH conditions, vertical-horizontal seismic coupling significantly exacerbates deformation demands. Conversely, in isolated cases, the pier top displacement increases slightly with the rise of α
VH, and the increment is much lower than that in common cases. This is because the isolation system effectively interrupts direct vertical-horizontal energy transfer paths, remarkably mitigating coupling-induced deformations and thereby enhancing structural safety.
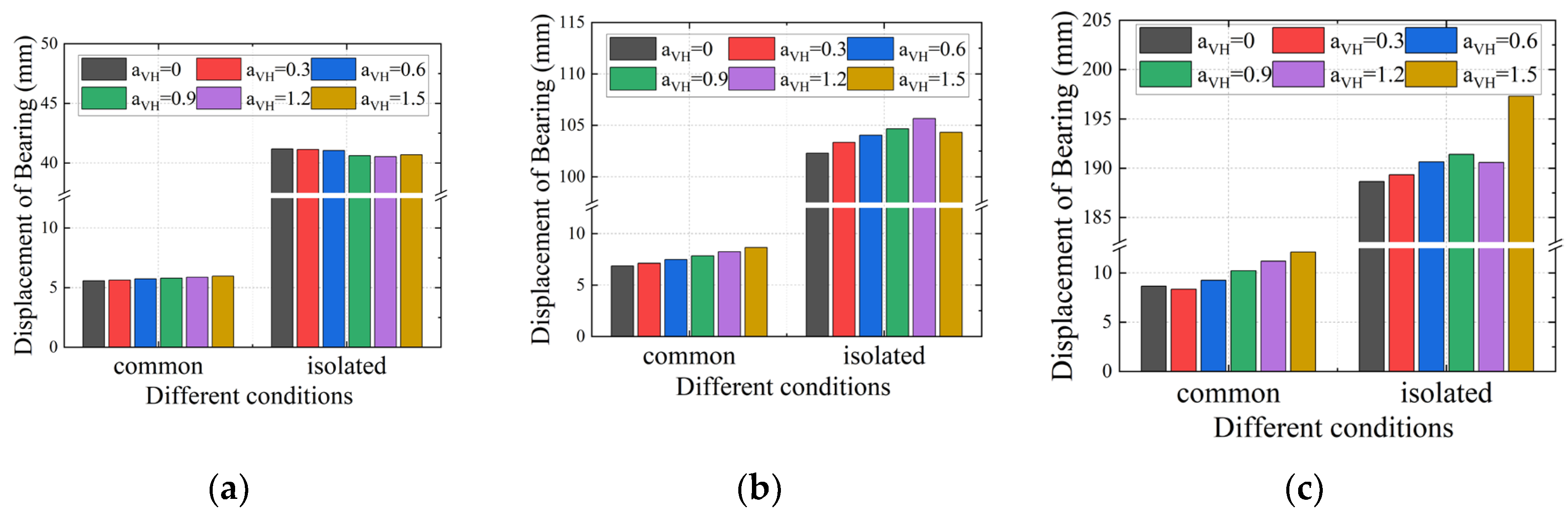
Figure 6 presents the displacement responses of the movable bearing at 3#Pier, where subfigures (a)-(c) display the displacement distributions of common and isolated conditions under FE, DE, and RE seismic levels respectively. The results indicate that under both conditions, the movable bearing displacement increases with the elevation of seismic level (FE→DE→RE). With the variation of α
VH: under the common case, at the FE level, minor movable bearing displacement (<6mm) are exhibited with low sensitivity to α
VH variations (difference <7%); at the DE level, the movable bearing displacement increases significantly with increasing α
VH (26% increase when α
VH=1.5 compared to α
VH=0); at the RE level, the displacement surges due to the superposition of high seismic energy and bidirectional earthquakes (40% increase when α
VH=1.5 compared to α
VH=0). Under the isolated case, all three seismic levels demonstrate maintained displacement sensitivity to α
VH variations below 5%, indicating effective displacement control. In addition, the movable bearing displacement under all isolated cases is significantly higher than that under common cases, which reflects the design concept of the isolation system that “uses large bearing deformations for energy dissipation to protect primary structures”. However, under high seismic intensity levels, displacement-restricting devices must be incorporated to strictly control isolated bearing deformations, as excessive displacements may lead to severe seismic damage such as girder unseating.
3.2. Effect of Seismic Response on Interlayer Components in Track Structure
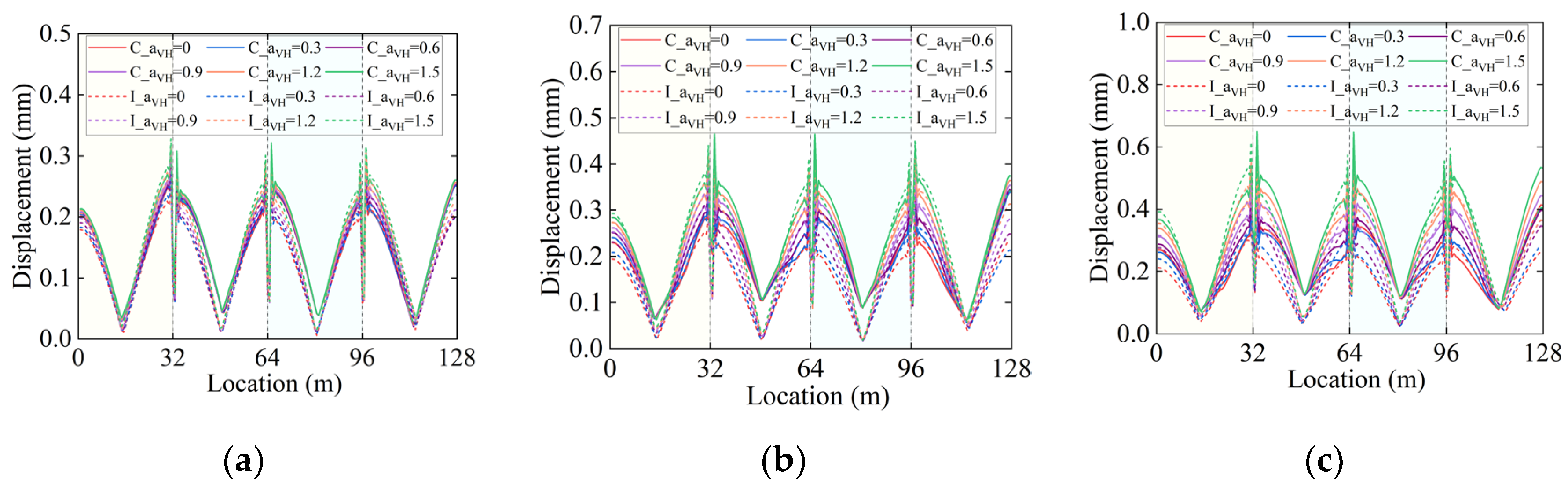
The displacement characteristics of interlayer components in track structures such as the sliding layer, CA mortar layer and fasteners are recognized as critical indicators for evaluating the seismic performance of HSR track-bridge systems. Based on three seismic levels: FE, DE, and RE, this study systematically investigates the influence of the vertical-to-horizontal PGA ratio αVH on the interlayer displacement responses of track structures under both common and isolated cases. The findings not only provide a theoretical foundation but also lay a solid basis for optimizing the seismic design of interlayer components in track-bridge systems.
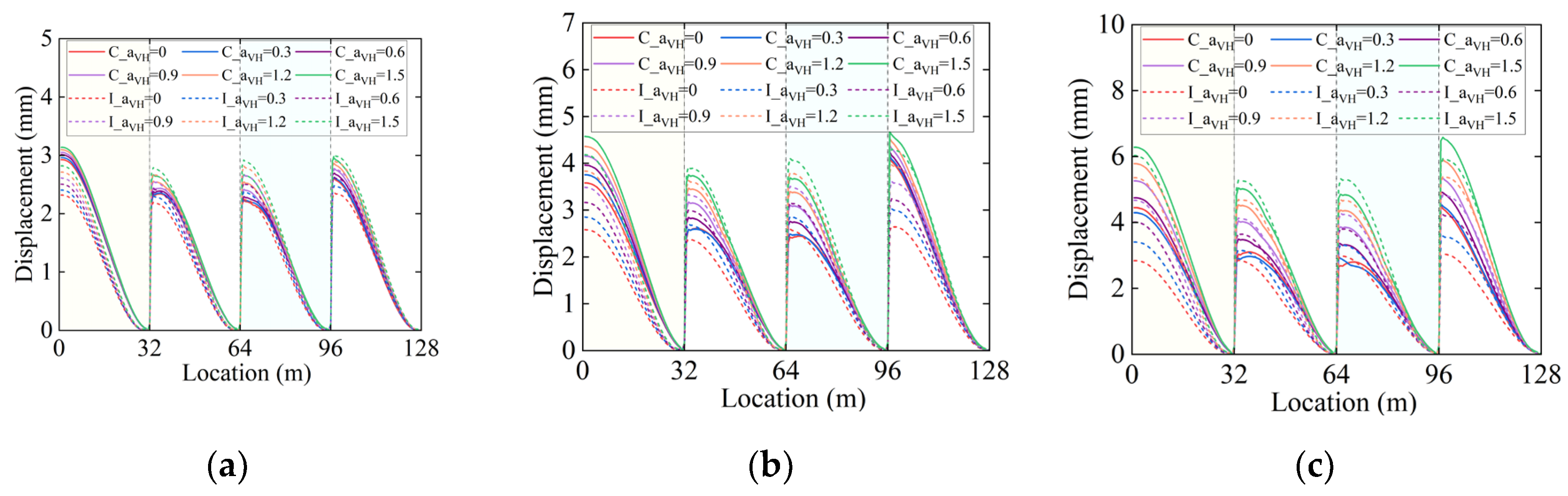
Figure 7a-c present the sliding layer displacement responses with different α
VH ratios under common case (denoted as C_α
VH=0~ C_α
VH=1.5 in the figures) and isolated case (denoted as I_α
VH=0~ I_α
VH=1.5 in the figures) at the FE, DE, and RE levels. The sliding layer displacements exhibit periodic variations along the bridge length, with peak values consistently observed at the simply-supported beam ends (0 m, 32 m, 64 m, and 96 m). For a given seismic intensity level, displacements in both conditions increase with the rise of α
VH, and this amplification effect becomes more pronounced as seismic intensity rises (FE→DE→RE); notably, the isolated condition exhibits greater displacement amplification than the common condition, particularly under the RE level where a 97% increase is recorded when α
VH=1.5 compared to α
VH=0. This phenomenon provides clear evidence that the coupling effect between vertical and horizontal ground motions can significantly amplify sliding layer deformations, and in near-fault regions where strong vertical ground motions may occur, seismic analyses considering only horizontal components while neglecting or underestimating vertical-horizontal coupling effects would lead to a substantial underestimation of sliding layer deformation demands, potentially resulting in safety hazards.
Under identical seismic intensity levels and αVH ratios, sliding layer displacements in isolated cases are generally smaller than those in common cases, demonstrating the protective effect of the isolation system on the sliding layer. However, the isolated displacement in the central two spans is observed to exceed that in common cases. This reversal is attributed to the flexibility introduced by the isolation system, which alters structural vibration modes, induces displacement redistribution among girders, and requires the central spans to accommodate additional deformation demands from the isolation layer—furthermore, the extension of the fundamental period and prolonged seismic excitation duration caused by isolation amplify these displacements. In terms of boundary effects, larger displacements in common systems are concentrated in end spans due to the direct transmission of seismic energy at supports and enhanced sensitivity of boundary constraints and dynamic responses; in contrast, under isolated cases, FPBs reduce inter-span displacement differences by dissipating energy and uniformizing vibration patterns, significantly mitigating the phenomenon of displacement concentration in end spans relative to central spans.
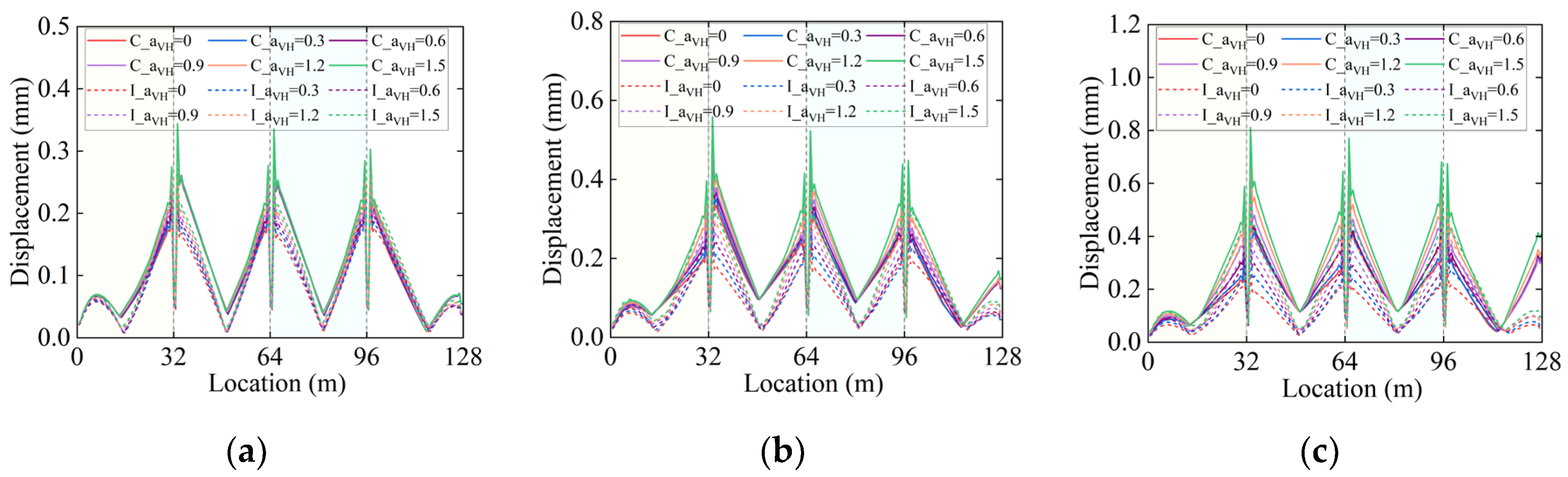
Figure 8a-c and
Figure 9a-c respectively present the displacement responses of CA mortar and fasteners under common and isolated conditions at FE, DE, RE seismic levels and α
VH (0~1.5) values. Compared with the sliding layer, the displacement values of the CA mortar layer and fasteners are smaller, which reflects the gradient distribution characteristics of interlayer deformations in the track structure. The displacements of both show an obvious increasing trend with the elevation of seismic levels (FE→DE→RE) and the increase of α
VH (0→1.5), and they present an inter-span periodic distribution along the bridge length, with peak values located at the ends of simply supported beams (32 m, 64 m, 96 m) — this is attributed to the weak constraints at the beam ends, where the vibration of the beam body during an earthquake leads to large relative displacements at the beam ends, and the complex stress and deformation at the connecting interface of the beam ends result in the concentration of displacements in interlayer components. Under identical seismic and α
VH conditions, reduced displacements are achieved in isolated cases compared to common conditions, demonstrating the protective role of seismic isolation in mitigating energy transmission. The isolation system is shown to effectively alleviate the adverse effects of vertical-horizontal seismic coupling on the deformation demands of track interlayer components.
4. Damage Analysis of Components Under Different αVH Ratios
Based on existing research [
24,
36], the damage states of HSR track-bridge structural components are classified into five levels: no damage, slight damage, moderate damage, serious damage, and failure. The boundaries between these levels are defined by four damage thresholds (DS1-DS4), with specific quantitative indicators shown in
Table 3. Herein, pier damage is represented by the pier drift ratio (equal to pier top displacement divided by pier height, %) [
36], and damage to other components by displacement values (disp, mm). By establishing a comparative system between the common model and the isolated model, the seismic performance of the track-bridge structure under FE, DE, and RE earthquakes was systematically investigated across different α
VH conditions (0–1.5). The study focuses on the peak displacement responses and damage distribution of the pier, bearings, and interlayer track components (as shown in
Figure 10 and
Figure 11), the influence of earthquake intensity on damage progression, the effectiveness of isolation measures in mitigating displacement responses and damage degrees, and the suggested reasonable values of α
VH based on damage control, so as to provide a theoretical basis for the seismic design of high-speed railway track-bridge systems.
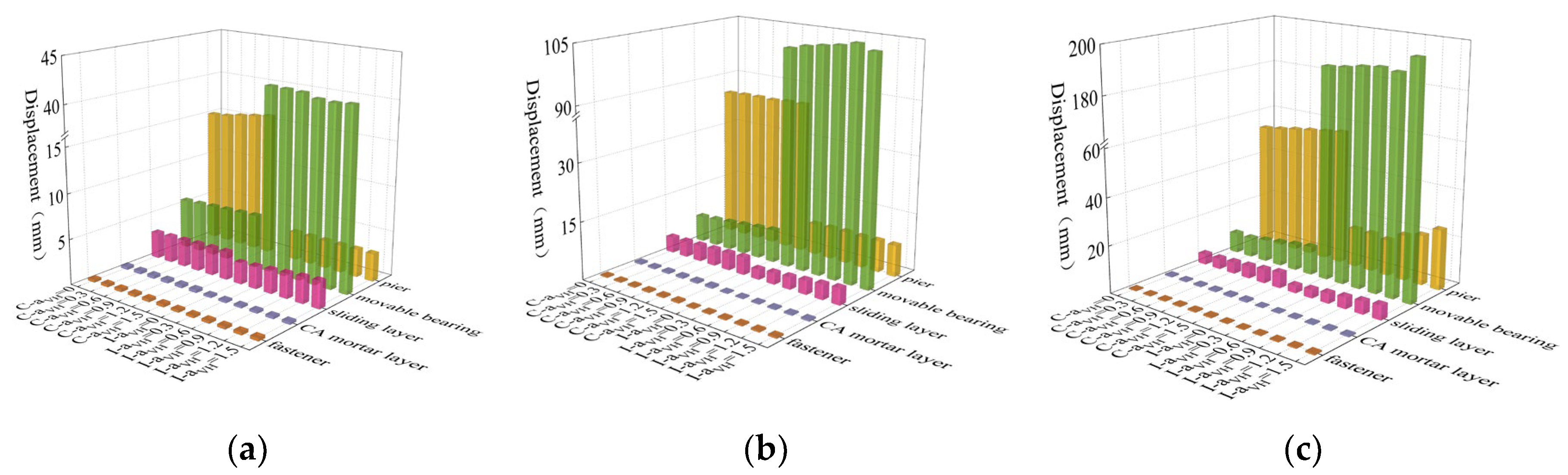
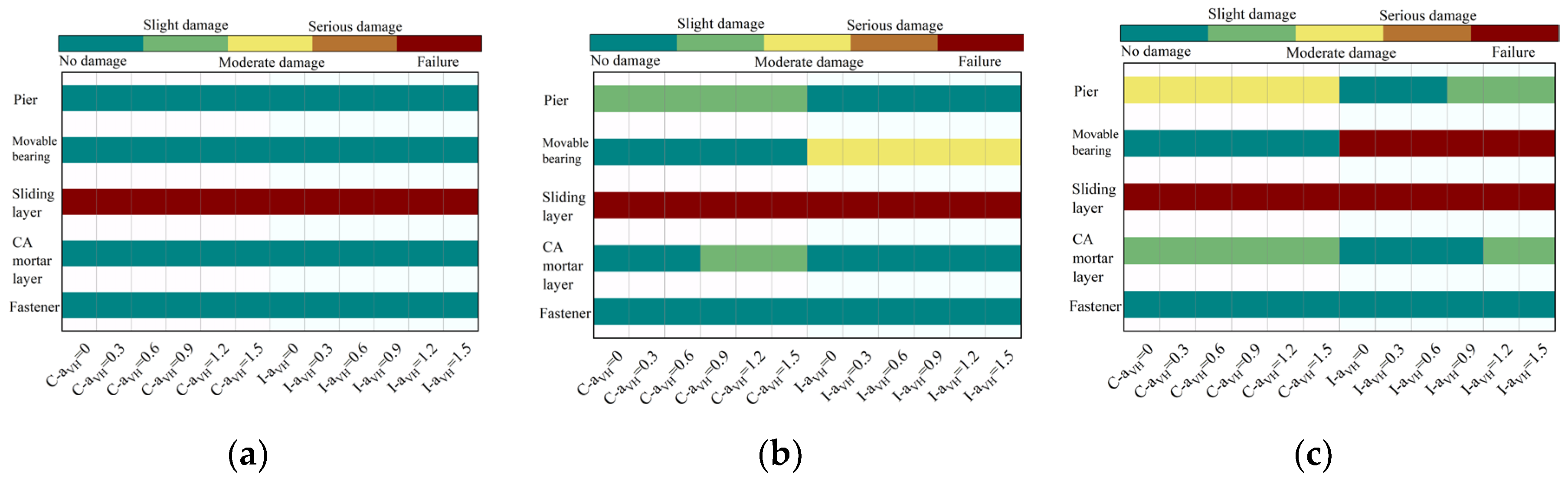
4.1. Displacement Response and Damage Degree Analysis
Based on the damage level criteria classified in
Table 3,
Figure 10 and
Figure 11 respectively illustrate the peak responses and damage degrees of piers, bearings, and track-structure interlayer components in the HSR track-bridge system under different seismic intensities. The analysis reveals the following:
Under the FE level, the displacement responses show that components under the common condition exhibit minor elastic deformations (e.g., movable bearing displacement ≤6mm), while displacements in the isolated condition are negligible. In terms of damage, the overall damage is minimal: components in the common model remain in the “No damage” state except for the sliding layer, which fails, and the αVH has no significant impact on the damage.
Under the DE level, displacement behaviors differ between the common condition and isolated condition: components under the common condition (e.g., CA mortar, piers) exceed elastic limits, whereas the isolated condition restricts displacements to the elastic range. Regarding damage, the common condition sees piers reaching “Slight damage” and when αVH=0.9 CA mortar entering “Slight damage”; in contrast, the isolated condition delays the initiation of CA mortar damage (remaining undamaged even at αVH=0.9) and reduces pier damage to “No damage”.
Under the RE level, displacement responses are more severe: displacement of components under the common condition surge, while the isolated condition can only delay but not prevent displacement exceedance. For damage, the common condition has piers in “Moderate damage” across all αVH conditions; the isolated condition, however, reduces pier damage to “Slight damage” (at αVH =0.9, 1.2, 1.5) or “No damage” (at αVH =0, 0.3, 0.6), though the sliding layer and isolation bearings fail. The effect of αVH becomes evident here: at αVH =0.9, piers reach “Slight damage,” and at αVH =1.2, CA mortar transitions from “No damage” to “Slight damage.”
The damage behavior of components is closely related to their inherent properties under varying seismic intensities. The isolation bearings serve as “buffers”, significantly reducing displacements and suppressing damage development in other components during FE and DE level. However, they sustain moderate damage under the DE level and fail completely under the RE level, while unable to prevent overall structural damage, they delay the failure of other components and reduce their damage severity. Displacement-restraining devices must be employed to prevent catastrophic seismic damage such as girder unseating. The sliding layer, being displacement-sensitive and functionally requiring large displacements, exhibits high damage risk and fails under all seismic intensities. Due to its weak load-bearing and deformation capacity, the CA mortar layer is prone to damage under complex seismic actions. In contrast, fasteners, protected by both bearings and the sliding layer, sustain the least damage, reflecting the differences in the “displacement-damage” relationship among components. Additionally, the vertical seismic effect acts as an “accelerator”: its influence is negligible under FE level, but under DE and RE level, increasing αVH leads to premature displacement exceedance and accelerated damage escalation, particularly in the sliding layer, CA mortar, and piers.
4.2. Recommended Values for αVH in Near-Fault Regions
Based on the longitudinal response and structural damage analysis under varying seismic intensities, along with the influence of the vertical-to-horizontal PGA ratio αVH in near-fault regions, the following αVH values are recommended to ensure structural safety and performance.
Under FE level, the variation of αVH has negligible effects on structural displacement and damage. It is recommended to adopt αVH =0.67 (as specified in the code), which meets safety requirements while ensuring redundant design.
As seismic intensity increases under DE level, a higher αVH exacerbates structural damage. If the value is lower than 0.9, the impact of vertical ground motion may be underestimated, leading to insufficient evaluation of CA mortar layer damage. Conversely, an excessively high value would overamplify the effect. A recommended αVH of 0.9 accurately reflects the damage state without underestimation.
Under high seismic intensity of RE, an increased αVH significantly amplifies damage, causing severe damage to components such as bridge piers. Adopting αVH =1.2 fully accounts for the influence of vertical ground motion, neither underestimating structural response due to an overly conservative value nor overestimating it, thereby effectively ensuring structural safety and performance.
In conclusion, the recommended αVH values comprehensively consider seismic intensity, structural damage characteristics, and economic feasibility. By adopting differentiated values, a balance is achieved between structural safety and cost control, providing a scientifically sound and rational parameter basis for seismic engineering design.
5. Conclusions
This study focuses on HSR track-bridge systems in near-fault regions. FEMs of both common and isolated systems were established to systematically investigate the influence of αVH (vertical-to-horizontal PGA ratio) on structural responses and damage under different seismic intensity levels. The main conclusions are as follows:
1. αVH distribution differs significantly from code-specified values: Statistics show that for reverse faults and strike-slip faults, αVH is mainly distributed in the interval of 0-1 (accounting for 75%-85%), while for normal faults, it is concentrated in the interval of 1-2 (approximately 60%). Moreover, the measured αVH values are densely distributed in the range of 0.5-1.5, which is significantly different from the unified value of 2/3 specified in the code.
2. αVH ‘s influence strengthens with seismic intensity: Under FE, the structural response is not sensitive to changes in αVH; under DE, an increase in αVH exacerbates the damage to the common condition, while the isolated condition can delay such damage; under RE, the amplification effect of αVH is significant—the common condition suffers severe damage, while the isolated condition can significantly reduce the damage level. This confirms that the VGM in near-fault regions cannot be ignored in seismic analysis.
3. Isolation offers differentiated protection: By utilizing large deformations of friction pendulum bearings for energy dissipation, isolation reduces displacements and damage in main structural components. However, it may lead to greater displacements in sliding layers of mid-span sections compared to non-isolated cases. Under rare earthquakes, isolation bearings themselves are prone to failure, necessitating optimized deformation control strategies.
4. Tiered αVH design recommendations: Based on the principle of balancing damage control and economy, it is suggested that αVH values under frequent, design, and rare earthquakes be 0.67, 0.9, and 1.2 respectively. Compared with the current code, this value system can more accurately reflect the characteristics of VGM in near-fault regions and provide a theoretical basis for the seismic design of HSR projects.
Author Contributions
Conceptualization, Haiyan Li and Jianfeng Mao; Data curation, Haiyan Li and Jinyu Ma; Formal analysis, Haiyan Li and Jianfeng Mao; Funding acquisition, Haiyan Li; Investigation, Jinyu Ma; Methodology, Haiyan Li; Project administration, Haiyan Li and Jianfeng Mao; Resources, Zhiwu Yu; Software, Haiyan Li and Jinyu Ma; Supervision, Zhiwu Yu and Jianfeng Mao; Visualization, Jinyu Ma; Writing – original draft, Haiyan Li; Writing – review & editing, Haiyan Li and Jinyu Ma.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 52308517) and the Open Foundation of National Engineering Research Center of High-Speed Railway Construction Technology (Grant No. HSR202107).
Data Availability Statement
The original contributions presented in the study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
In this section, you can acknowledge any support given which is not covered by the author contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments). Where GenAI has been used for purposes such as generating text, data, or graphics, or for study design, data collection, analysis, or interpretation of data, please add “During the preparation of this manuscript/study, the author(s) used [tool name, version information] for the purposes of [description of use]. The authors have reviewed and edited the output and take full responsibility for the content of this publication.”
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| HSR |
High-speed railway |
| VGM |
Vertical ground motion |
| FEM |
Finite element model |
| PGA |
Peak ground acceleration |
| FPB |
Friction pendulum bearing |
| FE |
Frequent earthquake |
| DE |
Design earthquake |
| RE |
Rare earthquake |
References
- He, X.; Wu, T.; Zou, Y.; Chen, Y.F.; Guo, H.; Yu, Z. Recent developments of high-speed railway bridges in China. Struct. Infrastruct. Eng. 2017, 13, 1584–1595. [Google Scholar] [CrossRef]
- Montenegro, P.A.; Carvalho, H.; Ribeiro, D.; Calçada, R.; Tokunaga, M.; Tanabe, M.; Zhai, W. Assessment of train running safety on bridges: A literature review. Eng. Struct. 2021, 241, 112425. [Google Scholar] [CrossRef]
- Billah, M.; Alam, M.S.; Bhuiyan, A. Fragility analysis of retrofitted multicolumn bridge bent subjected to near-fault and far-field ground motion. J. Bridge Eng. 2013, 18, 992–1004. [Google Scholar] [CrossRef]
- Taslimi, A.; Petrone, F.; Pitarka, A. Characteristics of Vertical Ground Motions and Their Effect on the Seismic Response of Bridges in the Near-Field: A State-of-the-Art Review. J. Bridge Eng. 2024, 29, 03124001. [Google Scholar] [CrossRef]
- Li, X.; Dou, H.; Zhu, X. Engineering characteristics of near-fault vertical ground motions and their effect on the seismic response of bridges. Earthq. Eng. Eng. Vib. 2007, 6, 345–350. [Google Scholar] [CrossRef]
- Malhotra, P.K. Response of buildings to near-field pulse-like ground motions. Earthq. Eng. Struct. Dyn. 1999, 28, 1309–1326. [Google Scholar] [CrossRef]
- MAKRIS, N. Rigidity–plasticity–viscosity: Can electrorheological dampers protect base-isolated structures from near-source ground motions? Earthq. Eng. Struct. Dyn. 1997, 26, 571–591. [Google Scholar] [CrossRef]
- Shaohui, L.; Lizhong, J.; Wangbao, Z.; Jian, Y.; Feng, Y.; Zhenbin, R. Influence of velocity pulse effect on earthquake-induced track irregularities of high-speed railway track–bridge system under near-fault ground motions. Arch. Civ. Mech. Eng. 2024, 24. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, N.; Jiang, L.; Zeng, Z.; Chen, G.; Guo, W. Near-fault directivity pulse-like ground motion effect on high-speed railway bridge. J. Cent. South Univ. 2014, 21, 2425–2436. [Google Scholar] [CrossRef]
- Adanur, S.; Altunişik, A.; Bayraktar, A.; Akkose, M. Comparison of near-fault and far-fault ground motion effects on geometrically nonlinear earthquake behavior of suspension bridges. Nat. Hazards 2012, 64. [Google Scholar] [CrossRef]
- Phan, V.; Saiidi, S.; Anderson, J.; Ghasemi, H. Near-Fault Ground Motion Effects on Reinforced Concrete Bridge Columns. J. Struct. Eng. 2007, 133. [Google Scholar] [CrossRef]
- Zhang, J.; Huo, Y. Evaluating effectiveness and optimum design of isolation devices for highway bridges using the fragility function method. Eng. Struct. 2009, 31, 1648–1660. [Google Scholar] [CrossRef]
- Liu, X.; Wang, W.; Li, J. Full-scale shaking table tests and numerical studies of structural frames with a hybrid isolation system. Eng. Struct. 2023, 292, 116545. [Google Scholar] [CrossRef]
- Xie, Y.; Zhang, J. Design and Optimization of Seismic Isolation and Damping Devices for Highway Bridges Based on Probabilistic Repair Cost Ratio. J. Struct. Eng. 2018, 144. [Google Scholar] [CrossRef]
- Papazoglou, A.; Elnashai, A. Analytical and field evidence of the damaging effect of vertical earthquake ground motion. Earthq. Eng. Struct. Dyn. 1996, 25, 1109–1137. [Google Scholar] [CrossRef]
- Tao, Y.; Yuan, X.; Zhong, J. Near-fault pulse seismic ductility spectra for bridge columns based on machine learning. Soil Dyn. Earthq. Eng. 2023, 164, 107582. [Google Scholar] [CrossRef]
- Jiang, L.; Zhong, J.; Yuan, W. The pulse effect on the isolation device optimization of simply supported bridges in near-fault regions. Structures 2020, 27, 853–867. [Google Scholar] [CrossRef]
- Jiang, L.; Duan, H.; Wen, T.; Jiang, L. Effects of Near-Fault Pulse-Like Ground Motions and Pulse Parameters on a High-Speed Railway Long-Span Arch Bridge–Track System. J. Bridge Eng. 2025, 30, 04024112. [Google Scholar] [CrossRef]
- Ismail, M.; Rodellar, J.; Pozo, F. An isolation device for near-fault ground motions. Struct. Control Health Monit. 2014, 21. [Google Scholar] [CrossRef]
- Dicleli, M.; Buddaram, S. Equivalent linear analysis of seismic-isolated bridges subjected to near-fault ground motions with forward rupture directivity effect. Eng. Struct. 2007, 29, 21–32. [Google Scholar] [CrossRef]
- Guo, W.; Yang, S.; Jiang, L.; Yu, Z.; Zeng, C.; Wang, Y.; Huang, R.; Wu, S.; Ren, S. Effect of near-fault vertical seismic excitation on running safety of trains on high-speed railway bridges. Eng. Struct. 2023, 296, 116880. [Google Scholar] [CrossRef]
- Ryan, K.; Mojidra, R. Analysis of effect of vertical ground shaking in bridges isolated with spherical sliding bearings. Earthq. Eng. Struct. Dyn. 2023, 52, 5010–5032. [Google Scholar] [CrossRef]
- Shao, Y.; Wei, Y.; Yang, T.; Ni, M.; Zhong, J. Empirical models of bridge seismic fragility surface considering the vertical effect of near-fault ground motions. Structures 2021, 34, 2962–2973. [Google Scholar] [CrossRef]
- Wei, B.; Zuo, C.; He, X.; Jiang, L.; Wang, T. Effects of vertical ground motions on seismic vulnerabilities of a continuous track-bridge system of high-speed railway. Soil Dyn. Earthq. Eng. 2018, 115, 281–290. [Google Scholar] [CrossRef]
- Zhou, F.; Tan, P.; Chen, Y.; Liu, Y. Recent Development and Application on Seismic Isolation, Energy Dissipation and Vibration Control in China. In Seismic Isolation, Energy Dissipation and Active Vibration Control of Structures; WCSI 2022. Lecture Notes in Civil Engineering; Springer: Cham, Switzerland, 2023; Volume 309. [Google Scholar] [CrossRef]
- Chen, L.; Jiang, L.; Qin, H.; Zhang, N.; Ling, L.; Zhang, Q.; Li, Q.; Cao, D. Nonlinear seismic assessment of isolated high-speed railway bridge subjected to near-fault earthquake scenarios. Struct. Infrastruct. Eng. 2019, 15, 1–19. [Google Scholar] [CrossRef]
- Liu, H.; Jiang, J.; Mao, N.; Mao, Y.; Mao, J. Design and Seismic Performance Study of Multistage Controllable Isolation Bearing for High-Speed Railway Simply Supported Beam. Buildings 2024, 14, 3539. [Google Scholar] [CrossRef]
- Li, H.; Yu, Z.; Mao, J.; Spencer, B.F. Effect of seismic isolation on random seismic response of High-Speed railway bridge based on probability density evolution method. Structures 2021, 29, 1032–1046. [Google Scholar] [CrossRef]
- Li, H.; Yu, Z.; Mao, J.; Jiang, L. Nonlinear random seismic analysis of 3D high-speed railway track-bridge system based on OpenSEES. Structures 2020, 24, 87–98. [Google Scholar] [CrossRef]
- Wei, B.; Yang, Z.; Fu, Y.; Xiao, B.; Jiang, L. Seismic displacement response analysis of Friction Pendulum Bearing under friction coupling and collision effects. Eng. Struct. 2024, 310, 118128. [Google Scholar] [CrossRef]
- Wang, D.; Guo, X.; Sun, Z.; Meng, Q.; Yu, D.; Li, X. Damage to highway bridges during wenchuan earthquake. J. Earthq. Eng. Eng. Vib. 2009, 29, 84–94. (In Chinese) [Google Scholar]
- Loghman, V.; Khoshnoudian, F.; Banazadeh, M. Effect of vertical component of earthquake on seismic responses of triple concave friction pendulum base-isolated structures. J. Vib. Control 2015, 21, 2099–2113. [Google Scholar] [CrossRef]
- Zhong, J.; Zhu, Y.; Han, Q. Impact of vertical ground motion on the statistical analysis of seismic demand for frictional isolated bridge in near-fault regions. Eng. Struct. 2023, 278, 115512. [Google Scholar] [CrossRef]
- Xiao, B.; Wei, B.; Zhao, H.; Zheng, X.; Zhang, R.; Chen, J.; Jiang, L. Effect of seismic isolation parameters on component damage and running safety performance of high-speed railway bridge-track system under near-fault earthquakes. Eng. Struct. 2025, 328, 119712. [Google Scholar] [CrossRef]
- Wei, B.; Wang, W.; Wang, P.; Yang, T.; Jiang, L.; Wang, T. Seismic Responses of a High-speed Railway (HSR) Bridge and Track Simulation under Longitudinal Earthquakes. J. Earthq. Eng. 2020, 26, 1–22. [Google Scholar] [CrossRef]
- Hu, Z.; Wei, B.; Jiang, L.; Li, S. Research on damage quantification of high-speed railway bridge piers. Chin. Civ. Eng. J. 2023, 56. (In Chinese) [Google Scholar]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).