Analogy of Space-Time as an Elastic Medium–State of the Art and Perspectives on the Knowledge of Time

1. Introduction

Time was studied a lot before the advent of physics by Galileo by Greek and later philosophers. Thus, since Antiquity, time has been at the heart of philosophical reflections. Plato (427–347 BCE) wrote in the Timaeus (37d) that time is "the moving image of eternity", created by the demiurge to order the sensible world. Aristotle (384–322 BC) stated in Physics (IV, 11, 219b) that "time is the number of motion according to the anterior and the posterior", insisting on its inseparable link with change. St. Augustine (354–430), in the Confessions (Book XI, chapters 26–28), described time as a distentio animi—a "distension of the soul"—made up of memory (past), attention (present), and expectation (future). René Descartes (1596–1650) argued in the Principles of Philosophy (II, § 23) that time is "the number of motions, or rather a certain way in which we conceive the duration of things", a divine creation, uniform and continuous, but not graspable by the senses. Baruch Spinoza (1632–1677), in his Ethics (part II, scolia of proposition 44), wrote that "time is only a modality of thought" and that it does not possess an objective reality, but is the result of an inadequate conception of duration. Immanuel Kant (1724–1804) argued in the Critique of Pure Reason (Transcendental Aesthetics, § 4) that "time is not an empirical concept," but "a pure form of sensible intuition"—a subjective structure necessary for the experience of phenomena. Henri Bergson (1859–1941), in Essay on the Immediate Data of Consciousness (1889), distinguished the measurable time of physicists from the "lived time" of consciousness, which he called "duration." Finally, Martin Heidegger (1889–1976), in Being and Time (1927), asserted that "time is the horizon of any understanding of being," an existential dimension of Dasein and not a simple physical framework.

With the scientific revolution and the writing of nature in mathematical language that began with Galileo Galilei, Isaac Newton (1643–1727) introduced into his “philosophiae naturalis Principia Mathematica” (1687) [1] the idea of an "absolute, true, and mathematical time, flowing uniformly" (tempus absolutum), independent of space and events. Albert Einstein (1879–1955) showed in 1905, and again in 1915 and 1916, in his theory of special [2] and general [3] [4] relativity, that time is relative, inseparable from the geometry of space-time, and influenced by gravitation. Quantum mechanics, on the other hand, retained an external and uniform time to describe probabilistic phenomena, without managing to unify it with general relativity. Since then, more than 120 years of measurements have shown that he was 100/100 right.

Time is no longer an independent and absolute entity. Since the work of Einstein, it must be considered as inseparable from space, together forming a four-dimensional structure: space-time. With special relativity, durations lengthen as we get closer to the speed of light: time becomes relative to motion. General relativity shows that time is sensitive to gravitation: it slows down near large masses.

But beyond these physical effects, a fundamental question remains: what is time? What is its driving force? What is it that makes each present moment tirelessly become past, replaced without interruption by a new present moment, since the dawn of time? Why is there an arrow of time, this irreversible orientation that prohibits us from rewriting the past, frozen forever?

What if time was not a primitive given, but an emergence linked to deeper phenomena — gravitation, entropy, temperature, the structure of space-time itself? Thus, each one, in his or her own way, has tried to unravel the mystery of time, but no one — neither philosopher nor physicist to our knowledge— has considered, as this work proposes, that time can be the manifestation of a mechanical deformation of a quantified elastic medium.

So, this paper does not claim to answer all these questions, far from it. He simply envisages approaching time from a different, more mechanistic angle since we will see that general relativity in weak fields can be modeled as an elastic medium that behaves like true space-time, an idea suggested by A Sakharov in his 1968 paper [5], taken up by two many authors behind [6] and [26] and in particular well formalized in his concept of "deformable elastic jelly" by T Damour in his book “Si Einstein m’était conté” [23] and in at least one of his lectures [24]. It is therefore this original approach to time associated with an equivalent elastic medium that we will study in this paper. Everything that is going to be announced may seem revolutionary but has already been justified by scattered publications that this paper brings together in a single paradigm for the first time. That’s its innovative and interesting side.

2. Methodology

We analyze the following aspects:

• We start by doing the state of the art overtime with:

  -

  Time according to I. Newton,

  -

  Relativistic time mixed with space-time according to the special relativity of A. Einstein,

  -

  The time bent by gravitation according to the general relativity of A. Einstein.

2

Then we look at contemporary developments on time, all published in reputable peer-reviewed journals:

-

Elastic time in the context of the analogy of space-time with an elastic medium,

-

Temperature-sensitive space-time according to Hawking radiation to temperature-sensitive elastic time,

-

Creep-sensitive elastic space-time and consequences on time,

-

Plasticity of the elastic medium and infinite stretching of time,

-

Time as an illusion with quantum gravity,

-

Foliation of space-time and time lapse in the case of gravitational waves - Modified theory of general relativity with addition of Einstein Cartan geometric torsion,

3

In the context of a Discussion about elastic medium analogy, we highlight the different consequences implied by the different research studied in 2:

-

Consequence of a variation of time and space as a function of temperature in connection with dark energy,

-

Consequence of a variation of time and space by creep of space-time in connection with dark matter,

-

Consequence of the foliation of space-time on the nature of time in the case of an equivalent elastic medium in connection with the possible emerging mechanistic nature of time.

3. State of the Art

3.1. Time According to I. Newton

In 1687, when Isaac Newton published the “Philosophiæ naturalis principia mathematica” [1], he considered that space and time are absolute, separate, a bit like a rigid stage that lives its life independently of the actors who are on it who express events, a story according to the time that passes separately. Gravitation is then an attraction force that pulls massive objects of mass M and m together in inverse proportion to the square of the distance between them r². He calibrates his equation via a proportionality constant G = 6.674x10^-11 m³/(kg.s²).

$$‖\overrightarrow{F}‖={\displaystyle \frac{GMm}{r^2}}$$

(1)

However, this approach fails to justify the delay in the perihelion of mercury of 43 seconds of arc. It is on this point that A. Einstein [3] [4] will triumph by finding it exactly with these equations of general relativity.

3.2. Relativistic Time Mixed with Space-Time According to A. Einstein

In 1905, Albert Einstein [2] overturned Newton’s view of absolute space and time by introducing special relativity. This new theory is based mathematically on Lorentz transformations (2), and conceptually on the principle of constancy of the speed of light: it remains the same for all observers, regardless of their relative motion with respect to the source.

This result stems in particular from the experiment of Michelson and Morley [27], which failed to detect a motion of the Earth in relation to a hypothetical luminiferous ether. This negative experiment suggested that light does not require a material medium to propagate, and that its speed is a universal constant.

However, according to the relationship$c=d/t$, if space contracts at high speed (contraction of lengths), then time must expand (time dilation) for the speed of light to remain constant. Thus, the faster an object moves, the slower the proper time measured in its frame of reference flows relative to an observer at rest.

The speed of light in a vacuum, c=299,792,458 m/s, constitutes an insurmountable limit for any form of matter or information. There is no longer a universal absolute time: each observer has his own time, depending on his movement. It should be noted that no one knows to date why and how this speed of light was calibrated precisely to this value. That is why it is today a fundamental physic constant.

The time dilation is described by the following formula with v the velocity:

$$t^{\prime }={\displaystyle \frac{t}{\sqrt{1-\frac{v^2}{c^2}}}}$$

(2)

If we compare the time measured by an observer who has remained on Earth with that of an observer moving at the speed v, we see that time slows down for the latter as v approaches the speed of light. This phenomenon, called time dilation, is a direct consequence of special relativity.

This phenomenon is illustrated by the famous paradox of the Langevin twins: if one of the twins embarks on a high-speed space journey, close to that of light, while the other remains on Earth, then on its return, the traveling twin will have aged less than its brother who remained on the ground. Its proper time has elapsed more slowly due to its high velocity, in accordance with the time dilation predicted by special relativity. This paradox, although counterintuitive and therefore slowing down of clocks in motion compared to those remaining on the ground, was measured experimentally in the famous experiments of Hafele and Keating (1972), [28] to [30] who embarked atomic clocks on board aircraft making terrestrial circumnavigations.

3.3. The Time Bent by Gravitation According to the General Relativity of A. Einstein

In 1915 [3] and again in 1916 [4], Albert Einstein published the theory of general relativity. This is based in particular on the principle of equivalence, according to which it is impossible to distinguish locally a physical experiment carried out in an elevator subject to the Earth’s gravity from an identical experiment conducted in an elevator located in a vacuum, far from any mass or energy that could generate gravitation but accelerated upwards.

Einstein shows that in an accelerated elevator, a ray of light passing horizontally through the elevator appears to deflect downwards, hitting the opposite wall at a lower position. By reciprocity, as stated according to his principle of equivalence, he concludes that gravity must also bend the path of light, even though it is devoid of mass. This revolutionary result contradicts Newtonian mechanics, which did not foresee such a curvature. Gravitation is therefore no longer considered a force in the classical sense, but a manifestation of the geometric curvature of space-time induced by the presence of mass and energy.

Einstein calculated his field equations (3) so that in the weak field regime (4), they found the Poisson equation (5), which in turn led to Newton’s law of gravitation (1) that works verry well in this low gravitation regime. Remarkably, this correspondence is obtained from the temporal component of Einstein’s equations (μ=0,ν=0), whereas Newton had based his mechanics on an exclusively spatial conception. This is a major conceptual reversal in the history of physics. Thus, the equation of general relativity without a cosmological constant Λ (we will come back to this when we talk about the effects of temperature on space and time) is written with $R_{\mu v}$the Ricci tensor, R the scalar curvature, $g_{\mu v}$ the metric and $T_{\mu v}$ the energy momentum tensor:

$$R_{\mathrm{\mu }\mathrm{v}}-{\displaystyle \frac{1}{2}}{g}_{\mathrm{\mu }\mathrm{v}}R={\displaystyle \frac{8\pi G}{c^4}}{T}_{\mathrm{\mu }\mathrm{v}}\mathrm{ }$$

(3)

In a weak field, this equation becomes, for the time component 00 with the Laplacian operator, $∆$ϕ the gravitational potential and ρ a mass density:

$$∆{\mathit{h}}_{\mathbf{00}}={\displaystyle \frac{\mathbf{2}}{{\mathit{c}}^{\mathbf{2}}}}∆\mathrm{\varphi }={\displaystyle \frac{\mathbf{8}\pi \mathit{G}}{{\mathit{c}}^{\mathbf{4}}}}{\mathsf{\rho }\mathit{c}}^{\mathbf{2}}$$

(4)

This gives the Poisson equation again:

$$∆\mathrm{\varphi }=\mathbf{4}\pi \mathit{G}\mathsf{\rho }$$

(5)

In a weak field, Einstein’s equation of the linearized gravitational field is written [31] :

$${{\mathsf{\partial }}^{\mathrm{\lambda }}{\mathsf{\partial }}_{\mathrm{\lambda }}{\overline{\mathit{h}}}_{\mathit{\mu }\mathit{\nu }}=◻\overline{\mathit{h}}}_{\mathit{\mu }\mathit{\nu }}=-{\displaystyle \frac{\mathbf{16}\pi \mathit{G}}{{\mathit{c}}^{\mathbf{4}}}}{\mathrm{ }\mathit{T}}_{\mathit{\mu }\mathit{\nu }}$$

(6)

h is the trace of ${\mathit{h}}_{\mathrm{\mu }\mathrm{v}}$, :$◻$ the D’Alembert operator and ${\mathit{T}}_{\mathrm{\mu }\mathrm{v}}\mathbf{ }$the stress energy tensor. The gauge state taken is  ${\mathsf{\partial }}^{\mathrm{\lambda }}{\overline{\mathit{h}}}_{\mathit{\mu }\mathrm{\lambda }}=0\mathbf{ }$with ${\overline{\mathit{h}}}_{\mathit{\mu }\mathit{\nu }}={\mathit{h}}_{\mathit{\mu }\mathit{\nu }}+{\displaystyle \frac{1}{2}}{\mathit{\eta }}_{\mathit{\mu }\mathit{\nu }}\overline{\mathit{h}}$.

Then he showed in 1916 [31] that in a vacuum, gravitational waves exist based on this equation:

$${{\mathsf{\partial }}^{\mathrm{\lambda }}{\mathsf{\partial }}_{\mathrm{\lambda }}{\overline{\mathit{h}}}_{\mathit{\mu }\mathit{\nu }}=◻\overline{\mathit{h}}}_{\mathit{\mu }\mathit{\nu }}=\mathbf{0}\mathrm{ }$$

(7)

Thus, the equation of general relativity of A. Einstein [31] uses ${\eta }_{\mu \nu }$ a flat metric called Minkowski to which is added a small geometric perturbation $h_{\mu v}$ related to gravitation. The indices μ and ν are 0 for time and 1 to 3 for space coordinates.

$$g_{\mathrm{\mu }\mathrm{v}}={\mathrm{\eta }}_{\mathrm{\mu }\mathrm{v}}+h_{\mathrm{\mu }\mathrm{v}}$$

(8)

It is recalled that in general relativity, each term constituting this metric $g_{\mu v}$constitutes the coefficients of the terms of an infinitesimal distance interval squared ${ds}^2$. The indices 00, 01, 02, 03 and their symmetric represent the components of the tensors related to time. Component 00 represents the 100/100 temporal aspect of this space-time metric. Thus, $g_{00}$is the term associated $c^2{dt}^2$with it therefore reflects the distortion of space-time related to time..

The proper time τ measured by a clock is then written:

$$d=\sqrt{g_{00}}dt$$

(9)

Gravity bends time. This is Einstein’s second great discovery. Since then, we have taken measures that confirm this. Indeed, a remarkable test of general relativity, demonstrating that gravitation curves time, is the Shapiro effect. Proposed by Irwin Shapiro in 1964 [32]. This effect consists of measuring the time delay experienced by a radio signal when it passes close to a massive body, such as the Sun. According to general relativity, the presence of mass bends spacetime, and this curvature slows down the propagation of the signal, even if it travels at the speed of light. This measurable delay — called Shapiro delay — is direct evidence that time is affected by gravitation. This phenomenon has been confirmed experimentally thanks to radar measurements sent to planets such as Venus or Mercury and is one of the four classic tests of general relativity. Thus, time is no longer a primitive and absolute quantity, but a dynamic physical variable that depends on motion and gravitation. This relativistic view, confirmed by more than a century of experiments, will serve as a foundation for the rest of this paper, where we propose to go further: to interpret time as a mechanical deformation within a quantized elastic medium — a paradigm shift that opens new perspectives on the nature of the vacuum and the structure of space-time

4. Contemporary Developments Over Time

4.1. Elastic Time in the Context of the Space-Time Analogy with an Elastic Medium

4.1.1. Elastic Analogy and Theory

In weak gravitational fields, A. Sakharov in [5] showed that space-time can be modeled as a quantized elastic medium, with a quantum microscopic structure. Thibault Damour in [22] to [24] shows that we can model elastic space-time, this new kind of deformable Ether (which we will call “elasther”) different from the old one [24], as a kind of "deformable elastic jelly [22] to [24]". Thus, the vacuum is no longer empty, it is inhabited by space-time and by the quantum fluctuations of the vacuum in field theory, as shown in particular by Casimir with the experiment of the two plates that come together under the effect of the fluctuations of the quantum vacuum, whose ground state is not zero [33] [34] or in 2012 with the HIGGS field and its famous boson which makes it possible to give mass to particles [35] [36]. This space-time, this "deformable elastic jelly [22] to [24]", this new ether or “elasther”, this cosmic web or cosmological crystal [38] to [43] according to the name given to it by the various authors follows Hooke’s law D(g) = K T [23] or D(g) represents the tensor of the Deformations as a function of the metric g, K the flexibility in the mechanical sense (force F, displacement δ) of space-time (F=kδ or δ=1/k F = K δ) and T the tensor of tensions within this space-time. This analogy was then mathematically developed by many authors [6] to [24] including T Tenev and M.F Horstemeyer who, in [12] and [13] have concretely shown that this perturbation of the metric $h_{\mu v}$ is equivalent to twice one elastic strain tensor ε_μv as described in continuum mechanics. We will come back on it later.

$$h_{\mathrm{\mu }\mathrm{v}}=2{\mathrm{\epsilon }}_{\mathrm{\mu }\mathrm{v}}$$

(10)

Applied to the 00 component, this means that the time associated with the speed of light (c x dt) becomes a full-fledged elastic displacement that must be added to the classical displacements of space studied in continuum mechanics for each of the spatial coordinates $dx,dy,dz$. The effect of time curvature by gravitation is thus by mirror effect, mechanized by a deformation ${\epsilon }_{00}$acting in the 4th dimension of a particular geometry linked to space-time.

Moreover, in the context of the analogy of the elastic medium, it is shown in the publications [12] [18] to [20]that the energy-momentum tensor $T_{\mu v}$ is equivalent to a 4-dimensional stress tensor ${\sigma }_{\mu v}$. Indeed, the expression of the stress tensor at low speed as a function of the energy density ρ and based on the multiplication of velocities $v_i$and $v_j$:

$${\sigma }_{ij}=\rho v_i{v}_j$$

(11)

The momentum energy tensor results from the product of the energy density and the multiplication of the four velocities (four dimensions of space-time) resulting from general relativity:

$$T_{\mu \nu }=\rho u_{\mu }{u}_{\nu }$$

(12)

Moreover, the constant $𝒦={\displaystyle \frac{8\mathit{\pi }G}{c^4}}$is strictly equivalent if we reduce it to m², to the elastic flexibility of space-time in Pa^-1, i.e. inversely to its Young modulus E=Y in Pa [18] to [20]. So, the state of the art is sufficiently consistent and verified to affirm that general relativity in a weak gravitational field is, by mirror effect or analogy, the equivalent of a Hooke’s law such as the one used in the strength of materials and well known in structural engineering. This Hooke’s law takes two forms depending on whether we are talking about elongations or shortening ε under normal stresses σ :

$$\mathrm{\epsilon }={\displaystyle \frac{1}{E}}\mathrm{\sigma }$$

(13)

Or that we talk about angular distortions γ under tangential stresses τ.

$$\gamma ={\displaystyle \frac{1}{G}}\mathrm{\tau }={\displaystyle \frac{2(1+\mathrm{\nu })}{E}}\mathrm{\tau }$$

(14)

Both depend on Young’s modulus E and the Poisson ratio ν characterizing the equivalent elastic medium.

The parallelism between each of the components of the perturbation tensor of the weak field metric $h_{\mu v}$and the deformation tensor of elastic space-time in 4 dimensions ${\epsilon }_{\mu v}$is detailed component by component in the publication [21]. Each of the components is identified with confirmed experiments of general relativity (Lense Thirring effect [46] [47], gravitational waves [62] [63], gravitational lensing effect [74]). But we also see in this publication that certain physical phenomena or complementary polarizations associated in particular with the $zz$components; i$z$,j$z$ remains to be discovered...

The parallelism between the equations of non-linearized general relativity (15), then linearized (16), then the elastic analogy with the equivalent generalized Hooke’s law (17) is given here in a tensor mathematical way to be valid regardless of the frame of reference considered below with E the young modulus, v the Poisson’s ratio of the equivalent material, $U_{ij}$the elastic strain energy,${\epsilon }_{ij}$the stain tensor and ${\delta }_{ij}$the Kronecker symbol:

$$\mathrm{ }\mathrm{ }\mathrm{ }{G}^{\mathrm{\mu }\nu }=R^{\mu \nu }-{\displaystyle \frac{1}{2}}{g}^{\mu \nu }\mathrm{R}=-{\displaystyle \frac{8\mathrm{\pi }G}{c^4}}{\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }T}^{\mathrm{\mu }\nu }$$

(15)

$$\mathrm{ }\mathrm{ }{{\partial }^{\lambda }{\partial }_{\lambda }{\overline{h}}_{\mu \nu }=◻\overline{h}}_{\mu \nu }=-{\displaystyle \frac{16\mathrm{\pi }G}{c^4}}{\mathrm{ }\mathrm{ }\mathrm{ }T}_{\mu \nu }$$

(16)

$${\left[\left({\epsilon }_{ij}+{\displaystyle \frac{\nu }{1-2\nu }}{\epsilon }_{kk}{\delta }_{ij}\right)\right]{\epsilon }^{ij}={\displaystyle \frac{2\left(1+\nu \right)}{E}}\mathrm{ }\mathrm{ }U}_{ij}={\displaystyle \frac{\left(1+\nu \right)}{E}}{\sigma }_{ij}{\epsilon }^{ij}\mathrm{ }\mathrm{ }\mathrm{ }$$

(17)

We see clearly that $\mathsf{𝒦}\to {\displaystyle \frac{\left(1+\mathrm{\nu }\right)}{E}}$, ${\epsilon }_{ij}\to {\overline{h}}_{\mu \nu }$ and ${\sigma }_{ij}\to {\mathrm{ }\mathrm{ }\mathrm{ }T}_{\mu \nu }$. Equivalent at Hooke’s law.

Noted that in the vacuum $T_{\mu v}=0$. We must then add a tensor $t_{\mu v,el}$related to the energy of the vacuum deformation to keep the complete analogy with Hooke’s law. This is explained in [20] and [21].

The various measurements of strains and angular distortions of space-time (gravitational lensing effect, Lense-Thirring effect) or space (gravitational waves) or time (Chapiro effect) have allowed us to be certain that Einstein is right. Space-time is a physical deformable elastic object. Space must be associated with time to constitute space-time. This space-time is not infinitely rigid and absolute, but deformable (very little in fact), this is what the constant κ=2.0766x10^-43N^-1 translates.

Another way to see how space is rigid is it order of magnitude of the Young modulus (10²⁰ x $Y_{steel}={2.1\times 10}^{31}Pa$ [15][75]) or the order of magnitude of the strain created by gravitational wave 10^-21! Space-time is elastic and malleable, a kind of "deformable elastic jelly" as Thibault Damour calls it in his lectures [24] or in his book [23]. The elastic aspect: i.e. its ability to return to its initial shape after loading without residual deformation was validated by measurements of the deviation of the positioning of stars during a solar eclipse in 1919 by Eddington [44]. The light manifesting the position of the stars shifted under the distortion of space-time in the presence of the sun, then the stars returned to their initial position when the sun left. Space-time did have an elastic response. No residual deformation once the "load" is removed. In structural engineering, this corresponds to the serviceability limit state. As opposed to the effect of a black hole, which corresponds to the achievement of the ultimate cost of ruin of space-time, i.e. in the engineering of structures in the ultimate limit state. Space-time is therefore not an immobile ether at rest; it behaves like a kind of "deformable elastic jelly" [22] to [24]. We will therefore call the elastic medium that behaves as if by analogy like space-time "Elasther" represented in Figure 1 so as not to confuse them.

In the context of this analogy, we can therefore take the expression of proper time and transpose it into an elastic deformation of a new elastic ether, different from the first called the Luminiferous Ether, which is perfectly immobile because it is supposed to vibrate and carry light, but Maxwell has shown that light is an electromagnetic wave that advances by itself by self-reaction between an electric field and a magnetic field.

We then obtain the expression of proper time in terms of equivalent elastic deformation associated with the fourth dimension of space-time within the framework of the analogy of the equivalent elastic medium as demonstrated by T Tenev and M.F. Horstemeyer in [12] and [13]:

$$d\mathrm{\tau }=\sqrt{g_{00}}dt=\sqrt{1+2{\mathrm{\epsilon }}_{00}}dt\approx \left(1+{\mathrm{\epsilon }}_{00}\right)dt$$

(18)

This leads to a missed period of time of their own with${\epsilon }^{3D}={\epsilon }_i^i$:

$${\displaystyle \frac{d\mathrm{\tau }}{dt}}={\displaystyle \frac{1}{1+{\mathrm{\epsilon }}^{3D}}}$$

(19)

In the context of this analogy, everything happens as if we had in the “elasther” a super-elastic material with 4 dimensions, one of the variations in geometric dimensions the ${(g}_{00}{c}^2{dt}^2)$ depends directly on the variations of time. Time is thus found in the "mechanized" analogy. We will see later the fundamental consequences of this point for dark energy and dark matter if we push the analogy of the elastic medium of this "deformable elastic jelly" $)$[22] to [24] to the end.

Thus, many theorists try either to develop a 4-dimensional mechanics of continuous media from the mechanics of 3-dimensional continuous media, or to start from general relativity and transform it into a mechanics of continuous media in 4 dimensions. We are in this second approach in this paper.

Another way to see these 4 dimensions, and to note the non-static nature of space-time on the one hand and to take into account the limit speed c of transport of deformations within it on the other hand. Thus, when an observer makes a measurement of deformation (elongation or shortening, angular variation) at a point in space-time, there are certainly the deformations that he measures in his own time instantaneously where he is, but there are also, in a way, complementary deformations in the process of arriving, given that nothing can go faster than the speed of light. It takes time for deformation to travel from one place in space-time to another. It’s not instantaneous. If the sun disappeared, it would take 8.20 minutes for us to realize on earth the change in deformation associated with this disappearance where the earth is positioned in relation to the sun. The final measurement will therefore take into account the instantaneous deformations and the delayed deformations of the “elasther”. This is why in all measurements of deformations of space-time in general, the final deformations are greater than those alone predicted by Newton (e.g. the angle of shift of light rays by the sun predicted and measured in general relativity is twice as large as that predicted by Newtonian calculation alone). So, the deformation measurements must be made in 4 dimensions, i.e. take into account those related to space but also those due to time. In the “elasther” model, time implies deformations complementary to that of space and therefore space-time must be considered in any elastic model.

4.1.2. Experimental Validation

At this point, the reader is entitled to ask what are the experimental validations of this elastic model that behaves like space-time?

There are 3 of them:

- as we have seen, each of the components of the perturbation tensor of the metric $h_{\mu v}$corresponds in their nature to the position and type to that of the associated deformation tensor of the “elasther” ${\epsilon }_{\mu v}$. When it is elongation, shortening (e.g. the Gravitational waves measured on February 11, 2016 GW150914 [46] or GW170817 [47]), it is indeed elongation and shortening, so the space ${\epsilon }_{ij}$components in the strain tensor ε_μv of a magnitude of 10^-21..Similarly, when angular distortions are involved (e.g. the Lense-Thirring effect [62] measured via gravity prob B in 2011 [63]), the same angular distortions are measured in the strain tensor (see 20,21). The time component $h_{00}$is associated with isotropic compression in all directions, Newtonian gravitation. Brief, all this prove that $h_{\mu v}=2{\epsilon }_{\mu v}$is effectively true physically and mathematically and is explained and demonstrated in detail in the publication [21].

$$\left[\begin{array}{cccc}{\mathit{h}}_{00}& {\mathit{h}}_{01}& {\mathit{h}}_{02}& {\mathit{h}}_{03}\\ {\mathit{h}}_{10}& {\mathit{h}}_{11}& {\mathit{h}}_{12}& {\mathit{h}}_{13}\\ {\mathit{h}}_{20}& {\mathit{h}}_{21}& {\mathit{h}}_{22}& {\mathit{h}}_{23}\\ {\mathit{h}}_{30}& {\mathit{h}}_{31}& {\mathit{h}}_{32}& {\mathit{h}}_{33}\end{array}\right]\to \left[\begin{array}{cccc}\mathit{G}\mathit{r}\mathit{a}\mathit{v}\mathit{i}\mathit{t}\mathit{a}\mathit{t}\mathit{i}\mathit{o}\mathit{n}\mathrm{ }\mathit{o}\mathit{r}\mathrm{ }\mathit{G}\mathrm{ }\mathit{L}\mathit{e}\mathit{n}\mathit{s}\mathit{e}& \mathit{L}\mathit{e}\mathit{n}\mathit{s}\mathit{e}-\mathit{T}\mathit{h}\mathit{i}\mathit{r}\mathit{r}\mathit{i}\mathit{n}\mathit{g}& \mathit{L}\mathit{e}\mathit{n}\mathit{s}\mathit{e}-\mathit{T}\mathit{h}\mathit{i}\mathit{r}\mathit{r}\mathit{i}\mathit{n}\mathit{g}& \mathit{L}\mathit{e}\mathit{n}\mathit{s}\mathit{e}-\mathit{T}\mathit{h}\mathit{i}\mathit{r}\mathit{r}\mathit{i}\mathit{n}\mathit{g}\\ \mathit{L}\mathit{e}\mathit{n}\mathit{s}\mathit{e}-\mathit{T}\mathit{h}\mathit{i}\mathit{r}\mathit{r}\mathit{i}\mathit{n}\mathit{g}& \mathit{G}\mathit{W}\mathrm{ }\mathit{L}\mathit{I}\mathit{G}\mathit{O}\mathrm{ }\mathit{o}\mathit{r}\mathrm{ }\mathit{G}\mathrm{ }\mathit{L}\mathit{e}\mathit{n}\mathit{s}\mathit{e}& \mathit{G}\mathit{W}& \mathit{N}\mathit{e}\mathit{w}\mathrm{ }\mathit{G}\mathit{W}\mathrm{ }\mathit{p}\mathit{o}\mathit{l}\mathit{a}\mathit{r}\mathit{i}\mathit{s}\mathit{a}\mathit{t}\mathit{i}\mathit{o}\mathit{n}?\\ \mathit{L}\mathit{e}\mathit{n}\mathit{s}\mathit{e}-\mathit{T}\mathit{h}\mathit{i}\mathit{r}\mathit{r}\mathit{i}\mathit{n}\mathit{g}& \mathit{G}\mathit{W}& \mathit{G}\mathit{W}\mathrm{ }\mathit{L}\mathit{I}\mathit{G}\mathit{O}\mathrm{ }\mathit{o}\mathit{r}\mathrm{ }\mathit{G}\mathrm{ }\mathit{L}\mathit{e}\mathit{n}\mathit{s}\mathit{e}& \mathit{N}\mathit{e}\mathit{w}\mathrm{ }\mathit{G}\mathit{W}\mathrm{ }\mathit{p}\mathit{o}\mathit{l}\mathit{a}\mathit{r}\mathit{i}\mathit{s}\mathit{a}\mathit{t}\mathit{i}\mathit{o}\mathit{n}?\\ \mathit{L}\mathit{e}\mathit{n}\mathit{s}\mathit{e}-\mathit{T}\mathit{h}\mathit{i}\mathit{r}\mathit{r}\mathit{i}\mathit{n}\mathit{g}& \mathit{N}\mathit{e}\mathit{w}\mathrm{ }\mathit{G}\mathit{W}\mathrm{ }\mathit{p}\mathit{o}\mathit{l}\mathit{a}\mathit{r}\mathit{i}\mathit{s}\mathit{a}\mathit{t}\mathit{i}\mathit{o}\mathit{n}?& \mathit{N}\mathit{e}\mathit{w}\mathrm{ }\mathit{G}\mathit{W}\mathrm{ }\mathit{p}\mathit{o}\mathit{l}\mathit{a}\mathit{r}\mathit{i}\mathit{s}\mathit{a}\mathit{t}\mathit{i}\mathit{o}\mathit{n}?& \mathit{N}\mathit{e}\mathit{w}\mathrm{ }\mathit{G}\mathit{W}?\mathrm{ }\mathit{o}\mathit{r}\mathrm{ }\mathit{G}\mathrm{ }\mathit{L}\mathit{e}\mathit{n}\mathit{s}\mathit{e}\end{array}\right]\mathrm{ }$$

(20)

$$\left[\begin{array}{cccc}{\mathit{h}}_{\mathit{t}\mathit{t}}& {\mathit{h}}_{\mathit{t}\mathit{x}}& {\mathit{h}}_{\mathit{t}\mathit{y}}& {\mathit{h}}_{\mathit{t}\mathit{z}}\\ {\mathit{h}}_{\mathit{x}\mathit{t}}& {\mathit{h}}_{\mathit{x}\mathit{x}}& {\mathit{h}}_{\mathit{x}\mathit{y}}& {\mathit{h}}_{\mathit{x}\mathit{z}}\\ {\mathit{h}}_{\mathit{y}\mathit{t}}& {\mathit{h}}_{\mathit{y}\mathit{x}}& {\mathit{h}}_{\mathit{y}\mathit{y}}& {\mathit{h}}_{\mathit{y}\mathit{z}}\\ {\mathit{h}}_{\mathit{z}\mathit{t}}& {\mathit{h}}_{\mathit{z}\mathit{x}}& {\mathit{h}}_{\mathit{z}\mathit{y}}& {\mathit{h}}_{\mathit{z}\mathit{z}}\end{array}\right]\to 2\times \left[\begin{array}{cccc}{\mathrm{\epsilon }}_{\mathit{t}\mathit{t}}& {\displaystyle \frac{1}{2}}{\gamma }_{\mathit{t}\mathit{x}}& {\displaystyle \frac{1}{2}}{\gamma }_{\mathit{t}\mathit{y}}& {\displaystyle \frac{1}{2}}{\gamma }_{\mathit{t}\mathit{z}}\\ {\displaystyle \frac{1}{2}}{\gamma }_{\mathit{x}\mathit{t}}& {\mathrm{\epsilon }}_{\mathit{x}\mathit{x}}& {\displaystyle \frac{1}{2}}{\gamma }_{\mathit{x}\mathit{y}}& {\displaystyle \frac{1}{2}}{\gamma }_{\mathit{x}\mathit{z}}\\ {\displaystyle \frac{1}{2}}{\gamma }_{\mathit{y}\mathit{t}}& {\displaystyle \frac{1}{2}}{\gamma }_{\mathit{y}\mathit{x}}& {\mathrm{\epsilon }}_{\mathit{y}\mathit{y}}& {\displaystyle \frac{1}{2}}{\gamma }_{\mathit{y}\mathit{z}}\\ {\displaystyle \frac{1}{2}}{\gamma }_{\mathit{z}\mathit{t}}& {\displaystyle \frac{1}{2}}{\gamma }_{\mathit{z}\mathit{x}}& {\displaystyle \frac{1}{2}}{\gamma }_{\mathit{z}\mathit{y}}& {\mathrm{\epsilon }}_{\mathit{z}\mathit{z}}\end{array}\right]\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }$$

(21)

- Any elastic medium, when dynamically stressed, presents elastic compression waves whose velocity is $c=\sqrt{{\displaystyle \frac{Y}{\rho }}}$and shear $c=\sqrt{{\displaystyle \frac{\mu }{\rho }}}$with Y the Young’s modulus,

μ the shear modulus sometimes noted G in engineer calculations, and ρ the density of the medium. Gravitational waves, being transverse waves, are a wave corresponding to the elastic space-time medium dynamically solicited in an extreme way given the extremely high rigidity of its structure (1/κ) [18,23]. By the way, the elastic model explains why the speed of light is what it is, it corresponds in a way to the ability of photons to penetrate the elastic medium constituting the “elasther”. At speed c, a screen effect of sorts prevents you from exceeding the 299792458 m/s whatever happens. To take an image, it is a bit like a bullet fired into a pile of sand and which loses its power of penetration at a certain speed, an impassable limit due in particular to the frictional forces exerted by the grains of sand throughout its course and to the effect of the bullet tip screen by the compressed grains. This is detailed in [12][13][18] and [20].

- General relativity in a vacuum implies, as we have seen, gravitational waves. They are manifested only by two polarizations A+ and Ax. Why physically two? mystery. The equivalent elastic medium provides an elegant response. Indeed, physically, the gravitational waves measured to date are generated by two black holes or neutron stars or mixed systems rotating relative to each other. In short, these two objects mechanically twist space-time. Well, in the mechanics of continuous media, the tensor of deformations and therefore of stresses takes two forms depending on the orientation of the facets considered, which are at 45° of each other. The first corresponds to pure tension-compression, i.e. elongation, shortening according to Hooke’s first law, the second to pure shear, i.e. angular distortion according to Hooke’s second law. The two polarizations A+ and Ax are also 45° apart. And the polarization measured to date by the LIGO/VIRGO/KAGRA interferometers are indeed elongations, shortenings. It works! The analogy of the elastic medium reproduces well and explains the physics of gravitational waves, Lense-Thirring effects, classical gravitation, observed today.

4.1.3. Predictive Power of the Model

Does the model have the power to predict new phenomena? ? The answer is yes by three criteria:

-the first one we have just seen is angular distortions related to shear stresses, so potentially interferometers have their arms moving laterally? having exchanged with Rainer Weiss, 2017 Nobel Prize in Physics on this subject, they are not designed to measure these potential lateral movements. On the other hand, the future LISA interferometer will. (see [20]),

-the second point is the analysis of the components of the perturbation tensor of the metric$h_{\mu v}$, there remain the components $h_{zx},h_{zy},h_{zz}$to be associated with a new physical phenomenon (see [21]),

-The third point is that space-time appears as layered and isotropic transverse when we analyze the deformations generated by gravitational waves calculated and measured according to traditional general relativity in weak fields [20]. To reconstitute a cohesive medium, and thus reassemble these sheets of space together, or what amounts to the same having possible deformations in the direction of propagation of gravitational waves, it is necessary to add geometric torsion to the Riemann tensor (whose mirror is the theory of defects in crystallography with plasticity [64]) and this generates complementary polarizations in the z direction. These potential new polarizations, if they exist, LISA will measure them (see [20]).

At this point, we can be confident about this elastic model of space-time to represent the real behaviour of the space and time when loaded and push it to its limits to see what it can teach us about physics and these contemporary mysteries. This is what we will do in the next paragraphs by studying other mechanical properties of all elastic media, and in particular its expansion coefficient α and its creep coefficient ϕ.

4.2. Temperature-Sensitive Space-Time According to Hawking Radiation to Temperature-Sensitive Elastic Time?

4.2.1. Elastic Analogy and Theory

When a massive giant star explodes, it generates, if its mass exceeds a certain threshold, such a localized density of energy that space-time, as if overloaded or locally plasticized, collapses. It is compressed, twisted, twisted so intensely that it generates a black hole. In his article [45] J.P. Luminet explains, and I quote, "The black hole must be understood not as a mass that attracts with an irresistible force, but as an extreme distortion of space-time". Gravitational waves have shown that mergers of black holes (GW150914) [46] or neutron stars (GW1701817) [47] do exist. The shadow of a black hole has been observed twice thanks to the global Event Horizon Telescope (EHT) collaboration. That of our galaxy Sagittarius A* on May 12, 2022 and that of the galaxy M87* on April 10, 2019. In short, today there is no longer any doubt. Black holes, which are intensely distorted space-time, do exist.

But within these black holes is a small seed called singularity, which means that quantum mechanics must be taken into account in addition to general relativity to know what is going on. This is what Stephen Hawking did in [48] to [51]. He discovered that black holes, and therefore intensely twisted space-time, emit radiation, that they have a temperature and that they end up evaporating in the very long term. However, a black hole is above all space and time, intensely distorted, as explained by J.P. Luminet [45]. The implacable consequence of having assembled space with time is therefore that not only is space sensitive to temperature, but also time must also be influenced by temperature, as envisaged in the publications [52] and [53] we will return to this. The radiation discovered by Hawking is written with the Boltzmann constant $k_B$.

$$T={\displaystyle \frac{1}{8\pi k_B}}{\displaystyle \frac{\mathrm{\hslash }{c}^3}{GM}}$$

(22)

This radiation from black holes has not yet been directly measured, but hydrodynamic-acoustic analogies have indeed highlighted this phenomenon [54].

This is why recent publications attempt to assess the sensitivity of weather to temperature. Thus, the authors of [52] and [53] define the time interval as a function of the local entropy S and its rate of change ̇$\dot{S}$:

$$t={\displaystyle \frac{S}{\acute{S}}}$$

(23)

By studying the variation of entropy, they then introduce a function τ related to the frequency ν of a physical system serving as a clock, in accordance with A. Einstein ’s idea. This time this clock depends on the temperature T, Planck’s constant h and Boltzmann’s constant $k_B$. They get:

$${\tau }_{\left(T\right)}={\displaystyle \frac{1}{\upsilon }}={\displaystyle \frac{h}{k_B}}\times {\displaystyle \frac{1}{T}}={\displaystyle \frac{4.799243\times {10}^{-11}\left[K.s\right]}{T\left[K\right]}}$$

(24)

In the case of blackbody radiation, the variation of the time flow t as a function of the temperature T can then be written as:

$$t_{\left(T\right)}=n\tau =n{\displaystyle \frac{h}{k_B}}\times {\displaystyle \frac{1}{T}}=n.{\displaystyle \frac{4.799243\times {10}^{-11}[K.s]}{T}}\approx n{\displaystyle \frac{4.80\times {10}^{-11}\left[Ks\right]}{T}}$$

(25)

According to Table 1 of [52], the effect remains extremely small: for example, for T = 10⁶ K (mean temperature of the cosmic web [68]) and n = 1, the temporal variation is of the order of 4.8 × 10⁻¹⁷ s. Although very small, this value is of the same order of magnitude as the space-time strain amplitude observed for gravitational waves (typically around 10⁻²¹), suggesting that such thermal effects on time, while subtle, may still be physically meaningful and potentially measurable in extreme astrophysical environments.

By inverting the expression and relating it to time t, we obtain a term that plays the role of a coefficient of thermal expansion of time:

$${\displaystyle \frac{t}{n\mathrm{\tau }}}={\displaystyle \frac{k_{B}t}{nh}}\times T={\mathrm{\alpha }}_{t}T$$

(26a)

And by identification it comes:

$${\displaystyle \frac{k_{B}t}{nh}}={\mathrm{\alpha }}_t$$

(26b)

where has the dimension of a time-dependent coefficient of thermal expansion ${\mathrm{\alpha }}_t$ (K^-1).

Thus, time appears to be influenced at the quantum level by the temperature T, the fundamental constants h, $k_B$ and therefore by the entropy of the medium S. In this sense, time is quantified in multiples of nh.

This result can be reconciled with what we have seen in section 3.4 in the case of “elasther”. Indeed, all elastic bodies are sensitive to temperature and have an expansion coefficient associated with is material. So, if space-time behaves by analogy like a quantized medium, then like any elastic medium it is sensitive to temperature and expands, contracts, and curves under the effect of a temperature gradient. So, by starting from analogy to physics by equivalence, then time becomes sensitive to temperature. Which is quite logical since already by special relativity we know that it lengthens when we reproach ourselves for the speed of light.

If we postulate that the analogy of the elastic medium continues to apply under temperature as it already applies well without temperature, then the strain ε₀₀ in the “elasther” must be sensitive to temperature and become ${\epsilon }_{00}\left(T\right).$The principle of equivalence between the elastic analogy and spacetime in weak fields being bijective and having to work in the analogy direction towards relativistic physics, then time must be effectively sensitive to temperature, as explicitly envisaged in publications $.$[52] and [53], and as implicitly envisaged by the Hawking radiation of black holes, which are infinitely distorted pure space-time.

The thermal elasticity of time can also be established in the following way as developed in [55] in connection with [52] and [53] and the Hawking radiation of black holes [48] to [51].

To do this, we start with the "cosmic fabric" model developed by T. Tenev and M.F. Horstemeyer [12, 13], in which the time lapse is related to the speed of propagation of a signal within space-time. The variation of this time lapse is then written:

$${\displaystyle \frac{d\mathrm{\tau }}{dt}}={\displaystyle \frac{1}{\left(1+{\mathrm{\epsilon }}^{3D}\right)}}$$

(27)

With:

$${\mathrm{\epsilon }}_{,kk}^{3D}=c^2\mathrm{\kappa }\mathrm{\rho }$$

(28)

where ${{\mathrm{\epsilon }}_{,kk}^{3D}\equiv \nabla }^2{\mathrm{\epsilon }}^{3D}$is the Laplacian of the volumetric deformation, c is the speed of light, κ Einstein’s constant, and ρ is the matter-energy density.

The term ${\mathrm{\epsilon }}^{3D}$represents a scalar field describing the fractional increase in the volume of a hypersurface of the tissue:

$${\mathrm{\epsilon }}^{3D}\equiv {\mathrm{\epsilon }}_i^i$$

(29)

and the usual strain tensor is:

$${\mathrm{\epsilon }}_{ij}={\displaystyle \frac{1}{2}}\left(g_{ij}-{\mathrm{\delta }}_{ij}\right)$$

(30)

Thus, time depends on a volume variation dV related to the energy-stress tensor, which acts as a tension on the elastic medium:

$${\displaystyle \frac{dV}{d\overline{V}}}=\left(1+{\mathrm{\epsilon }}^{3D}\right)$$

(31)

By analogy with a classical elastic medium, this volume variation can also come from a temperature rise related to a temperature gradient ΔT and a coefficient of thermal expansion ${\mathrm{\alpha }}_S$:

$${\displaystyle \frac{dV}{d\overline{V}}}={\mathrm{\alpha }}_S\Delta T$$

(32)

Finally, transposed to time, this relationship is expressed as a ratio between the length of the spatial fabric (in which the speed of light plays an intrinsic role) and thermal expansion:

$${\displaystyle \frac{ct}{cn\mathrm{\tau }}}={\displaystyle \frac{k_{B}t}{nh}}\times \Delta T$$

(33)

This expression is thus demonstrated in [55] and shows how time should vary as a function of temperature if we believe the analogy of the equivalent elastic medium in a weak gravitational field. Of course, all his articles related to a possible variation of time as a function of temperature [52] [53] [55] [56] to [60] remain for the moment theoretical as long as a real measurement experiment has not been carried out to confirm or refute this prediction.

4.2.2. Experimental Validation

The idea of a variation of time as a function of temperature raises a fundamental question: Is it a change in the weather itself or simply an alteration in the behaviour of the measuring instrument under the effect of temperature variation? [57] to [60]. Atomic clocks, although extremely accurate, are still physical systems subject to thermodynamic laws. An experiment consisting of comparing two identical clocks, one at room temperature and the other subjected to a heated environment, could reveal a temporal drift. However, this drift would probably be due to thermal effects on the clock components, and not to a change in universal time. To test the hypothesis of a fundamental link between temperature and temporality, it would be necessary to design an experiment capable of isolating time as an independent physical quantity, eliminating all instrumental influence. This could involve the study of quantum or cosmological phenomena where temperature plays a dynamic role in the very structure of space-time.

4.3. Elastic Space-Time Sensitive to Creep and Consequences on Time?

4.3.1. Elastic Analogy and Theory

If we continue the analogy of the elastic medium as a model of the functioning of space-time in a weak field, any elastic medium that can exhibit viscoelastic behavior is also sensitive to creep, i.e. to amplifications of deformations in time under constant loading. This approach to space-time that can flow has been studied in [61]. In this publication we show for the first time, as a logical consequence of all that we have seen so far, that time within the framework of the analogy of the elastic medium could flow if the analogy still applies.

In the analogy with an elastic medium, spacetime is thought of as a fabric that includes both space and time [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. To introduce the idea of time creep, we need to relate the potential time drift to the time elasticity in general relativity. In a weak field, we have [12,13]:

$$1+2{\mathrm{\epsilon }}_{00}\approx g_{00}$$

(34)

Proper time is then written, with the interval convention (+---):

$$d\mathrm{\tau }=g_{00}dt$$

(35)

Either:

$${\displaystyle \frac{d\mathrm{\tau }}{dt}}=\left(1+2{\mathrm{\epsilon }}_{00}\right)$$

(36)

Compare with the usual expression of general relativity:

$${\displaystyle \frac{d\mathrm{\tau }}{dt}}=\left(1-{\displaystyle \frac{GM}{r{c}^2}}\right)$$

(37)

Where we see that $d\tau <dt$:

By identification, we obtain:

$${\mathrm{\epsilon }}_{00}=-{\displaystyle \frac{GM}{2r{c}^2}}$$

(38)

Hence the temporal distortion:

$${\displaystyle \frac{d\mathrm{\tau }-dt}{dt}}=-{\displaystyle \frac{GM}{r{c}^2}}$$

(39)

By introducing the creep effect, modeled by an increase in the gravitational factor of G according to $G\left(1+\phi \right)$as done in [61], we have:

$${\displaystyle \frac{d\mathrm{\tau }-dt}{dt}}=-{\displaystyle \frac{GM\left(1+\mathrm{\phi }\right)}{r{c}^2}}$$

(40)

The creep coefficient φ can be isolated:

$$-\left({\displaystyle \frac{d\mathrm{\tau }-dt}{dt}}\right){\displaystyle \frac{r{c}^2}{GM}}-1=\mathrm{\phi }$$

(41)

Let us also:

$$\left({\displaystyle \frac{dt-d\mathrm{\tau }}{dt}}\right){\displaystyle \frac{r{c}^2}{GM}}-1={\displaystyle \frac{\mathrm{\delta }t}{{\mathrm{\delta }t}_0}}{\displaystyle \frac{r{c}^2}{GM}}-1=\left({\displaystyle \frac{\frac{\mathrm{\delta }t}{{\mathrm{\delta }t}_0}}{\frac{GM}{r{c}^2}}}-1\right)=\mathrm{\phi }$$

(42)

This relationship, which links temporal drift to a creep effect, was published in [61].

4.3.2. Experimental Validation

Again, only a measurement of the variation of time by the creep effect of space-time will be able to confirm or inform this prediction. To do this, it would be necessary to reproduce a Shapiro-type measurement [32] over time to see if there is indeed a deviation in the measurement of the effect of gravitation related to time, all other parameters being kept fixed elsewhere.

4.4. Plasticity of the Elastic Medium and Infinite Stretching of Time

Until now, we have been interested in deformations in weak gravitational fields, which are already partly covered by Newtonian gravitation, but general relativity aims, and this is its whole interest, at gravitation in strong fields such as neutron stars or black holes. In this case, it is well known that space-time at the level of these singularities is intensely distorted until it breaks, giving rise to the singularity. The mirror effect of this in the case of elastic medium analogy is plasticization. The fibers that make up the fabric of space-time plasticize and stretch until they break. If space-time can be modeled as an elastoplastic crystal as the authors do in [41] to [43], the small quantum beams constituting the equivalent crystal lattice [12] [13] [18] [21] are as if subject to plastic ball joints and the crystal collapses. The answer for time in this elastic-plastic model is then the plastic bearing of the material in the law of stresses on the $y$-axis and strain on the $x$-axis. Time stretches infinitely within a black hole like plasticized fibers that leave Hooke’s law, i.e. we enter the realm of plastic irreversible deformations.

4.5. Time as an Illusion with Quantum Gravity

String theories [65], or loop quantum gravity [66] and general relativity suggest that time could be an illusion emerging from a more fundamental substrate. We refer the reader to these two theories for more details.

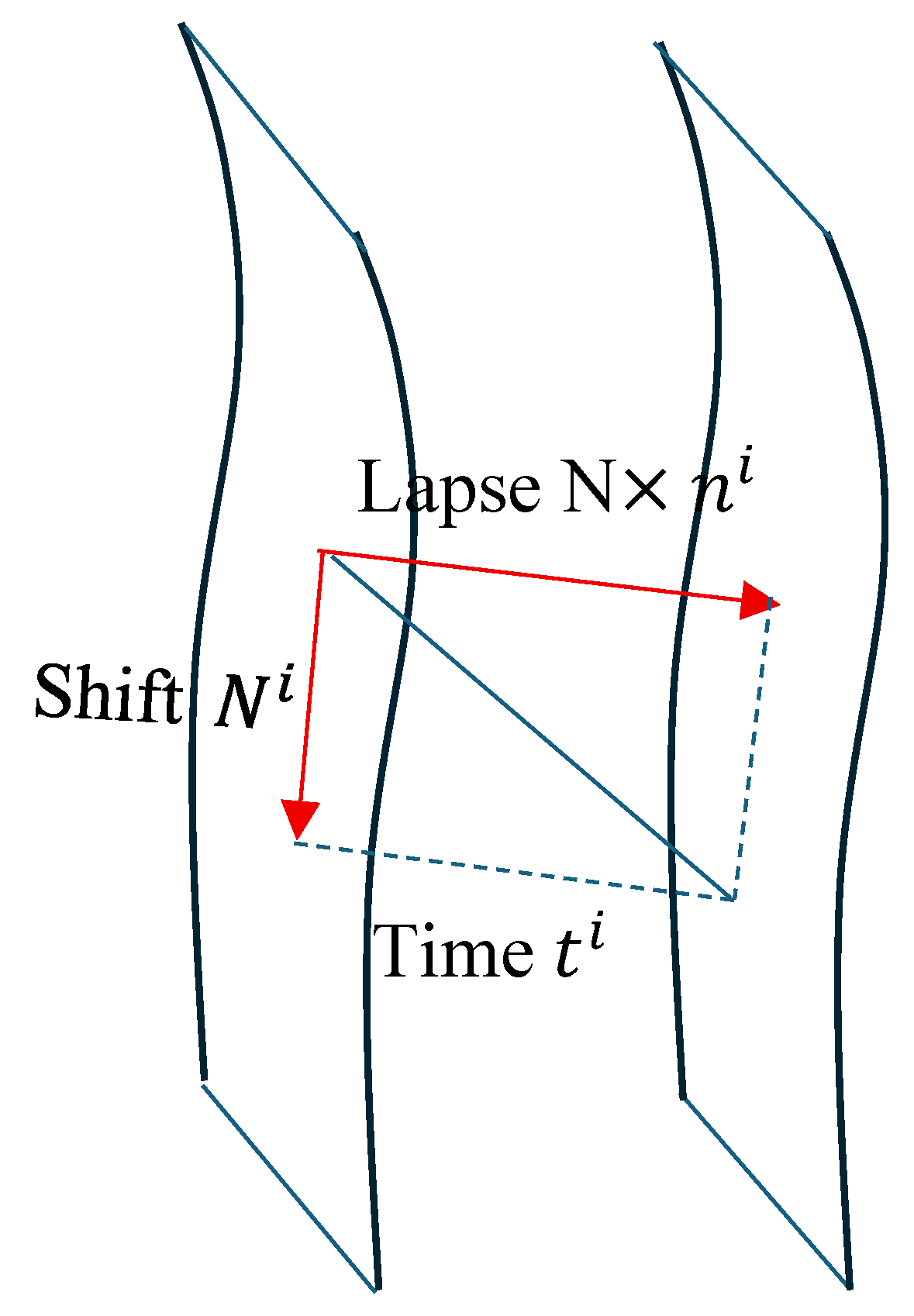
4.6. Space-Time Lamination and Time Lapse in the Case of Gravitational Waves – Einstein Cartan’s Modified Theory of General Relativity

In his publication [31] A. Einstein showed that in the case of general relativity in a weak field, gravitational waves are transverse plane waves generating deformations in planes perpendicular to the direction of propagation (Figure 2). The publication [20] studies these deformations from the point of view of elastic analogy. It emerges that space appears as laminated or a kind of multi-sandwich with deformations localized in these transverse planes, as if space were a particular elastic medium made up of a stack of sheets of equivalent elastic materials without any coherence between them. Based on the Poisson coefficient of such a medium equal to ν=1 as shown by [12] and [13], then space and therefore space-time becomes by analogy an anisotropic elastic medium, i.e. isotropic transverse. To reconstruct a coherent medium, the authors show in [20] that it is necessary to use general relativity with geometric torsion, i.e. to add a complementary term called torsion tensor to the traditional Riemann tensor. In this model, the time interval intervenes to transmit information from one sheet of space to another.

In [67], spacetime is divided into a family of spatial hypersurfaces ${\mathrm{\sum }}_t$, parameterized by a time of coordinate t. Each ${\mathrm{\sum }}_t$is a three-dimensional hypersurface, provided with a spatial metric ${\mathrm{\gamma }}_{ij}(x)$, on which the initial data is defined.

To describe the transition from ${\mathrm{\sum }}_t$ to ${\mathrm{\sum }}_{t+dt}$, Arnowitt, Deser, and Misner (ADM) introduce two gauge functions (Figure 3):

• The lapse $N(t,x)$, which measures the normal proper time interval at ${\mathrm{\sum }}_t$between two hypersurfaces;
• The shift$N^i\left(t,x\right)$, which describes the spatial shift of points from one hypersurface to another.

The spatio-temporal metric then takes the form:

$${ds}^2=-N^2{dt}^2+{\mathrm{\gamma }}_{ij}\left({dx}^i+N^{i}dt\right)\left({dx}^j+N^{j}dt\right)$$

(43)

Moving on to Hamiltonian formalism, ADM chooses t as the evolution parameter and defines for each hypersurface the canonical variables (${\mathrm{\gamma }}_{ij},{\mathrm{\pi }}^{ij}$), where ${\mathrm{\pi }}^{ij}$is conjugated to ${\mathrm{\gamma }}_{ij}$. Two types of constraints appear:

• the Hamiltonian stress H≈0, which generates the normal evolution at the surface (via lapse),
• $H_i$≈0 moment constraints, which describe tangent rearrangements (via shift).

Time then becomes a generator of transformations, and the total Hamiltonian is written:

$$H_{ADM}=\underset{{\mathrm{\Sigma }}_t}{\int }\left(NH+N^i{H}_i\right)d^{3}x$$

(44)

Thus, choosing a lapse function N is equivalent to fixing the way in which time flows from one hypersurface to another, while the shift $N^i$adjusts the spatial coordinate system.

The interpretation of time that results from this is twofold:

• There is a relativity of time: no absolute time, but a plurality of internal "clocks" depending on the choices of lapse and shift.
• Time is dynamic: it corresponds to the successive sliding of spatial hypersurfaces, which reflects the evolution of the gravitational metric.

In summary, the ADM formulation describes time as a foliation parameter of space-time, defined by gauge functions (lapse and shift), and integrated into a Hamiltonian formalism where it becomes the generator of dynamical evolution. This vision is in line with both our elastic analogy (transmission of deformations from one leaf to another) and the foliation of space-time revealed by gravitational waves [20] or hypersurfaces developed by T Tenev and M.F Horstemeyer in [12] and [13].

5. Discussion

5.1. Consequence of a Variation in Time and Space as a Function of Temperature

We have seen whether it is through Hawking radiation [48] to [51] or in publications [52] [53] [55] [56] to [60], that time, in the context of a 4-dimensional elastic medium, can be sensitive to temperature since it becomes associated with a deformation of an equivalent elastic medium that can be dilated (the “Elasther”, the "deformable elastic jelly" [22] to [24], the cosmic crystal [41] to [43]). In these same publications, based on physics experiments, the publication ${\epsilon }_{00\left(T\right)}$[55] shows that naturally space is also sensitive to temperature. As a result, space-time is sensitive to temperature and therefore temperature gradients within space-time, if they exist, can, according to the model of the "elastic space-time jelly" [22] to [24] generate a thermal curvature of it. Thus, a thermal gradient between the cosmic web and the vacuum applied to Planck thickness sheets of thermal conductivity of vacuum λ=0 W/m².K, which would constitute it [12][13][20][67], would bend space-time in the opposite direction of gravitation, giving us the illusion of a mysterious dark energy. This is therefore equivalent to placing the cosmological constant Λ on the left side of Einstein’s equation on the curvature side and not on the right on the dark energy side (46). The following two equations show the parallelism between the one-dimensional elastic beam model and Einstein’s 4-dimensional equation. In summary, what can create curvature in space-time is not only the density of mass energy, but also a temperature gradient applied between two faces of a laminated insulating medium [12] [13] [20] [67] as it is taken into account in structural engineering and as envisaged in the ADM model.

Expression in structural engineering with R the radius of curvature of the beam, I its inertia, L its span U the different bending energies M and thermal energy ΔT, E its Young’s modulus, α its coefficient of thermal expansion, e its thickness:

$${\displaystyle \frac{1}{R^2}}+{\left({\displaystyle \frac{\mathit{\alpha }\Delta \mathit{T}}{\mathit{e}}}\right)}^{\mathbf{2}}={\displaystyle \frac{\mathbf{2}}{EI}}\left({\displaystyle \frac{U_M}{L}}\right)+{\displaystyle \frac{2}{\mathit{E}\mathit{I}}}\left({\displaystyle \frac{{\mathit{U}}_{\Delta \mathit{T}}}{\mathit{L}}}\right)={\displaystyle \frac{2}{EI}}\left({\displaystyle \frac{W_{ext\left(total(M+\Delta T\right)}}{L}}\right)$$

(45)

In parallelism with the expression of general relativity:

$$G_{\mathrm{\mu }\mathrm{v}}=R_{\mathrm{\mu }\mathrm{v}}-{\displaystyle \frac{1}{2}}{g}_{\mathrm{\mu }\mathrm{v}}R+\Lambda g_{\mathrm{\mu }\mathrm{v}}=-{\displaystyle \frac{8\pi G}{c^4}}{T}_{\mathrm{\mu }\mathrm{v}}$$

(46)

In the publication [55], it is shown that such a process is conceivable and that in the case of space as in the case of time we obtain a coefficient of thermal expansion α= 12x10^-6 if we consider a thermal gradient between the cosmic web and the vacuum as given in the publication [68]. This phenomenon of thermal curvature linked to a thermal gradient would then, within the framework of our elastic model, be an excellent candidate to explain what dark energy is and where dark energy comes from, which would then be, according to the publication [55], only an intrinsic thermal curvature of space-time and therefore of the space and time of the different leaves that would constitute it according to the formulation with Λ the cosmological constant:

$${\left({\displaystyle \frac{{\mathrm{\alpha }}_S\Delta T}{e}}\right)}^2={\left({\displaystyle \frac{1}{R_0}}\right)}^2=\Lambda$$

(47)

With e the thickness of the space-time sheet of Planck size, $R_0$the curvature of the space sheet under the effect of the thermal gradient ΔT and ${\mathrm{\alpha }}_s$the coefficient of thermal expansion of the "jelly [22] to [24] " space-time. Figure 4 illustrates this thermal curvature on a space sheet.

This effect of thermal curvature and therefore of dark energy may have varied over time since the cosmic web that is the source of the thermal gradient has only evolved since the Big Bang, as shown in the recent publication [71] [72].

5.2. Consequence of a Variation in Time and Space by Creep of Space-Time

To explain the stability of stars on the periphery of galaxies that should be ejected due to a lack of gravitation calculated from visible mass alone, physicists, based on Newton’s law, have assumed the existence of a hidden or black mass (Fritz Zwicky) to amplify the effects of gravitation and hold the various stars in place. The same principle has been considered to explain the increase in gravitational lensing effect or at the time of the CMB to explain the small anisotropies in the emission of the cosmic microwave background. The problem is that this hidden mass to generate this missing gravitation has remained hopelessly untraceable for 60 years despite the colossal deployment of experiments around the world to bring it to light. As a result, some physicists have been led to transform this ontological problem into a legislative solution. Change Newton’s law in certain regime. And it works. This is the approach developed by Mordehai Milgrom and which became the MOND theory "Modified Newtonian dynamics"[69] to [70] but this is done at the cost of a new constant of unknown origin $a_0$ = 1.2 × 10⁻¹⁰ m s⁻² which would be, I quote wikipedia, "roughly the acceleration it would take to go from rest to the speed of light during the life of the Universe. It is also the order of magnitude of the recently discovered acceleration of the expansion of the Universe."

The analogy of the elastic medium allows us to consider a completely different approach. Not like the MOND theory by modifying Newton’s law or like Zwicky by adding dark matter, but to return to what we learned from general relativity by using the elastic medium that reproduces the deformations of space-time. Gravitation is not a force linked to masses as I. Newton had envisaged, it is an illusion, it is a deformation of space and time. So, if there is more gravity needed to keep stars on the periphery of the galaxy, or in the case of gravitational lensing or at the time of CMB emission with all the anisotropies observed at the level of the temperatures of the cosmic microwave background, it is because there are more deformations than the visible mass alone can provide, whatever the origin of this excess deformation. This second part is the key part here. The elastic analogy then allows us to consider another solution than adding mass or changing Newton’s simplified law. Once again, the solution is not external through densities of mass, energy that loads elastic space-time within it, but within space-time itself, as Einstein taught us to solve Newton’s paradox with its mysterious forces acting at a distance, forces that moreover could not act on light which has no mass, and which is nevertheless bent by gravitation. This is shown in the publication [61] based on the well-known knowledge of structural engineering. An increase in deformation can also occur under constant load if the medium constituting the structure is subject to creep, i.e. a reorganization of the molecules noting the elastic material under the effect of prolonged loading over time, typical of viscoelastic behaviour. The creep of space-time and therefore of time like space can therefore alone explain the physical observations of gravity more intensely than mass produce it without adding missing or black mass. This is the great consequence of the creep of time via ${\epsilon }_{00\left(\phi ,t\right)}$and space-time. In the publication [61], it is thus shown that the MOND law, which works well to explain the stability of stars on the periphery of galaxies, can be reformulate as a creep coefficient of space-time according to the formulation:

$${\mathrm{\phi }}_{\mathit{s}\mathit{p}\mathit{a}\mathit{c}\mathit{e}}={\displaystyle \frac{{\mathit{a}}_{\mathbf{0}}}{\mathit{a}}}-\mathbf{1}$$

(48)

With $a={\displaystyle \frac{GM}{r^2}}$ and $a_0=1.2\times {10}^{-10}m/s^2$which suddenly takes on a mechanical origin.

Figure 4 shows the amplification of space-time deformations by creep effect.

Figure 5. Deformation of space-time by creep effect.

Figure 5. Deformation of space-time by creep effect.

This creep effect, and therefore dark matter, may have varied over time depending on the texture of the elastic deformable jelly [22] to [24] as shown by the recent publication resulting from the DESI experiment [73].

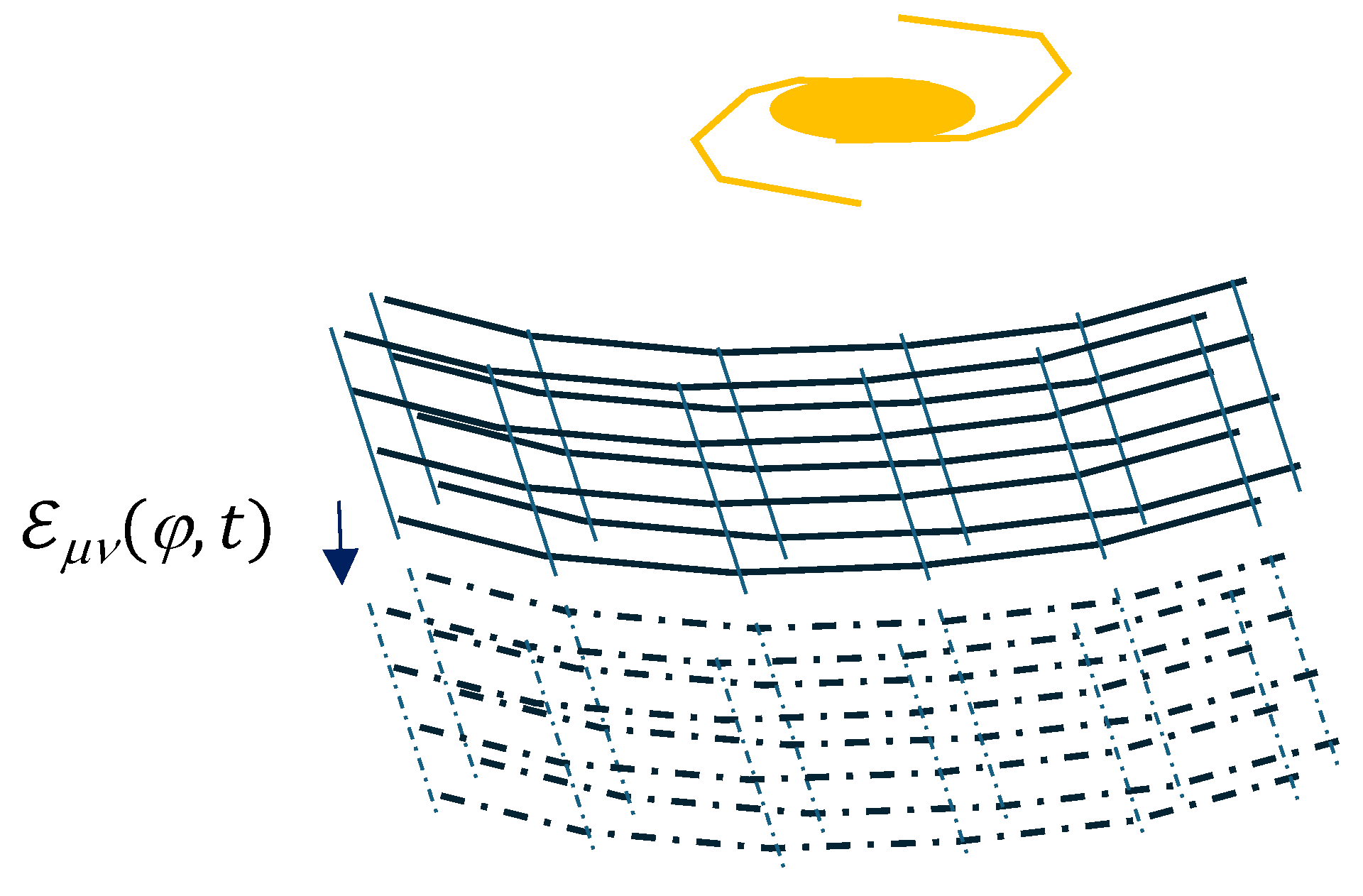
5.3. Consequence of the Foliation of Space-Time on the Nature of Time in the Case of an Equivalent Elastic Medium

The consequence of this whole study is to try to understand what becomes of time in the case of our analogy of the elastic medium. Like an investigator, we must gather all the clues at our disposal.

a)

First of all, in any elastic medium, the relations between the speed of propagation of the waves and the elastic characteristics of the medium Y, ν and ρ are written according to [12] [13]:

$$v_{longitudinal}=\sqrt{{\displaystyle \frac{Y}{\mathrm{\rho }}}}$$

(49)

$$v_{transversal}=\sqrt{{\displaystyle \frac{E}{2(1+\nu )\mathrm{\rho }}}}$$

(50)

However, it is well known that in the case of space-time there are gravitational waves predicted by A. Einstein [31] and measured for the first time during the GW150914 event [46].

Moreover, it was shown during the GW170817 event [47] that these waves propagate precisely at the speed of light c which is therefore, on the basis of our analogy and the two formulations above, a key parameter that characterizes the space-time elastic crystal structure, the “elasther”.

b)

Then, according to special relativity, time expands [2].

c)

In general relativity, time can indeed be associated with deformation, and we have seen that this translates into the 00 component of the tensors involved in general relativity $h_{00}=2{\epsilon }_{00}$ [12] [13] [18] [20] [21]. And we have seen that time can be expressed from this deformation in the 4th dimension of general relativity $d\tau =\sqrt{g_{00}}dt=\sqrt{1+2{\epsilon }_{00}}dt\approx \left(1+{\epsilon }_{00}\right)dt$.

d)

Space-time appears to consist of thin sheets of Planck thickness if we refer to deformations related to gravitational waves, so it takes some time for a deformation to pass from one slice to another [12] [13] [18] [20] [21].

e)

Finally, in physics, time is defined as the ratio between distance and speed

$$v={\displaystyle \frac{d}{t}}\to t={\displaystyle \frac{d}{v}}$$

(51)

All these elements put together invite us to postulate that time could also be "mechanized" and defined in the framework of our elastic analogy as a deformation that propagates over a given distance more or less quickly depending on the characteristics of the environment, its Young’s modulus, its Poisson ratio, its density, etc. and would be influenced by the coefficient of creep ${\epsilon }_{00}$φ and expansion. α The overall vision of the elastic paradigm then appears as follows:

-

Gravitation curves time [3] [4] and slows it down since space-time is bent, so "the deformable elastic jelly" [22] to [24] lengthens, thus increases the travel time of the deformation compared to the initial flat length not deformed before the effect of gravitation.

-

Nothing, not even information, can exceed the speed of light since this is a characteristic of elastic space-time [12] [13] [18] [20] [21].

-

An increase in temperature slows down time since lengths dilate and the travel time to transmit a deformation increases relative to an initial L length [48] to [51] [52] [53] [55] [56] to [60].

-

The creep of space-time increases gravitation and therefore the curvatures and therefore the distances to be covered to transmit information with respect to an initial length L [61].

-

In a black hole, time dilates, until it seems to stop since the deformation enters the plastic regime and stretches to infinity.

Thus, mathematically, proper time becomes, following the direction considered, since according to publication [20] space is isotropic transverse:

$$d\tau =\left(1+{\epsilon }_{00}\right)dt$$

(52)

$${\displaystyle \frac{d\tau -dt}{dt}}={\epsilon }_{00}$$

(53)

With therefore as a logical consequence of all our reasoning the mechanical definition of tenses defined as:

$$t_{longitudinal}={\displaystyle \frac{d}{v}}={\displaystyle \frac{L_{longitudinal}{\epsilon }_{00,longitudinal}}{\sqrt{\frac{Y_{longitudinal}}{\rho }}}}$$

(54)

$$t_{transversal}={\displaystyle \frac{L_{transversal}{\epsilon }_{00,transversal}}{\sqrt{\frac{Y_{transversal}}{2(1+\nu )\rho }}}}$$

(55)

Let us take a metaphor to explain these mechanical formulations of time. A human being who has aged over time is characterized, among other things, by the wrinkles on his face. However, these wrinkles or deformation waves depend on the elasticity and density of his skin. These wrinkles are deformities that spread over a given distance, the face and which are more or less important depending on the elasticity and density of the skin, its curvature, its tensions, its creep with the relaxation of the muscles, and the dilation with temperature. Time as such does not exist, it emerges through the transfer of deformations which solicits the elastic medium according to the flexibility and density of the medium.

6. Limitations and Future Challenges

While the elastic medium analogy offers a compelling framework to unify gravitational, thermal, and quantum effects on spacetime, several limitations must be acknowledged. First, the model relies heavily on weak-field approximations, and its extension to extreme regimes (e.g., near singularities or during cosmic inflation) remains speculative. Second, key predictions—such as temperature-dependent time dilation or spacetime creep—lack direct experimental validation, though future missions like LISA may provide critical tests. Third, the analogy implicitly assumes a classical continuum description, while quantum gravity effects (e.g., spacetime discreteness at Planck scales) might require deeper modifications. Lastly, the theoretical equivalence between mechanical deformations and relativistic curvature does not yet resolve the ontological question of whether spacetime is fundamentally elastic or merely behaves as such phenomenologically. Addressing these gaps will demand tighter integration with quantum field theory, high-precision astrophysical measurements, and possibly novel experimental paradigms.

7. Conclusion

Space-time can be interpreted as a quantized elastic medium whose mechanical properties govern the behavior of time. In nature, every structure—whether biological, inert, or engineered, follows mechanical laws. From bridges and cathedrals to DNA molecules and living organisms, all exhibit elastic and structural behavior. Why should the vacuum be exempt?

This perspective opens the door to an elastic and plastic mechanization of gravitation. Within a unified paradigm, where the vacuum is structured as a crystal or a "deformable elastic jelly" [22,23,24], several major enigmas of modern physics find coherent and pragmatic resolution. Dark matter emerges as a consequence of the long-term creep of the elastic medium constituting the space-time crystal, charged by the cosmic web [61]. Dark energy arises from thermal curvature induced by differential heating between the cosmic web and the vacuum [55].

In this framework, space-time appears foliated, and general relativity must be extended to include geometric torsion, as in Einstein–Cartan theory. Time ceases to be an abstract parameter and becomes a dynamic manifestation of the universe’s structure—an emergent phenomenon resulting from the propagation of elastic or plastic deformations at a speed determined by the medium’s texture, i.e., the square root of Young’s modulus over its density.

The vacuum is no longer empty; it possesses deformation energy that drives the propagation of these deformations—and thus, time itself. Future experiments, particularly LISA, by detecting or refuting the predicted complementary deformations and polarizations, will test the validity of this global paradigm and potentially redefine our understanding of the vacuum and the architecture of space-time.