1. Introduction
In recent years, the study of fractional differential inclusions has attracted significant attention due to their capacity to model uncertain and memory-dependent phenomena across various scientific fields. In particular, Shahid et al. [25] investigated nonlinear fractional differential inclusions involving fuzzy set-valued mappings of q-rung orthopair (q-ROF), establishing new existence results through fixed point theory. Recent research has expanded the analytical foundation of differential and integro-differential inclusions, particularly in the context of fractional and delayed systems. For example, Sasikumar and Vijayakumar [24] investigated approximate controllability results for second-order differential inclusions with state-dependent delay, highlighting the impact of damping in dynamic systems. Alshehri et al. [4] tackled delay integro-differential inclusions with practical applications, extending the solution framework for real-world systems involving memory effects. Bensalem et al. [5] studied infinite delay in second-order integro-differential inclusions, offering results on the topological structure of solution sets. In a coupled framework, Ma et al. [17] addressed existence results for nonlinear Hilfer fractional differential systems, combining differential equations and inclusions. A comprehensive survey on boundary value problems involving Hilfer-type fractional inclusions was presented by Ntouyas [19], offering a detailed classification of various solution methods. Khan et al. [13] proposed an abstract formulation for delayed fractional integro-differential systems using the -resolvent operator, thereby making a notable contribution to the theory of fractional abstract Cauchy problems. In a related development, Jing et al. [12] examined hemivariational inequalities governed by Hilfer fractional differential evolution equations with history-dependent operators, which significantly enriched the theory of inclusion problems involving nonsmooth analysis and memory-based dynamics.
With these advances, fractional differential equations (FDEs) have gained increasing relevance in modeling systems that exhibit memory and long-range dependence. Unlike classical models relying on standard derivatives, FDEs employ fractional (non-integer order) derivatives, enabling more accurate descriptions of phenomena such as viscoelasticity, anomalous diffusion, and biological processes [14,18]. Their wide applicability spans disciplines such as physics, engineering, biology, and economics. When coupled with differential inclusion theory, fractional calculus offers a more robust analytical framework, facilitating deeper investigation into existence, stability, and control of solutions under broad settings.
A general form of a fractional differential equation with boundary conditions is given by:
where
denotes the Caputo fractional derivative and
is a given function. The boundary conditions may incorporate both the function and its fractional derivatives, for instance:
These boundary conditions impose essential constraints within a prescribed domain. The study of boundary value problems (BVPs) for FDEs represents an important field of mathematical analysis, with both theoretical and practical implications. Solving such problems often necessitates sophisticated mathematical tools since the inclusion of fractional-order derivatives at the boundaries introduces additional complexity [22?].
A powerful tool in this context is the Bohnenblust-Karlin fixed point theorem, which is widely used to prove existence results in set-valued analysis. This theorem guarantees the existence of fixed points for certain multivalued mappings defined on convex subsets of Banach spaces. Its application becomes especially valuable in the framework of differential inclusions, where the derivative of an unknown function is allowed to take values in a set. Such inclusions frequently appear in models involving uncertainties—examples include problems in economics, biological systems, and control theory [1,8].
We generalize the analysis by considering the nonlinear fractional differential inclusion:
subject to boundary conditions
Here, denotes a multivalued (set-valued) mapping that characterizes the possible values of the derivative. This generalization permits the modeling of systems whose evolution may not be uniquely determined and reflects multiple potential outcomes depending on system states.
The analysis of BVPs involving multivalued maps and fractional derivatives is intricate and often requires fixed-point techniques adapted to the multivalued setting [10,20]. The presence of integral and multipoint conditions involving both the function and its fractional derivatives further increases the analytical challenges. Yet, this formulation enhances the flexibility and realism of the models, making them more applicable to real-world phenomena.
The growing interest in these models is largely motivated by the limitations of classical integer-order differential equations when applied to systems with memory. Many real-world problems, especially in engineering and physics, inherently involve memory effects, which are more naturally described using fractional operators [26]. Moreover, the use of multivalued maps enables modeling of systems with uncertainty or nondeterminism, which frequently arise in areas such as decision theory, neural dynamics, and material science [7,9].
This paper focuses on proving the existence of solutions to a class of fractional differential inclusions governed by complex boundary conditions incorporating both fractional derivatives and multivalued terms. The Bohnenblust-Karlin fixed point theorem will be employed to derive sufficient conditions ensuring the existence of solutions. In doing so, this work extends existing results on fractional differential equations and broadens the analytical scope for solving practical problems in applied sciences [20].
2. Main Results
Before we proceed to the existence result for the nonlinear inclusion, we first consider the solution of the associated linear problem. For a given function , the solution of a linear fractional differential equation.
The following lemma is cruicial for the existence of solutions to the proposed differential inclusion.
Lemma 1.
For the solution of the following linear problem
with boundary conditions is
where
Proof. The general solution for linear problem
is written as
for some real constants
and
. Now using first boundary condition from
i.e.,
and obtain,
simplifying above equation, we have Further simplification gives
with second boundary condition
so
as
□
In our next result we use (Bohnenblust-Karlin Thoerem) to show the existance of our result. We consider the following inclusion
with boundary conditions
.
For this purpose we need to assume the following statements on given functions.
Let
be measurable with respect to j for each
upper semi continuous with respect to
for a.e
and for each fixed
the set of selections
for a.e
be nonempty.
For every
there is a function
such that,
for all
satisfying
and
Definition 1.
A function is solution of the problem if there exists a function such that a.e on and
Theorem 1. (Bohnenblust-Karlin). Let D be a non-void subset of a Banach space X, which is bounded, convex and closed. Suppose that the mapping is upper semi-continuous with closed, convex values satisfying and is a compact set. Then has a fixed point.
Lemma 2. Let I be a closed interval. Let ϝ be multivalued map satisfying and letbe linear continuous from then the operator is closed graph operator in
Theorem 2.
Suppose that the assumputions and are satisfiedwith
then the problem has at least one solution on
Proof. The problem can be transformed into a fixed point problem by defining a set-valued mapping
and proving that
satisfies all the assumptions of Theorem 1, and has a fixed point. This fixed point will be the solution of the problem
In first step, we show that
is convex set for each
For this choose any
Then there exist
such that for each
we have
let
For all
we have
as
is convex, therefore it follows that
Now to show that is closed for each Let be such thatin
Then for
there exists a
such that
since
has compact values, we obtain a convergent subsequence, so that
converges to
v.
which shows that
In next we prove
where
Clearly
is bounded closed and convex set in
. If it is not true, on contrary for each positive number
thereexists a function
with
and
on the other hand,
dividing both side by
and taking lower limit as
we find that
which contradicts
Hence there exists a positive number
such that
Now we show that
is continuous. Let
with
Let
and
then there exists
such that for each
we have
using
obviously the right hand side of above inequality tends to zero independent of
as
Thus,
is equicontinous. So
and
satisfies, therefore by Ascoli-Arzela theorem follows that
is compact multivalued map.
Finally we show that
has a closed graph. Let
and
Wewillshow
By this relation mean that there exists
such that for each
thus we need to show that there exists
such that for each
Let us consider the continuous linear operator
so that
observe that
as
Thus, it follows by Lemma
that
is closed graph operator. Further, we have
Since
therefore, Lemma
implies that
for some
Hence we conclude that
is a compact multivalued map, upper semi continuous with convex closed values. Thus all assumptions of Theorem 1 are satisfied. Therefore
has a fixed point
which is solution of given problem
. □
3. Applications and Examples
The practical relevance and applicability of the theoretical results established in this work have been demonstrated through detailed examples of fractional differential inclusion problems with nonlocal boundary conditions. These examples are constructed to illustrate how abstract fixed point theorems particularly the Bohnenblust Karlin theorem can be employed to guarantee the existence of solutions in appropriate function spaces. By incorporating explicit function definitions, boundary data, and fractional derivatives of non-integer order, we aim to bridge the gap between theory and application.
To enhance intuition and facilitate deeper understanding, we also provide diagrams that visually depict the structure of the multivalued operator and the fixed point construction, highlighting the critical roles of convexity, compactness, and upper semicontinuity in ensuring solvability.
In particular, Example 3.2 presents a concrete application to heat transfer modeling in heterogeneous media. This example captures memory effects through fractional derivatives and incorporates nonlocal boundary conditions derived from distributed sensor measurements. Such models are widely relevant in engineering and applied sciences, including the simulation of heat flow in layered composites, pollutant transport in porous soils, temperature distribution in biological tissues during hyperthermia treatment, and thermal regulation in nuclear fuel rods. The problem formulation uses a fractional differential inclusion with a convex-compact interval-valued right-hand side and demonstrates how the abstract assumptions of the main existence theorem are verified in a physically meaningful setting.
Example 3.1: Consider the Banach space with the supremum norm , and let be a non-void subset, where is chosen such that , ensuring boundedness, convexity, and closedness. Define the set-valued mapping corresponding to the fractional differential inclusion problem:
where
for
. The mapping
is the set of functions
such that
belongs to the interval
, satisfying the boundary conditions. Since
is upper semi-continuous with closed, convex values,
, and
is compact (by the Arzela Ascoli theorem due to uniform boundedness and equicontinuity), the Bohnenblust-Karlin theorem ensures the existence of a fixed point
such that
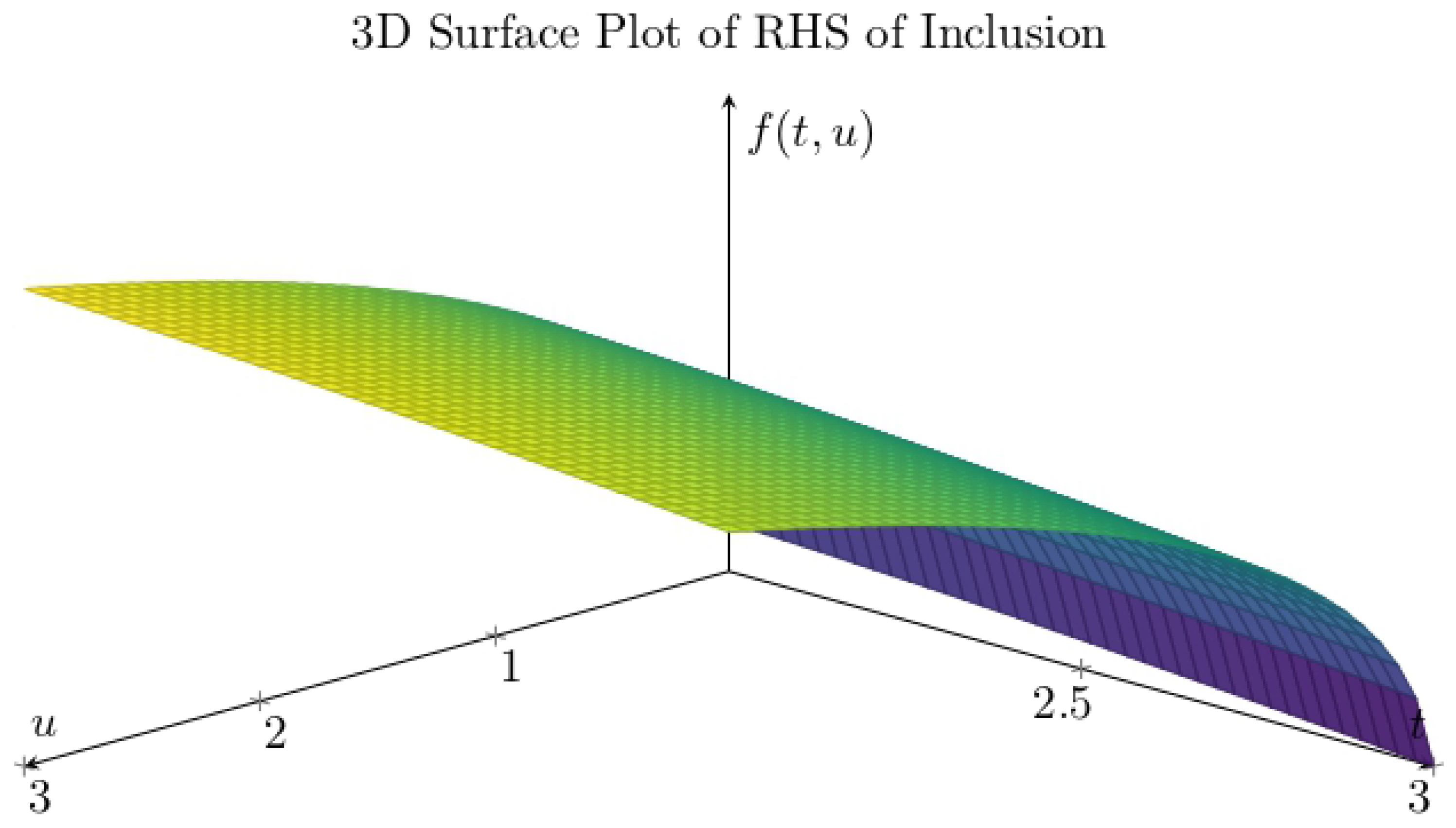
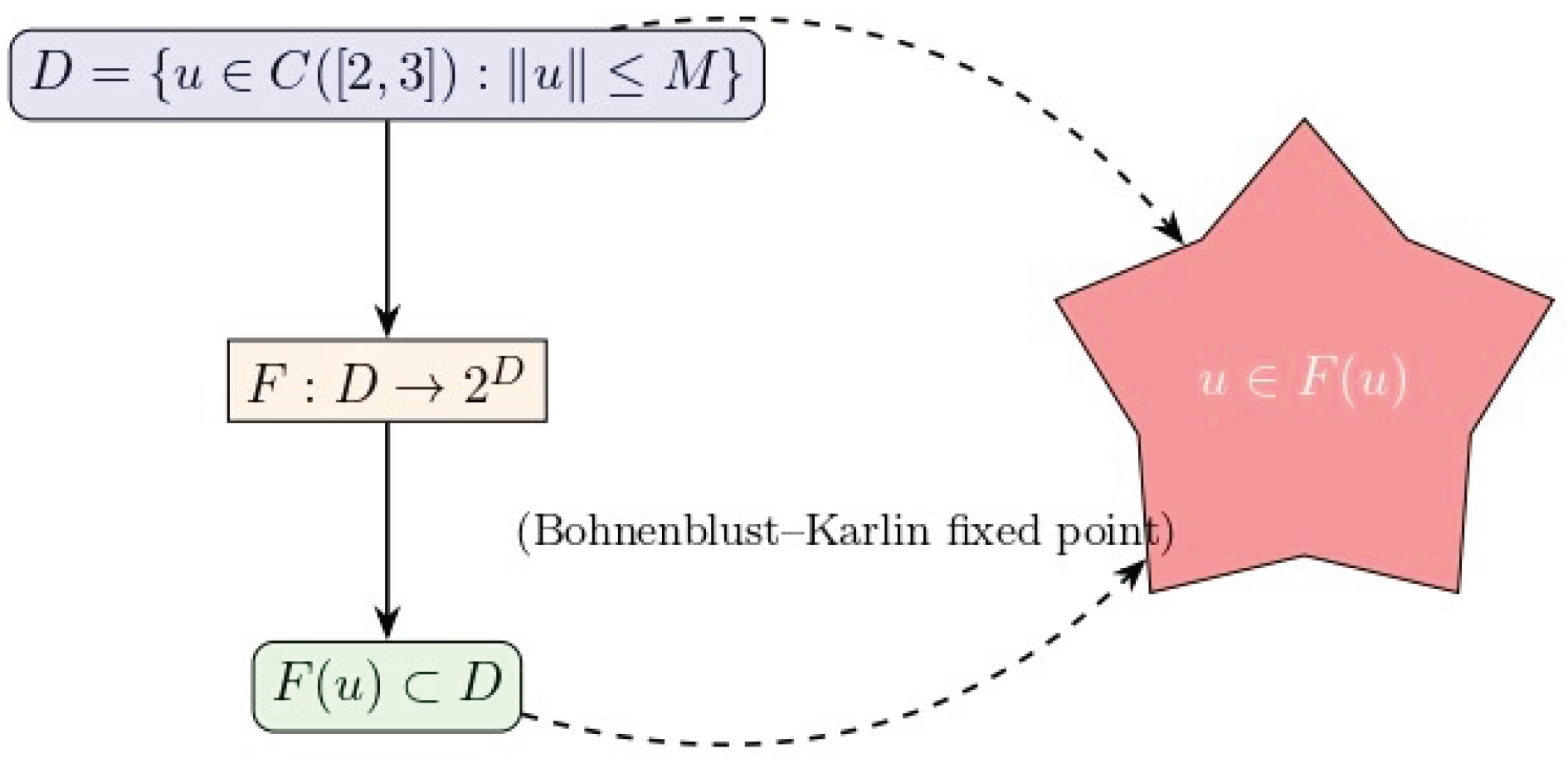
. For better understanding how a solution exists for the fractional differential inclusion, we provide two simple visual illustrations.
Figure 1 shows a 3D plot where the inclusion operator is interval-valued. For each (t,u), the output ranges from 0 up to a surface value—helping us visualize the uncertainty and variability in the system.
Figure 2 offers a schematic of the fixed point approach. It shows how the multivalued operator F maps a function space D into itself. Due to essential properties such as compactness and convexity, the Bohnenblust–Karlin fixed point theorem ensures that some point u in D lies within its image F(u). This fixed point, shown as a red star, represents the solution to our problem under the given boundary conditions.
We now present an example from heat transfer modeling, where fractional derivatives reflect memory effects, and nonlocal boundary conditions arise from sensor data. This modeling framework is widely applicable, for instance, in simulating heat flow in layered materials, tracking pollutant dispersion in soil, analyzing heat propagation in biological tissues during medical treatments, and predicting temperature distributions in nuclear fuel rods. By combining fractional calculus, set-valued mappings, and sensor-based data, the model effectively captures systems where uncertainty and memory effects play a key role
Example 3.2: Consider a physical model involving heat transfer in a rod of unit length subjected to spatially varying heat sources with uncertain intensity. The temperature distribution
, at position
, is governed by the fractional differential inclusion
where the right-hand side is an interval-valued map defined by
This inclusion models the effect of uncertain heat sources in a heterogeneous medium. The order
of the Caputo derivative reflects super-diffusion behavior due to long-range memory effects typical of fractal or porous materials. The boundary behavior is defined by non-separated multipoint conditions given as:
with the parameters
,
, and sensor locations
, while the integral bounds are
,
. These boundary conditions incorporate both pointwise evaluations and averaged measurements over the segment
, simulating a practical scenario where temperature and heat flux are monitored using discrete sensors and integrated thermocouple arrays. The function
is convex-compact valued for each
, measurable in
, and upper semicontinuous in
u, satisfying assumption (A1) of the main theorem. For bounded
u, the upper bound of the multifunction satisfies assumption (A2) with
where
. One computes
ensuring that the measure of noncompactness condition is satisfied. Additionally, the technical condition required in Theorem 2.0,
holds. Therefore, by Theorem 2.0, we conclude that the problem (3.1), (3.2) admits at least one continuous solution
.
4. Conclusions
This study considered a class of fractional differential inclusions with nonlocal and multipoint boundary conditions, where the nonlinearity is described by an interval-valued set-valued mapping to account for uncertainty in the internal source terms. The framework incorporates Caputo fractional derivatives to model memory effects commonly observed in complex physical media. Under suitable compactness and continuity assumptions, the existence of solutions was established using fixed point theorems for upper semicontinuous set-valued maps with convex values.
A representative application to heat transfer in a rod with uncertain internal heating and distributed sensor feedback was provided to illustrate the theoretical results. The model demonstrates how memory effects, measurement uncertainty, and nonlocal interactions can be captured within a unified analytical framework. The results are broadly applicable to problems arising in materials science, biomechanics, environmental modeling, and nuclear engineering.
The methodology presented herein contributes to the mathematical analysis of real-world systems governed by fractional dynamics and uncertainty. Possible extensions include the investigation of uniqueness, stability, and the development of numerical methods for approximating such fractional inclusion problems.
Author Contributions
Conceptualization, Akbar Azam and Ahsan Abbas; Methodology, Ahsan Abbas and Nayyar Mehmood; Formal analysis, Faryad Ali and Nayyar Mehmood; Investigation, Ahsan Abbas and Faryad Ali; Writing—original draft preparation, Ahsan Abbas; Writing—review and editing, Akbar Azam and Nayyar Mehmood; Supervision, Akbar Azam. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported and funded by the Deanship of Scientific Research of Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-DDRSP2503).
Data Availability Statement
This study is purely theoretical in nature. No empirical datasets were created or utilized; all results stem from analytical reasoning and previously established mathematical frameworks.
Conflicts of Interest
The authors declare that they have no known competing interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Abbasbandy, S., Nieto, J. J., and Alavi, M. (2005). Tuning of reachable set in one dimensional fuzzy differential inclusions. Chaos, Solitons & Fractals, 26(5), 1337–1341.
- Ahmad, B., Ntouyas, S. K., Alsaedi, A., Shammakh, W., and Agarwal, R. P. (2018). Existence theory for fractional differential equations with non-separated type nonlocal multi-point and multi-strip boundary conditions. Advances in Difference Equations, 2018(1), 89.
- Ahmad, B., and Otero-Espinar, V. (2009). Existence of solutions for fractional differential inclusions with antiperiodic boundary conditions. Boundary Value Problems, 2009(1), 625347.
- Alshehri, M. G., Aydi, H., and Hammad, H. A. (2024). Solving delay integro-differential inclusions with applications. AIMS Mathematics, 9, 16313–16334.
- Bensalem, A., Salim, A., and Benchohra, M. (2024). Solution sets for second-order integro-differential inclusions with infinite delay. Qualitative Theory of Dynamical Systems, 23(3), 144.
- Bohnenblust, H. F., and Karlin, S. (1950). On a theorem of Ville. Contributions to the Theory of Games, 1, 155–160.
- Chang, Y. K., and Nieto, J. J. (2009). Existence of solutions for impulsive neutral integro-differential inclusions with nonlocal initial conditions via fractional operators. Numerical Functional Analysis and Optimization, 30(3–4), 227–244.
- Chang, Y. K., Li, W. T., and Nieto, J. J. (2007). Controllability of evolution differential inclusions in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications, 67(2), 623–632.
- Chang, Y. K., Nieto, J. J., and Li, W. S. (2009). On impulsive hyperbolic differential inclusions with nonlocal initial conditions. Journal of Optimization Theory and Applications, 140(3), 431.
- Frigon, M. (2007). Systems of first order differential inclusions with maximal monotone terms. Nonlinear Analysis: Theory, Methods & Applications, 66(9), 2064–2077.
- Henderson, J., and Ouahab, A. (2009). Fractional functional differential inclusions with finite delay. Nonlinear Analysis: Theory, Methods & Applications, 70(5), 2091–2105.
- Jing, Z., Liu, Z., and Papageorgiou, N. S. (2024). A class of Hilfer fractional differential evolution hemivariational inequalities with history-dependent operators. Fractional Calculus and Applied Analysis, 27(1), 190–217.
- Khan, I., Zada, A., Popa, I. L., and Kallekh, A. (2025). Analysis of an abstract delayed fractional integro-differential system via the α-resolvent operator. Axioms, 14(2), 111.
- Kilbas, A. A., Srivastava, H. M., and Trujillo, J. J. (2006). Theory and Applications of Fractional Differential Equations. North-Holland Mathematics Studies, Vol. 204.
- Li, W. S., Chang, Y. K., and Nieto, J. J. (2009). Solvability of impulsive neutral evolution differential inclusions with state-dependent delay. Mathematical and Computer Modelling, 49(9–10), 1920–1927.
- Losta, A., and Opial, Z. (1965). Application of the Kakutani-Ky-Fan theorem in the theory of ordinary differential equations or noncompact acyclic-valued map. Bull. Acad. Pol. Sci., Sér. Sci. Math. Astron. Phys, 13, 781–786.
- Ma, R., Meng, Y., and Pang, H. (2024). The existence results of solutions to the nonlinear coupled system of Hilfer fractional differential equations and inclusions. Fractal Fract., 8(4), 194.
- Miller, K. S., and Ross, B. (1993). An Introduction to the Fractional Calculus and Fractional Differential Equations. Wiley.
- Ntouyas, S. K. (2021). A survey on existence results for boundary value problems of Hilfer fractional differential equations and inclusions. Foundations, 1(1), 63–98.
- Nieto, J. J., and Rodríguez-López, R. (2007). Euler polygonal method for metric dynamical systems. Information Sciences, 177(20), 4256–4270.
- Ouahab, A. (2008). Some results for fractional boundary value problem of differential inclusions. Nonlinear Analysis: Theory, Methods & Applications, 69(11), 3877–3896.
- Oldham, K., and Spanier, J. (1974). The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order. Vol. 111. Elsevier.
- Samko, S. G., Kilbas, A. A., and Marichev, O. I. (1993). Fractional Integrals and Derivatives. Vol. 1993. Gordon and Breach Science Publishers, Yverdon-les-Bains.
- Sasikumar, R., and Vijayakumar, V. (2024). A note on the approximate controllability of damped second-order differential inclusions with state-dependent delay. Optimization, 1–19.
- Shahid, L., Rashid, M., Azam, A., and Ali, F. (2023). Existence results for nonlinear fractional differential inclusions via q-ROF fixed point. Fractal Fract., 7(1), 41.
- Smirnov, G. V. (2002). Introduction to the Theory of Differential Inclusions. Vol. 41. American Mathematical Society.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).