1. Introduction
One of the unsolved questions in the study of heavy-ion collisions is understanding how the properties of matter in the Quark-Gluon Plasma (QGP) phase evolves with decreasing beam energy, and determining the energy threshold below which QGP formation no longer occurs. The main goal of relativistic heavy-ion collision experiments is to explore the phase structure of Quantum Chromodynamics (QCD) matter. Lattice QCD calculations predict a smooth crossover from hadronic matter to a deconfined state of quarks and gluons at high temperatures and vanishing net baryon chemical potential (
) [
1]. But at higher values of
, theoretical QCD-based models suggest the existence of a first-order phase transition boundary [
2,
3]. This boundary is expected to terminate at a critical point [
4,
5]. However, due to the sign problem in Lattice QCD at finite baryon density, the location of the critical point remains highly uncertain [
4].
Fluctuations of different conserved quantities, such as net-baryon (B), net-charge (Q) and net-strangeness (S) number, are analyzed on an event-by-event basis, where each event corresponds to the collision of two nuclei. Study of these fluctuations allows to probe the system’s correlation length (
), which characterizes the extent of spatial and temporal correlations among variables. Near the QCD critical point, the correlation length is expected to diverge in an infinite system. As a result, fluctuation measurements provide a sensitive tool for exploring critical phenomena and searching for the QCD critical point [
6,
7,
8,
9,
10].
The CBM experiment at FAIR, Darmstadt, will offer a unique opportunity to investigate the model-predicted first-order phase transition from hadronic matter to the QGP with high precision, enabled by its exceptionally high collision rate of up to 10 MHz, significantly exceeding that of previous experiments.
In this study, we present the first measurements of the moments of net-proton (a proxy for net-baryon) distributions in Au+Au collisions at ranging from 3.5 to 19.6 GeV, using the PHQMD model within the Solenoidal Tracker at Relativistic Heavy Ion Collider (STAR) acceptance i.e., <0.5, 0.42.0 and CBM detector acceptance i.e., 1.082.08, 0.42.0 (y is the rapidity and is the transverse momentum). These results serve as baseline calculations for proton cumulants and correlation functions from the PHQMD model, contributing to the ongoing search for the QCD critical point in heavy-ion collisions. At low collision energies, the net-proton number is primarily dominated by protons, making it a sensitive observable in this regime.
The paper is organized as follow : At first we will introduce the observables of fluctuation study, the relation between the cumulants. Then, we will discuss the PHQMD model. In the results, we will show the energy dependence and centrality dependence of net-proton cumulants in Au+Au collisions at ranging from 3.5 to 19.6 GeV with the PHQMD model generated data. We will finalize by giving a summary and a conclusion.
2. Cumulants
To quantify the intricacies of the distribution, fluctuations are typically characterized using cumulants. The cumulants of a distribution up to the fourth order are defined as follows,
where, N is the net-particle number in a single event and
is the average of N across all the events and
. The first and second-order moments represent the mean and variance whereas the third and fourth-order moments reflect its skewness and kurtosis, respectively.
The products of moments
and
can be expressed in terms of cumulant ratios:
The moment
, skewness
S, and kurtosis
have been found to be proportional to the powers of the correlation length
, specifically
,
, and
[
7], respectively. The n
th order susceptibilities
are related to the cumulant
as
[
11], where V and T represent the volume and temperature of the system. The event-by-event fluctuation of the net-proton number (the difference between the number of protons and antiprotons observed) has been proposed as a key observable for signaling the QCD critical end point. In the energy range (
=3.5-4.9 GeV) of the CBM experiment, there is a hopeful expectation that the QCD critical point can be discovered.
3. PHQMD
The Parton-Hadron-Quantum-Molecular-Dynamics (PHQMD) model is developed to explore the complex dynamics of heavy-ion collisions and the formation of clusters and hypernuclei over a broad spectrum of beam energies, from several hundred AMeV up to the ultra-relativistic scales. It builds upon the Quantum Molecular Dynamics (QMD) model and the Parton-Hadron-String Dynamics (PHSD). The PHQMD model describes the particle production from SIS up to the LHC energies [
12].
Baryon Propagation (QMD Approach): In PHQMD, baryons are treated as Gaussian wave packets and propagated using the QMD model, which includes density-dependent two-body potential interactions. This approach enables the preservation of full n-body phase-space correlations among the baryons, contrasting with traditional mean-field models that average out such correlations [
13,
14].
Collision Dynamics (via PHSD): PHQMD considers the collision integral from PHSD to simulate the full evolution of the system, including hadronic collisions, QGP formation, partonic scatterings, hadronization, propagation of mesons and final-state hadronic interactions. The partonic phase is treated using the Kadanoff-Baym equations [
15,
16]. The model also incorporates in-medium effects such as collisional broadening and modifications of spectral functions for vector mesons (e.g.,
,
,
) and strange mesons (
K,
,
,
), enabling a realistic description of hadronic dynamics in dense and hot nuclear matter.
Dynamic Cluster Formation: PHQMD takes a dynamic approach to cluster formation with QMD. Instead of applying a static coalescence criterion at a specific time, it allows clusters to emerge through ongoing potential interactions throughout the system’s evolution. Cluster recognition is carried out using the Simulated Annealing Clusterization Algorithm (SACA) [
17] or the Minimum Spanning Tree (MST) method [
12]. The baryon resonances which do not participate in the cluster formation continue to propagate within the PHQMD framework until they undergo their natural decay.
QGP Phase Identification: In PHQMD, the region where the local energy density exceeds 0.5 GeV/fm³, that regions are considered to be in the quark-gluon plasma (QGP) phase, as hadrons are expected to dissolve into their constituent quarks and gluons. In the QGP phase, the partons-quarks, antiquarks, and gluons are scattered and dynamically propagated within a self-generated scalar mean-field potential. As the system expands and the local energy density decreases to the critical value, the partons undergo hadronization into color-neutral off-shell hadrons—mesons and baryons. This process is described by covariant transition rates that conserve energy, momentum, and quantum numbers on an event-by-event basis.
In the PHQMD model, cluster identification is not inherently performed during the dynamical evolution. Instead, all clusters are initially counted without distinguishing their physical relevance. Not all clusters with mass number A<9 are considered physical; for instance, unbound systems such as a proton-proton pair are excluded from the final list of physical clusters. In our analysis, we have used MST in the PHQMD model for clusterization. In this approach, cluster formation is determined purely based on coordinate space information. Two nucleons are considered part of the same cluster if their spatial separation is less than a threshold distance . Nucleons connected by this spatial criterion collectively form a cluster.
In our analysis, we have used the PHQMD physical cluster QGP ON and Physical cluster QGP OFF data sets. The QGP ON state refers to the system being in the QGP phase, characterized by a local energy density exceeding 0.5 GeV/fm³. If this condition is not met, the system is considered to be in the QGP OFF state.
4. Results
Two million minimum-bias Au+Au collision events generated using the PHQMD model, are used to conduct this study. We analyzed the net-proton cumulants in Au+Au collisions at =3.5, 4.0, 4.9, 7.7 and 19.6 GeV for STAR acceptance and =3.5, 4.0, 4.9 for CBM acceptance.
Although PHQMD offers the flexibility to explore by changing the input parameters, resource and storage constraints prevented the generation of 2 million minimum-bias events for every QGP-ON and QGP-OFF scenario involving physical clustering. To study how the centralitywise
,
differs for the QGP ON and QGP OFF case, we have compared 2 million minimum bias events for the
= 7.7 GeV. Our analysis, based on varying model parameters, focuses on results obtained using a reduced maximum impact parameter of
fm (
value is obtained as
fm by using the Glauber model [
18]), corresponding to the 0-5% most central collision events. This data set allows us to investigate and compare the effects of physical clustering and QGP dynamics under top central collision condition.
In the model calculations, we have not applied the volume fluctuations whereas this analysis technique has been used in the real data analysis of STAR. Instead of applying volume fluctuation, we performed the analysis considering smaller bin width. We determined centrality using the multiplicity distribution of all particles, whereas the STAR experiment employed a different method for centrality determination in BES-II [
19] for centrality determination. In addition, the Delta theorem method [
20,
21] has been used to estimate the statistical error in cumulants. In this paper, we focus on the results from the 0-5% most central Au+Au collisions events and also centrality dependent results.
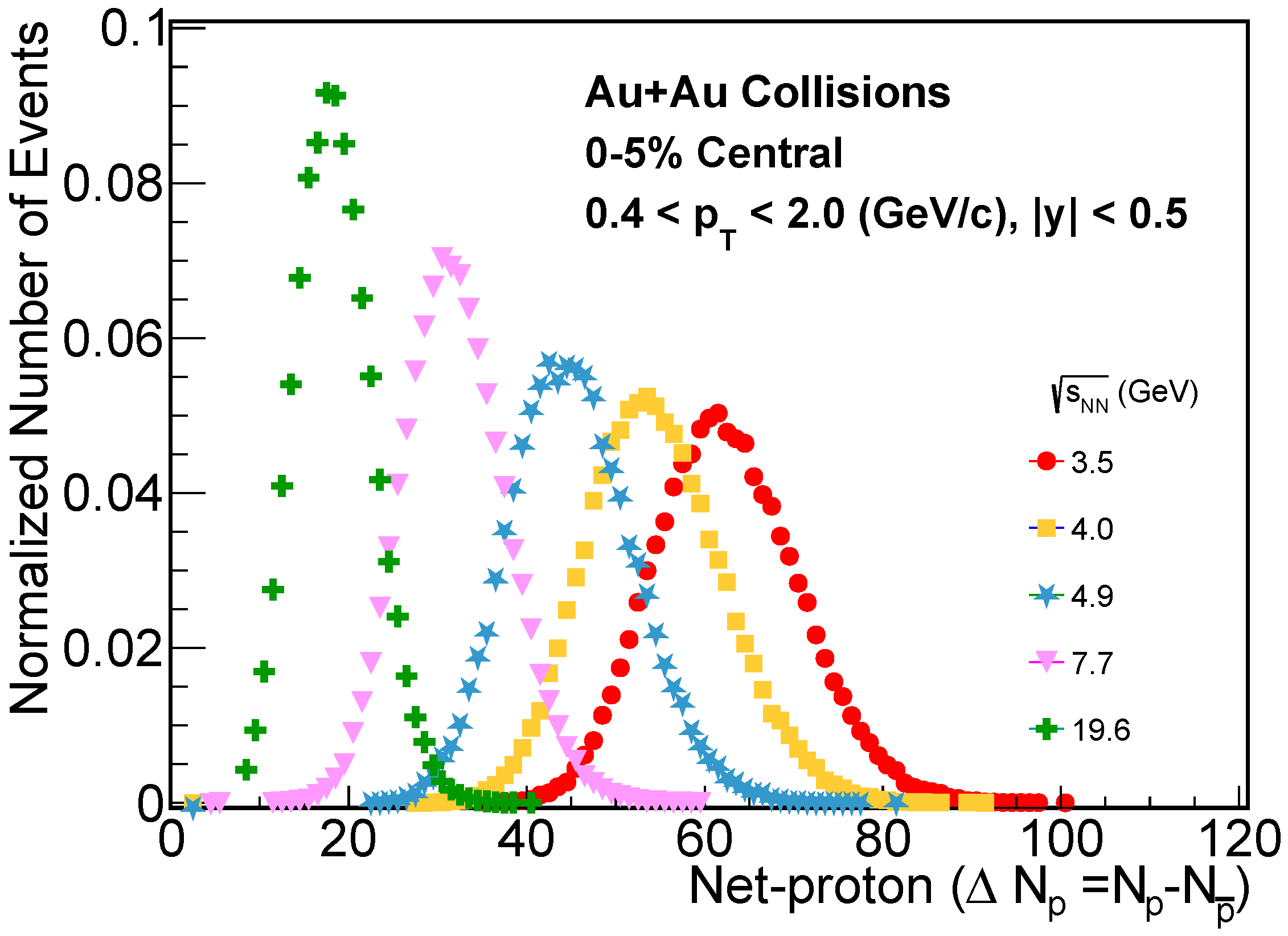
Figure 1 shows the net-proton multiplicity distributions for 0-5% collision centrality for Au+Au collisions at different collision energies from 3.5 GeV to 19.6 GeV considering the STAR acceptance. With increasing energy, proton number as well as net-proton number decrease because the net baryon number tend to be zero at higher energy range.
Figure 2 and
Figure 3 shows the centrality dependence of net-proton cumulants (
) up to the fourth order in Au+Au collisions from PHQMD model for STAR and CBM acceptance, respectively. In
Figure 2, the cumulant values tend to deviate towards the central collisions, while for the peripheral collisions, the values are close to zero across all energies. The trend observed in the net-proton
(mean) reflects an increase in particle production, favoring matter over antimatter, as collisions go from peripheral to central. Similarly, the
(variance) rises due to the same effect. As both proton and antiproton yields increase with the increasing centrality, the variance of their distributions also becomes larger. It is important to note that higher-order cumulants are associated with greater statistical uncertainties.
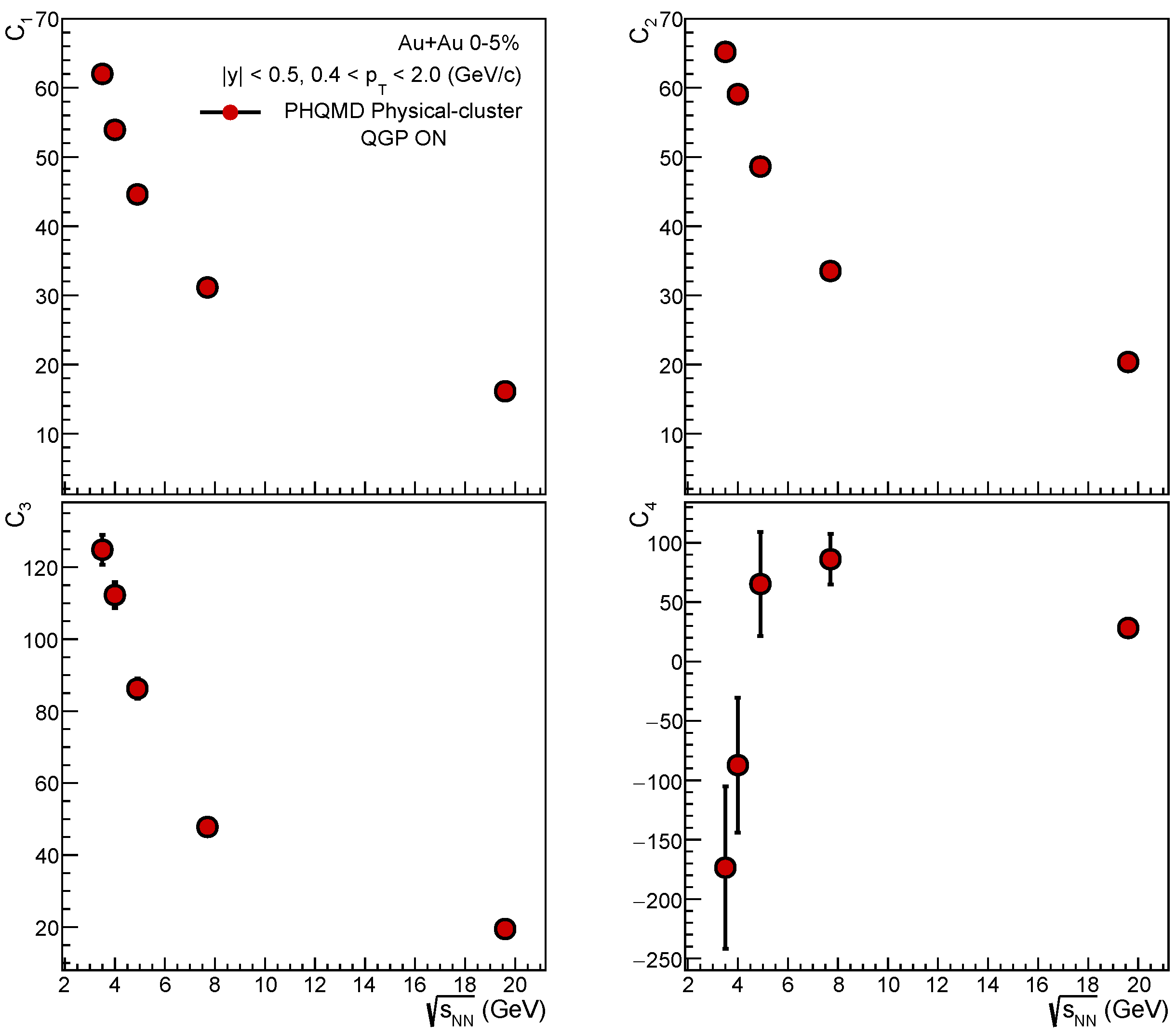
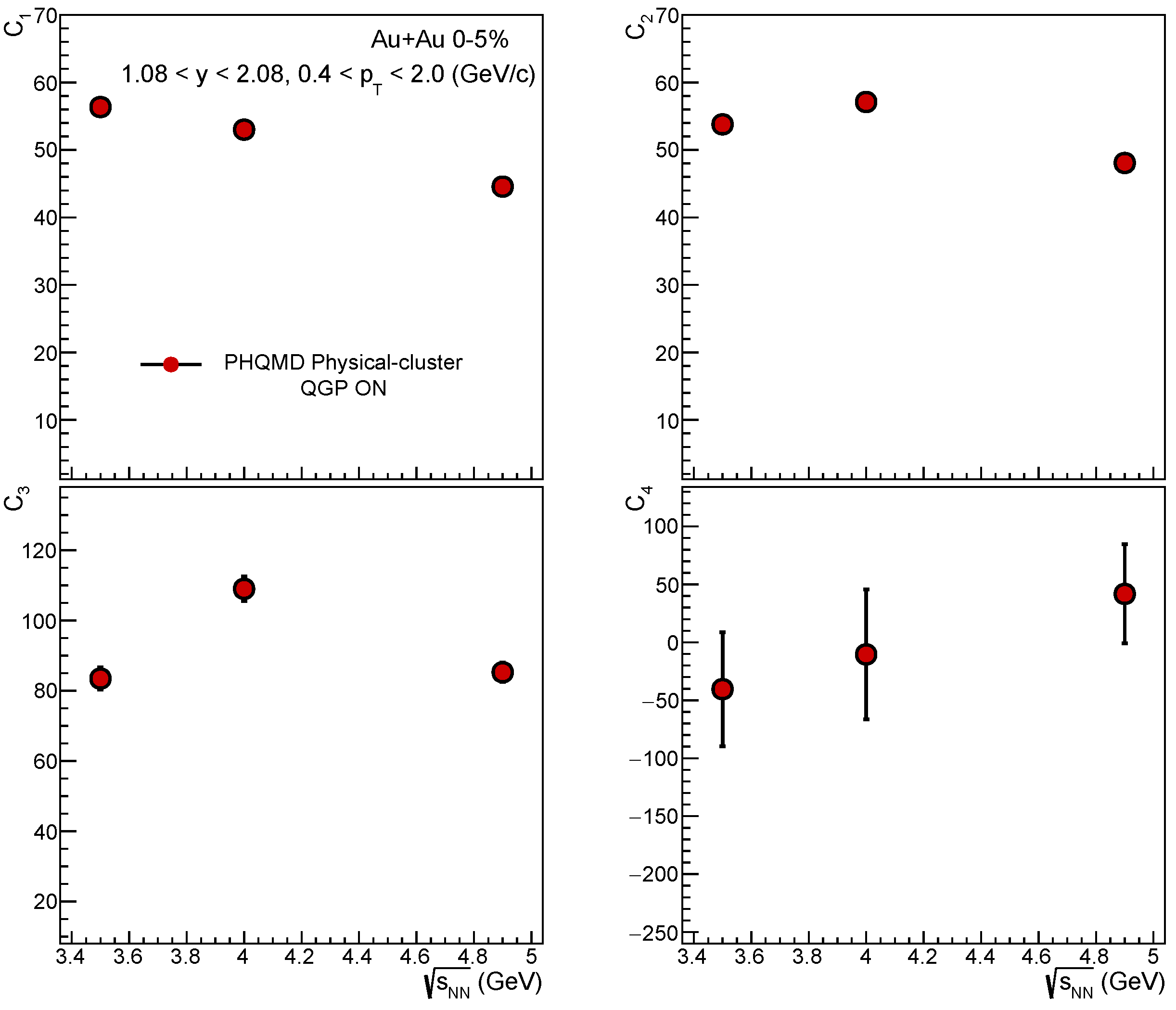
Figure 4 and
Figure 5 shows the same observables as in
Figure 2 and
Figure 3, but for 0-5% central events and here we replace the centrality with
in the x-axis in the corresponding
y and
cut for STAR acceptance and CBM acceptance. For
,
and
, the cumulant values decrease with increase in
but for
opposite trend has been seen with more statistical error for lower energies. In
Figure 2,
Figure 3,
Figure 4 and
Figure 5 the error bars for
,
, and
are not visibly prominent, as they lie mostly within the marker size. However, for
, being a higher-order cumulant, the statistical fluctuations are larger, resulting in clearly visible error bars.
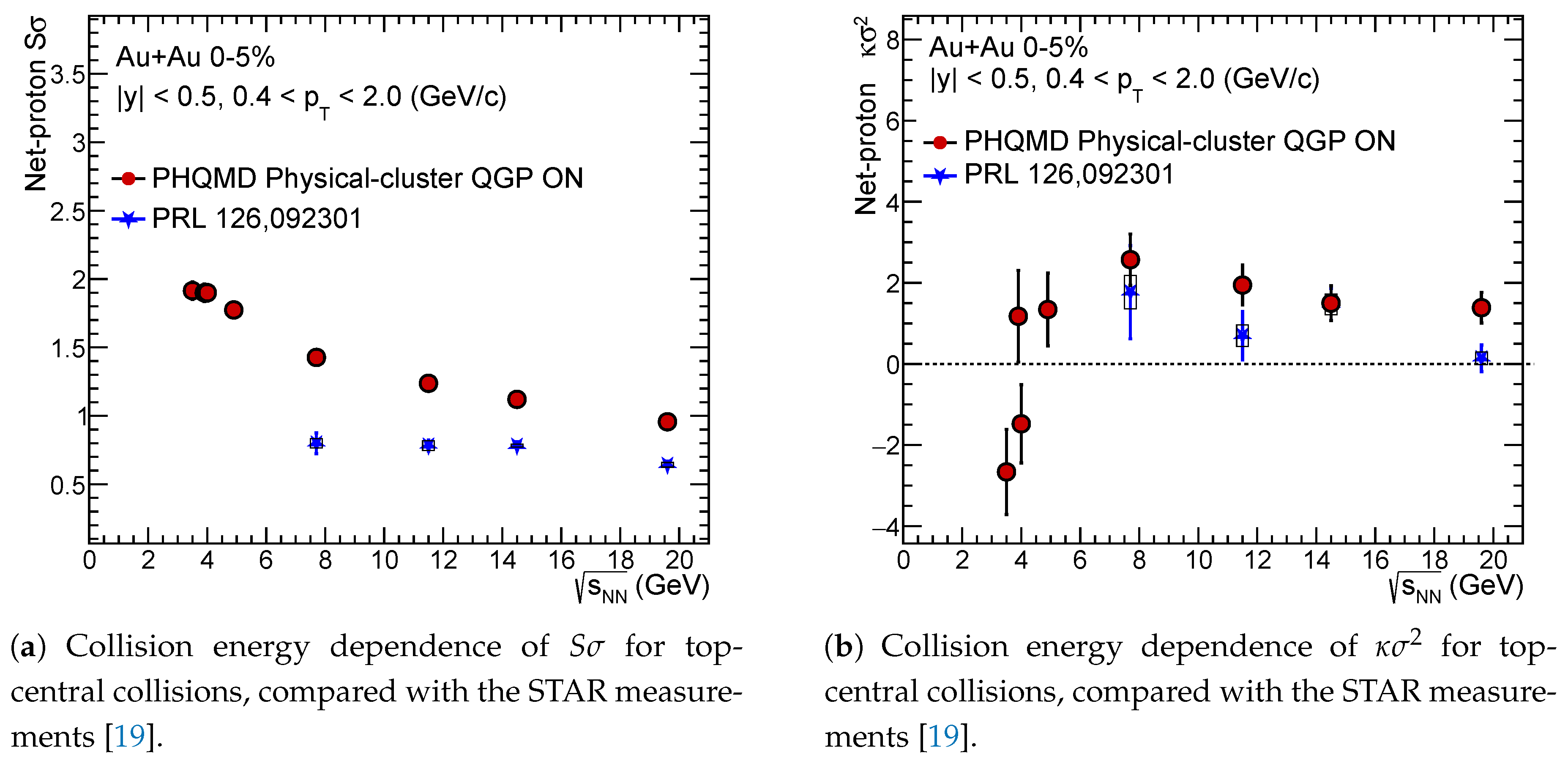
The collision energy dependence of the cumulant ratios,
(
Figure 6a) and
(
Figure 6b) for net-proton distributions in Au+Au collisions with PHQMD model generated data are presented at the energy range
= 3.5-19.6 GeV considering the STAR acceptance. To eliminate volume dependence, the ratios of cumulants of different orders are utilized. The results are shown for the most central (0-5%) collisions. The STAR data [
19] are compared to calculations of PHQMD without a critical point.
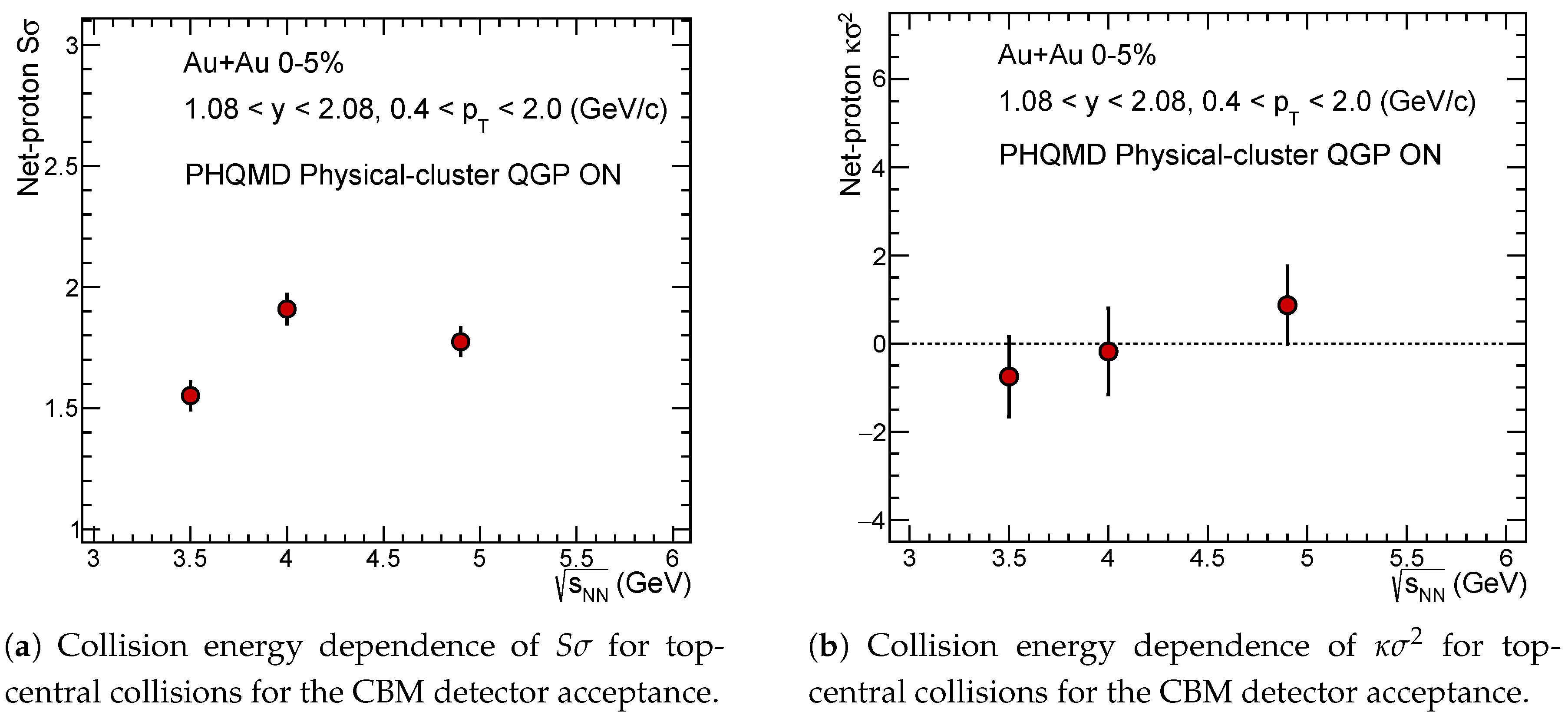
Figure 7a,b show the
and
of net-proton distribution for top central PHQMD data for the CBM acceptance.
values are negative at lower energies but appear to approach zero or slightly positive at higher energies. This might suggest a non-Gaussian distribution, possibly reflecting critical dynamics or non-Poissonian fluctuations.
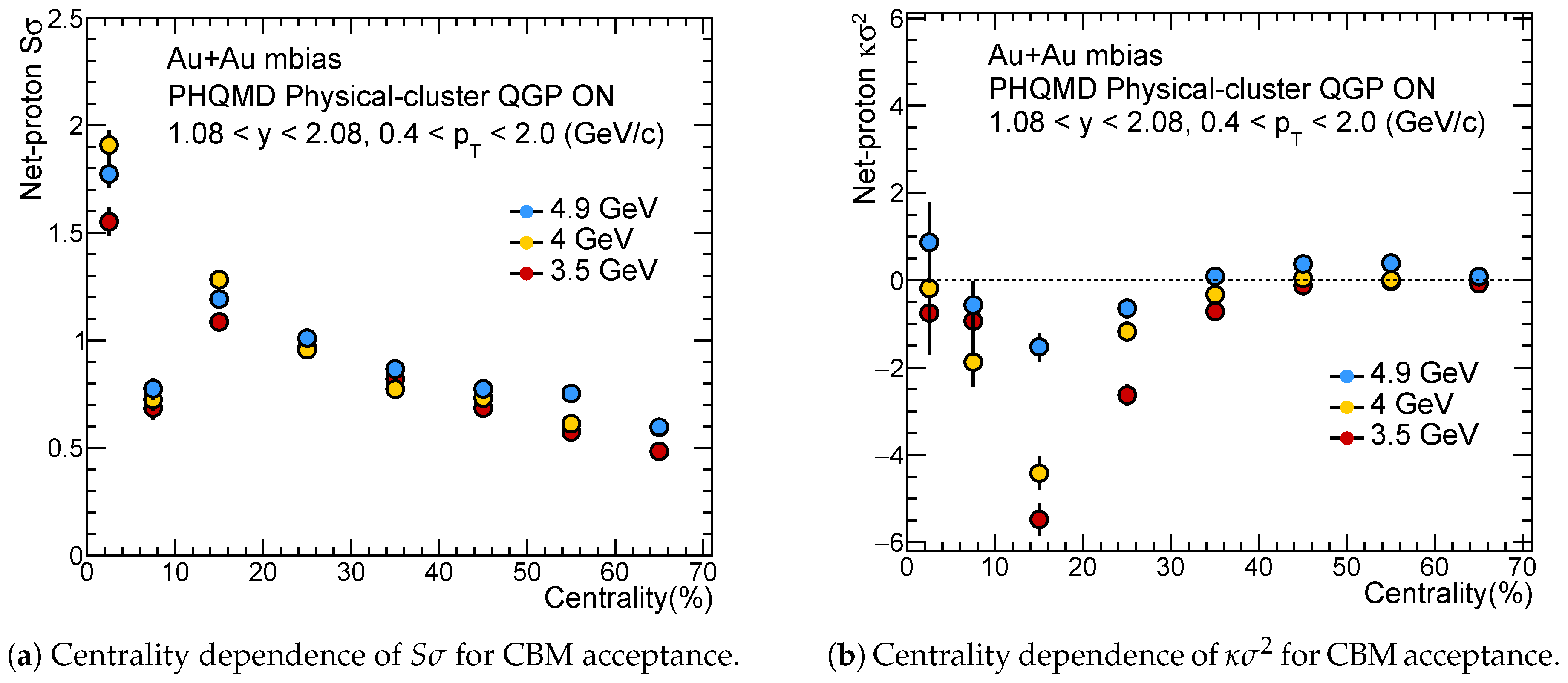
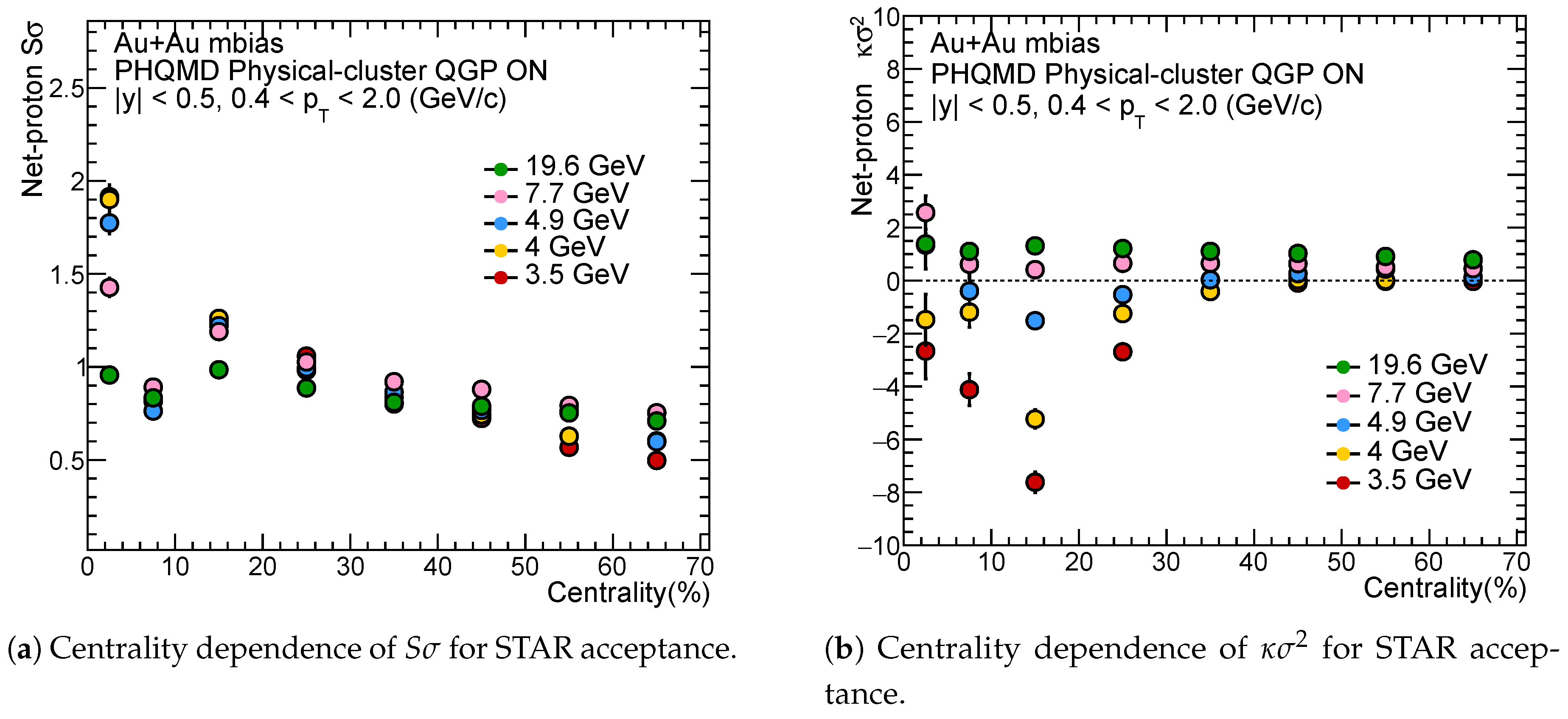
Figure 8a,b shows the centrality dependence of cumulant ratios of net-proton in PHQMD data for Au+Au collisions at
= 3.5-19.6 GeV for STAR acceptance. In case of CBM acceptance, the centrality dependence of
and
are shown in
Figure 9a,b, respectively. Overall
decrease from central to peripheral collisions and more pronounced negative
values at lower energies and in central events. For the energy range
–4.9 GeV, the values of
(
Figure 8b) initially decrease with centrality and then exhibit a rise in the peripheral region. In contrast, for higher beam energies such as 7.7 and 19.6 GeV,
decreases with centrality and remains approximately constant towards the peripheral region.
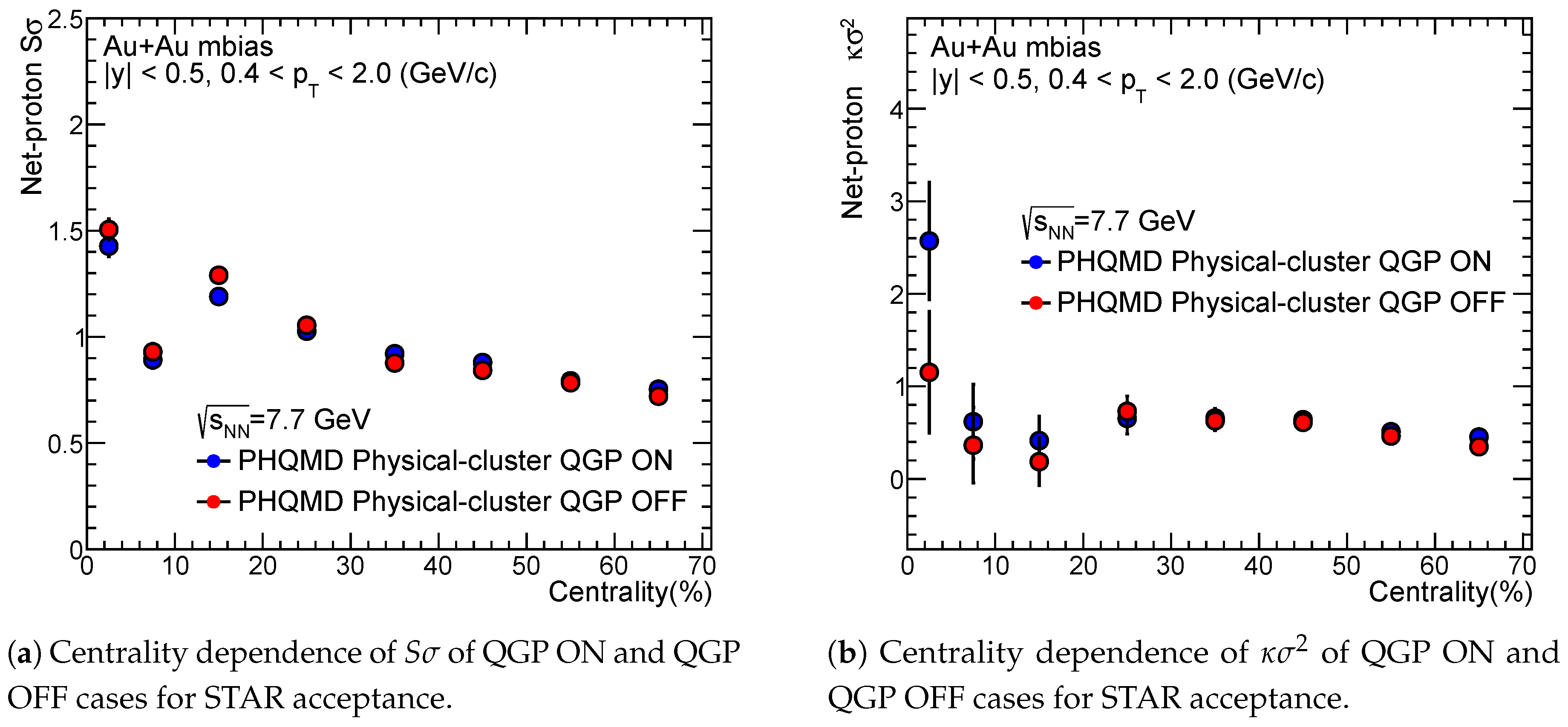
We present the comparison of centrality dependent PHQMD results for QGP ON and QGP OFF scenarios, showing
and
of the net-proton multiplicity distribution in Au+Au collisions at
GeV, within the STAR acceptance in the
Figure 10. In the
Figure 10a, both the blue (QGP ON) and red (QGP OFF) points show a decreasing trend with centrality, indicating that the values of
are more pronounced in central collisions. The difference between QGP ON and OFF is small but visible at central collisions, where QGP effects are expected to be stronger due to higher energy density.
At the top central collisions (0–5%), there is a noticeable difference between the QGP ON (blue) and QGP OFF (red) scenarios, which we can see in the
Figure 10b. QGP ON shows a significantly larger value of possibly reflecting enhanced critical fluctuations or non-Gaussian tails. At mid-central to peripheral collisions, both QGP ON and OFF values remain nearly constant and close to unity. Large error bars at top centrality reflect statistical uncertainty due to a lower number of events.
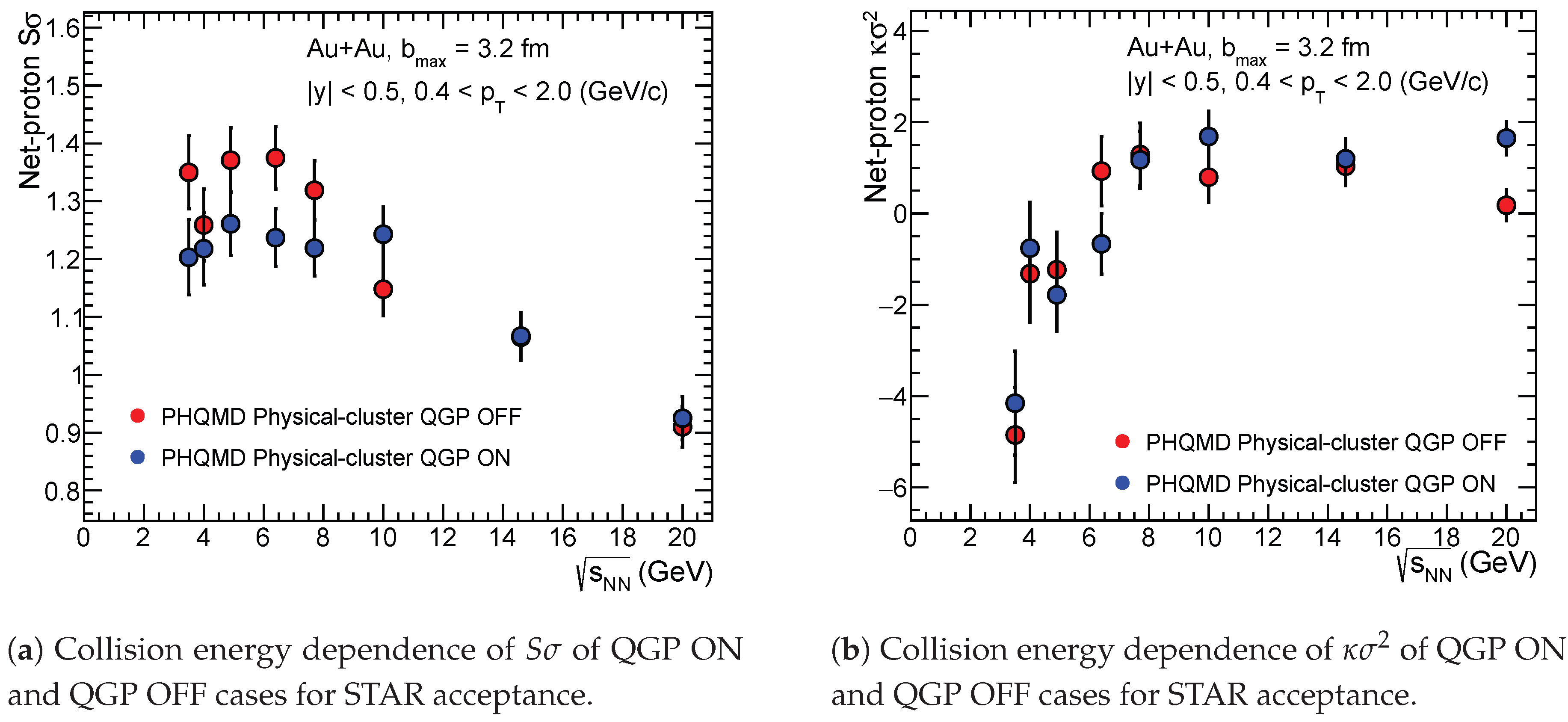
Figure 11 shows the collision energy dependence of net-proton fluctuations observables
and
obtained from PHQMD simulations for Au+Au collisions under STAR acceptance (
,
GeV/
c) with
fm. The results compare the scenarios with and without a QGP phase (QGP ON and QGP OFF). A noticeable difference is observed in
at lower energies (
GeV), where the QGP ON case shows suppressed values, suggesting a damping of fluctuations due to QGP formation. The
exhibits the non-monotonic behavior in both cases, with a slightly stronger suppression in the QGP ON scenario.
5. Discussion
It is important to note that in peripheral collisions, the system formed may not reach the necessary temperature and density to undergo a phase transition or approach the QCD critical point. Therefore, our calculations mainly focus on the most central collisions. The STAR Collaboration [
19] observed a non-monotonic energy dependence of net-proton kurtosis (
) in central Au+Au collisions, suggesting possible signatures of the QCD critical point. In contrast, peripheral collisions showed a monotonic trend consistent with non-critical models. Within uncertainties, the values of
of our analysis are consistent with STAR experimental data for central (0-5%) Au+Au collisions energy for 7.7 & 14.5 GeV. The fluctuations decrease with increasing centrality, showing some abrupt behavior in the 5–10% centrality range in
Figure 8a and
Figure 9a. For
, similar irregularities are observed in
Figure 8b and
Figure 9b, particularly within the 0–30% centrality range. Using our generated dataset, we investigated the differences between the QGP ON and QGP OFF scenarios as implemented in the PHQMD model. A clear distinction is observed in the
values for central (0–5%) Au+Au collisions at
GeV within the STAR acceptance in the
Figure 10b, highlighting the sensitivity of higher-order fluctuations to the presence of a QGP phase. The results shown in the
Figure 11 considering
=3.2 fm indicate that the presence of a QGP phase can significantly influence net-proton fluctuation observables, particularly at lower collision energies, where a suppression in
and a stronger non-monotonic trend in
are observed in the QGP ON scenario.
The exploration of the energy region ( = 3.0 - 4.9 GeV) with precision measurements is currently underway using STAR’s FXT program. It is important to note that the PHQMD model does not explicitly incorporate the critical point in its current implementation. While a non-monotonic behavior in observables such as is often regarded as a potential signal for the existence of the QCD critical point, its presence alone does not provide conclusive evidence.
Furthermore, conventional transport models like UrQMD do not account for realistic cluster formation, which plays a significant role in the evolution and final-state composition of the system. In contrast, PHQMD includes a dynamic cluster formation mechanism, allowing for the generation of light nuclei and fragments based on nucleon correlations in phase space. This aspect provides a more realistic scenario for studying fluctuations of conserved quantities, particularly in the high baryon density regime relevant to FAIR energies. As a result, PHQMD offers a more comprehensive framework for investigating fluctuation observables in heavy-ion collisions. The upcoming CBM experiment will explore this region and is expected to provide high-statistics data. A significantly higher-statistics dataset is required to investigate the QCD critical point.
6. Conclusions
By maintaining n-body correlations and dynamically modeling interactions from early to late stages, PHQMD enhances the capabilities of earlier models and offers a comprehensive picture of both hadronic and partonic matter, as well as cluster and hypernuclei formation in heavy-ion collisions.
Fluctuations of conserved quantities-such as baryon number, electric charge, and strangeness-are considered sensitive probes in heavy-ion collisions for investigating the QCD phase transition and identifying the critical point. The STAR experiment has reported measurements of the moments of net-proton distributions in Au+Au collisions over a collision energy range of
= 7.7-200 GeV [
19]. The PHQMD calculations for
are consistent with the trend of STAR data for the most central 0-5% Au+Au collisions within current uncertainties, whereas the same for
slightly overestimate the data.
QCD-based model calculations suggest that net-proton fluctuations are particularly sensitive observables. In this study, the cumulant ratios of net-proton distributions from PHQMD simulations display a non-monotonic trend as a function of collision energy within the CBM energy range, albeit within the current statistical uncertainties. This analysis offers new insights into the behavior of net-proton fluctuations in the CBM energy domain and contributes to establishing a baseline for interpreting net-proton and net-baryon fluctuations. Such a baseline is essential for future high-statistics measurements with the CBM experiment aimed at probing possible critical phenomena near the QCD critical end point.
Author Contributions
Rudrapriya Das - Conceptualization, Methodology, Software, Validation, Formal Analysis, Investigation, Data Curation, Writing – Original Draft Preparation, Visualization; Anjali Sharma - Software, Methodology, Data Curation, Writing – Review & Editing, Susanne Glaessel- Software, Data Curation, Methodology, Writing – Review & Editing; Supriya Das - Writing – Review & Editing, Supervision.
Funding
Rudrapriya Das acknowledges the Inspire Fellowship [DST/INSPIRE Fellowship/2020/ IF200305], and Anjali Sharma is grateful for financial support from grant SR/MF/PS-02/2010.
Acknowledgments
The authors want to thank to the PHQMD group, especially Prof. Elena Bratkovskaya, for her valuable suggestions. Authors acknowledge Dr. Sanchari Thakur for the fruitful discussion relevant to this study.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Aoki, Y. and Endrődi, G. and Fodor, Z. and Katz, S. D. and Szabó, K. K. The order of the quantum chromodynamics transition predicted by the standard model of particle physics. Nature, Springer Science and Business Media LLC., 2006, 443, 1476–4687. [Google Scholar]
- Ejiri, S. Canonical partition function and finite density phase transition in lattice QCD. Phys. Rev. D, 2008, 78. [Google Scholar] [CrossRef]
- Bowman, E.S.; Kapusta, J.I. Critical Points in the Linear Sigma Model with Quarks. Phys. Rev. C, 2009, 79, 015202. [Google Scholar] [CrossRef]
- Stephanov, M. A. QCD phase diagram and the critical point. Int. J. Mod. Phys. A, 2005, 20, 4387. [Google Scholar] [CrossRef]
- Gavai, R.V.; Gupta, S. QCD at finite chemical potential with six time slices. Phys. Rev. D, 2008, 78, 114503. [Google Scholar] [CrossRef]
- Ejiri, S. and Karsch, F. and Redlich, K. Hadronic fluctuations at the QCD phase transition. Phys. Lett. B 2006, 633, 275.
- Stephanov, M. A. Non-Gaussian fluctuations near the QCD critical point. Phys. Rev. Lett. 2009, 102, 032301. [Google Scholar] [CrossRef] [PubMed]
- Stephanov, M.A. On the sign of kurtosis near the QCD critical point. Phys. Rev. Lett., 2011, 107, 052301.
- Schaefer, B. J. and Wagner, M. QCD critical region and higher moments for three flavor models. Phys. Rev. D, 2012, 85, 034027. [Google Scholar] [CrossRef]
- Schaefer, B.J.; Wagner, M. QCD critical region and higher moments for three flavor models. Phys. Rev. Lett., 2009, 103, 262301. [Google Scholar] [CrossRef]
- Gupta, S; Luo, X.; Mohanty, B.; Ritter, H.G.; Xu, Nu. Scale for the Phase Diagram of Quantum Chromodynamics. Science 2011, 332, 1525–1528. [Google Scholar] [CrossRef] [PubMed]
- Aichelin, J. Quantum molecular dynamics: A Dynamical microscopic n body approach to investigate fragment formation and the nuclear equation of state in heavy ion collisions. Phys. Rept., 1991, 202, 233–360. [Google Scholar] [CrossRef]
- Marty, R. and Aichelin, J. Molecular dynamics description of an expanding q/q¯ plasma with the Nambu–Jona-Lasinio model and applications to heavy ion collisions at energies available at the BNL Relativistic Heavy Ion Collider and the CERN Large Hadron Collider. Phys. Rev. C, 2013, 87(3), 034912.
- Marty, R., Bratkovskaya, E., Cassing, W., and Aichelin, J. Observables in ultrarelativistic heavy-ion collisions from two different transport approaches for the same initial conditions. Phys. Rev. C, 2015, 92(1), 015201.
- Cassing, W. From Kadanoff-Baym dynamics to off-shell parton transport. Eur. Phys. J. ST, 2009, 168, 3–87. [Google Scholar] [CrossRef]
- Cassing, W. and Bratkovskaya, E. L. Parton transport and hadronization from the dynamical quasiparticle point of view. Phys. Rev. C, 2008, 78, 034919. [Google Scholar] [CrossRef]
- Puri, C, H., and J., A. Early fragment formation in heavy-ion collisions. Phys. Rev. C Nucl Phys., 2008, 54, R28–R31.
- Miller, Michael L. and others. Glauber modeling in high energy nuclear collisions. Ann. Rev. Nucl. Part. Sci., 2007, 57, 205-243.
- Adam, J. and others. Nonmonotonic Energy Dependence of Net-Proton Number Fluctuations. Phys. Rev. Lett., 2021, 126, 9, 092301.
- Luo, X. Error Estimation for Moments Analysis in Heavy Ion Collision Experiment. J. Phys. G, 2012, 39, 025008. [Google Scholar] [CrossRef]
- Luo, X. Unified description of efficiency correction and error estimation for moments of conserved quantities in heavy-ion collisions. Phys. Rev. C, 2015, 91, 3, 034907.
Figure 1.
Event-by-event net-proton number distribution for top central (0-5%) Au+Au collisions from PHQMD.
Figure 1.
Event-by-event net-proton number distribution for top central (0-5%) Au+Au collisions from PHQMD.
Figure 2.
Cumulants (, , , ) of net-proton multiplicity distribution from = 3.5 – 19.6 GeV as a function of collision centrality in the STAR acceptance (<0.5, 0.42.0) with PHQMD.
Figure 2.
Cumulants (, , , ) of net-proton multiplicity distribution from = 3.5 – 19.6 GeV as a function of collision centrality in the STAR acceptance (<0.5, 0.42.0) with PHQMD.
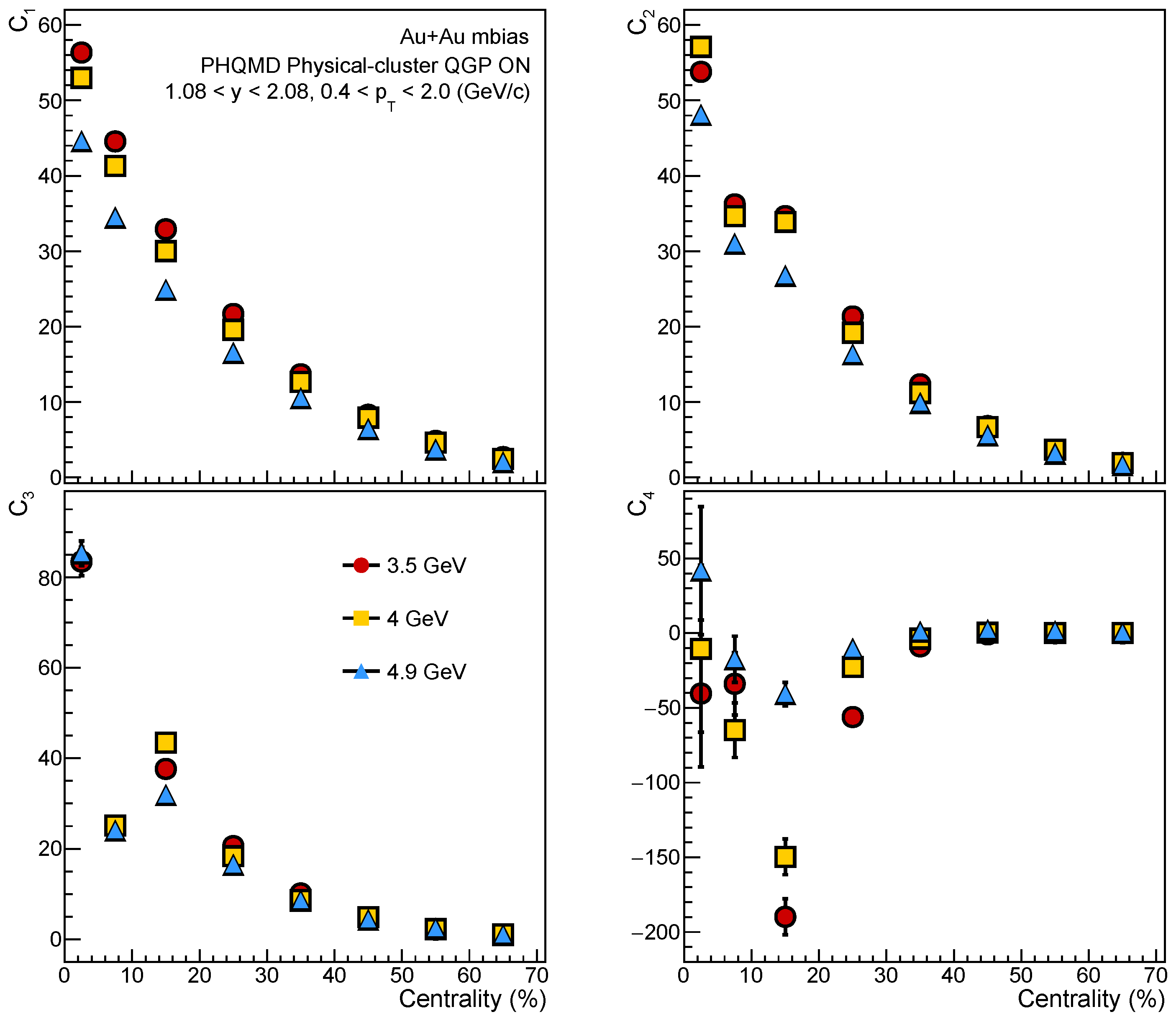
Figure 3.
Cumulants (, , , ) of net-proton multiplicity distribution for = 3.5, 4.0 and 4.9 GeV as a function of collision centrality in the CBM acceptance (1.082.08, 0.42.0) with PHQMD.
Figure 3.
Cumulants (, , , ) of net-proton multiplicity distribution for = 3.5, 4.0 and 4.9 GeV as a function of collision centrality in the CBM acceptance (1.082.08, 0.42.0) with PHQMD.
Figure 4.
Cumulants (, , , ) of net-proton multiplicity distribution from = 3.5 – 19.6 GeV as a function of collision energy in the STAR acceptance (<0.5, 0.42.0) with PHQMD.
Figure 4.
Cumulants (, , , ) of net-proton multiplicity distribution from = 3.5 – 19.6 GeV as a function of collision energy in the STAR acceptance (<0.5, 0.42.0) with PHQMD.
Figure 5.
Cumulants (, , , ) of net-proton multiplicity distribution as a function of collision energy in the CBM acceptance (1.082.08, 0.42.0) with PHQMD.
Figure 5.
Cumulants (, , , ) of net-proton multiplicity distribution as a function of collision energy in the CBM acceptance (1.082.08, 0.42.0) with PHQMD.
Figure 6.
Collision energy dependence of (a) and (b) of net-proton multiplicity distribution in Au+Au collisions for STAR ( = 3.5-19.6 GeV) acceptance with PHQMD.
Figure 6.
Collision energy dependence of (a) and (b) of net-proton multiplicity distribution in Au+Au collisions for STAR ( = 3.5-19.6 GeV) acceptance with PHQMD.
Figure 7.
Collision energy dependence of (a) and (b) of net-proton multiplicity distribution in Au+Au collisions for CBM ( = 3.5-4.9 GeV) acceptance with PHQMD.
Figure 7.
Collision energy dependence of (a) and (b) of net-proton multiplicity distribution in Au+Au collisions for CBM ( = 3.5-4.9 GeV) acceptance with PHQMD.
Figure 8.
Centrality dependence of (a) and (b) of net-proton multiplicity distribution in Au+Au collisions for STAR ( = 3.5-19.6 GeV) acceptance with PHQMD.
Figure 8.
Centrality dependence of (a) and (b) of net-proton multiplicity distribution in Au+Au collisions for STAR ( = 3.5-19.6 GeV) acceptance with PHQMD.
Figure 9.
Centrality dependence of (a) and (b) of net-proton multiplicity distribution in Au+Au collisions for CBM ( = 3.5-4.9 GeV) acceptance with PHQMD.
Figure 9.
Centrality dependence of (a) and (b) of net-proton multiplicity distribution in Au+Au collisions for CBM ( = 3.5-4.9 GeV) acceptance with PHQMD.
Figure 10.
Comparison between QGP ON and QGP OFF cases for centrality dependence PHQMD results of (a) and (b) of net-proton multiplicity distribution in Au+Au collisions for STAR acceptance at = 7.7 GeV.
Figure 10.
Comparison between QGP ON and QGP OFF cases for centrality dependence PHQMD results of (a) and (b) of net-proton multiplicity distribution in Au+Au collisions for STAR acceptance at = 7.7 GeV.
Figure 11.
Comparison between QGP ON and QGP OFF cases for collision energy dependence PHQMD results of (a) and (b) of net-proton multiplicity distribution in Au+Au collisions for STAR acceptance considering =3.2 fm for 0.1 million events.
Figure 11.
Comparison between QGP ON and QGP OFF cases for collision energy dependence PHQMD results of (a) and (b) of net-proton multiplicity distribution in Au+Au collisions for STAR acceptance considering =3.2 fm for 0.1 million events.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).