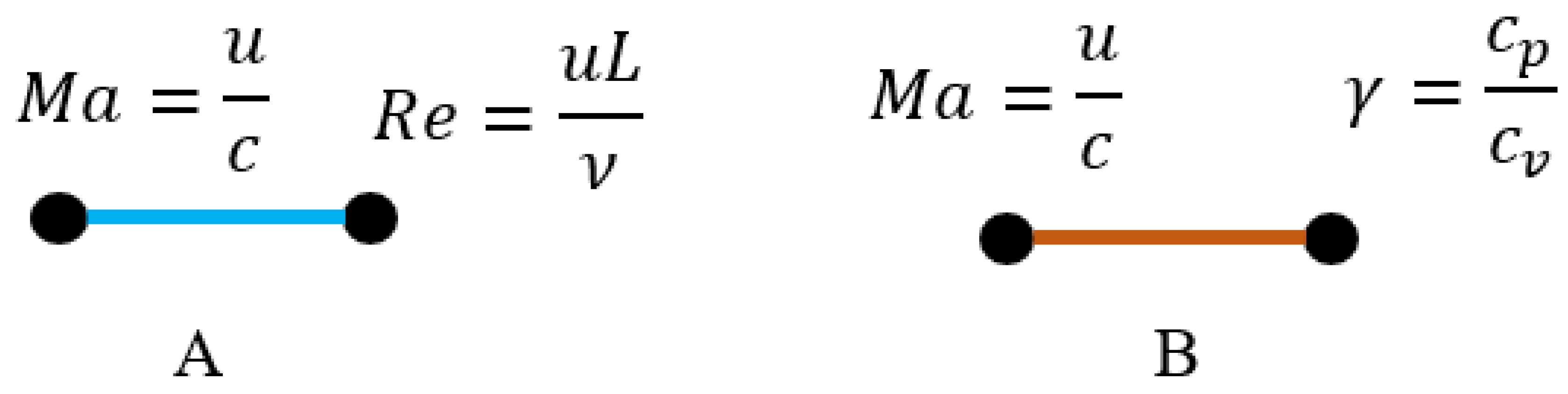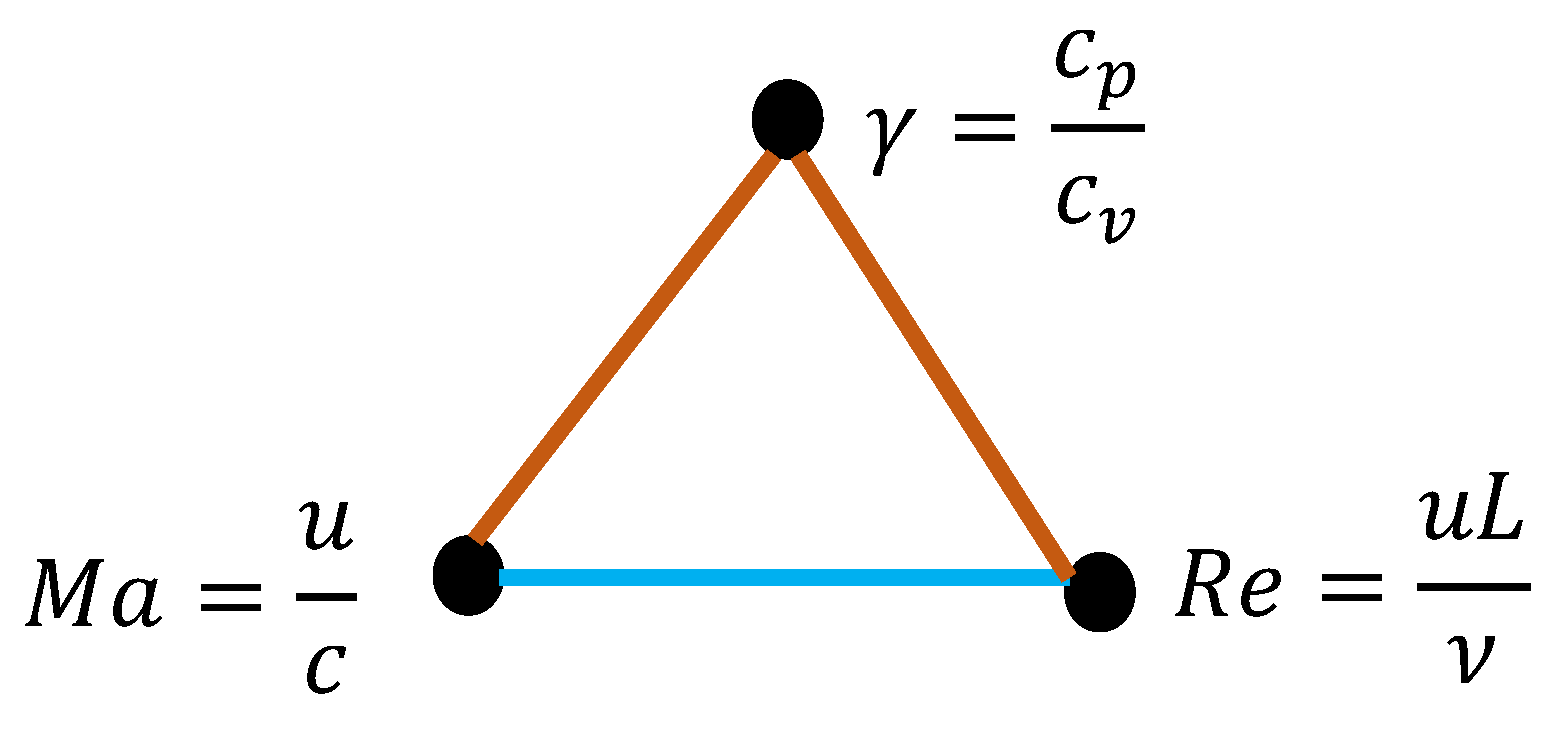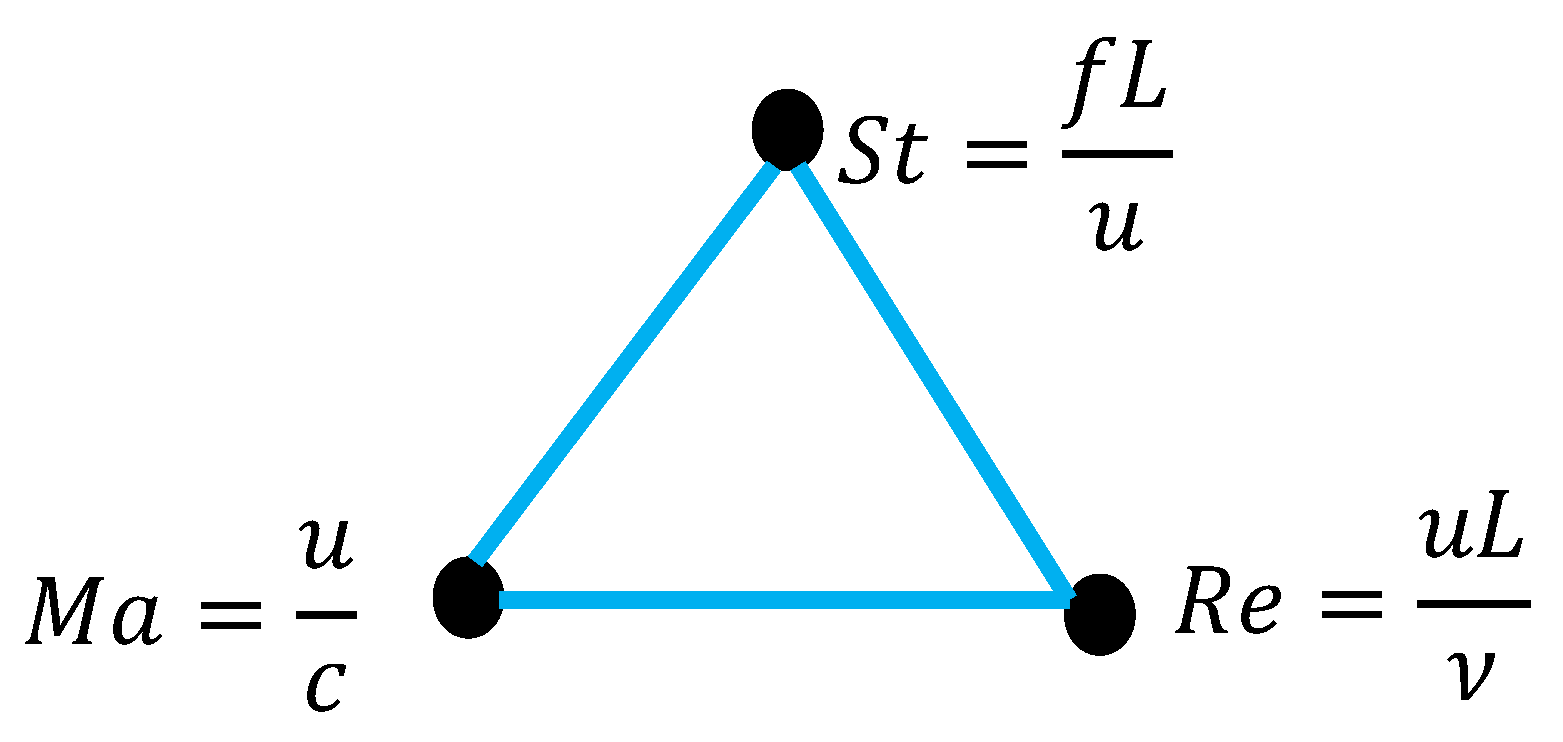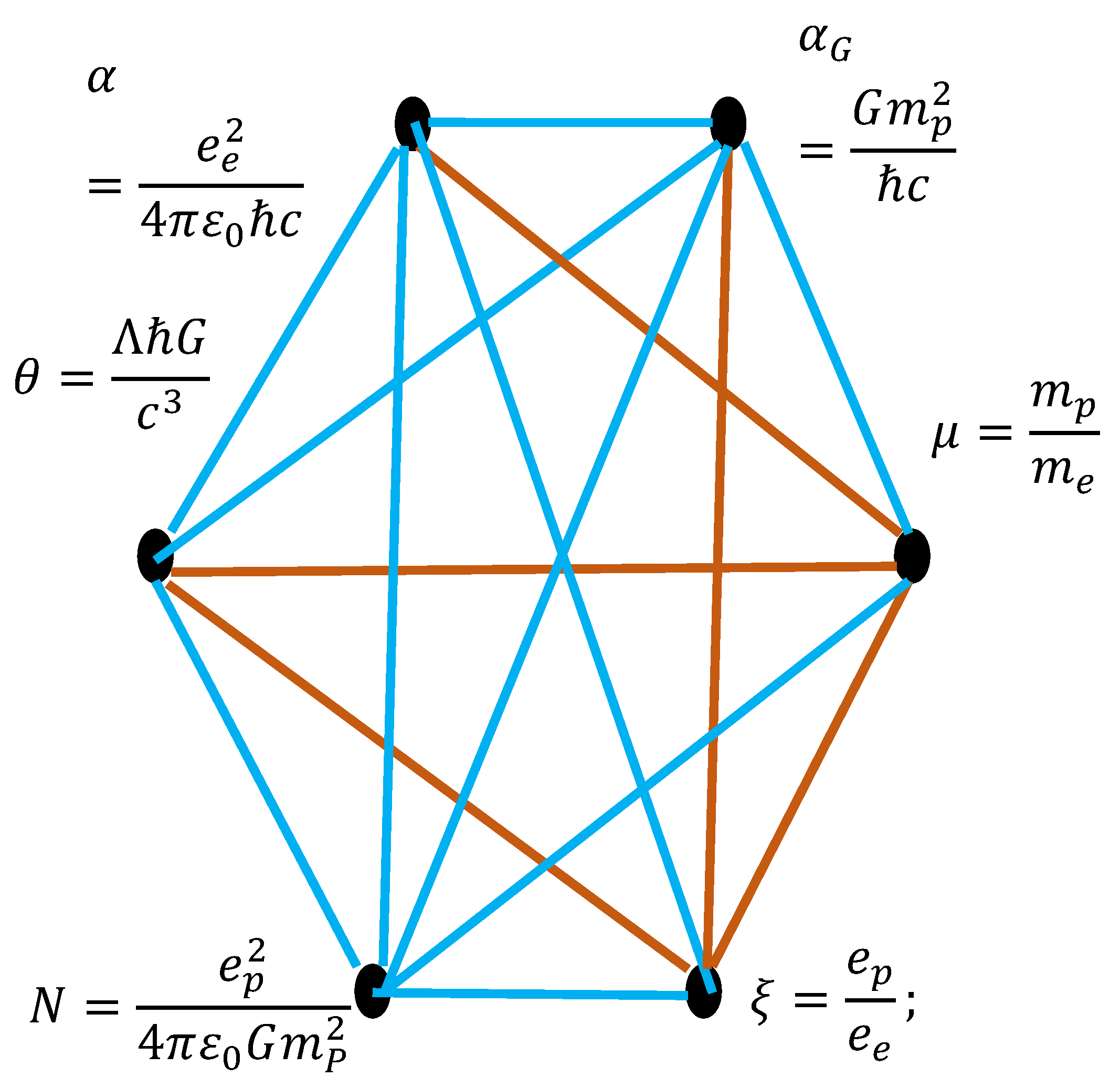Advanced Ramsey Dimensional Analysis

1. Introduction

The dimensional analysis, introduced by Joseph Fourier, James Clerk Maxwell and developed by Lord Rayleigh remains one of the most powerful, important and elegant approaches for qualitative analysis and solving of physical problems [1,2,3,4,5]. The dimensional analysis is based on the extremely simple, intuitively clear, however, fundamental idea: physical laws do not depend on arbitrarily chosen basic units of measurement. In spite of its simplicity, the dimensional analysis enables obtaining remarkably deep, general and important results, including the progress in the theories of gravity and turbulence [3,6]. Recently the principle of dimensional invariance was embedded into a two-level machine learning scheme to automatically discover dominant dimensionless numbers and governing laws (including scaling laws and differential equations) from scarce measurement data [4].

One of the basic theorem of dimensional analysis is the famous so-called Buckingham $\pi$-theorem [4,5,6,7]. Consider the arbitrary physical system, described by a number of physical quantities/parameters denoted $Q_i(i=1,\dots ,n)$ and their ratios denoted $r_j\left(j=1,\dots l\right).$ The most general form of physical equations, describing behaviour of this system is given by Equation (1):

$$f\left(Q_1,Q_2\dots Q_n,r_1,\dots ,r_l\right)=0$$

(1)

If it is assumed that the ratios do not vary during the evolution of the system described by the equation, i.e., the system remains similar to itself during the changes of quantities/parameters $Q_i(i=1,\dots ,n)$, Equation (1) is reduced to Equation (2):

$$f\left(Q_1,Q_2\dots Q_n\right)=0$$

(2)

The seminal Buckingham theorem (which is also known the “$\pi$ - theorem”) states, that Equation (2) may be re-shaped in the terms of $\zeta$ dimensionless parameters $\zeta =n-k$, where k is the maximal number of values possessing independent dimensions among n values of parameters $Q_i$, denoted $Q_m,\left(m=1,\dots ,k\right).$ Parameters $Q_m(i=1,\dots ,k)$ are considered as dimensionally independent, if the dimensions of any of $Q_m$ cannot be expressed through dimensions of other quantities from that subset [7,8,9]. Although named for Edgar Buckingham, the “π-theorem” was first proved by the French mathematician Joseph Bertrand in 1878 [10]. From the pure mathematical point of view, the Buckingham theorem is rooted in the rank-nullity theorem of the linear algebra [11]. Our paper presents the new approach to the dimensional analysis, which is complementary to the Buckingham theorem. This approach is based on the Ramsey theorem, applied in its graph form. One of the most advanced fields of modern mathematics is a graph theory, which was extensively developed in last decades [12,13,14,15,16,17,18,19]. Mathematical graph is a structure used to represent pairwise relationships between objects. Simply and briefly speaking, graphs represent a set of objects and a set of pairwise relations between them [12,13,14,15,16,17,18,19]. It consists of vertices/nodes, which are the fundamental units or points of the graph and edges/links, which are the connections between the vertices [12,13,14,15,16,17,18,19]. One of the varieties of graphs are the so-called “colored graphs”, which are graphs, where colors are assigned to its elements, typically vertices or edges [12,13,14,15,16,17,18,19]. The classical result in theory of colored graph is the Ramsey theorem, which states that for any pair of positive integers r and s, there exists a smallest integer $R\left(r,s\right)$, called the Ramsey number, such that: in any aqua-brown edge coloring of the complete graph $K_n$ with $n\ge R\left(r,s\right)$ vertices, there exists either: an aqua-colored clique of size r (i.e., a set of r vertices where every pair is connected by an aqua edge), or a brown-colored clique of size s (i.e., a set of s vertices where every pair is connected by a brown edge) [18,19]. In particular, if we have bi-colored graph, built of six vertices, it will inevitably contain at least one mono-colored triangle, in other words $R\left(\mathrm{3,3}\right)=6.$

2.1. Graph Analysis of Dimensional Problems

Let us introduce the procedure enabling converting the dimensional analysis of the problem into the bi-colored, complete graph. We examplify our approach with the compressible fluid/gas flow in a nozzle [20,21,22]. This problem is described with three dimensionless constants ($\pi$ – groups) namely: the Mach number Ma, the Reynolds number Re and the specific heat ratio $\gamma$, i.e., the triad of condtants, supplied by Equation (3):

$$Ma={\displaystyle \frac{u}{c}};Re={\displaystyle \frac{uL}{\upsilon }};\gamma ={\displaystyle \frac{c_p}{c_v}}$$

(3)

where u is the velocity of flow, c is the sound speed, L is the characteristic spatial scale, $\nu$, $c_{p}and{c}_v$ are the kinematic viscosity, and the thermal capacities of the fluid/gas corrrespondingly. This problem illustrates perfectly the Buckinghem theorem. Indeed, the full list of relevant physical values is: $Q_i(i=1,\dots ,6)=\left\{u,c,L,\nu ,c_p,c_v\right\}$, the set of dimensionally independent values is $Q_m(m=1,\dots ,3)=\left\{u,L,c_p\right\}$. Thus, $\mathsf{\zeta }=n-k=6-3=3$ dimensionless $\pi$-groups will describe the problem. These dimensionless Buckingham $\pi$-groups are listed in Equation (3). Now we introduce the mathematical procedure enabling converting the dimensionless groups and relations between them into a bi-colored graph The dimemensionless contstants, i.e.,: $Ma,Re$ and $\gamma$ serve as the vertices of the graph, as shown in Figure 1.

The vertices are connected with the aqua link when they contain at least one common physical value. Different physical values possessing the same dimensions (u and c) are considered as different, distinguishable values. The Mach number Ma and the Reynolds number Re contain the common for both of them physical value and it is the characterstic velocity u. These vertices are connected with the aqua-colored link, as depicted in inset A of Figure 1. In contrast, the Mach number $Ma$ and and the specific heat ratio $\gamma$ do not contain any common physical value. These vertices are connected with the brown link, as shown in inset B of Figure 1.

Now we present the complete, bi-colored graph emerging from the dimensional analysis of the compressible fluid flow in a nozzle. This graph, depicted in Figure 2 is addressed by the Ramsey theory [12,13]. Recall that, a complete graph is a type of graph in mathematics (specifically in graph theory) in which every pair of distinct vertices is connected by a unique edge [12,13].

Figure 2 illustrates a very important idea: the property “to be connected with a brown” link is not transitive. Vertices Ma and $\gamma$ are connected with a brown link, and vertices $\gamma$ and Re are connected with a brown link; and it is does not imply that vertices Ma and Re are necessarily connected with the brown link.

Figure 2 depicts the bi-colored, complete graph, adressed by the Ramsey theory. It should be mentioned that mono-colored triangles built on the dimensionless constants, seen as vertices of the graph, are possible. Consider oscillatory phenomena occuring in incompressible liquids described by the triad of dimensionless constants, supplied by Equation (4):

$$Ma={\displaystyle \frac{u}{c}};Re={\displaystyle \frac{uL}{\upsilon }};St={\displaystyle \frac{fL}{u}}$$

(4)

where St is the Strouhal number, and f is the oscillation or vortex shedding frequency. The full list of relevant physical values is: $Q_i(i=1,\dots ,5)=\left\{u,c,f,L,\nu \right\}$, the set of dimensionally independent values is $Q_m(m=\mathrm{1,2})=\left\{f,L,\right\}$. Thus, $\mathsf{\zeta }=n-k=5-2=3$ dimensionless $\pi$-groups will describe the problem. However, in this case the graph corresponding to the problem will be monochromatic.

We label the graphs depicted in Figure 2 and Figure 3 as the “dimensions graphs”. The dimensions graph depicted in Figure 3 is monochromatic due to the fact that all of the vertices/dimensionless numbers contain the velocity of the flow, denoted u; i.e., the triad of the dimensionless numbers is velocity-dependent.

Obviously, the property “to be connected with an auqa-link” is not necessarily transititive, i.e., if groups ${\pi }_i$ and ${\pi }_k$ are connected with an aqua-colored-link and groups ${\pi }_k$ and ${\pi }_l$are also connected with an aqua-colored-link, it does not necessarily imply that groups ${\pi }_i$ and ${\pi }_l$are connected with the aqua-colored-link. Non-transitivity of the connection is crucial for the future application of the Ramsey theorem for the analysis of the dimensions graphs.

2.2. Dimensions Graphs Built of Six Vertices and the Ramsey Theorem

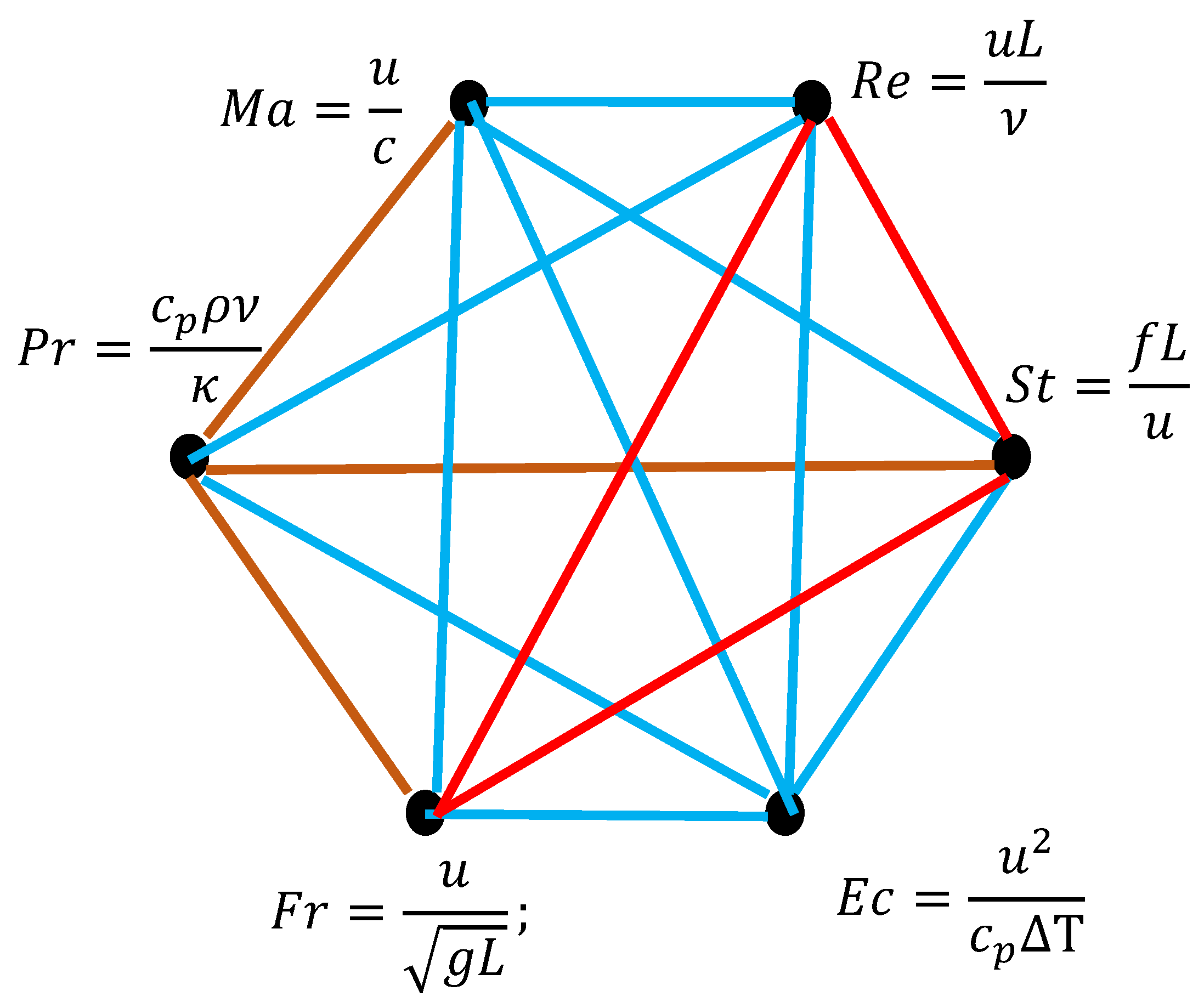
Consider now the flow of a incompressible, viscous, heat-conducting fluid under general/non-simplified conditions. This complex hydrodynamic system is governed by the Navier–Stokes equations (for momentum), the continuity equation (for mass conservation), and the energy equation (for heat transfer) [20,21,22]. This problem is typically quantified with six dimensionless numbers, listed in Equation (5):

$$Ma={\displaystyle \frac{u}{c}};Re={\displaystyle \frac{uL}{\upsilon }};St={\displaystyle \frac{fL}{u}};Pr={\displaystyle \frac{c_p\rho \nu }{\kappa }};Fr={\displaystyle \frac{u}{\sqrt{gL}}};Ec={\displaystyle \frac{u^2}{c_p\Delta \mathrm{T}}}$$

(5)

where Pr, Fr and Ec are the Prandtl, Froude and Eckert numbers correspondingly, $\rho$ and $\upsilon$ are density and kinematic viscosity of the liquid, $\Delta T,$ is the difference between wall temperature and local temperature and g is gravity. The Prandtl number Pr quantifies the ratio of momentum diffusivity to thermal diffusivity $\kappa$, the Eckert number Ec expresses the relationship between a flow’s kinetic energy and the boundary layer enthalpy difference, and is used to characterize heat transfer dissipation. 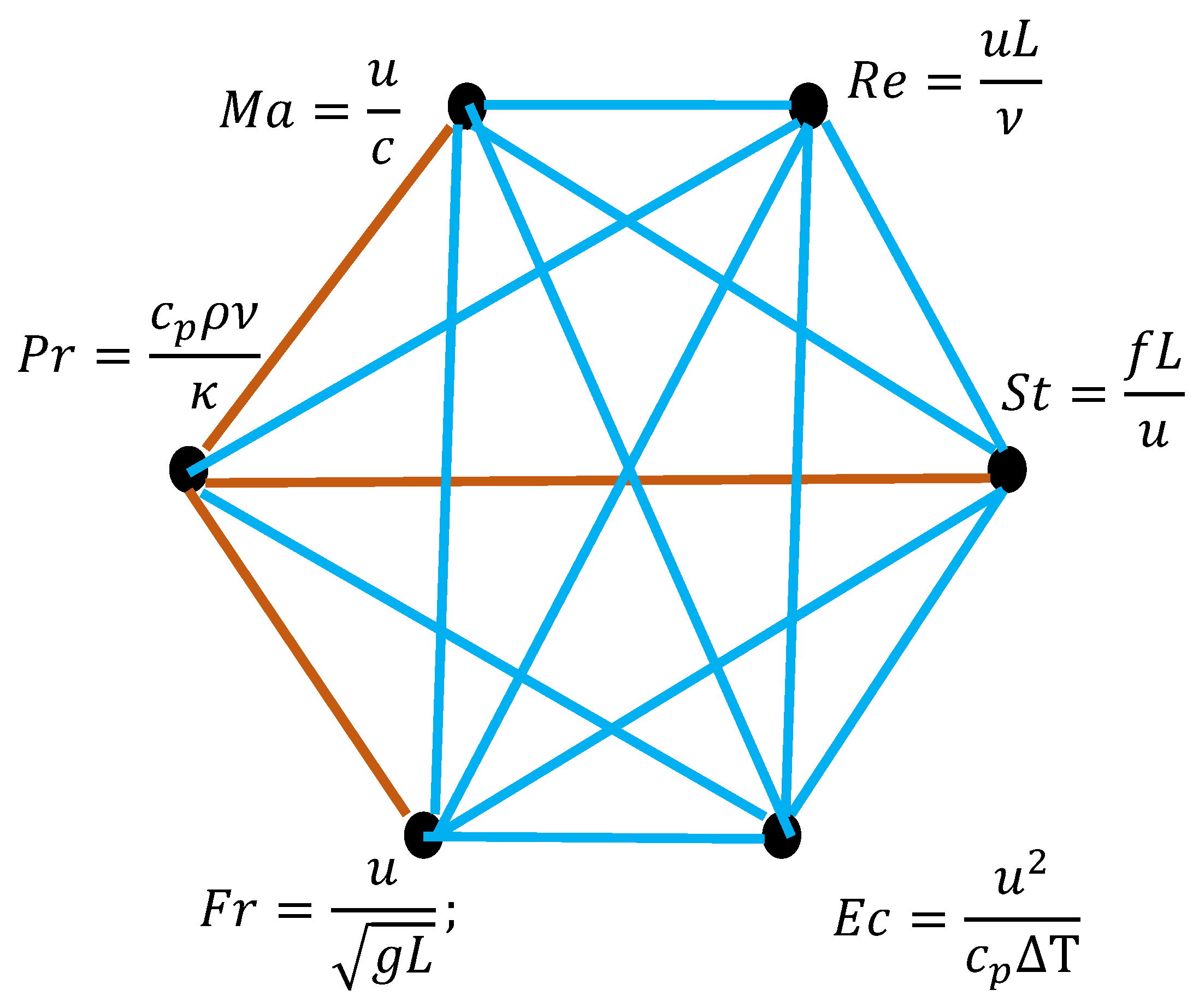The Froude number Fr defines the ratio of the flow inertia to gravity g. Let us built the dimensions graph; dimensionless $\pi -$groups listed in Equation (5) serve as the vertices of the graph, depicted in Figure 4.

The full list of relevant physical values is: $Q_i(i=1,\dots ,10)=\left\{u,c,f,L,\nu ,T,\rho ,\kappa ,c_p,g\right\}$. The set of dimensionally independent values is $Q_m(m=1,\dots 4)=\left\{f,L,T,\rho \right\}$. Thus, according to the Buckingham theorem $\mathsf{\zeta }=n-k=10-4=6$ dimensionless $\pi$-groups/vertices appear in the dimensions graph; and this is the case shown in Figure 4.

The graph, containing six $\pi -\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}\mathrm{s}/$vertices is of a particular interest. According to the seminal Ramsey theorem the Ramsey number $R\left(\mathrm{3,3}\right)=6$[17,18] (see the Introduction Section). Thus, the bi-colored, complete graph containing six vertices inentably includes at least one mono-colored triangle. Indeed, triangles $\left\{Ma,Fr,Ec\right\}$, $\left\{Pr,Re,Ec\right\}$ $\left\{Ma,Re.Ec\right\}$, $\left\{Ma,St,Ec\right\}$,$\left\{Ec,St,Re\right\}$,$\left\{Ma,Re,St\right\},\left\{Re,St,Fr\right\},$and $\left\{Ma,St,Fr\right\}$ are monochromatic aqua-colored ones. The mono-chromatic triangle will be present in any dimensions compete, bi-colored graph built of six vertices. Moreover, for a given problem changing the order of the vertices of the dimension graph does not change the distribution of monochromatic triangles. When we permute the vertices of the dimension graph, we are simply relabeling them. This does not affect the edge colors; it just changes their names. Therefore, the structure of the dimension graph remains the same, and so does the number and type of monochromatic triangles. Thus, we demonstrated the following theorem:

Theorem

Consider the dimensions graph built of six vertices. Every vertex represents the dimensionless number ($\pi$ –group) built of dimensional physical values. Vertices are connected with the aqua-colored link, when they contain at least one dimensional physical value common for both vertices. Vertices are connected with a brown link, when they do not contain any physical value common for both vertices. The dimensions graph inevitably contains at least one mono-colored triangle, whatever aqua- or brown-colored.

Straightforward application of the Ramey theorem became possible due to the fact that the relations “to be connected with the aqua-colored link” and “to be connected with the brown link” are both non-transitive. This is illustated with triangles $\left\{Pr,Ec,Fr\right\}$, $\left\{Pr,Ec,Ma\right\}$ and $\left\{Pr,St,Ma\right\}$. The Ramsey numbers for the graphs in which vertices are related with transitive relations are different from the “regular non-transitive Ramsey numbers” [23].

Now we address the physical meaning of the Ramsey analysis of the dimension graph. Ramsey theory, simply speaking, asserts that if some set of objects is large enough, the prescribed patterns are guaranteed to appear. In our case, the Ramsey theorem states that the mono-chromatic triangle will necessarily appear in any dimensions graph built of six vertices. This, surprising result does not follow from Buckingham theorem. Thus, it is complementary to the Buckingham theorem. If the monochromatic triangle is aqua-coloured, this means that the triad of physical phenomena, depending on the same physical value/pair of the same physical values is necessarily present in the graph. Consider, for example, the aqua-coloured triangle $\left\{Ma,Re,St\right\}.$ The triad of its vertices contains the velocity of the flow u. Thus, we have in our problem the triad of flow-velocity-dependent physical phenomena. The same is true for the triangles $\left\{Ma,Fr,Ec\right\},\left\{Re,St.Ec\right\}.$ On the other hand, the triangle $\left\{Pr,Re,Ec\right\}$ does not contain any physical value common for all of its vertices/$\pi$-groups.

If the monochromatic triangle is brown-coloured, we have a triangle representing a triad of independent physical events. Regrettably, the Ramsey theorem does not predict the exact colour of the mono-coloured triangle to be present in the graph built of six vertices [18,19].

The Buckingham $\pi$-theorem guarantees the existence of dimensionless groups, but it does not uniquely specify which groups to choose. The set of dimensionless groups is not unique, and there can be many mathematically valid, but physically different, choices. Our choice of $\pi$-groups should be physically justified, and this choice is defined until now by our physical intuition. So, various dimensions graphs, related to the same physical problem are possible, and their analysis is based on our physical understanding of the problem.

2.2. Dimensions Graph and Fundamental Physical Constants

Now we apply the developed approach to the analysis of the dimensionless numbers built of fundamental physical constants. We disconnect from the specific physical problem and address dimensionless numbers uniting basic physical constants. The set of addressed dimensionless numbers include:

$$\begin{gathered} \alpha ={\displaystyle \frac{e_e^2}{4\pi {\epsilon }_0\mathrm{\hslash }c}};{\alpha }_G={\displaystyle \frac{G{m}_p^2}{\mathrm{\hslash }c}};N={\displaystyle \frac{e_p^2}{4\pi {\epsilon }_{0}G{m}_P^2}};\mu ={\displaystyle \frac{m_p}{m_e}}; \\ \xi ={\displaystyle \frac{e_p}{e_e}};\theta ={\displaystyle \frac{\Lambda \hslash G}{c^3}}=\Lambda l_p^2 \end{gathered}$$

(6)

where $e_e$ and $m_e$ are the electrical charge and mass of electron, $e_p$ and $m_p$ are electrical charge and mass of proton, G and $\Lambda$ are the gravitation and cosmological constants, $\hslash$ and c are the Planck constant and light velocity in vacuum, and $l_p=\sqrt{{\displaystyle \frac{\hslash G}{c^3}}}$ is the Planck length. In Equation (6) $\alpha \cong {\displaystyle \frac{1}{137}}$ is the fine structure constant, which quantifies the strength of the electromagnetic interaction between elementary charged particles ${\alpha }_G\cong 5.9\times {10}^{-39}$ is the gravitation coupling constant, which measures the strength of gravity between two protons, analogous to the fine-structure constant for gravity; $\mu ={\displaystyle \frac{m_p}{m_e}}\cong 1836$ compares the mass of the proton to that of the electron, dimensionless constant N relates electric interaction between protons to gravitational interaction $N\cong 1.23\times {10}^{36},$the dimensional constant $\xi ={\displaystyle \frac{e_p}{e_e}}=1$ compares the charge of proton to that of electron, and $\theta ={\displaystyle \frac{\Lambda \hslash G}{c^3}}=\Lambda l_p^2=2.87\times {10}^{-122}$; this extremely small dimensionless number is often cited in discussions of the cosmological constant problem, indicating how unnaturally small the observed value is relative to Planck-scale expectations. Let us respresent these numbers with the dimensions graph, depicted in Figure 5.

The scroll of dimensional physical quantities includes now

$$Q_i\left(i=1,\dots ,10\right)=\left\{m_p,m_e,e_p,e_e,G,\mathrm{\hslash },c,G,\Lambda ,{\epsilon }_0\right\}.$$

The set of dimensionally independent values is: $Q_m(m=1,\dots 4)=\left\{m_p,e_p,c,\hslash \right\}$. Thus, $\mathsf{\zeta }=n-k=10-4=6$ dimensionless groups/vertices appear in the bi-colored, complete dimensions graph; depicted in Figure 5. Recall that we use the SI system of units; this explains appearence of ${\epsilon }_0$ in the list of dimensional values. The Ramsey theorem states that at least one mono-colored triangle will be necessarily present in the graph. Indeed we recongnized aqua-colored triangles $\left\{\alpha ,\xi ,N\right\}$, $\left\{{\alpha }_G,\theta ,N\right\}$, $\left\{{\alpha }_G,\theta ,\alpha \right\}$ and $\left\{{\alpha }_G,\mu ,N\right\}$ and the brown triangle $\left\{\theta ,\mu ,\xi \right\}$ in the graph, shown in Figure 5. Let us analyze the mono-colored triangles. Values ${\epsilon }_0,e_e,e_p$ make the triangle$\left\{\alpha ,\xi ,N\right\}$aqua-colored. This means that just electrical phenomena unite the triad of dimensionless constants $\left\{\alpha ,\xi ,N\right\}$. Now consider the aqua-colored triangle $\left\{{\alpha }_G,\theta ,N\right\}$. Just the gravitation constant G makes it aqua-monochromatic. In other words, gravitation unites the triad of dimensionless constants $\left\{{\alpha }_G,\theta ,N\right\}.$ Address now the aqua-colored triangle $\left\{{\alpha }_G,\theta ,\alpha \right\}.$ Pair of fundamenal constants G and c make it monochromatic. Consider aqua-colored triangle $\left\{{\alpha }_G,\mu ,N\right\}.$ Just the proton mass $m_p$ makes it monochromatic, i.e., inertia/gravity joints the effects described by the triad of dimensionless constants $\left\{{\alpha }_G,\mu ,N\right\}$.

Now address the brown triangle $\left\{\theta ,\mu ,\xi \right\}$. The vertices of this triangle does not contain common physical values. This means that the triad of dimensionless values $\left\{\theta ,\mu ,\xi \right\}$ describe physical phenomena which are different in their physical nature.

Again, the dimensions graph emerging from the basic physical interactions is not unique [24]. A diversity of fundmental constants relating basic physical interactions was suggested [24]. In our future investigations we plan to address transformations of the dimensions graph, under various mathematical procedures.

2.3. Extension of the Ramsey Approach to-Multi-Colored Dimension Graphs

The introduced Ramsey approach is easily generalized for multi-colored dimensions graphs, such as those depicted in Figure 6, illustrating the flow of a incompressible, viscous, heat-conducting fluid, already discussed in Section 2.1. Now we contact two vertices with the red link, when they contain at least two physical values common for both of vertices/dimensionless groups. Indeed, Re, St and Fr numbers contain velocity u and characteristic spatial scale L, and they are connected with the red links, as shown in Figure 6.

The rest of edges coloring remains untouched. Now we recongize $\left\{Ma,Fr,Ec\right\}$, $\left\{Ma,Re,Ec\right\}$, $\left\{Ma,St,Ec\right\}$ aqua-colored triangles, and $\left\{Re,St,Fr\right\}$ red-colored triangle in the dimensions graph, presented in Figure 6. The red triangle $\left\{Re,St,Fr\right\}$ evidences the triad of physical phenomena, which are both dependent on the characteristic spatial scale L and velocity of the flow u. The same three-colored approach may be appplied for the analysis of complete graphs built of fundamental physical constants, such as the graph depicted in Figure 5. It is noteworthy that $R\left(\mathrm{3,3},3\right)=17$; hence, in the dimensions three-colored, complete graph built of 17 vertices will be necessarily present at least one mono-colored triangle.

2.4. Generalization of the Ramsey Approach to the Infinite Dimensions Graphs

The introduced approach may be generalized for infinite sets of dimensionless constants. Consider infinite, however, countable set of dimensionless constants. The constants are connected with the aqua-colored link if they contain at least one common for both of them physical value. The constants are connected with a brown link if they do not contain common for both of them physical value. In this case the infinite Ramsey theorem becomes apllicable. Let us rigorously formulate the infinite Ramsey theorem. Let $K_{\omega }$ denote the complete colored graph on the vertex set N. For every $\Gamma >0$, if we color the edges of $K_{\omega }$ with $\Gamma$ distinguishable colors, then an infinite monochromatic clique must be present [25]. An infinite monochromatic clique in a colored graph is a subset of vertices that are all pairwise-adjacent (in other words, that form a clique) and whose edges/links are all the same color in a given edge/link coloring of the given infinitegraph. The infinite Ramsey theorem re-formulates the well-known Dirichlet pigeonhole principle, which states that if n pigeonholes exist containing $n+1$ pigeons, one of the pigeonholes necessarily must contain at least two pigeons [25]. Thus, a monochromatic aqua-colored or brown-colored clique will necessarily appear in the infinite dimensions graph. The infinite Ramsey theorem does not predict the exact color of the monochromatic clique to be present in the infinite graph.

3. Conclusions

Ramsey theory is a branch of discrete mathematic/combinatorics that studies conditions under which order must appear in sufficiently large or complex systems, demonstrates an essential potential for physics. Its power lies in guaranteeing structure in sufficiently large systems. The immediate conclusion emerging from the Ramsey theory is formulated as follows: in sufficiently large systems the complete chaos is impossible. Patterns inevitably appear in the systems, when their size is larger than the critical one. At least one monochromatic triangle will inevitably appear in the complete, bi-colored graphs built of six vertices. In spite of this, the applications of the Ramsey theory to physical problems are still rare in occurrence [26,27].

We apply the Ramsey theory for revealing hidden patterns inherent for sets of dimensionless numbers, used for the qualitative analysis of physical problems. These dimensionless numbers are built from dimensional physical values, appearing in a given physical problem. The number of these dimensionless groups (known also as $\pi -\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}\mathrm{s})$ is established by the seminal Buckingham $\pi -\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{m},$ arising from the rank-nullity theorem of the linear algebra [7,8,9,10,11]. We suggest the mathematical scheme complementary to the Buckingham $\pi -$ theorem, based on the theory of complete, bi-colored graphs. Consider a given physical problem. Dimensionless $\pi -\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}\mathrm{s}$ defining qualitatively the system serve as the vertices of the graph. Vertices are connected with the aqua-colored link, when they contain at least one dimensional physical value common for both vertices. Vertices are connected, in turn, with a brown link, when they do not contain any physical value common for both vertices. Thus, the complete, bi-colored graph, labeled as the “dimensions graph” emerges. If this graph contains six vertices, it will inevitably contain at least one mono-colored triangle; whatever, aqua- or brown-colored.

We applied the suggested mathematical procedure, uniting Bickingham $\pi$ – groups into the bi-colored complete graph, for the analysis of the specific physical problem of the flow of a incompressible, viscous, heat-conducting fluid. This problem is qualitaively characterized with six dimensionless numbers ($\pi$- groups). Appearance and physical meaning of mono-chromatic triangles recognized within the graph were analyzed. The same mathematical scheme was applied for the analysis of the graph, built of dimensionless numbers comprising fundamental physical constants. It is noteworthy that the introduced dimensions graphs are invariant relatively to rotations of frames, but they are sensitive to the Galilean and Lorentz transformations. The suggested mathematical scheme is suitable for dimensional machine learning [4].

Generalization of the Ramsey graph approach, exploited for the analysis of multi-colored and infinite dimensions graphs is discussed. In our future investigations we plan to study the symmetry of the dimensions graphs.