Submitted:
19 May 2025
Posted:
20 May 2025
You are already at the latest version
Abstract

Keywords:
1. Introduction
2. Literature Review
3. Preliminaries
3.1. General Type-2 Fuzzy Sets
3.2. Interval Type-2 Fuzzy Sets
3.3. Arithmetic Operations in Type-2 Fuzzy Sets
3.4. Interval Type-2 Fuzzy VIKOR Method (IT2 F-VIKOR)
-
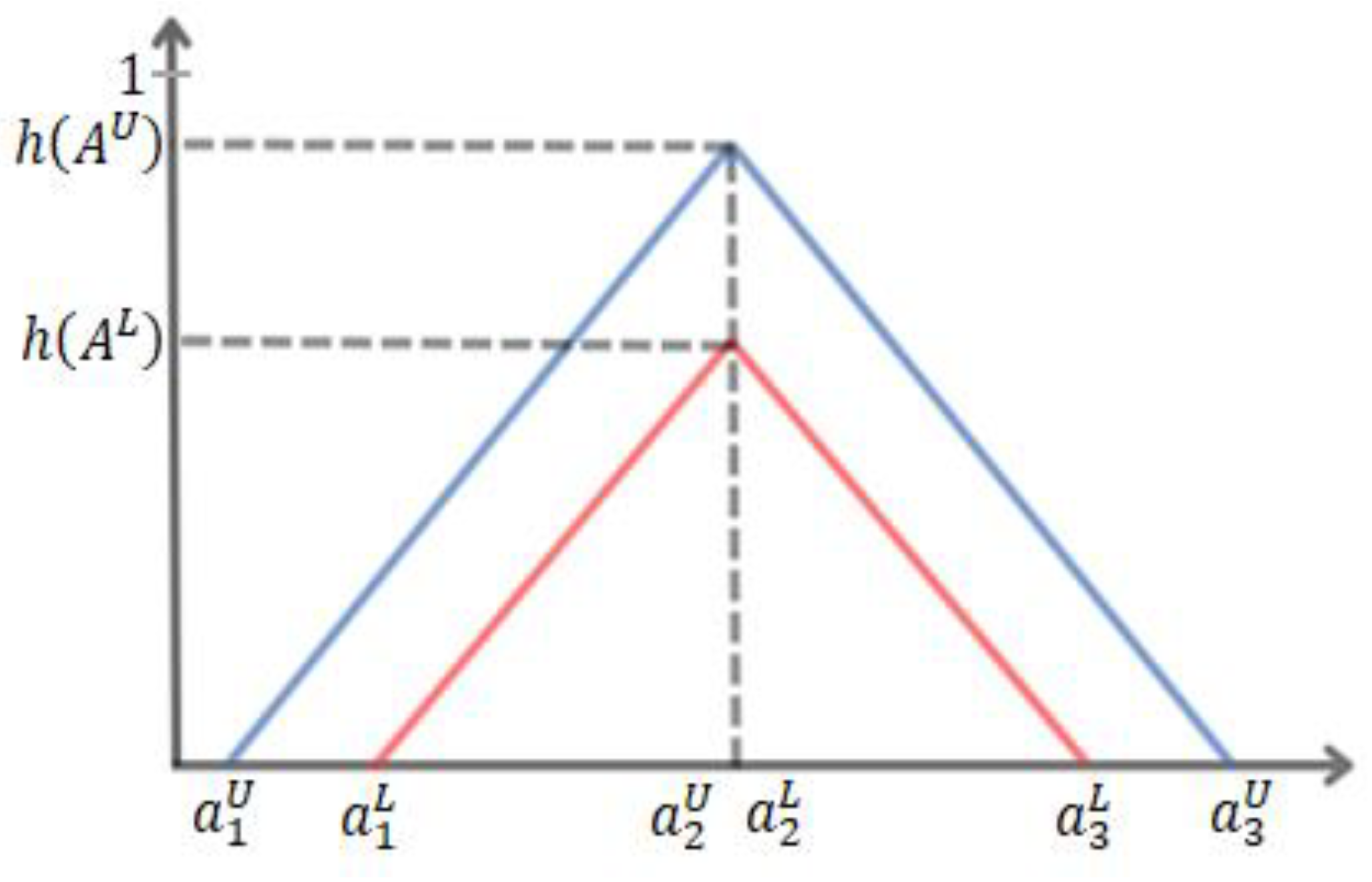
Transformation of Upper and Lower Membership Functions into Type-1 Fuzzy Sets: Here, to obtain a Type-1 fuzzy set, the average of the upper and lower membership functions is calculated.Here; represents the value of the upper membership function, and represents the value of the lower membership function.As a result of this process, our type-2 fuzzy set is transformed into a type-1 fuzzy set.
- Defuzzification: Here, the Weighted Average (Centroid) Method is applied to defuzzify the type-1 fuzzy set: This significantly simplifies the computation required to find the center of a two-dimensional shape, thus enhancing the efficiency of the defuzzification process [13].
3.5. DEMATEL Method (The Decision Making Trial and Evaluation Laboratory Method)
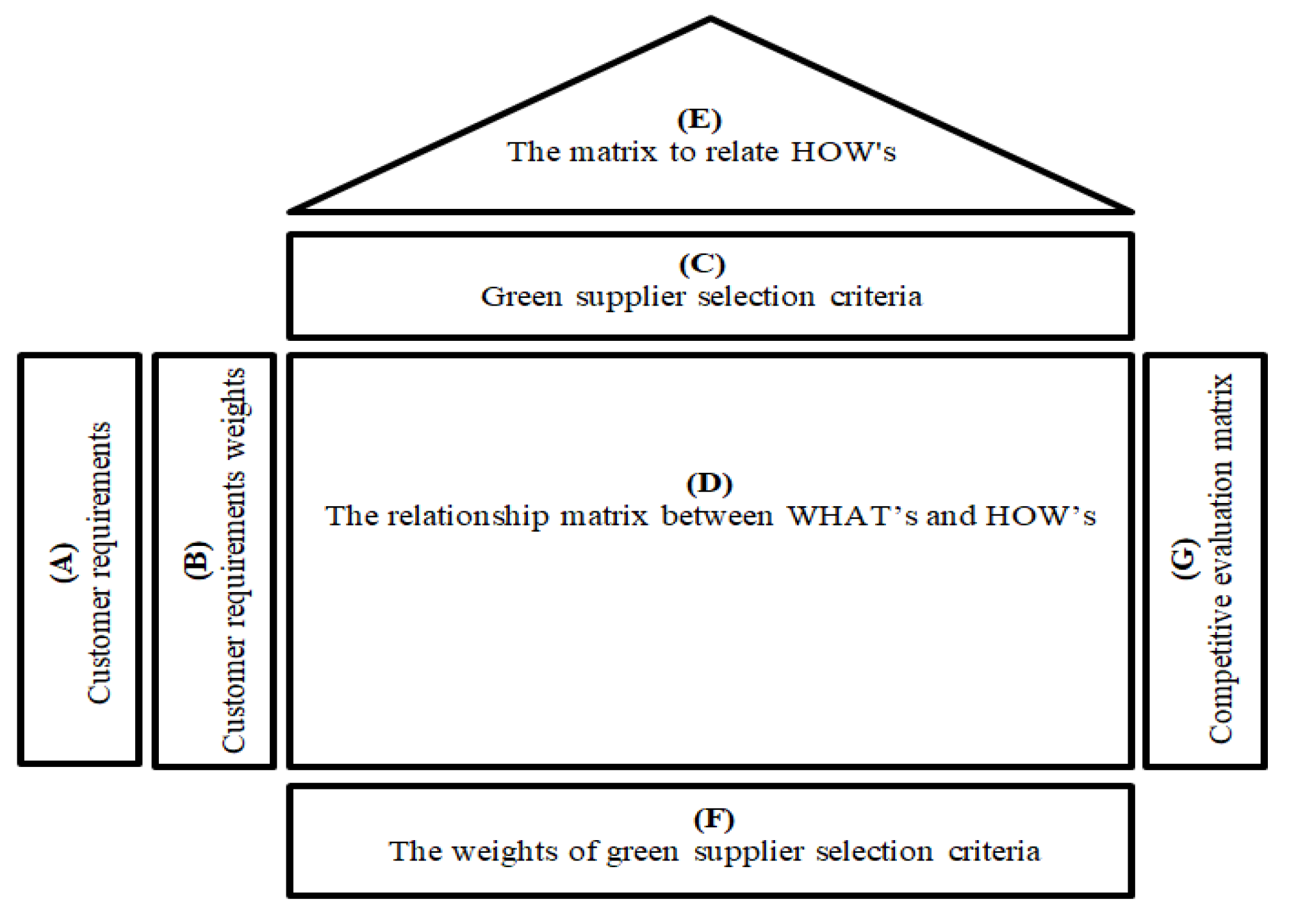
3.6. QFD Model
4. A Combined Selection Method for Green Supplier Selection
4.1. Stage I: Identification of Customer, Green Supplier Selection Requirements, and Alternatives
4.2. Stage II: Weighting of Customer and Green Supplier Selection Criteria
4.3. Stage III: Weighting of Suppliers According to Each Green Supplier Selection Criterion
4.4. Stage IV: Ranking Alternatives Using the IT2 F-VIKOR Method
5. Application of the Proposed Method
5.1. Ranking of Alternatives Using IT2 VIKOR
6. Analysis of Result
7. Conclusion and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
AI Declaration Statement
Abbreviations
| MCDM | Multi-Criteria Decision-Making |
| IT2 F-VIKOR | Interval Type-2 Fuzzy VIKOR |
| QFD | Quality Function Deployment |
| DEMATEL | Decision-Making Trial and Evaluation Laboratory |
| LR | Long range |
| FCT | Fast charging time |
| S | Safety |
| EFR | Environmental friendliness and recyclability |
| LC | Low cost |
| CF | Carbon Footprint (CO₂ Emissions) |
| WMRR | Waste Management and Recycling Rate |
| TCMU | Use of Toxic and Critical Materials |
| GEU | Use of Green Energy |
| EELI | Energy Efficiency and Lifetime Impact |
References
- Khorram, M., Sheibani, M., & Niroomand, S. (2024). A Decision Framework Based on Integration of DEMATEL, QFD, TOPSIS and VIKOR Approaches for Fuzzy Multi-Criteria Supplier Selection Problem. Journal of Uncertain Sys tems, 17(01), 2440002. https://. [CrossRef]
- Wu, S. M., Liu, H. C., & Wang, L. E. (2017). Hesitant fuzzy integrated MCDM approach for quality function deployment: a case study in electric vehicle. International Journal of Production Research, 55(15), 4436-4449. https://. [CrossRef]
- Chen, Y., Ran, Y., Huang, S., Xiao, L., & Zhang, S. (2021). A new integrated MCDM approach for improving QFD based on DEMATEL and extended MULTIMOORA under uncertainty environment. Applied Soft Computing, 105, 107222. https://. [CrossRef]
- Zhou, F., Wang, X., Lin, Y., He, Y., & Zhou, L. (2016). Strategic part prioritization for quality improvement practice using a hybrid MCDM framework: a case application in an auto factory. Sustainability, 8(6), 559. https://. [CrossRef]
- Uygun, O., Kacamak, H., Aysim, S., & Simsir, F. (2013). Supplier selection for automotive industry using multi-criteria deci sion making techniques. TOJSAT, 3(4), 126-137.
- Mousakhani, S., Nazari-Shirkouhi, S., & Bozorgi-Amiri, A. (2017). A novel interval type-2 fuzzy evaluation model based group decision analysis for green supplier selection problems: A case study of battery industry. Journal of cleaner produc tion, 168, 205-218. https://. [CrossRef]
- Seikh, M. R., & Chatterjee, P. (2025). Sustainable strategies for electric vehicle adoption: A confidence level-based interval- valued spherical fuzzy MEREC-VIKOR approach. Information Sciences, 699, 121814. https://. [CrossRef]
- Liang, Y., Ju, Y., Martínez, L., & Tu, Y. (2022). Sustainable battery supplier evaluation of new energy vehicles using a distribu ted linguistic outranking method considering bounded rational behavior. Journal of Energy Storage, 48, 103901. https://. [CrossRef]
- Babar, A. H. K., & Ali, Y. (2021). Enhancement of electric vehicles’ market competitiveness using fuzzy quality function dep loyment. Technological Forecasting and Social Change, 167, 120738. https://. [CrossRef]
- Deveci, M., Gokasar, I., Pamucar, D., Zaidan, A. A., Wen, X., & Gupta, B. B. (2023). Evaluation of Cooperative Intelligent Transportation System scenarios for resilience in transportation using type-2 neutrosophic fuzzy VIKOR. Transportation research part a: policy and practice, 172, 103666. https://. [CrossRef]
- Rohit, K., Verma, A., Dhairiyasamy, R., & Gabiriel, D. (2025). A continuous supply chain management approach using SPJS-Fuzzy DEMATEL and LPWBN for automotive electric vehicles in India. Sustainable Futures, 9, 100518. https://. [CrossRef]
- Digalwar, A. K., Saraswat, S. K., Rastogi, A., & Thomas, R. S. (2022). A comprehensive framework for analysis and evalua tion of factors responsible for sustainable growth of electric vehicles in India. Journal of Cleaner Production, 378, 134601. https://. [CrossRef]
- Yilmaz, O., Eyercioglu, O., & Gindy, N. N. (2006). A user-friendly fuzzy-based system for the selection of electro disc harge machining process parameters. Journal of Materials Processing Technology, 172(3), 363-371. https://. [CrossRef]
- Aksakal, E., & Dagdeviren, M. (2010). ANP ve DEMATEL yöntemleri ile personel seçimi problemine bütünleşik bir yaklaşım. Journal of the Faculty of Engineering and Architecture of Gazi University, 25(4), 905–913.
- Tsai, W. H., & Chou, W. C. (2009). Selecting management systems for sustainable development in SMEs: A novel hybrid model based on DEMATEL, ANP, and ZOGP. Expert systems with applications, 36(2), 1444-1458. https://. [CrossRef]
- Khademi-Zare, H., Zarei, M., Sadeghieh, A., & Owlia, M. S. (2010). Ranking the strategic actions of Iran mobile cellular telecommunication using two models of fuzzy QFD. Telecommunications Policy, 34(11), 747-759. https://. [CrossRef]
- Tang, J., Zhang, Y. E., Tu, Y., Chen, Y., & Dong, Y. (2005). Synthesis, evaluation, and selection of parts design scheme in supplier involved product development. Concurrent Engineering, 13(4), 277-289. https://. [CrossRef]
- Cuthbertson, R., & Piotrowicz, W. (2008). Supply chain best practices–identification and categorisation of measures and benefits. International Journal of productivity and performance management, 57(5), 389-404.
- Bhattacharya, A., Mohapatra, P., Kumar, V., Dey, P. K., Brady, M., Tiwari, M. K., & Nudurupati, S. S. (2014). Green supply chain performance measurement using fuzzy ANP-based balanced scorecard: a collaborative decision- making appro ach. Production Planning & Control, 25(8), 698-714. https://. [CrossRef]

| Author / Authors | Applied Method | Application Area |
| [8] | ORESTE method | Automotive-Battery Supplier Selection |
| [9] | Fuzzy QFD- Multiple regression Method | Automotive - Hybrid electric vehicles |
| [6] | Type-2 Fuzzy TOPSIS, Type-2 Fuzzy Hamming | Energy-Battery industry |
| [10] | Classical VIKOR- Fuzzy VIKOR | Transportation-Energy-Sensors |
| [11] | Fuzzy DEMATEL- LPWBN | Automotive - Electric vehicle - Battery supplier selection |
| [12] | DEMATEL-ISM | Automotive - Electric vehicle selection |
| Customer Requirements (Customer Demands) (CRs) | Explanation |
| Long range (LR) | It is the maximum distance that an electric vehicle can travel on a single full charge. |
| Fast charging time (FCT) | It refers to the time required for the battery to reach a specific charge level. |
| Safety (S) | It refers to the level of protection the vehicle and battery provide to the user against physical hazards. |
| Environmental friendliness and recyclability (EFR) | It refers to the minimal environmental impact of the battery's production, use, and disposal processes, as well as the inclusion of recyclable materials. |
| Low cost (LC) | It refers to the minimal impact of the battery on the vehicle's price or ensuring that its total cost remains at an acceptable level. |
| Green Supplier Selection Criteria | Explanation |
| Carbon Footprint (CO₂ Emissions) (CF) | It refers to the total greenhouse gas emissions (especially CO₂) generated throughout the process from raw material extraction to production, transportation, and usage of the battery. Low emissions are crucial for reducing environmental impacts. |
| Waste Management and Recycling Rate (WMRR) | It refers to how much of the battery can be recycled when its lifespan ends and how environmentally friendly this process is. A high recycling rate reduces resource waste and environmental pollution. |
| Use of Toxic and Critical Materials (TCMU) | It refers to the amount and type of materials used in the battery that are harmful to the environment and human health (e.g., cobalt, lead, fluoride electrolytes) or are at risk in terms of sourcing. Reducing the use of such materials is important both environmentally and ethically. |
| Use of Green Energy (GEU) | It refers to whether renewable energy sources (such as solar, wind, etc.) are used in the battery production processes. The use of green energy significantly reduces the environmental impact of the production process. |
| Energy Efficiency and Lifetime Impact (EELI) | It refers to how efficiently the battery provides energy and the total environmental impact throughout its entire life cycle. Long-lasting and highly efficient batteries reduce resource usage and waste generation |
| Abbreviation of the Alternatives | Battery Type / Criteria | Carbon Footprint (CO2 Emissions) | Recycling and Waste Management | Use of Toxic / Critical Materials | Use of Green Energy | Energy Efficiency and Lifetime Impact |
| A1 | NMC (Li-ion) |
High Intensive mining and processing process |
Medium It has existing infrastructure but is costly |
High Contains Cobalt and Nickel |
Low-Medium Typically produced using fossil energy |
Medium-High Good range but limited cycle life |
| A2 | LFP (LiFePO₄) |
Medium Simpler structure, production with lower energy |
High Easy and safe recycling |
Low Does not contain critical materials |
Medium-High Production is increasing with solar energy |
High Long cycle life and stable performance |
| A3 | Solid-State |
Medium-High Its production is complex; however, there is potential for cost reduction |
Medium As an emerging system, it encompasses both advantages and disadvantages |
Low-Medium It may vary depending on the material selection |
High (Objective) It is planned to increase the use of clean energy in production in the future. |
Very High Very long lifespan and high energy density |
| A4 | Li-S (Lithium Sulfur) |
Medium Lightweight material but inefficient production |
Low Sulfur-based structure poses challenges in recycling |
Low Does not contain critical materials |
Low In R&D-focused production, conventional energy is typically used |
Medium High capacity but short lifespan |
| A5 | Sodium-Ion |
Low Abundant resources, low-temperature production |
High Easy recycling due to its simple structure |
Low Does not contain toxic materials |
High Low temperature and production are easy with green energy |
Medium Low energy density, but durable structures are possible |
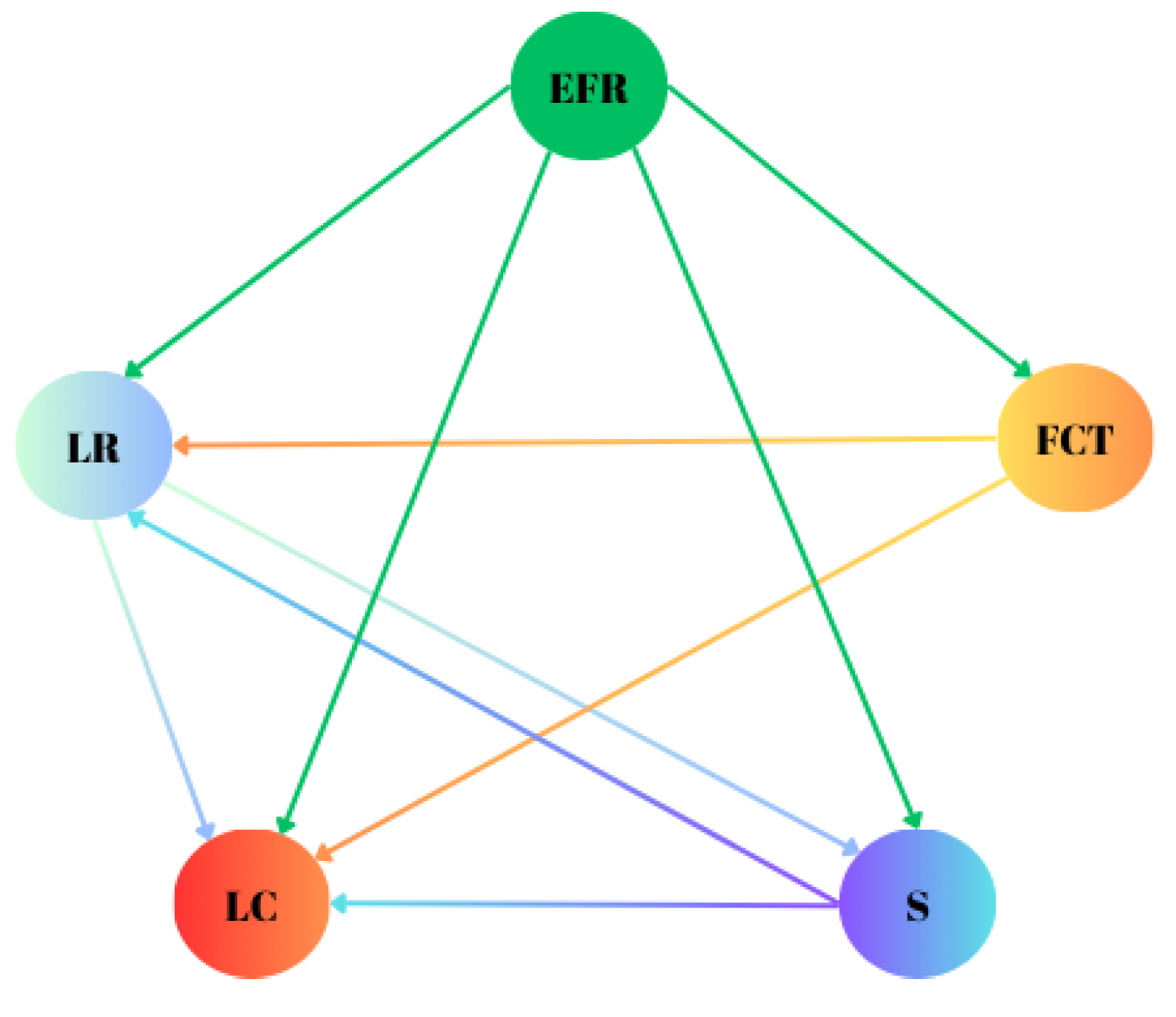
| CRs | LR | FCT | S | EFR | LC |
| LR | 0 | 1 | 2 | 2 | 3 |
| FCT | 2 | 0 | 1 | 1 | 3 |
| S | 3 | 2 | 0 | 1 | 2 |
| EFR | 3 | 3 | 3 | 0 | 3 |
| LC | 1 | 1 | 1 | 2 | 0 |
| CRs | LR | FCT | S | EFR | LC |
| LR | 0.0000 | 0.0833 | 0.1667 | 0.1667 | 0.2500 |
| FCT | 0.1667 | 0.0000 | 0.0833 | 0.0833 | 0.2500 |
| S | 0.2500 | 0.1667 | 0.0000 | 0.0833 | 0.1667 |
| EFR | 0.2500 | 0.2500 | 0.2500 | 0.0000 | 0.2500 |
| LC | 0.0833 | 0.0833 | 0.0833 | 0.1667 | 0.0000 |
| CRs | LR | FCT | S | EFR | LC |
| LR | 0.2810 | 0.3055 | 0.3752* | 0.3619 | 0.5497* |
| FCT | 0.3732* | 0.1844 | 0.2693 | 0.2668 | 0.5010* |
| S | 0.4791* | 0.3575 | 0.2233 | 0.2926 | 0.4862* |
| EFR | 0.6029* | 0.5221* | 0.5279* | 0.3038 | 0.6952* |
| LC | 0.2782 | 0.2409 | 0.2436 | 0.2941 | 0.2439 |
| CRs | Dk (Influencing) | Rk (Influenced) |
| LR | 1.8733 | 2.0144 |
| FCT | 1.5947 | 1.6104 |
| S | 1.8387 | 1.6393 |
| EFR | 2.6519 | 1.5192 |
| LC | 1.3007 | 2.4760 |
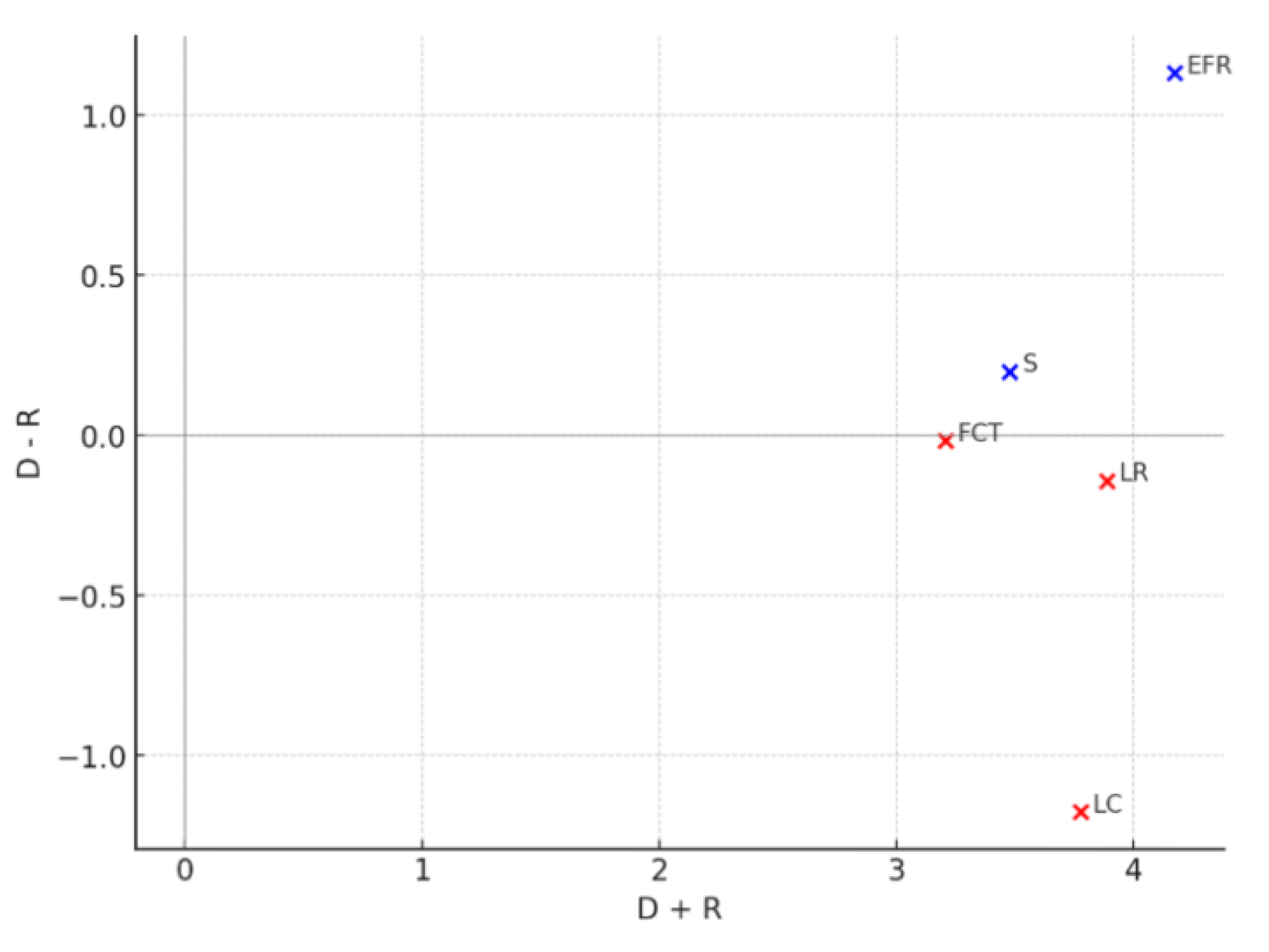
| CRs | D + R | D - R | Group |
| LR | 3.8877 | -0.1411 | Conclusion |
| FCT | 3.2051 | -0.0157 | Conclusion |
| S | 3.4780 | 0.1994 | Reason |
| EFR | 4.1711 | 1.1327 | Reason |
| LC | 3.7767 | -1.1753 | Conclusion |
| CRs | LR | FCT | S | EFR | LC |
| Ağırlıklar | 0.2099 | 0.1731 | 0.1878 | 0.2252 | 0.2039 |
| HOW’s (CRs) | WHAT’s (Green Supplier Selection Criteria) | Weights of CRs | |||||
| CF | WMRR | TCMU | GEU | EELI | |||
| LR | 3 | 1 | 1 | 1 | 9 | 0.2099 | |
| FCT | 1 | 1 | 1 | 1 | 6 | 0.1731 | |
| S | 3 | 3 | 9 | 1 | 6 | 0.1878 | |
| EFR | 9 | 9 | 3 | 6 | 6 | 0.2252 | |
| LC | 3 | 3 | 6 | 3 | 3 | 0.2039 | |
| Absolute Importance Values | 4.0047 | 3.2093 | 3.9722 | 2.5337 | 6.0174 | ||
| Normalized Criterion Weights | 0.2029 | 0.1626 | 0.2013 | 0.1284 | 0.3049 | ||
| Alternatives | Criteria | ||||
|
CF (Minimize) (0-10) |
WMRR (Maximize) (0-10) |
TCMU (Minimize) (0-10) |
GEU (Maximize) (0-10) |
EELI (Maximize) (0-10) |
|
| A1 | (2, 3.5, 5;1,1) (2.5, 3.5, 4.5;0.8, 0.8) |
(4, 5.5, 7;1,1) (4.4, 5.5, 6.6;0.8, 0.8) |
(1, 2.5, 4;1,1) (1.3, 2.5, 3.7;0.8, 0.8) |
(4, 5, 6;1,1) (4.2, 5, 5.8;0.8, 0.8) |
(5, 6, 7;1,1) (5.2, 6, 6.8;0.8, 0.8) |
| A2 | (5, 6.5, 8;1,1) (5.4, 6.5, 7.6;0.8, 0.8) |
(7, 8.5, 10;1,1) (7.3, 9, 9.7;0.8, 0.8) |
(8, 9, 10;1,1) (8.4, 9, 9.6;0.8, 0.8) |
(5, 7, 8;1,1) (5.6, 7, 7.4;0.8, 0.8) |
(7, 9, 10;1,1) (7.3, 9, 9.7;0.8, 0.8) |
| A3 | (5, 6, 7;1,1) (5.5, 6, 6.5;0.8, 0.8) |
(4.5, 5.5, 6.5;1,1) (5, 5.5, 6;0.8, 0.8) |
(4.5, 6, 7.5;1,1) (5, 6, 7;0.8, 0.8) |
(7, 9, 10;1,1) (7.6, 9, 9.4;0.8, 0.8) |
(8, 9, 10;1,1) (8.3, 9, 9.7;0.8, 0.8) |
| A4 | (5.5, 6.4, 8;1,1) (6, 6.4, 7.5;0.8, 0.8) |
(3, 4, 5.5;1,1) (3.3, 4, 5.2;0.8, 0.8) |
(6, 7.5, 9;1,1) (6.6, 7.5, 8.4;0.8, 0.8) |
(3, 4, 5;1,1) (3.4, 4, 4.6;0.8, 0.8) |
(2, 3.5, 5;1,1) (2.5, 4, 4.5;0.8, 0.8) |
| A5 | (8, 9, 10;1,1) (8.5, 9, 9.5;0.8, 0.8) |
(9, 9.5, 10;1,1) (9.2, 9.5, 9.8;0.8, 0.8) |
(9, 9.5, 10;1,1) (9.3, 9.5, 9.7;0.8, 0.8) |
(9, 9.5, 10;1,1) (9.2, 9.5, 9.8;0.8, 0.8) |
(5, 6, 7;1,1) (5.5, 6, 6.5;0.8, 0.8) |
| Criterion | Best | |
| CF (Minimize) | (2, 3.5, 5;1,1) (2.5, 3.5, 4.5;0.8, 0.8) |
(8, 9, 10;1,1) (8.5, 9, 9.5;0.8, 0.8) |
| WMRR (Maximize) | (9, 9.5, 10;1,1) (9.2, 9.5, 9.8;0.8, 0.8) |
(3, 4, 5.5;1,1) (3.3, 4, 5.2;0.8, 0.8) |
| TCMU (Minimize) | (1, 2.5, 4;1,1) (1.3, 2.5, 3.7;0.8, 0.8) |
(9, 9.5, 10;1,1) (9.3, 9.5, 9.7;0.8, 0.8) |
| GEU (Maximize) | (9, 9.5, 10;1,1) (9.2, 9.5, 9.8;0.8, 0.8) |
(3, 4, 5;1,1) (3.4, 4, 4.6;0.8, 0.8) |
| EELI (Maximize) | (8, 9, 10;1,1) (8.3, 9, 9.7;0.8, 0.8) |
(2, 3.5, 5;1,1) (2.5, 4, 4.5;0.8, 0.8 |
| Alternatives |
CF (Minimize) |
WMRR (Maximize) |
TCMU (Minimize) |
GEU (Maximize) |
EELI (Maximize) |
| A1 | (0, 0, 0;1,1) (0, 0, 0;0.8, 0.8) |
(0.1355, 0.1183, 0.1084;1,1) (0.1323, 0.1183, 0.1131;0.8, 0.8) |
(0, 0, 0;1,1) (0, 0, 0;0.8, 0.8) |
(0.1070, 0.1051, 0.1027;1,1) (0.1107, 0.1051, 0.0988;0.8, 0.8) |
(0.1525, 0.1663, 0.1829;1,1) (0.1630, 0.1829, 0.1700;0.8, 0.8) |
| A2 | (0.1015, 0.1107, 0.1217;1,1) (0.0981, 0.1107, 0.1258;0.8, 0.8) |
(0.0542, 0.0296, 0.0000;1,1) (0.0524, 0.0148, 0.0035;0.8, 0.8) |
(0.1761, 0.1869, 0.2013;1,1) (0.1787, 0.1869, 0.1979;0.8, 0.8) |
(0.0856, 0.0584, 0.0514;1,1) (0.0797, 0.0584, 0.0593;0.8, 0.8) |
(0.0508, 0.0000, 0.0000;1,1) (0.0526, 0.0000, 0.0000;0.8, 0.8) |
| A3 | (0.1015, 0.0922, 0.0812;1,1) (0.1015, 0.0922, 0.0812; 0.8, 0.8) |
(0.1220, 0.1183, 0.1138;1,1) (0.1157, 0.1183, 0.1343;0.8, 0.8) |
(0.0881, 0.1007, 0.1174;1,1) (0.0931, 0.1007, 0.1107;0.8, 0.8) |
(0.0428, 0.0117, 0.0000;1,1) (0.0354, 0.0117, 0.0099;0.8, 0.8) |
(0, 0, 0;1,1) (0, 0, 0;0.8, 0.8) |
| A4 | (0.2367, 0.2213, 0.2029;1,1) (0.2266, 0.2213, 0.2151; 0.8, 0.8) |
(0.1626, 0.1626, 0.1463;1,1) (0.1626, 0.1626, 0.1626;0.8, 0.8) |
(0.1258, 0.1438, 0.1678;1,1) (0.1334, 0.1438, 0.1577;0.8, 0.8) |
(0.1284, 0.1284, 0.1284;1,1) (0.1284, 0.1284, 0.1284;0.8, 0.8) |
(0.3049, 0.3049, 0.3049;1,1) (0.3049, 0.3049, 0.3049;0.8, 0.8) |
| A5 | (0.2029, 0. 2029, 0. 2029;1,1) (0.1961, 0.2029, 0.2110; 0.8, 0.8) |
(0, 0, 0;1,1) (0, 0, 0;0.8, 0.8) |
(0.2013, 0.2013, 0.2013;1,1) (0.2013, 0.2013, 0.2013;0.8, 0.8) |
(0, 0, 0;1,1) (0, 0, 0;0.8, 0.8) |
(0.1525, 0.1663, 0.1839;1,1) (0.1472, 0.1829, 0.1876;0.8, 0.8) |
| Alternatives | (The sum of all criteria) | (he largest criterion value) |
| A1 | (0.3950, 0.3897, 0.3940;1,1) (0.4060, 0.4063, 0.3819;0.8, 0.8) |
(0.1525, 0.1663, 0.1829;1,1) (0.1630, 0.1829, 0.1700;0.8, 0.8) |
| A2 | (0.4682, 0.3856, 0.3744;1,1) (0.4615, 0.3708, 0.3865;0.8, 0.8) |
(0.1761, 0.1869, 0.2013;1,1) (0.1787, 0.1869, 0.1979;0.8, 0.8) |
| A3 | (0.3544, 0.3229, 0.3124;1,1) (0.3457, 0.3229, 0.3361;0.8, 0.8) |
(0.1220, 0.1183, 0.1174;1,1) (0.1157, 0.1183, 0.1343;0.8, 0.8) |
| A4 | (0.9584, 0.9610, 0.9503;1,1) (0.9559, 0.9610, 0.9684;0.8, 0.8) |
(0.3049, 0.3049, 0.3049;1,1) (0.3049, 0.3049, 0.3049;0.8, 0.8) |
| A5 | (0.5567, 0.5705, 0.5881;1,1) (0.5446, 0.5871, 0.5999;0.8, 0.8) |
(0.2029, 0.2029, 0.2029;1,1) (0.2013, 0.2029, 0.2110;0.8, 0.8) |
| Alternative | VIKOR Index () |
| A1 | (0.1170, 0.1810, 0.2386;1, 1) (0.1744, 0.2384, 0.1408;0.8, 0.8) |
| A2 | (0.2421, 0.2329, 0.2723;1, 1) (0.2614, 0.2213, 0.2263;0.8, 0.8) |
| A3 | (0.0000, 0.0000, 0.00000;1, 1) (0.0000, 0.0000, 0.0000;0.8, 0.8) |
| A4 | (1.0000, 1.0000, 1.00000;1, 1) (1.0000, 1.0000, 1.0000;0.8, 0.8) |
| A5 | (0.3886, 0.4207, 0.4441;1, 1) (0.3892, 0.4337, 0.4334;0.8, 0.8) |
| has been taken | |
| Alternative | |
| A1 | 0.1817 |
| A2 | 0.2427 |
| A3 | 0.0000 |
| A4 | 1.0000 |
| A5 | 0.4183 |
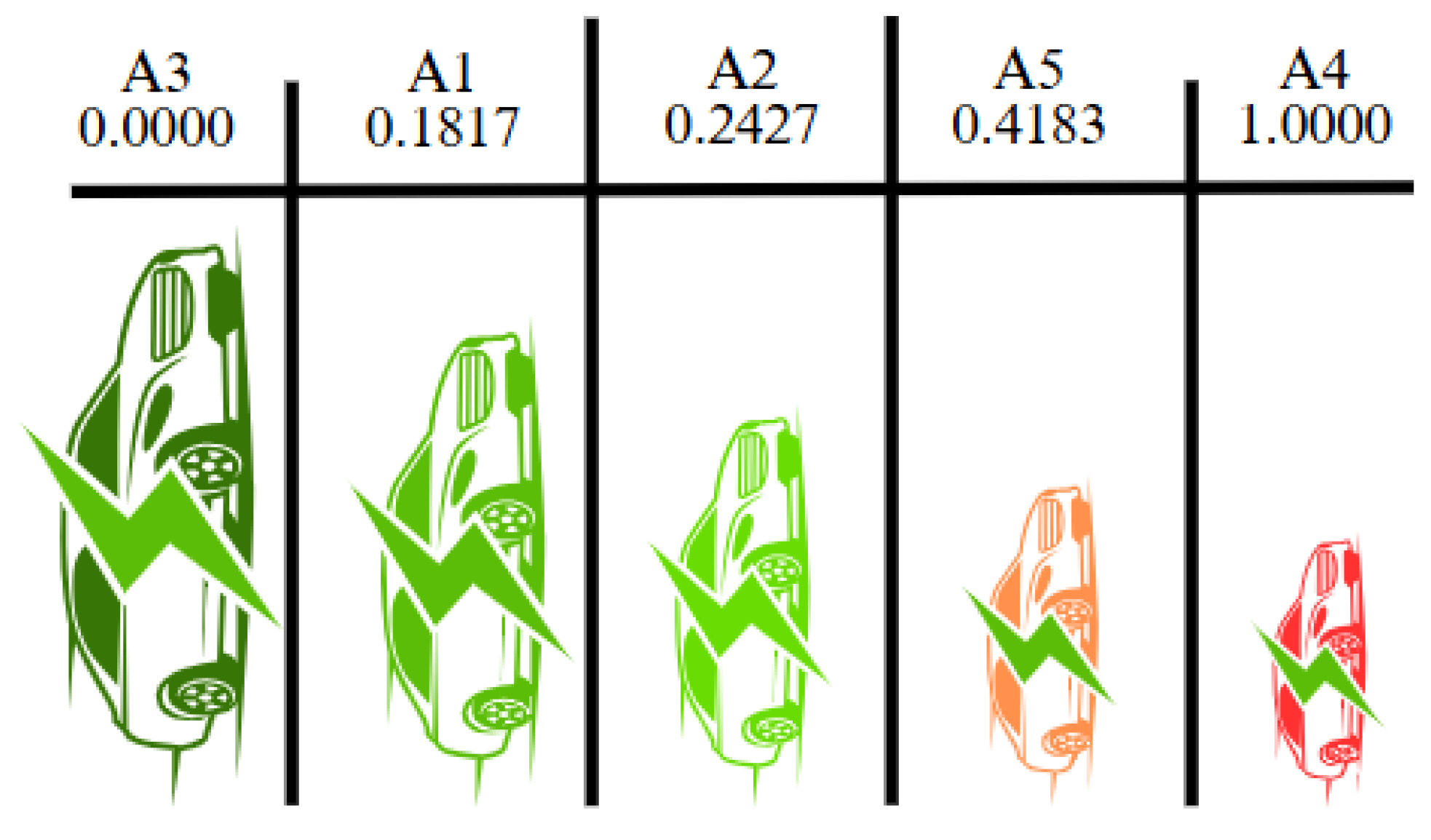
| Alternatives | A3 | A1 | A2 | A5 | A4 |
| Values of Alternatives Calculated Using the DEMATEL-QFD-IT2 F-VIKOR Method | 0.0000 | 0.1817 | 0.2427 | 0.4183 | 1.0000 |
| Ranking Performance of Alternatives | 1 | 2 | 3 | 4 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





