Submitted:
23 April 2025
Posted:
24 April 2025
You are already at the latest version
Abstract

Keywords:
Introduction
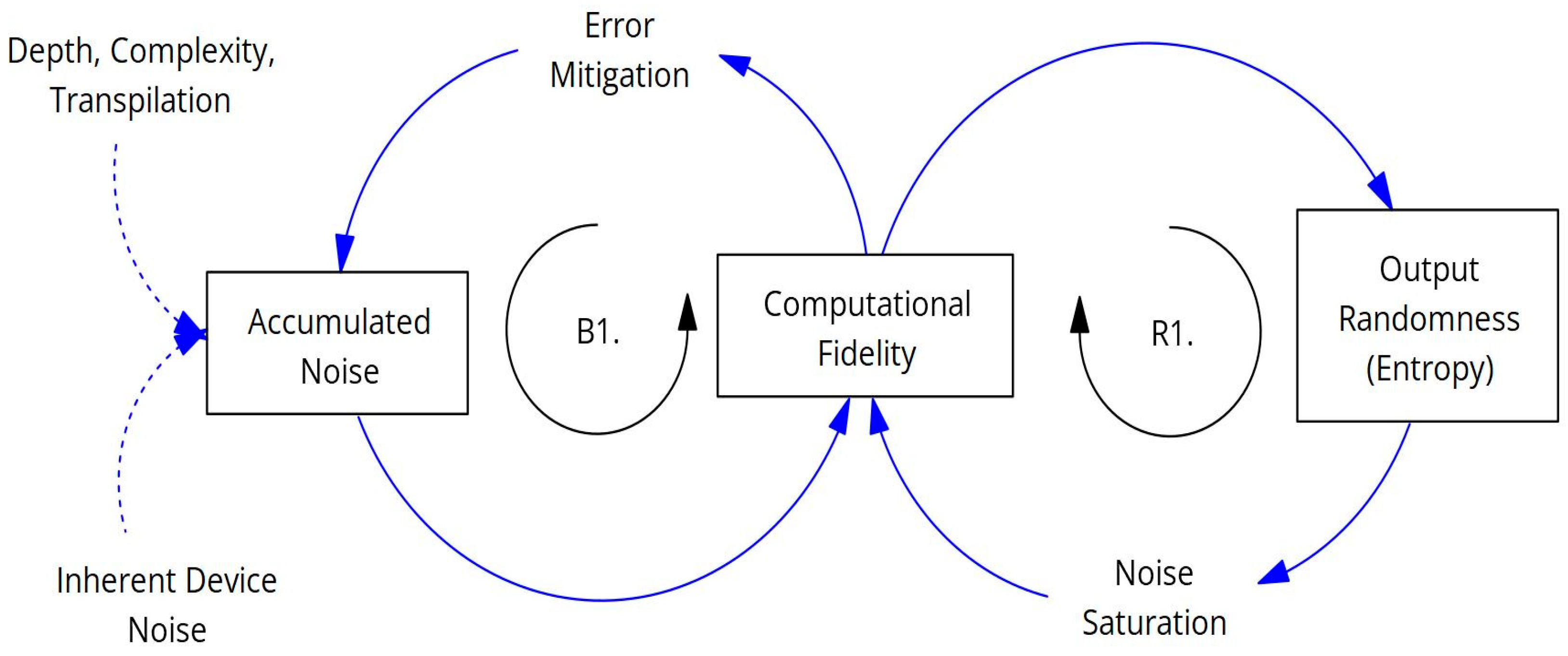
Methods
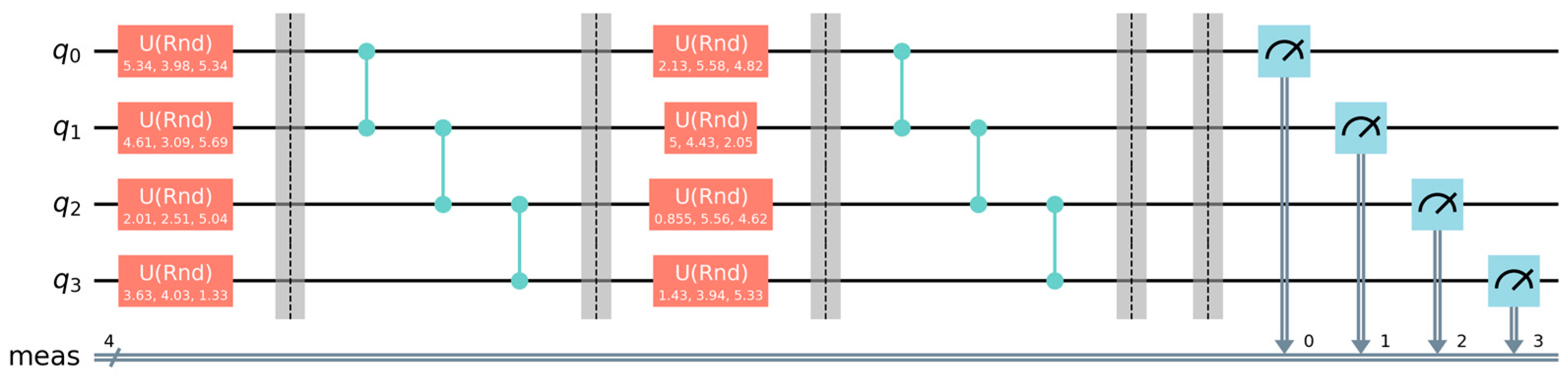
- (i)
- The total number of unique observed 127-bit outcomes.
- (ii)
- The Shannon entropy H of the measured probability distribution p(x) over the output bitstrings x is calculated as:
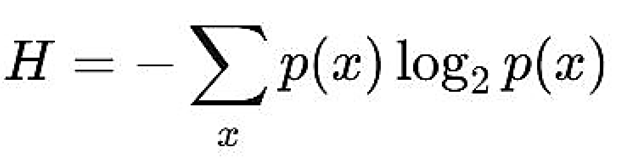
- (iii)
- The average magnetization (or expectation value of the Pauli-Z operator) for a specific qubit i, denoted ⟨Zi⟩, is calculated from the measurement counts as:
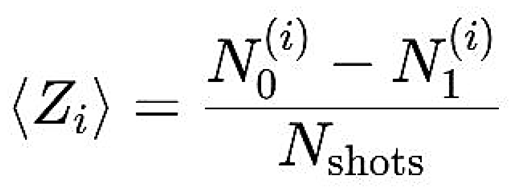

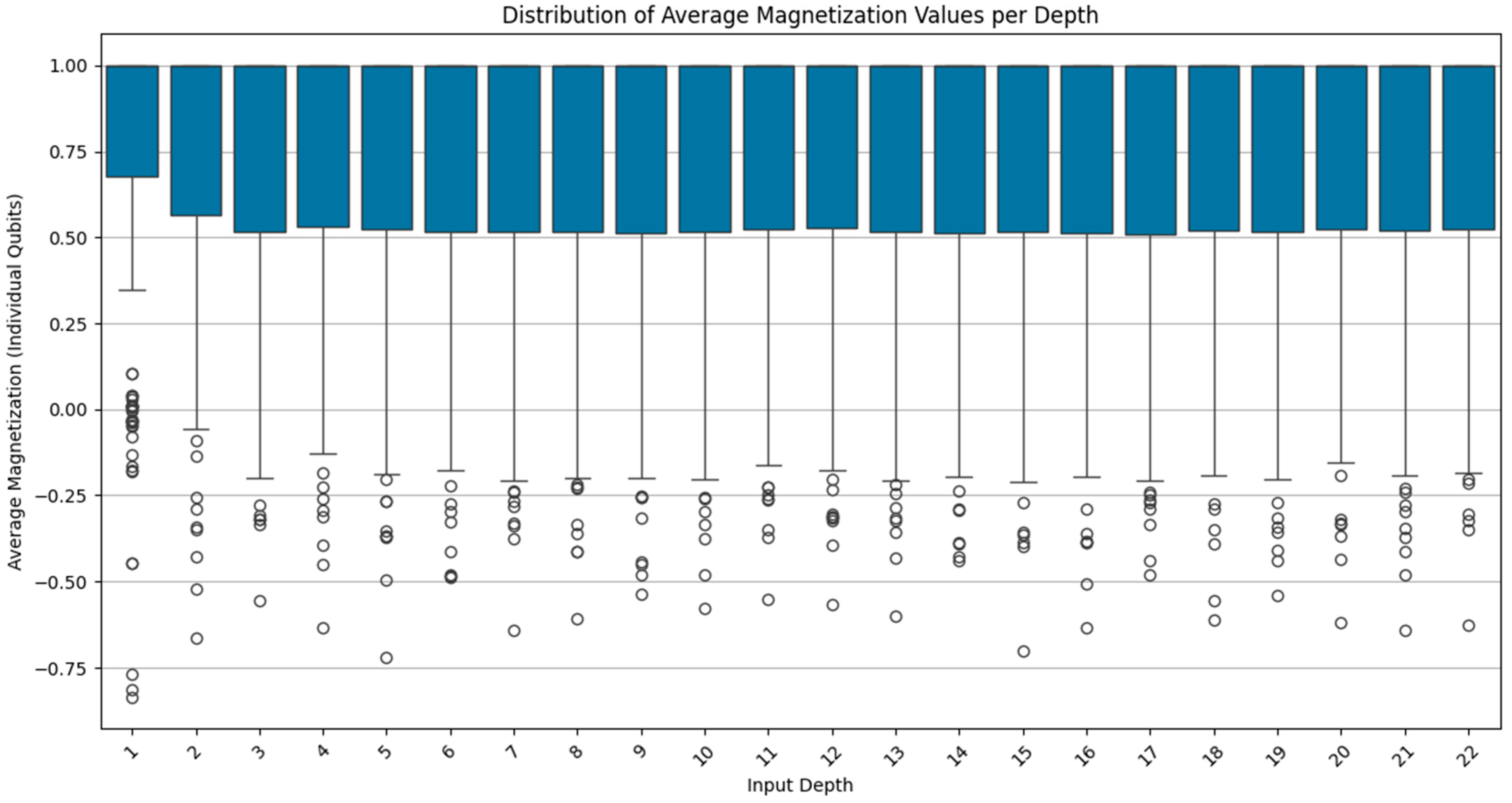
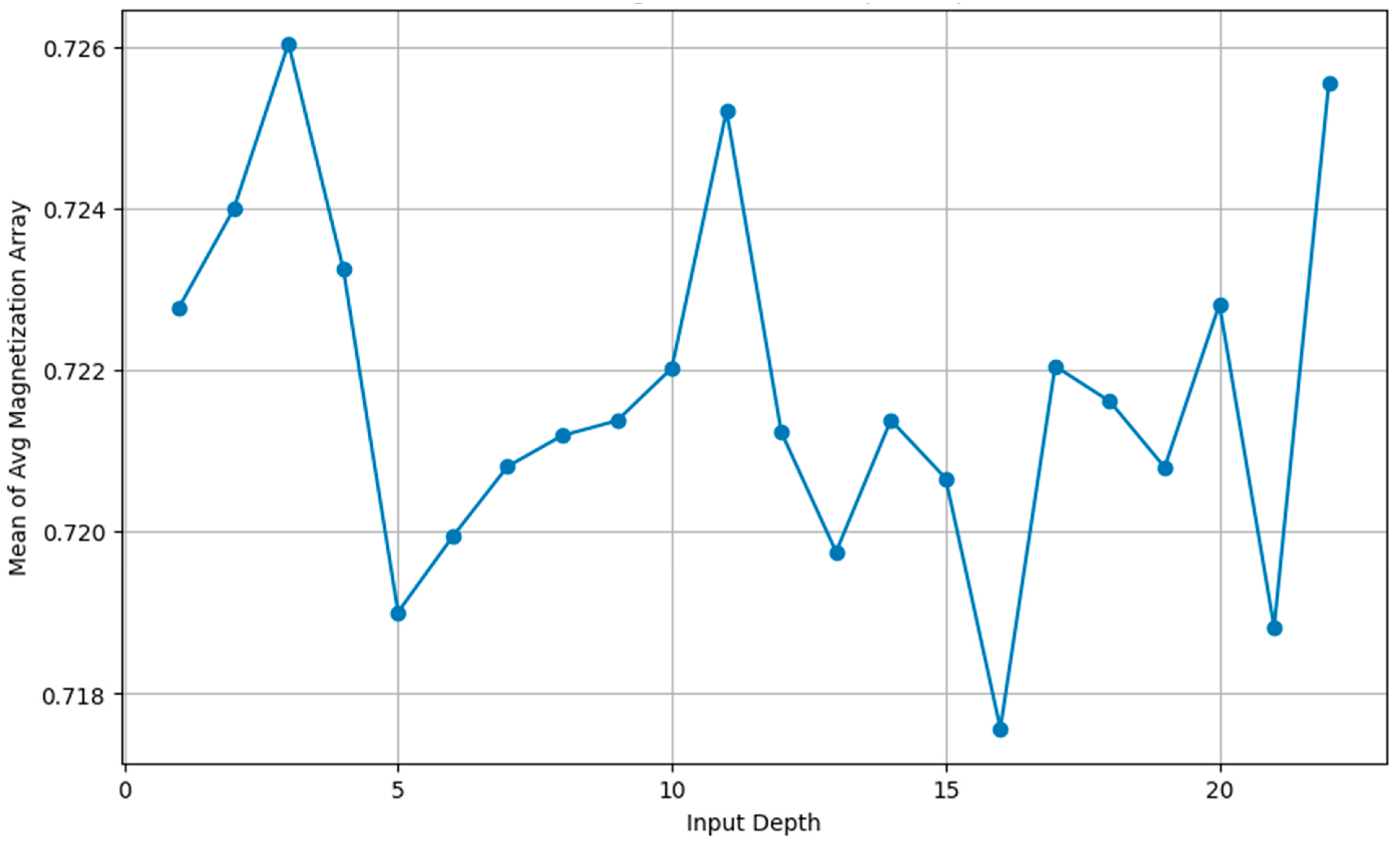
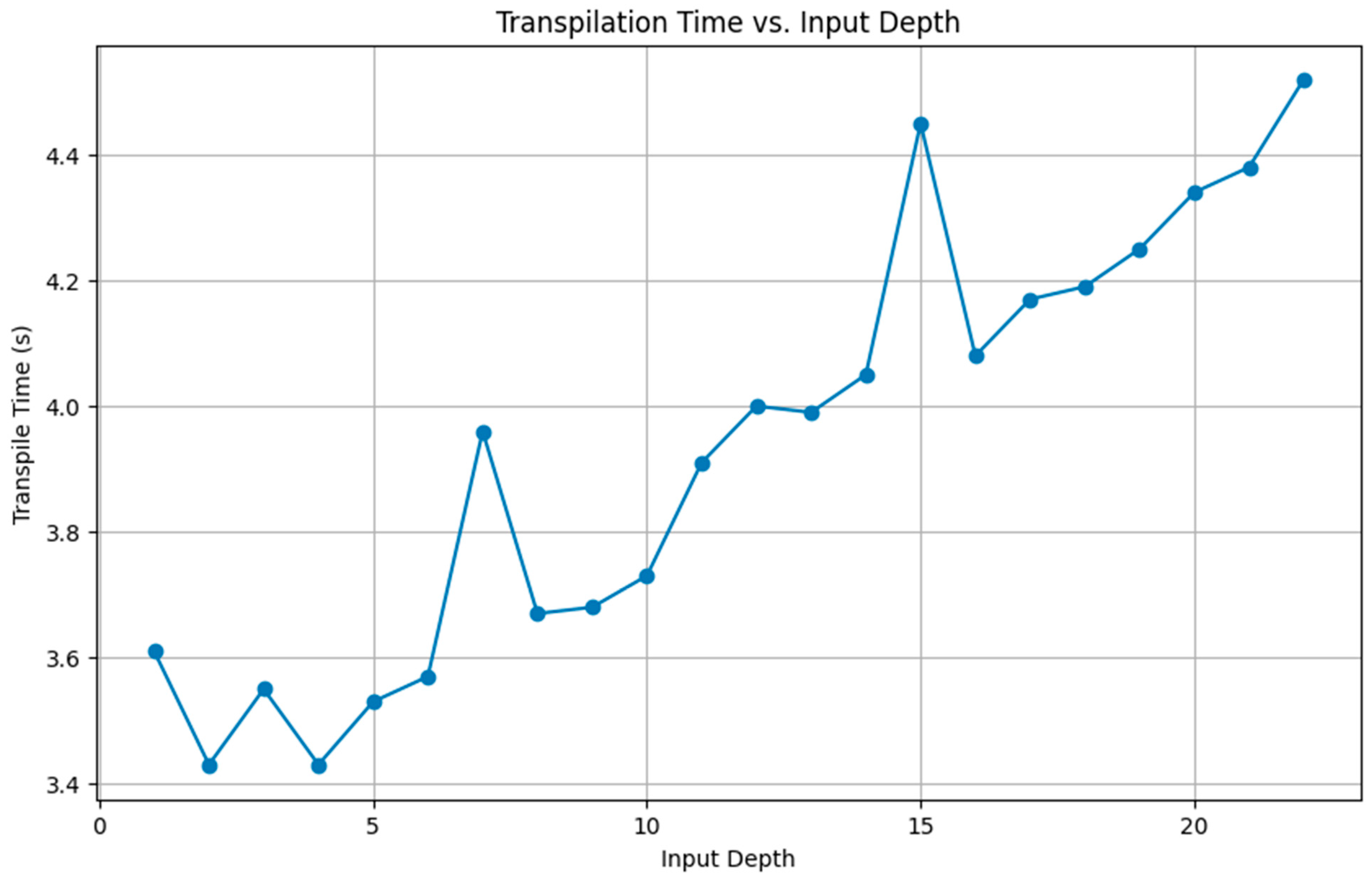
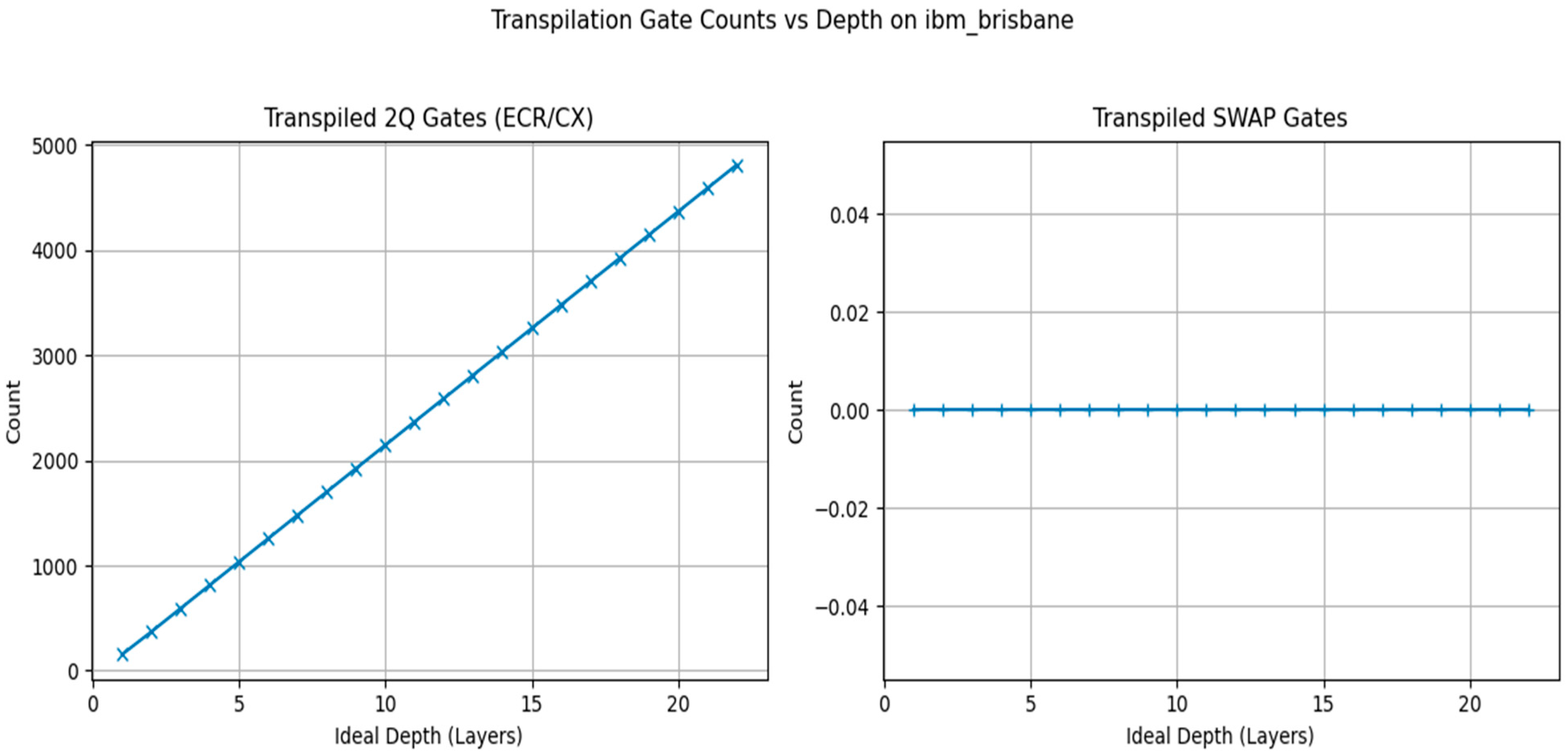
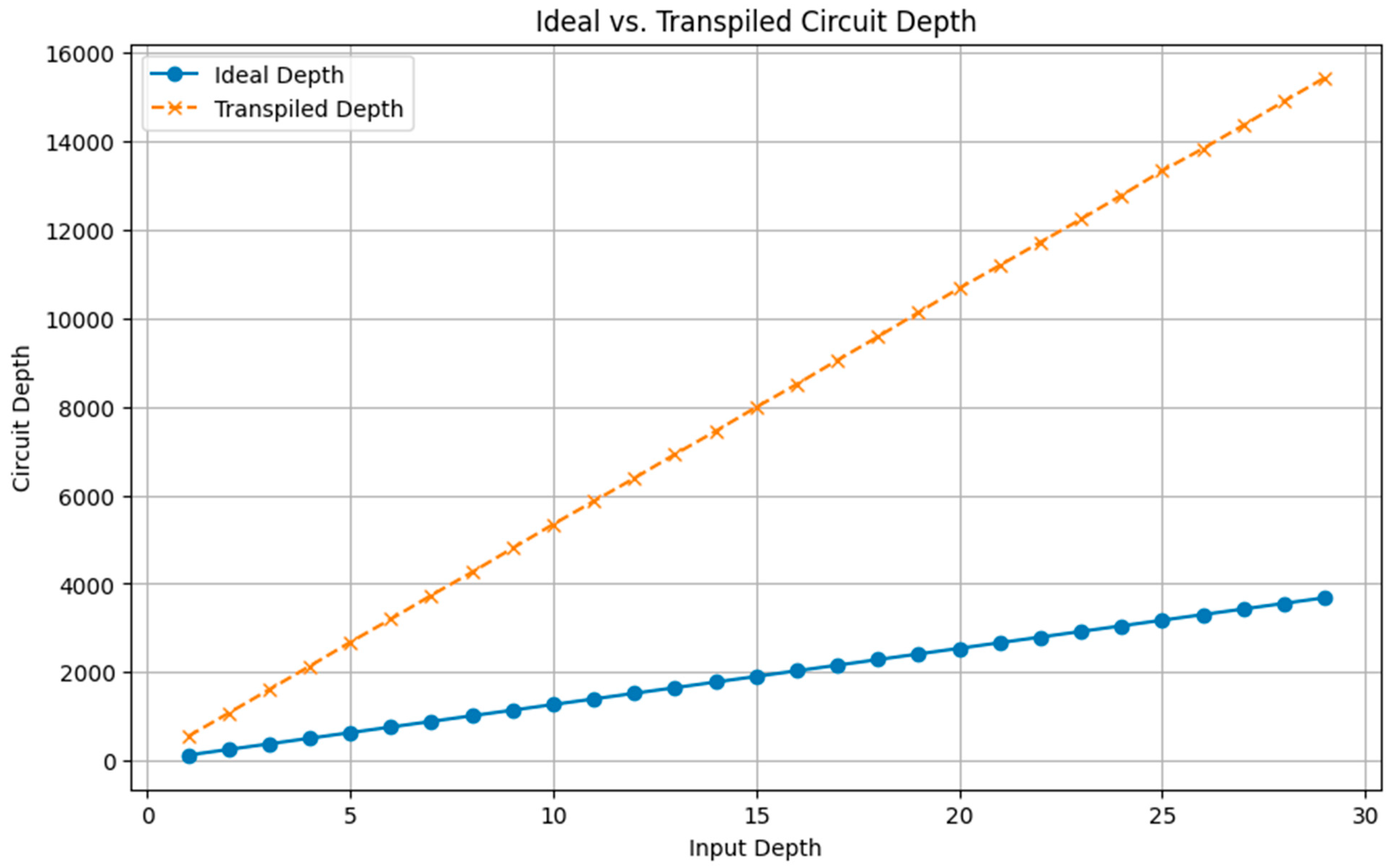
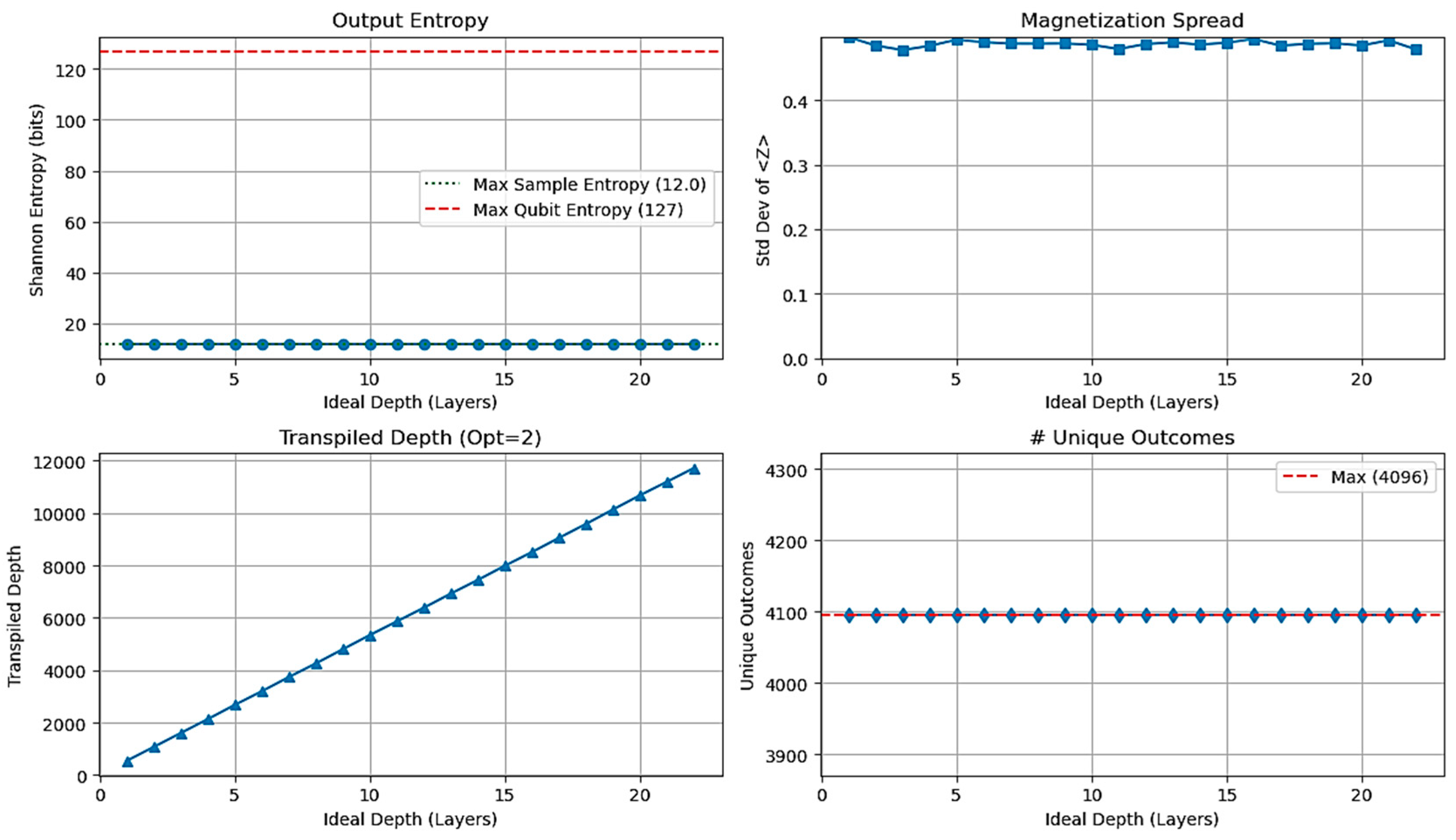
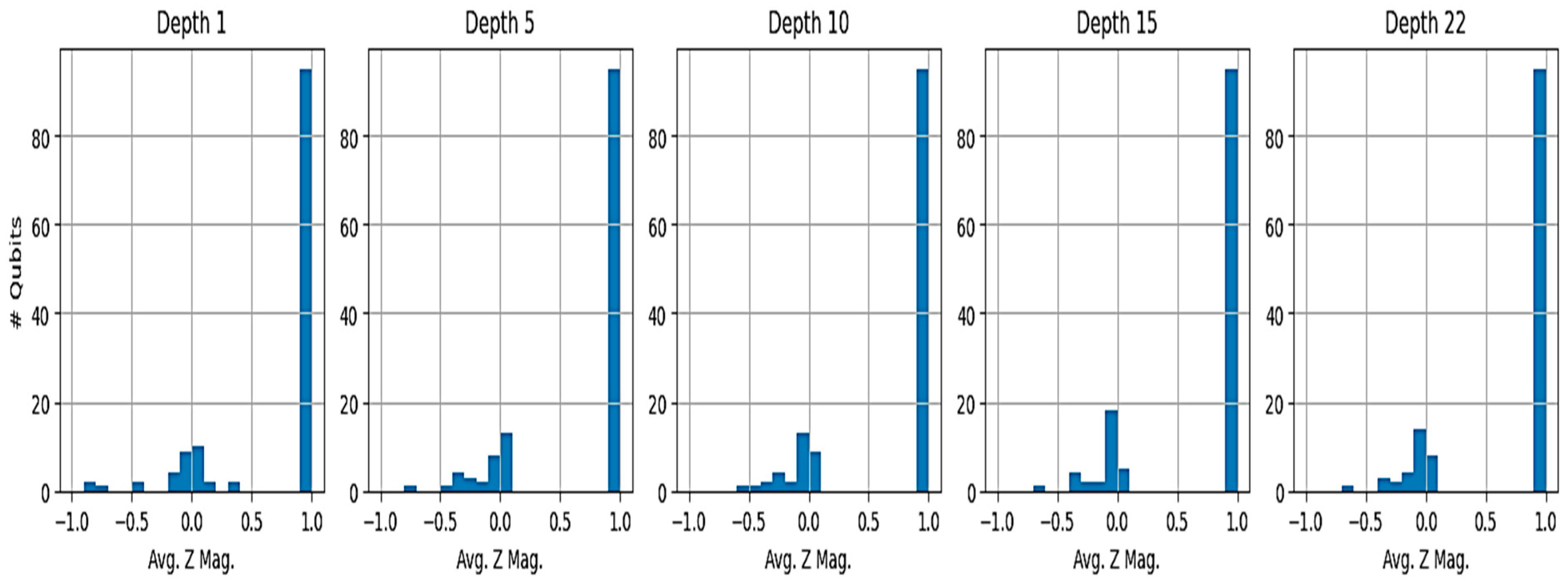
Results
Discussion
Conclusion
Appendix


|
Visual Studio Code Miniconda Qiskit Environment |
|
pip install qiskit qiskit-ibm-runtime matplotlib numpy scipy pandas # --- Run this code block ONCE securely --- from qiskit_ibm_runtime import QiskitRuntimeService # Replace the placeholder below with your REAL API token from IBM Quantum my_api_token = "INSERT YOUR IBM QUANTUM API KEY HERE" try: # Save the account information for Qiskit to use later # Use channel='ibm_quantum' for the cloud service # overwrite=True allows updating if you saved before QiskitRuntimeService.save_account(channel="ibm_quantum", token=my_api_token, overwrite=True) print("--- IBM Quantum Account Saved Successfully! ---") print("You can now run the main experiment script.") except Exception as e: print(f"--- ERROR saving account: {e} ---") print("Please double-check your API token and try again.") # --- End of secure setup code --- |
|
# --- Prerequisites --- import time import math import json import os import traceback import numpy as np import pandas as pd import matplotlib.pyplot as plt from qiskit import QuantumCircuit, transpile # Corrected Imports for v0.37.0 from qiskit_ibm_runtime import QiskitRuntimeService, Sampler, Session, Options from qiskit_ibm_runtime.constants import JobStatus from qiskit_ibm_runtime.exceptions import JobError from qiskit.visualization import plot_histogram, circuit_drawer print("--- IBM Quantum Shallow Depth Stress Test (Pinpoint Noise Onset) ---") print("!!! Running shallow depths on hardware. Expect queue times. !!!") # --- Configuration --- BACKEND_NAME = "ibm_brisbane" NUM_SHOTS = 4096 OPTIMIZATION_LEVEL = 2 # <<< --- Testing SHALLOW Depths --- >>> DEPTHS_TO_TEST = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30] # <<< ----------------------------- >>> RESULTS_FILE = 'stress_test_shallow_depth_results.json' # Use a NEW file name # --- Initialize Service --- try: service = QiskitRuntimeService() # Uses saved account print(f"QiskitRuntimeService initialized. Using account: {service.active_account()}") except Exception as e: print(f"ERROR init service: {e}"); traceback.print_exc(); exit() # --- Select Backend --- try: backend = service.backend(BACKEND_NAME) num_qubits = backend.num_qubits print(f"Selected backend: {backend.name} ({num_qubits} qubits)") if backend.simulator: print("ERROR: Selected backend is a simulator."); exit() except Exception as e: print(f"ERROR accessing backend: {e}"); traceback.print_exc(); exit() # --- Helper Function for Circuit Creation --- def create_stress_circuit(depth, num_qubits): qc = QuantumCircuit(num_qubits, name=f"Stress_{depth}L_{num_qubits}q") for layer in range(depth): for i in range(num_qubits): theta, phi, lam = 2 * np.pi * np.random.rand(3); qc.u(theta, phi, lam, i) qc.barrier() if num_qubits > 1: for i in range(num_qubits - 1): qc.cz(i, i + 1) qc.barrier() qc.measure_all(inplace=True) return qc # --- Load Previous Results or Initialize Data Storage --- results_data = [] if os.path.exists(RESULTS_FILE): # Load from the SHALLOW results file try: with open(RESULTS_FILE, 'r') as f: content = f.read() if content: results_data = json.loads(content); print(f"Loaded {len(results_data)} previous results from {RESULTS_FILE}") else: print(f"{RESULTS_FILE} was empty. Starting fresh."); results_data = [] except json.JSONDecodeError: print(f"Warning: {RESULTS_FILE} invalid JSON. Starting fresh."); results_data = [] except Exception as e: print(f"Warning: Could not load previous results: {e}. Starting fresh."); results_data = [] else: print(f"No previous results file found ({RESULTS_FILE}). Starting fresh.") processed_depths = {res.get("depth") for res in results_data if res.get("depth") is not None and res.get("status") != "PENDING"} # --- Main Loop --- for depth in DEPTHS_TO_TEST: if depth in processed_depths: print(f"\n--- Skipping Depth: {depth} (already found in results file) ---"); continue print(f"\n--- Processing Depth: {depth} ---") run_data = { "depth": depth, "job_id": None, "status": "PENDING", "ideal_depth": None, "ideal_size": None, "transpiled_depth": None, "transpiled_ops": None, "transpile_time": None, "unique_outcomes": None, "shannon_entropy": None, "avg_magnetization": None, "std_magnetization": None, "shots_returned": None } try: ideal_circuit = create_stress_circuit(depth, num_qubits) run_data["ideal_depth"] = ideal_circuit.depth(); run_data["ideal_size"] = ideal_circuit.size() print(f"Ideal circuit created (Depth={run_data['ideal_depth']}, Size={run_data['ideal_size']}).") print(f"Transpiling (level {OPTIMIZATION_LEVEL})...") t_start = time.time() isa_circuit = transpile(ideal_circuit, backend=backend, optimization_level=OPTIMIZATION_LEVEL) t_end = time.time() run_data["transpile_time"] = round(t_end - t_start, 2); run_data["transpiled_depth"] = isa_circuit.depth(); run_data["transpiled_ops"] = dict(isa_circuit.count_ops()) print(f"Transpiled in {run_data['transpile_time']:.2f}s (Depth={run_data['transpiled_depth']}, Size={isa_circuit.size()}).") job = None; result = None; session = None try: with Session(backend=backend) as session: print(f"Session opened: {session.session_id}") sampler = Sampler(options={}) # Use default options print("Sampler initialized.") print(f"Submitting job...") job = sampler.run([isa_circuit], shots=NUM_SHOTS) run_data["job_id"] = job.job_id() print(f"Job submitted: {run_data['job_id']}. Waiting for results...") # Still need to wait result = job.result() # BLOCKING CALL run_data["status"] = job.status() print(f"Job {run_data['job_id']} finished with status: {run_data['status']}") except JobError as job_err: print(f"ERROR: Job {job.job_id() if job else 'UNKNOWN'} failed! Error: {job_err}"); run_data["status"] = "ERROR"; except Exception as e: print(f"ERROR during job execution:"); traceback.print_exc(); run_data["status"] = "ERROR_UNKNOWN" # 'with Session' handles closing if result and run_data["status"] == "DONE": print("Processing results...") # ... (results processing logic remains the same) ... if not result or len(result) == 0: print("ERROR: No results data found."); run_data["status"] = "ERROR_NO_RESULT_DATA"; raise Exception("Result object empty") pub_result = result(0; counts = {}; register_name = None; data_bin = pub_result.data if hasattr(data_bin, 'meas'): register_name = 'meas'; counts = data_bin.meas.get_counts() elif hasattr(data_bin, 'c'): register_name = 'c'; counts = data_bin.c.get_counts() if register_name: binary_counts = {}; shots_returned = 0; bitmask = (1 << num_qubits) - 1 print(f"Processing counts using {num_qubits}-bit mask...") processed_counts = {} for k, v in counts.items(): try: raw_val = int(k, 16); masked_val = raw_val & bitmask; bitstring = format(masked_val, f'0{num_qubits}b'); processed_counts[bitstring] = processed_counts.get(bitstring, 0) + v; shots_returned += v except ValueError: print(f" Warning: Skipping key '{k}' (not hex?)."); continue except Exception as parse_err: print(f" Warning: Error parsing key '{k}': {parse_err}"); continue binary_counts = processed_counts print(f"Processed {len(binary_counts)} unique {num_qubits}-bit outcomes.") run_data["shots_returned"] = shots_returned; run_data["unique_outcomes"] = len(binary_counts) if shots_returned > 0: entropy = 0.0 for count in binary_counts.values(): prob = count / shots_returned; entropy -= prob * math.log2(prob) if prob > 0 else 0 run_data["shannon_entropy"] = round(entropy, 4) avg_magnetization = np.zeros(num_qubits); processed_shots_mag = 0 for bitstring, count in binary_counts.items(): if len(bitstring) != num_qubits: continue processed_shots_mag += count for qubit_idx, bit in enumerate(bitstring[:num_qubits]): z_value = 1.0 if bit == '0' else -1.0; avg_magnetization[qubit_idx] += z_value * count if processed_shots_mag > 0: avg_magnetization /= processed_shots_mag; run_data["avg_magnetization"] = np.round(avg_magnetization, 4).tolist(); run_data["std_magnetization"] = round(np.std(avg_magnetization), 4) else: print("No valid shots for magnetization.") else: print("No valid shots returned.") else: print("ERROR: No 'meas' or 'c' register."); run_data["status"] = "ERROR_NO_REGISTER" # Append/Update results data found_existing = False for i, existing_run in enumerate(results_data): if existing_run.get("depth") == depth: results_data[i] = run_data; found_existing = True; break if not found_existing: results_data.append(run_data) try: with open(RESULTS_FILE, 'w') as f: json.dump(results_data, f, indent=2) print(f"Intermediate results saved to {RESULTS_FILE}") except Exception as save_e: print(f"Warning: Failed to save intermediate results: {save_e}") except Exception as outer_e: print(f"ERROR processing depth {depth}:"); traceback.print_exc(); run_data["status"] = "ERROR_PROCESSING"; results_data.append(run_data) finally: # Save intermediate results even on outer error try: with open(RESULTS_FILE, 'w') as f: json.dump(results_data, f, indent=2) except Exception as save_e: print(f"Warning: Failed to save error state: {save_e}") # --- Final Analysis & Plotting --- print("\n--- Finished processing all requested depths ---") try: df = pd.DataFrame(results_data) print("\nSummary DataFrame (Shallow Depths):") print(df[['depth', 'status', 'job_id', 'transpiled_depth', 'shannon_entropy', 'std_magnetization']].to_string()) df_done = df[(df['status'] == "DONE") & (df['shannon_entropy'].notna())].copy() df_done.sort_values(by='depth', inplace=True) if not df_done.empty: print("\nGenerating plots for completed runs...") plt.figure(figsize=(12, 8)); plt.suptitle(f'Shallow Depth Stress Test Metrics on {BACKEND_NAME}') # ... (Plotting code remains the same) ... plt.subplot(2, 2, 1); plt.plot(df_done['depth'], df_done['shannon_entropy'], marker='o'); plt.axhline(y=num_qubits, color='r', linestyle='--', label=f'Max ({num_qubits})'); plt.xlabel("Ideal Depth (Layers)"); plt.ylabel("Shannon Entropy (bits)"); plt.title("Output Entropy"); plt.legend(); plt.grid(True) plt.subplot(2, 2, 2); plt.plot(df_done['depth'], df_done['std_magnetization'], marker='s'); plt.xlabel("Ideal Depth (Layers)"); plt.ylabel("Std Dev of <Z>"); plt.title("Magnetization Spread"); plt.grid(True) plt.subplot(2, 2, 3); plt.plot(df_done['depth'], df_done['transpiled_depth'], marker='^'); plt.xlabel("Ideal Depth (Layers)"); plt.ylabel("Transpiled Depth"); plt.title(f"Transpiled Depth (Opt={OPTIMIZATION_LEVEL})"); plt.grid(True) plt.subplot(2, 2, 4); plt.plot(df_done['depth'], df_done['unique_outcomes'], marker='d'); plt.axhline(y=NUM_SHOTS, color='r', linestyle='--', label=f'Max ({NUM_SHOTS})'); plt.xlabel("Ideal Depth (Layers)"); plt.ylabel("Unique Outcomes"); plt.title("# Unique Outcomes"); plt.legend(); plt.grid(True) plt.tight_layout(rect=[0, 0.03, 1, 0.95]); plt.show() # plt.savefig(f'shallow_depth_scaling_{BACKEND_NAME}.png') else: print("\nNo successfully completed jobs with data found in the results file to plot.") except ImportError: print("\nPlotting requires pandas. `pip install pandas`") except Exception as plot_e: print(f"\nError plotting: {plot_e}"); traceback.print_exc() print("\n--- End of Script ---") ) |
|
# --- Script to Analyze Existing Stress Test Results with Enhancements --- import json import os import traceback import numpy as np import pandas as pd import matplotlib.pyplot as plt import math print("--- Analyzing Shallow Depth Stress Test Results (Enhanced Analysis) ---") # --- Configuration --- NUM_QUBITS = 127 NUM_SHOTS = 4096 # Assuming this was used for all runs in the file BACKEND_NAME = "ibm_brisbane" OPTIMIZATION_LEVEL = 2 # As used in the runs RESULTS_FILE = 'stress_test_shallow_depth_results.json' # File with your results # --- Load Results --- results_data = [] if os.path.exists(RESULTS_FILE): try: with open(RESULTS_FILE, 'r') as f: content = f.read() if content: results_data = json.loads(content); print(f"Loaded {len(results_data)} results from {RESULTS_FILE}") else: print(f"{RESULTS_FILE} is empty. Nothing to analyze."); exit() except Exception as e: print(f"ERROR loading or parsing {RESULTS_FILE}: {e}"); traceback.print_exc(); exit() else: print(f"ERROR: Results file not found: {RESULTS_FILE}"); exit() # --- Data Processing and Metric Calculation --- print("\n--- Processing Stored Results ---") processed_results = [] bitmask = (1 << NUM_QUBITS) - 1 for run_data in results_data: depth = run_data.get("depth") status = run_data.get("status") print(f"Processing entry for depth {depth} (Status: {status})...") # Copy existing data processed_entry = run_data.copy() # --- Recalculate metrics for DONE jobs --- # Ensures consistency even if file was manually edited or partially processed if status == "DONE" and run_data.get("job_id"): # Need to retrieve results again if counts aren't stored directly # For simplicity here, we assume counts WERE processed correctly and saved # If not, you'd need to add job retrieval: # job = service.job(run_data["job_id"]) # result = job.result() # etc. # For now, assume counts need re-processing from raw IF available # NOTE: This part requires the raw counts stored in JSON, which wasn't done previously. # We will proceed assuming the calculated values in the JSON are correct, # but add calculation for Hamming weight if possible from avg_magnetization # A better approach would be to save raw counts dict in the JSON. # Let's recalculate Hamming stats if avg_magnetization exists (as a proxy for counts processing) if run_data.get("avg_magnetization") is not None and run_data.get("shots_returned") == NUM_SHOTS: # Placeholder: Cannot recalculate Hamming weight without raw counts. # We'll add columns but leave them empty if raw counts aren't saved. processed_entry["hamming_mean"] = None # Requires raw counts processed_entry["hamming_std"] = None # Requires raw counts print(" (Skipping Hamming calc - needs raw counts stored in JSON)") else: processed_entry["hamming_mean"] = None processed_entry["hamming_std"] = None # --- Extract Gate Counts --- if run_data.get("transpiled_ops"): ops_dict = run_data["transpiled_ops"] # Adjust gate name if 'ecr' wasn't the primary 2Q gate for Brisbane in that transpilation processed_entry['ecr_count'] = ops_dict.get('ecr', 0) + ops_dict.get('cx', 0) # Sum common 2Q gates processed_entry['swap_count'] = ops_dict.get('swap', 0) else: processed_entry['ecr_count'] = None processed_entry['swap_count'] = None processed_results.append(processed_entry) # --- Final Analysis & Plotting --- print("\n--- Generating DataFrame and Plots ---") try: df = pd.DataFrame(processed_results) print("\nFull Summary DataFrame with Extracted Gates:") cols_to_show = ['depth', 'status', 'job_id', 'transpiled_depth', 'ecr_count', 'swap_count', 'shannon_entropy', 'std_magnetization', 'unique_outcomes'] existing_cols = [col for col in cols_to_show if col in df.columns] print(df[existing_cols].to_string()) # Filter DataFrame for DONE status and valid entropy df_done = df[(df['status'] == "DONE") & pd.notna(df.get('shannon_entropy'))].copy() if not df_done.empty and 'depth' in df_done.columns: df_done.sort_values(by='depth', inplace=True) max_depth_plotted = df_done['depth'].max() print(f"\nGenerating plots for {len(df_done)} completed runs (up to depth {max_depth_plotted})...") # --- Create Figure 1: Core Metrics --- plt.figure(figsize=(12, 8)); plt.suptitle(f'Stress Test Core Metrics vs Depth on {BACKEND_NAME} (Up to Depth {max_depth_plotted})') # Plot Entropy if 'shannon_entropy' in df_done.columns: plt.subplot(2, 2, 1); plt.plot(df_done['depth'], df_done['shannon_entropy'], marker='o'); plt.axhline(y=math.log2(NUM_SHOTS), color='g', linestyle=':', label=f'Max Sample Entropy ({math.log2(NUM_SHOTS):.1f})'); plt.axhline(y=NUM_QUBITS, color='r', linestyle='--', label=f'Max Qubit Entropy ({NUM_QUBITS})'); plt.xlabel("Ideal Depth (Layers)"); plt.ylabel("Shannon Entropy (bits)"); plt.title("Output Entropy"); plt.legend(); plt.grid(True) # Plot Magnetization Spread if 'std_magnetization' in df_done.columns: plt.subplot(2, 2, 2); plt.plot(df_done['depth'], df_done['std_magnetization'], marker='s'); plt.xlabel("Ideal Depth (Layers)"); plt.ylabel("Std Dev of <Z>"); plt.title("Magnetization Spread"); plt.grid(True); plt.ylim(bottom=0) # Plot Transpiled Depth if 'transpiled_depth' in df_done.columns: plt.subplot(2, 2, 3); plt.plot(df_done['depth'], df_done['transpiled_depth'], marker='^'); plt.xlabel("Ideal Depth (Layers)"); plt.ylabel("Transpiled Depth"); plt.title(f"Transpiled Depth (Opt={OPTIMIZATION_LEVEL})"); plt.grid(True) # Plot Unique Outcomes if 'unique_outcomes' in df_done.columns: plt.subplot(2, 2, 4); plt.plot(df_done['depth'], df_done['unique_outcomes'], marker='d'); plt.axhline(y=NUM_SHOTS, color='r', linestyle='--', label=f'Max ({NUM_SHOTS})'); plt.xlabel("Ideal Depth (Layers)"); plt.ylabel("Unique Outcomes"); plt.title("# Unique Outcomes"); plt.legend(); plt.grid(True) plt.tight_layout(rect=[0, 0.03, 1, 0.95]); plt.show() # plt.savefig(f'final_core_metrics_{BACKEND_NAME}.png') # --- Create Figure 2: Transpilation Metrics --- plt.figure(figsize=(12, 5)); plt.suptitle(f'Transpilation Gate Counts vs Depth on {BACKEND_NAME}') # Plot 2Q Gate Counts if 'ecr_count' in df_done.columns: plt.subplot(1, 2, 1); plt.plot(df_done['depth'], df_done['ecr_count'], marker='x'); plt.xlabel("Ideal Depth (Layers)"); plt.ylabel("Count"); plt.title("Transpiled 2Q Gates (ECR/CX)"); plt.grid(True) # Plot SWAP Gate Counts if 'swap_count' in df_done.columns: plt.subplot(1, 2, 2); plt.plot(df_done['depth'], df_done['swap_count'], marker='+'); plt.xlabel("Ideal Depth (Layers)"); plt.ylabel("Count"); plt.title("Transpiled SWAP Gates"); plt.grid(True) plt.tight_layout(rect=[0, 0.03, 1, 0.95]); plt.show() # plt.savefig(f'final_transpilation_gates_{BACKEND_NAME}.png') # --- Create Figure 3: Magnetization Distribution --- depths_to_plot_mag = [d for d in [1, 5, 10, 15, df_done['depth'].max()] if d in df_done['depth'].values] # Select depths if 'avg_magnetization' in df_done.columns and depths_to_plot_mag: print("\nGenerating Magnetization Distribution plots...") plt.figure(figsize=(min(15, 3*len(depths_to_plot_mag)), 4)) plt.suptitle(f'Distribution of Single-Qubit <Z> on {BACKEND_NAME}') for i, depth_val in enumerate(depths_to_plot_mag): mags = df_done.loc[df_done['depth'] == depth_val, 'avg_magnetization'].iloc(0 if mags: # Check if list is not None/empty plt.subplot(1, len(depths_to_plot_mag), i+1) plt.hist(mags, bins=20, range=(-1, 1)) )plt.xlabel("Avg. Z Mag.") if i == 0: plt.ylabel("# Qubits") plt.title(f"Depth {depth_val}") plt.grid(True); plt.ylim(bottom=0) else: print(f"No magnetization data for depth {depth_val}") plt.tight_layout(rect=[0, 0.03, 1, 0.93]); plt.show() # plt.savefig(f'final_magnetization_dist_{BACKEND_NAME}.png') else: print("No magnetization data available to plot distributions.") # Hamming Weight calculation requires raw counts, which were not saved in the previous script. # Add code here if you modify the main script to save `binary_counts` to the JSON file. print("\n(Skipping Hamming Weight analysis - requires raw counts saved in JSON)") else: print("\nNo successfully completed jobs with processed data found in the results file to plot.") except ImportError: print("\nPlotting requires pandas. `pip install pandas`") except Exception as plot_e: print(f"\nError during analysis/plotting: {plot_e}"); traceback.print_exc() print("\n--- End of Analysis ---") |
|
Visual Studio Code Result |
        
|
References
- Arute, F., Arya, K., Babbush, R., Bacon, D., Bardin, J. C., Barends, R., Biswas, R., Boixo, S., Brandao, F. G. S. L., Buell, D. A., Burkett, B., Chen, Y., Chen, Z., Chiaro, B., Collins, R.,... & Martinis, J. M. (Google AI Quantum). (2019). Quantum supremacy using a programmable superconducting processor. Nature, 574(7779), 505-510. [CrossRef]
- Baldwin, C. L., Mayer, K., Ryan, C. A., & Scarmeas, D. (2022). Re-examining the quantum volume test: Ideal distributions, practical compiling limits, and comparison to other methodologies. Quantum, 6, 758. [CrossRef]
- Bharti, K., Cervera-Lierta, A., Kyaw, T. H., Haug, T., Alperin-Lea, S., Anand, A., Degroote, M., Heimonen, H., Kottmann, J. S., Melnikov, A. A., Romero, J., Kwek, L.-C., & Aspuru-Guzik, A. (2022). Noisy intermediate-scale quantum (NISQ) algorithms. Reviews of Modern Physics, 94(1), 015004. [CrossRef]
- Blume-Kohout, R., Gamble, J. K., Nielsen, E., Rudinger, K., Mizrahi, J., Fortier, K., & Maunz, P. (2017). Demonstration of qubit operations at the error correction threshold. Nature Communications, 8(1), 14485. [CrossRef]
- Bravyi, S., Sheldon, S., Kandala, A., Mckay, D. C., & Gambetta, J. M. (2021). Mitigating measurement errors in multiqubit experiments. Physical Review A, 103(4), 042605. [CrossRef]
- Bruzewicz, C. D., Chiaverini, J., McConnell, R., & Sage, J. M. (2019). Trapped-ion quantum computing: Progress and challenges. Applied Physics Reviews, 6(2), 021314. [CrossRef]
- Bylander, J., Gustavsson, S., Yan, F., Yoshihara, F., Harrabi, K., Fitch, G., Cory, D. G., Nakamura, Y., Tsai, J.-S., & Oliver, W. D. (2011). Noise spectroscopy through dynamical decoupling with a superconducting flux qubit. Nature Physics, 7(7), 565–570. [CrossRef]
- Cardani, L., Valenti, F., Casali, N., Catelani, G., Charpentier, T.,... & Córcoles, A. D. (2021). Reducing the impact of radioactivity on quantum circuits in a deep-underground facility. Nature Communications, 12(1), 2733. [CrossRef]
- Chow, J. M., Dial, O., & Gambetta, J. M. (2021, November 16). IBM Quantum breaks the 100-qubit processor barrier. IBM Research Blog. https://www.ibm.com/quantum/blog/127-qubit-quantum-processor-eagle.
- Cross, A. W., Bishop, L. S., Sheldon, S., Nation, P. D., & Gambetta, J. M. (2019). Validating quantum computers using randomized model circuits. Physical Review A, 100(3), 032328. [CrossRef]
- Earnest, N., Tornow, S., & Egger, D. J. (2021). Pulse-efficient circuit transpilation for quantum applications on cross-resonance-based hardware. Physical Review Research, 3(4), 043088. [CrossRef]
- Eisert, J., Hangleiter, D., Walk, N., Roth, I., Naghiloo, M., Pashayan, H.,... & Krastanov, S. (2020). Quantum certification and benchmarking. Nature Reviews Physics, 2(7), 382–390. [CrossRef]
- Endo, S., Cai, Z., Benjamin, S. C., & Yuan, X. (2021). Hybrid quantum-classical algorithms and quantum error mitigation. Journal of the Physical Society of Japan, 90(3), 032001. [CrossRef]
- Fowler, A. G., Mariantoni, M., Martinis, J. M., & Cleland, A. N. (2012). Surface codes: Towards practical large-scale quantum computation. Physical Review A, 86(3), 032324. [CrossRef]
- Gambetta, J. M., Chow, J. M., & Steffen, M. (2017). Building logical qubits in a superconducting quantum computing system. npj Quantum Information, 3(1), 2. [CrossRef]
- Gambetta, J. M., Córcoles, A. D., Merkel, S. T., Johnson, B. R., Smolin, J. A., Chow, J. M., Ryan, C. A., Rigetti, C., Poletto, S., Ohki, T. A., Ketchen, M. B., & Steffen, M. (2012). Characterization of addressability by simultaneous randomized benchmarking. Physical Review Letters, 109(24), 240504. [CrossRef]
- Google AI Quantum and Collaborators. (2023). Suppressing quantum errors by scaling a surface code logical qubit. Nature, 614(7949), 676–681. [CrossRef]
- Hangleiter, D., Kliesch, M., Schwarz, M., & Eisert, J. (2021). Direct certification of a class of quantum simulations. Quantum Science and Technology, 6(2), 025004. [CrossRef]
- IBM Quantum. (n.d.-a). Configure error mitigation options. IBM Quantum Documentation. Retrieved April 21, 2025, from https://docs.quantum.ibm.com/run/configure-error-mitigation.
- IBM Quantum. (n.d.-b). Introduction to transpilation. IBM Quantum Documentation. Retrieved April 21, 2025, from https://docs.quantum.ibm.com/guides/transpile.
- IBM Quantum. (n.d.-c). Qiskit Runtime overview. IBM Quantum Documentation. Retrieved April 21, 2025, from https://docs.quantum.ibm.com/run/runtime.
- Jurcevic, P., Javadi-Abhari, A., Bishop, L. S., Lauer, I., Bogorin, D. F., Brink, M., Capelluto, L., Günther, O., Itoko, T., Kanazawa, N., Kandala, A., Keefe, G. A., Kenerelman, K., Klaus, D., Koch, J.,... & Gambetta, J. M. (2021). Demonstration of quantum volume 64 on a superconducting quantum computing system. Quantum Science and Technology, 6(2), 025020. [CrossRef]
- Kandala, A., Mezzacapo, A., Temme, K., Takita, M., Brink, M., Chow, J. M., & Gambetta, J. M. (2017). Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature, 549(7671), 242–246. [CrossRef]
- Kim, Y., Eddins, A., Anand, S., Wei, K. X., van den Berg, E., Rosenblatt, S., Nayfeh, H., Wu, Y., Zoufaly, M., Kurečić, P., Haide, I., & Temme, K. (2023). Evidence for the utility of quantum computing before fault tolerance. Nature, 618(7965), 500–505. [CrossRef]
- Klimov, P. V., Kelly, J., Chen, Z., Neeley, M., Megrant, A., Burkett, B., Barends, R., Arya, K., Chiaro, B., Chen, Y.,... & Martinis, J. M. (2018). Fluctuations of energy-relaxation times in superconducting qubits. Physical Review Letters, 121(9), 090502. [CrossRef]
- Krinner, S., Lacroix, N., Remm, A., Di Paolo, A., Genois, E., Leroux, C., Hellings, C., Lazar, S., Swiadek, F., Herrmann, J., Norris, G. J., Andersen, C. K., Müller, C., Wallraff, A., & Eichler, C. (2022). Realizing repeated quantum error correction in a distance-three surface code. Nature, 605(7911), 669–674. [CrossRef]
- Li, Y., & Benjamin, S. C. (2017). Efficient variational quantum simulator incorporating active error minimization. Physical Review X, 7(2), 021050. [CrossRef]
- Magesan, E., Gambetta, J. M., & Emerson, J. (2011). Scalable and robust randomized benchmarking of quantum processes. Physical Review Letters, 106(18), 180504. [CrossRef]
- Mariantoni, M., Lang, H., Chuang, I. L., Shor, P. W., Wang, T., & Bialczak, R. C. (2011). Implementing the quantum von Neumann architecture with superconducting circuits. Science, 334(6052), 61–65. [CrossRef]
- Müller, C., Cole, J. H., & Lisenfeld, J. (2019). Towards understanding two-level-systems in amorphous solids – insights from quantum circuits. Reports on Progress in Physics, 82(12), 124501. [CrossRef]
- Mundada, P. S., Zhang, G., Hazard, T., & Houck, A. A. (2019). Suppression of qubit crosstalk in a tunable coupling superconducting circuit. Physical Review Applied, 12(5), 054023. [CrossRef]
- Murali, P., Linke, N. M., Martonosi, M., Abhari, A. J., Nguyen, N. H., & Alderete, C. H. (2019). Noise-adaptive compiler mappings for noisy intermediate-scale quantum computers. Proceedings of the Twenty-Fourth International Conference on Architectural Support for Programming Languages and Operating Systems (ASPLOS '19), 1027–1040. [CrossRef]
- Nielsen, M. A., & Chuang, I. L. (2010). Quantum Computation and Quantum Information: 10th Anniversary Edition (Chapter 8: Quantum Noise and Quantum Operations). Cambridge University Press.
- Preskill, J. (2018). Quantum Computing in the NISQ era and beyond. Quantum, 2, 79. [CrossRef]
- Qiskit Development Team. (2024). Qiskit Textbook (Online). https://learn.qiskit.org.
- Sarovar, M., Blume-Kohout, R., Clader, B. D., & Rudinger, K. M. (2020). Detecting crosstalk errors in quantum information processors. Quantum, 4, 321. [CrossRef]
- Takita, M., Cross, A. W., Córcoles, A. D., Chow, J. M., & Gambetta, J. M. (2017). Experimental demonstration of fault-tolerant state preparation with superconducting qubits. Physical Review Letters, 119(18), 180501. [CrossRef]
- Tannu, S. S., & Qureshi, M. K. (2019). Not all qubits are created equal: A case for variability-aware policies for NISQ-era quantum computers. Proceedings of the Twenty-Fourth International Conference on Architectural Support for Programming Languages and Operating Systems (ASPLOS '19), 987–999. [CrossRef]
- Temme, K., Bravyi, S., & Gambetta, J. M. (2017). Error mitigation for short-depth quantum circuits. Physical Review Letters, 119(18), 180509. [CrossRef]
- Terhal, B. M. (2015). Quantum error correction for quantum memories. Reviews of Modern Physics, 87(2), 307-346. [CrossRef]
- van den Berg, Z. K., Kandala, A., & Temme, K. (2023). Probabilistic error cancellation with sparse Pauli-Lindblad models on noisy quantum processors. Nature Physics, 19(9), 1341-1346. [CrossRef]
- van den Berg, E., Temme, K., & Bravyi, S. (2023). Model-free readout error mitigation for quantum computers. Nature Physics, 19(9), 1336-1340. [CrossRef]
- Viola, L., Knill, E., & Lloyd, S. (1999). Dynamical decoupling of open quantum systems. Physical Review Letters, 82(12), 2417–2421. [CrossRef]
- Werning, L., Steckmann, H. T., Kramer, J. G., Sonner, P. M., Egger, D. J., & Wilhelm, F. K. (2021). Leakage reduction in quantum gates using optimal control. PRX Quantum, 2(2), 020343. [CrossRef]
- Willsch, D., Willsch, M., De Raedt, H., & Michielsen, K. (2020). Benchmarking the quantum approximate optimization algorithm. Quantum Information Processing, 19(8), 261. [CrossRef]
- Wright, K., Beck, K. M., Debnath, S., Amini, J. M., Avsar, Y., Figgatt, C. E.,... & Kim, J. (2019). Benchmarking an 11-qubit quantum computer. Nature Communications, 10(1), 5464. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).