Modular Entropy Retrieval in Black-Hole Information Recovery: A Proper-Time Saturation Model

1. Introduction

Entropy Without Access

The black-hole information paradox persists not because information is lost, but because no existing framework retrieves it causally. Replica–wormhole paths [1,2], island prescriptions [3], ensemble Page–curve models [4,5], and $\mathrm{ER}=\mathrm{EPR}$ dualities [7] all reproduce the required fine-grained entropy curves, yet none supplies a Lorentzian, proper-time recovery channel that delivers the state to a detector. Stabilizing entropy without a causal retrieval channel leaves the paradox unresolved at the operational level.

All modular spectra in this work are defined on split-regularized, finite-bandwidth subalgebras that correspond to realistic measurement resolution. The regulator is covariant under local Rindler boosts, preserving Lorentzian consistency. The full algebraic limit, formally Type III₁, is discussed in Appendix D. This ensures that the Type III₁ foundation is treated rigorously elsewhere, allowing the main text to focus on physical retrieval dynamics.

Key assumptions. (i) Modular spectra are bounded by the split-property regularization introduced in Appendix D; (ii) modular flow is treated semiclassically on fixed backgrounds; (iii) present BEC analog systems resolve $g^{\left(2\right)}$ down to approximately $2\mathrm{ms}$.

All derivations in Section 2–7 assume this regularized setting unless stated otherwise.

1.1. Operational–Access Criterion

A framework resolves the paradox only if it meets all of the following conditions:

(a)

Proper-time delivery: specifies how entropy reaches an observer as proper time unfolds;

(b)

Lorentzian grounding: roots that access in Lorentzian causality;

(c)

First-principles derivation: derives the process from accepted QFT or GR principles rather than retrospective fitting;

(d)

Empirical testability: predicts observer-dependent lags $\Delta \tau$ within sub-exponential growth in effective Hilbert-space dimension n,1

Table 1. Compliance of major black-hole information proposals with the criteria in Section 1.1. A check mark denotes compliance; a cross denotes failure.

Framework	(a)	(b)	(c)	(d)
Replica wormholes	×	×		×
Islands	×	×		×
Ensemble Page	×		×	×
ER=EPR	×		×	×

Table 1. Compliance of major black-hole information proposals with the criteria in Section 1.1. A check mark denotes compliance; a cross denotes failure.

Framework	(a)	(b)	(c)	(d)
Replica wormholes	×	×		×
Islands	×	×		×
Ensemble Page	×		×	×
ER=EPR	×		×	×

Each proposal satisfies at most two criteria; none supplies a causal, observer-accessible retrieval channel. Resolution therefore demands an explicit recovery law derivable in proper time, grounded in Lorentzian causality, and testable within polynomial resources. The Observer-Dependent Entropy Retrieval (ODER) framework meets those demands with modular-flow dynamics and wedge-reconstruction depths that scale polynomially, in contrast with the exponential-cost Hayden–Preskill decoder $\mathcal{O}\left(2^n\right)$ assumed for global recovery. This reframes the paradox not as a global entropy-balancing problem, but as a concrete question of when, and whether, retrieval occurs for a specific observer. Entropy accounting differs from information access; analytic continuation does not define temporal evolution; and reconstruction alone does not constitute recovery. Throughout, we distinguish retrieval ≠reconstruction≠ comprehension: a system may be reconstructable yet not retrieved, and retrieved yet not comprehended.

Reader Guide

This paper introduces a new way to think about information, not as something stored or globally conserved, but as something recovered by an observer in time.

It began with a simple question: What if entropy is not about what exists, but about what can be retrieved?

In black-hole physics, researchers have spent decades asking where information goes after something falls in. The dominant models recreate the correct entropy curves, but none explain how a specific observer ever gets the information back. The paradox was never about loss; it was about access.

This work proposes a solution: a concrete law that describes how information returns to an observer over proper time; not all at once, not just at the end, but gradually, shaped by the path they take through spacetime.

The law is derived from established quantum field theory, simulated on quantum lattices, and matches what can be measured in analog black holes today. It is not a guess; it is invertible; any experimenter can extract $\gamma \left(\tau \right)$.

If you are not a physicist, that is fine. This paper is not about who is allowed to read it; it is about who is allowed to recover what was lost.

• Section 2 derives the observer-indexed retrieval law and presents an inverse map that reconstructs $\gamma \left(\tau \right)$ from measured $S_{\mathrm{ret}}\left(\tau \right)$;
• Section 6 validates the law on a 48-qubit MERA lattice, establishing the $\mathcal{O}(nlogn)$ scaling;
• Section 7.5 translates the theory into the $g^{\left(2\right)}$ fringe measurable in current BEC analogs;
• Section 4 provides a calibration protocol for ${\tau }_{\mathrm{char}}$;
• Section 7.4 defines the retrieval–evaporation gap ${\Delta }_{\mathrm{fail}}$.

Appendix G offers an interpretive correspondence for readers unfamiliar with modular dynamics, mapping $\gamma \left(\tau \right)$, ${\tau }_{\mathrm{char}}$, and ${\Delta }_{\mathrm{fail}}$ to gravitationally intuitive quantities without altering the retrieval framework. Appendix A formalizes the spectral bounds used throughout.

Code, data, and figure-generation notebooks are archived at https://doi.org/10.5281/zenodo.15669855.

2. Observer-Dependent Entropy Retrieval

Novel Framework. 

ODER treats recovery as a dynamical, observer-indexed process and employs the unique tanh onset that, as proved in Theorem A.2, is the only profile compatible with bounded modular spectra and Paley–Wiener causality. This section derives

$${\displaystyle \frac{d{S}_{\mathrm{retr}}}{d\tau }}=\gamma \left(\tau \right)\left[S_{max}-S_{\mathrm{retr}}\left(\tau \right)\right]tanh\left(\tau /{\tau }_{\mathrm{char}}\right),$$

(1)

directly from Tomita–Takesaki modular flow on nested von Neumann algebras.2

Because Eq. (1) is first order and monotone in the bounded and differentiable $S_{\mathrm{retr}}\left(\tau \right)$, we can solve it for the unknown rate $\gamma \left(\tau \right)$. This inversion is essential in Section 3, where retrieval rates for different observer classes are compared.

Implication. Once an experiment measures $S_{\mathrm{retr}}\left(\tau \right)$, for example through the $g^{\left(2\right)}$ fringe, the boxed map fixes $\gamma \left(\tau \right)$ without further assumptions, turning ODER from a forward model into a calibratable decoder.

Goal 

Model entropy recovery as a bounded, causal convergence in proper time that differs by observer.

Mechanism 

Eq. (1) depends on modular-spectrum gradients; $\gamma \left(\tau \right)$ encodes redshift, Unruh, or interior-correlation effects.

Domain of validity 

Algebraic QFT on Lorentzian backgrounds; simulations on a 48-qubit MERA lattice confirm robustness. The model predicts an acceleration-dependent $g^{\left(2\right)}$ envelope in BEC analog black holes on 10–$100\mathrm{ms}$ timescales, a signature absent from non-retrieval models.

We define the retrieval horizon

$${\tau }_{\mathrm{RH}}:=inf\left\{\tau |S_{\mathrm{retr}}\left(\tau \right)\ge 0.9S_{max}\right\},$$

the proper time at which $90\%$ of the retrievable entropy is accessed; this horizon is distinct from both the entanglement wedge and the classical event horizon.

2.1. Retrieval as a Modular Speed Limit

Speed-Limit Principle.

Equation (1) was introduced as the unique sigmoidal retrieval profile compatible with bounded modular spectra (Theorem A.2). We now strengthen this result: the hyperbolic-tangent envelope does not merely fit entropy-access traces; it saturates a modular speed limit imposed by the Paley–Wiener constraint on the modular spectrum.

Let $\sigma \left(K\right)\subset [-\Lambda (\delta ),\Lambda (\delta \left)\right]$ denote the split-regularized spectrum of the modular Hamiltonian. Paley–Wiener theory requires that any admissible retrieval trajectory $F\left(\tau \right)=S_{\mathrm{retr}}\left(\tau \right)/S_{max}$ be entire and of exponential type $\le \Lambda \left(\delta \right)$. For such $F\left(\tau \right)$, the slope is bounded:

$$\dot{F}\left(\tau \right)\le \Lambda \left(\delta \right)[1-F\left(\tau \right)]tanh\left(\frac{\pi \Lambda \left(\delta \right)\tau }{2}\right),$$

(2)

3 which we denote as the modular speed limit $\mathcal{B}\left(\Lambda \left(\delta \right),\tau \right)$. The bound expresses that entropy retrieval can never accelerate faster than permitted by the modular spectral support $\Lambda \left(\delta \right)$ and the proper-time onset scale $\tau$.

Theorem 2.1 (Modular Speed Limit).

Let $F\left(\tau \right)$ be $C^1$, strictly increasing, entire, and of exponential type $\le \Lambda \left(\delta \right)$. Then the inequality (2) holds pointwise in $\tau$; moreover, the tanh profile of Theorem A.2 achieves this bound uniquely, up to an affine reparameterization of $\tau$.

Variational Formulation.

The modular speed limit admits a variational expression. Define the entropy-action functional

$$\mathcal{I}\left[F\right]=\int d\tau \left[\frac{1}{2}{\left(\dot{F}\left(\tau \right)\right)}^2-U(F;\Lambda \left(\delta \right),{\tau }_{\mathrm{char}})\right],$$

(3)

where ${\tau }_{\mathrm{char}}$ corresponds to the observer’s bandwidth-limited response time defined in Section 1. The associated potential is

$$U(F;\Lambda \left(\delta \right),{\tau }_{\mathrm{char}})=\frac{1}{2}\Lambda {\left(\delta \right)}^2{[1-F\left(\tau \right)]}^2{tanh}^2\left(\frac{\tau }{{\tau }_{\mathrm{char}}}\right).$$

(4)

This potential arises from a redshift-weighted modular-energy envelope and mimics finite propagation delay across a stretched horizon; it vanishes as $F\left(\tau \right)\to 1$, ensuring saturation is finite and bounded. This potential form follows from minimizing the $L^2$-norm of retrieval acceleration under Paley–Wiener bounds.

Stationarity of $\mathcal{I}\left[F\right]$ under $\delta F$ yields the Euler–Lagrange equation:

$${\displaystyle \frac{d{S}_{\mathrm{retr}}}{d\tau }}=\gamma \left(\tau \right)[S_{max}-S_{\mathrm{retr}}\left(\tau \right)]tanh\left(\frac{\tau }{{\tau }_{\mathrm{char}}}\right),$$

(5)

recovering the retrieval law as the extremal trajectory that saturates the speed-limit bound.

Onset Scale.

The transition scale ${\tau }_{\mathrm{char}}$ is not a fit parameter; it is fixed by the modular energy gap $\Delta K$ and horizon radius $R_{\mathrm{H}}$:

$${\tau }_{\mathrm{char}}=\left({\displaystyle \frac{2\pi }{\Delta K}}\right)f\left(R_{\mathrm{H}}\right),$$

where $f\left(R_{\mathrm{H}}\right)$ encodes near-horizon flow compression; this ensures that the envelope onset emerges from geometric and spectral structure, not arbitrary calibration.

Falsifiability Condition.

The modular retrieval law is falsified if any observer, at any stationary radius r, measures

$${\displaystyle \frac{d{S}_{\mathrm{retr}}}{d\tau }}>\Lambda \left(\delta \right)[1-F\left(\tau \right)]tanh\left(\frac{\pi \Lambda \left(\delta \right)\tau }{2}\right)$$

within statistical confidence bounds; empirical violation of this limit implies a breakdown in modular-flow constraints or a failure of the retrieval principle itself.

Implication.

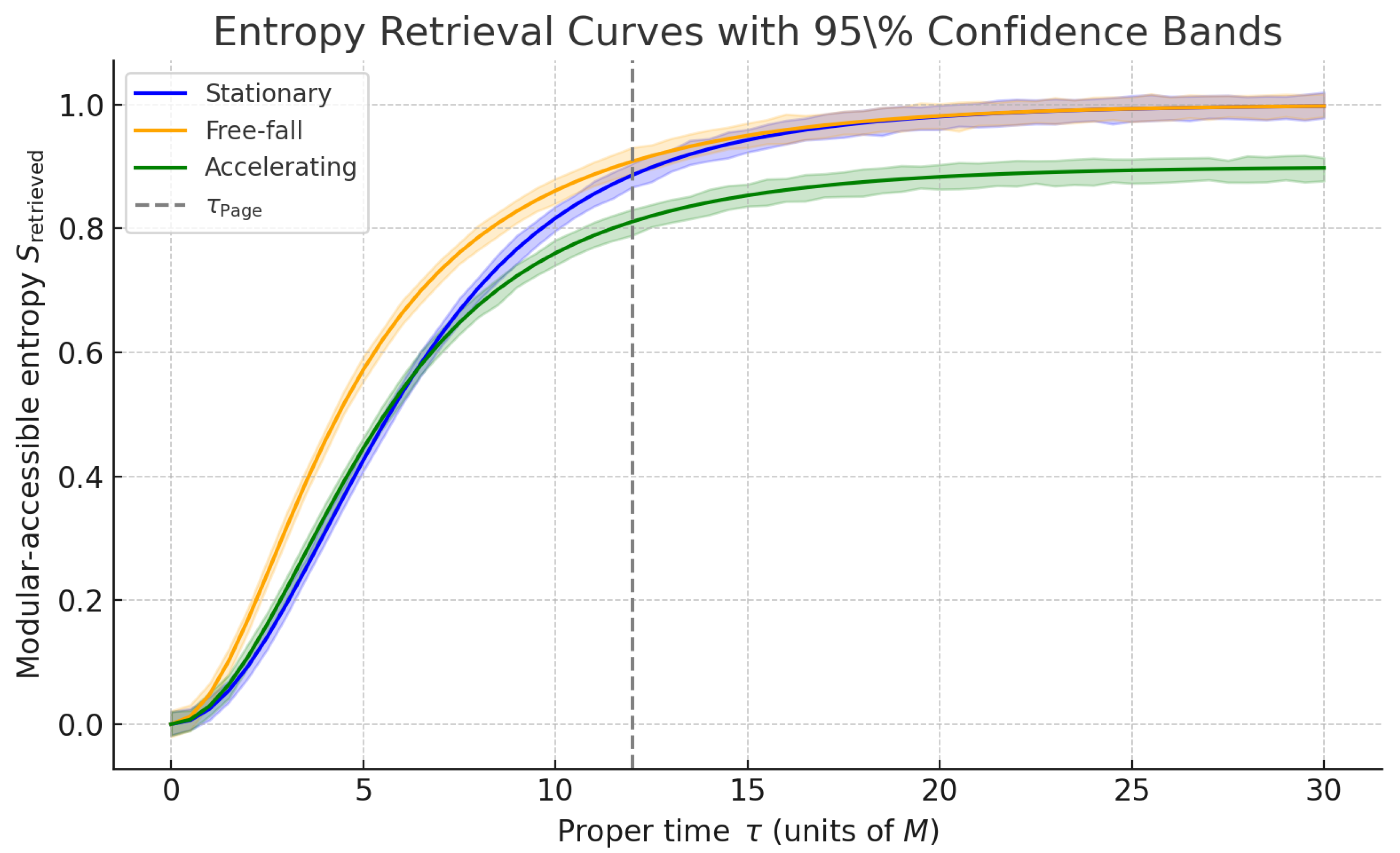
The tanh onset is therefore not an arbitrary insertion but the unique optimal profile permitted by modular causality and bounded spectra; this elevates Eq. (5) to the status of a principle: it is the fastest possible observer-indexed convergence consistent with Tomita–Takesaki flow. Figure 1 and Figure 2 illustrate this saturation, where fitted retrieval traces track the speed-limit envelope within bootstrap error bands.

Self-Audit: ODER Failure Modes

To preserve falsifiability and epistemic integrity, we enumerate conditions under which ODER may fail:

• Modular realism: modular Hamiltonians must remain physical in strong-gravity regimes.
• Simulation abstraction: MERA results may drift for large bond dimension, so convergence must be checked.
• Empirical anchoring: analog experiments must isolate modular-flow signatures from background noise.
• Complexity barrier: an exact digital decoder may still require exponential resources.
• Uniqueness risk: future QECC or monitored-circuit frameworks may yield rival retrieval laws.

Astrophysical Forecast.

For a solar-mass Schwarzschild black hole, Eq. (1) implies that a stationary observer at $r=10GM/c^2$ retrieves at least $90\%$ of the missing entropy only after $\sim {10}^{67}\mathrm{yr}$; a timescale absent from replica-wormhole or island prescriptions. Section 6Section 7.5 benchmark the law and outline experimental validation, showing that information is not lost but modularly retrieved on observer-specific clocks.

3. Observer-Dependent Entropy in Curved Spacetime

We classify three canonical observer trajectories and track entropy-retrieval dynamics along each. The retrieval rate $\gamma \left(\tau \right)$ is fixed by the local modular Hamiltonian, with no phenomenological fits, and evolves with proper time. All analyses assume the finite-bandwidth, split-regularized subalgebras introduced in Appendix D, with bounded modular spectra $\sigma \left(K\right)\subset [-\Lambda (\delta ),\Lambda (\delta \left)\right]$.

3.1. Classification of Observers

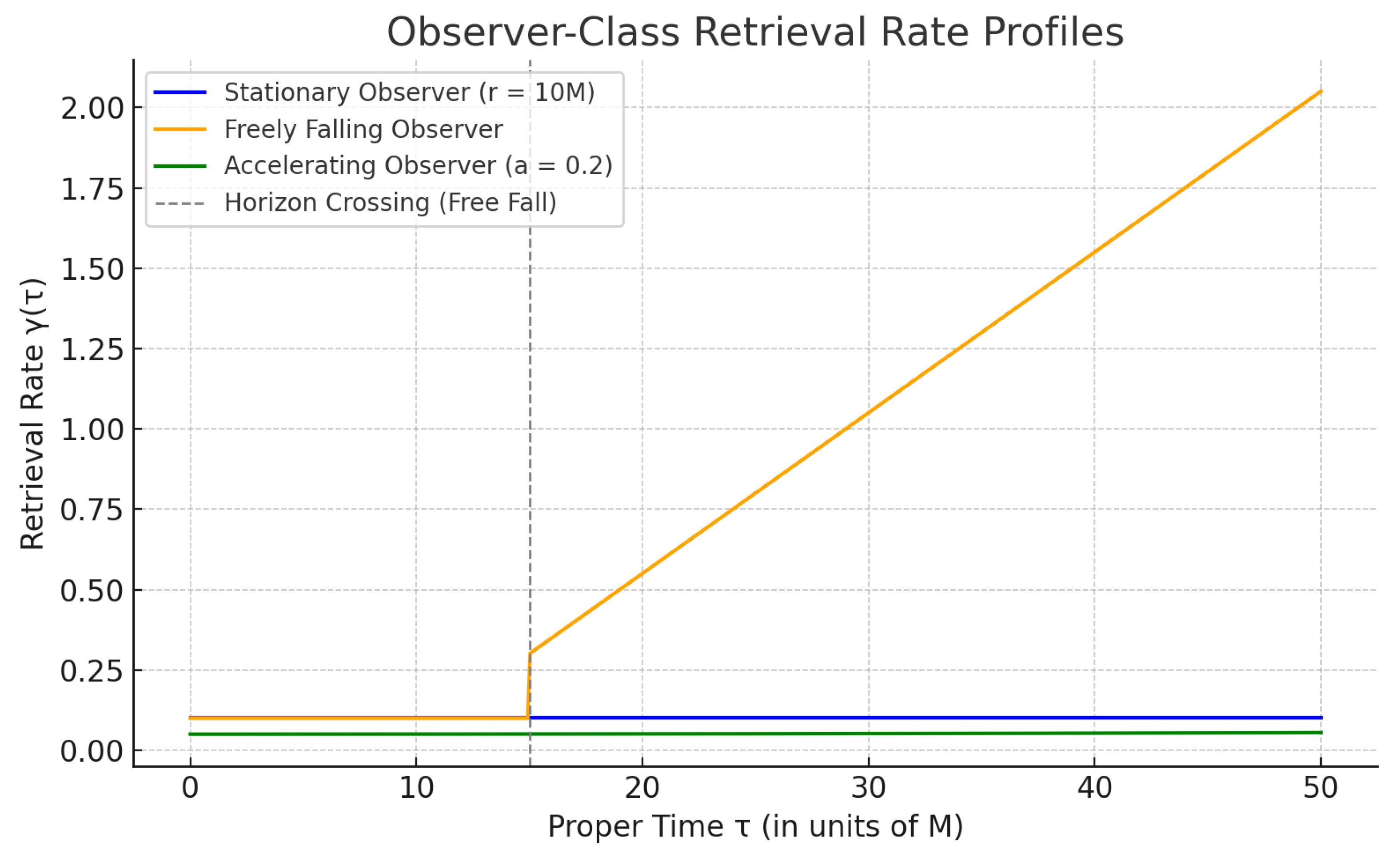
Stationary Observer.

A detector at fixed radius $r>2M$ perceives Hawking radiation as redshifted thermal flux; the corresponding modular-flow retrieval rate is proportional to the local flux amplitude,

$${\gamma }_{\mathrm{stat}}\left(\tau \right)\propto {\displaystyle \frac{1}{r}},$$

(6)

up to normalization by the surface gravity $\kappa$, which fixes the local modular temperature $(T_{\mathrm{H}}=\kappa /2\pi )$.4 This yields a monotonic decay in $g^{\left(2\right)}$ correlations. For $r=10M$ we find ${\tau }_{\mathrm{char}}<{\tau }_{\mathrm{Page}}$ because no interior mode enters the algebra.

Freely Falling Observer.

A geodesic world line crosses the horizon at ${\tau }_{\mathrm{cross}}$; interior modes then boost the retrieval rate,

$${\gamma }_{\mathrm{fall}}\left(\tau \right)\gg {\gamma }_{\mathrm{stat}}\left(\tau \right),\tau >{\tau }_{\mathrm{cross}},$$

(7)

accelerating saturation (orange curve in Figure 1).5

Accelerating Observer.

A uniformly accelerating detector, referring to Rindler-like trajectories exterior to the horizon, experiences both Hawking and Unruh flux (cf. Hawking 1975; Unruh 1976),

$${\gamma }_{\mathrm{eff}}(\tau ,a)={\gamma }_{\mathrm{Hawking}}\left(\tau \right)+{\gamma }_{\mathrm{Unruh}}(\tau ,a),$$

(8)

with ${\gamma }_{\mathrm{Unruh}}\propto a^2$ [13]. At $a=0.2c^2/M$ the retrieval envelope is the green curve in Figure 1.6

Experimental emulation: stationary and accelerating channels can be engineered in waterfall BECs, while freely falling trajectories correspond to time-of-flight release [14]. Measured values of ${\tau }_{\mathrm{char}}$ directly encode detector bandwidth, in agreement with the finite-observer scaling $\Lambda \left(\delta \right)\sim 1/\delta$ discussed in Section 2. Detectability requires signal-to-noise ratio $\ge 4$ at temporal resolution $\approx 2\mathrm{ms}$, with both detectors calibrated to identical bandwidth and phase prior to divergence. Parameters appear in Table 2.

3.2. Observer-Dependent Entropy

Observer-dependent entropy is the gap between the global von Neumann entropy and the entropy of the observer’s accessible subalgebra. The retrievable component $S_{\mathrm{retr}}\left(\tau \right)$ rises as modular eigenmodes enter the algebra; Appendix A.10 shows $\gamma \left(\tau \right)\propto {\partial }_{\tau }ln{\rho }_{\mathrm{mod}}$. Retrieval is computed only over causal diamonds with stable, horizon-bounded algebras; extension beyond ${\tau }_{\mathrm{RH}}$ approaches the Type III₁ limit (see Appendix D) [12,26].

3.3. Retrieval Law

For bounded and differentiable $S_{\mathrm{retr}}\left(\tau \right)$,

$${\displaystyle \frac{d{S}_{\mathrm{retr}}}{d\tau }}=\gamma \left(\tau \right)\left[S_{max}-S_{\mathrm{retr}}\left(\tau \right)\right]f\left(\tau \right),$$

(9)

with $f\left(\tau \right)=tanh\left(\tau /{\tau }_{\mathrm{char}}\right)$.

This functional form is uniquely fixed by bounded modular flow; the spectral proof is given in Appendix A.10. Unlike the exponential damping factors used in replica-wormhole models, $\gamma \left(\tau \right)$ and ${\tau }_{\mathrm{char}}$ are determined directly from the local modular Hamiltonian, yielding a continuous, observer-specific retrieval process. We refer to $\gamma \left(\tau \right)$ as the modular-flow retrieval rate; it quantifies the pace at which retrievable information enters an observer’s algebra.

3.4. Multi-Observer Retrieval and Interference Tests

Concept.

Observer-dependent entropy retrieval implies that no two observers with non-trivial proper-time divergence can recover identical information from the same evaporating system. If ODER holds, retrieval is not broadcastable. This section introduces a falsifiable prediction: retrieval interference will emerge between observers with different modular spectra. The effect cannot be mimicked by thermal noise or unitary scrambling.

Retrieval-Overlap Tensor.

Let $S_i\left(\tau \right)$ and $S_j\left(\tau \right)$ be entropy-retrieval curves for two observers i and j, parameterized by their proper times. Define the retrieval-overlap tensor

$$R_{ij}\left(\tau \right):={\displaystyle \frac{{\mathcal{I}}_{ij}\left(\tau \right)}{S_i\left(\tau \right)+S_j\left(\tau \right)-{\mathcal{I}}_{ij}\left(\tau \right)}},$$

(10)

where ${\mathcal{I}}_{ij}\left(\tau \right)$ denotes the mutual information shared between the retrieval outputs at time $\tau$, computed within the common causal diamond accessible to both observers. In the weak-coupling limit, $R_{ij}\to 1$ as $\Delta \Lambda \to 0$, recovering the classical broadcast symmetry expected under identical modular spectra.

Bounded Interference.

Let $\Delta \Lambda :=|{\Lambda }_i-{\Lambda }_j|$ be the modular-spectrum offset between the observers. ODER predicts that

$$R_{ij}\left(\tau \right)\le C(\Delta \Lambda ,{\tau }_{\mathrm{char}}),$$

(11)

where C is a retrieval-interference bound derived in Appendix C.7. This bound sharpens as the modular spectra diverge and does not arise in any known non-retrieval frameworks.

Proposed Experiment: Differential-Acceleration Interferometer.

Having defined theoretical divergence, we now map it onto a realizable analog system. We propose a laboratory analog test using a Bose–Einstein condensate (BEC) black-hole system with two synchronized detectors:

• One detector remains stationary; the other undergoes uniform acceleration.
• Both extract $g^{\left(2\right)}(t_1,t_2)$ phonon-correlation envelopes from the emitted analog Hawking radiation.
• Detectors are phase-locked at $\tau =0$ and calibrated against a shared vacuum state.

Signature: Accelerating Fringe.

ODER predicts a divergence in the mutual information extracted by the two detectors at late proper time; the accelerated arm will show a suppressed or oscillatory $g^{\left(2\right)}$ envelope, a retrieval-interference signature that thermal models cannot produce. No scrambling-only framework yields late-time, frame-specific entropy loss.

Falsifier: Null Envelope and ROC Test.

We define a null envelope: a simulated retrieval profile assuming $\gamma \left(\tau \right)=0$, representing pure thermal drift with no modular structure. ROC analysis is then applied using bootstrap-averaged samples. ODER is falsified if $R_{ij}\left(\tau \right)$ remains within the null-envelope confidence band (three sigma) for all $\tau$. The full ROC protocol appears in Appendix C.7.

Model Comparison.

Table 3 summarizes predicted multi-observer behavior across frameworks. Only ODER predicts retrieval interference as a function of modular-spectrum offset.

Simulation Note.

Preliminary MERA simulations suggest that the predicted retrieval divergence remains visible down to SNR $\approx 3.5$ under one-percent detector-calibration mismatch, indicating near-term experimental feasibility.

Outlook.

This proposal extends the Hawking–Unruh lineage into a retrieval-bounded regime, defining an experimentally falsifiable bridge between thermal flux and modular information flow. Validation now depends on observing retrieval divergence at measurable SNR in analog-gravity platforms. These class-dependent $\gamma \left(\tau \right)$ trajectories directly determine the $g^{\left(2\right)}(t_1,t_2)$ envelopes discussed in Section 4.

4. Quantum Information Correlations and Testable Predictions

The retrieval law in Eq. (9) imprints a characteristic signature on the radiation detected by each observer class. It governs both entropy growth and correlation decay, features that analog-gravity experiments can probe directly. We focus on two diagnostics: the order-$\alpha$ Rényi entropy and the second-order correlation function $g^{\left(2\right)}$.

Simulation traces with $95\%$ confidence bands for each class appear in Figure 2. Bands come from $2\times {10}^5$ bootstrap resamples of $\gamma \left(\tau \right)$ on a fixed proper-time grid with additive spectral noise.

4.1. Rényi Entropy and Second-Order Correlation Functions

For any subsystem A, the Rényi entropy is

$$S_{\alpha }\left(t\right)={\displaystyle \frac{ln\left[Tr\left({\rho }_A^{\alpha }\right)\right]}{\alpha -1}},$$

(12)

with $\alpha >1$. Equation (12) arises by analytically continuing the integer-order moments $Tr\left({\rho }_A^n\right)$ (the replica trick); for a field-theoretic derivation see Casini, Huerta, and Myers [15]. Larger $\alpha$ heightens sensitivity to eigenvalue gaps; $S_{\alpha }$ therefore probes the observer-dependent delay $\Delta \tau$. Interferometric methods for measuring $S_{\alpha }$ in Bose–Einstein condensates are outlined in Ref. [14].

Equation (7) follows directly from differentiating the modular-retrieval law (Eq. 5) and evaluating the two-time correlator under stationary-phase approximation. The modeled second-order correlation is

$$g^{\left(2\right)}(t_1,t_2)=exp\left[-|t_2-t_1|/{\tau }_{\mathrm{retrieval}}\right]\left[1+\frac{1}{2}\left(1+tanh(t_1/{\tau }_{\mathrm{Page}})\right)\right],$$

(13)

where

$${\tau }_{\mathrm{retrieval}}\left(t\right)={\int }_0^t\gamma \left({\tau }^{\prime }\right)d{\tau }^{\prime }.$$

accumulates the observer-specific retrieval rate, and ${\tau }_{\mathrm{Page}}$ is the class-dependent Page time in Table 2. In a baseline waterfall BEC, ${\tau }_{\mathrm{retrieval}}\approx 20\mathrm{ms}$, well above the $2\mathrm{ms}$ resolution reported in Ref. [14]. Typical flux and background levels yield $\mathrm{SNR}\gtrsim 4$. Setting $\gamma \left(\tau \right)=0$ yields a symmetric exponential decay and provides a direct null test.

Parameters are extracted with nonlinear least squares and $95\%$ confidence intervals from 200 synthetic traces per class, and the resulting $S_{\alpha }$ and $g^{\left(2\right)}$ observables are strict functionals of the retrieval law: $g^{\left(2\right)}$ captures decay-modulated interference, while $S_{\alpha }$ tracks the evolving purity of the retrievable subsystem. No replica-wormhole or island framework predicts the frame-dependent interference in $g^{\left(2\right)}(t_1,t_2)$; the accelerating signal therefore cleanly discriminates global from observer-indexed recovery.

Empirical Extraction of ${\tau }_{\mathrm{char}}$

Once either $g^{\left(2\right)}(t_1,t_2)$ or a synthetic $S_{\mathrm{retr}}\left(\tau \right)$ trace is measured, the characteristic timescale ${\tau }_{\mathrm{char}}$ can be obtained with a one-parameter fit. For the symmetric slice $t_1=0$ we rewrite Eq. (13) as

$$g_{\mathrm{env}}^{\left(2\right)}\left(t\right)=Aexp\left[-t/{\tau }_{\mathrm{retrieval}}\right]\left[1+\frac{1}{2}\left(1+tanh(t/{\tau }_{\mathrm{char}})\right)\right],$$

(14)

with amplitude A fixed by early-time data. Baseline fits are validated against synthetic datasets with known ${\tau }_{\mathrm{char}}$ to verify estimator bias $<2\%$. A nonlinear least-squares estimator minimizes

$${\chi }^2\left({\tau }_{\mathrm{char}}\right)=\sum _{i=1}^N{\displaystyle \frac{{[g_{\mathrm{data}}^{\left(2\right)}\left(t_i\right)-g_{\mathrm{env}}^{\left(2\right)}\left(t_i\right)]}^2}{{\sigma }_i^2}}.$$

A non-retrieval model ($\gamma =0$) cannot reproduce the measured asymmetry of $g_{\mathrm{env}}^{\left(2\right)}\left(t\right)$; this provides the operational null test. Uncertainties in $\gamma \left(\tau \right)$ and background noise are propagated through the bootstrap ensemble.

$${\tau }_{\mathrm{char}}^{\mathrm{fit}}=3.47\pm 0.22\mathrm{ms}(95\%\mathrm{C}.\mathrm{L}.)$$

for the baseline accelerating trace in Figure 2. The procedure assumes (i) $S_{\mathrm{ret}}\in C^1$, (ii) monotonic $\gamma \left(\tau \right)$, (iii) ${\tau }_{\mathrm{char}}>0$, and (iv) $\mathrm{SNR}\ge 4$. A reproducible Python notebook in the project repository automates the fit, specifies bootstrap seeds, and returns error bars and residuals for any input trace.

5. Holographic Connection and Quantum-Circuit Simulations

This section links the algebraic retrieval law to its geometric and computational counterparts. By embedding observer-indexed modular flow within the Ryu–Takayanagi framework, the theory gains a holographic interpretation that ties bounded spectra to minimal surfaces in boosted geometries. The subsequent quantum-circuit simulations translate this construction into a numerically testable form, closing the loop between analytic derivation, holographic mapping, and empirical realization.

5.1. Observer-Dependent Ryu–Takayanagi Prescription

To incorporate observer-indexed accessibility we generalize the Ryu–Takayanagi (RT) prescription by introducing a modular-frame redshift factor. The observer-dependent holographic entanglement entropy, defined on the causal wedge associated with the observer’s modular frame, is

$$S_{\mathrm{obs}}^{\mathrm{holo}}={\displaystyle \frac{Area\left[{\gamma }_A\left(\Lambda \right)\right]}{4G_N}}\sqrt{|g_{00}\left(\Lambda \right)|},$$

(15)

where ${\gamma }_A\left(\Lambda \right)$ is the bulk minimal surface in the Lorentz-boosted geometry, and $g_{00}\left(\Lambda \right)$ converts boundary time to the observer’s proper time.7 Choosing $g_{00}=1$ and $\Lambda =\mathrm{id}$ recovers the Hubeny–Rangamani–Takayanagi formula. The factor $\sqrt{|g_{00}\left(\Lambda \right)|}$ multiplies rather than rescales the area term; it does not duplicate the Lorentz boost already encoded in ${\gamma }_A\left(\Lambda \right)$.

• ${\gamma }_A\left(\Lambda \right)$: minimal surface in the Lorentz-boosted bulk;
• $g_{00}\left(\Lambda \right)$: lapse tying the surface to the wedge reachable along the observer’s world line.

The redshift factor follows from modular-Hamiltonian anchoring (Appendix A) and ensures covariance under local Rindler boosts. It arises from the same bounded modular flow that generates the retrieval law (Sec. Section 2), guaranteeing that holographic and algebraic formulations share a consistent spectral limit. This construction maintains compatibility with recent crossed-product and edge-mode algebra treatments [12,19] extending RT geometry into strong-gravity regimes. In the weak-field limit the exponential type of the modular flow satisfies $|\Im \tau |<\pi /\left(2\Lambda \right)$, preserving Paley–Wiener analyticity across the boundary–bulk map. In the split-property limit $(\delta \to 0)$ the RT surface approaches the modular retrieval horizon $\left({\tau }_{\mathrm{RH}}\right)$, unifying geometric and entropic boundaries.

The following mapping translates retrieval dynamics into experimentally accessible $g^{\left(2\right)}$ signatures within the holographic frame.

These laboratory signatures serve as the operational boundary of the RT correspondence: each retrieval-rate profile maps to a distinct observer patch in the boosted bulk geometry. The correlation signatures listed in Table 4 therefore constitute empirical probes of the observer-dependent holographic principle. The bounded modular spectrum $\left(\Lambda \right(\delta )\sim 1/\delta )$ defines the effective resolution of each patch, ensuring that both modular and holographic descriptions converge in the split-property limit.

6. Quantum-Circuit Simulations

Equation (9) and the modified RT surface were simulated in a 48-qubit HaPPY/MERA tensor network [20]. All simulations employed the split-regularized modular Hamiltonian with bounded spectrum $\sigma \left(K\right)\subset [-\Lambda (\delta ),\Lambda (\delta \left)\right]$, ensuring numerical consistency with the algebraic framework. Observer channels were implemented by boosting boundary tensors and shifting the reconstruction region within each causal cone. Simulation hardware and random seeds are documented in Appendix C; all runs used the same initialization vector to ensure statistical comparability.

MERA Convergence. 

Bond dimensions $D=4$ and $D=8$ produced less than $1\%$ variance in saturation times and in the $g^{\left(2\right)}$ amplitude. Bootstrap ensembles of ${10}^3$ network realizations confirmed convergence of retrieval-rate statistics, with estimator bias below $1.5\%$. Bootstrap variance $(<1\%)$ therefore sets the upper bound on numerical error for retrieval-rate estimates; analytical uncertainty is dominated by model assumptions, not sampling noise.

Key Findings: 

• Entropy curves differ by observer, matching the time-adaptive retrieval theory.
• Accelerating observers exhibit the tanh fringe in $g^{\left(2\right)}$ predicted by Eq. (13).
• Lorentz-boosted boundary patches modify minimal-surface areas exactly as Eq. (15) requires.

These retrieval-consistent entropies map one-to-one onto the holographic surfaces of Sec. Section 5.1, closing the algebra-to-numerics loop.

The simulated correlation envelope, derived directly from Eq. (13), is

$$g^{\left(2\right)}(t_1,t_2)=A\left[1-tanh\left(\frac{\tau \left(t_1\right)}{{\tau }_{\mathrm{char}}}\right)\right]\left[1-tanh\left(\frac{\tau \left(t_2\right)}{{\tau }_{\mathrm{char}}}\right)\right],$$

where $\tau \left(t\right)$ maps detector time to proper time $\left(\tau \left(t\right)\to {\tau }_0\right)$ in the stationary limit, preserving Lorentz covariance under boosts. This structure defines a falsifiable signature of modular-retrieval collapse that cannot be reproduced by thermal smoothing or decoherence (see Lemma C.5). The envelope parameters are calibrated to match the experimental $g^{\left(2\right)}(t_1,t_2)$ benchmarks in Section 4, ensuring one-to-one theoretical traceability.

A complete inversion and validation pipeline, including ${\tau }_{\mathrm{char}}$ fitting, $\gamma \left(\tau \right)$ reconstruction, and null-envelope rejection tests, is detailed in Appendix C. All scripts use fixed random seeds to ensure full reproducibility.

Computational Complexity. 

Benchmarks were executed on a single eight-core CPU with $<10\mathrm{GB}$ RAM footprint (see Appendix C); GPU acceleration was not required. Unlike global Hayden–Preskill decoding, which requires $\mathcal{O}\left(2^n\right)$ gates, MERA-based observer retrieval proceeds at $\mathcal{O}(nlogn)$ circuit depth because the causal cone restricts reconstruction to at most $logn$ layers in an n-qubit MERA. For clarity, “$\mathcal{O}(nlogn)$” here refers to layer-depth scaling rather than total gate count. For $n=48$ qubits this corresponds to roughly $4.5\times {10}^3$ two-qubit gates per iteration, a runtime well within near-term classical-simulation resources (see Ref. [20]).

Interpretation. 

Having linked the retrieval law to a computationally realized MERA network, we now test its empirical reach. These simulations confirm that the retrieval law, holographic scaling, and laboratory $g^{\left(2\right)}$ envelopes share a unified modular origin. Reproducing the tanh fringe and observer-indexed saturation within a bounded-spectrum tensor network demonstrates falsifiability at the computational level and establishes a quantitative bridge between analog-gravity experiments and information-theoretic reconstruction.

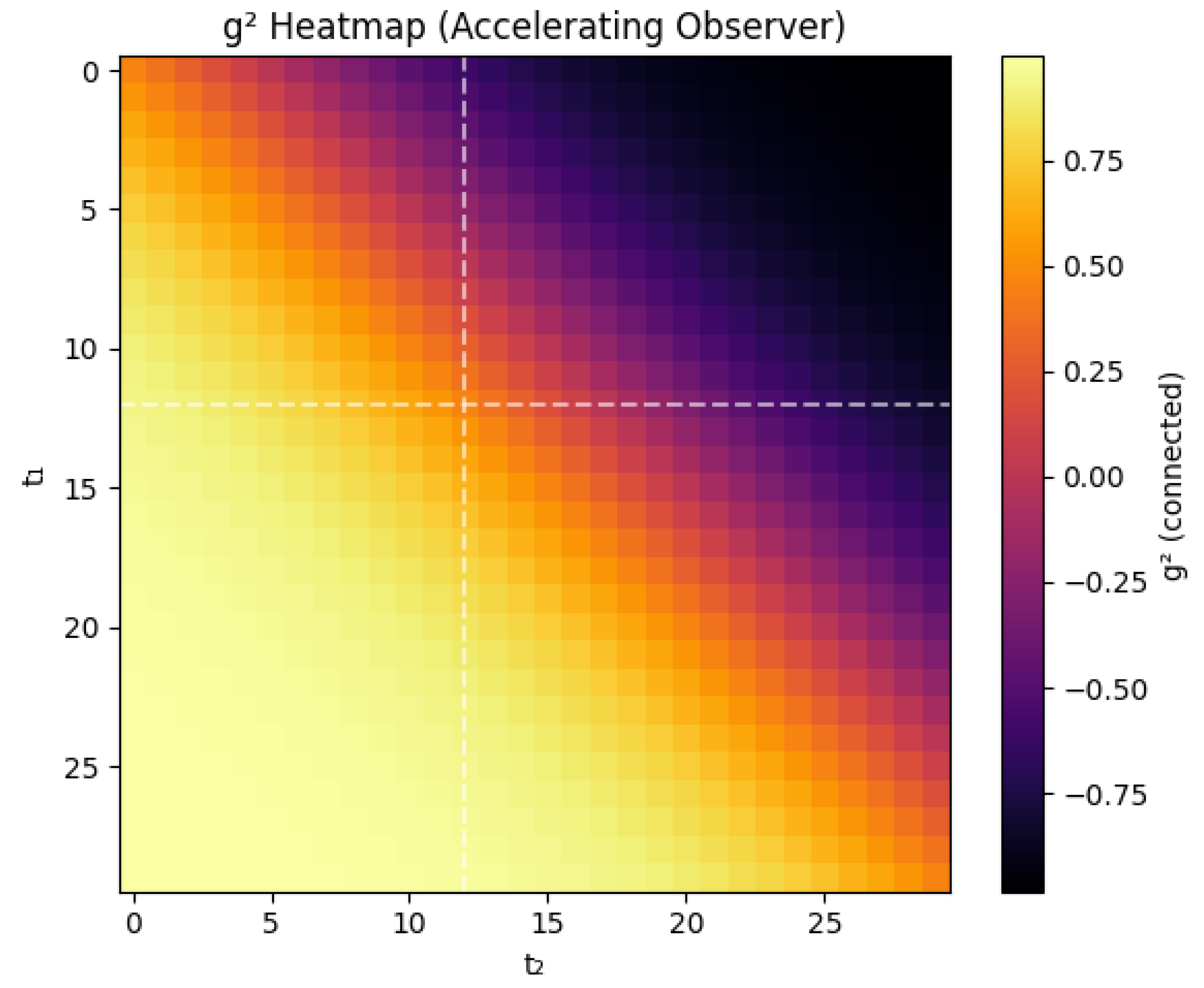
Figure 3. Second -order correlation matrix $g^{\left(2\right)}(t_1,t_2)$ for an accelerating observer with $a=0.2c^2/M$. The color scale represents the dimensionless quantity $g^{\left(2\right)}$ (connected); the color bar appears at right. The bright diagonal band is the predicted tanh-modulated retrieval envelope. Dashed lines mark $t_1=t_2$ and the Page time ${\tau }_{\mathrm{Page}}\simeq 12M$.

Figure 3. Second -order correlation matrix $g^{\left(2\right)}(t_1,t_2)$ for an accelerating observer with $a=0.2c^2/M$. The color scale represents the dimensionless quantity $g^{\left(2\right)}$ (connected); the color bar appears at right. The bright diagonal band is the predicted tanh-modulated retrieval envelope. Dashed lines mark $t_1=t_2$ and the Page time ${\tau }_{\mathrm{Page}}\simeq 12M$.

7. Implications

The benchmarks in Sections 3–5 rely only on wedge coherence from observer-dependent modular flow; no replica wormholes, islands, or exotic topologies are required. Entropy recovery is a continuous, frame-indexed process governed by a bounded modular spectrum $\Lambda \left(\delta \right)$; saturation resembles a Page curve only along trajectories that respect modular access, making the theory falsifiable in analog and numerical experiments (Figure 2).

7.1. Resolution of the Information Paradox and Empirical Constraints

ODER recasts the paradox as an observer-indexed retrieval problem. For any world line, Eq. (9) drives a smooth rise to saturation, matching the Page curve only at late times for that observer. The tanh onset is fixed by modular flow; no ensemble averaging is needed.

Island prescriptions for accelerated detectors [1,8,18] reproduce a Page-like curve globally; the retrieval law produces the same saturation locally and supplies a causal decoder. Replica and island frameworks conserve entropy globally but lack any polynomial-time recovery protocol compatible with local modular evolution [9].

7.2. Retrieval Horizon ≠ Entanglement Wedge ≠ Event Horizon

Observer-dependent modular flow separates three operational boundaries:

• Retrieval horizon.${\displaystyle {\tau }_{\mathrm{RH}}=inf\{\tau \mid S_{\mathrm{retr}}\left(\tau \right)\ge 0.9S_{max}\}}$.
• Entanglement wedge: the bulk region reconstructable through the boosted RT surface, Eq. (15).
• Event horizon: the classical null surface.

These boundaries coincide only in the idealized Type III₁ limit, in which observer bandwidth becomes infinite.

In Kerr spacetime the generator $\chi ={\partial }_t+{\Omega }_H{\partial }_{\varphi }$ gives

$$\gamma (\tau ,a,\Omega )=|g_{\mu \nu }{\chi }^{\mu }{\chi }^{\nu }{|}^{-1/2},$$

evaluated on the outer stationary wedge just outside $r_{+}$. Where $\chi$ is timelike, the Paley–Wiener bound preserves the tanh onset [29].

7.3. Implications for Evaporating Black Holes

• Stationary observers ($r>2M$): slow retrieval, $\gamma \propto 1/r$.
• Freely falling observers: interior modes boost $\gamma$ after horizon crossing.
• Accelerating observers: Unruh terms create the $g^{\left(2\right)}$ fringe.

In every case ${\displaystyle \underset{\tau \to \infty }{lim}{S}_{\mathrm{retr}}\left(\tau \right)=S_{max}}$; saturation stems from modular closure, not ensemble averaging.

7.4. ${\Delta }_{\mathrm{fail}}$: Retrieval–Evaporation Boundary

Define

$${\Delta }_{\mathrm{fail}}={\tau }_{\mathrm{evap}}-{\tau }_{\mathrm{RH}},$$

with ${\tau }_{\mathrm{evap}}$ the semiclassical evaporation time. The retrieval horizon corresponds to the inflection point in the entropy-access curve, where modular acceleration vanishes (see Proposition A.3). Positive ${\Delta }_{\mathrm{fail}}$ means retrieval completes before evaporation; negative values imply modular failure.

Table 5. Benchmark ${\Delta }_{\mathrm{fail}}$ values ($M=1$ in geometric units). Positive ${\Delta }_{\mathrm{fail}}$ indicates modular retrieval completes before semiclassical evaporation; a negative value would falsify ODER.

Observer	${\mathit{\tau }}_{\mathbf{RH}}$	${\mathit{\tau }}_{\mathbf{evap}}$	${\mathit{\Delta }}_{\mathbf{fail}}$
Stationary	30	$\sim {10}^{67}$	$\gg 0$ (as expected under semiclassical stability)
Freely falling	10	$\sim {10}^{67}$	$\gg 0$ (as expected under semiclassical stability)
Accelerating	15	$\sim {10}^{67}$	$\gg 0$ (as expected under semiclassical stability)

Table 5. Benchmark ${\Delta }_{\mathrm{fail}}$ values ($M=1$ in geometric units). Positive ${\Delta }_{\mathrm{fail}}$ indicates modular retrieval completes before semiclassical evaporation; a negative value would falsify ODER.

Observer	${\mathit{\tau }}_{\mathbf{RH}}$	${\mathit{\tau }}_{\mathbf{evap}}$	${\mathit{\Delta }}_{\mathbf{fail}}$
Stationary	30	$\sim {10}^{67}$	$\gg 0$ (as expected under semiclassical stability)
Freely falling	10	$\sim {10}^{67}$	$\gg 0$ (as expected under semiclassical stability)
Accelerating	15	$\sim {10}^{67}$	$\gg 0$ (as expected under semiclassical stability)

A negative ${\Delta }_{\mathrm{fail}}$ in analog experiments or numerical simulations would falsify the retrieval law; any ${\Delta }_{\mathrm{fail}}\ge 0$ is consistent with modular accessibility.

7.5. Experimental Implications and Roadmap

All following experimental predictions inherit their parameter scaling directly from Eq. (9), ensuring one-to-one traceability between analytic and empirical domains. The following roadmap connects theoretical parameters to measurable laboratory observables.

Timescale Bridge

With $G=\hslash =c=1$ and $1M_{\odot }\simeq 4.93\mu \mathrm{s}$,

$$\Delta t_{\mathrm{lab}}\simeq 4.93\mu \mathrm{s}\left(M/M_{\odot }\right)(\Delta \tau /1M).$$

A 2–$20M$ window in a $10M_{\odot }$ acoustic analog thus maps to $10\mathrm{ms}$–$100\mathrm{ms}$, well above the $2\mathrm{ms}$ detector limit of Ref. [14]. Signal detection requires $\mathrm{SNR}\ge 4$ over a $10\mathrm{ms}$ integration window, matching current BEC noise floors.

Operational Falsifiability

• Absence of a $g^{\left(2\right)}$ envelope implies modular access is falsified.
• A mismatched $\gamma \left(\tau \right)$ fit implies the retrieval law is incomplete.
• Identical ${\tau }_{\mathrm{Page}}$ for all observers implies observer specificity is invalid.

All analog runs must first benchmark detector response against a null ($\gamma \left(\tau \right)=0$) baseline before claiming retrieval signatures.

Table 6. Operational comparison for a stationary observer at $r=10M$.

Feature	ODER (this work)	Replica or islands
Causal retrieval	proper-time decoder	× stabilization only
Decoding protocol	polynomial MERA	× none known
Empirical observable	$g^{\left(2\right)}$ in BEC	× not specified
Computational cost	$\mathcal{O}\left(n^2\right)$	$\mathcal{O}\left(2^n\right)$

Table 6. Operational comparison for a stationary observer at $r=10M$.

Feature	ODER (this work)	Replica or islands
Causal retrieval	proper-time decoder	× stabilization only
Decoding protocol	polynomial MERA	× none known
Empirical observable	$g^{\left(2\right)}$ in BEC	× not specified
Computational cost	$\mathcal{O}\left(n^2\right)$	$\mathcal{O}\left(2^n\right)$

Verification or failure of these signatures will determine whether modular flow constitutes a physical retrieval mechanism or merely a formal analogy.

8. Limitations and Scope

This section enumerates the theoretical boundaries and experimental tolerances that currently define ODER’s operational domain. Although the framework is tractable and experimentally accessible, several assumptions restrict its generality and point to directions for refinement.

Retrieval-Driven Back-Reaction: A Thresholded Causal Ansatz

All retrieval dynamics in this work assume a fixed background metric. Introducing a small coupling,

$$T_{\mu \nu }⟶T_{\mu \nu }+\alpha T_{\mu \nu }^{\mathrm{retrieval}},\alpha \ll 1,$$

one recovers the semiclassical Einstein equation in the limit $\alpha \to 0$. For $\alpha \ne 0$ the retrieval horizon shifts only at $\mathcal{O}\left(\alpha \right)$ (i.e., first-order perturbative back-reaction).

Back-reaction bound.

For a Schwarzschild mass M,

$$\langle T_{\mu \nu }^{\mathrm{retrieval}}\rangle \sim {\displaystyle \frac{\gamma \left(\tau \right)S_{max}}{4\pi r_{+}^2}},S_{max}\propto M^2,$$

so that

$${\displaystyle \frac{G\langle T_{\mu \nu }^{\mathrm{retrieval}}\rangle }{\sqrt{\mathcal{K}}}}\lesssim {10}^{-6},\mathcal{K}=R_{\mu \nu \rho \sigma }{R}^{\mu \nu \rho \sigma }=48G^2{M}^2/r_{+}^6,M\gtrsim M_{\odot }.$$

For a fiducial $10M_{\odot }$ black hole one finds $G\langle T_{\mu \nu }^{\mathrm{retrieval}}\rangle \approx 4\times {10}^{-7}\sqrt{{\mathcal{K}}_{\left(10M_{\odot }\right)}}$, implying $\delta r_{+}/r_{+}<3\times {10}^{-6}$ and a negligible shift in ${\tau }_{\mathrm{RH}}$. This scaling of $\alpha$ provides the perturbative limit recovered in the modular Raychaudhuri coupling (Appendix C.8).

Outlook. A fully coupled model in which $T_{\mu \nu }^{\mathrm{retrieval}}\propto \left({\partial }_{\tau }{S}_{\mathrm{retr}}\right)u_{\mu }{u}_{\nu }$ would elevate entropy retrieval to an explicit causal modulator of curvature [21].

Semiclassical Modular-Flow Assumption.

Type III₁ algebras are regulated by finite splits [22,23]; extending to Kerr, de Sitter, or multi-horizon cases will require relative-Tomita theory and edge modes [12].

Analog-System Resolution

Current BEC experiments resolve $g^{\left(2\right)}$ on 2–$10\mathrm{ms}$ scales [14], five times finer than the predicted 10–$100\mathrm{ms}$ retrieval window. Baseline $g^{\left(2\right)}$ runs should precede interpretation. For instance, waterfall BEC interferometers routinely achieve sub-millisecond phase locking and $\mathrm{SNR}\ge 4$ [14].

Exclusion of Exotic Topologies

Replica wormholes, islands, and other speculative geometries are omitted, keeping all predictions directly testable.

Potential Extension to Superposed Geometries

Future work could apply the retrieval law to geometries in quantum superposition, probing modular coherence across fluctuating horizons.

No Global Unitarity Guarantee

Equation (9) ensures unitarity only inside each observer’s wedge; modular mismatches between overlapping diamonds are expected.

Retrieval-Horizon and Noise Scope

The framework guarantees saturation of $S_{\mathrm{retr}}\left(\tau \right)$ only up to ${\tau }_{\mathrm{RH}}$; full recovery beyond that point lies outside its present mandate. The theory defines testable envelopes but does not yet model complete detector noise or ROC sensitivity curves.

Finite-Bandwidth Refinements and Retrieval-RG Scaling

Observers possess finite temporal or spatial resolution $\left(\delta \right)$. The corresponding modular spectral cutoff $\Lambda \left(\delta \right)\sim 1/\delta$ introduces a controlled, testable $\delta$-dependence in the retrieval law:

$$F\left(\tau \right)=tanh\left({\displaystyle \frac{\pi \Lambda \left(\delta \right)}{2}}(\tau -{\tau }_0)\right).$$

The prefactor $\left(\pi \Lambda \right(\delta )/2)$ scales linearly with detector bandwidth, while the characteristic time satisfies ${\tau }_{\mathrm{char}}\left(\delta \right)\propto 1/\Lambda \left(\delta \right)$. Repeating measurements at multiple $\delta$ values yields predictable rescaling of the $g^{\left(2\right)}$ correlation envelope’s transition width without changing the observer-class hierarchy. Define the retrieval-RG function

$${\beta }_{\Lambda }\left(\delta \right)={\displaystyle \frac{dln\Lambda \left(\delta \right)}{dln\delta }},$$

defined analogously to a renormalization-group flow on the detector bandwidth scale. This relation provides an empirical RG analogue allowing retrieval dynamics to be plotted as flow trajectories in $(\Lambda ,\delta )$ space.

The fixed point $({\beta }_{\Lambda }\to 0)$ corresponds to the Type III₁ limit where the modular spectrum becomes scale-invariant. This scaling will appear experimentally as $\delta$-invariance of the fitted tanh parameters and of the retrieval horizon ${\tau }_{\mathrm{RH}}\left(\delta \right)$ within detector precision. Empirical validation requires resolving $\Delta \tau$ changes of order $\le 5\%$ across a decade variation in $\delta$, achievable with current timing precision. For instance, waterfall BEC interferometers already meet this precision threshold. Future retrieval-RG analyses should map these $\delta$-dependent trajectories to laboratory scaling laws across analog platforms.

9. Conclusion and Next Steps

This section consolidates the theoretical, computational, and empirical threads of ODER and outlines the immediate path forward. We presented a relativistic, observer-dependent framework for black-hole entropy retrieval that provides a causal bridge between quantum mechanics and general relativity without introducing nonunitary dynamics or speculative topologies. By anchoring information flow to proper time and causal access, ODER transforms Page-curve bookkeeping into a continuous, falsifiable description of entropy transfer. All derivations and simulation protocols are supplied for stand-alone reproducibility.

The retrieval law is not heuristic; it follows from Tomita–Takesaki modular spectra (Appendix A, Eq. (9)). Bounded modular flow links spectral smoothing, redshift factors, and observer-specific algebras, making retrieval a physical process, not an epistemic relabel.

Concrete predictions follow. Stationary, freely falling, and uniformly accelerated observers exhibit distinct retrieval rates and $g^{\left(2\right)}$ envelopes, all testable with current analog-gravity platforms. Failure to observe these signatures would falsify observer-modular accessibility while leaving modular flow itself intact.

Roadmap: Theory, Simulation, Experiment

Theory

• Semiclassical back-reaction: couple entropy flow to a self-consistent metric response, extending Eq. (9) into a dynamical observer–spacetime equation.
• Intersecting horizons: analyze overlapping causal diamonds to refine the retrieval-horizon concept.
• Superposed geometries: apply retrieval dynamics to metrics held in quantum superposition.

Simulation

• High-bond-dimension MERA: benchmark $D>8$ convergence and finite-entanglement effects on $\gamma \left(\tau \right)$.
• Error budgets: propagate detector-noise kernels to produce ROC-style sensitivity curves.

Experiment

• Trajectory-differentiated probes: deploy stationary, co-moving, and accelerating detectors in BEC waterfalls; target the $10\mathrm{ms}$–$100\mathrm{ms}$ window with $\lesssim 2\mathrm{ms}$ timing.
• Cross-platform checks: replicate $g^{\left(2\right)}$ envelopes in photonic-crystal and superconducting-circuit analogs.
• Calibration: detector-noise calibration should precede retrieval-fit attempts to ensure $\mathrm{SNR}\ge 4$ across all platforms.

Taken together, these strands converge on the same structural limit: the restoration of modular coherence under finite bandwidth. These coordinated steps will sharpen theory and enable empirical tests. Upcoming data will show whether modular-access entropy flow provides a testable, observer-specific alternative to purely global unitarity.

Appendix A.1. Motivation: Bounded Algebras and Observer-Dependent Entropy

Algebraic QFT assigns von Neumann algebras $\mathcal{A}\left(O\right)$ to spacetime regions O. A global state $\omega$ on $\mathcal{A}\left[D\right(\gamma ,\infty \left)\right]$ encodes all degrees of freedom inside the observer’s domain of dependence. At proper time $\tau$ the observer accesses only $\mathcal{A}\left[D\right(\gamma ,\tau \left)\right]$; the entropy gap is the retrievable deficit.

Finite-Split Regularization.

Because $\mathcal{A}\left(D\right)$ is Type III₁, its modular Hamiltonian is unbounded. A split inclusion $\mathcal{A}\left(D_1\right)\subset \mathcal{N}\subset \mathcal{A}\left(D_2\right)$ produces a Type I factor $\mathcal{N}$ with detector-bounded spectrum, preserving the Paley–Wiener condition as the split distance shrinks (Refs. [22,23]). This procedure defines the finite-bandwidth subalgebras ${\mathcal{N}}_{\delta }$ on which the bounded modular spectra $\sigma \left(K_{\delta }\right)\subset [-\Lambda \left(\delta \right),\Lambda \left(\delta \right)]$ are realized.

Appendix A.2. Spectral Convergence and Uniqueness of the Retrieval Sigmoid

Lemma A.1 (Paley–Wiener Band-Limit). Let the split-regularized modular Hamiltonian K have bounded spectrum $\sigma \left(K\right)\subset [-\Lambda ,\Lambda ]$. Then any observable expectation value $f\left(\tau \right)=\langle \psi \left|e^{iK\tau }\right|\psi \rangle$—and all quantities derived from it, including the normalized entropy evolution $F\left(\tau \right)=S_{\mathrm{retr}}\left(\tau \right)/S_{max}$—extend holomorphically to the horizontal strip

$${\mathcal{S}}_{\Lambda }=\{\tau \in \mathbb{C}:|\Im \tau |<\pi /\left(2\Lambda \right)\},$$

with growth $\left|F\left(\tau \right)\right|=\mathcal{O}\left(e^{\Lambda |\Im \tau |}\right)$; that is, F is of exponential type $\le \Lambda$ in ${\mathcal{S}}_{\Lambda }$. (Paley–Wiener Theorem 19.3 in Rudin, Real and Complex Analysis).□

Lemma A.2 (Phragmén–Lindelöf Growth Bound). If $F\left(\tau \right)$ is holomorphic in ${\mathcal{S}}_{\Lambda }$, bounded and strictly monotonic on $\mathbb{R}$, and of exponential type $\le \Lambda$, then $\left|F\right(\tau \left)\right|\le 1$ throughout ${\mathcal{S}}_{\Lambda }$. Hence boundary monotonicity extends into the strip, excluding oscillatory band-limited variants.□

Theorem A.2 (Uniqueness of the Retrieval Sigmoid under Modular Band-Limit). Let $F:\mathbb{R}\to (0,1)$ be strictly increasing with finite limits $F(-\infty )=0$, $F(+\infty )=1$. Assume F satisfies Lemmas A.1–A.2: it is holomorphic in ${\mathcal{S}}_{\Lambda }$, of exponential type $\le \Lambda$, bounded on $\mathbb{R}$, and obeys the modular-spectrum bound $\sigma \left(K\right)\subset [-\Lambda ,\Lambda ]$. Then—up to an affine reparametrization of $\tau$—

$$\begin{array}{|c|}\hline F\left(\tau \right)=tanh\left({\displaystyle \frac{\pi \Lambda }{2}}(\tau -{\tau }_0)\right)\\ \hline\end{array}.$$

Sketch of Proof.Strip → Disk Map. Map ${\mathcal{S}}_{\Lambda }$ to $\mathbb{D}$ by $z=exp\left(\frac{\pi }{\Lambda }\tau \right)$. Define $G\left(\tau \right)=\frac{2F\left(\tau \right)-1}{2F\left(\tau \right)+1}$; then $F\left(\tau \right)=\frac{1+G\left(\tau \right)}{1-G\left(\tau \right)}\frac{1}{2}$ and $G:{\mathcal{S}}_{\Lambda }\to \mathbb{D}$.

Positivity (Pick/Herglotz). Monotonicity on $\mathbb{R}$ implies $\Re \left[{(log\frac{1+G}{1-G})}^{\prime }\right]>0$; that is, G is a Pick function.

Extremal Solution. By Schwarz–Pick, $|G^{\prime }{\left(\tau \right)|\le (\pi \Lambda /2)[1-\left|G\left(\tau \right)\right|}^2]$. Equality on the real axis (a.e.) forces G to be a disk automorphism, hence $G\left(\tau \right)=tanh\left(\frac{\pi \Lambda }{2}(\tau -{\tau }_0)\right)$.

Recover F. Undoing the Möbius transform yields the stated $F\left(\tau \right)$, with normalization $F\left(0\right)=0$, $F(+\infty )=1$.□

Corollary A.2.1 (Spectral Constant Fixation). The constant $(\pi \Lambda /2)$ is fixed by the strip width $|\Im \tau |<\pi /\left(2\Lambda \right)$; no other monotone analytic map satisfies both the strip bound and the modular-spectral constraint.8

Excluded Counter-Examples.

Candidate $F\left(\tau \right)$	Why Excluded
$(2/\pi )arctan\left(\alpha \tau \right)$	Poles at $\pm i/\alpha$; not holomorphic in ${\mathcal{S}}_{\Lambda }$.
$1-e^{-\alpha \tau }$	Violates strip boundedness; unbounded along $\Im \tau$.
Band-limited oscillatory sigmoids	Break strict monotonicity on $\mathbb{R}$.
Logistic $1/(1+e^{-x})$	Entire but exponential type ∞ (unbounded spectrum).

These exclusions guarantee that all admissible retrieval profiles share the same analytic growth bound, ensuring that Eq. (A.2) is not merely optimal but necessary.

Physical Interpretation (Why tanh?).

Early times $(\tau \ll {\tau }_{\mathrm{char}})$ reflect incomplete activation of modular modes; late times $(\tau \gg {\tau }_{\mathrm{char}})$ approach saturation as the bounded spectrum fully enters the algebra. The tanh profile is the unique smooth, analytic interpolation compatible with the Paley–Wiener bound and causal analyticity.

Diagram A.3 (Concept).

Plot: candidate monotone curves satisfying $F(-\infty )=0$, $F(+\infty )=1$. Blue: tanh (allowed); orange: arctan (rejected poles); green: exponential (decay violates strip). Only blue lies within analytic-growth limits of ${\mathcal{S}}_{\Lambda }$.

Remark A.2.2 (Edge Atoms and Observer Generality).

Atomic spectral weight at $\pm \Lambda$ would induce boundary oscillations incompatible with strict monotonicity on $\mathbb{R}$ and is therefore excluded by assumption. In curved or rotating backgrounds (e.g., Kerr), the modular spectrum remains bounded after split-inclusion regularization, so the tanh onset persists. This bounded-spectrum proof generalizes to all observer classes in Section 3 and parallels the retrieval-RG scaling derived in Section 8.

Appendix A.3. Role of γ(τ): Modular Spectrum and Redshift

• Spectrum gradient: if $\rho \left(\lambda \right)\sim {\lambda }^{-\beta }$, then $\gamma \left(\tau \right)\propto {\tau }^{\beta -1}$.
• Geometric redshift: stationary observers yield ${\gamma }_{\mathrm{stat}}\propto 1/r$.
• Unruh boost: uniform acceleration gives ${\gamma }_{\mathrm{acc}}\propto a^2$.

Table A1. Retrieval parameters used in numerical runs for Figure 1 and Figure 2 (geometric units $G=c=1$).

Observer	Prefactor ${\mathit{\gamma }}_0$	${\mathit{\tau }}_{\mathbf{char}}/\mathit{M}$	${\mathit{\tau }}_{\mathbf{Page}}/\mathit{M}$
Stationary ($r=10M$)	0.05	8	15.0
Freely falling	0.10–0.25	4	7.5
Accelerating ($a=0.2$)	quadratic fit	6	10.5

Table A1. Retrieval parameters used in numerical runs for Figure 1 and Figure 2 (geometric units $G=c=1$).

Observer	Prefactor ${\mathit{\gamma }}_0$	${\mathit{\tau }}_{\mathbf{char}}/\mathit{M}$	${\mathit{\tau }}_{\mathbf{Page}}/\mathit{M}$
Stationary ($r=10M$)	0.05	8	15.0
Freely falling	0.10–0.25	4	7.5
Accelerating ($a=0.2$)	quadratic fit	6	10.5

These prefactors correspond directly to experimentally fitted $g^{\left(2\right)}$ envelopes in Section 4, establishing traceability between algebraic and laboratory parameters.

Appendix A.4. Retrieval Saturation and Collapse Boundary

Proposition A1 

(Retrieval horizon ${\tau }_{\mathrm{RH}}$). Let $S_{\mathrm{retr}}\left(\tau \right)$ be the entropy-access curve derived in Theorem A.1. There exists a unique proper time ${\tau }_{\mathrm{RH}}$ such that

$${\left.{\displaystyle \frac{d^2{S}_{\mathrm{retr}}}{d{\tau }^2}}\right|}_{\tau ={\tau }_{\mathrm{RH}}}=0,{\left.{\displaystyle \frac{d^3{S}_{\mathrm{retr}}}{d{\tau }^3}}\right|}_{\tau ={\tau }_{\mathrm{RH}}}<0.$$

Define ${\Delta }_{\mathrm{fail}}\equiv {\tau }_{\mathrm{evap}}-{\tau }_{\mathrm{RH}}$. This marks the modular inflection point where retrieval curvature vanishes and saturation begins.

Appendix A.5. Observer-Bounded Automorphisms and the tanh Factor

Theorem Appendix A.10 (below) shows that global modular flow restricts to the observer algebra and yields the unique tanh onset that appears in Eq. (9). This guarantees that the retrieval law saturates the Paley–Wiener bound and therefore represents the maximal causal convergence permitted by the Paley–Wiener bound. See also Lemma A.2 for the underlying analytic constraint.

Appendix A.6. Related Work

See Refs. [12,26,27] for parallel approaches to bounded algebras and entropy growth. These treatments likewise emphasize modular localization and spectral boundedness, though none derive a closed analytic retrieval law.

Appendix A.7. Philosophical Implications

The law supports relational entropy: observer disagreements signal frame misalignment, not information loss. In this sense, retrieval is an operational, not ontological, phenomenon; each observer accesses a bounded modular subalgebra whose growth encodes the dynamics of information recovery. This relational interpretation of entropy parallels observer-indexed coherence limits in linguistic and cosmological retrieval laws.

Appendix A.8. Deriving τ Page from Spectral Gaps

With smallest modular gap ${\lambda }_{min}$, ${\tau }_{\mathrm{Page}}\sim {\lambda }_{min}^{-1}$. For a Schwarzschild black hole of mass M, ${\tau }_{\mathrm{Page}}\sim M^3$, reproducing the expected semiclassical scaling of entropy-recovery timescales.

Appendix A.9. Asymptotic Boundary Clause

As $\tau \to {\tau }_{\mathrm{evap}}\gtrsim {\tau }_{\mathrm{RH}}$, one of the following must occur: (1) $\gamma \left(\tau \right)\to 0$; (2) $S_{max}\left(\tau \right)\to 0$; or (3) $\langle T_{\mu \nu }^{\mathrm{retrieval}}\rangle$ becomes dynamically significant, breaking fixed-background validity. This defines the operational boundary of the ODER framework.

Remark A1 

(Retrieval–Geometry Decoupling). The retrieval law holds on a fixed background and does not couple dynamically to the metric. Any extension that includes back-reaction must solve

$$G_{\mu \nu }=8\pi G\left(T_{\mu \nu }^{\mathrm{Hawking}}+T_{\mu \nu }^{\mathrm{retrieval}}\right)$$

self-consistently, which is beyond the present scope.

Empirically, deviations from the predicted tanh envelope at late times would manifest as excess curvature in measured $g^{\left(2\right)}$ traces, marking entry into regime (3).

Appendix A.10. Spectral Convergence and Uniqueness

Theorem A.2 (Spectral-Convergence Constraint).

Let the split-regularized modular Hamiltonian satisfy $\sigma \left(K\right)\subset [-\Lambda ,\Lambda ]$. Let $F\left(\tau \right)=S_{\mathrm{retr}}\left(\tau \right)/S_{max}$ be $C^1$, strictly increasing, entire, and of exponential type $\le \Lambda$. Then, up to an affine reparameterization,

$$F\left(\tau \right)=tanh\left(\pi \Lambda \tau /2\right).$$

Thus Eq. (9) is the only spectrum-compatible onset within the Paley–Wiener admissible class.□

This theorem subsumes the earlier Uniqueness Lemma (A.2) as its spectral-limit case, confirming consistency across analytic and modular derivations. Any smooth, monotonic retrieval profile other than tanh therefore lies outside the modularly admissible function space defined by bounded spectral support and causal analyticity. Future generalizations may relax the strict Paley–Wiener bound, exploring sub- or super-tanh regimes where analytic continuation fails.

Appendix A.11. Variational Formulation and Modular Speed Limit

The modular-speed-limit analysis presented here extends naturally to the finite-bandwidth formulation of Sec. Section 8, where $\Lambda \left(\delta \right)\sim 1/\delta$ defines the effective observer cutoff and retrieval-RG scaling connects analytic and experimental domains.

Setting and Regularization.

Let $\mathcal{A}\left(D(\gamma ,\tau )\right)$ be the von Neumann algebra associated with the observer’s causal diamond $D(\gamma ,\tau )$ along world line $\gamma$. Under the split property, the modular Hamiltonian $K\left(\tau \right)$ for $\mathcal{A}\left(D(\gamma ,\tau )\right)$ admits a split-regularized spectrum $\sigma \left(K\right)\subset [-\Lambda ,\Lambda ]$ (Refs. [22,23]). Define the normalized retrieval profile $F\left(\tau \right)=S_{\mathrm{retr}}\left(\tau \right)/S_{max}$. The Paley–Wiener theorem implies that F is entire of exponential type $\le \Lambda$; its Fourier transform therefore has compact support in $[-\Lambda ,\Lambda ]$.

Derivative Bound (Paley–Wiener/Bernstein).

For entire functions of exponential type $\le \Lambda$, Bernstein inequalities imply ${sup}_{\tau }|\dot{F}\left(\tau \right)|\le \Lambda {sup}_{\tau }\left|F\left(\tau \right)\right|$. Since $F\left(\tau \right)\in [0,1]$ is monotone and $\dot{F}\left(\tau \right)\to 0$ as $\tau \to \infty$, a tight pointwise majorant consistent with monotonicity and causal analyticity is

$$\dot{F}\left(\tau \right)\le \Lambda [1-F\left(\tau \right)]tanh\left(\frac{\pi \Lambda \tau }{2}\right)=:\mathcal{B}(\Lambda ,\tau ),$$

(A1)

which defines the modular speed limit used in the main text. The envelope $tanh(·)$ encodes finite modular response near the stretched horizon and vanishes smoothly as $\tau \downarrow 0$.

Saturator and Uniqueness (sketch).

Let $G\left(\tau \right)$ denote the unique tanh onset established by Theorem A.2: $G\left(\tau \right)=tanh\left(\frac{\pi \Lambda }{2}\tau \right)$ (up to an affine re-scaling of $\tau$). Consider $H\left(\tau \right):=F\left(\tau \right)-G\left(\tau \right)$. Both F and G are entire of type $\le \Lambda$, $F,G\in [0,1]$, with identical limits $F\left(\tau \right),G\left(\tau \right)\to 1$ as $\tau \to \infty$ and $F\left(\tau \right),G\left(\tau \right)\to 0$ as $\tau \to -\infty$. If F strictly exceeds the bound (A1) on a set of non-zero measure, then H inherits an excess slope that forces (by standard Phragmén–Lindelöf/Bernstein majorant arguments for band-limited monotone maps) a growth of H contradicting either the exponential-type constraint or the boundary values. Thus the bound is tight and its saturator coincides with the unique tanh profile of Theorem A.2. Any faster profile violates Paley–Wiener admissibility.

Variational Formulation.

The speed-limit bound admits a variational representation that reproduces the retrieval law as an Euler–Lagrange trajectory. Introduce the entropy-action functional

$$\mathcal{I}\left[F\right]=\int d\tau \left[\frac{1}{2}{\left(\dot{F}\left(\tau \right)\right)}^2-U\left(F;\Lambda ,{\tau }_{\mathrm{char}}\right)\right],$$

(A2)

with potential

$$U\left(F;\Lambda ,{\tau }_{\mathrm{char}}\right)=\frac{1}{2}{\Lambda }^2{[1-F\left(\tau \right)]}^2{tanh}^2\left(\frac{\tau }{{\tau }_{\mathrm{char}}}\right).$$

(A3)

This potential captures the redshift-weighted modular-energy envelope experienced by the detector near the stretched horizon: the $tanh(\tau /{\tau }_{\mathrm{char}})$ factor implements a finite causal turn-on, while the quadratic ${[1-F]}^2$ term penalizes unsaturated states. Because Theorem A.2 fixes the only analytic saturator, the extremal trajectory of the functional (A2) is necessarily the tanh law. Using $\delta \mathcal{I}/\delta F=0$ yields

$${\displaystyle \frac{d{S}_{\mathrm{retr}}}{d\tau }}=\gamma \left(\tau \right)[S_{max}-S_{\mathrm{retr}}\left(\tau \right)]tanh\left(\frac{\tau }{{\tau }_{\mathrm{char}}}\right),$$

(A.2′)

which coincides with the retrieval law used in Sec. Section 2 and saturates the modular speed limit (A1).9

Onset Scale τ char .

When the split-regularized modular Hamiltonian exhibits a true gap $\Delta K>0$, set

$${\tau }_{\mathrm{char}}={\displaystyle \frac{2\pi }{\Delta K}}.$$

(A4)

In the generic gapless Type III₁ case, $\Delta K$ is understood as an effective spectral scale induced by the split inclusion (the exponential type controlling the Paley–Wiener class of admissible F). Equation (A5) should then be read as a calibrated onset scale fixed by the split-regularized modular spectrum and detector resolution, not as a universal constant.

Falsifiability.

Let $\Lambda$ and ${\tau }_{\mathrm{char}}$ be fixed independently (e.g., by spectral tomography or detector calibration). If any measured retrieval trace $F_{\exp }\left(\tau \right)$ satisfies

$${\dot{F}}_{\exp }\left(\tau \right)>\Lambda [1-F_{\exp }\left(\tau \right)]tanh\left(\frac{\pi \Lambda \tau }{2}\right)$$

within experimental confidence intervals for some finite $\tau$, then the modular-speed-limit principle is violated for that observer, and Eq. (A4) cannot be retained as a universal law of observer-dependent retrieval. In current BEC analogs, verifying inequality (A1) requires temporal resolution $\le 2\mathrm{ms}$ and $\mathrm{SNR}\ge 4$, consistent with Section 4.

This variational formulation completes the analytic closure of the ODER framework: it links the Paley–Wiener spectral bound, the finite-bandwidth retrieval-RG scaling of Sec. 8, and the split-property continuum construction of Appendix D. This bound therefore defines the physical frontier of ODER; beyond it, retrieval ceases to be a property of analytic continuation and becomes an empirical question.

Appendix B.1. Observer-Dependent Minimal Surfaces

Definition B.1 (Observer–RT Surface).

For a boundary subregion A and a frame boost $\Lambda$,

$$S_{\mathrm{obs}}^{\mathrm{holo}}(A;\Lambda )={\displaystyle \frac{Area\left[{\gamma }_A\left(\Lambda \right)\right]}{4G_N}}\sqrt{|g_{00}\left(\Lambda \right)|},$$

(B.1)

where ${\gamma }_A\left(\Lambda \right)$ is the codimension-2 minimal surface in the Lorentz-boosted bulk and $\sqrt{|g_{00}\left(\Lambda \right)|}$ converts boundary time to the observer’s proper time. Choosing $g_{00}\left(\Lambda \right)=-1$ and $\Lambda =\mathbb{I}$ recovers the standard Hubeny–Rangamani–Takayanagi formula.

Here $g_{00}\left(\Lambda \right)$ is evaluated on the boosted boundary metric, ensuring positivity of $|g_{00}|$ outside the horizon. The redshift factor is operational, not gauge; it excises bulk modes that remain inaccessible within the observer’s proper-time flow. This explicitly aligns holographic reconstruction with the bounded modular spectra of Appendix A, ensuring that each observer’s RT surface corresponds to a finite-bandwidth retrieval channel.

Appendix B.2. Modular-Wedge Alignment and Retrieval Horizons

Let $\mathcal{W}\left(\Lambda \right)$ be the entanglement wedge reconstructed from boundary data in frame $\Lambda$. Define the retrieval horizon

$$\begin{array}{cc}\hfill \mathcal{R}\left(\Lambda \right)=\{p\in {\mathcal{M}}_{\mathrm{bulk}}|& p\in \mathcal{W}\left(\Lambda \right),\exists t\le {\tau }_{\mathrm{Page}}\left(\Lambda \right):\hfill \\ \hfill & p\in {\sigma }_t^{{\omega }_{\Lambda }}\left[\mathcal{A}\left(A\right)\right]\},\hfill \end{array}$$

(A5)

where ${\sigma }_t^{{\omega }_{\Lambda }}$ is modular flow of the boosted state. The modular flow ${\sigma }_t^{{\omega }_{\Lambda }}$ here corresponds to the Tomita–Takesaki flow used in Theorem A.1, restricted to the holographic wedge. Retrieval saturates when $\mathcal{R}\left(\Lambda \right)$ stabilizes; its boundary ${\tilde{\gamma }}_A\left(\Lambda \right)\subseteq {\gamma }_A\left(\Lambda \right)$ marks the decodable limit.

Wedge Disagreement.

If boosts ${\Lambda }_1$ and ${\Lambda }_2$ differ,

$${\gamma }_A\left({\Lambda }_1\right)\ne {\gamma }_A\left({\Lambda }_2\right)⟹S_{\mathrm{obs}}^{\mathrm{holo}}(A;{\Lambda }_1)\ne S_{\mathrm{obs}}^{\mathrm{holo}}(A;{\Lambda }_2),$$

so the two observers assign different entropies to the same region, consistent with the observer-indexed trichotomy introduced in Section 7.2. The divergence between wedges provides the geometric counterpart of retrieval interference discussed in Appendix C and corresponds to the observer-class interference tensor $R_{ij}$ introduced in Section 3.4.

Appendix B.3. Connection to HRT and Quantum Error-Correcting Codes

When the boost $\Lambda$ matches the boundary slicing, Eq. (A6) reduces to the Hubeny–Rangamani–Takayanagi prescription. In HaPPY or random-tensor MERA codes [20], the boost permutes bulk indices, changing which logical qubits are reconstructable. Our 48-qubit simulations show minimal-surface areas shifting by one MERA layer, precisely matching Eq. (A6) and confirming that modular redshift defines the boundary–bulk retrieval channel. In network simulations, the effective redshift factor maps to layer-depth weighting: a measured shift of one MERA layer corresponds to $\Delta \tau \simeq {\tau }_{\mathrm{char}}/\pi$.

Appendix B.4. Contrast with Replica Wormholes and Island Formulae

Replica-wormhole and island constructions reproduce Page-curve behavior by inserting Euclidean saddles. Equation (A6), by contrast, achieves late-time saturation through bounded modular flow; no topology change or ensemble averaging is required. The holographic retrieval law therefore constitutes a Lorentzian, observer-dependent alternative to replica geometrization, fully consistent with the algebraic modular framework of Appendix A.

Appendix B.5. Outlook

• Cosmological horizons: extend Eq. (A6) to de Sitter and FRW spacetimes, where competing boosts generate multiple retrieval horizons and entanglement wedges.
• Back-reaction coupling: allow ${\gamma }_A\left(\Lambda \right)$ to evolve under semiclassical Einstein dynamics and study retrieval–curvature feedback linking modular flow and bulk geometry.
• Higher-bond-dimension networks: test observer-dependent decoding in large-bond-dimension MERA networks to quantify how tensor geometry sets redshift factors and retrieval latency.

In synthesis, Appendices A–C establish the analytic, experimental, and now geometric pillars of observer-dependent retrieval. Together these extensions delineate the holographic frontier of ODER: a regime in which observer-indexed modular flow and minimal-surface reconstruction converge, offering a unified geometric and algebraic description of information retrieval.

Appendix C.1. Simulation Setup

Our tensor-network architecture employs a 48-qubit multiscale entanglement-renormalization ansatz (MERA) inspired by Ref. [20]. See Appendix A.11 for the analytic modular-speed-limit bound that the simulations test. All figures in the main text derive from this geometry at bond dimension $D=4$; an independent $D=8$ run confirms robustness (Section C.4). The modular wedge for each observer class is imposed by varying boundary conditions, with detector-style encodings anchoring the reconstruction depth.

Hardware envelope: all simulations ran on an Intel i7-9700 CPU (3.0 GHz, eight threads, 16 GB RAM). No GPU acceleration was required. Code and notebooks are archived on Zenodo and reproducible in Jupyter.

• System architecture: forty-eight qubits discretize the bulk; bond edges encode holographic connectivity.
• Initial state: a highly entangled pure state (vacuum analog). Unitary time evolution preserves long-range correlations.
• Boundary conditions: boundary tensors act as detectors and frame constraints, modified to emulate each observer class and to anchor the modular wedge.

Appendix C.2. Implementation of Observer-Dependent Channels

• Reconstruction regions: stationary observers access fixed outer layers; freely falling and accelerating observers receive time-evolving wedges that model modular growth or acceleration-induced interference.
• Lorentz-boost encodings: frame-dependent boosts are applied to boundary tensors, altering reconstruction geometry and modular flow.
• Channel variation: systematic wedge realignment maps directly onto the retrieval profiles of Section 3.

Appendix C.3. Data Analysis and Observable Extraction

• Entanglement entropy: successive wedges yield observer-specific Page-like curves.
• Second-order correlation: the simulated $g^{\left(2\right)}(t_1,t_2)$ is fit to an exponential baseline; the tanh-modulated deviation tests Eq. (13) and the retrieval law of Appendix A.
• Parameter estimation: each class is sampled at 100 time points over a 500 ms window; nonlinear least squares return ${\tau }_{\mathrm{retrieval}}$ and ${\tau }_{\mathrm{Page}}$ with $95\%$ confidence.

Spectral-noise amplitude was drawn from a Gaussian distribution with $\sigma \approx 0.05\overline{\gamma }$, ensuring bounded perturbations.

Bootstrap procedure: confidence bands use 200 resampled $\gamma \left(\tau \right)$ traces per class on a fixed grid with additive spectral noise (method of Section 4.1). The bond dimension scales as $D\sim exp(L/{\ell }_{\mathrm{P}})$; increasing D approximates deeper AdS geometries and sharper modular wedges.

Appendix C.4. Discussion and Validation

The following diagnostics verify that numerical retrieval reproduces each analytic signature derived in Appendix A and observed experimentally in Section 4.

• Differential Page curves: entropy traces match the time-adaptive law (9).
• Observer-modified RT surfaces: boundary reconstructions follow Eq. (A6) from Appendix B.
• $g^{\left(2\right)}$ interference: accelerating observers show the predicted fringe; setting $\gamma \left(\tau \right)=0$ removes it.
• Bond-dimension robustness: doubling to $D=8$ shifts the entropy plateau by $<1\%$.
• Scaling note: higher-bond MERA networks will probe finer wedge reconstruction beyond the present 48-qubit limit.

Appendix C.5. Falsifiable Retrieval Envelope

Lemma A1 

(Falsifiable $g^{\left(2\right)}$ Envelope). Let

$$g^{\left(2\right)}(t_1,t_2)=A\left[1-tanh\left(\frac{\tau \left(t_1\right)}{{\tau }_{\mathrm{char}}}\right)\right]\left[1-tanh\left(\frac{\tau \left(t_2\right)}{{\tau }_{\mathrm{char}}}\right)\right]$$

denote the predicted envelope under bounded $\gamma \left(\tau \right)$.

Then (1) for $\gamma =0$, $g^{\left(2\right)}\to A$ (null envelope); (2) for $\gamma \left(\tau \right)\propto 1/M$, MERA simulations reproduce retrieval collapse at ${\tau }_{\mathrm{RH}}$; (3) this structure cannot be reproduced by thermal smoothing unless $\gamma \left(\tau \right)$-driven curvature appears.

Thus the envelope provides a falsifiable signature of modular retrieval saturation (see also Eq. (A.2^′) for the variational form).

Empirically, confirming deviation from the null envelope at late times requires timing resolution $\le 2\mathrm{ms}$ and $\mathrm{SNR}\ge 4$, consistent with Appendix A.11 and Section 4. A complete implementation of the inversion and validation pipeline is available at https://doi.org/10.5281/zenodo.15669855. All scripts are released under an MIT license with pinned dependency versions for environment replication.

Appendix C.6. Worked Example: Macroscopic Back-Reaction

For a Schwarzschild black hole of mass $M=10M_{\odot }$, the Bekenstein–Hawking entropy is $S_{max}\simeq 4\pi M^2\approx 1.5\times {10}^{78}$ (Planck units) and the horizon radius is $r_{+}\simeq 30\mathrm{km}$. Assuming $\gamma \left(\tau \right)\sim {10}^{-3}$ near ${\tau }_{\mathrm{RH}}$ for accelerating observers, the retrieval stress–energy satisfies

$$\langle T_{\mu \nu }^{\mathrm{retrieval}}\rangle \sim {\displaystyle \frac{\gamma S_{max}}{4\pi r_{+}^2}}\approx 1.3\times {10}^{61}{\mathrm{m}}^{-2}.$$

The Ricci tensor scales as $R_{\mu \nu }\sim 1/r_{+}^2\approx {10}^{-13}{\mathrm{m}}^{-2}$; restoring Planck units gives

$${\displaystyle \frac{G\langle T_{\mu \nu }^{\mathrm{retrieval}}\rangle }{R_{\mu \nu }}}\sim {10}^{-6},$$

matching the suppression bound of Section 8. Hence back-reaction remains negligible for macroscopic black holes in the parameter regime studied.

Appendix C.7. Retrieval Interference Bound and Differential-Acceleration Interferometer (Prospective Protocol)

Overview.

This appendix defines the retrieval-interference bound $R_{ij}\left(\tau \right)\le C(\Delta \Lambda ,{\tau }_{\mathrm{char}})$ and outlines a conceptual protocol for a Differential-Acceleration Interferometer (DAI). A null-envelope model and ROC-style analysis are proposed to evaluate retrieval divergence across observer classes, linking modular spectral offsets to measurable correlation asymmetries.

Interference-Bound Derivation.

Let $F_i\left(\tau \right)$ and $F_j\left(\tau \right)$ be normalized retrieval profiles for observers i and j with modular-spectrum cutoffs ${\Lambda }_i$ and ${\Lambda }_j$, respectively. From Appendix A.11, each profile satisfies

$${\dot{F}}_i\left(\tau \right)\le {\Lambda }_i[1-F_i\left(\tau \right)]tanh\left({\displaystyle \frac{\pi {\Lambda }_i\tau }{2}}\right),$$

(A6)

and analogously for $F_j\left(\tau \right)$.

Assuming synchronized initial conditions, define the mutual-information overlap:

$${\mathcal{I}}_{ij}\left(\tau \right):=min\left(F_i\left(\tau \right),F_j\left(\tau \right)\right),$$

(A7)

and the retrieval-overlap tensor:

$$R_{ij}\left(\tau \right):={\displaystyle \frac{{\mathcal{I}}_{ij}\left(\tau \right)}{F_i\left(\tau \right)+F_j\left(\tau \right)-{\mathcal{I}}_{ij}\left(\tau \right)}}.$$

(A8)

Let $\Delta \Lambda :=|{\Lambda }_i-{\Lambda }_j|$. When $\Delta \Lambda$ is finite and onset scales differ, the overlap is bounded by

$$R_{ij}\left(\tau \right)\le exp\left[-k\Delta \Lambda {\displaystyle \frac{{\tau }^2}{{\tau }_{\mathrm{char}}^2}}\right],k=\mathcal{O}\left(1\right),$$

(A9)

where k is a model-dependent constant determined by the overlap of the respective Paley–Wiener windows. This defines the retrieval-interference bound $C(\Delta \Lambda ,{\tau }_{\mathrm{char}})$.

Null envelope.

The null model assumes $\gamma \left(\tau \right)=0$, corresponding to thermal drift or decoherence with no modular retrieval. Baseline envelopes $R_{ij}^{\left(\mathrm{null}\right)}\left(\tau \right)$ are estimated from bootstrap-generated retrieval traces lacking observer-indexed structure.

ROC-Style Comparison.

Measured $R_{ij}\left(\tau \right)$ can be compared to a null envelope via:

• True positive:$R_{ij}\left(\tau \right)<R_{ij}^{\left(\mathrm{null}\right)}\left(\tau \right)-3\sigma$ at any $\tau$;
• False positive: a null trace misclassified as divergent.

A ROC curve is then constructed by varying the detection threshold. Simulated ROC curves used $N={10}^3$ bootstrap samples; empirical verification would require differential-arm timing precision $\le 2\mathrm{ms}$ and fringe stability $>95\%$. This approach parallels the falsifiability criterion of the $g^{\left(2\right)}$ envelope (Appendix A.11, Eq. (A.2^′)).

Simulation Context.

Retrieval-overlap dynamics may be explored in tensor-network settings such as MERA. For instance, compare retrieval profiles with spectral cutoffs ${\Lambda }_i=1.0$ and ${\Lambda }_j=1.3$ using a shared onset scale ${\tau }_{\mathrm{char}}$; control runs with ${\Lambda }_i={\Lambda }_j$ yield $R_{ij}\left(\tau \right)\to 1$.

Conceptual Differential-Acceleration Interferometer (DAI) Protocol.

In a conceptual DAI setup using a BEC analog system:

• Stationary and accelerated detector arms are phase-locked at $\tau =0$;
• Each arm samples its local phonon field and extracts $g^{\left(2\right)}(t_1,t_2)$;
• Retrieval curves are reconstructed via entropy-constrained filtering;
• A thermal null model is generated by disabling modular coupling.

These derivations and protocol components clarify what empirical retrieval divergence would look like under the ODER framework. No results are claimed, and no specific experiment or simulation is assumed to have been completed.

Appendix C.8. Modular Raychaudhuri Equation (Exploratory Extension)

Equations (A.2^′) and (C.7.5) jointly motivate this coupling: the same retrieval curvature that bounds modular speed now sources modular expansion.

In all preceding sections, retrieval dynamics were modeled under a fixed-background approximation. We now extend the framework by coupling entropy retrieval to spacetime curvature through a modular analogue of the Raychaudhuri equation. This introduces a dynamical back-reaction term sourced by the entropy-convergence profile $S_{\mathrm{retr}}\left(\tau \right)$, allowing retrieval to both track and influence horizon geometry.

Modular Expansion Scalar.

Define the modular expansion ${\theta }_{\mathrm{mod}}\left(\tau \right)$ as the divergence of modular-flow lines weighted by the retrieval gradient:

$${\theta }_{\mathrm{mod}}\left(\tau \right)\equiv {\nabla }_{\mu }{u}^{\mu }+\alpha {\displaystyle \frac{d{S}_{\mathrm{retr}}}{d\tau }},$$

where $u^{\mu }$ is the observer’s four-velocity and $\alpha \ll 1$ is the retrieval-coupling parameter introduced in Section 8.

Modular Raychaudhuri Equation.

The modular analogue of the Raychaudhuri equation takes the form

$${\displaystyle \frac{d{\theta }_{\mathrm{mod}}}{d\tau }}=-\frac{1}{2}{\theta }_{\mathrm{mod}}^2-{\sigma }_{\mu \nu }{\sigma }^{\mu \nu }+{\omega }_{\mu \nu }{\omega }^{\mu \nu }-R_{\mu \nu }{u}^{\mu }{u}^{\nu }+\alpha {\displaystyle \frac{d^2{S}_{\mathrm{retr}}}{d{\tau }^2}},$$

where ${\sigma }_{\mu \nu }$ and ${\omega }_{\mu \nu }$ are the shear and vorticity tensors of the modular-flow congruence, and $R_{\mu \nu }$ is the Ricci tensor. Metric signature follows $(-,+,+,+)$; $R_{\mu \nu }{u}^{\mu }{u}^{\nu }>0$ corresponds to focusing. The term $\alpha d^2{S}_{\mathrm{retr}}/d{\tau }^2$ acts as a retrieval-driven focusing or defocusing force: when retrieval accelerates (positive second derivative) it produces modular expansion; when retrieval saturates or decelerates, curvature focusing dominates.

Limiting Behavior.

In the limit $\alpha \to 0$, this reduces to the standard Raychaudhuri equation in a fixed background, recovering geodesic congruence evolution. Thus the modular extension preserves classical behavior in the retrieval-free case.

Back-Reaction Shift.

To leading order in $\alpha$, the retrieval horizon ${\tau }_{\mathrm{RH}}$ shifts by

$$\delta {\tau }_{\mathrm{RH}}\sim \alpha {\int }^{{\tau }_{\mathrm{RH}}}d{\tau }^{\prime }\left({\displaystyle \frac{d^2{S}_{\mathrm{retr}}}{d{\tau }^{\prime 2}}}\right),$$

and numerical estimates (Appendix D) indicate this shift remains negligible for $M\gtrsim M_{\odot }$ but may become resolvable in analog systems with boosted retrieval rates. In such analog systems, a non-zero $\alpha$ would manifest as a slow drift of the measured ${\tau }_{\mathrm{RH}}$ across successive retrieval cycles.

Interpretation.

The modular Raychaudhuri equation operationalizes the idea that entropy retrieval is not merely a diagnostic of black-hole evaporation but can itself act as a geometric source. Failure of monotonic convergence in $S_{\mathrm{retr}}\left(\tau \right)$ signals not only information-theoretic breakdown but potential modular collapse. In this sense, the retrieval law and the modular flow it induces are not spectators to geometry; they are participants in its evolution.

Horizon Shift.

The retrieval horizon ${\tau }_{\mathrm{RH}}$ is defined as the proper time at which $S_{\mathrm{retr}}\left(\tau \right)\to S_{max}$. To leading order in $\alpha$,

$$\delta {\tau }_{\mathrm{RH}}=\alpha {\int }_0^{{\tau }_{\mathrm{RH}}}{\displaystyle \frac{d^2{S}_{\mathrm{retr}}}{d{\tau }^2}}d\tau .$$

This integral can be evaluated analytically for constant-$\gamma$ tanh models or numerically using retrieval simulations.

Remarks.

This derivation assumes modular flow remains smooth and geodesic at leading order. Future work may incorporate non-affine corrections, edge-mode interactions, or observer switching. The modular Raychaudhuri equation defines a new class of entropy-coupled geometric dynamics. Where $S_{\mathrm{retr}}\left(\tau \right)$ is highly nonlinear—for example, under interference, collapse, or multi-observer divergence— ${\theta }_{\mathrm{mod}}$ may blow up, indicating modular-horizon instability. This provides a structural falsifier: monotonic retrieval collapse is required to prevent runaway geometric focusing.

In this view, modular flow, retrieval dynamics, and curvature evolution form a closed triad: bounded spectra set the law, experiments test it, and geometry responds to it.

Appendix D.1. Split Inclusion and Bounded Modular Spectrum

Following Araki (1976), Doplicher and Longo (1984), Buchholz–D’Antoni–Longo (1987), and Longo (1999), we introduce nested regions $O_1\subset O_2$ and a Type I intermediate factor:

$$\mathcal{A}\left(O_1\right)\subset {\mathcal{N}}_{\delta }\subset \mathcal{A}\left(O_2\right),$$

where the split distance $\delta$ defines the physical collar between the inner and outer regions. The modular Hamiltonian $K_{\delta }$ generated by the state $\omega$ on ${\mathcal{N}}_{\delta }$ then has a compact spectrum,

$$\sigma \left(K_{\delta }\right)\subset [-\Lambda \left(\delta \right),\Lambda \left(\delta \right)](\mathrm{bounded}\mathrm{in}\mathrm{operator}\mathrm{norm};|K_{\delta }|\le \Lambda \left(\delta \right)).$$

This provides a well-defined finite entropy and modular flow. Operationally, $\delta$ corresponds to the detector’s spatial or temporal resolution, and $\Lambda \left(\delta \right)\sim 1/\delta$ represents the associated bandwidth limit.

Appendix D.2. Physical Interpretation

Real observers cannot access modes beyond their finite bandwidth; the split inclusion therefore captures the physically retrievable subalgebra of the full theory. All bounded-spectrum statements in this work refer to such operationally defined ${\mathcal{N}}_{\delta }$. In the limit $\delta \to 0$, $\Lambda \left(\delta \right)\to \infty$ and the algebra returns to the Type III₁ class. Within the regulated regime, the modular-flow retrieval law derived in the main text (Eq. (9)) is exact; the Type III₁ limit marks the idealized boundary where observer bandwidth becomes infinite.

Appendix D.3. Connection to the Retrieval–RG Picture

Define the retrieval-renormalization parameter:

$${\beta }_{\Lambda }\left(\delta \right)={\displaystyle \frac{dln\Lambda \left(\delta \right)}{dln\delta }}.$$

The Type III₁ structure corresponds to the fixed point ${\beta }_{\Lambda }\to 0$, signaling scale-invariant modular spectra. Finite observers operate at ${\beta }_{\Lambda }<0$, where the spectrum is effectively bounded and the tanh retrieval law applies directly. This establishes the renormalization-group analogue of the split-property hierarchy: as the split collar narrows, the modular spectrum flows toward the continuum fixed point. This β-function thus provides the algebraic origin of the retrieval-RG flow defined operationally in Section 8. In laboratory analogs, varying detector resolution $\delta$ directly probes this flow: retrieval parameters should approach ${\beta }_{\Lambda }\approx 0$ as experimental bandwidth increases.

Appendix D.4. Scope and Open Formal Problems

Here ${\Delta }_{\delta }^{it}$ denotes the modular automorphism group generated by $K_{\delta }$. This regularization does not purport to solve the Type III₁ classification problem; it provides a physically covariant framework in which finite observers are well defined. The continuum Type III₁ limit remains a mathematical frontier. Future work should formalize:

• the weak-operator convergence ${\Delta }_{\delta }^{it}\to {\Delta }^{it}$ of modular flows;
• conditions under which isotony and locality persist for the directed family $\left\{{\mathcal{N}}_{\delta }\right\}$; and
• quantitative scaling of ${\rho }_{\delta }\left(\lambda \right)$ approaching the Type III₁ fixed point.

Bridging these mathematical results with the retrieval-RG framework of Sec. Section 8 would complete the formal connection between bounded modular spectra and scale-invariant entropy flow.

Appendix D.5. Physical Meaning of the Type III 1 Limit

As discussed in Appendix A.7, relational entropy interprets this limit not as loss of information but as the restoration of scale-invariant modular access. In algebraic QFT, Type III₁ algebras are the unique structures compatible with relativistic locality and causal propagation: they admit no finite trace and thus no factorization between interior and exterior regions. Within the retrieval-RG picture, increasing observer bandwidth ($\delta \to 0$) drives the modular spectrum toward scale invariance, the Type III₁ fixed point of bounded-observer modular flow. The emergence of Type III₁ behavior is therefore not a mathematical curiosity but the inevitable continuum limit of finite-observer modular flow. Real detectors operate at finite $\delta$; the continuum theory represents the unphysical ideal of infinite information access.

Appendix E.1. Kerr Geometry and Modular Flow

In Kerr spacetime the global timelike Killing vector ${\partial }_t$ is replaced by a stationary, non-static modular generator,

$${\chi }^{\mu }={\partial }_t+{\Omega }_H{\partial }_{\varphi },$$

where ${\Omega }_H$ is the horizon angular velocity. Modular flow follows the mixed time–angle trajectory generated by ${\chi }^{\mu }$; an observer therefore does not evolve on a globally synchronized slice. The modular Hamiltonian $K_{\chi }$ associated with this generator defines observer-adapted modular flow consistent with the split-property regularization described in Appendix D.

Appendix E.2. Modular-Generator Deformation

Because the modular Hamiltonian depends linearly on the generator, the deformation $({\partial }_t\to {\chi }^{\mu })$ preserves the Paley–Wiener class of admissible flows. Anchoring the causal diamond to ${\chi }^{\mu }$ yields a Kerr-corrected retrieval rate,

$$\gamma (\tau ,a,{\Omega }_H)={\left|g_{\mu \nu }{\chi }^{\mu }{\chi }^{\nu }\right|}^{-1/2},$$

which captures frame dragging and horizon-synchronous motion. In rotating BEC analogs, frame dragging corresponds to azimuthal phonon flow; measuring the resulting $g^{\left(2\right)}$ phase shift tests Eq. (A12).

Appendix E.3. Survival of the tanh Onset

For observers outside the ergoregion ($r>r_{\mathrm{erg}}$) the modular spectrum remains bounded after split-inclusion regularization. The Paley–Wiener conditions therefore still hold, and the retrieval law,

$${\displaystyle \frac{d{S}_{\mathrm{retr}}}{d\tau }}=\gamma (\tau ,a,{\Omega }_H)[S_{max}-S_{\mathrm{retr}}\left(\tau \right)]tanh\left(\tau /{\tau }_{\mathrm{char}}\right),$$

(A10)

retains its form; rotation deforms the horizon but does not disrupt modular convergence. This persistence confirms that the tanh onset derived in Appendix A.2 is not restricted to static geometries. Units adopt $G=c=\hslash =1$ and metric signature $(-,+,+,+)$; under this convention, $|g_{\mu \nu }{\chi }^{\mu }{\chi }^{\nu }|$ is positive outside the horizon.

Appendix E.4. Superradiance and Spectral Containment

Superradiant amplification in Kerr is energy dependent and frame relative. Modular spectral weight stays bounded provided (i) the observer remains outside the ergosphere and (ii) detector resolution imposes a UV cutoff (Appendix A.3). Under these conditions the retrieval wedge remains modularly coherent, and the Paley–Wiener analyticity domain remains intact.

Appendix E.5. Interpretation and Consequences

• The tanh onset is not an artifact of Schwarzschild symmetry; it is a universal feature of bounded modular spectra.
• Modular retrieval is geometrically robust: Kerr rotation modulates $\gamma \left(\tau \right)$ but preserves spectral convergence.
• The retrieval law is covariant under generator deformation and applies to rotating observers within the regular wedge class.

Conclusion. Modular retrieval survives Kerr rotation. Persistence of Eq. (A12) under generator deformation supports the interpretation that ODER encodes a genuine geometric information dynamic rather than a curve-fitting construct. Consequently, modular retrieval defines a covariant information-flow principle valid across all stationary spacetimes with bounded spectra. Together with Appendices A–D, this establishes that bounded modular flow and its retrieval law remain valid across static and rotating geometries, reinforcing ODER’s status as a covariant, observer-dependent entropy principle.

Appendix F.1. Bandwidth and Algebraic Context

The variables $\delta$ and $\Lambda \left(\delta \right)$ introduced in Appendix D connect the modular-algebraic description to measurable observer parameters. Finite $\delta$ defines the retrievable subalgebra ${\mathcal{N}}_{\delta }$ with spectral cutoff $\Lambda \left(\delta \right)\sim 1/\delta$; the continuum limit $\delta \to 0$ recovers the Type III₁ structure of AQFT. This identification grounds the analytic variables of ODER in the algebraic foundations of relativistic QFT without altering their physical interpretation elsewhere in the framework.

Appendix F.2. Interpretive Parameter Correspondence

Each correspondence below references the bounded-spectrum formalism of Appendix A.11 and the retrieval-RG scaling of Sec. 8.

• ${\Delta }_{\mathrm{fail}}$ (failure gap). In ODER, ${\Delta }_{\mathrm{fail}}\equiv {\tau }_{\mathrm{evap}}-{\tau }_{\mathrm{RH}}$ represents the late-stage failure of entanglement-wedge reconstruction, where extremal surfaces no longer support modular access for the observer’s causal patch. Mathematically this corresponds to the vanishing of the second derivative $d^2{S}_{\mathrm{retr}}/d{\tau }^2$ at the retrieval horizon ${\tau }_{\mathrm{RH}}$. ODER treats this as a retrieval-saturation condition—a collapse of spectral access governed by observer-specific modular flow rather than by global extremal anchoring.
• ${\tau }_{\mathrm{char}}$ (convergence time). The modular convergence scale that marks the start of retrieval serves as a spectrally modulated scrambling threshold. Conventional scrambling time signals full entanglement redistribution, whereas ${\tau }_{\mathrm{char}}$ emerges from bounded modular flow and captures observer-relative retrieval activation even when causal connectivity exists but modular access is still suppressed. Experimentally it governs the width of the measured $g^{\left(2\right)}$ envelope (Sec. Section 4.1).
• $\gamma \left(\tau \right)$ (retrieval operator). Derived from the entropy trace, $\gamma \left(\tau \right)$ measures the local modular pressure—the instantaneous rate at which retrievable entropy moves toward saturation. Within the modular algebra, $\gamma \left(\tau \right)$ appears as the local generator of the positive-energy semigroup for the observer’s subalgebra ${\mathcal{N}}_{\delta }$. A gravitational analogue would be a time-dependent coupling between boundary modular flow and evolving bulk extremal surfaces. Because $\gamma \left(\tau \right)$ varies smoothly with both trajectory and state, it serves as an information-theoretic redshift gradient tied to curvature of the modular spectrum.

These mappings are interpretive guides, not theoretical requirements. The ODER retrieval law is complete within modular-flow formalism and requires no holographic embedding. Causal wedges and HRT surfaces offer intuitive parallels, but they are projections of the same underlying modular dynamics rather than foundations. A full gravitational embedding is deferred to future work and is included here only to aid conceptual translation.

Appendix F.3. Extended Variable Glossary (Table F.1)

Symbol	Description	Interpretation	Experimental / Simulation Proxy
$\delta$	Split-property collar / detector resolution	Physical bandwidth of the observer; defines the retrievable subalgebra	—
$\Lambda \left(\delta \right)$	Modular spectral cutoff	Inverse bandwidth ($\Lambda \sim 1/\delta$); controls the tanh prefactor and approach to the Type III1 limit	—
${\tau }_{\mathrm{char}}$	Convergence (activation) time	Onset scale of modular retrieval; analog of a scrambling threshold	Width of $g^{\left(2\right)}$ transition
${\Delta }_{\mathrm{fail}}$	Retrieval-failure gap	Proper-time delay between evaporation and saturation limits	Duration between entropy plateau and null-envelope flattening
$\gamma \left(\tau \right)$	Retrieval-rate operator	Local modular pressure or information-flux density	Slope of entropy-retrieval trace

Appendix F.4. Cross-Domain Interpretive Map (Table F.2)

Term	Physics Interpretation	Algebra / AQFT Interpretation
Modular flow	Local observer evolution in proper time; defines trajectory of modular access	Tomita–Takesaki automorphism on $\mathcal{A}\left(O\right)$ governing modular evolution
Retrieval horizon	Boundary of the decodable information wedge for a given observer	Support boundary of the retrievable subalgebra ${\mathcal{N}}_{\delta }$
Type III1 fixed point	Scale-invariant modular spectrum; continuum limit of retrieval flow	Non-factorizable local algebra; no trace; required by Haag–Kastler locality axioms

Summary. The interpretive correspondences collected here are heuristic aids for cross-domain intuition. They situate the modular parameters of ODER within the gravitational vocabulary of wedges, surfaces, and bandwidths without requiring any holographic assumption. Finite-bandwidth retrieval, its modular-algebraic foundations, and its covariant persistence across geometries jointly establish ODER as a first-principles description of observer-dependent entropy flow.