Submitted:
04 March 2025
Posted:
05 March 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
1.1. Motivation and Related Work
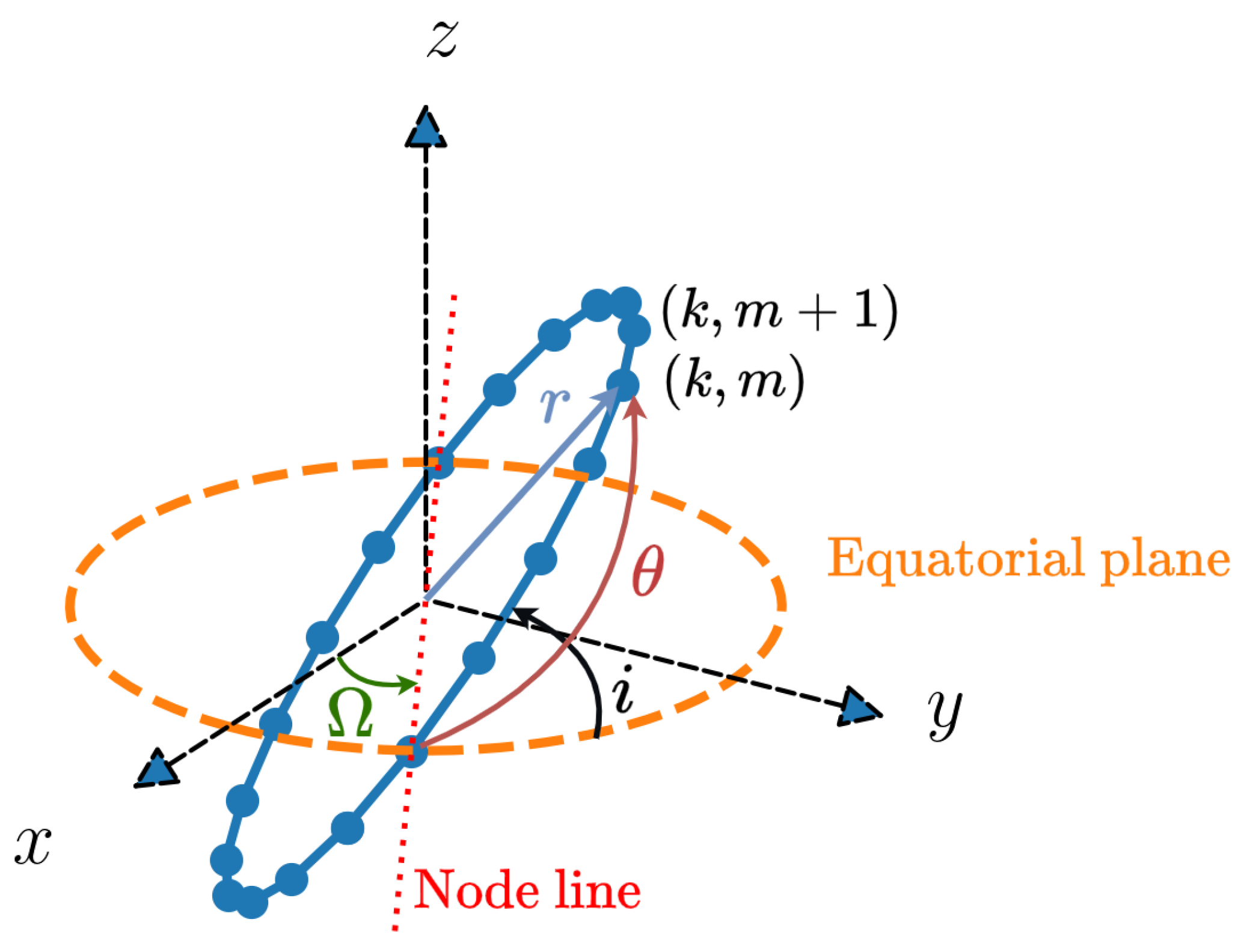
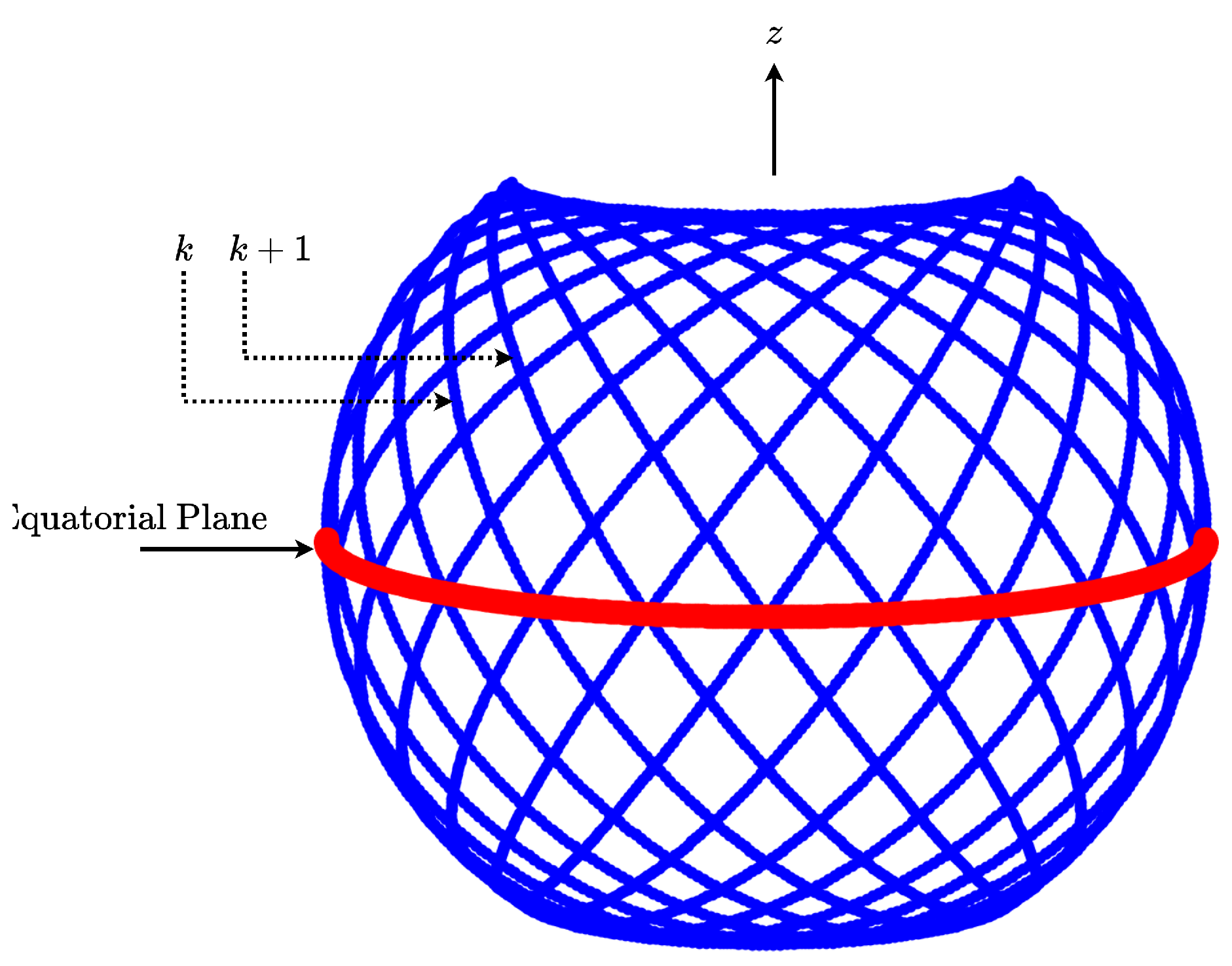
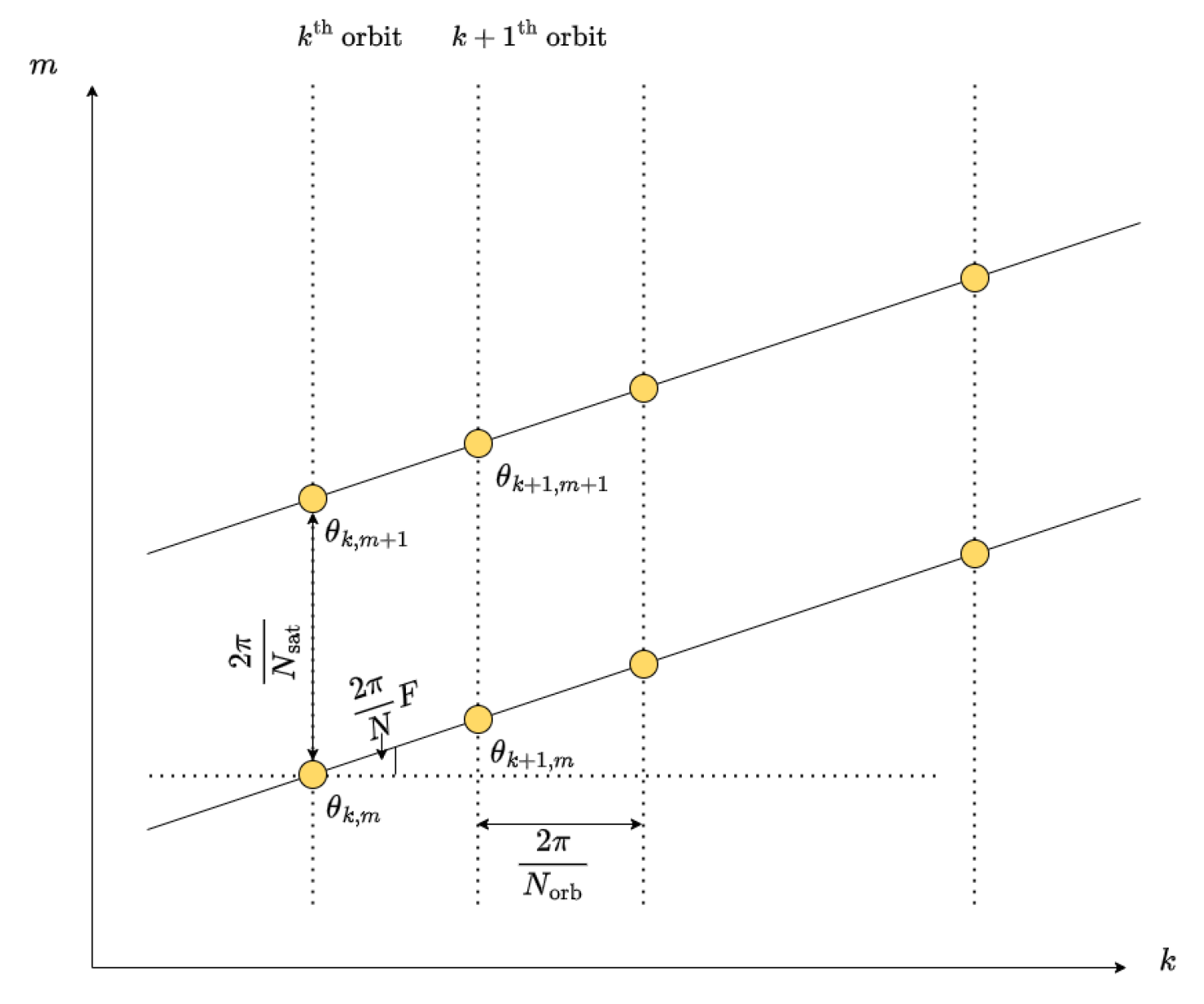
2. Constellation Model
2.1. Constellation Dynamics
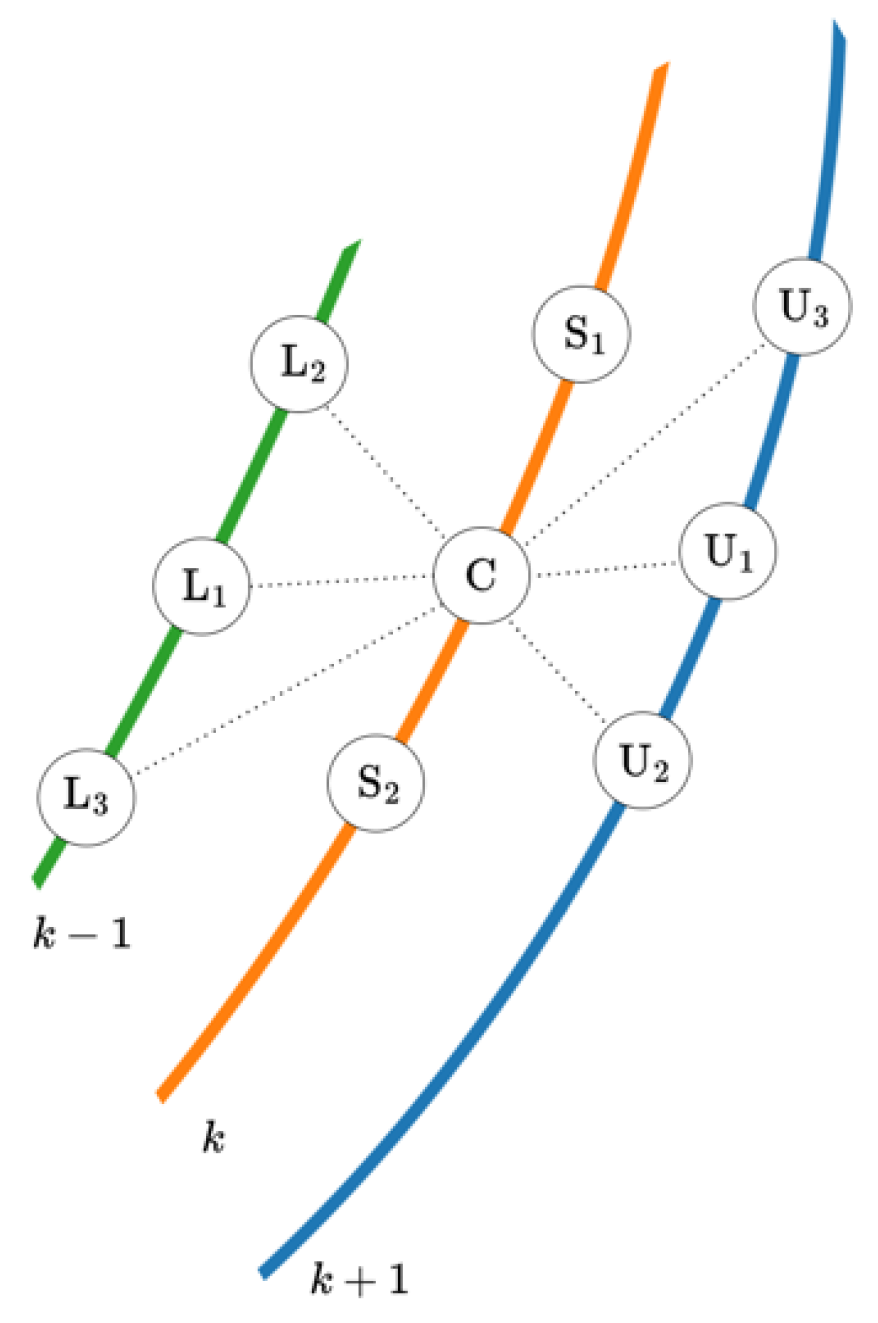
2.2. Collision Avoidance
2.3. Connectivity Requirements
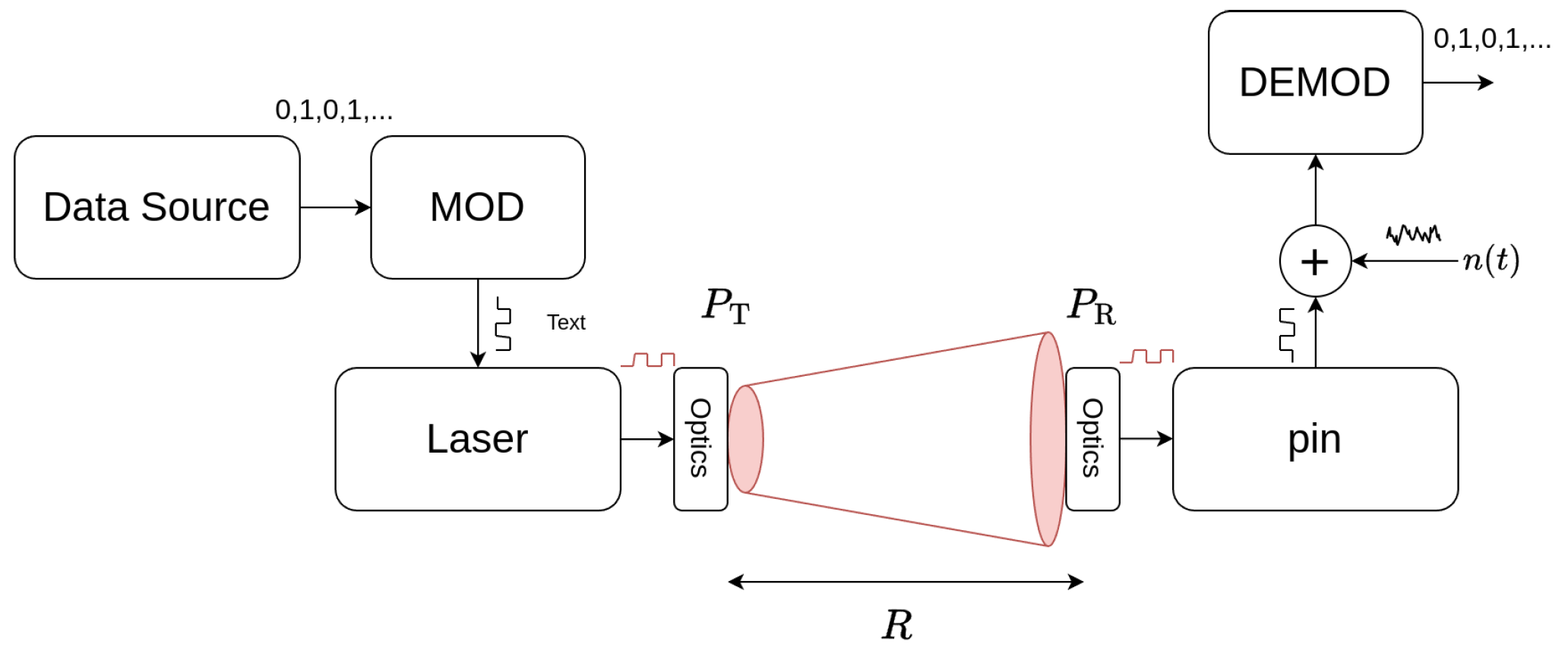
3. Link Model
3.1. Link Budget
3.2. Bit error rate
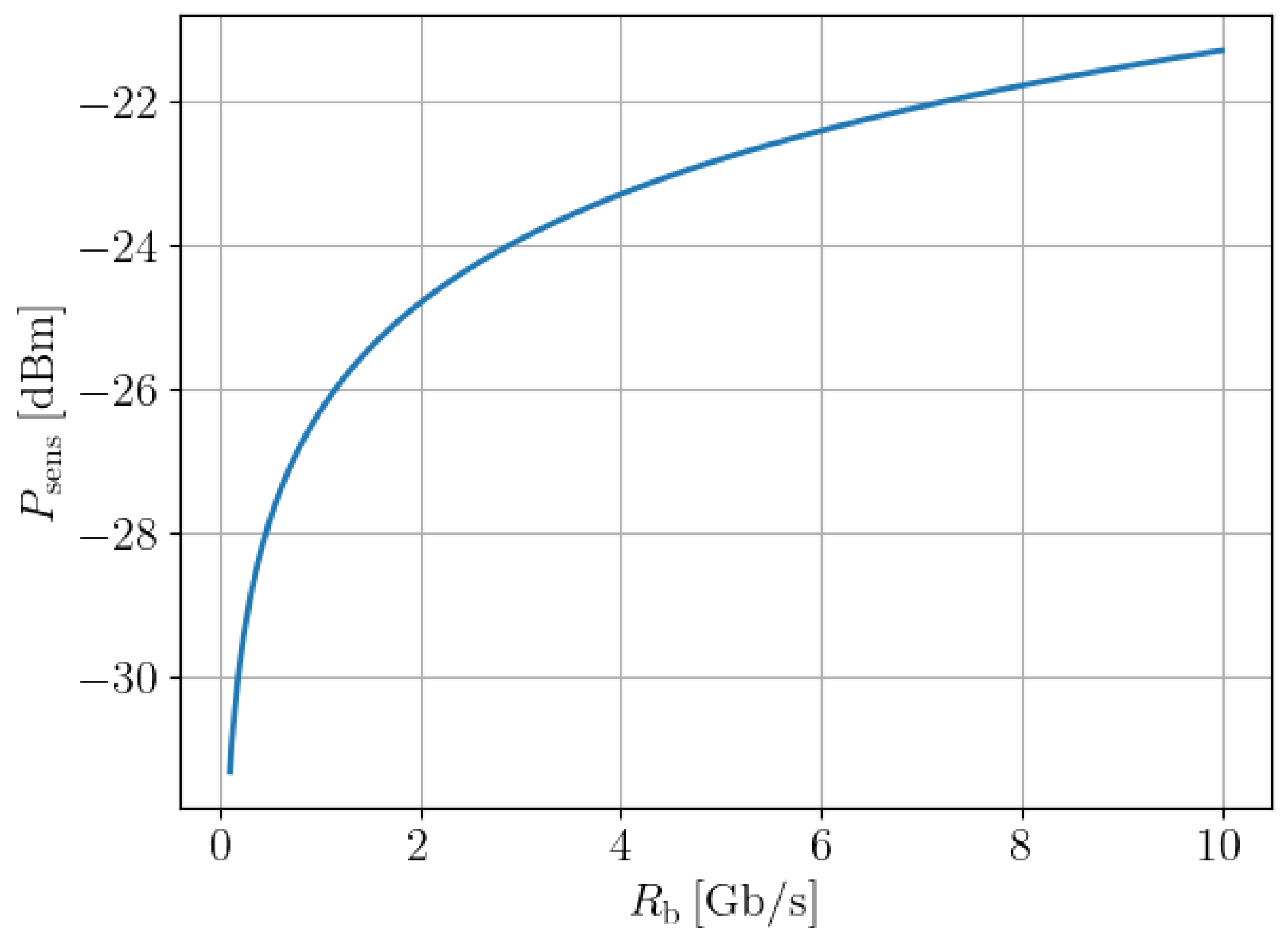
3.3. Receiver Sensitivity
4. Pyminisat Module Implementation
5. Results
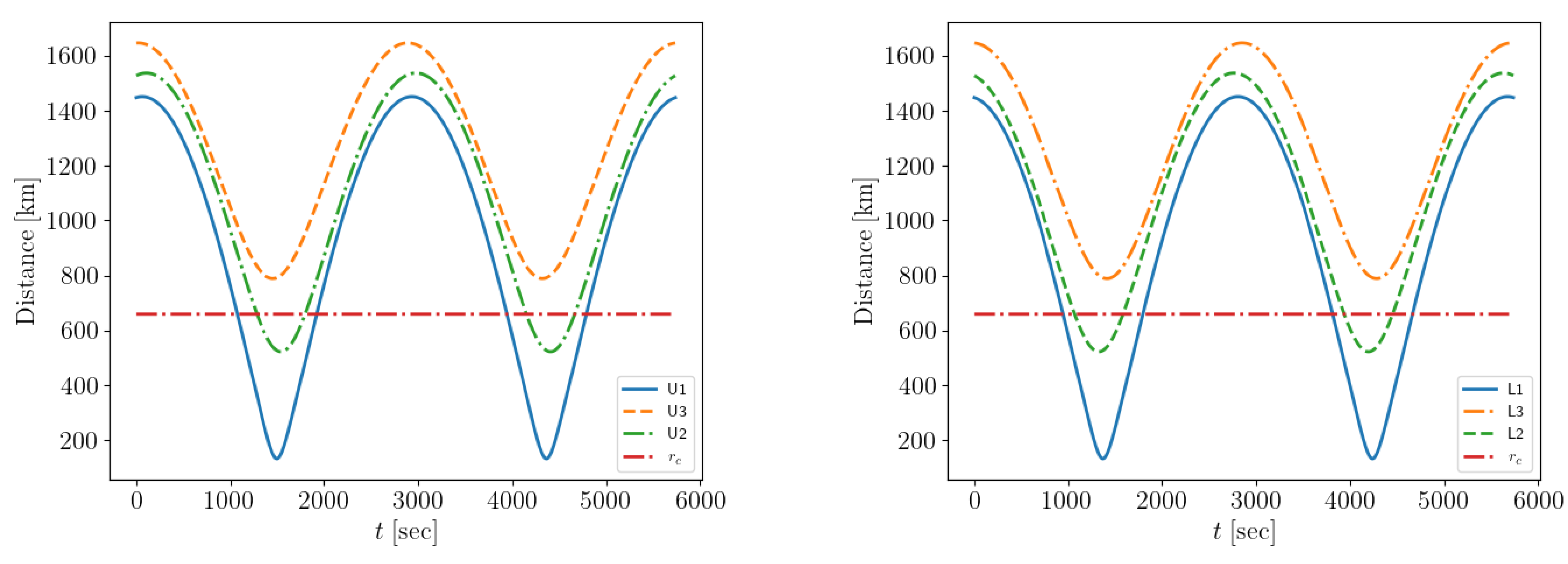
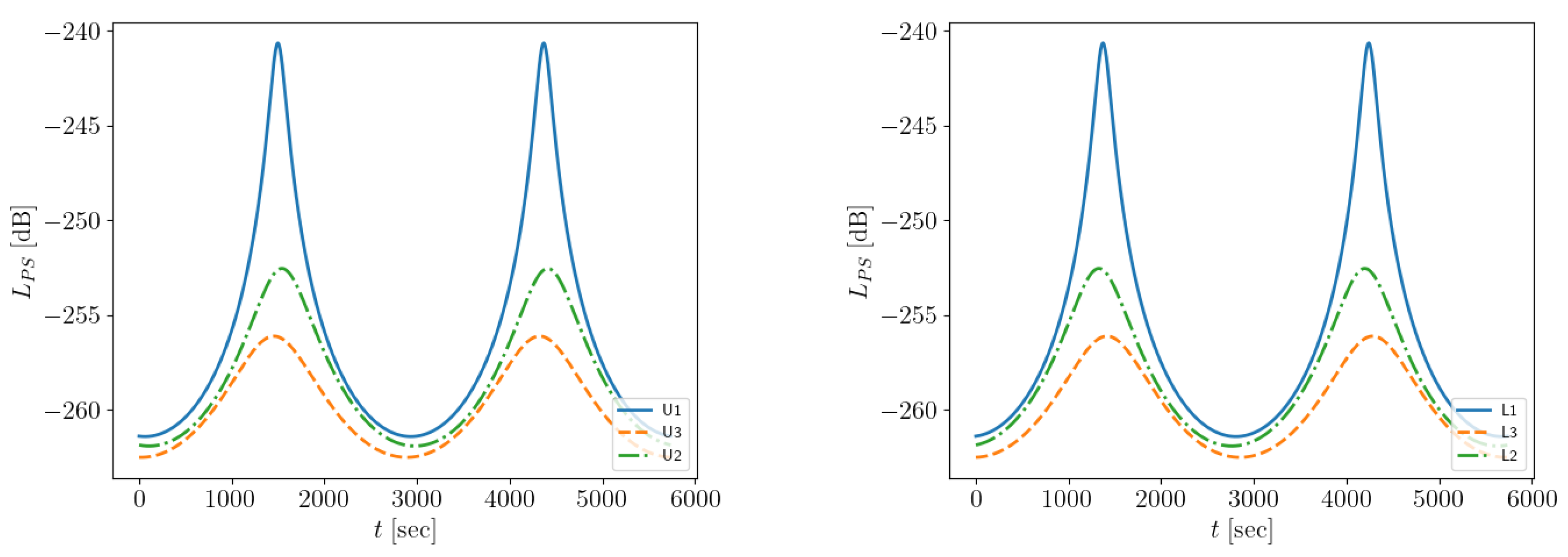
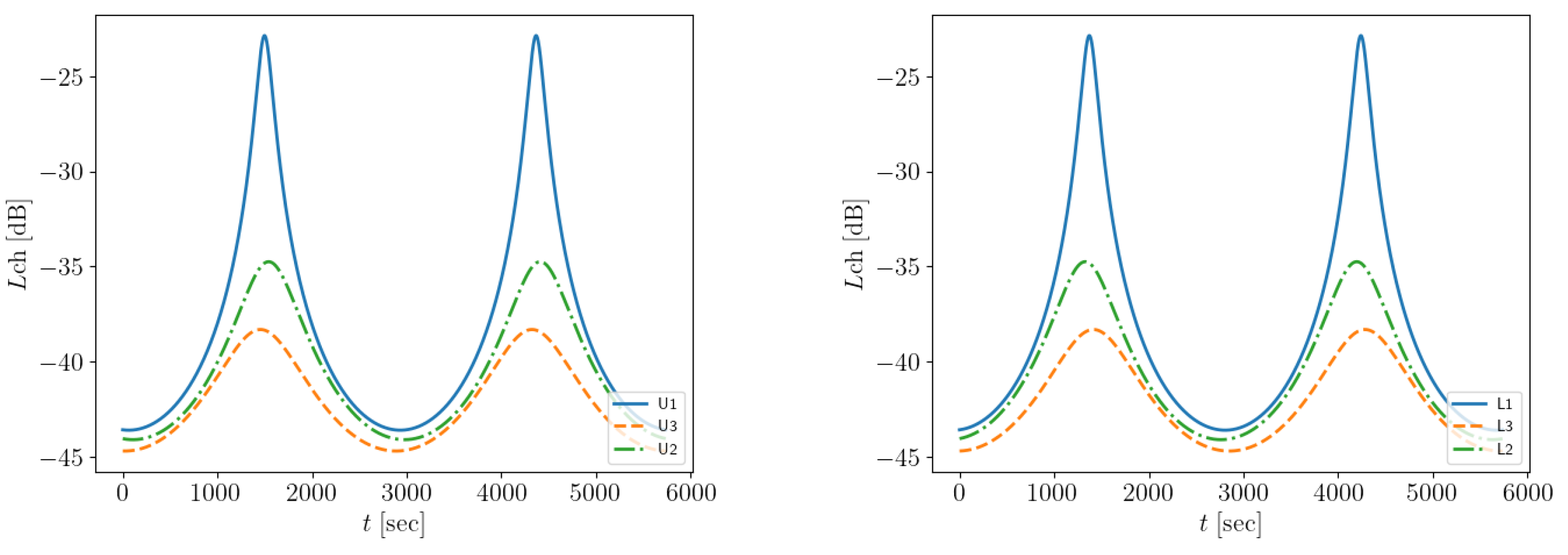
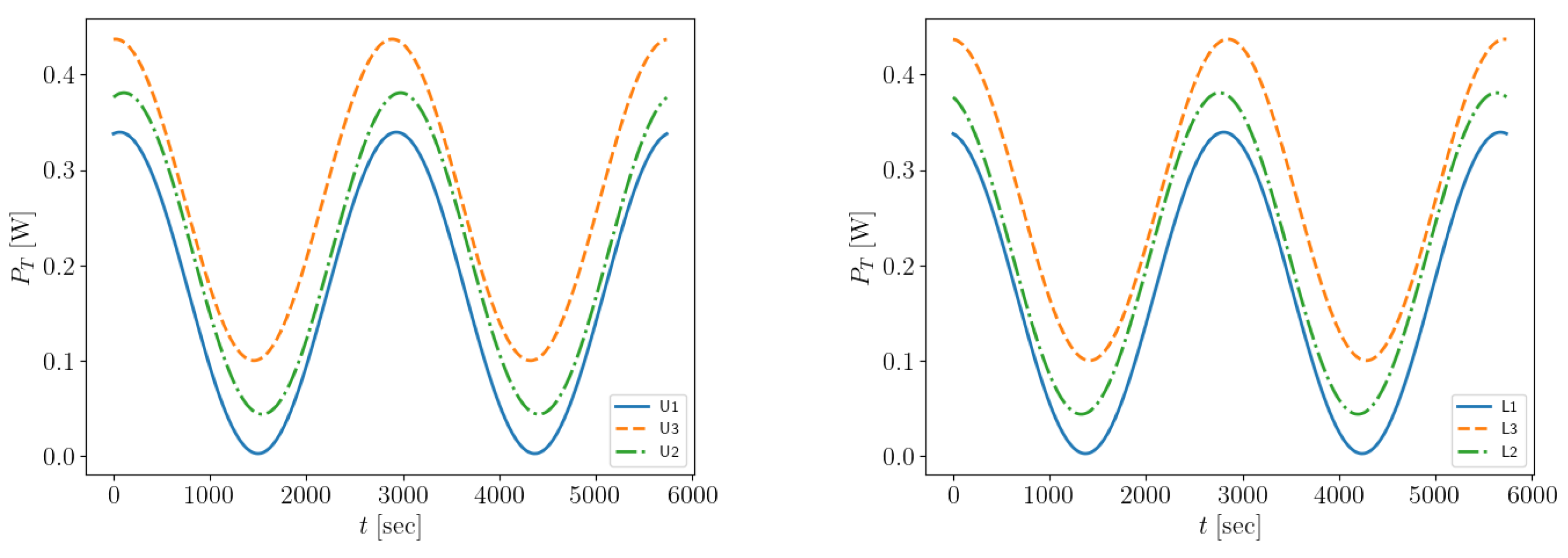
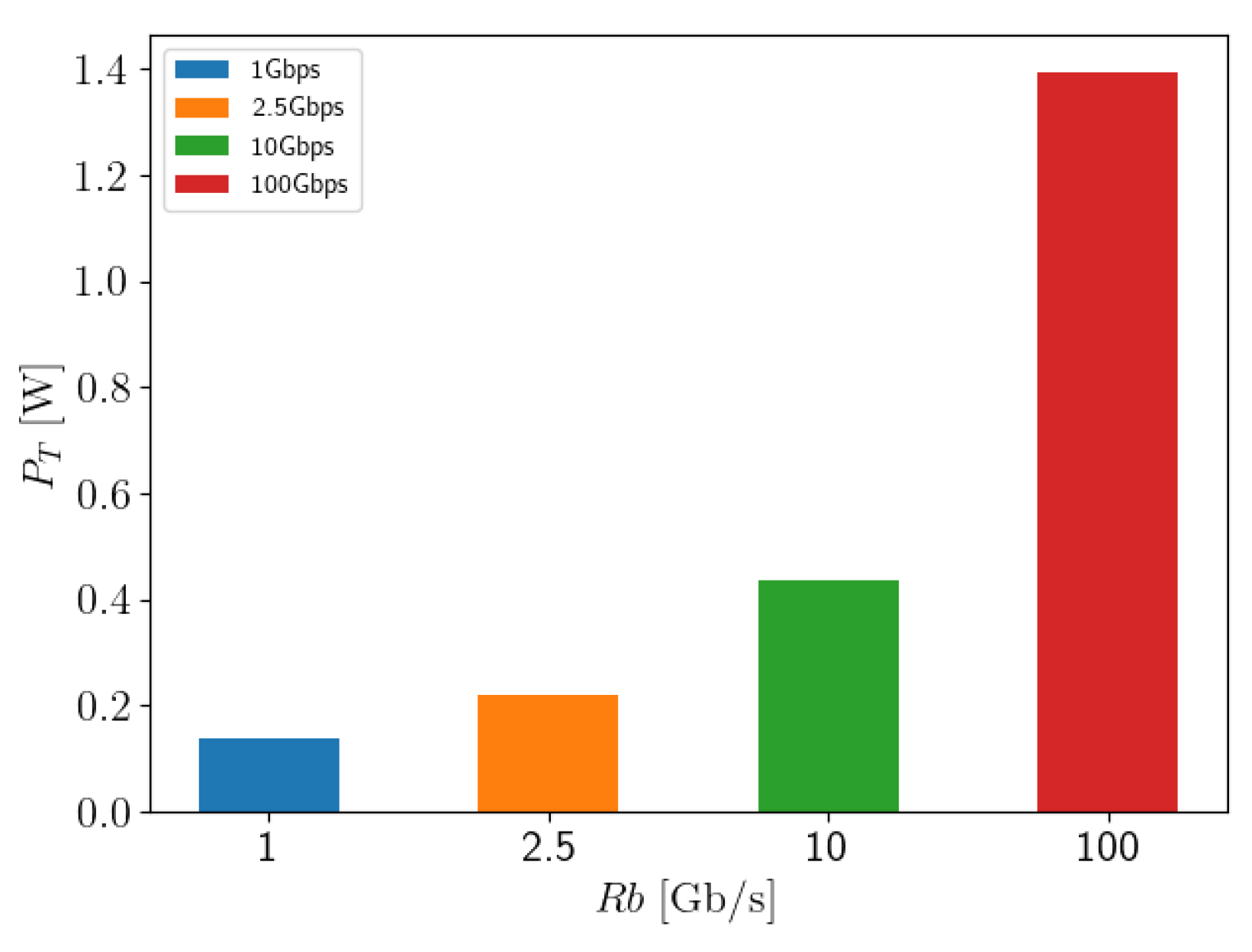
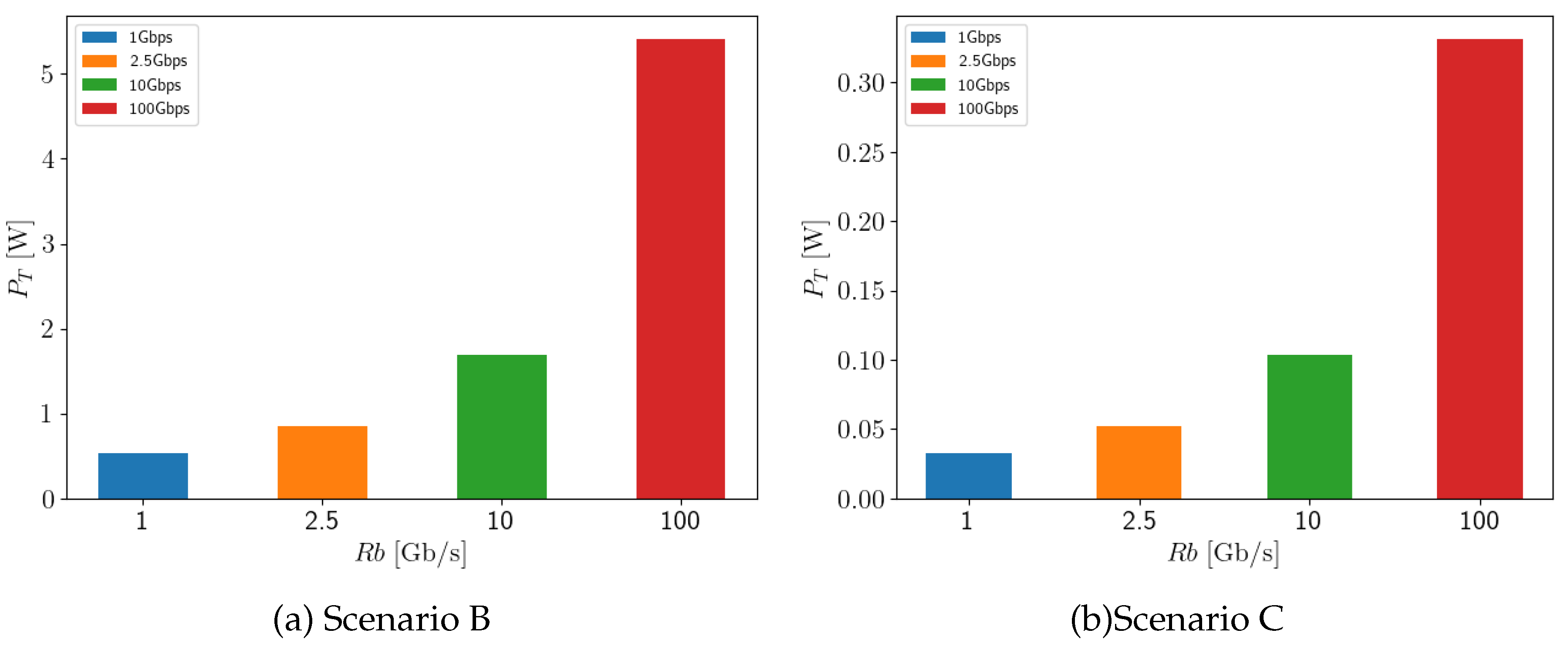
5.1. Scenario A
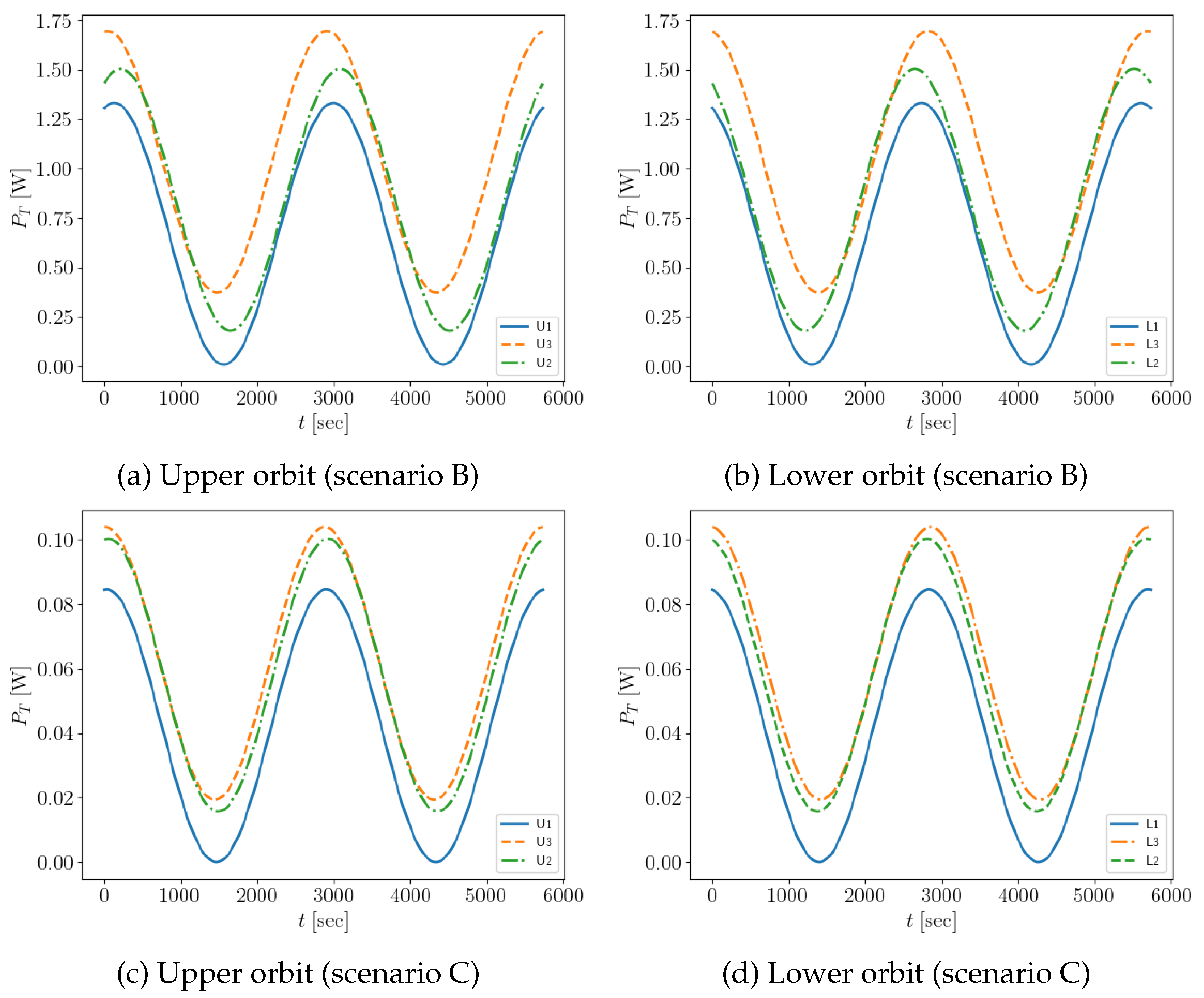
5.2. Alternative Scenarios
6. Conclusions and Outlook
References
- Carrizo, C.; Knapek, M.; Horwath, J.; Gonzalez, D.D.; Cornwell, P. Optical inter-satellite link terminals for next generation satellite constellations. In Proceedings of the Free-Space Laser Communications XXXII. SPIE, 2020, Vol. 11272, pp. 8–18.
- Kemih, K.; Yaiche, Y.; Benslama, M. Optimization of Transmitter Aperture by Genetic Algorithm in Optical Satellite. World Academy of Science, Engineering and Technology, International Journal of Electrical, Computer, Energetic, Electronic and Communication Engineering 2007, 1, 1261–1267. [Google Scholar]
- Kim, G.N.; Park, S.Y.; Seong, S.; Choi, J.Y.; Han, S.K.; Kim, Y.E.; Choi, S.; Lee, J.; Lee, S.; Ryu, H.G.; et al. Design of Novel Laser Crosslink Systems Using Nanosatellites in Formation Flying: The VISION. Aerospace 2022, 9, 423. [Google Scholar] [CrossRef]
- Zhu, Q.; Tao, H.; Cao, Y.; Li, X. Laser inter-satellite link visibility and topology optimization for mega constellation. Electronics 2022, 11, 2232. [Google Scholar] [CrossRef]
- Liang, J.; Chaudhry, A.U.; Erdogan, E.; Yanikomeroglu, H. Link Budget Analysis for Free-Space Optical Satellite Networks. In Proceedings of the 2022 IEEE 23rd International Symposium on a World of Wireless, Mobile and Multimedia Networks (WoWMoM), Los Alamitos, CA, USA, jun 2022; pp. 471–476. [Google Scholar]
- Liang, J.; Chaudhry, A.U.; Erdogan, E.; Yanikomeroglu, H.; Kurt, G.K.; Hu, P.; Ahmed, K.; Martel, S. Free-Space Optical (FSO) Satellite Networks Performance Analysis: Transmission Power, Latency, and Outage Probability. IEEE Open Journal of Vehicular Technology 2024, 5, 244–261. [Google Scholar] [CrossRef]
- update, S.F. SpaceX non-geostationary satellite system, attachment a, technical information to supplement schedule S. Accessed: Dec. 6, 2023. [Online]. Available: https://fcc, report/IBFS/SAT-MOD-20181108-00083/1569860.pdf 2018.
- Carrasco-Casado, A.; Biswas, A.; Fields, R.; Grefenstette, B.; Harrison, F.; Sburlan, S.; Toyoshima, M. Optical communication on CubeSats — Enabling the next era in space science. In Proceedings of the 2017 IEEE International Conference on Space Optical Systems and Applications (ICSOS), 2017, pp. 46–52. [CrossRef]
- Goorjian, P.M. Free-space optical communication for spacecraft and satellites, including cubesats in low earth orbit (LEO). In Proceedings of the Photonic Networks and Devices. Optica Publishing Group, 2019, pp. NeM2D–4.
- Saathof, R.; Crowcombe, W.; Kuiper, S.; van der Valk, N.; Pettazzi, F.; de Lange, D.; Kerkhof, P.; van Riel, M.; de Man, H.; Truyens, N.; et al. Optical satellite communication space terminal technology at TNO. In Proceedings of the International Conference on Space Optics — ICSO 2018; Sodnik, Z.; Karafolas, N.; Cugny, B., Eds. International Society for Optics and Photonics, SPIE, 2019, Vol. 11180, p. 111800K. [CrossRef]
- Benzi, E.; Troendle, D.C.; Shurmer, I.; James, M.; Lutzer, M.; Kuhlmann, S. Optical inter-satellite communication: the Alphasat and Sentinel-1A in-orbit experience. In Proceedings of the 14th International Conference on Space Operations, 2016, p. 2389.
- Li, L.; Xuejiao, Z.; Jianhua, Z.; Changzhi, X.; Yi, J. Advanced space laser communication technology on cubesats. ZTE communications 2021, 18, 45–54. [Google Scholar]
- Schmidt, C.; Rödiger, B.; Rosano, J.; Papadopoulos, C.; Hahn, M.T.; Moll, F.; Fuchs, C. DLR’s Optical Communication Terminals for CubeSats. In Proceedings of the 2022 IEEE International Conference on Space Optical Systems and Applications (ICSOS), 2022, pp. 175–180. [CrossRef]
- Velazco, J.; Boyraz, O. High data rate inter-satellite omnidirectional optical communicator. 32 Annual AIAA/USU Conference on Small Satellites 2018.
- Zaman, I.U.; Velazco, J.E.; Boyraz, O. Omnidirectional optical crosslinks for CubeSats: Transmitter optimization. IEEE transactions on aerospace and electronic systems 2020, 56, 4556–4566. [Google Scholar] [PubMed]
- Saeed, N.; Almorad, H.; Dahrouj, H.; Al-Naffouri, T.Y.; Shamma, J.S.; Alouini, M.S. Point-to-Point Communication in Integrated Satellite-Aerial 6G Networks: State-of-the-Art and Future Challenges. IEEE Open Journal of the Communications Society 2021, 2, 1505–1525. [Google Scholar] [CrossRef]
- Chaudhry, A.U.; Yanikomeroglu, H. Free Space Optics for Next-Generation Satellite Networks. IEEE Consumer Electronics Magazine 2021, 10, 21–31. [Google Scholar] [CrossRef]
- Liang, J.; Chaudhry, A.U.; Yanikomeroglu, H. Phasing parameter analysis for satellite collision avoidance in starlink and kuiper constellations. In Proceedings of the 2021 IEEE 4th 5G world forum (5GWF). IEEE, 2021, pp. 493–498.
- Chaudhry, A.U.; Yanikomeroglu, H. Laser Intersatellite Links in a Starlink Constellation: A Classification and Analysis. IEEE Vehicular Technology Magazine 2021, 16, 48–56. [Google Scholar] [CrossRef]
- Chaudhry, A.U.; Yanikomeroglu, H. Temporary laser inter-satellite links in free-space optical satellite networks. IEEE Open Journal of the Communications Society 2022, 3, 1413–1427. [Google Scholar] [CrossRef]
- Liang, J.; Chaudhry, A.U.; Chinneck, J.W.; Yanikomeroglu, H.; Kurt, G.K.; Hu, P.; Ahmed, K.; Martel, S. Latency Versus Transmission Power Trade-Off in Free-Space Optical (FSO) Satellite Networks With Multiple Inter-Continental Connections. IEEE Open Journal of the Communications Society 2023, 4, 3014–3029. [Google Scholar] [CrossRef]
- Handley, M. Delay is Not an Option: Low Latency Routing in Space. In Proceedings of the Proceedings of the 17th ACM Workshop on Hot Topics in Networks, New York, NY, USA, 2018; HotNets ’18, p. 85–91. [CrossRef]
- Walker, J.G. Satellite constellations. Journal of the British Interplanetary Society 1984, 37, 559. [Google Scholar]
- Wenzel, H.; Klehr, A.; Braun, M.; Bugge, F.; Erbert, G.; Fricke, J.; Knauer, A.; Ressel, P.; Sumpf, B.; Weyers, M.; et al. Design and realization of high-power DFB lasers. In Proceedings of the Physics and Applications of Optoelectronic Devices. SPIE, 2004, Vol. 5594, pp. 110–123.
- McDowell, J.C. The low earth orbit satellite population and impacts of the SpaceX Starlink constellation. The Astrophysical Journal Letters 2020, 892, L36. [Google Scholar] [CrossRef]
- Kotake, H.; Abe, Y.; Fuse, T.; Kubooka, T.; Toyoshima, M. Adaptive optical satellite network architecture. In Proceedings of the International Conference on Space Optics—ICSO 2020. SPIE, 2021, Vol. 11852, pp. 685–693.
- Gioulis, M.; Kamalakis, T. Pyminisat: A Python package for simulating optical intersatellite links in a minisat constellation. https://github.com/thomaskamalakis/pyminisat, 2024.
- C.H. Orbital Mechanics for Engineering Students, 7 ed.; Elsevier Butterworth Heinemann, 2005.
- Sumathi, K.; Balasaraswathi, M.; Boopathi, C.; Singh, M.; Malhotra, J.; Dhasarathan, V. Design of 3.84 Tbps hybrid WDM–PDM based inter-satellite optical wireless communication (IsOWC) system using spectral efficient orthogonal modulation scheme. Journal of Ambient Intelligence and Humanized Computing 2020, 11, 4167–4175. [Google Scholar] [CrossRef]
- Chaudhary, S.; Chaudhary, N.; Sharma, S.; Choudhary, B. High speed inter-satellite communication system by incorporating hybrid polarization-wavelength division multiplexing scheme. Journal of Optical Communications 2017, 39, 87–92. [Google Scholar] [CrossRef]
- Betti, S.; Carrozzo, V.; Parca, G. Optical Intersatellite hybrid network links based on WDM technology. In Proceedings of the 2008 10th Anniversary International Conference on Transparent Optical Networks. IEEE, 2008, Vol. 4, pp. 209–212.
- Horst, Y.; Bitachon, B.I.; Kulmer, L.; Brun, J.; Blatter, T.; Conan, J.M.; Montmerle-Bonnefois, A.; Montri, J.; Sorrente, B.; Lim, C.B.; et al. Tbit/s line-rate satellite feeder links enabled by coherent modulation and full-adaptive optics. Light: Science & Applications 2023, 12, 153. [Google Scholar]
- Rajiv Ramaswami, Kumar N.Sivarajan, G.H.S. Optical Networks, A Practical Perspective, 3 ed.; Elsevier, 2010.
- Brashears, T.R. Achieving 99% link uptime on a fleet of 100G space laser inter-satellite links in LEO. In Proceedings of the Free-Space Laser Communications XXXVI. SPIE, 2024, Vol. 12877, p. 1287702.
- Kato, W.; Kawamoto, Y.; Kato, N.; Ariyoshi, M.; Sugyo, K.; Funada, J. Stable and Efficient Inter-Satellite Optical Wireless Communications Through Connection of Intersecting Orbits. In Proceedings of the 2024 IEEE 99th Vehicular Technology Conference (VTC2024-Spring). IEEE, 2024, pp. 1–5.
- Zhu, Y.; Xu, G.; Gao, M.; Chu, H.; Song, Z. Average bit-error rate analysis of an inter-satellite optical communication system under the effect of perturbations. Optics Express 2024, 32, 36796–36810. [Google Scholar] [PubMed]
- Stampoulidis, L.; Osman, A.; Sourikopoulos, I.; Winzer, G.; Zimmermann, L.; Dorward, W.; Rodrigo, A.S.; Chiesa, M.; Rotta, D.; Maho, A.; et al. H2020-SPACE-ORIONAS Miniaturized optical transceivers for high-speed optical inter-satellite links. arXiv preprint arXiv:2210.17304 2022. arXiv:2210.17304 2022.
- Rödiger, B.; Fuchs, C.; Nonay, J.R.; Jung, W.; Schmidt, C. Miniaturized optical Intersatellite communication terminal–CubeISL. In Proceedings of the 2021 IEEE International Conference on Communications Workshops (ICC Workshops). IEEE, 2021, pp. 1–5.
- Edmunds, J.; Thipparapu, N.; Kechagias, M.; Hall, K.; Donnot, A.; Kean, P.; Kehayas, E.; Welch, M. Designing transmit optical amplifiers for the current roll out of optical communication constellations. In Proceedings of the International Conference on Space Optics—ICSO 2022. SPIE, 2023, Vol. 12777, pp. 1497–1504.
- Carrasco-Casado, A.; Shiratama, K.; Kolev, D.; Trinh, P.V.; Ishola, F.; Fuse, T.; Toyoshima, M. Development and space-qualification of a miniaturized CubeSat’s 2-W EDFA for space laser communications. Electronics 2022, 11, 2468. [Google Scholar] [CrossRef]
- Morthier, G.; Roelkens, G.; Baets, R. Optical versus RF free-space signal transmission: A comparison of optical and RF receivers based on noise equivalent power and signal-to-noise ratio. IEEE Journal of Selected Topics in Quantum Electronics 2021, 28, 1–8. [Google Scholar]
| Parameter | Symbol | Value |
|---|---|---|
| Number of orbits | 24 | |
| Number of satellites per orbit | 66 | |
| Total number of satellites | N | 1584 |
| Altitude | a | 550 km |
| Distance from earth center | r | 6921 km |
| Orbital period | T | 5730.11 s |
| Angular momentum | h | 52523.60/s |
| Inclination | i | |
| Optimal phasing parameter | F | 13 |
| Parameter | Symbol | Units | Value |
|---|---|---|---|
| Laser wavelength | nm | 1550 | |
| Transmitter optical efficiency | 0.8 | ||
| Receiver optical efficiency | 0.8 | ||
| Data rate | Gbps | 1 - 100 | |
| Receiver telescope diameter | mm | 80 | |
| Transmitter pointing error | rad | 1 | |
| Receiver pointing error | rad | 1 | |
| Full transmitting divergence angle | rad | 4 | |
| Target BER | |||
| Extinction ratio | dB | 20 | |
| Quantum efficiency | 1 | ||
| Amplifier noise figure | dB | 3 | |
| Load resistor | 100 | ||
| Temperature in Kelvin | K | 300 | |
| Link margin | dB | 3 |
| Parameters | A | B | C |
|---|---|---|---|
| 66 | 33 | 132 | |
| 24 | 12 | 48 | |
| N | 1584 | 396 | 6336 |
| i | |||
| a [Km] | 550 | 550 | 550 |
| F | 13 | 6 | 19 |
| [Km] | 659.3 | 1317.1 | 329.7 |
| [Km] | |||
| [Km] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





