Submitted:
29 January 2025
Posted:
30 January 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
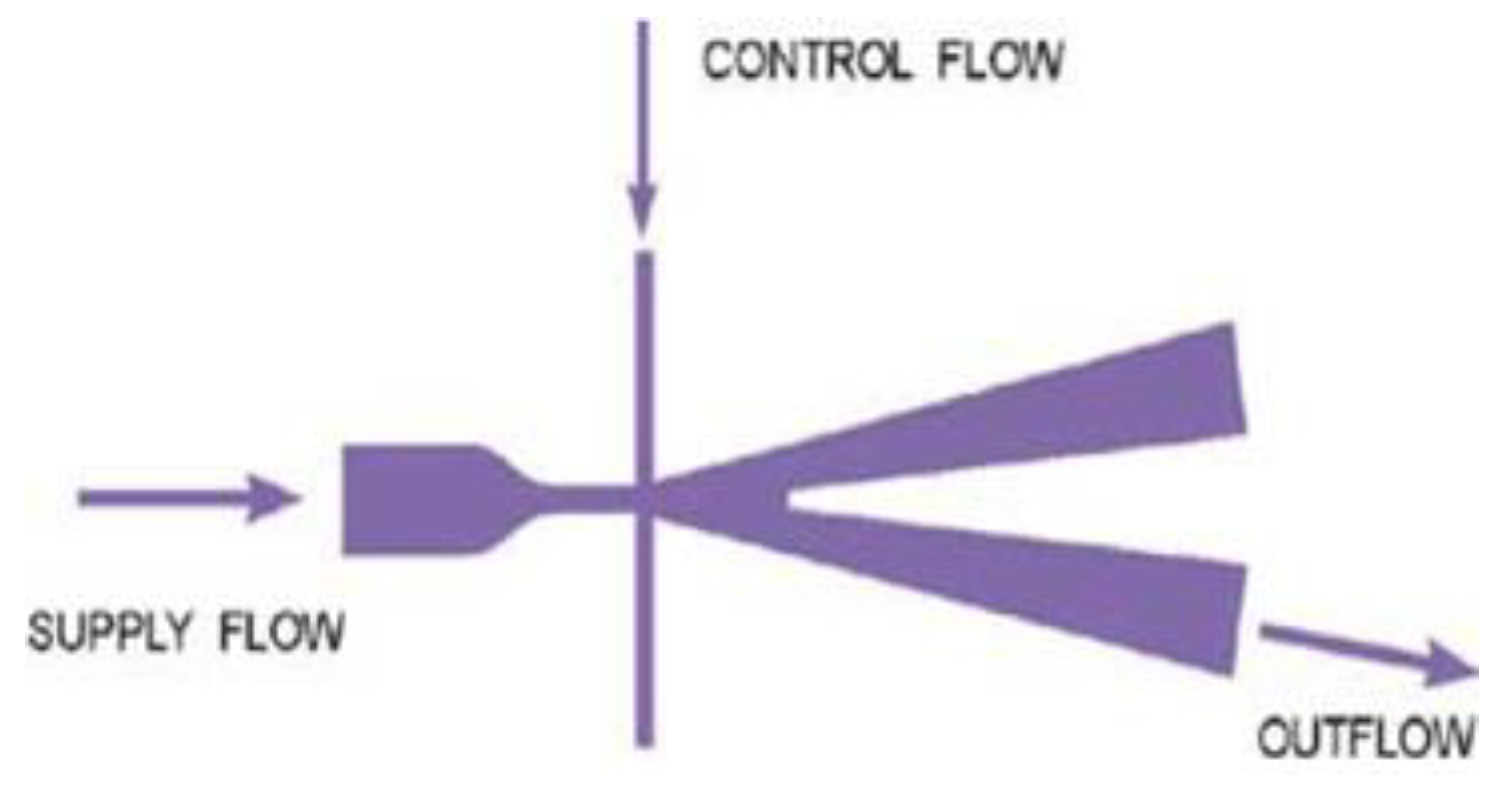
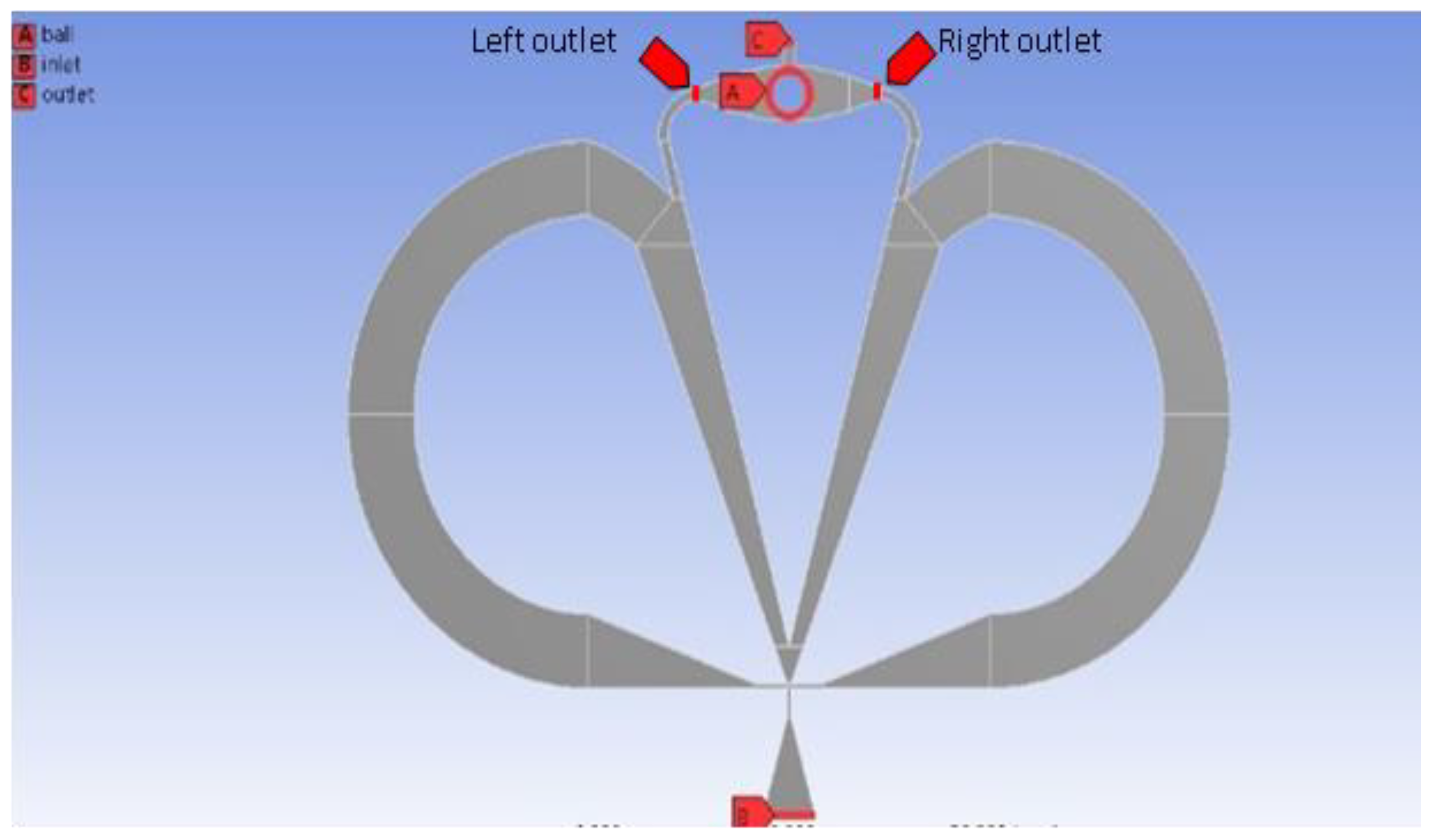
2. Simulation of Fluidic Actuation with Mobile Object
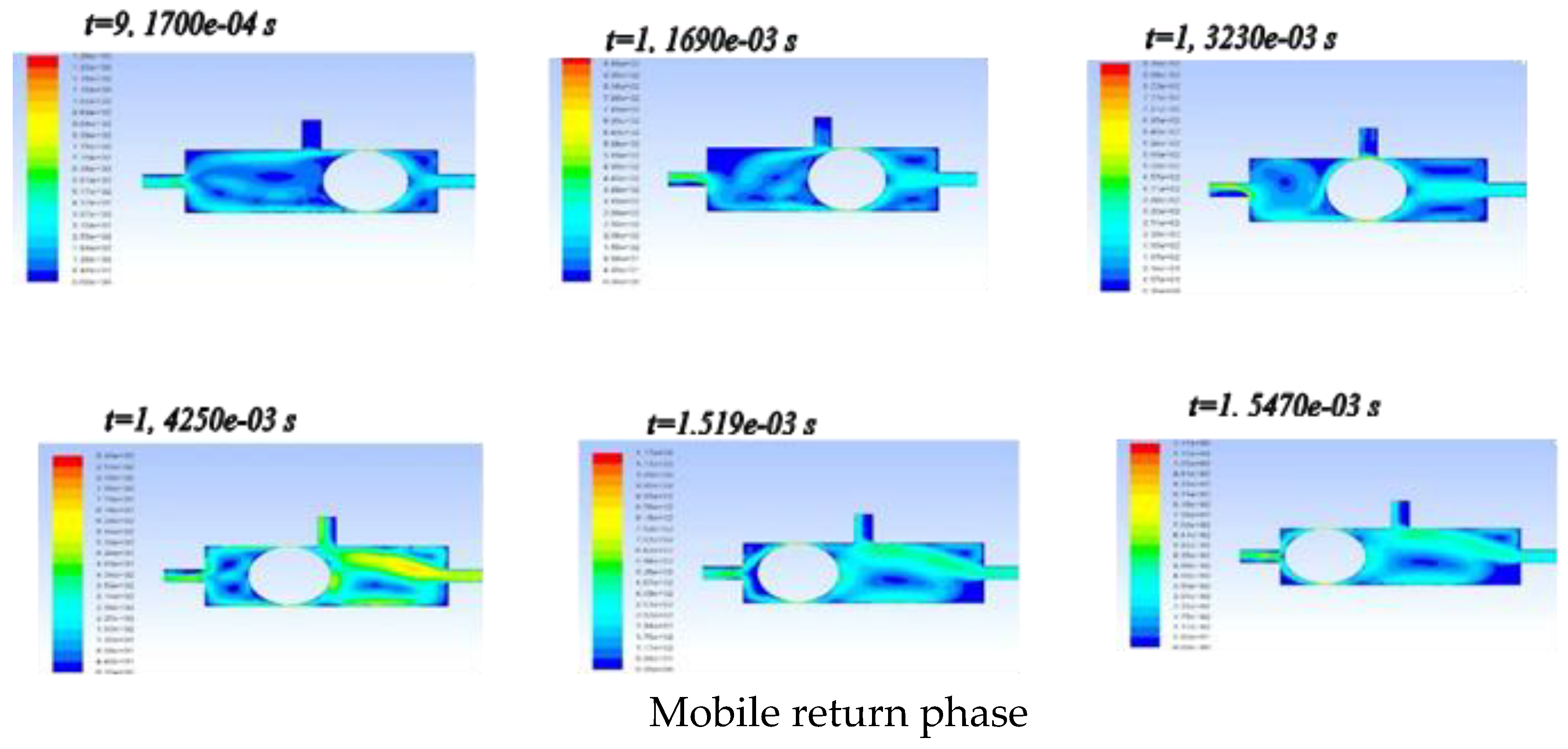
3. Simulation Results
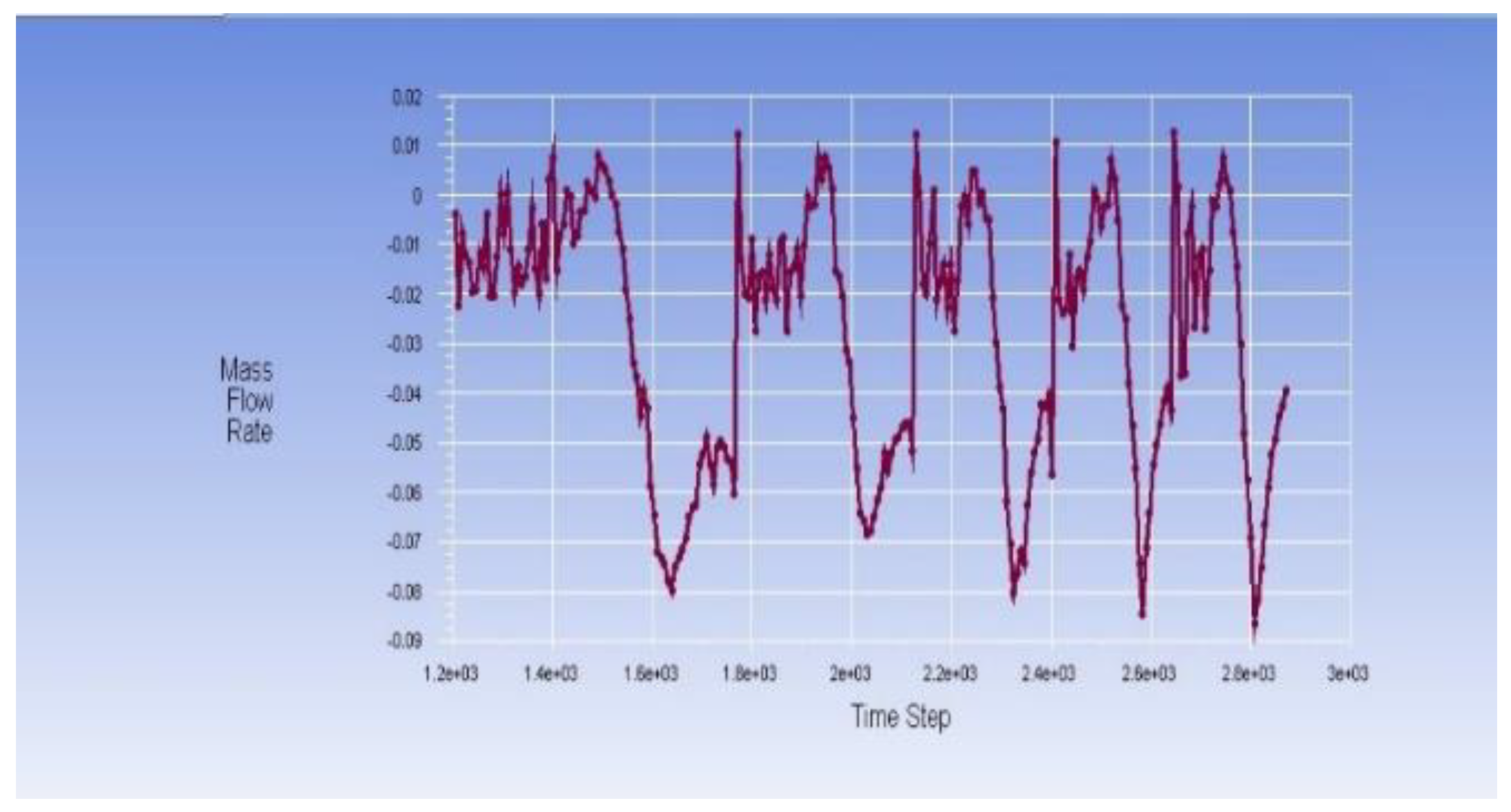
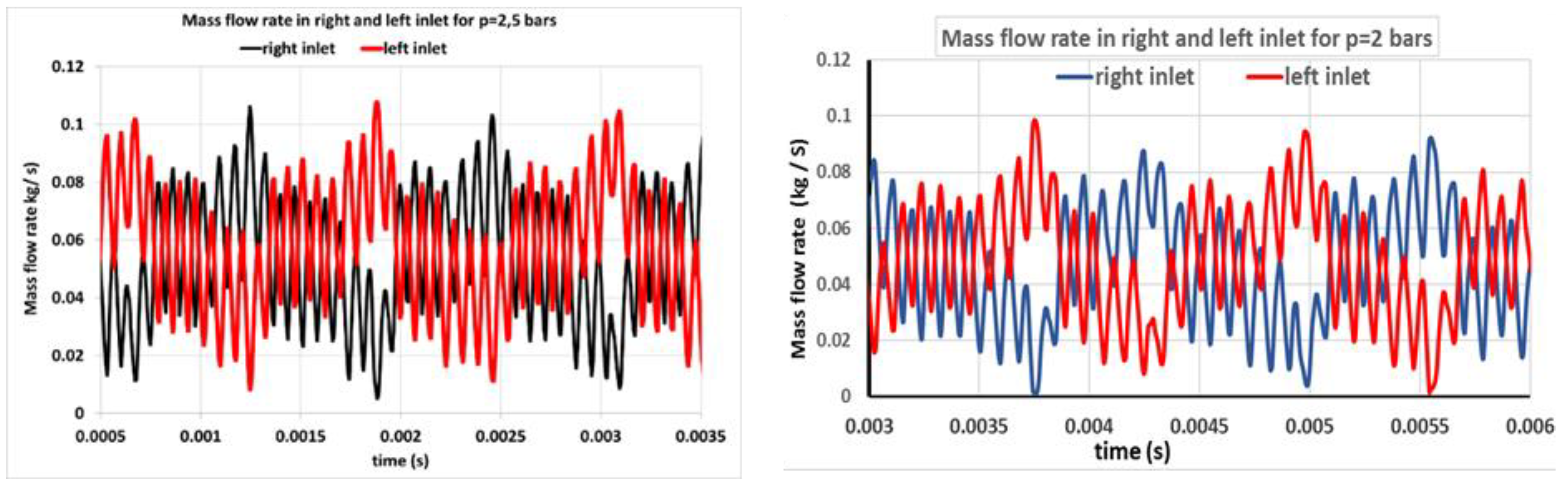
3.1. Evolution of Mass Flow at the Left and Right Outputs of the Oscillator-Actuator Combination
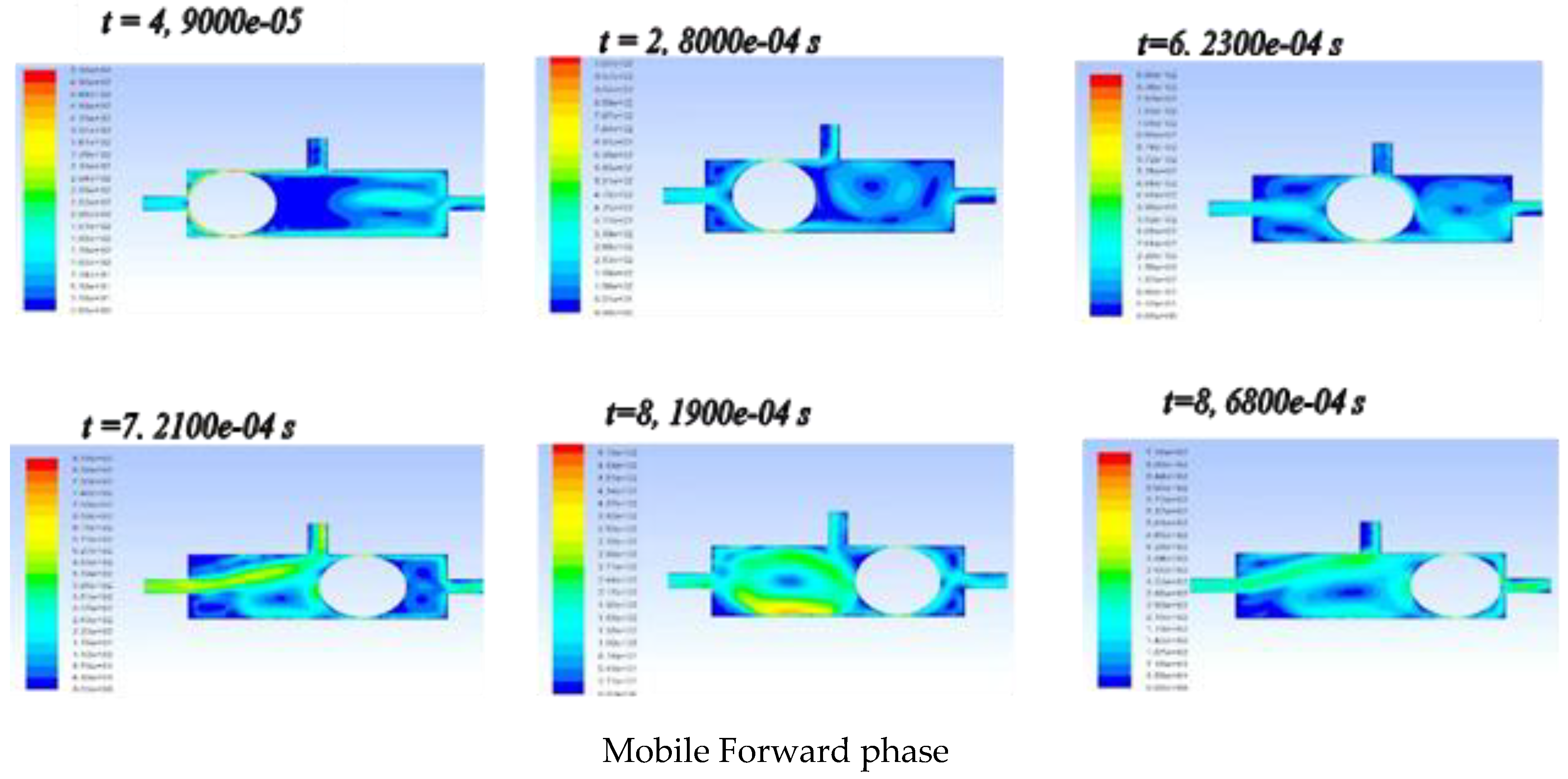
3.2. Evolution of Mobile Velocity
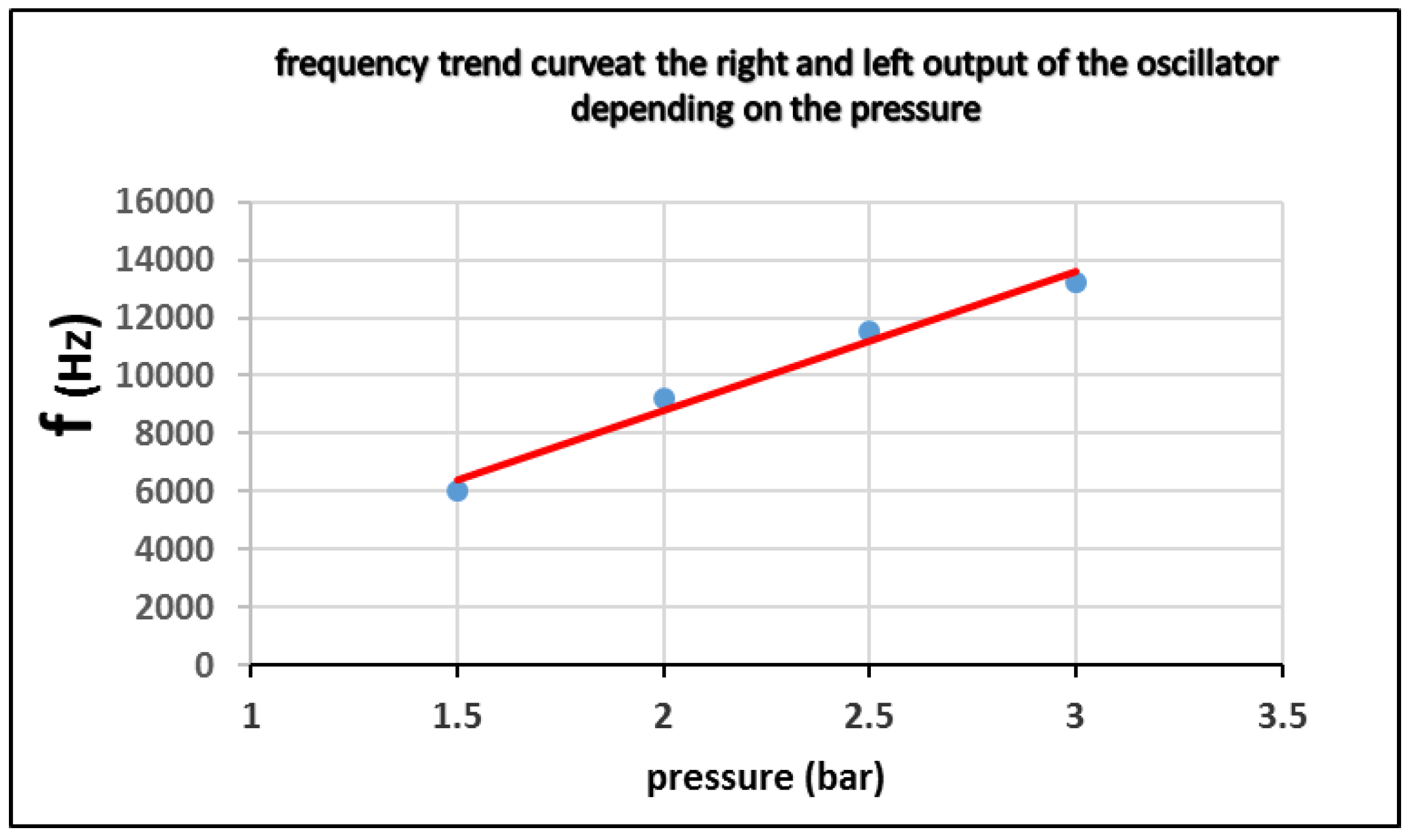
3.3. Trend Curve
5. Conclusions
References
- Sebastiano, M. : Analyse et mise en oeuvre d'un moteur électromagnétique micro fabriqué. Ph.D Thesis, federal instate of technology in LAUANNE, N° 4801 (2010).
- Piyabongkarn, D. , Rajamani R., Sezen A., and Nelson B.J.: Travel Range Extension of a MEMS Electrostatic Micro actuator. IEEE transactions on control systems technology, vol. 13, N°1 (2005).
- Cédric, A. : conception d'un micro robot à actionneur asservi électropneumatique pour l'inspection intratubulaire- Ph.D Thesis, INSA of Lyon (1999).
- Shikida, M. : basic 05 Micro actuator Electrostatic actuator. COE for education and research of Micro-Nano mechatronics, Nagoya University (2010).
- Jeffry, J.S. , Garcia E.J.: Micro fabricated Actuators and Their Application to Optics – SAND-2270C (1997).
- Felix, B. , Adrian N., Stefano O., Dominik J. B., Yu S., Jürg D., and Bradley J. N.: Monolithically Fabricated Micro gripper With Integrated Force Sensor for Manipulating Micro objects and Biological Cells Aligned in an Ultrasonic Field. Journal of micro electromechanical systems, vol. 16, no. 1, February (2007).
- Volland, B.E. , Heerlein H., and Rangelow I.W.: electrostatically driven micro gripper- mne (2001).
- Tao, C. , Liguo C., Lining S., Xinxin L.: Electro statically Driven Micro gripper Integrated Piezoresistive Force Sensor. EDA Publishing/DTIP (2008).
- Varona, J.; Saenz, E.; Fiscal-Woodhouse, S.; Hamoui, A.A. Design and fabrication of a novel microgripper based on electrostatic actuation. 2009 52nd IEEE International Midwest Symposium on Circuits and Systems (MWSCAS). LOCATION OF CONFERENCE, MexicoDATE OF CONFERENCE; pp. 827–832.
- Yukun, J. and Qingsong X.: Design of a Monolithic Dual-Axis Electrostatic Actuation MEMS Micro gripper with Capacitive Position/Force Sensors. Proceedings of the 13th IEEE International Conference on Nanotechnology Beijing, China, -8, (2013). 5 August.
- Yukun, J. and Qingsong X. Recent Patents on Mechanical Engineering ( 2013.
- Vitório, A. , Paulo H., Emilio C.N.S., Ricardo C. I.: Micro grippers Driven by Electrostatic Comb Drive Actuators. ABCM Symposium series in Mechatronics- Vol. 1-pp.682-687 (2004).
- Sam Jebar Kumar, J. , Enoch A.T., Paul Braineard E.: A study of why electrostatic actuation is preferred and a simulation of an electro statically actuated cantilever beam for mems applications. International Journal of Engineering Sciences & Emerging Technologies, Volume 6, Issue 5, pp: 441-446 (2014).
- Pan, C.T. , Cheng P.J., Yen C.K., Hsieh C.C.: Application of polyimide to bending-mode micro actuators with Ni/Fe and Fe/Pt magnet. Microelectronics Reliability 46, 1369–1381(2006).
- Pessiot-Bonvilain, A. : Etude et réalisation d'un micro robot a pattes structure mécanique et micro-actionnement. Ph.D Thesis, University of Franche-Comte, HAL Id: tel-00010356 (2002).
- Deok-Ho, K. , Moon G.L., Byungkyu K., and Yu S.: A super elastic alloy micro gripper with embedded electromagnetic actuators and piezoelectric force sensors: a numerical and experimental study. Smart Mater. Struct. 14 pp.1265–1272 (2005).
- CHONG H., A. , YOUG J. IEEE ( 1993.
- Guckel, H. , ChristensonT.R., Skrobis K.J., JungT.S., KleinJ., Hartojo K.V., and Widjaja I.: A first functional current excited planar rotational magnetic micro motor. IEEE (1993).
- Wagner, B. , Kreutzer M., and Benecke W.: Permanent Magnet Micro motors on Silicon Substrates. J. Of MEMS, VOL. 1993; 2. [Google Scholar]
- Chunsheng, Y. , Xiaolin Z., Guifu D., Chen Z. and Bingchu C.: An axial flux electromagnetic micro motor. J. Micro mech. Micro eng. 11, pp 113–117, (2001).
- Matthieu, C. : Microactionneurs piézoélectriques. Ph.D Thesis, University of Grenoble, (2011).
- Silvestri, M.; Confalonieri, M.; Ferrario, A. Piezoelectric actuators for micro positioning stages in automated machines: experimental characterization of open loop implementations. FME Trans. 2017, 45, 331–338. [Google Scholar] [CrossRef]
- Nah, S.K. , Zhong Z.W.: A micro gripper using piezoelectric actuation for micro-object manipulation. Sensors and Actuators A 133, 218–224 (2007).
- Ramadan, K.S.; Sameoto, D.; Evoy, S. A review of piezoelectric polymers as functional materials for electromechanical transducers. Smart Mater. Struct. 2014, 23. [Google Scholar] [CrossRef]
- Tadigadapa, S. , Materi K.: Piezoelectric MEMS sensors, state of the art and perspectives. Measurement Science and Technology, vol. 20, p. 092001, September (2009).
- Koh, K.H. , Kobayashi T., Xie J., Yu A., Lee C.: Novel piezoelectric actuation mechanism for a gimbal-less mirror in 2D raster scanning applications. J. Micro mech. Micro eng. 21, 075001 (2011).
- Fu, Y.Q. , Luo J.K., Flewitt A.J., Huang W.M., Zhang S., Du H.J., and Milne W.I.: Thin film shape memory alloys and micro actuators. Int. J. Computational Materials Science and Surface Engineering, Vol. 2, Nos. 3/4, (2009).
- Mohamed, S.M.A. , Shafishuhaza S., and Mohammad A.Z.: Micro machined Shape Memory Alloy Micro actuators and Their Application in Biomedical Devices. Micro machines, VOL. 6, pp.879-901, (2015).
- Gabriel, K.; Trimmer, W.; Walker, J. A micro rotary actuator using shape memory alloys. Sensors Actuators 1988, 15, 95–102. [Google Scholar] [CrossRef]
- Han, Z. , Yves B., Etienne B., Reymond C., Aun-Neow P., Diebnar W. H.: Shape Memory Alloy Micro gripper for Robotic Micro assembly of Tissue Engineering Scaffolds. International Conference on Robotics &Automation New Orleans, LA April (2004).
- Kyung, J.H. , Ko B.G., Ha Y.H., and Chung G.J.: Design of a micro gripper for micro manipulation of micro components using SMA wires and flexible hinges. Sensor Actuator A-Phys, 141(1): 144-50, (2008).
- Sinclair, M. A high force low area MEMS thermal actuator. ITHERM 2000. The Seventh Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE; pp. 127–132.
- Hsu, C.; Hsu, W. A two-way membrane-type micro-actuator with continuous deflections. J. Micromechanics Microengineering 2000, 10, 387–394. [Google Scholar] [CrossRef]
- Qing-An, H. , and Neville K.L.: Analysis and design of polysilicon thermal flexure actuator. J. Micro mech. Micro eng. Vol.9, pp.64–70, (1999).
- Lerchyx, Ph. , Kara S.C., Romanowiczy B., and Renaud Ph.: Modelization and characterization of asymmetrical thermal micro actuators. J. Micro mech. Micro eng. Vol.6, (1996).
- Bordatchev, E.V. , & Nikumb S.K.: Micro gripper design, finite element analysis and laser micro fabrication. Proceedings of the International Conference on MEMS, NANO and Smart Systems, pp. 308-313, (2003).
- Marija, C. , Pierluigi M. International CAE Conference ( 2016.
- Chi, S.P. , and Wensyang H.: An electro-thermally and laterally driven polysilicon micro actuator. J. Micro mech. Micro eng. Vol.7, pp.7–13, (1997).
- Niels, T. , Jeroen W., Louis S., Theo L., Miko E.: Modeling, design and testing of the electrostatic shuffle motor. Sensors and Actuators, A 70, pp.171-178, (1998).
- Just, E. , Kohl M., Pfleging W., Miyazaki S.: SMA Micro gripper with Integrated Antagonism. In: Proc. Transducers, 10th Int. Conf. Solid-State Sensors and Actuators. S. 1768-1771, (1999).
- de Bhailis, D. , Murray C., Duffy M., Alderman J., Kelly G., and O Mathuna S.C.: Modelling and analysis of a magnetic micro actuator. Sensors and Actuators, Vol.81, pp.285–289, (2000).
- Fuller, S.B. , Wilhelm E.J., and Jacobson J.M.: Ink-jet printed nano particle micro electromechanical systems. J. MEMS, Vol.11, pp.54–60, (2002).
- Abadie, J.; Chaillet, N.; Lexcellent, C. An integrated shape memory alloy micro-actuator controlled by thermoelectric effect. Sensors Actuators A: Phys. 2002, 99, 297–303. [Google Scholar] [CrossRef]
- Olivier, M. , Paul B., Stéphane R., Philippe B., Elli T., Dominique C., and Lionel B.: Electrostatic actuated micro gripper using an amplification mechanism. Sensors and Actuators, (2004).
- Jing, Y.; Luo, J.; Yi, X.; Gu, X. Design and evaluation of PZT thin-film micro-actuator for hard disk drives. Sensors Actuators A: Phys. 2004, 116, 329–335. [Google Scholar] [CrossRef]
- Ahn, S.H. , Kim Y.K.: Silicon scanning mirror of two DOF with compensation current routing. J. Micro mech. Micro eng, 14, 1455 (2004).
- Fu, Y. , Du H., Huang W., Zhang S., Hu M.: TiNi-based thin film in MEMS applications: A review. Sens. Actuators A Phys, Vol.112, pp.395–408, (2004).
- Mitsui, T.; Takahashi, Y.; Watanabe, Y. A 2-axis optical scanner driven nonresonantly by electromagnetic force for OCT imaging. J. Micromechanics Microengineering 2006, 16, 2482–2487. [Google Scholar] [CrossRef]
- Xinyu, L. , Keekyoung K., and Yu S.: A MEMS stage for 3-axis nano positioning. J. Micro mech. Micro eng. Vol.17, pp.1796–1802, (2007).
- Young, H.C. and Ji-Chul R.: Transverse Electromagnetic Micro actuators Using Electroplated Planar Coil Driven by Symmetric Twin Magnets. Sensors & Materials, Vol. 19, N° 2, (2007).
- Andrew, C. , Jongbaeg K. and Liwei L.: Bidirectional electrothermal electromagnetic actuators. J. Micro mech. Micro eng. Vol.17, pp.975–982, (2007).
- Marialena, V. , George N., Anthony T.: Design of a robust PID control switching scheme for an electrostatic micro actuator. Control Engineering Practice, 16, pp.1321– 1328, (2008).
- Gustavo, A.A.R. : Conception, simulation et réalisation d'un micro actionneur à base de matériau énergétique pour l'actionnement micro fluidique. Ph.D Thesis, Paul Sabatier University - Toulouse III, HAL Id: tel-00258425 (2008).
- Guo, S. , Sun X. In , Ishii K., Guo J.: SMA actuator-based novel type of peristaltic micro pump. In Proceedings of the International Conference on Information and Automation, ICIA; pp. 1620–23.
- Nieva, P.M. , Topaloglu N., Elbuken C., Yavuz M., Huissoon J.P.: Modeling and simulation of a 2-DOF bidirectional electro thermal micro actuator. Proc. of SPIE Vol. 6926, 692605-1, (2008).
- Jia, K. , Pal S., Xie H.: An electro thermal tip-tilt-piston micro mirror based on folded dual S-shaped bimorphs. J. Micro electro mechanical System, Vol.19, pp.1004–1015, (2009).
- Micky, R. , and Ioan A.I.: Development and Force Position Control of a New Hybrid Thermo Piezoelectric micro gripper dedicated to micromanipulation tasks. IEEE transactions on automation, science. First submission: april 19th, (2010).
- Zhu, Y. , Liu W., Jia K., Liao W., Xie H.: A piezoelectric unimorph actuator based tip-tilt-piston micro mirror with high fill factor and small tilt and lateral shift. Sensors & Actuators A Phys. Vol.167, pp.495–501, (2011).
- Chao-Chieh, L. , Che-Min L., and Chen-Hsien F.: A self sensing micro gripper module with wide handling ranges. IEEE/ASME Trans. Mechatron. Vol.16, pp.141–150, (2011).
- Liu, L. , Pal S. In , Xie H.: MEMS mirrors based on curved concentric electro thermal actuators with very small lateral shift and tilt. In Proceedings of the International Conference on Solid-State Sensors Actuators and Microsystems (TRANSDUCERS); pp. 2522–9.
- Qingsong, X. : Precision Position Force Interaction Control of a Piezoelectric Multimorph Micro gripper for Micro assembly. IEEE transactions on automation science and engineering, vol. 10, N°. 3, (2013).
- Park, E.S. , Chen Y., Liu T.K., and Subramanian V.: A New Switching Device for Printed Electronics: Inkjet-Printed Micro electromechanical Relay. Nano Lett. Vol.13, pp.5355−5360, (2013).
- Ren-Jung, C. , Chih-Cheng S. and Chih-Yi C.: Self-Biased-SMA Drive PU Micro gripper with Force Sensing in Visual Servo. International Journal of Advanced Robotic Systems, Vol. 10, (2013).
- Bessonov, A.; Kirikova, M.; Haque, S.; Gartseev, I.; Bailey, M.J. Highly reproducible printable graphite strain gauges for flexible devices. Sensors Actuators A Phys. 2014, 206, 75–80. [Google Scholar] [CrossRef]
- Sharma, A. , Olszewski Z., Torres J., Mathewson A., Houlihan R.: Fabrication, Simulation and Characterization of MEMS Piezoelectric Vibration Energy Harvester for Low Frequency. Procedia Engineering, Vol.120, pp.645 – 650, (2015).
- Saadon, S.; Sidek, O. Micro-Electro-Mechanical System (MEMS)-Based Piezoelectric Energy Harvester for Ambient Vibrations. Procedia - Soc. Behav. Sci. 2015, 195, 2353–2362. [Google Scholar] [CrossRef]
- Andò, B. , Marletta V.: An All-InkJet Printed Bending Actuator with Embedded Sensing Feature and an Electromagnetic Driving Mechanism. Actuators MDPI, (2016).
- Yamamoto, Y.; Harada, S.; Yamamoto, D.; Honda, W.; Arie, T.; Akita, S.; Takei, K. Printed multifunctional flexible device with an integrated motion sensor for health care monitoring. Sci. Adv. 2016, 2, e1601473–1601473. [Google Scholar] [CrossRef]
- HAIJUN, Z. , QINGYANG Y., YINGDA W., JIAJUN C.: Dynamic properties of symmetric opto thermal micro actuator. J. Micro mech. Micro eng. at press. [CrossRef]
- Kachroudi, A.; Basrour, S.; Sylvestre, A. Thermal Stability of Micro-Structured PDMS Piezo-Electrets under Various Polymeric Reticulation Ratios for Sensor Applications. Eurosensors. LOCATION OF CONFERENCE, COUNTRYDATE OF CONFERENCE; p. 310.
- Eakkachai, P. , Kanty R., Micky., and Nicolas A.,: Scanning Micro mirror Platform Based on MEMS Technology for Medical Application. Micro machines 7, 24, (2016).
- JackW Judy – Micro Electro Mechanical Systems (MEMS): fabrication, design and applications. Smart Mater. Struct. Vol.10, pp.1115–1134, (2001).
- Andrew, C. , Jongbaeg K., and Liwei L.: Bidirectional electro thermal electromagnetic actuators. J. Micro mech. Micro eng. Vol.17, pp.975–982, (2007).
- Bhushan, P.; Tomlin, C. Design of an Electromagnetic Actuator for an Insect-Scale Spinning-Wing Robot. IEEE Robot. Autom. Lett. 2020, 5, 4188–4193. [Google Scholar] [CrossRef]
- Fan, J.; Wang, S.; Yu, Q.; Zhu, Y. Experimental Study on Frog-inspired Swimming Robot Based on Articulated Pneumatic Soft Actuator. J. Bionic Eng. 2020, 17, 270–280. [Google Scholar] [CrossRef]
- Mansour, N.A.; Shin, B.; Ryu, B.; Kim, Y. Development of a Novel Miniaturized Electromagnetic Actuator for a Modular Serial Manipulator. Actuators 2021, 10, 14. [Google Scholar] [CrossRef]
- Cheng, P.; Ye, Y.; Jia, J.; Wu, C.; Xie, Q. Design of cylindrical soft vacuum actuator for soft robots. Smart Mater. Struct. 2021, 30, 045020. [Google Scholar] [CrossRef]
- Jadhav, S.; Glick, P.E.; Ishida, M.; Chan, C.; Adibnazari, I.; Schulze, J.P.; Gravish, N.; Tolley, M.T. Scalable Fluidic Matrix Circuits for Controlling Large Arrays of Individually Addressable Actuators. Adv. Intell. Syst. 2023, 5. [Google Scholar] [CrossRef]


| reference | First Author | Year | Actuation Type |
Size L*w*h (in µm) |
Operating Conditions |
|---|---|---|---|---|---|
| [36] | Chi S.P. | 1997 | Electro thermal | 1000*700*3 | 15V 2,8µN |
| [37] | Neils T. | 1998 | Electrostatic | 200*100*0,5 | 40V |
| [38] | Just E. | 1999 | SMA | 2000*3900*100 | 22mW 17mN |
| [39] | Bhailis D. | 2000 | Electromagnetic | 5000*5000*2000 | 1A 15mN |
| [05] | Volland B.E. | 2001 | Electrostatic | 3300*1250*5 | 80V 170µm Ø |
| [40] | Fuller, S.B. | 2002 | Electro thermal | / | 300 °C 5V |
| [41] | Abadie J. | 2002 | SMA | 3000*800*200 | 0,8A 68° |
| [25] | Bordatchev E.V. | 2003 | Electro thermal | 2800*1400*12,5 | 1,9V |
| [42] | Olivier. M | 2004 | Electrostatic | 1200*800*10 | 75V |
| [43] | Yang J. | 2004 | Piezoelectric | 1200*320*1,5 | 15V 16,67kHz |
| [44] | Vitorio. A | 2004 | Electrostatic | / | 400V |
| [33] | Zhang H. | 2004 | SMA | 4000*3000*290 | 1A 81µm Ø |
| [45] | Ahn | 2004 | Electromagnetic | 3500*3500 | 20mA 920Hz |
| [46] | Fu | 2004 | SMA | 2200*2200 | 5V 30mA |
| [02] | D.Piyabongkarn | 2005 | Electrostatic | 3200*3000*50 | 10V |
| [29] | C.T. Pan | 2005 | Electromagnetic | 1000*1000*10 | 5V 17,5° |
| [31] | D.H. Kim | 2005 | Electromagnetic | 15500*5220*500 | 8V 18mN |
| [47] | Mitsui | 2006 | Electromagnetic | 7400*9800 | 4.6mA 80,5Hz |
| [13] | S.K.Nah | 2007 | Piezoelectric | 36000*30000*3 | 0-100V |
| [06] | Felix. B | 2007 | Electrostatic | 7700*5600*50 | 150V 100µm Ø |
| [48] | Liu X. | 2007 | Electrostatic | 4000*4000 | 30V |
| [49] | Young-ho C. | 2007 | Electromagnetic | 4000*4000*570 | 27mA 11kHz |
| [50] | Andrew C. | 2007 | Electromagnetic | 200*2*3.5 | 4V 200µN |
| [51] | Kim | 2007 | Electromagnetic | 2400*2900 | 3V 350Hz |
| [52] | Vagia. M | 2008 | Electrostatic | 400*400 | / |
| [07] | Chen. T | 2008 | Electrostatic | 6200*3500*50 | 30V 150µm Ø |
| [53] | Gustavo.A. | 2008 | Electro thermal | 500*500*30 1000*1000*30 |
70mW 79mW |
| [54] | Guo S. | 2008 | SMA | 45000*30000*30000 | 1000µL 50 Hz |
| [55] | P. M. Nieva | 2008 | Electro thermal | 200*25*2 | 10V 3.7-13.3µm |
| [08] | Varona. J | 2009 | Electrostatic | 100*100*3,5 | 45V |
| [56] | Jia | 2009 | Electro thermal | 1000*1000 | 8V 336Hz |
| [57] | Micky.R. | 2010 | Piezoelectric | 15000*2000*300 | 100V 15mN |
| [58] | Zhu | 2011 | Piezoelectric | 2000*2000 | 2V 316Hz |
| [16] | Koh | 2011 | Piezoelectric | 5000*5000 | 9V 30Hz |
| [59] | Lan C.C. | 2011 | SMA | 45000*70000*20500 | 3.6 V 490mN |
| [60] | Liu | 2012 | Electro thermal | 2000*2000 | 0,6V 197Hz |
| [09] | Jia. Y | 2013 | Electrostatic | 6900*6500*50 | 120V |
| [61] | Q. Xu | 2013 | Piezoelectric | 26000*5000*860 | 2V 500Hz |
| [62] | Park, E.S. | 2013 | Electrostatic | 650*90*2.25 | 200°C 10Ω |
| [63] | Ren-Jung Chang | 2013 | SMA | 937*477 | 50mA 3V |
| [64] | Bessonov, A. | 2014 | Piezoelectric | 25000*1000*6.6 | / |
| [65] | A. Sharma | 2015 | Piezoelectric | 7100*2300*566 | 114Hz 54nW |
| [66] | Salem Saadon | 2015 | Piezoelectric | 2450*780*512 | 0,4V 6,8µW |
| [67] | Hussein hussein | 2015 | Electro thermal | 3200*400*100 | 15V 18V |
| [68] | Marija Cauchi | 2016 | Electro thermal | 411*45*4 | 0,22V 9µm Ø |
| [69] | Bruno Andò | 2016 | Electromagnetic | 95000*20000*140 | 4.1 Hz 37.1 mT |
| [70] | Yuki Yamamoto | 2016 | Electrostatic | 10000*10000*38 | 38mg |
| [71] | Haijun Zhang | 2017 | Electro thermal | 580*105 | 13.7 µm 2 Hz |
| [72] | Achraf Kachroudi | 2017 | Piezoelectric | 20000*20000*150 | d33=750 at 25°C |
| [73] | Yingxiang Liu | 2018 | Piezoelectric | 80800*48000*24000 | 427 mm/s |
| [27] | Marija Cauchi | 2018 | Electro thermal | 606*169*28 | 3V (5-9)µm |
| [74] | Ying Wu | 2019 | Piezoelectric | 12000*10000*8000 | 5.86 x 105 µrad/s |
| [28] | Rolend Elsen | 2019 | Electro thermal | / | 1V (55-110) µm |
| [75] | Palak Bhushan | 2020 | Electromagnetic Actuator | 4cm and weighs 133 mil-gr | voltage (<3 V) |
| [76] | Fan, J. | 2020 | Pneumatic actuator | 175000 × 100000 × 60000 | 0.01 to 0.09 |
| [77] | Nader A. Mansour | 2021 | Electromagnetic Actuator | 15000 × 15000 × 40 000 | 0 to 100 mA |
| [78] | Cheng, P. | 2021 | Vacuum buckling | 220000 | −0.002 to −0.1 MPA 0.6 to 2 HZ |
| [79] | Saurabh .Jadhav | 2023 | Pneumatic actuators | 60000 x60000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




