Phenomenological Model for Kinematic Description of the Universe

1. Introduction

The current standard cosmological model, the $\Lambda$-cold dark matter ($\Lambda$CDM) model, has been successful in explaining both the homogeneous expansion of the Universe and the 2.7 K cosmic microwave background (CMB) radiation [1]. Although $\Lambda$CDM provides a remarkable fit to most available cosmological data, it lacks the deeper underpinnings necessary to connect with fundamental physical laws. In particular, the physical evidence for inflation, dark matter (DM), and dark energy (DE) so far arises only from cosmological and astrophysical observations [2]. Moreover, as measurements become increasingly precise, discrepancies among key cosmological parameters have emerged. For example, Planck measurements of the CMB at redshift $z\approx 1100$ yield a $\Lambda$CDM-based value for the present-day Hubble constant $\left(H_0\right)$ of $67.4\pm 0.5\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$ [3,4]. In contrast, several late-time, model-independent measurements of distances and redshifts give $H_0=73.2\pm 1.3\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$ [5]. Furthermore, recent observations by the James Webb Space Telescope (JWST) indicate that the structure and masses of very early galaxies at high redshift are in strong tension with the $\Lambda$CDM model, given that the Universe’s age of about 13.8 Gyr leaves insufficient time for the formation of massive galaxies at high redshifts [6]. In addition, the tension of the curvature parameter is measured between the Planck 2018, CMB lensing, and baryon acoustic oscillation (BAO) data [4]. Especially, Planck 2018 CMB data alone indicate a strong preference for closed universes over open ones [4,7]. This result contrasts with other data sets such as Planck CMB lensing or BAO which suggest a flat universe. However, in the modern era there is a strong research community bias toward a flat universe. It should be noted that very few conclusions about the kinematics and dynamics of the universe have been drawn without relying on model assumptions, typically those of the $\Lambda$CDM model. In this predicament, it is crucial not to adhere too tightly to the standard model [2]. Consequently, the precise measurements from various astronomical missions have led to a striking tension in cosmological parameters, underscoring the strong need for alternative cosmologies to the canonical $\Lambda$CDM paradigm.

In recent decades, the application of fractional calculus in a wide range of fields—such as biology [8], quantum mechanics [9], and neuroscience [10,11]—has grown rapidly. Moreover, experimental evidence shows that anomalous diffusion, characterized by a mean-square displacement of particles $\langle r^2\left(t\right)\rangle \sim t^{\alpha }$$(\alpha \ne 1)$, is ubiquitous in nature, indicating that slow transport $\alpha <1$ may be generic for complex heterogeneous systems [12]. This type of dynamics is generally understood to arise from two distinct mechanisms [13]. The first mechanism is formulated within the framework of the generalized Langevin equation, which incorporates a slowly relaxing memory-friction term [14,15,16,17]. The second mechanism is based on the concept of continuous-time random walks (CTRW) [18,19], wherein the time dependence of the random walk is governed by a slowly decaying waiting-time distribution $\Psi \left(t\right)\sim t^{-(1+\alpha )}$ for $0<\alpha <1$, reflecting the presence of deep traps in the system [20]. A convenient description of the continuous realization of the CTRW scheme—via a random operational time known as the subordination procedure—was proposed in [21]. Comprehensive treatments of the subordinated process within the CTRW framework, along with discussions on how these approaches can be generalized for different diffusive scenarios in complex systems, are given in [22,23,24,25,26,27].

In the present paper, inspired by the Bohr model of the atom, in which electron orbitals correspond to stationary energy levels, we consider the primordial Universe as undergoing a sharp (vacuum-phase) transition at a specific internal (operational) time $\tau ={\tau }_c$ between two Einstein Universes. Each of these Universes is characterized by a distinct stationary energy level with scale factors: $\tilde{a}\left(\tau \right)=a_1=\mathrm{const}$ for $\tau <{\tau }_c$, and $\tilde{a}\left(\tau \right)=a_2=\mathrm{const}$ for $\tau >{\tau }_c$. Additionally, we assume that the ticks of the internal clock are accumulated from two independent channels of activity: one corresponding to ordinary matter and the other to dark matter. This sharp transition, described above, is treated as the parent process evolving in internal time.

To determine the scale factor $a\left(t\right)$ of the Robertson–Walker (RW) metric,

$$d{s}^2=c^{2}d{t}^2-a^2\left(t\right)\left[{\displaystyle \frac{d{r}^2}{1-k{r}^2}}+r^2\left(d{\Theta }^2+{sin}^2\Theta d{\varphi }^2\right)\right],$$

(1)

at the observable (physical) time t, we introduce an inverse Lévy-type subordinator to relate the internal and physical times. Here, c is the speed of light, r, $\Theta$, and $\varphi$ are spherical coordinates, and $k\in \{-1,0,1\}$ determines the geometry of the space. We then assume that the scale factor $a\left(t\right)$ can be obtained as the mean of $\tilde{a}\left(\tau \right)$ over an ensemble of realizations of the inverse subordinator, i.e., $a\left(t\right)=\langle \tilde{a}\left(\tau \right)\rangle .$

The main contribution of this paper is as follows. Within the framework of the proposed subordinated model, we provide exact analytical formulas for the dependence of the scale factor $a\left(t\right)$ on observable time. Based on these expressions, we find that the kinematics of $a\left(t\right)$ in physical time qualitatively mimic the well-known expansion history of the Universe through three distinct eras: inflation, decelerated expansion, and cosmic acceleration. Moreover, by invoking energy conservation, we attempt to phenomenologically include the effects of the subordinated process by describing the evolution of the matter density in the model. It is shown that this approach predicts the emergence of a time-dependent dark energy, which vanishes as $t\to \infty$. In this scenario, the accelerated expansion of the Universe eventually ceases, leading to a new period of decelerated expansion; the Universe then continues to grow forever at an ever-decreasing rate.

The structure of the paper is as follows. In Section 2, we present the proposed model. In Section 3, we derive asymptotic formulas for the scale factor $a\left(t\right)$. In Section 4, we discuss the behavior of $a\left(t\right)$ and illustrate its characteristic features. Section 5 addresses the inclusion of matter-energy in the model, deriving formulas for the evolution of the matter and dark energy densities. Section 6 offers brief concluding remarks. Finally, additional formulas are provided in the Appendixes.

2. The Model

For the reader’s convenience, we briefly summarize the main features of the subordination method in subsection 2.1, adapted from Ref. [11].

2.1. Subordination Procedure

The formulation of the subordination scheme is based on a system of coupled Langevin equations [10,21,22],

$${\displaystyle \frac{d}{d\tau }}X\left(\tau \right)=F\left(X\left(\tau \right)\right)+\xi \left(\tau \right),{\displaystyle \frac{d}{d\tau }}T\left(\tau \right)=\delta \left(\tau \right),$$

(2)

where $F\left(x\right)$ is a time-independent function, and the trajectories $y\left(t\right)=x\left(\tau \right(t\left)\right)$ of the random walk are parameterized by the variable $\tau$. The Markovian noises $\xi \left(\tau \right)$ and $\delta \left(\tau \right)$ are assumed to be independent. In the context of the CTRW scheme, $\delta \left(\tau \right)$ must be positive due to causality. Here and in the following, stochastic variables are denoted with capital letters (e.g., T), and possible values of these variables with the corresponding lowercase letters (e.g., t). The system (2) can be interpreted as a standard Langevin equation in an internal time $\tau$ that is subjected to a random time change described by the second equation. The internal time $\tau$ plays the role of the number of jumps (clock ticks) performed along the trajectory $x\left(\tau \right)$ and is successively delayed by trapping events. The physical time t is modeled by an independent process $T\left(\tau \right)$, known as the subordinator. It is the sum of independent, identically distributed random waiting time intervals between the jumps. The subordinator $T\left(\tau \right)$ is defined as a strictly increasing Lévy motion with the characteristic function

$$\langle e^{-sT\left(\tau \right)}\rangle ={\int }_0^{\infty }{e}^{-st}P(t,\tau )dt=e^{-\tau \varphi \left(s\right)},$$

(3)

where $P(t,\tau )$ is the probability density function (PDF) of $T\left(\tau \right)$, and $\varphi \left(s\right)$ is called the Lévy exponent [25]. If $\varphi \left(s\right)$ is a Bernstein function, then the subordinator $T\left(\tau \right)$ is well-defined: it starts from zero and is a pure-jump process with strictly increasing sample paths [25]. To complete the subordination procedure, an inverse subordinator $\tau \left(t\right)$ is introduced, which measures the evolution of the internal (operational) time $\tau$ as a stochastic function on physical time t and fulfills the following first passage time relation:

$$\tau \left(t\right)=\inf \{\tau >0:T(\tau )>t\}.$$

(4)

The PDF $h(t,\tau )$ of $\tau \left(t\right)$ is given by

$$h(\tau ,t)=-{\displaystyle \frac{𝜕}{𝜕\tau }}{\int }_0^{t}P(t^{\prime },\tau )d{t}^{\prime }.$$

(5)

If the Lévy exponent $\varphi \left(s\right)$ is a Bernstein function, then the inverse subordinator $\tau \left(t\right)$, which has nondecreasing continuous trajectories, can be used as a time arrow [25]. The process of primary interest, i.e., the random walk motion as seen by the observer in physical time t, is now obtained as a combined random function $Y\left(t\right)=X\left(\tau \right(t\left)\right)$. The process $X\left(\tau \right)$ is called a parent process, and the resulting process $Y\left(t\right)$ is subordinated to the parent process (referred to as the subordinated process).

2.2. Einstein Universe

The key equations of spatially homogeneous and isotropic cosmology are the Friedman equations, which are the field equations of general relativity applied to the RW metric (1):

$${\left({\displaystyle \frac{\dot{a}}{a}}\right)}^2=-{\displaystyle \frac{k{c}^2}{a^2}}+{\displaystyle \frac{\Lambda c^2}{3}}+{\displaystyle \frac{8\pi G}{3c^2}}ϵ,$$

(6)

$$\left({\displaystyle \frac{\ddot{a}}{a}}\right)={\displaystyle \frac{\Lambda c^2}{3}}-{\displaystyle \frac{4\pi G}{3c^2}}(3p+ϵ),$$

(7)

where an overdot denotes a time derivative, $ϵ$ is the total energy density of the Universe (sum of ordinary matter, radiation, dark matter), p is the total pressure (sum of pressures from each component i), and $\Lambda$ and G are the cosmological and gravitational constants, respectively [1]. As the metric (1) requires the stress-energy to take the perfect fluid form, the evolution of the energy density is governed by the ratio of pressure to energy density for each component i:

$${\gamma }_i\equiv {\displaystyle \frac{p_i}{{ϵ}_i}}.$$

(8)

Hereafter, $\gamma$ without a subscript refers to

$$\gamma \equiv {\displaystyle \frac{p}{ϵ}}={\displaystyle \frac{{\sum }_i{\gamma }_i{ϵ}_i}{{\sum }_i{ϵ}_i}}.$$

(9)

Under physically reasonable assumptions

$$ϵ>0,\gamma >-1,$$

(10)

a static solution of equations (6)-(9) is possible only if $k=1,$ i.e., the Universe is closed with a finite volume $V=2{\pi }^2{a}^3$. The corresponding solution, called the Einstein Universe, is characterized by two free parameters (a and $\gamma$) as follows:

$$ϵ={\displaystyle \frac{c^4}{4\pi G(1+\gamma )a^2}},\Lambda ={\displaystyle \frac{1+3\gamma }{(1+\gamma )a^2}}.$$

(11)

Eventually, the total energy E of the Universe is given by

$$E=Vϵ={\displaystyle \frac{\pi c^{4}a}{2G(1+\gamma )}}.$$

(12)

However, it should be noted that the Einstein Universe is unstable against expansion or contraction.

2.3. Kinematic Model for the Scale Factor

2.3.1. Fundamentals

The main assumptions of the model are as follows:

1.

Drawing an analogy with the Bohr model of the atom, we assume that the primordial Universe, in internal time $\tau$, can only exist in sharply defined stationary states with unique energies, which are described by Einstein Universes. The ability for transitions between these states is also postulated.

2.

The internal and physical times are interconnected via a Lévy-type subordinator. It is hypothesized that the corresponding Lévy exponent accounts for the aggregation of ticks from two independent clocks, representing ordinary matter and dark matter.

3.

The observable scale factor $a\left(t\right)$ in physical time t is conceptualized as the mean outcome of a scale factor jump between two stationary states of the primordial Universe, averaged over an ensemble of realizations of the inverse subordinator.

Hypothesis 3 is partially suggested from the Feynman’s path (histories) integral approach in the quantum field theory [28,29] with the difference being the use Levy distributions instead of Gaussian distributions for the set of possible paths.

2.3.2. Subordinated Scale Factor

The parent process $\tilde{a}\left(\tau \right)$ is modeled as a jump process:

$$\tilde{a}\left(\tau \right)=\left\{\begin{array}{cc}{a}_1=\mathrm{const},\hfill & \tau <{\tau }_c,\hfill \\ a_2=\mathrm{const},\hfill & \tau >{\tau }_c,\hfill \end{array}\right.$$

(13)

where $a_2\gg a_1$. Here, $\tilde{a}$ represents the scale factor of an Einstein Universe, and ${\tau }_c$ is the critical time at which the transition between these states occurs. According to Hypothesis 3 from Subsection 2.3.1, the observable scale factor can be expressed as:

$$\begin{array}{c}\hfill a\left(t\right)=\langle \tilde{a}\left(\tau \right)\rangle ={\int }_0^{\infty }\tilde{a}\left(\tau \right)h(\tau ,t)d\tau =a_1+(a_2-a_1){\int }_0^{t}P(t^{\prime },{\tau }_c)d{t}^{\prime }.\end{array}$$

(14)

This formulation uses the relationship defined in equation (5). Consequently, the expansion rate $\dot{a}\left(t\right)$ is given by:

$$\dot{a}\left(t\right)=(a_2-a_1)P(t,{\tau }_c)\approx a_{2}P(t,{\tau }_c),$$

(15)

indicating that it is proportional to the (PDF) of the subordinator $T\left({\tau }_c\right)$. Completing the model description requires specifying the structure of the Lévy exponent $\varphi \left(s\right)$, a critical component of the model. Typically, for subdiffusion phenomena, the Lévy exponent is given as:

$$\varphi \left(s\right)={\displaystyle \frac{{\left({\tau }_{0}s\right)}^{\alpha }}{{\tau }_0\Gamma (1+\alpha )}},0<\alpha <1,$$

(16)

where ${\tau }_0$, a constant, has the dimension of time, $\Gamma \left(x\right)$ is the gamma function, and $\alpha$ is known as the memory exponent [27]. In this particular case, following from Equations (3) and (5), the mean number of ticks of the internal clock within the time interval $(0,t)$ is:

$${\displaystyle \frac{\langle \tau \left(t\right)\rangle }{{\tau }_0}}={\left({\displaystyle \frac{t}{{\tau }_0}}\right)}^{\alpha },$$

(17)

and the corresponding PDF of $T\left(\tau \right)$ is:

$$P_{\alpha }(t,\tau )={\displaystyle \frac{1}{{\tau }_0}}{\left({\displaystyle \frac{{\tau }_0\Gamma (1+\alpha )}{\tau }}\right)}^{{\displaystyle \frac{1}{\alpha }}}{g}_{\alpha }\left({\displaystyle \frac{t}{{\tau }_0}}{\left({\displaystyle \frac{{\tau }_0\Gamma (1+\alpha )}{\tau }}\right)}^{{\displaystyle \frac{1}{\alpha }}}\right),$$

(18)

where $g_{\alpha }\left(x\right)$ is the one-sided $\alpha$-stable PDF [30].

As demonstrated by Ref. [30], one-sided laws $g_{\alpha }\left(x\right)$ can be transformed into non-oscillating integrals, which are more convenient for numerical calculations:

$$g_{\alpha }\left(x\right)={\displaystyle \frac{\alpha }{1-\alpha }}{x}^{-{\displaystyle \frac{1}{1-\alpha }}}{\int }_0^{1}A(\xi ;\alpha )exp\left[-x^{-{\displaystyle \frac{\alpha }{1-\alpha }}}A(\xi ;\alpha )\right]d\xi ,$$

(19)

where

$$A(\xi ;\alpha )={\displaystyle \frac{sin\left[(1-\alpha )\pi \xi \right]{\left[sin\left(\alpha \pi \xi \right)\right]}^{\frac{\alpha }{1-\alpha }}}{{\left[sin\left(\pi \xi \right)\right]}^{\frac{1}{1-\alpha }}}}.$$

(20)

To determine the Lévy exponent in our model, we consider baryon matter and dark matter as two independent escape (clock ticks) channels acting in parallel. It is assumed that for both channels, their contributions to the number of ticks of the internal clock are determined by Eq. (17), with different memory exponents: $\alpha$ for dark matter and $\beta \ne \alpha$ for baryon matter. The total mean number of escape events (ticks) of the internal clock within the time interval $(0,t)$ can be expressed as:

$${\displaystyle \frac{\langle \tau \left(t\right)\rangle }{{\tau }_0}}=\eta {\left({\displaystyle \frac{t}{{\tau }_0}}\right)}^{\alpha }+(1-\eta ){\left({\displaystyle \frac{t}{{\tau }_0}}\right)}^{\beta },$$

(21)

where the non-negative coefficient $\eta \le 1$ characterizes the relative weight of the dark matter compared to the total matter (baryon matter plus dark matter). From Eqs. (3) and (5), it follows that the Lévy exponent $\varphi \left(s\right)$ is related to the Laplace transform of the mean value $\langle \tau \left(t\right)\rangle$ through:

$${\displaystyle \frac{1}{s\varphi \left(s\right)}}={\int }_0^{\infty }{e}^{-st}\langle \tau \left(t\right)\rangle dt.$$

(22)

Thus, the appropriate Lévy exponent can be expressed as:

$$\varphi \left(s\right)={\displaystyle \frac{1}{{\tau }_0}}{\left[\eta \Gamma (1+\alpha ){\left({\tau }_{0}s\right)}^{-\alpha }+(1-\eta )\Gamma (1+\beta ){\left({\tau }_{0}s\right)}^{-\beta }\right]}^{-1}.$$

(23)

Equation (23) along with Eq. (3) completes the subordinated model for the scale factor $a\left(t\right)$, as considered in this paper. Finally, we note that properties of the $\varphi \left(s\right)$ with similar structure have been considered in [23] and [25], where it is shown that such a Lévy exponent is a Bernstein function (see also Appendix A).

3. Asymptotic Behavior of the Scale Factor

Hereafter, we assume that the memory exponent $\alpha$ for DM is much smaller than the memory exponent $\beta$ for the baryon matter, i.e.,

$$\alpha \ll \beta \approx 1.$$

(24)

In this context, it is important to note that in the specific case where $\eta =0$ and $\beta =1$, the PDF of the subordinator $T\left(\tau \right)$ reduces to a $\delta$-function:

$$P(t,\tau )=\delta (t-\tau ),$$

(25)

i.e., in the case of ideally homogeneous baryon matter distribution (without DM), the physical time and the operational time coincide. A slight deviation of $\beta$ from 1, in inequality (24) is assumed to model the heterogeneity of the baryon matter, such as the time dilation effects observed at black holes, neutron stars, etc.

3.1. The Short-Time Limit

From Eqs. (21) and (24), it follows that in the short-time limit, $t\ll {\tau }_0$ (or $s\gg 1/{\tau }_0$), the smaller memory exponent, $\alpha$, dominates. Thus, the limiting behavior of $P(t,\tau )$ for $t\ll {\tau }_0$ is related to the one-sided Lévy $\alpha$-stable PDF $g_{\alpha }\left(z\right)$ as follows (see Eqs. (18)-(20)):

$$P(t,\tau )\approx P_{\alpha }(t,\tau )={\displaystyle \frac{z}{t}}{g}_{\alpha }\left(z\right),z={\displaystyle \frac{t}{{\tau }_0}}{\left({\displaystyle \frac{{\tau }_0\eta \Gamma (1+\alpha )}{\tau }}\right)}^{{\displaystyle \frac{1}{\alpha }}}.$$

(26)

Referring to the behavior of the function $g_{\alpha }\left(z\right)$, as discussed in Refs. [30] and [31], we conclude that $P_{\alpha }(t,\tau )$ is monomodal. As t increases, $P_{\alpha }(t,\tau )$ increases exponentially from zero to a maximum, then decreases monotonically. If z is sufficiently small ($z\ll 1$), i.e.,

$${\displaystyle \frac{t}{{\tau }_0}}\ll {\left({\displaystyle \frac{\tau }{{\tau }_0\eta \Gamma (1+\alpha )}}\right)}^{{\displaystyle \frac{1}{\alpha }}},$$

(27)

the position, $t_m$, of the maximum of $P_{\alpha }(t,\tau )$ is given by (see Appendix B):

$$t_m\approx {\tau }_0{\left({\displaystyle \frac{\alpha \tau }{{\tau }_0\eta \Gamma (1+\alpha )}}\right)}^{{\displaystyle \frac{1}{\alpha }}}{\left(1+{\displaystyle \frac{\alpha }{2(1-\alpha )}}\right)}^{-{\displaystyle \frac{1-\alpha }{\alpha }}},$$

(28)

and

$$P_{\alpha }\left(t_m,\tau \right)=\sqrt{{\displaystyle \frac{e}{2\pi (1-\alpha )}}\left(1+{\displaystyle \frac{\alpha }{2(1-\alpha )}}\right)}{\displaystyle \frac{e^{-\frac{1}{\alpha }}}{t_m}}.$$

(29)

In this case, the PDF of the subordinator $T\left(\tau \right)$ is given by

$$\begin{array}{cc}\hfill P(t,\tau )& \approx P_{\alpha }(t_m,\tau ){\left({\displaystyle \frac{t_m}{t}}\right)}^{1+{\displaystyle \frac{\alpha }{2(1-\alpha )}}}exp\left\{\left({\displaystyle \frac{1}{\alpha }}-{\displaystyle \frac{1}{2}}\right)\left[1-{\left({\displaystyle \frac{t_m}{t}}\right)}^{{\displaystyle \frac{\alpha }{1-\alpha }}}\right]\right\}.\hfill \end{array}$$

(30)

The cumulative probability $G(t,\tau )$ of the subordinator can be expressed as

$$G(t,\tau )={\int }_0^{t}P(t^{\prime },\tau )d{t}^{\prime }\approx \sqrt{{\displaystyle \frac{1}{2\alpha }}}\left[1-{\displaystyle \frac{2}{\sqrt{\pi }}}{\int }_0^y{e}^{-{\xi }^2}d\xi \right],$$

(31)

where

$$y=\sqrt{{\displaystyle \frac{2-\alpha }{2\alpha }}}{\left({\displaystyle \frac{t_m}{t}}\right)}^{{\displaystyle \frac{\alpha }{2(1-\alpha )}}}.$$

(32)

Here, we emphasize that the formulas (28)-(32) are applicable only within a finite time interval, determined by the condition $t\ll {\tau }_0$ and Eq. (27). Eqs. (28)-(32) are particularly suitable for analyzing the behavior of the scale factor $a\left(t\right)$ and the expansion rate $\dot{a}\left(t\right)$ at small time values, e.g., for describing the inflation era of the Universe. Notably, from Eqs. (28) and (29), it is observed that the peak of $P(t,\tau )$ becomes more pronounced and its position $t_m$ rapidly shifts towards shorter times as the memory exponent $\alpha$ decreases.

3.2. The Long-Time Limit

In the long-time limit, where $t\gg {\tau }_0$ (or $s\to 0$), the larger memory exponent $\beta$ in Eq. (21) dominates. The limiting behavior of $P(t,\tau )$, as encoded in expression (23), yields the asymptotic form:

$$P(t,\tau )\sim {\displaystyle \frac{1}{\pi }}sin\left(\beta \pi \right){\displaystyle \frac{\tau }{(1-\eta ){\tau }_0^2}}{\left({\displaystyle \frac{{\tau }_0}{t}}\right)}^{1+\beta },t\gg {\tau }_0.$$

(33)

Thus, in this asymptotic limit, only the baryon matter contributes, causing $\dot{a}\left(t\right)$ to tend to zero like $1/t^{1+\beta }$.

Numerical investigations of the inverse Laplace transform of Eq. (3) with the Lévy exponent (23) indicate that under condition (24), a bimodal dependence of $P(t,\tau )$ on t may be generic, especially if $\tau >{\tau }_0$. Although we are not able to derive a simple estimator for the position of the second peak, $t_m^{*}$, of $P(t,\tau )$ at moderate time values, it seems that in the particular case given by Eq. (24), $t_m^{*}$ is approximately determined by:

$$t_m^{*}\approx {\displaystyle \frac{\tau }{1-\eta }},\tau >{\tau }_0.$$

(34)

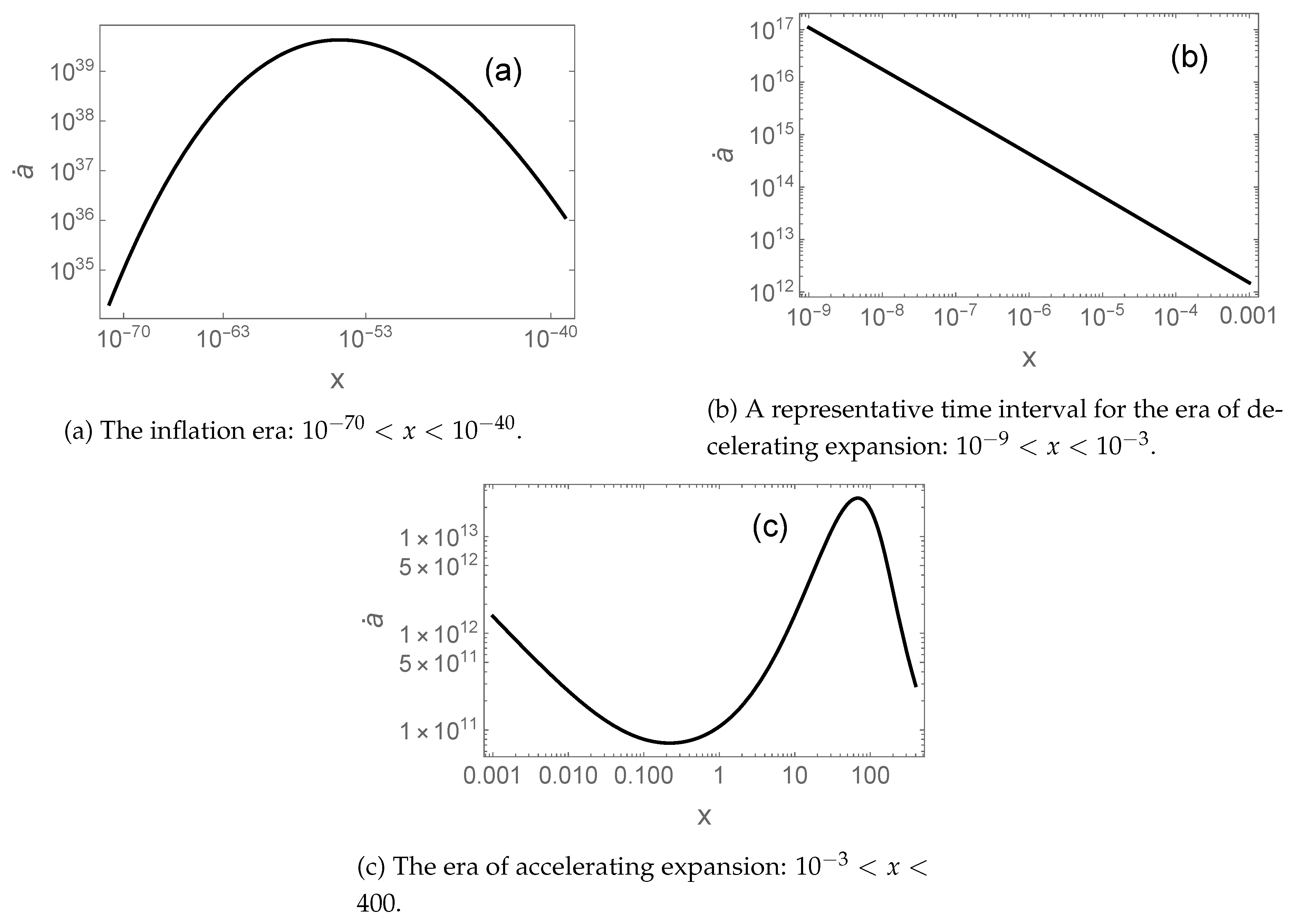
4. A Numerical Illustration of Kinematic of the Scale Factor

In the case of the Lévy exponent (23) a convinient formula for the calculation of $P(t,\tau )$ can be obtained if $\alpha <0.5$, [10,11]. In this case the appropriate contour in complex plane $\left\{s\right\}$ for the evaluation of the inverse Laplace transform of $exp(-\tau \varphi (s\left)\right)$ can be transformed to the Hankel contour with a cut along the real negative semiaxis (in the half-plane $\mathrm{Re}\left(s\right)<0$ the poles are absent). Thus, the PDF of the subordinator is given by

$$P(t,\tau )=-{\displaystyle \frac{1}{\pi }}{\int }_0^{\infty }dr{e}^{-rt}\mathrm{Im}\left[exp(-\tau \varphi (-r\left)\right)\right],\alpha <0.5.$$

(35)

Three of the most important parameters of the Universe described with the metric (1) are the values of the Hubble parameter

$$H\left(t\right)\equiv {\displaystyle \frac{\dot{a}\left(t\right)}{a\left(t\right)}},$$

(36)

and the deceleration parameter

$$q\left(t\right)\equiv -{\displaystyle \frac{\ddot{a}\left(t\right)}{a\left(t\right)H^2\left(t\right)}},$$

(37)

in the present epoch (i.e., $H_0$ and $q_0$), and the redshift $z=({\lambda }_{obs}/{\lambda }_{em})-1$ of photons (with wavelengths $\lambda$) emitted from a distant source at time t

$$z={\displaystyle \frac{a_0}{a\left(t\right)}}-1.$$

(38)

Here and below, a subscript “0” on a parameter denotes its value at the present. Our model for expansion of the Universe is described by 7 parameters: $a_1,$$a_2$, $\eta$, $\alpha$, $\beta$, ${\tau }_c$ and ${\tau }_0$. To illustrate a possible evolution of the scale factor in physical time, Eqs. (14) and (15), we specify these parameters as follows:

$$\begin{array}{cc}\hfill & a_1\approx a_{pl}=1.6\times {10}^{-33}\mathrm{cm},a_2=3\times {10}^{32}\mathrm{cm},\eta =0.85,\hfill \\ \hfill & \beta =0.92,\alpha =1/70,{\tau }_c=9.8{\tau }_0,{\tau }_0=1.09\times {10}^{17}\mathrm{s}.\hfill \end{array}$$

(39)

The parameter $a_1$ value $a_{pl}$ (Planck-length) is partly inspired by the paper [32], where the Universe was modeled as a closed RW spacetime which starts with inflation from a nonsingular state characterized by the Planck density ${\rho }_{pl}=5.2\times {10}^{93}{\mathrm{g}/\mathrm{cm}}^3$ and the Planck radius $a_{pl}$. The parameter value $\eta =0.85$, which characterizes the relative weight of the dark matter in comparison with total matter, corresponds to the observed rotation velocities of stars in galaxies, and is also required to give an account of cosmological structure formation and gravitational lensing, [1]. As mentioned in the Section 3, a slight deviation of the memory exponent $\beta =0.92$ from 1 is assumed to model heterogeneity of the baryon matter. The maximum radius $a_2$ of the Universe is a free parameter, which must be large enough to guarantee the observed fact that the Universe is nearly spatially flat [1]. The remaining parameters $\alpha$, ${\tau }_c$, and ${\tau }_0$ are chosen so that duration of the inflation era is comparable with $t_{inf}\sim {10}^{-38}$s, Eq. (28), and that the well established today’s values of $H_0=72\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$ and the age of the Universe $t_r=t\left(z_r\right)=0.38\mathrm{Myr}$, $z_r=1100$, in the epoch of last scattering, when photons and baryons decoupled, are in accordance with results computed from Eqs. (36) and (38), respectively.

Table 1 presents cosmological parameters computed from Eqs. (14), (23), and (35)-(39) for our model (OM), comparing them with the consensus $\Lambda$CDM model and the hybrid tired light model with covarying coupling constants (CCC+TL) [6].

It is remarkable that our model predicts the age of the Universe at $t_0=34.5$ Gyr, compared to the generally accepted value of 13.8 Gyr. This significant difference also extends to values $t(z=10)$ and $t(z=20)$ when compared to those predicted by the $\Lambda$CDM model. Although such discrepancies may raise concerns, they potentially resolve the “impossible early galaxy” problem identified by recent JWST observations. These observations confirm the existence of galaxies at high redshifts $(z\sim 15)$ that, according to the $\Lambda$CDM model, would have existed only about 0.3 Gyr after the Big Bang—much sooner than expected from traditional galaxy formation models [6]. Notably, the CCC+TL model [6] was developed specifically to address this issue. As evident from Table 1, both our model and the CCC+TL model predict a sufficient extension of cosmic time to allow for the formation of large galaxies at these high redshifts.

Figure 1 illustrates how the expansion rate $\dot{a}\left(t\right)$ evolves over time under the parameters specified by Eq. (39). Notably, $\dot{a}\left(t\right)$ exhibits a bimodal form, indicating significant dynamic changes in the Universe’s expansion rate at different epochs. It is seen that the evolution of the expansion rate is characterized by the following scenarios: by increasing time it starts from zero at $t=0$ and increases very rapidly to the maximum value ${\dot{a}}_{inf}=4.6\times {10}^{39}$ cm/s at $t_{inf}=1.7\times {10}^{-38}$ s. In this time interval the scale factor a, see Eqs. (14) and (31), increases from the Planck length ($\sim {10}^{-33}$ cm) to the macroscopic value $a\left(t_{inf}\right)\approx 78$ cm displaying so the inflation era of the Universe. For further increasing values of t the expansion rate decreases monotonously to a minimum ${\dot{a}}_{min}\approx 7.4\times {10}^{10}$ cm/s at $t_{min}=0.82$ Gyr $\left(z=185,q\left(t_{min}\right)=0\right)$. After that the expansion of the Universe is accelerating $\left(q\right(t)<0)$ up to the time $t_{max}=237$ Gyr at which the second maximum of the function $\dot{a}\left(t\right)$ appears, $\dot{a}\left(t_{max}\right)=2.5\times {10}^{13}\mathrm{cm}/\mathrm{s}\left(q\left(t_{max}\right)=0\right)$. At larger times, $t>t_{max}$, $\dot{a}\left(t\right)$ is again monotonically decreasing $\left(q\left(t\right)>0\right)$, and tends to zero at $t\to \infty$, $a(\infty )=a_2$.

5. Matter and Radiation in the Universe

In the proposed model, we utilize the concept of a sharp transition at an internal time $\tau ={\tau }_c$ from one Einstein Universe (EU1) with total energy $E_1$ to another (EU2) with total energy $E_2$. This approach builds on the notion that the evolution of energy in the internal time can be modeled as a jump process:

$$\tilde{E}\left(\tau \right)=\left\{\begin{array}{cc}{E}_1=\mathrm{const}.,\hfill & \tau <{\tau }_c,\hfill \\ E_2=\mathrm{const}.,\hfill & \tau >{\tau }_c.\hfill \end{array}\right.$$

(40)

Accordingly, in physical time, the total energy evolves as follows:

$$E\left(t\right)=\langle \tilde{E}\left(\tau \right)\rangle =E_1+(E_2-E_1){\int }_0^{t}P(t^{\prime },{\tau }_c)d{t}^{\prime }.$$

(41)

Given that the scale factor $a_2$ is significantly larger than $a_1=a_{pl}$ (Planck length), it is reasonable to assume that the dominant contributions to the energy in $E_2$ are from dust matter (cold dark matter plus non-relativistic baryon matter) and isotropic radiation, with pressures $p_m=0$ and $p_r={\displaystyle \frac{1}{3}}{ϵ}_r$ (where ${ϵ}_r$ is the radiation energy density), respectively. From Eqs. (8), (9), and (12), we derive:

$$E_1={\displaystyle \frac{\pi E_{pl}}{2(1+\gamma )}},E_2={\displaystyle \frac{\pi a_2{E}_{pl}}{2a_{pl}\left[1+\left(\frac{E_r}{3E_2}\right)\right]}},$$

(42)

where $E_{pl}$ is the Planck energy and $E_r$ represents the total energy of radiation and relativistic particles in $E_2$, with $E_{pl}/a_{pl}={\displaystyle \frac{c^4}{G}}$.

To proceed further, it is reasonable divide the energy density $ϵ\left(t\right)$ into three parts

$$ϵ\left(t\right)={\displaystyle \frac{E\left(t\right)}{2{\pi }^2{a}^3\left(t\right)}}={ϵ}_m\left(t\right)+{ϵ}_r\left(t\right)+{ϵ}_t\left(t\right),$$

(43)

where ${ϵ}_m\left(t\right)$, ${ϵ}_r\left(t\right)$, and ${ϵ}_t\left(t\right)$ correspond to dust-matter, radiation, and DE, respectively. Using the energy conservation for each component separately

$$d\left(a^3\left(t\right){ϵ}_i\left(t\right)\right)=-p_{i}d\left(a^3\left(t\right)\right),$$

(44)

the expanding Universe analogue of the first law of thermodynamics $(dE=-pdV)$, one can write

$${ϵ}_m\left(t\right)={ϵ}_m\left(t_0\right){\left({\displaystyle \frac{a_0}{a\left(t\right)}}\right)}^3,{ϵ}_r\left(t\right)={ϵ}_r\left(t_0\right){\left({\displaystyle \frac{a_0}{a\left(t\right)}}\right)}^4.$$

(45)

In addition to these equations we define two parameters

$$\rho \equiv {\displaystyle \frac{{ϵ}_r\left(t_0\right)}{{ϵ}_m\left(t_0\right)}},\kappa ={\displaystyle \frac{{ϵ}_m\left(t_0\right)}{{ϵ}_t\left(t_0\right)}},$$

(46)

which can be estimated via observations. In the consensus cosmological model presented in [1] the current values of these parameters are given by $\rho \approx 0.8\times {10}^{-4}$ and $\kappa \approx 0.33$. With the help of Eqs. (14) and (41)-(46), it is possible to express the energy densities ${ϵ}_i\left(t\right)$ and the state-parameter $\gamma$ as (see also Appendix C)

$${ϵ}_m\left(t\right)={\displaystyle \frac{a_2{E}_{pl}}{4\pi a_{pl}{a}^3\left(t\right)}}·{\displaystyle \frac{1}{\left[1+\frac{4}{3}\rho \frac{a_0}{a_2}\right]}},{ϵ}_r\left(t\right)={\displaystyle \frac{\rho a_0}{a\left(t\right)}}{ϵ}_m\left(t\right),$$

(47)

$${ϵ}_t\left(t\right)=\rho {ϵ}_m\left(t\right)\left(1-{\displaystyle \frac{a\left(t\right)}{a_2}}\right)\left[1-{\displaystyle \frac{a_0}{a\left(t\right)}}+{\displaystyle \frac{1}{\kappa \rho }}{\left(1-{\displaystyle \frac{a_0}{a_2}}\right)}^{-1}\right],$$

(48)

and

$$\begin{array}{c}\hfill \gamma =-1+{\displaystyle \frac{a_{pl}}{a_2}}\left[1+{\displaystyle \frac{4}{3}}\rho {\displaystyle \frac{a_0}{a_2}}\right]{\left\{1+\rho {\displaystyle \frac{a_0}{a_2}}+\left(1-{\displaystyle \frac{a_{pl}}{a_2}}\right)\left[\rho +{\displaystyle \frac{1}{\kappa }}{\left(1-{\displaystyle \frac{a_0}{a_2}}\right)}^{-1}\right]\right\}}^{-1}.\end{array}$$

(49)

Let us take, to be specific, the parameter values from Eq. (39); in this case $a_0=6.6\times {10}^{29}\mathrm{cm}\ll a_2$. In the case of large time, $t\to \infty$, the contribution of the EU2 to $E\left(t\right)$ is dominant

$$E(\infty )=E_2\approx {\displaystyle \frac{\pi a_2{E}_{pl}}{2a_{pl}}}\approx 5.7\times {10}^{81}\mathrm{erg}$$

(50)

and the density of the DE tends to zero, ${ϵ}_t(\infty )=0$, indicating that the DE is generated by a contribution of the primordial EU1 to $E\left(t\right)$. For limiting values of the energy densities ${ϵ}_m\left(t\right)$ and ${ϵ}_r\left(t\right)$ we obtain

$$\begin{array}{cc}\hfill {ϵ}_m(\infty )& \approx {\displaystyle \frac{E_{pl}}{4\pi a_{pl}{a}_2^2}}\approx 1.06\times {10}^{-17}\mathrm{erg}{\mathrm{cm}}^{-3},\hfill \\ \hfill {ϵ}_r(\infty )& ={\displaystyle \frac{\rho a_0}{a_2}}{ϵ}_m(\infty )\approx 1.8\times {10}^{-7}{ϵ}_m(\infty ).\hfill \end{array}$$

(51)

Thus in this epoch the dust-matter (cold DM + nonrelativistic baryon matter) dominates. It is notable that corresponding value of the cosmological constant ${\Lambda }_2$ in the Einstein Universe is very small (see also Eq. (11)).

$${\Lambda }_2=1.1\times {10}^{-65}{\mathrm{cm}}^{-2}.$$

(52)

We will now consider the behavior of the energy $E\left(t\right)$ at short-time limit, $t\to 0$, where the contribution of the primordial Einstein Universe (with $E_1$) to $E\left(t\right)$ dominates. In the parameter regime described by Eq. (39), from Eq. (49) we get

$$\gamma \approx -1+{\displaystyle \frac{a_{pl}}{a_2}}·{\displaystyle \frac{\kappa }{1+\kappa }},$$

(53)

so that in this Einstein Universe the universe matter had an equation of state

$$p\approx -ϵ,$$

(54)

which is usually assumed by inflation models (see, e.g., [1] and [32]). Because this, in the very early period of the Universe, the matter behaved very differently from the matter we know. In the short-time limit, $t\to 0$, from Eqs. (11), (12), (41), and (53) it follows that

$$E\left(0\right)=E_1\approx {\displaystyle \frac{1+\kappa }{\kappa }}{E}_2\approx 4E_2,$$

(55)

with $ϵ\left(0\right)\approx 2.8\times {10}^{179}\mathrm{erg}{\mathrm{cm}}^{-3}$ and

$${\Lambda }_1\approx -{\displaystyle \frac{2a_2}{a_{pl}^3}}\left({\displaystyle \frac{1+\kappa }{\kappa }}\right)\approx -6\times {10}^{131}{\mathrm{cm}}^{-2}.$$

(56)

It is somewhat surprising that the described model predicts a transition from a higher energy level $E_1$ to a lower one $E_2$, with $E_1>E_2$. At first glance, Eq. (12) seems to suggest that energy E increases as the scale factor a increases. However, this conclusion is misleading because it does not consider potential changes in the equations of state. The estimated value of $ϵ\left(0\right)\approx 2.8\times {10}^{179}\mathrm{erg}{\mathrm{cm}}^{-3}$ greatly exceeds the Planck density ${ϵ}_{pl}\approx 4.6\times {10}^{114}\mathrm{erg}{\mathrm{cm}}^{-3}$. This suggests that the classical description may not hold for such extreme densities, indicating the need for a quantum gravity theory—which remains undeveloped—to unify gravity with other fundamental interactions as suggested by [1].

Given this situation, we consider two possibilities. The first is that the model proposed here may only be applicable after a certain time, $t>t_1\sim {10}^{-49}$ seconds, where $ϵ\left(t_1\right)⩾{ϵ}_{pl}$. It is remarkable that the time interval $(0,t_1)$ is much shorter as the Planck time $t_{pl}=5.391\ast {10}^{-44}$ s. The second possibility involves interpreting the cosmological constant $\Lambda$ in Eqs. (6) and (7) as a representation of vacuum energy, with an energy density given by:

$${ϵ}_{vac}={\displaystyle \frac{c^4}{8\pi G}}\Lambda ={\displaystyle \frac{1}{8\pi }}{\displaystyle \frac{E_{pl}}{a_{pl}}}\Lambda ,$$

(57)

where the vacuum pressure $p_{vac}=-{ϵ}_{vac}$. Consequently, the total energy density of an Einstein Universe can be expressed as:

$${ϵ}_{tot}=ϵ+{ϵ}_{vac}={\displaystyle \frac{3E_{pl}}{8\pi a_{pl}{a}^2}}.$$

(58)

It should be noted that the value of ${ϵ}_{1vac}$, corresponding to the very large magnitude of the cosmological constant ${\Lambda }_1$ from Eq. (56), aligns with some estimates from quantum field theory for the energy density associated with the quantum vacuum. Within the $\Lambda$CDM model, such a significant quantum vacuum energy density presents a well-known issue—referred to as the cosmological constant problem—where the quantum vacuum energy density exceeds the density predicted by the $\Lambda$CDM model by approximately 120 orders of magnitude [1].

In our proposed model, the total energy density ${ϵ}_{1tot}$, corresponding to ${\Lambda }_1$, is on the order of the Planck density:

$${ϵ}_{1tot}=\left({\displaystyle \frac{3}{8\pi }}\right){ϵ}_{pl},$$

(59)

and the total energy of EU1 is given by:

$$E_{tot}\left(0\right)=E_{1tot}={\displaystyle \frac{3\pi }{4}}{E}_{pl}.$$

(60)

To an observer, the universe appears to begin expanding at time $t=0$ from a state characterized by the Planck scale factor $a_{pl}$, the Planck energy density ${ϵ}_{pl}$, and the total mass of the universe being the Planck mass $M_{pl}=E_{pl}/c^2$ (approximately $2.2\times {10}^{-5}$ g). It remains an open question whether our model can shed light on the vacuum-energy problem in cosmology.

Finally, our analysis is restricted to a single transition between two stationary states of the parent process (refer to Eq.(13)). Here, the model predicts that the accelerated expansion of the universe eventually ceases, followed by perpetual expansion at an ever-decreasing rate. Our findings serve as a promising foundation for exploring more elaborate models. For example, the model could be extended to include an inverse transition from EU2 back to EU1 at a specific internal time ${\tau }_c^{*}>{\tau }_c$. According to this version, the universe would reach a maximum radius before contracting back to EU1, allowing the cycle of expansion and contraction to repeat, akin to features proposed in recent cyclic models of the universe [33].

6. Conclusion

We believe that this paper introduces a novel application of fractional calculus to cosmology. Our proposed model, a singularity-free and spatially closed universe characterized by a bifractional Lévy exponent, qualitatively captures the principal phases of the universe’s expansion: inflation, subsequent decelerated expansion, cosmic acceleration, and potential future deceleration. Within this model, dark energy (DE) emerges as an imprint of the primary Einstein Universe, characterized by Planck-scale radius and total mass, including the mass associated with the vacuum.

The model demonstrates that the time dependence of the DE density is nonmonotonic, initially increasing before eventually vanishing at large times. Intriguingly, it suggests potential resolutions to the “impossible early galaxy” problem, as recently highlighted by JWST observations, and the “large cosmological constant” problem, which challenge the conventional $\Lambda$CDM model.

However, for this “multiverse” model to be considered a viable alternative to the $\Lambda$CDM framework, it must undergo rigorous testing against empirical data. This includes fitting the model to Type Ia supernova data, as compiled in Ref. [34], and assessing its compatibility with observations related to the Cosmic Microwave Background (CMB), structure formation, big-bang nucleosynthesis, and baryonic acoustic oscillations, as well as how well it aligns with Planck data [4]. Whether or not the present model can be made consistent with the wealth of precision cosmological data remains to be seen. Finally, we like to point out that this work is only a preliminary study and we hope that it will stimulate deeper investigations of applicability of fractional calculus in cosmology.