Differential Quasilinearization Method for Solving Initial Value Problems of Ordinary Differential Equations

1. Introduction

It is often challenging to obtain analytical solutions to ordinary differential equations (ODEs), leading to the development of various methods for finding approximate solutions^1–10. These approximation methods can be categorized into two main types: numerical methods and analytical methods. Analytical methods, in particular, are widely used in solving many scientific and engineering problems due to their straightforward formulation, good continuity, and clearer physical interpretation.

Among the analytical methods, successive approximation techniques are especially valued for their simplicity, broad applicability, and controllable accuracy. As a result, they have garnered increasing attention from researchers across various fields. Notable successive approximation methods include the Picard iteration method^5,11,12, the Adomian decomposition method (ADM) ^6,7,13–16, the homotopy analysis method (HAM) ^8,17–21, the variational iteration method (VIM) ^10,22–25, and the quasilinearization method ¹². However, these methods typically require that the equation(s) be explicit or have a linear differential operator, that is, the equation(s) can be written in the following form

$$\begin{array}{c}L\left[y\left(x\right)\right]=N[x,y\left(x\right)]\end{array}$$

(1)

where $L$ is a linear differential operator and $N$ is either a linear or nonlinear operator. For example, consider the equation:

$$\begin{array}{c}{\displaystyle \frac{dy}{dx}}=f(x,y)\end{array}$$

(2)

In this case, the linear differential operator $L$ can be expressed as:

$$\begin{array}{c}L={\displaystyle \frac{d}{dx}}\end{array}$$

(3)

The operator $N$ can be expressed as:

$$\begin{array}{c}N=f(.,.)\end{array}$$

(4)

Similarly, for the equation:

$$\begin{array}{c}{y}^{‴}+{3y}^{″}+2y^{\prime }=g(x,y,y^{\prime })\end{array}$$

(5)

The linear differential operator $L$ can be expressed as:

$$\begin{array}{c}L={\displaystyle \frac{d^3}{d{x}^3}}+3{\displaystyle \frac{d^2}{d{x}^2}}+2{\displaystyle \frac{d}{dx}}\end{array}$$

(6)

The operator $N$ can be expressed as:

$$\begin{array}{c}N=g(.,.,.)\end{array}$$

(7)

In this work, the differential quasilinearization method (DQM), free from the previously mentioned limitations, is presented for solving initial value problems of ordinary differential equations (ODEs), especially for implicit or nonlinear cases. The validity of this method are verified through two examples.

2. The basic principle of differential quasilinearization method

2.1. Quasilinearization of ordinary differential equations

To illustrate the basic concept of the DQM, we consider the following general system of ODEs:

$$\begin{array}{c}\mathit{F}\left(\mathit{Y},x\right)=0\end{array}$$

(8)

subject to the initial condition:

$$\begin{array}{c}\mathit{G}\left(\mathit{Y}\left(x_0\right)\right)=0\end{array}$$

(9)

where:

$$\begin{array}{c}\mathit{Y}=\left(\begin{array}{c}{\mathit{y}}^{\left(\mathit{n}\right)}\\ {\mathit{y}}^{\left(\mathit{n}-1\right)}\\ ⋮\\ {\mathit{y}}^{\prime }\\ \mathit{y}\end{array}\right)\end{array}$$

(10)

$$\begin{array}{c}\mathit{y}=\left(\begin{array}{c}{y}_m\\ y_{m-1}\\ ⋮\\ y_2\\ y_1\end{array}\right)\end{array}$$

(11)

$\mathit{F}\left(\mathit{Y},x\right)$ and $\mathit{G}\left(\mathit{Y}\left(x_0\right)\right)$ are considered as column vectors. Taking the derivative of both sides of Equation (2.1), we obtain:

$$\begin{array}{c}{\displaystyle \frac{𝜕\mathit{F}\left(\mathit{Y},x\right)}{𝜕\mathit{Y}}}{\mathit{Y}}^{\prime }\left(x\right)+{\displaystyle \frac{𝜕\mathit{F}(\mathit{Y},x)}{𝜕x}}=0\end{array}$$

(12)

If the ${\displaystyle \frac{𝜕\mathit{F}\left(\mathit{Y},x\right)}{𝜕\mathit{Y}}}$ and ${\displaystyle \frac{𝜕\mathit{F}(\mathit{Y},x)}{𝜕x}}$ are regarded as known functions with respect to $x$, Equation (2.5) can be treated as a system of linear ODEs. Consequently, the initial value problem described by Equations (2.1) and (2.2) is converted to the initial value problem of ODEs with a linear differential operator, as follows:

$$\begin{array}{c}\left\{\begin{array}{c}{\displaystyle \frac{𝜕\mathit{F}\left(\mathit{Y},x\right)}{𝜕\mathit{Y}}}{\mathit{Y}}^{\prime }\left(x\right)+{\displaystyle \frac{𝜕\mathit{F}(\mathit{Y},x)}{𝜕x}}=0\\ \mathit{F}\left(\mathit{Y}\left(x_0\right),x_0\right)=0\\ \mathit{G}\left(\mathit{Y}\left(x_0\right)\right)=0\end{array}\right.\end{array}$$

(13)

The existence and uniqueness of the solution to the initial value problem (2.6) can be determined by the principle of contraction mapping or the Picard–Lindelöf theorem¹¹. Successive approximations of the solution can then be obtained using the Picard iteration method or other established methods applicable to ODEs with a linear part¹¹.

2.2. Quasilinearization recursion equations of ODEs

To solve the initial value problem described by Equation (2.6), we aim to construct a sequence of vector-valued functions $\left\{{\mathit{\phi }}_{\left(i\right)}\left(x\right)\right\}$ that converges to the solution of this initial value problem, such that:

$$\begin{array}{c}\underset{i\to \infty }{\lim }{\mathit{\phi }}_{\left(i\right)}\left(x\right)=\mathit{\phi }\left(x\right)\end{array}$$

(2.7)

$$\begin{array}{c}{\displaystyle \frac{𝜕\mathit{F}\left(\mathbf{\Phi },x\right)}{𝜕\mathbf{\Phi }}}{\mathbf{\Phi }}^{\prime }\left(x\right)+{\displaystyle \frac{𝜕\mathit{F}(\mathbf{\Phi },x)}{𝜕x}}=0\end{array}$$

(2.8)

where:

$$\begin{array}{c}\mathbf{\Phi }=\left(\begin{array}{c}{\mathit{\phi }}^{\left(\mathit{n}\right)}\\ {\mathit{\phi }}^{\left(\mathit{n}-1\right)}\\ ⋮\\ {\mathit{\phi }}^{\prime }\\ \mathit{\phi }\end{array}\right)\end{array}$$

(2.9)

$$\begin{array}{c}\mathit{\phi }=\left(\begin{array}{c}{\phi }_m\\ {\phi }_{m-1}\\ ⋮\\ {\phi }_2\\ {\phi }_1\end{array}\right)\end{array}$$

(2.10)

$$\begin{array}{c}{\mathit{\phi }}_{\left(i\right)}=\left(\begin{array}{c}{\phi }_{\left(i\right),m}\\ {\phi }_{\left(i\right),m-1}\\ ⋮\\ {\phi }_{\left(i\right),2}\\ {\phi }_{\left(i\right),1}\end{array}\right)\end{array}$$

(2.11)

By substituting the components of $\mathit{\phi }$ with the components in the corresponding dimension of element(s) in $\left\{{\mathit{\phi }}_{\left(i\right)}\left(x\right)\right\}$, a recurrence equation based on Equation (2.8) can be obtained:

$$\begin{array}{c}\mathit{A}\left({\mathbf{\Phi }}_{\left(k-1\right)},\cdots ,{\mathbf{\Phi }}_{\left(i\right)},\cdots ,{\mathbf{\Phi }}_{\left(0\right)},x\right){\mathbf{\Phi }}_{\left(k\right)}^{\prime }=\mathit{G}\left({\mathbf{\Phi }}_{\left(k-1\right)},\cdots ,{\mathbf{\Phi }}_{\left(i\right)},\cdots ,{\mathbf{\Phi }}_{\left(0\right)},x\right)\end{array}$$

(2.12)

where:

$$\begin{array}{c}{\mathbf{\Phi }}_{\left(i\right)}=\left(\begin{array}{c}{\mathit{\phi }}_{\left(i\right)}^{\left(\mathit{n}\right)}\\ {\mathit{\phi }}_{\left(i\right)}^{\left(\mathit{n}-1\right)}\\ ⋮\\ {\mathit{\phi }}_{\left(i\right)}^{\prime }\\ {\mathit{\phi }}_{\left(i\right)}\end{array}\right)\end{array}$$

(2.13)

Each term in the sequence $\left\{{\mathit{\phi }}_{\left(i\right)}\left(x\right)\right\}$ can typically be deduced successively. It is important to note that in Equation (2.12), the largest subscript of ${\mathbf{\Phi }}_{\left(i\right)}$ in $\mathit{A}\left({\mathbf{\Phi }}_{\left(k-1\right)},\cdots ,{\mathbf{\Phi }}_{\left(i\right)},\cdots ,{\mathbf{\Phi }}_{\left(0\right)},x\right)$ and $\mathit{G}\left({\mathbf{\Phi }}_{\left(k-1\right)},\cdots ,{\mathbf{\Phi }}_{\left(i\right)},\cdots ,{\mathbf{\Phi }}_{\left(0\right)},x\right)$ must be smaller than $k$. In addition, the elements of $\left\{{\mathit{\phi }}_{\left(i\right)}\left(x\right)\right\}$ must satisfy the initial conditions:

$$\begin{array}{c}\left\{\begin{array}{c}\mathit{F}\left({\mathbf{\Phi }}_{\left(i\right)}\left(x_0\right),x_0\right)=0\\ \mathit{G}\left({\mathbf{\Phi }}_{\left(i\right)}\left(x_0\right)\right)=0\end{array}\right.\end{array}$$

(2.14)

and an initial guess for ${\mathit{\phi }}_{\left(0\right)}$ is required. By substituting the known elements of $\left\{{\mathit{\phi }}_{\left(i\right)}\left(x\right)\right\}$ with smaller subscripts ($k-1$, $k-2$, …, $0$) into the recursive Equation (2.12), the Equation can be viewed as a linear Equation with respect to ${\mathbf{\Phi }}_{\left(k\right)}^{\prime }$ Thus, ${\mathit{\phi }}_{\left(i\right)}$ can typically be obtained by solving a system of linear differential equations. Repeating this process allows us to obtain any term in the sequence $\left\{{\mathit{\phi }}_{\left(i\right)}\left(x\right)\right\}$. If the initial value problem described by Equation (2.6) has a unique solution, ${\mathit{\phi }}_{\left(i\right)}$ can be regarded as an approximate solution to the initial value problem.

3. A simplified version of the differential quasilinearization method: converting to lower-order quasilinear ODEs and recursive equations

3.1. General system of ODEs

Even linear ODEs can be challenging to solve when the order is relatively high, although they are generally simpler than nonlinear ODEs. To simplify the problem, Equation (2.5) can be transformed into a system of lower-order ODEs, ideally first-order ODEs.

Let:

$$\begin{array}{c}\left\{\begin{array}{c}{\mathit{y}}^{\prime }={\mathit{y}}_1\\ {\mathit{y}}_1^{\prime }={\mathit{y}}_2\\ ⋮\\ {\mathit{y}}_{n-1}^{\prime }={\mathit{y}}_n\end{array}\right.\end{array}$$

(3.1)

then:

$$\begin{array}{c}\mathit{Y}=\left(\begin{array}{c}{\mathit{y}}_n\\ {\mathit{y}}_{n-1}\\ ⋮\\ {\mathit{y}}_1\\ \mathit{y}\end{array}\right)\end{array}$$

(3.2)

$$\begin{array}{c}{\mathit{Y}}^{\prime }=\left(\begin{array}{c}{\mathit{y}}_n^{\prime }\\ {\mathit{y}}_n\\ ⋮\\ {\mathit{y}}_2\\ {\mathit{y}}_1\end{array}\right)\end{array}$$

(3.3)

Thus, Equation (2.5) can be converted into the following first-order ODEs:

$$\begin{array}{c}\left\{\begin{array}{c}{\mathit{y}}^{\prime }={\mathit{y}}_1\\ {\mathit{y}}_1^{\prime }={\mathit{y}}_2\\ ⋮\\ {\mathit{y}}_{n-1}^{\prime }={\mathit{y}}_n\\ {\displaystyle \frac{𝜕\mathit{F}\left(\mathit{Y},x\right)}{𝜕\mathit{Y}}}{\mathit{Y}}^{\prime }\left(x\right)+{\displaystyle \frac{𝜕\mathit{F}(\mathit{Y},x)}{𝜕x}}=0\end{array}\right.\end{array}$$

(3.4)

and the initial value problem expressed in Equation (2.6) can be transformed into:

$$\begin{array}{c}\left\{\begin{array}{c}{\mathit{y}}^{\prime }={\mathit{y}}_1\\ {\mathit{y}}_1^{\prime }={\mathit{y}}_2\\ ⋮\\ {\mathit{y}}_{n-1}^{\prime }={\mathit{y}}_n\\ {\displaystyle \frac{𝜕\mathit{F}\left(\mathit{Y},x\right)}{𝜕\mathit{Y}}}{\mathit{Y}}^{\prime }\left(x\right)+{\displaystyle \frac{𝜕\mathit{F}(\mathit{Y},x)}{𝜕x}}=0\\ \mathit{F}\left(\mathit{Y}\left(x_0\right),x_0\right)=0\\ \mathit{G}\left(\mathit{Y}\left(x_0\right)\right)=0\end{array}\right.\end{array}$$

(3.5)

where the expressions for $\mathit{Y}$ and ${\mathit{Y}}^{\prime }$ are shown in Equations (3.2) and (3.3), respectively. Next, proceed with the method outlined in last section for further processing. To provide a more intuitive introduction to the simplified version of DQM, first-order ODE and system of first-order ODEs will be used as examples for a more detailed discussion in the following sections.

3.2. First order ODE

For example, consider the ODE:

$$\begin{array}{c}F(y^{\prime },y,x)=0\end{array}$$

(3.6)

subject to the initial condition:

$$\begin{array}{c}y\left(x_0\right)=y_0\end{array}$$

(3.7)

where $F$ has continuous partial derivatives with respect to $y^{\prime },y$, and $x$, and $y$ has continuous second derivatives.

The solution can be found by combining Equations (3.6) and (3.7):

$$\begin{array}{c}{y}^{\prime }\left(x_0\right)=\phi \left(x_0,y_0\right)\end{array}$$

(3.8)

If the solution is not unique, separate cases need to be considered. Taking the derivative of both sides of Equation (3.6), we obtain:

$$\begin{array}{c}{\displaystyle \frac{𝜕F}{𝜕y^{\prime }}}{y}^{″}+{\displaystyle \frac{𝜕F}{𝜕y}}{y}^{\prime }+{\displaystyle \frac{𝜕F}{𝜕x}}=0\end{array}$$

(3.9)

Let

$$\begin{array}{c}{y}^{\prime }=z\end{array}$$

(3.10)

then Equation (3.9) can be rewritten as:

$$\begin{array}{c}{\displaystyle \frac{𝜕F}{𝜕z}}{z}^{\prime }+{\displaystyle \frac{𝜕F}{𝜕y}}z+{\displaystyle \frac{𝜕F}{𝜕x}}=0\end{array}$$

(3.11)

If:

$$\begin{array}{c}{\displaystyle \frac{𝜕F}{𝜕z}}\ne 0\end{array}$$

(3.12)

then from Equation (3.11), it follows that:

$$\begin{array}{c}{z}^{\prime }=-{\displaystyle \frac{1}{\frac{𝜕F}{𝜕z}}}\left({\displaystyle \frac{𝜕F}{𝜕y}}z+{\displaystyle \frac{𝜕F}{𝜕x}}\right)\end{array}$$

(3.13)

For points that do not satisfy Inequality (3.12), from the previous continuity condition, the left side of Equation (3.13) equals the limit of the right side as $x$ approaches the corresponding points. Let:

$$\begin{array}{c}\left\{\begin{array}{c}\mathit{y}=\left(\begin{array}{c}y\\ z\end{array}\right)\\ f\left(x,\mathit{y}\right)=\left(\begin{array}{c}z\\ -{\displaystyle \frac{1}{\frac{𝜕F}{𝜕z}}}\left({\displaystyle \frac{𝜕F}{𝜕y}}z+{\displaystyle \frac{𝜕F}{𝜕x}}\right)\end{array}\right)\end{array}\right.\end{array}$$

(3.14)

Equations (3.10) and (3.13) form a system of differential equations that can be expressed in vector notation as:

$$\begin{array}{c}{\displaystyle \frac{d\mathit{y}}{dx}}=\mathit{f}(x,\mathit{y})\end{array}$$

(3.15)

Let:

$$\begin{array}{c}{\mathit{y}}_0=\left(\begin{array}{c}{y}_0\\ y^{\prime }\left(x_0\right)\end{array}\right)\end{array}$$

(3.16)

According to Equations (3.7), (3.10), and (3.14), we have

$$\begin{array}{c}\mathit{y}\left(x_0\right)={\mathit{y}}_0\end{array}$$

(3.17)

Hence, the initial value problem described by Equations (3.6) and (3.7) is transformed into:

$$\begin{array}{c}\left\{\begin{array}{c}{\displaystyle \frac{d\mathit{y}}{dx}}=\mathit{f}(x,\mathit{y})\\ \mathit{y}\left(x_0\right)={\mathit{y}}_0\end{array}\right.\end{array}$$

(3.18)

The Picard–Lindelöf theorem provides the conditions under which the initial value problem described by Equation (3.18) has a unique solution, and successive approximations of the solution can be obtained using the Picard iteration method¹¹.

3.3. System of first order ODEs

Consider the system of ODEs:

$$\begin{array}{c}\left\{\begin{array}{c}F(y^{\prime },z^{\prime },y,z,x)=0\\ G(y^{\prime },z^{\prime },y,z,x)=0\end{array}\right.\end{array}$$

(3.19)

subject to the initial conditions:

$$\begin{array}{c}\left\{\begin{array}{c}y\left(x_0\right)=y_0\\ z\left(x_0\right)=z_0\end{array}\right.\end{array}$$

(3.20)

where $F$ and $G$ have continuous partial derivatives with respect to $y^{\prime },z^{\prime },y,z,x$ and both $y$ and $z$ have continuous second derivatives.

From Equations (3.19) and (3.20), we obtain:

$$\begin{array}{c}\left\{\begin{array}{c}F(y^{\prime }\left(x_0\right),z^{\prime }\left(x_0\right),y_0,z_0,x_0)=0\\ G(y^{\prime }\left(x_0\right),z^{\prime }\left(x_0\right),y_0,z_0,x_0)=0\end{array}\right.\end{array}$$

(3.21)

These equations can be solved to find:

$$\begin{array}{c}\left\{\begin{array}{c}{y}^{\prime }\left(x_0\right)=g\left(x_0,y_0\right)\\ z^{\prime }\left(x_0\right)=h\left(x_0,y_0\right)\end{array}\right.\end{array}$$

(3.22)

Similar to the case discussed in last subsection, if the solution is not unique, separate cases need to be considered. Differentiating both sides of Equation (3.19), we get:

$$\begin{array}{c}\left\{\begin{array}{c}{\displaystyle \frac{𝜕F}{𝜕y^{\prime }}}{y}^{″}+{\displaystyle \frac{𝜕F}{𝜕z^{\prime }}}{z}^{″}+{\displaystyle \frac{𝜕F}{𝜕y}}{y}^{\prime }+{\displaystyle \frac{𝜕F}{𝜕z}}{z}^{\prime }+{\displaystyle \frac{𝜕F}{𝜕x}}=0\\ {\displaystyle \frac{𝜕G}{𝜕y^{\prime }}}{y}^{″}+{\displaystyle \frac{𝜕G}{𝜕z^{\prime }}}{z}^{″}+{\displaystyle \frac{𝜕G}{𝜕y}}{y}^{\prime }+{\displaystyle \frac{𝜕G}{𝜕z}}{z}^{\prime }+{\displaystyle \frac{𝜕G}{𝜕x}}=0\end{array}\right.\end{array}$$

(3.23)

Let:

$$\begin{array}{c}\left\{\begin{array}{c}{y}^{\prime }=u\\ z^{\prime }=v\end{array}\right.\end{array}$$

(3.24)

Substituting these into Equation (3.23), we can rewrite it as:

$$\begin{array}{c}\left\{\begin{array}{c}{\displaystyle \frac{𝜕F}{𝜕u}}{u}^{\prime }+{\displaystyle \frac{𝜕F}{𝜕v}}{v}^{\prime }+{\displaystyle \frac{𝜕F}{𝜕y}}u+{\displaystyle \frac{𝜕F}{𝜕z}}v+{\displaystyle \frac{𝜕F}{𝜕x}}=0\\ {\displaystyle \frac{𝜕G}{𝜕u}}{u}^{\prime }+{\displaystyle \frac{𝜕G}{𝜕v}}{v}^{\prime }+{\displaystyle \frac{𝜕G}{𝜕y}}u+{\displaystyle \frac{𝜕G}{𝜕z}}v+{\displaystyle \frac{𝜕G}{𝜕x}}=0\end{array}\right.\end{array}$$

(3.25)

If:

$$\begin{array}{c}\left|\begin{array}{cc}{\displaystyle \frac{𝜕F}{𝜕u}}& {\displaystyle \frac{𝜕F}{𝜕v}}\\ {\displaystyle \frac{𝜕G}{𝜕u}}& {\displaystyle \frac{𝜕G}{𝜕v}}\end{array}\right|\ne 0\end{array}$$

(3.26)

then Equation (3.25) can be solved to find:

$$\begin{array}{c}\left\{\begin{array}{c}{u}^{\prime }=-{\displaystyle \frac{\left|\begin{array}{cc}\frac{𝜕F}{𝜕y}u+\frac{𝜕F}{𝜕z}v+\frac{𝜕F}{𝜕x}& \frac{𝜕F}{𝜕v}\\ \frac{𝜕G}{𝜕y}u+\frac{𝜕G}{𝜕z}v+\frac{𝜕G}{𝜕x}& \frac{𝜕G}{𝜕v}\end{array}\right|}{\left|\begin{array}{cc}\frac{𝜕F}{𝜕u}& \frac{𝜕F}{𝜕v}\\ \frac{𝜕G}{𝜕u}& \frac{𝜕G}{𝜕v}\end{array}\right|}}\\ v^{\prime }=-{\displaystyle \frac{\left|\begin{array}{cc}\frac{𝜕F}{𝜕u}& \frac{𝜕F}{𝜕y}u+\frac{𝜕F}{𝜕z}v+\frac{𝜕F}{𝜕x}\\ \frac{𝜕G}{𝜕u}& \frac{𝜕G}{𝜕y}u+\frac{𝜕G}{𝜕z}v+\frac{𝜕G}{𝜕x}\end{array}\right|}{\left|\begin{array}{cc}\frac{𝜕F}{𝜕u}& \frac{𝜕F}{𝜕v}\\ \frac{𝜕G}{𝜕u}& \frac{𝜕G}{𝜕v}\end{array}\right|}}\end{array}\right.\end{array}$$

(3.27)

Similar to the situation in last subsection, for points that do not satisfy Inequality (3.26), the left side of Equation (3.27) equals the limit of the right side as $x$ approaches these points, as guaranteed by the continuity conditions. This same principle applies to similar scenarios later on.

Define:

$$\begin{array}{c}\left\{\begin{array}{c}\mathit{y}=\left(\begin{array}{c}y\\ z\\ u\\ v\end{array}\right)\\ \mathit{f}\left(x,\mathit{y}\right)=\left(\begin{array}{c}u\\ v\\ -{\displaystyle \frac{\left|\begin{array}{cc}\frac{𝜕F}{𝜕y}u+\frac{𝜕F}{𝜕z}v+\frac{𝜕F}{𝜕x}& \frac{𝜕F}{𝜕v}\\ \frac{𝜕G}{𝜕y}u+\frac{𝜕G}{𝜕z}v+\frac{𝜕G}{𝜕x}& \frac{𝜕G}{𝜕v}\end{array}\right|}{\left|\begin{array}{cc}\frac{𝜕F}{𝜕u}& \frac{𝜕F}{𝜕v}\\ \frac{𝜕G}{𝜕u}& \frac{𝜕G}{𝜕v}\end{array}\right|}}\\ -{\displaystyle \frac{\left|\begin{array}{cc}\frac{𝜕F}{𝜕u}& \frac{𝜕F}{𝜕y}u+\frac{𝜕F}{𝜕z}v+\frac{𝜕F}{𝜕x}\\ \frac{𝜕G}{𝜕u}& \frac{𝜕G}{𝜕y}u+\frac{𝜕G}{𝜕z}v+\frac{𝜕G}{𝜕x}\end{array}\right|}{\left|\begin{array}{cc}\frac{𝜕F}{𝜕u}& \frac{𝜕F}{𝜕v}\\ \frac{𝜕G}{𝜕u}& \frac{𝜕G}{𝜕v}\end{array}\right|}}\end{array}\right)\\ {\mathit{y}}_0=\left(\begin{array}{c}{y}_0\\ z_0\\ g\left(x_0,y_0\right)\\ h\left(x_0,y_0\right)\end{array}\right)\end{array}\right.\end{array}$$

(3.28)

where $F=F\left(u,v,y,z,x\right)$ and $G=G\left(u,v,y,z,x\right)$. Based on Equations (3.20), (3.22), (3.24), (3.27), and (3.28), the initial value problem described by Equations (3.19) and (3.20) can be transformed into the following initial value problem in vector form:

$$\begin{array}{c}\left\{\begin{array}{c}{\displaystyle \frac{d\mathit{y}}{dx}}=\mathit{f}(x,\mathit{y})\\ \mathit{y}\left(x_0\right)={\mathit{y}}_0\end{array}\right.\end{array}$$

(3.29)

The Picard–Lindelöf theorem provides the conditions under which the initial value problem in Equation (3.29) has a unique solution, and successive approximations of the solution can be obtained using the Picard iteration method¹¹.

4. Existence and uniqueness of solutions

Definition 1 (Lipschitz condition)¹¹ A vector function $\mathit{f}(x,\mathit{y}):D\to R^n$ is said to satisfy a uniform Lipschitz condition with respect to $\mathit{y}$ on the open set $D\subset R\times R^n$ provided there is a constant $L$ such that:

$$\begin{array}{c}\left|\mathit{f}\left(x,{\mathit{y}}_1\right)-\mathit{f}(x,{\mathit{y}}_2)\right|\le L\left|{\mathit{y}}_1-{\mathit{y}}_2\right|\end{array}$$

(3.30)

for all $\left(x,{\mathit{y}}_1\right),(x,{\mathit{y}}_2)\in D$. The constant $L$ is called a Lipschitz constant for $\mathit{f}(x,\mathit{y})$ with respect to $\mathit{y}$ on $D$.

Theorem 1 (Picard-Lindelöf theorem)¹¹ Assume that $\mathit{f}$ is a continuous vector function on the rectangle:

$$\begin{array}{c}D=\left\{\left(x,\mathit{y}\right):x_0\le x\le x_0+a,\left|\mathit{y}-{\mathit{y}}_0\right|\le b\right\}\end{array}$$

(3.31)

and that $\mathit{f}(x,\mathit{y})$ satisfies a uniform Lipschitz condition with respect to $\mathit{y}$ on $D$. Let:

$$\begin{array}{c}M=\underset{\left(x,\mathit{y}\right)\in D}{\max }\left|\mathit{f}(x,\mathit{y})\right|,h=\min \left\{a,{\displaystyle \frac{b}{M}}\right\}\end{array}$$

(3.32)

Then the initial value problem described by Equations (3.18) and (3.29) has a unique solution $\mathit{y}\left(x\right)$ on $\left[x_0,x_0+h\right]$.

According to Picard iteration method, the sequence $\left\{{\mathit{\phi }}_n\left(x\right)\right\}$ defined as:

$$\begin{array}{c}\left\{\begin{array}{c}{\mathit{\phi }}_0\left(x\right)={\mathit{y}}_0\\ {\mathit{\phi }}_{n+1}\left(x\right)={\mathit{y}}_0+{\int }_{x_0}^x\mathit{f}\left(\xi ,{\mathit{\phi }}_n\left(\xi \right)\right)\mathrm{d}\xi \end{array}\right.\end{array}$$

(3.33)

converges uniformly to the unique solution of the initial value problem described by Equations (3.18) and (3.29) over the interval $\left[x_0,x_0+h\right]$, and:

$$\begin{array}{c}\left|\mathit{y}\left(x\right)-{\mathit{\phi }}_n\left(x\right)\right|\le {\displaystyle \frac{M{L}^n{\left(x-x_0\right)}^{n+1}}{\left(n+1\right)!}}\end{array}$$

(3.34)

where $L$ is a Lipschitz constant. Hence, ${\mathit{\phi }}_n\left(x\right)$ can be regarded as an approximate solution to the initial value problem, and the error can be estimated using equation (3.34).

5. Examples

5.1. First order ODE

Consider the following initial value problem for the ODE:

$$\begin{array}{c}\left\{\begin{array}{c}{y^{\prime }}^2+y^2=1\\ y\left(0\right)=0\\ 0\le x<2\pi \end{array}\right.\end{array}$$

(4.1)

where $y$ has continuous second derivative.

From Equation (4.1), we obtain:

$$\begin{array}{c}{y^{\prime }\left(0\right)}^2+{y\left(0\right)}^2=1\end{array}$$

(4.2)

Combining Equations (4.1) and (4.2), we solve:

$$\begin{array}{c}{y}^{\prime }\left(0\right)=\pm 1\end{array}$$

(4.3)

By differentiating both sides of the ODE in Equation (4.1), we get:

$$\begin{array}{c}2y^{\prime }{y}^{″}+2y{y}^{\prime }=0\end{array}$$

(4.4)

Using the continuity condition, we derive:

$$\begin{array}{c}{y}^{″}\left(x\right)=\underset{t\to x}{\lim }{\displaystyle \frac{-y\left(t\right)y^{\prime }\left(t\right)}{y^{\prime }\left(t\right)}}=-y\left(x\right)\end{array}$$

(4.5)

Let:

$$\begin{array}{c}{y}^{\prime }=z\end{array}$$

(4.6)

The initial value problem described by Equation (4.1) is then transformed into:

$$\begin{array}{c}\left\{\begin{array}{c}{\displaystyle \frac{d\mathit{y}}{dx}}=\mathit{f}(x,\mathit{y})\\ \mathit{y}\left(x_0\right)={\mathit{y}}_0\\ 0\le x<2\pi \end{array}\right.\end{array}$$

(4.7)

where:

$$\begin{array}{c}\mathit{y}=\left(\begin{array}{c}y\\ z\end{array}\right),\mathit{f}\left(x,\mathit{y}\right)=\left(\begin{array}{c}z\\ -y\end{array}\right),{\mathit{y}}_0=\left(\begin{array}{c}0\\ \pm 1\end{array}\right)\end{array}$$

(4.8)

When:

$$\begin{array}{c}{\mathit{y}}_0=\left(\begin{array}{c}0\\ 1\end{array}\right)\end{array}$$

(4.9)

According to Equation (3.33), we can calculate:

$$\begin{array}{c}\left\{\begin{array}{c}{\mathit{\phi }}_0\left(x\right)={\mathit{y}}_0=\left(\begin{array}{c}0\\ 1\end{array}\right)\\ {\mathit{\phi }}_1\left(x\right)=\left(\begin{array}{c}0\\ 1\end{array}\right)+{\int }_0^x\left(\begin{array}{c}1\\ 0\end{array}\right)\mathrm{d}\xi =\left(\begin{array}{c}x\\ 1\end{array}\right)\\ {\mathit{\phi }}_2\left(x\right)=\left(\begin{array}{c}0\\ 1\end{array}\right)+{\int }_0^x\left(\begin{array}{c}1\\ -x\end{array}\right)\mathrm{d}\xi =\left(\begin{array}{c}x\\ 1-{\displaystyle \frac{x^2}{2}}\end{array}\right)\\ {\mathit{\phi }}_3\left(x\right)=\left(\begin{array}{c}0\\ 1\end{array}\right)+{\int }_0^x\left(\begin{array}{c}1-{\displaystyle \frac{x^2}{2}}\\ -x\end{array}\right)\mathrm{d}\xi =\left(\begin{array}{c}x-{\displaystyle \frac{x^3}{3!}}\\ 1-{\displaystyle \frac{x^2}{2}}\end{array}\right)\\ {\mathit{\phi }}_4\left(x\right)=\left(\begin{array}{c}0\\ 1\end{array}\right)+{\int }_0^x\left(\begin{array}{c}1-{\displaystyle \frac{x^2}{2}}\\ -x+{\displaystyle \frac{x^3}{3!}}\end{array}\right)\mathrm{d}\xi =\left(\begin{array}{c}x-{\displaystyle \frac{x^3}{3!}}\\ 1-{\displaystyle \frac{x^2}{2}}+{\displaystyle \frac{x^4}{4!}}\end{array}\right)\\ {\mathit{\phi }}_5\left(x\right)=\left(\begin{array}{c}x-{\displaystyle \frac{x^3}{3!}}+{\displaystyle \frac{x^5}{5!}}\\ 1-{\displaystyle \frac{x^2}{2}}+{\displaystyle \frac{x^4}{4!}}\end{array}\right)\\ ⋮\end{array}\right.\end{array}$$

(4.10)

It is not difficult to prove that:

$$\begin{array}{c}\underset{n\to \infty }{\mathbf{lim}}{\mathit{\phi }}_n\left(x\right)=\left(\begin{array}{c}{\displaystyle \sum _{n=0}^{\infty }}{\left(-1\right)}^n{\displaystyle \frac{x^{2n+1}}{\left(2n+1\right)!}}\\ {\displaystyle \sum _{n=0}^{\infty }}{\left(-1\right)}^n{\displaystyle \frac{x^{2n}}{\left(2n\right)!}}\end{array}\right)=\left(\begin{array}{c}\sin \left(x\right)\\ \cos \left(x\right)\end{array}\right)\end{array}$$

(4.11)

which implies:

$$\begin{array}{c}\left\{\begin{array}{c}y=\sin \left(x\right)\\ y^{\prime }=\cos \left(x\right)\end{array}\right.\end{array}$$

(4.12)

Similarly, when:

$$\begin{array}{c}{\mathit{y}}_0=\left(\begin{array}{c}0\\ -1\end{array}\right)\end{array}$$

(4.13)

we obtain:

$$\begin{array}{c}\left\{\begin{array}{c}y=-\sin \left(x\right)\\ y^{\prime }=-\cos \left(x\right)\end{array}\right.\end{array}$$

(4.14)

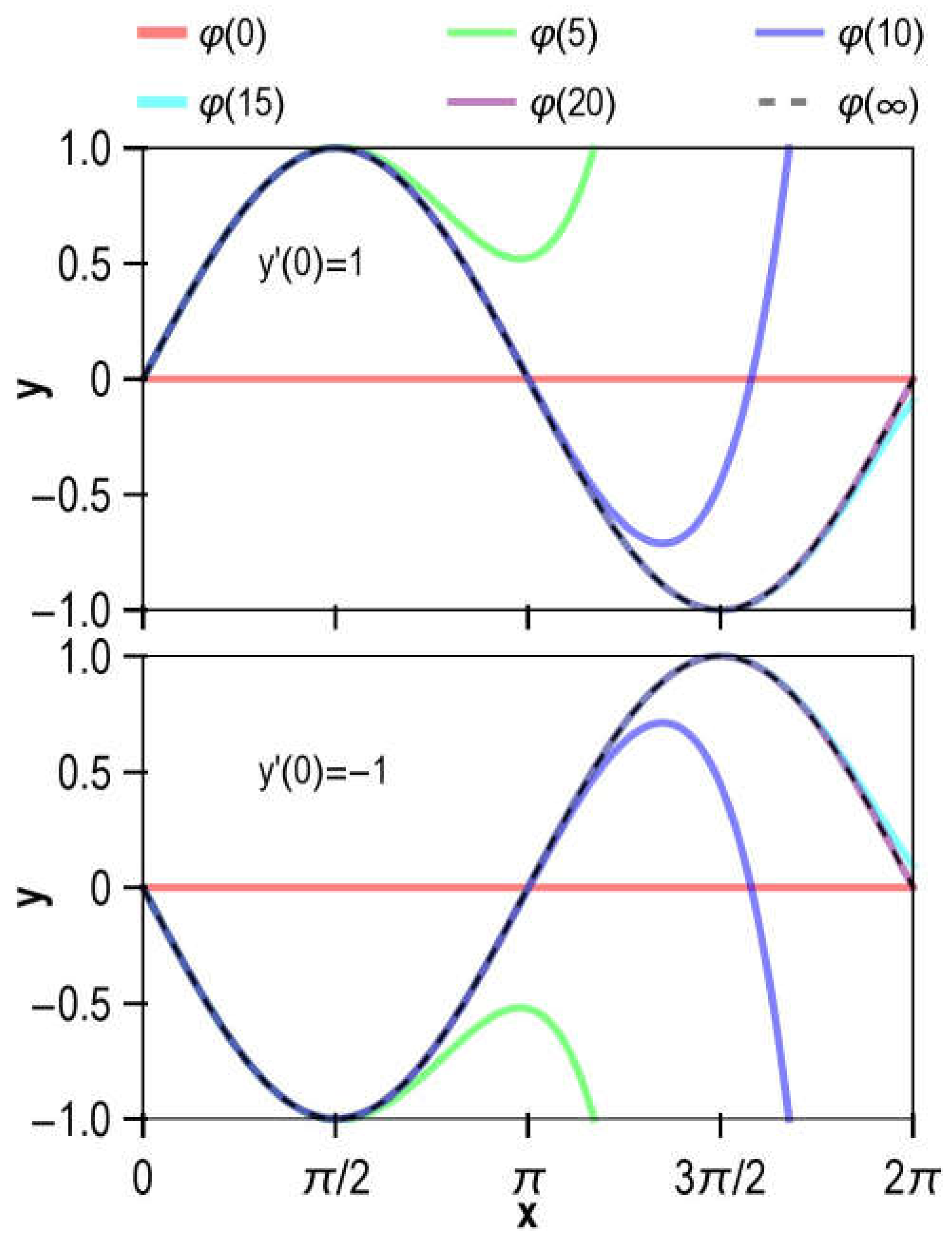
In conclusion, the solution to the initial value problem described by Equation (4.1) is

$$\begin{array}{c}y=\pm \sin \left(x\right),0\le x<2\pi \end{array}$$

(4.15)

This solution can be easily obtained or verified by other methods. The approximate analytical solutions of Equation (4.1) using the DQM and the exact solution are plotted in Figure 1. As seen in the figure, the approximate solution ${\mathit{\phi }}_5\left(x\right)$ is already very close to the exact solution.

5.2. System of first order ODEs

Consider an object of mass $2$ moving in a uniform circle under the gravitational pull of another object with mass ${\displaystyle \frac{1}{2G}}$ located at the origin $\left(\mathrm{0,0}\right)$, where $G$ is the gravitational constant. The initial position of the orbiting object is $\left(\mathrm{0,1}\right)$. The goal is to determine the position coordinates of this object at any time.

Let $\left(x,y\right)$ represent the coordinates of the object at time $t$. The zero potential energy point is selected at infinity. Using the principles of energy conservation and angular momentum conservation, the following ODEs and initial conditions can be derived:

$$\begin{array}{c}\left\{\begin{array}{c}{x^{\prime }}^2+{y^{\prime }}^2-{\displaystyle \frac{1}{\sqrt{x^2+y^2}}}=-{\displaystyle \frac{1}{2}}\\ x{y}^{\prime }-x^{\prime }y={\displaystyle \frac{1}{\sqrt{2}}}\\ x\left(0\right)=0\\ y\left(0\right)=1\\ t\ge 0\end{array}\right.\end{array}$$

(4.16)

where $x$ and $y$ are functions of $t$. From Equation (4.16), we find:

$$\begin{array}{c}\left\{\begin{array}{c}x\left(0\right)=0\\ y\left(0\right)=1\\ x^{\prime }\left(0\right)=-{\displaystyle \frac{1}{\sqrt{2}}}\\ y^{\prime }\left(0\right)=0\end{array}\right.\end{array}$$

(4.17)

Taking the derivatives of both sides of the ODEs in Equation (4.16), we obtain:

$$\begin{array}{c}\left\{\begin{array}{c}2x^{\prime }{x}^{″}+2y^{\prime }{y}^{″}+{\left(x^2+y^2\right)}^{-{\displaystyle \frac{3}{2}}}\left(x{x}^{\prime }+y{y}^{\prime }\right)=0\\ x{y}^{″}-x^{″}y=0\end{array}\right.\end{array}$$

(4.18)

Using the continuity condition, we derive:

$$\begin{array}{c}\left\{\begin{array}{c}{x}^{″}=-{\displaystyle \frac{x{\left(2{x^{\prime }}^2+2{y^{\prime }}^2+1\right)}^3}{16}}\\ y^{″}=-{\displaystyle \frac{y{\left(2{x^{\prime }}^2+2{y^{\prime }}^2+1\right)}^3}{16}}\end{array}\right.\end{array}$$

(4.19)

Let:

$$\begin{array}{c}\left\{\begin{array}{c}{x}^{\prime }=z\\ y^{\prime }=w\end{array}\right.\end{array}$$

(4.20)

The initial value problem described by Equation (4.16) is then transformed into:

$$\begin{array}{c}\left\{\begin{array}{c}{\displaystyle \frac{d\mathit{y}}{dt}}=\mathit{f}(t,\mathit{y})\\ \mathit{y}\left(x_0\right)={\mathit{y}}_0\\ t\ge 0\end{array}\right.\end{array}$$

(4.21)

where:

$$\begin{array}{c}\mathit{y}=\left(\begin{array}{c}x\\ y\\ z\\ w\end{array}\right),\mathit{f}\left(t,\mathit{y}\right)=\left(\begin{array}{c}z\\ w\\ -{\displaystyle \frac{x{\left(2z^2+2w^2+1\right)}^3}{16}}\\ -{\displaystyle \frac{y{\left(2z^2+2w^2+1\right)}^3}{16}}\end{array}\right),{\mathit{y}}_0=\left(\begin{array}{c}0\\ 1\\ -{\displaystyle \frac{1}{\sqrt{2}}}\\ 0\end{array}\right)\end{array}$$

(4.22)

Using Equation (3.33), we obtain:

$$\begin{array}{c}\left\{\begin{array}{c}{\mathit{\phi }}_0\left(t\right)={\mathit{y}}_0=\left(\begin{array}{c}0\\ 1\\ -{\displaystyle \frac{1}{\sqrt{2}}}\\ 0\end{array}\right)\\ {\mathit{\phi }}_1\left(t\right)=\left(\begin{array}{c}0\\ 1\\ -{\displaystyle \frac{1}{\sqrt{2}}}\\ 0\end{array}\right)+{\int }_0^t\left(\begin{array}{c}-{\displaystyle \frac{1}{\sqrt{2}}}\\ 0\\ 0\\ -{\displaystyle \frac{1}{2}}\end{array}\right)\mathrm{d}t=\left(\begin{array}{c}-{\displaystyle \frac{1}{\sqrt{2}}}t\\ 1\\ -{\displaystyle \frac{1}{\sqrt{2}}}\\ -{\displaystyle \frac{1}{2}}t\end{array}\right)\\ {\mathit{\phi }}_2\left(t\right)=\left(\begin{array}{c}-{\displaystyle \frac{1}{\sqrt{2}}}t\\ 1-{\displaystyle \frac{1}{4}}{t}^2\\ -{\displaystyle \frac{1}{\sqrt{2}}}+{\displaystyle \frac{1}{4\sqrt{2}}}{t}^2+{\displaystyle \frac{3}{32\sqrt{2}}}{t}^4+{\displaystyle \frac{1}{64\sqrt{2}}}{t}^6+{\displaystyle \frac{1}{1024\sqrt{2}}}{t}^8\\ -{\displaystyle \frac{1}{2}}t-{\displaystyle \frac{1}{8}}{t}^3-{\displaystyle \frac{3}{160}}{t}^5-{\displaystyle \frac{1}{896}}{t}^7\end{array}\right)\\ {\mathit{\phi }}_3\left(t\right)=\left(\begin{array}{c}-{\displaystyle \frac{1}{\sqrt{2}}}t+{\displaystyle \frac{1}{12\sqrt{2}}}{t}^3+{\displaystyle \frac{3}{160\sqrt{2}}}{t}^5+{\displaystyle \frac{1}{448\sqrt{2}}}{t}^7+{\displaystyle \frac{1}{9216\sqrt{2}}}{t}^9\\ 1-{\displaystyle \frac{1}{4}}{t}^2-{\displaystyle \frac{1}{32}}{t}^4-{\displaystyle \frac{1}{320}}{t}^6-{\displaystyle \frac{1}{7168}}{t}^8\\ -{\displaystyle \frac{1}{\sqrt{2}}}+{\displaystyle \frac{1}{4\sqrt{2}}}{t}^2+{\displaystyle \frac{1}{64\sqrt{2}}}{t}^6+{\displaystyle \frac{81}{10240\sqrt{2}}}{t}^8+{\displaystyle \frac{3663}{1433600\sqrt{2}}}{t}^{10}+\cdots \\ -{\displaystyle \frac{1}{2}}t+{\displaystyle \frac{1}{24}}{t}^3-{\displaystyle \frac{3}{160}}{t}^5-{\displaystyle \frac{51}{8960}}{t}^7-{\displaystyle \frac{31}{28672}}{t}^9-\cdots \end{array}\right)\\ ⋮\end{array}\right.\end{array}$$

(4.23)

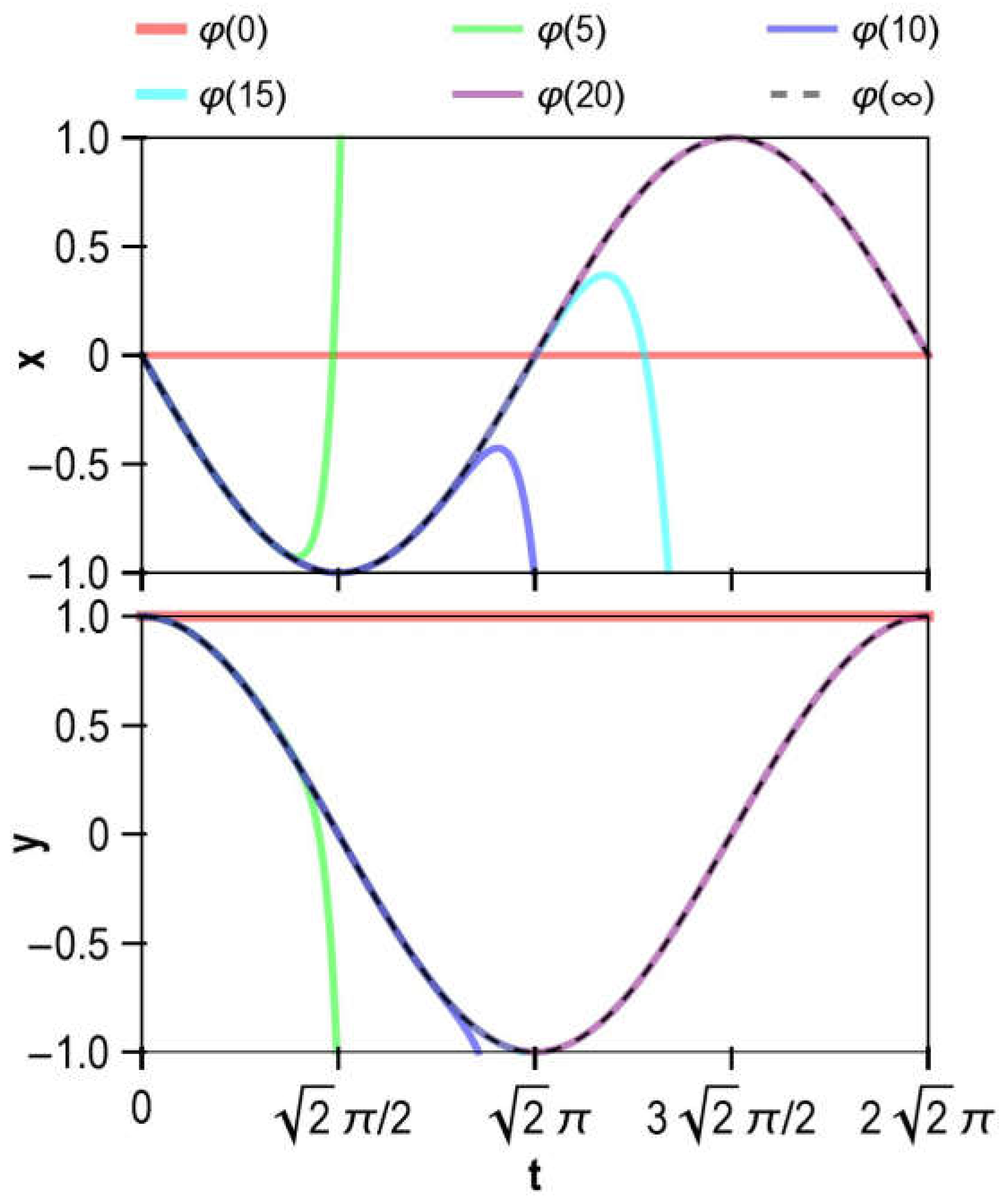
For convenience, terms in the sequence $\left\{{\mathit{\phi }}_n\right\}$ that exceed the 20th power are excluded from the calculation in Equation (4.23); however, this approach may lead to different convergence speeds. From a physical standpoint, it is straightforward to show that the solution to the initial value problem described by Equation (4.16) is:

$$\begin{array}{c}\left\{\begin{array}{c}x=-\sin \left({\displaystyle \frac{t}{\sqrt{2}}}\right)\\ y=\cos \left({\displaystyle \frac{t}{\sqrt{2}}}\right)\\ t\ge 0\end{array}\right.\end{array}$$

(4.24)

The approximate analytical solutions of Equation (4.16), obtained via the DQM, along with the exact solution, are plotted in Figure 2. As observed from the figure, within the interval $\left[\mathrm{0,2}\sqrt{2}\pi \right]$, the approximate solution ${\mathit{\phi }}_{20}\left(x\right)$ closely matches the exact solution.

6. Conclusion

The differential quasilinearization method (DQM) for obtaining approximate analytical solutions of ordinary differential equations (ODEs) was presented in this study. DQM is a widely applicable approach for solving initial value problems of ODEs, especially well-suited for addressing implicit or nonlinear ODEs. The effectiveness of this method was verified by solving specific examples of both single ODE and system of ODEs.