New Bayesian Estimation Method Based on Particle Flow Velocity

1. Introduction

In recent years, numerous mathematical models of engineering systems have exhibited strong nonlinear characteristics, which has rendered traditional Kalman Filter (KF) methods relying on linear assumptions ineffective when dealing with state estimation problems [1,2,3]. To address this challenge, academia has conducted in-depth research into nonlinear filtering techniques. Among these studies, the Extended Kalman Filter (EKF) emerged as an early solution, which linearizes nonlinear systems through Taylor series expansion and then applies the KF algorithm [4]. However, truncation errors introduced during the linearization process limit the accuracy of state estimation.

To overcome this limitation, Julier, Uhlmann, and others proposed the Unscented Kalman Filter (UKF) [5]. UKF avoids errors resulting from linearization by selecting a specific set of sample points to approximate nonlinear transformations, significantly improving the accuracy of state estimation.

Recently, Bayesian-based nonlinear filtering methods have become a research hotspot [6,7,8,9,10,11,12,13,14]. These methods are mainly divided into two categories: one approximates the state distribution in state space, with Particle Filter (PF) being one of the most representative algorithms [15]. PF represents the required posterior probability density through a weighted sum of random samples to estimate the state. Although PF theoretically approximates optimal Bayesian estimation, it still faces challenges in terms of estimation accuracy, implementation difficulty, and computational complexity in practical applications [16,17,18,19,20]. The other category directly approximates the state probability density function in function space. For example, the nonlinear projection filter algorithm proposed by Randal Beard and John Kenney addresses state estimation problems for low-dimensional nonlinear Gaussian systems [21,22,23]. Subsequently, scholars such as Zhao Yuxin proposed projection filter algorithms for one-dimensional nonlinear non-Gaussian systems, greatly reducing computational time complexity and memory usage [3].

It is worth noting that both EKF and UKF aim to solve for the second-order moments of the system state probability distribution, but the actual distribution of the system state may not be normal. Therefore, Bayesian estimation methods have advantages in non-Gaussian nonlinear systems, as they can directly solve for the system state probability density function, better capturing possible abrupt changes in the target state [16,17,18,19,20].

Literature [23] introduced a projection filtering method limited to low-dimensional state estimation problems. To overcome this limitation, this paper proposes a new Bayesian estimation method based on particle flow velocity(PFV-BEM)and extends it to nonlinear systems. Through numerical approximation solutions, simulation results demonstrate that this method not only relaxes the restrictive condition that system noise must be Gaussian but also outperforms PF algorithms in estimation accuracy and has lower computational complexity than general particle filters. Additionally, this method exhibits stable performance and has certain practical application value.

This paper is organized as follows. In Section 2, an Bayesian Estimation Model in NLSs is given, and the Bayesian equation of Bayesian Estimation Model is given. In Section 3, the (PFV-BEM) program is divided into two parts to solve the state solution: solving the prior probability for status update and using particle flow velocity for measurement update. In Section 4, two illustrative examples and their simulation results are given. Then, the conclusions of this paper are analyzed in detail In Section 5.

2. Bayesian Estimation Model

In nonlinear systems, the state estimation model consists of state equation and measurement equation, formulated as follows [24]:

$$\left\{\begin{array}{l}d{x}_t=F\left(x_t,t\right)dt+G\left(t\right)d{\beta }_t\\ z_k=H\left(x_k,t_k\right)+e_k\end{array}\right.$$

(1)

where: $x_t$ denotes the state vector at time t, $F\left(x_t,t\right)$ is the state transition matrix, $G\left(t\right)$ represents the system noise driving matrix, ${\beta }_t$ is the standard Brownian motion and $e_k$ represents measurement noise, respectively, with $z_k$ denoting the measurement vector, and $H\left(x_k,t_k\right)$ being the measurement matrix. ${\beta }_t$ and $e_k$ are mutually independent and satisfy:

$$\left\{\begin{array}{c}\mathrm{E}\left\{{\beta }_t\right\}=0,\begin{array}{c} \end{array}\mathrm{E}\left\{{\beta }_t{{\beta }_t}^{\mathrm{T}}\right\}=\mathit{Q}\left(t\right)\\ \mathrm{E}\left\{{\mathrm{e}}_k\right\}=0,\begin{array}{c} \end{array}\mathrm{E}\left\{{\mathrm{e}}_k{{\mathrm{e}}_k}^{\mathrm{T}}\right\}=\mathit{R}\left(k\right)\\ \mathrm{E}\left\{{\mathrm{e}}_k{{\beta }_{\mathrm{k}}}^{\mathrm{T}}\right\}=0\end{array}\right.$$

(2)

where: $\mathit{Q}\left(t\right)$ is given as the system noise covariance matrix; $\mathit{R}\left(k\right)$ represents the measurement noise covariance matrix.

According to a theorem in reference [25], the probability density function（PDF）of the state equation satisfies the Fokker-Planck Equation (FPE):

$$\dot{p}\left(x,t_k^{-}|z_{k-1}\right)={\displaystyle \frac{1}{2}}{\displaystyle \sum _{r,s=1}^n\frac{{𝜕}^2\left(G\left(t\right)Q\left(t\right)G^{\mathrm{T}}\left(t\right)\cdot p\left(x,t_k^{-}|z_{k-1}\right)\right)}{𝜕x_r𝜕x_s}}-{\displaystyle \sum _{r=1}^n\frac{𝜕\left(F\left(x_t,t\right)\cdot p\left(x,t_k^{-}|z_{k-1}\right)\right)}{𝜕x_r}}$$

(3)

Where $p\left(x,t_k^{-}|z_{k-1}\right)$ is defined as prior probability density.

the likelihood probability density $p\left(z_{k+1}|x\right)$ of the measurement equation is defined as:

$$p\left(z_k|x\right)={\displaystyle \frac{1}{\sqrt{{\left(2\pi \right)}^m\left|R_k\right|}}}exp\left\{-{\displaystyle \frac{1}{2}}{\left(z_k-h\left(x_{k-1},t_k\right)\right)}^{\mathrm{T}}{R}_k^{-1}\left(z_k-h\left(x_{k-1},t_k\right)\right)\right\}$$

(4)

In reference [17], the state estimate solution of Bayesian estimation models needs to calculate the probability density function $p\left(x,t_k|z_k\right)$, which is defined as the posterior PDF of Bayesian Estimation Model. the posterior PDF $p\left(x,t_k|z_k\right)$ satisfies Bayesian equation:

$$p\left(x,t_k|z_k\right)={\displaystyle \frac{p\left(z_k|x\right)p\left(x,t_k^{-}|z_{k-1}\right)}{{\displaystyle {\int }_{\Omega }p\left(z_k|x\right)p\left(x,t_k^{-}|z_{k-1}\right)dx}}}$$

(5)

3. Bayesian Filter Estimator Design-Based Projection Flow Velocity

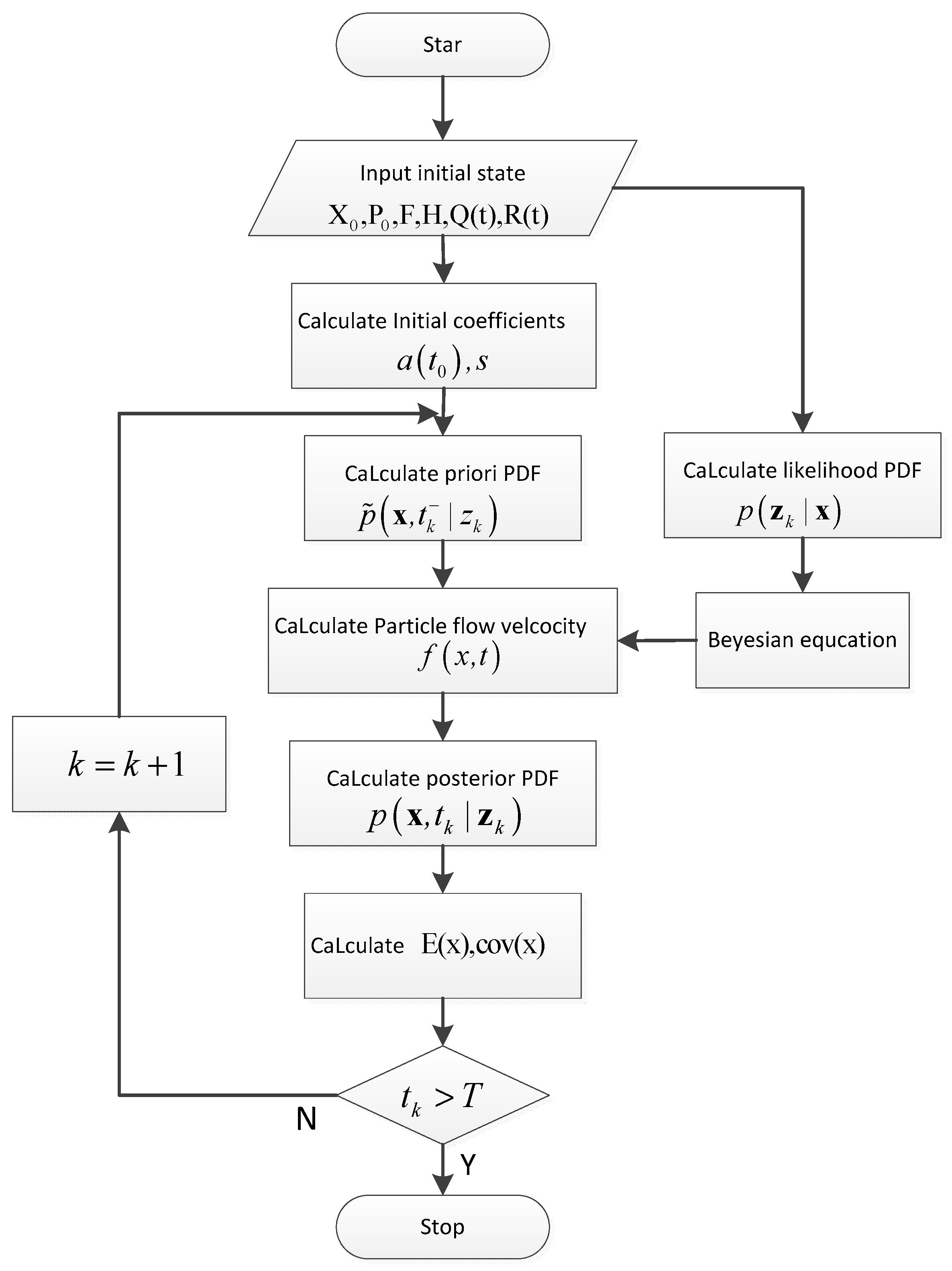
Bayesian estimation method based on particle flow velocity(PFV-BEM) is a state estimation method that approximates the PDF of the state. First, in the projection space, the prior PDF of the state can be calculated in its projection space. Second, the particle points of the prior PDF are obtained, through calculating the particle flow velocity, the particle information of the posterior PDF can be obtained, finally, the estimated solution and estimated variance of the system state can be calculated. Therefore, PFV-EMD is an effective method for solving Bayesian estimation problems. The flowchart of the PFV-BEM algorithm is shown in Figure 1.

3.1. Solving the Prior Probability for State Updates

State vector of state estimation model is given as $x=\left(x_1,\cdots ,x_n\right)$, the PDF can be denoted as $p\left(x,t\right)$, $t\ge 0$, assume that the PDF of x can be expressed as the following form in reference [24]

$$p\left(x,t\right)={\displaystyle \sum _{i=0}^{\infty }{a}_i\left(t\right){\varphi }_i\left(x\right)}$$

(6)

where ${\varphi }_i\left(x\right)$ denotes standard orthogonal basis function in projection subspace, $m_i\left(t\right)$ can be denoted as the coefficients of $p\left(x,t\right)$ in Eq. (1), we definite $〈\eta ,\varphi 〉={\displaystyle {\int }_{\Omega }\eta \left(x\right)\varphi \left(x\right)dx}$, $\Omega \subset R^n$ denotes the inner- product equation.

$$a_i\left(t\right)=〈p\left(x,t\right),{\varphi }_i\left(x\right)〉$$

(7)

where $V_N=span{\left\{{\varphi }_i\right\}}_0^{N-1}\subset V$ denotes a complete set of basis functions for $L_2$. $p\left(x,t\right)$ could be denoted as the following form:

$$\tilde{p}\left(x,t\right)={\displaystyle \sum _{i=0}^{N-1}{a}_i\left(t\right){\varphi }_i\left(x\right)}$$

(8)

where coefficients $a_i\left(t\right)$ is denoted as $a_i\left(t\right)=〈p\left(x,t\right),{\varphi }_i\left(x\right)〉$.These basis functions ${\varphi }_i\left(x\right)$ are given as：

$${\left[M\right]}_{q+1,i+1}=〈{\varphi }_i,{\varphi }_q〉=\left\{\begin{array}{l}0\hspace{1em}\hspace{0.17em}i\ne q\\ 1\hspace{1em}\hspace{0.33em}i=q\end{array}\right.$$

(9)

where $\hspace{0.17em}i,q=0,1,2,\cdots ,N-1$.

Simplify the above equation $M=E_{N\times N}$, $a\left(t\right)={\left[a_0\left(t\right)\hspace{1em}{a}_1\left(t\right)\hspace{1em}\cdots a_{N-1}\left(t\right)\right]}^T$,

$$\Phi \left(x\right)={\left[{\varphi }_0\left(x\right)\hspace{1em}{\varphi }_1\left(x\right)\cdots {\varphi }_{N-1}\left(x\right)\right]}^T.$$

Simplify the Eq.(8), $p\left(x,t\right)=a{\left(t\right)}^T\Phi \left(x\right)$.

In reference [24],basic functionsis ${\varphi }_i\left(x\right)$ were given, According to solve the coefficients matrix $a\left(t\right)$, the PDF solution of $x$ can be solved.

Substitute Eq. (7) into Eq. (3), Eq. (3) can be rewritten as

$${\displaystyle \frac{𝜕{\displaystyle \sum _{i=0}^{N-1}{a}_i{\varphi }_i}}{𝜕t}}={\displaystyle \sum _{i=0}^{N-1}{m}_i\left\{\frac{1}{2}{\displaystyle \sum _{r,s=1}^n\frac{{𝜕}^2\left(gQ\left(t\right)g^{\mathrm{T}}\cdot {\varphi }_i\right)}{𝜕x_r𝜕x_s}}\right\}}-{\displaystyle \sum _{i=0}^{N-1}{m}_i\left\{{\displaystyle \sum _{r=1}^n\frac{𝜕\left(f\left(x,t\right)\cdot {\varphi }_i\right)}{𝜕x_r}}\right\}}$$

(10)

Projecting Eq.(9) onto the project space $V_N=span{\left\{{\varphi }_q\right\}}_0^{N-1}$, Eq. (9) can be rewritten as

$${\displaystyle \frac{𝜕{\displaystyle \sum _{i=0}^{N-1}〈a_i{\varphi }_i,{\varphi }_q〉}}{𝜕t}}={\displaystyle \sum _{i=0}^{N-1}{a}_i\left\{\frac{1}{2}{\displaystyle \sum _{r,s=1}^n〈\frac{{𝜕}^2\left(gQ\left(t\right)g^{\mathrm{T}}\cdot {\varphi }_i\right)}{𝜕x_r𝜕x_s},{\varphi }_q〉}\right\}}-{\displaystyle \sum _{i=0}^{N-1}{a}_i\left\{{\displaystyle \sum _{r=1}^n〈\frac{𝜕\left(f\left(x,t\right)\cdot {\varphi }_i\right)}{𝜕x_r},{\varphi }_q〉}\right\}}$$

(11)

If $Q$, $f$ and $g$ are given in Eq. (1) and Eq. (2). so Eq. (11) can be rewritten as

$${\displaystyle \sum _{i=0}^{N-1}{\dot{a}}_i\cdot 〈{\varphi }_i,{\varphi }_q〉}={\displaystyle \sum _{i=0}^{N-1}{a}_i\left\{\frac{1}{2}{\displaystyle \sum _{r,s=1}^n〈\frac{{𝜕}^2\left(gQ\left(t\right)g^{\mathrm{T}}\cdot {\varphi }_i\right)}{𝜕x_r𝜕x_s},{\varphi }_q〉}\right\}}-{\displaystyle \sum _{i=0}^{N-1}{a}_i\left\{{\displaystyle \sum _{r=1}^n〈\frac{𝜕\left(f\left(x,t\right)\cdot {\varphi }_i\right)}{𝜕x_r},{\varphi }_q〉}\right\}}$$

(12)

Simplify the Eq.(12), we defined

$$\left\{\begin{array}{l}gQ\left(t\right)g^{\mathrm{T}}=B\\ {\left[A\right]}_{q,i}=〈{\varphi }_{i-1},{\varphi }_{q-1}〉=\left\{\begin{array}{l}1\hspace{1em}i=q\\ 0\hspace{1em}i\ne q\end{array}\right.\end{array}\right.$$

(13)

Eq. (12) can be rewritten as

$${\left[A\right]}_{q+1,i+1}=〈\left\{{\displaystyle \frac{1}{2}}{\displaystyle \sum _{r,s=1}^n\frac{B{𝜕}^2\left({\varphi }_i\right)}{𝜕x_r𝜕x_s}}-{\displaystyle \sum _{r=1}^n\frac{𝜕\left(f\left(x,t\right)\cdot {\varphi }_i\right)}{𝜕x_r}}\right\},{\varphi }_q〉$$

(14)

where $i,q=0,1,\cdots N-1$, ${\left[A\right]}_{qi}$ is the element of matrix $A$ in Equation (14).

When $M=E_{N\times N}$, Eq. (12) can be rewritten as

$$M\dot{a}\left(t\right)=Aa\left(t\right)$$

(15)

Eq. (15) can be rewritten as

$$\dot{a}\left(t\right)=Aa\left(t\right)$$

(16)

Set initial time $t=t_0$,the initial information $p_0=p\left(x_0,t_0|z_0\right)$, the initial coefficients $a\left(t_0\right)$ of PDF can be given

$$〈p_0,{\varphi }_j〉=〈{\displaystyle \sum _{i=0}^{N-1}{a}_i\left(t_0\right){\varphi }_i},{\varphi }_j〉={\displaystyle \sum _{i=0}^{N-1}{a}_i\left(t_0\right)\cdot 〈{\varphi }_i,{\varphi }_j〉}$$

(17)

$$s={\left[〈p_0,{\varphi }_0〉\hspace{1em}\cdots 〈p_0,{\varphi }_{N-1}〉\right]}^T$$

(18)

$$a\left(t_0\right)=M^{-1}s=s$$

(19)

Substitute Eq. (19) into Eq. (16), $a\left(t\right)$ can be obtained:

$$a\left(t\right)=exp\left\{{\displaystyle {\int }_{t_0}^{t}Ad\tau }\right\}s$$

(20)

If $\mathrm{t}\in \left[t_{k-1},t_k\right)$, Eqs. (20) have the following simple solution

$$a\left(t\right)=exp\left(A\left(t-t_{k-1}\right)\right)a\left(t_{k-1}\right)$$

(21)

priori coefficients $a^{-}\left(t_k\right)$ can be given：

$$a^{-}\left(t_k\right)=exp\left(A\left(t_k-t_{k-1}\right)\right)a\left(t_{k-1}\right)$$

(22)

where $a\left(t_{k-1}\right)$ are posterior coefficients of state $x$ at the time $\mathrm{t}=t_{k-1}$.

A priori PDF of state $x$ is given as

$$\tilde{p}\left(x,t_k^{-}|z_k\right)={\displaystyle \sum _{i=0}^{N-1}{a_i}^{-}\left(t_k\right){\varphi }_i}=a^{-}{\left(t_k\right)}^T\Phi \left(x\right)$$

(23)

3.2. Using Particle Flow Velocity for Measurement Update

Randomly extract particle points based on the prior PDF at time $t_k$. The posterior PDF of the state estimation model at time can be obtained by Bayesian formula Eq. (4). Homotopy function is expressed as:

$$p\left(x,\lambda \right)={\displaystyle \frac{g\left(x\right)h^{\lambda }\left(x\right)}{{\displaystyle \underset{x}{\int }g\left(x\right)h^{\lambda }\left(x\right)dx}}}$$

(24)

where $p\left(x,\lambda \right)$ is the conditional PDF, $g\left(x\right)$ represents the prior PDF, and $h\left(x\right)$ represents the likelihood PDF.

Taking the logarithm of the above equation yields:

$$log p\left(x,\lambda \right)=log g\left(x\right)+\lambda log h\left(x\right)-log K\left(\lambda \right)$$

(25)

In the equation, $K\left(\lambda \right)={\displaystyle \underset{x}{\int }g\left(x\right)h^{\lambda }\left(x\right)dx}$ is the normalization constant independent of x. Let λ change continuously from 0 to 1, and the homotopy function $p\left(x,\lambda \right)$ defines the probability distribution of the change from the prior distribution ($\lambda =0$) to the posterior distribution ($\lambda =1$). The flow velocity of the state particle x during this process is described as the following differential equation.

$${\displaystyle \frac{𝜕x}{𝜕\lambda }}=f\left(x,\lambda \right)+{\displaystyle \frac{\mathrm{d}\omega }{𝜕\lambda }}$$

(26)

The particle flow velocity $f\left(x,\lambda \right)$ satisfies FPE, which is the process noise. It can be obtained that:

$${\displaystyle \frac{𝜕p}{𝜕\lambda }}=-div\left(fp\right)+{\displaystyle \frac{1}{2}}div\left(Q{\displaystyle \frac{𝜕p}{𝜕x}}\right)$$

(27)

Simplify the above equation:

$${\displaystyle \frac{𝜕log p\left(x,\lambda \right)}{𝜕\lambda }}p\left(x,\lambda \right)=-div\left(fp\right)+{\displaystyle \frac{1}{2}}div\left(Q{\displaystyle \frac{𝜕p}{𝜕x}}\right)$$

(28)

Substituting equation (25) into equation (28) yields:

$$\left[log h\left(x\right)-{\displaystyle \frac{dlog K\left(\lambda \right)}{d\lambda }}\right]p\left(x,\lambda \right)=-div\left(fp\right)+{\displaystyle \frac{1}{2}}div\left(Q{\displaystyle \frac{𝜕p}{𝜕x}}\right)$$

(29)

Simplify the above equation

$$log h-{\displaystyle \frac{dlog K}{d\lambda }}=-div\left(f\right)-{\displaystyle \frac{𝜕log p}{𝜕x}}f+{\displaystyle \frac{1}{2p}}div\left(Q{\displaystyle \frac{𝜕p}{𝜕x}}\right)$$

(30)

The particle flow velocity field can be obtained as follows:

$$f=-{\left[{\displaystyle \frac{{𝜕}^{2}log p}{𝜕x^2}}\right]}^{-1}{\left({\displaystyle \frac{𝜕log h}{𝜕x}}\right)}^T$$

(31)

The variance $Q$ is:

$$Q=-{\left[{\displaystyle \frac{{𝜕}^{2}log p}{𝜕x^2}}\right]}^{-1}{\displaystyle \frac{{𝜕}^{2}log h}{𝜕x^2}}{\left[{\displaystyle \frac{{𝜕}^{2}log p}{𝜕x^2}}\right]}^{-1}$$

(32)

By using the velocity field calculation equation (31), the numerical integration of the prior particles $x_k^{-}$ with the posterior particles $x_k^{+}$ can be obtained as follows:

$$x_k^{+}=x_k^{-}+{\displaystyle \underset{0}{\overset{1}{\int }}f\left(x,\lambda \right)d\lambda }$$

(33)

The estimated value $\stackrel{⌢}{x}$ of the state can be denoted as:

$$\stackrel{⌢}{x}={\displaystyle \frac{1}{N}}{\displaystyle \sum _{k=1}^N{x}_k^{+}}$$

(34)

4. Illustrative Simulations Examples and Analysis

4.1. Example 1 and Analysis

For the first simulation example, In reference [26] considered a scalar signal process $x\left(t\right)$ is observed through a scalar measurement process $\mathrm{y}\left(t\right)$, and the NLSs model is given as.

$$\left\{\begin{array}{l}\mathrm{d}x\left(t\right)=sin\left(x/2\right)+\mathrm{d}\beta \left(t\right)\\ \mathrm{dy}\left(t\right)=\mathrm{d}x\left(t\right)+d\eta \left(t\right)\end{array}\right.$$

(35)

where β(t) and η(t) are standard Brownian motions, and Initial state x(0) = 0, y(0) = 0.

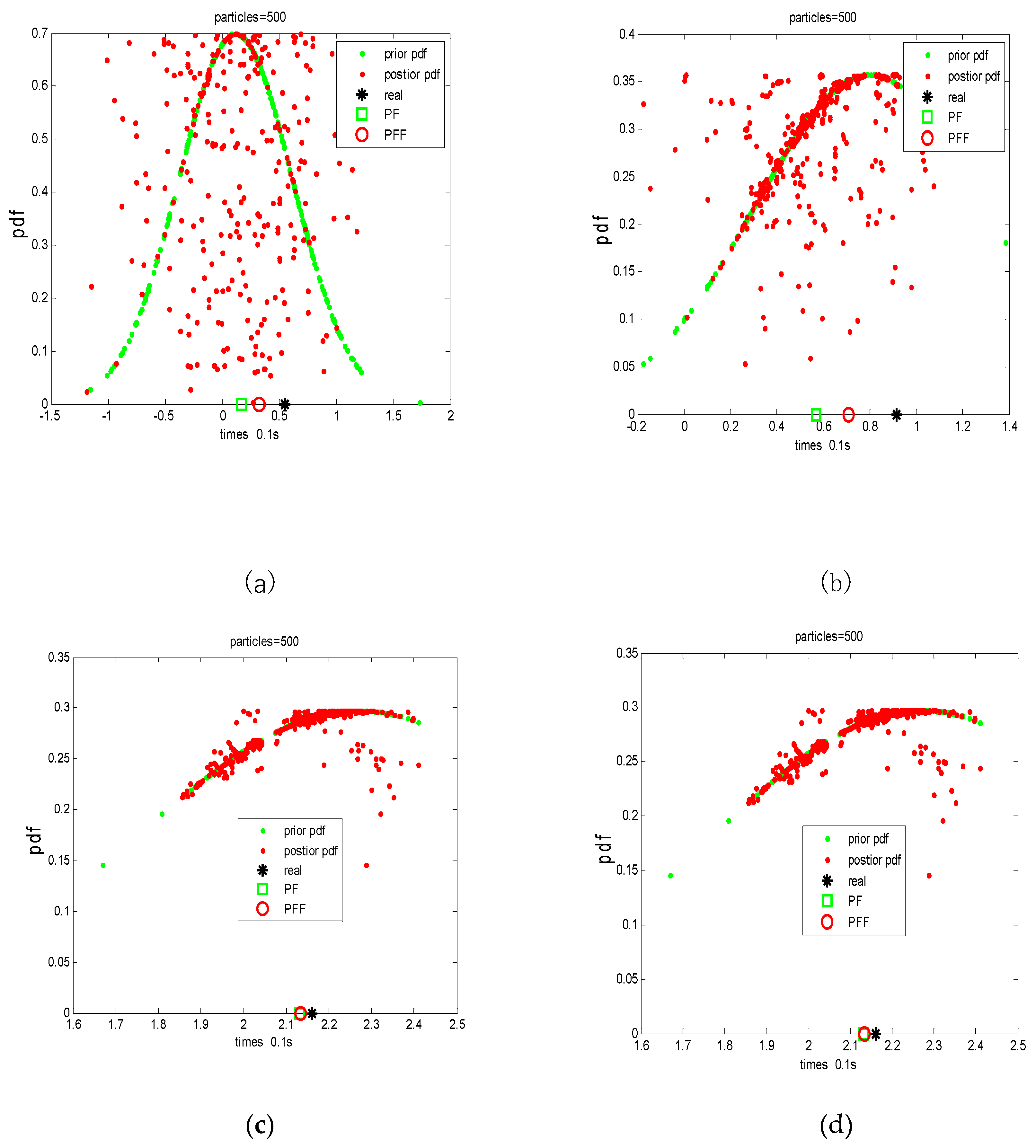
The simulation time is T=2 seconds, and the number of particles is 1000. The estimate results are shown in Figure 2 and Figure 3. The priori PDF and posterior PDFs are plotted in Figure 2. The normalized density functions are plotted every other 0.1s. The partial results have been shown in Figure 2, where the actual position information (represented by black stars), PF estimated position information (represented by green squares), and PFV-BEM estimated position information (represented by red circles) are all displayed in Figure 2. The approximate particle flow in the PDF of the state is shown through the four graphs in Figure 2. 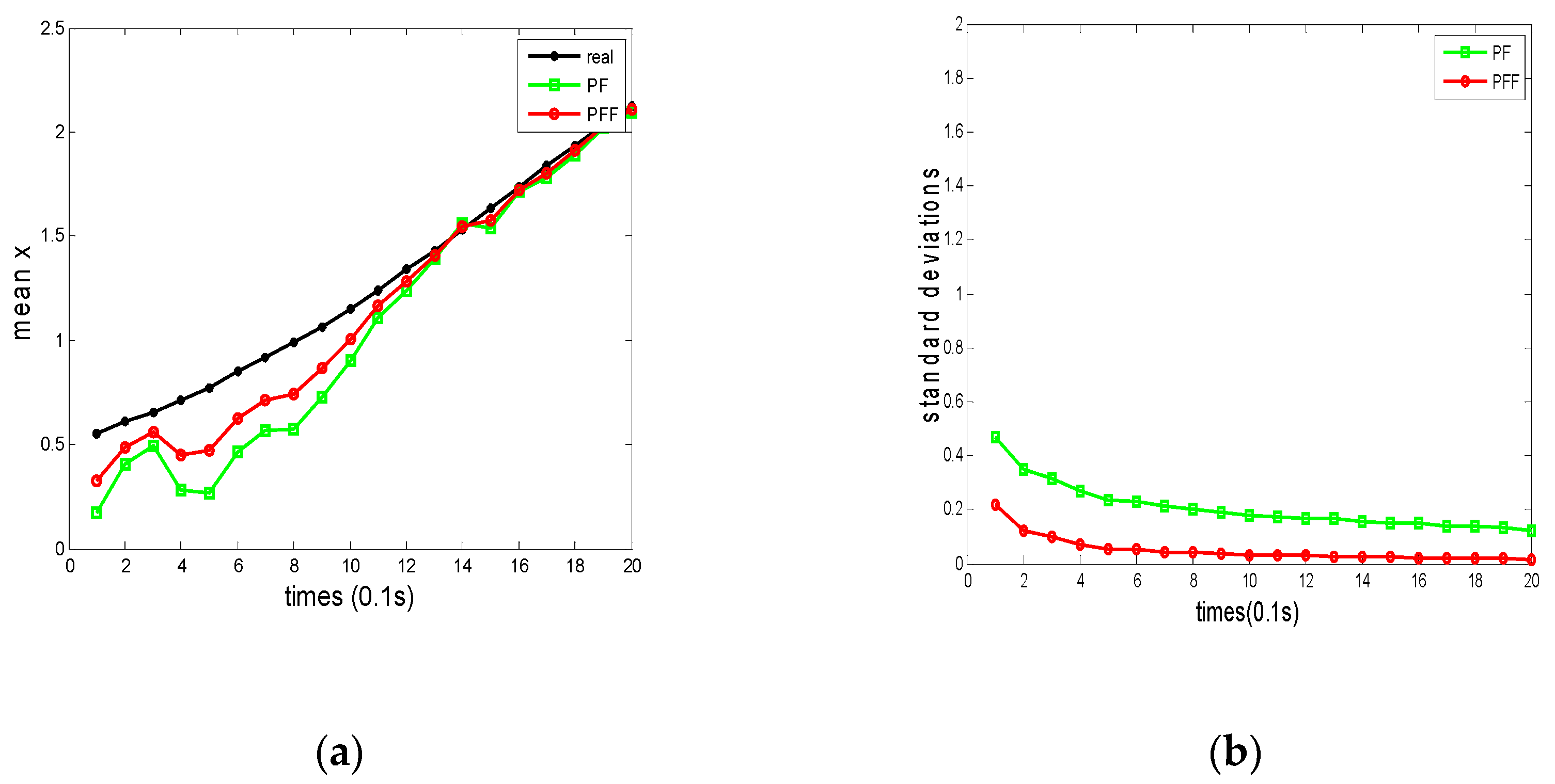Figure 3 provides a comparison chart of the estimated mean and variance of the two algorithms, where the PF estimation error is represented by a green line and the PFV-BEM estimation error is marked by a red line.

Figure 2a–d showcase partial estimation results of both particle filtering (PF) and the filtering algorithm proposed in this paper, along with the evolution of particles over time t. From Figure 2, it is evident that, in comparison to the PF algorithm, the proposed algorithm exhibits higher estimation accuracy, faster convergence speed, enhanced precision, and stable performance in system state estimation. The simulation results clearly demonstrate its capability to track the system state effectively. The feasibility of the proposed algorithm has been validated, making it apparent that PFV-BEM stands as an effective Bayesian estimation method for addressing state estimation problems in one-dimensional nonlinear systems.

4.2. Example 2 and Analysis

The continuous time stochastic differential equation interpretation of the dynamic tracking model is given by reference [27], which is described as follows:

State vector is defined as: $X\left(t\right)={\left[x\left(t\right)\hspace{1em}{v}_x\left(t\right)\hspace{1em}y\left(t\right)\hspace{1em}{v}_y\left(t\right)\right]}^T$

Measurement vector is defined as: $z\left(t\right)={\left[{\mathrm{r}}_{\mathrm{k}}\hspace{1em}{\theta }_{\mathrm{k}}\right]}^T$

state estimation model is given as: .

$$\dot{X}\left(t\right)=F_{k}X\left(t\right)+Q_k$$

(36)

the measurement model is denoted as

$$z_k=\left[\begin{array}{l}\sqrt{{\mathrm{x}}^2+{\mathrm{y}}^2}\\ \arctan ({\displaystyle \raisebox{1ex}{$y$}\!\left/ \!\raisebox{-1ex}{$x$}\right.})\end{array}\right]+R_{\mathrm{k}}$$

(37)

where: $Q_{\mathrm{k}},R_k$ are respectively described as process noise of state equation and measurement noise of measurement equation, the covariance matrix respectively are $Q$ and $R$.State Transition Matrix is given as

$$F_k=\left[\left[1, 1, 0, 0\right], \right[0, 1, 0, 0\left], \right[0, 0, 1, 1\left], \right[0, 0, 0, 1]]$$

Set the number of targets is 4, time steps are 400s, filter sampling time interval $\Delta T=1s$, running time T=400s, the number of particles is 2000.

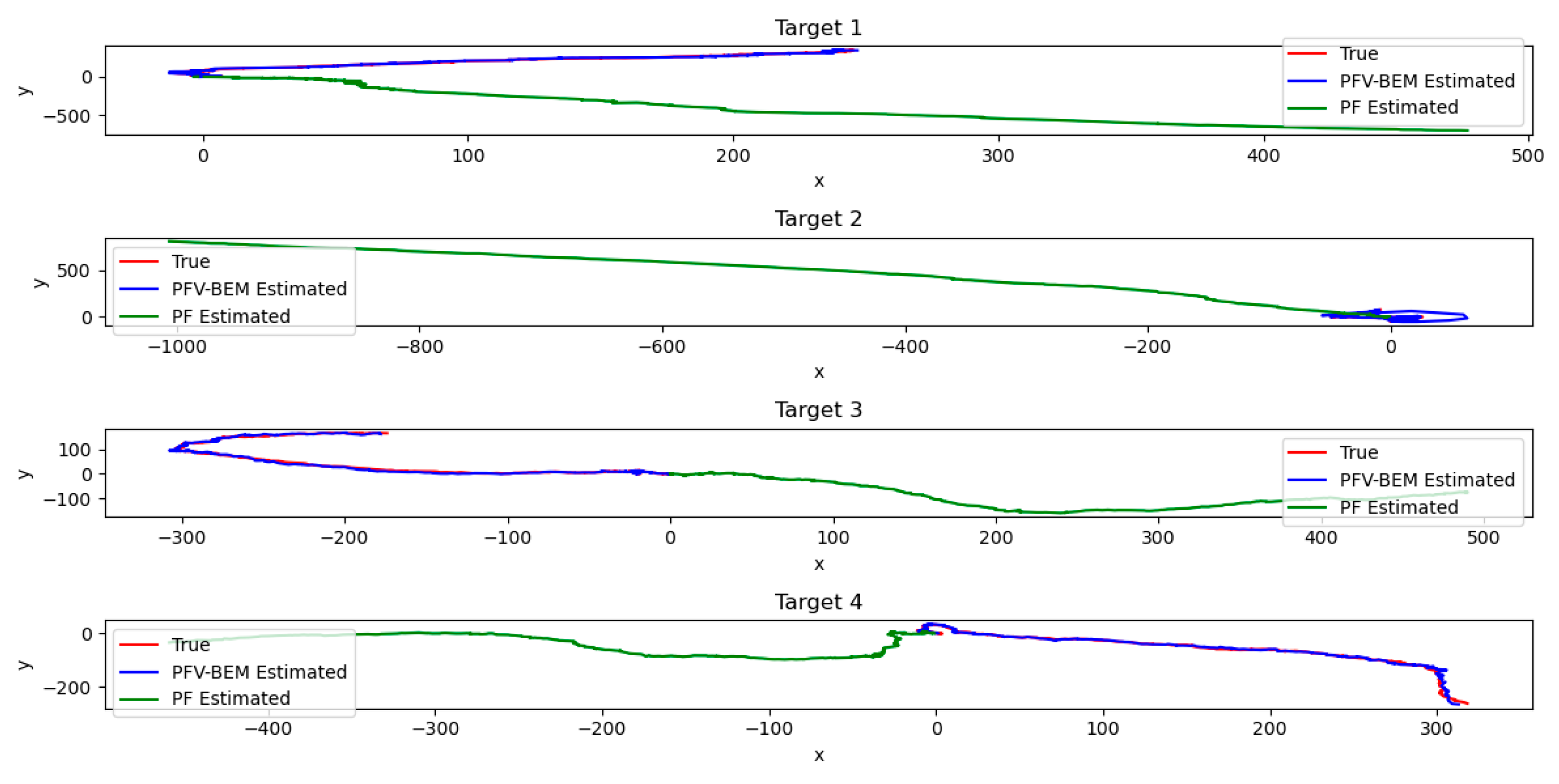
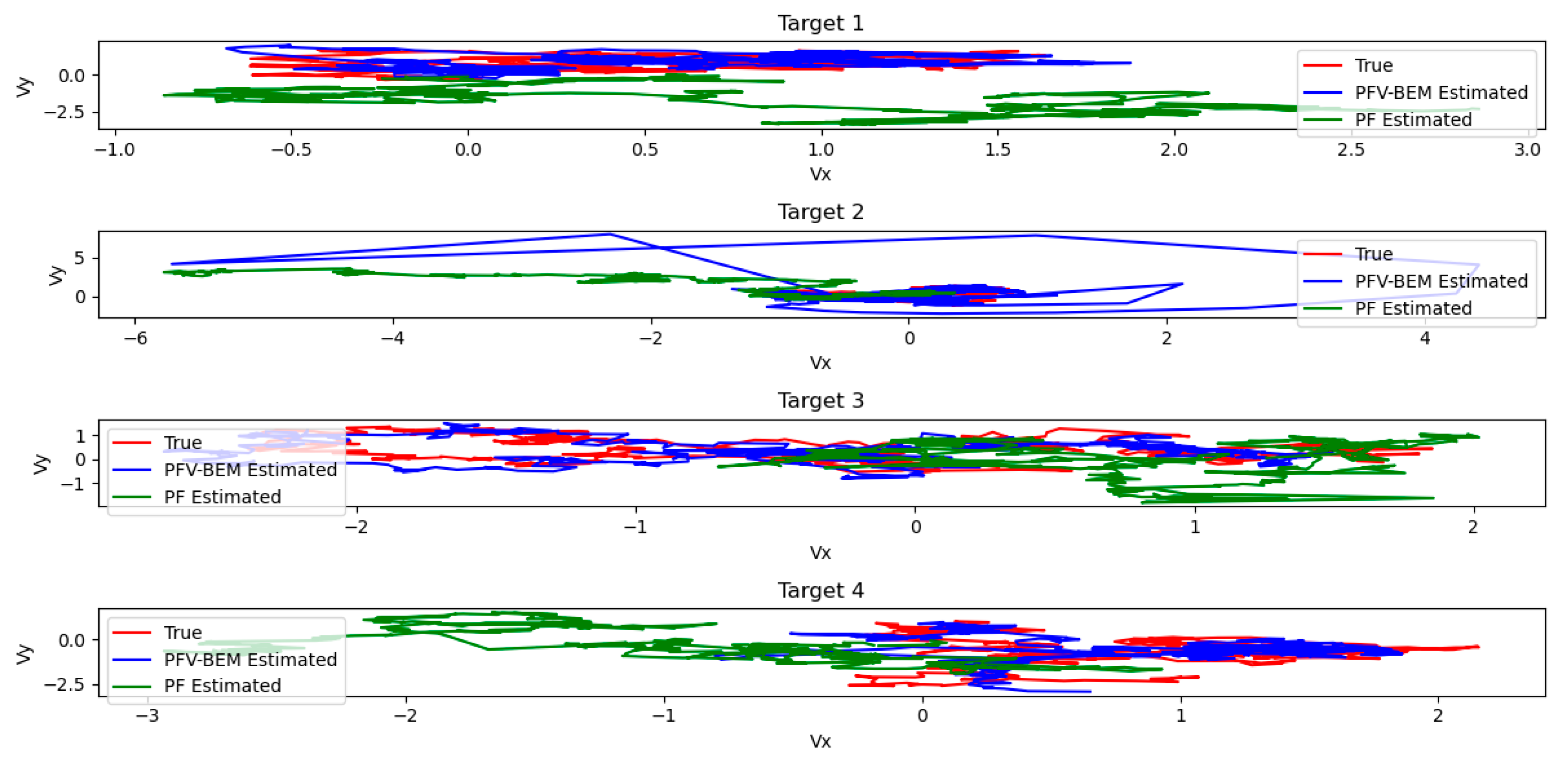
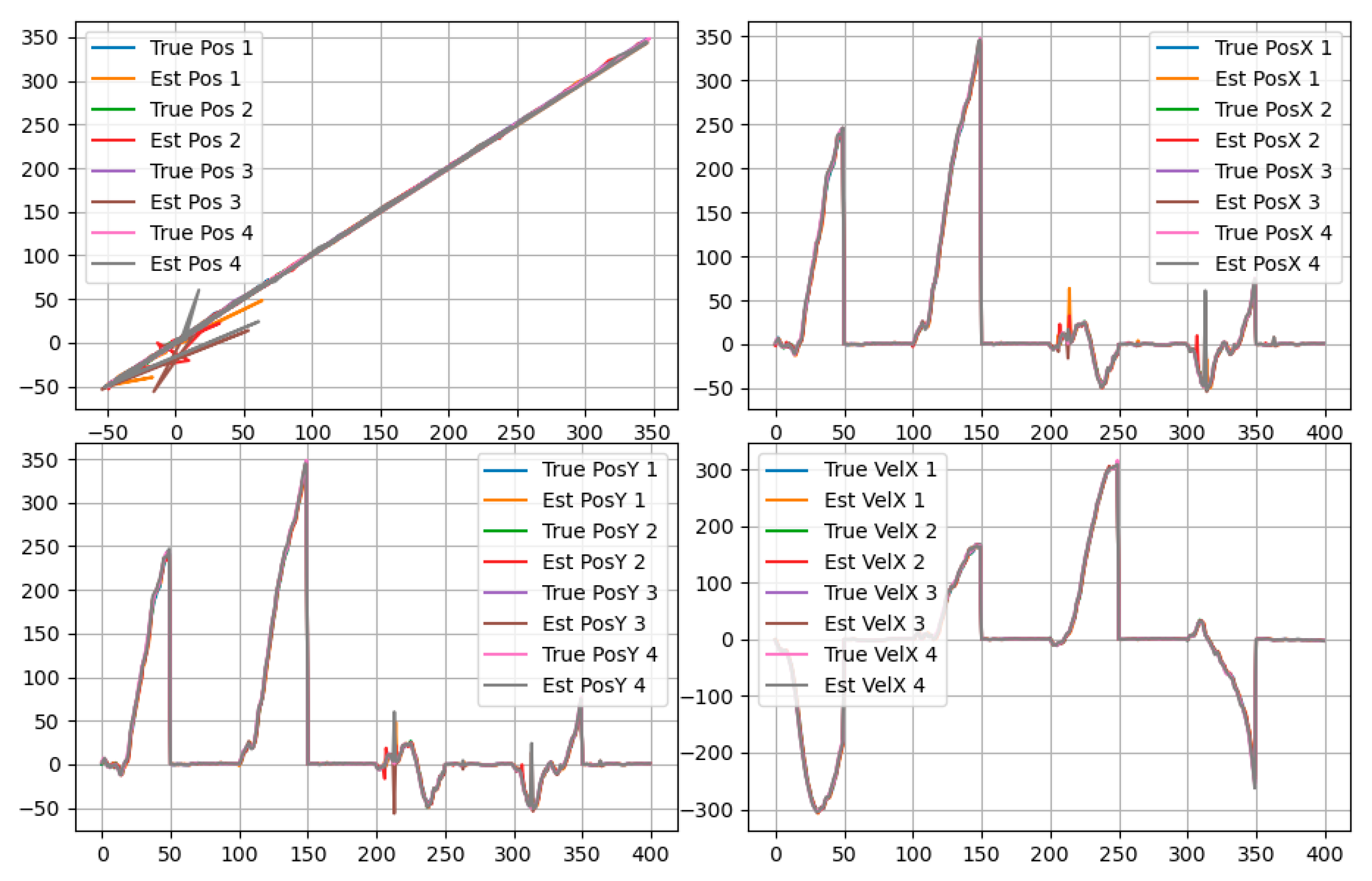
For the three non-linear filtering methods of PF and PFV-BEM. The state estimation results based on PF and PFV-BEM are shown in Figure 4, Figure 5, Figure 6 and Figure 7. Figure 4 displays the state estimation results for four targets based on PFV-BEM, including comparisons between the true position information of the four targets and the position estimates obtained using the proposed algorithm, as well as comparisons between the true velocity information of the four targets and the velocity estimates derived from the proposed algorithm. Figure 5 presents a comparison of the position estimates for the four targets using PF and PFV-BEM. Additionally, Figure 5 also shows a comparison of the velocity estimates for the four targets based on PF and PFV-BEM. 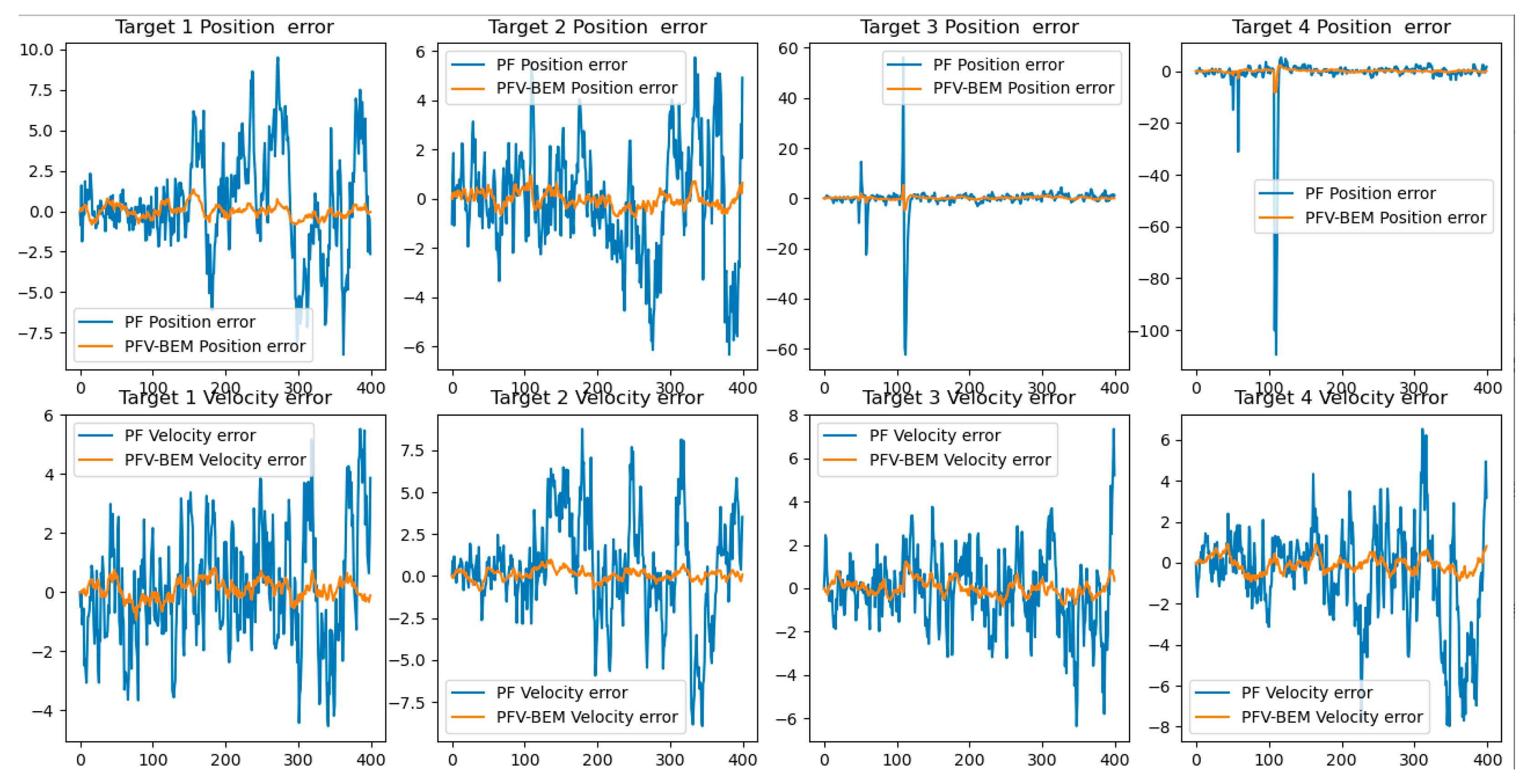Figure 6 demonstrates the position and velocity estimation errors for the four targets tracked by the two algorithms. Figure 7 provides a comparison chart of the estimated mean of the two algorithms, where the PF estimation error is represented by a blue line and the PFV-BEM estimation error is marked by a orange line.

The figure presents partial estimation results obtained using particle filtering (PF) and the filtering algorithm proposed in this paper. As observed in Figure 4, the algorithm proposed in this paper demonstrates high estimation accuracy and provides precise estimation results in system state estimation. The simulation results indicate that PFV-BEM can effectively track changes in the system state. This verifies the feasibility of the algorithm. Evidently, for high-dimensional nonlinear systems, PFV-BEM serves as an effective Bayesian estimation method for solving the problem of state estimation in nonlinear systems.

5. Conclusions

This article validates one of the effective algorithms of PFV-BEM in Bayesian estimation methods. The basic core of its algorithm is that the filter estimator accurately calculates the prior and posterior probability density functions (PDF) through Bayesian iteration, and then estimates the mean and standard deviation of the system state. The article elaborates on the theoretical derivation in detail, mainly covering two aspects: obtaining prior PDFs through state updates and obtaining posterior PDFs through measurement updates. Through simulation experiments, the PFV-BEM filter outperforms the particle filter (PF) method in estimation accuracy. It has shown significant advantages in processing sensor data of complex nonlinear systems, especially in high-dimensional state estimation problems. It not only improves performance, but also accelerates computation speed and reduces computational complexity. Although the algorithm provides high-precision approximate solutions through time iteration, the selection of iteration time intervals is still challenging, and the convergence and robustness of the algorithm need further research. Therefore, we are committed to exploring more robust Bayesian estimation methods. These unresolved issues will become the focus of our future research.