Submitted:
02 January 2025
Posted:
03 January 2025
You are already at the latest version
Abstract
The Yang–Baxter equation emerged from a theoretical physics article written by the Nobel laureate C.N. Yang and from statistical mechanics work of R.J. Baxter. Attempts to unify the algebra structures and the coalgebra structures have eventually led to new solutions of the Yang-Baxter equation. But, in order to capture the information encapsulated in modules over algebras and comodules over coalgebras, we will need some kind of extensions of the Yang-Baxter equation, called Yang-Baxter systems. Also, the Tzitzeica-Johnson theorem is generalized in the curent paper.
Keywords:
MSC: 16T05; 16T25; 53C05; 51N20; 01A60; 00A05 (Primary); 17C05; 17C50 (Secondary)
1. Introduction
2. Yang-Baxter Equations and Yang-Baxter Systems
3. Unifications Using Yang-Baxter Systems
4. On the Tzitzeica-Johnson Theorem
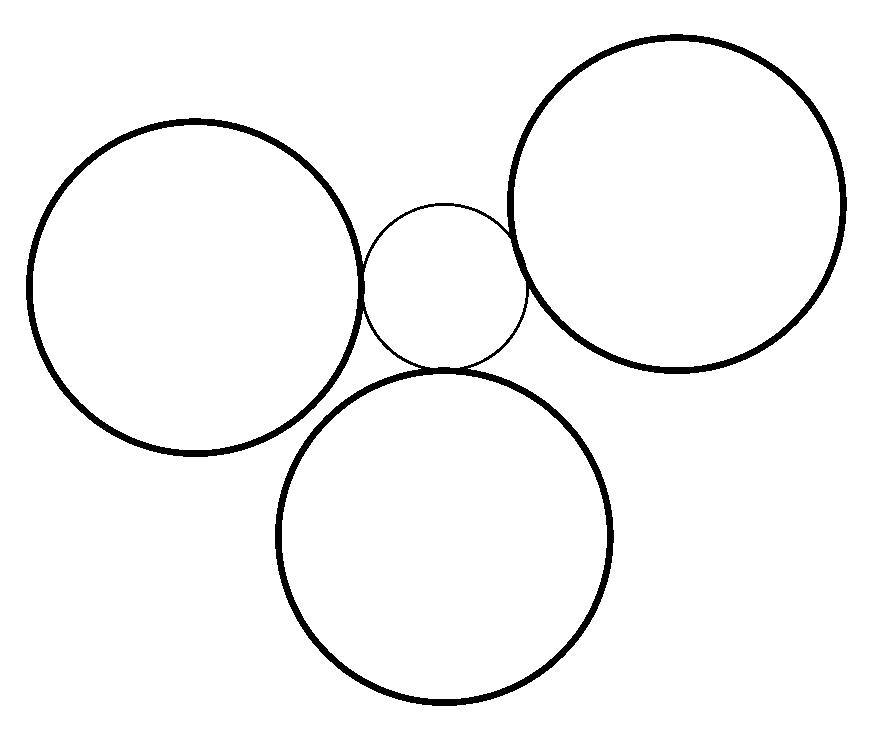
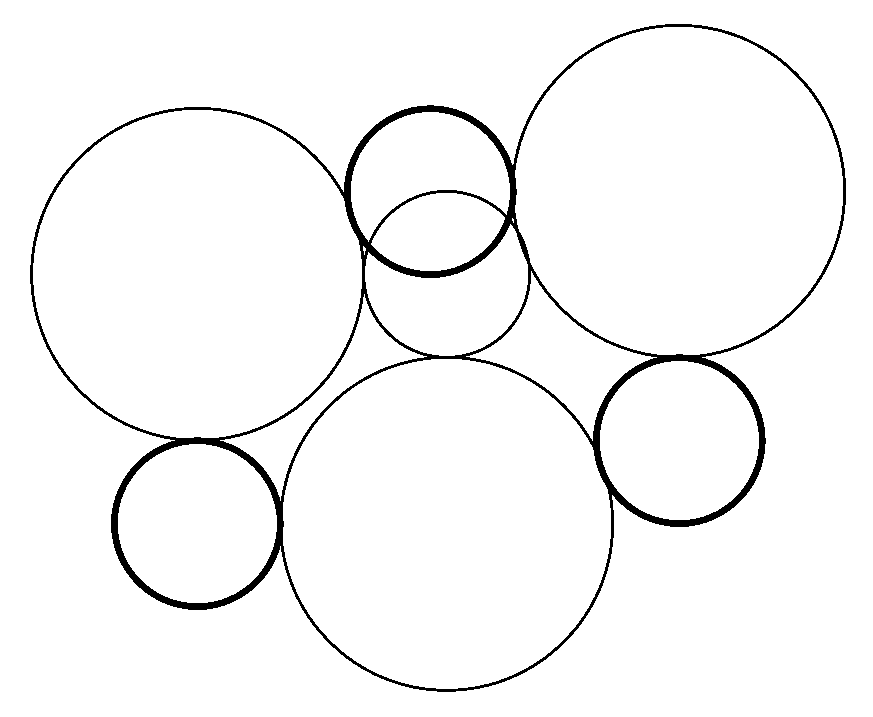
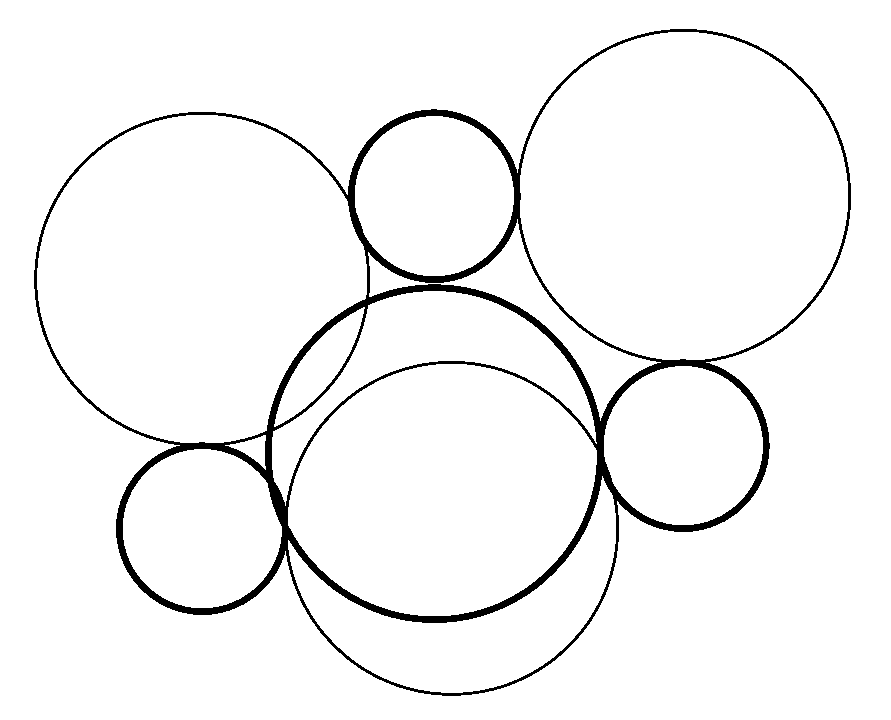
5. Conclusions and Further Comments
References
- C. N. Yang, Some exact results for the many-body problem in one dimension with repulsive delta-function interaction, Phys. Rev. Lett. 19(1967), 1312-1315. [CrossRef]
- R.J. Baxter, Exactly Solved Models in Statistical Mechanics, Acad. Press, London,1982.
- R.J. Baxter, Partition function for the eight-vertex lattice model, Ann. Physics 70(1972), 193-228. [CrossRef]
- F.F. Nichita, Self-Inverse Yang-Baxter Operators from (Co)Algebra structures, Journal of Algebra, Volume 218, Number 2, 738-759(1999). [CrossRef]
- V. Turaev, The Yang-Baxter equation and invariants of links, Invent. Math. 1988 92 527-553.
- V. F. R. Jones, A polynomial invariant for knots via von Neumann algebras, Bull. Amer. Math. Soc. 12 (1985), 103–111. [CrossRef]
- Nichita, F.F.(Ed.): Hopf Algebras, Quantum Groups and Yang-Baxter Equations, MDPI, (2019), ISBN 978-3-03897-325-6 (PDF), ISBN 978-3-03897-324-9 (Pbk).
- Elisabeth Remm, On filiform Lie algebras. Geometric and algebraic studies, Revue Roumaine de Mathematiques Pures et Appliquees, Selected papers from the 13th International Workshop on Differential Geometry and its Applications (September, 2017) TOME LXIII, NO 2, 2018, 179-209. [CrossRef]
- Nichita, F.F., Yang–Baxter Equations, Computational Methods and Applications. Axioms 2015, 4, 423-435. [CrossRef]
- Nichita, F.F., On Jordan algebras and unification theories, Revue Roumaine de Mathematiques Pures et Appliquees 61(4), 2016, 305-316.
- N. Anghel, Heron Triangles with constant area and perimeter, talk, Differential Geometry and its Applications, UPG, 9 - 11 July, 2019, submitted to Revue Roumaine de Mathematiques Pures et Appliquees.
- Paolo Bellingeri, Virtual braid groups and permutations, talk, Differential Geometry and its Applications, UPG, 9 - 11 July, 2019.
- Tomasz Brzeziński, Towards semi-trusses Revue Roumaine de Mathematiques Pures et Appliquees, No. 2 (2018), pp. 75-89.
- T. Brzezinski, T.; Nichita, F.F. Yang-Baxter systems and entwined structures, Communications in Algebra 2005, vol. 33(4), pp. 1083–1093. [CrossRef]
- S. Dăscălescu and F. F. Nichita, Yang-Baxter operators arising from (co)algebra structures. Comm. Algebra 1999, 27, 5833–5845. [CrossRef]
- P. Freyd, D. Yetter, J. Hoste, W. B. R. Lickorish, K. Millett, A. Ocneanu, A new polynomial invariant of knots and links, Bull. Amer. Math. Soc. 12 (1985), 239–246. [CrossRef]
- L. Hlavaty and L. Snobl, Solution of the Yang-Baxter system for quantum doubles, Int. J. Mod. Phys. A14 (1999), 3029–3058. [CrossRef]
- M. Jimbo, Quantum R matrix for the generalized Toda system, Lett. Math. Phys. 11 (1986), 247–252.
- L. H. Kauffman, New invariants in the theory of knots, Astérisque 163-164 (1988), 137–219. [CrossRef]
- V. Lebed, Braided Systems: A Unified Treatment of Algebraic Structures with Several Operations, Homology, Homotopy and Applications, vol. 19(2), (2017), pp. 141-174. [CrossRef]
- V. Lebed, Homologies of algebraic structures via braidings and quantum shuffles, Journal of Algebra 391, 152-192 (2013). [CrossRef]
- Majid, S., Markl, M., Glueing operations for R-Matrices, quantum groups and link-invariants of Hecke type, Math. Proc. Cambridge Philos. Soc. 119 (1996), 139–166. [CrossRef]
- G. Massuyeau and F.F. Nichita, Yang-Baxter operators arising from algebra structures and the Alexander polynomial of knots, Comm. Algebra 2005, 33 (7) 2375-2385. [CrossRef]
- Moise, L.D.; Cristea, R Gheorghe Titeica - reverbertii si permanente ale geometriei in contemporaneitate, Proceedings, Conferinta Nationala de Invatamant Virtual, editia a XI-a, 2013, 150-156.
- J. Murakami, A state model for the multi–variable Alexander polynomial, Pacific J. Math. 157, 1 (1993), 109–135. [CrossRef]
- Florin Nichita, On Applications of UJLA Structures, talk, Differential Geometry and its Applications, UPG, 9 - 11 July, 2019.
- Nichita, F.F. Unification Theories: Examples and Applications. Axioms 2018, 7, 85. [CrossRef]
- Nichita, F.F. Unification Theories: New Results and Examples. Axioms 2019, 8, 60. [CrossRef]
- Nichita, F.F. Mathematics and Poetry • Unification, Unity, Union. Sci 2020, 2, 58.
- Nichita, F.F. (Ed.) Hopf Algebras, Quantum Groups and Yang-Baxter Equations, MDPI, 2019, ISBN 978-3-03897-324-9 (Pbk); ISBN 978-3-03897-325-6 (PDF).
- J. H.H. Perk and H. Au-Yang, Yang-Baxter Equations, Encyclopedia of Mathematical Physics, eds. J.-P. Françoise, G.L. Naber and Tsou S.T., Oxford: Elsevier, 2006 (ISBN 978-0-1251-2666-3), volume 5, pages 465-473.
- Radu Popescu, Resonance varieties. Definition and applications, talk, Differential Geometry and its Applications, UPG, 9 - 11 July, 2019.
- J. H. Przytycki, P. Traczyk, Invariants of links of Conway type, Kobe J. Math. 4, 2 (1987), 115–139. [CrossRef]
- Elisabeth Remm, Rigidity of Lie algebras, poster, Differential Geometry and its Applications, UPG, 9 - 11 July, 2019, submitted to Revue Roumaine de Mathematiques Pures et Appliquees.
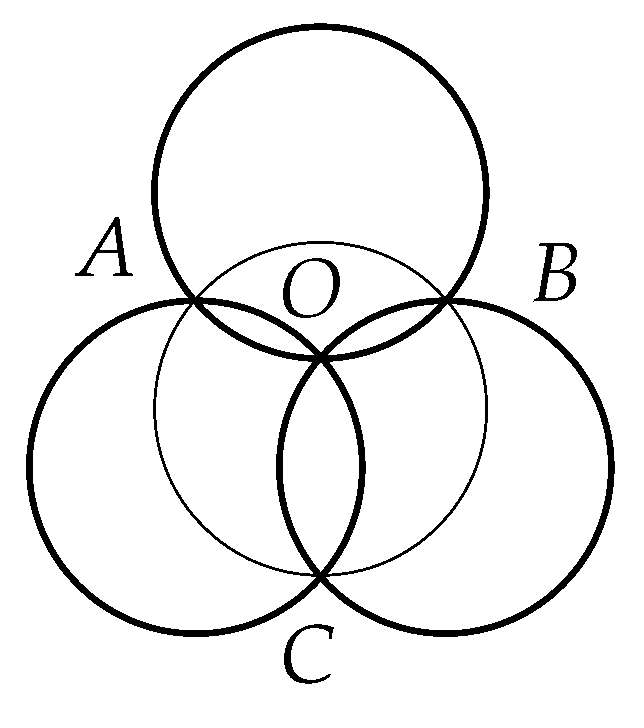

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




