Submitted:
31 December 2024
Posted:
31 December 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Methods
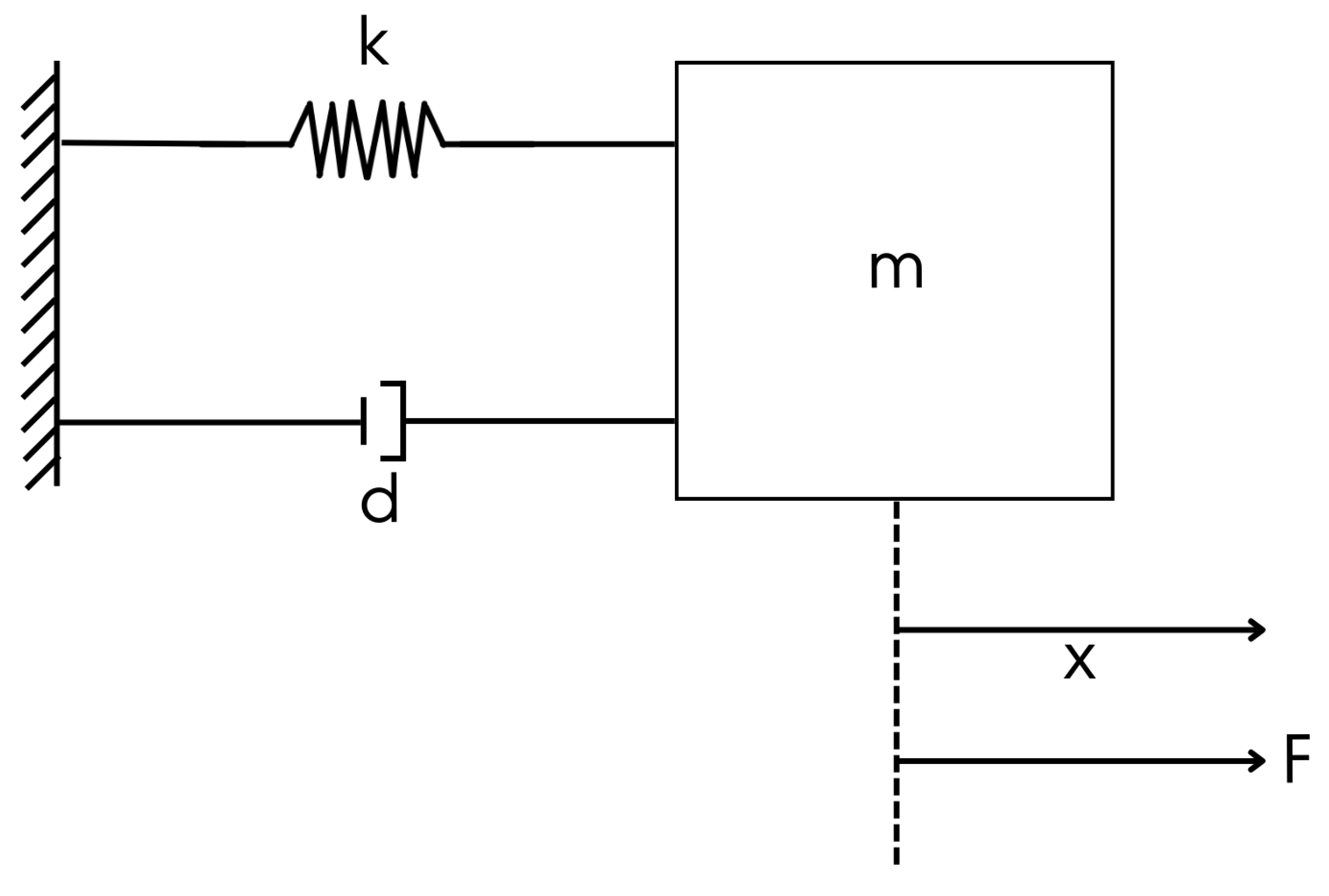
2.1. Mathematical Formulation
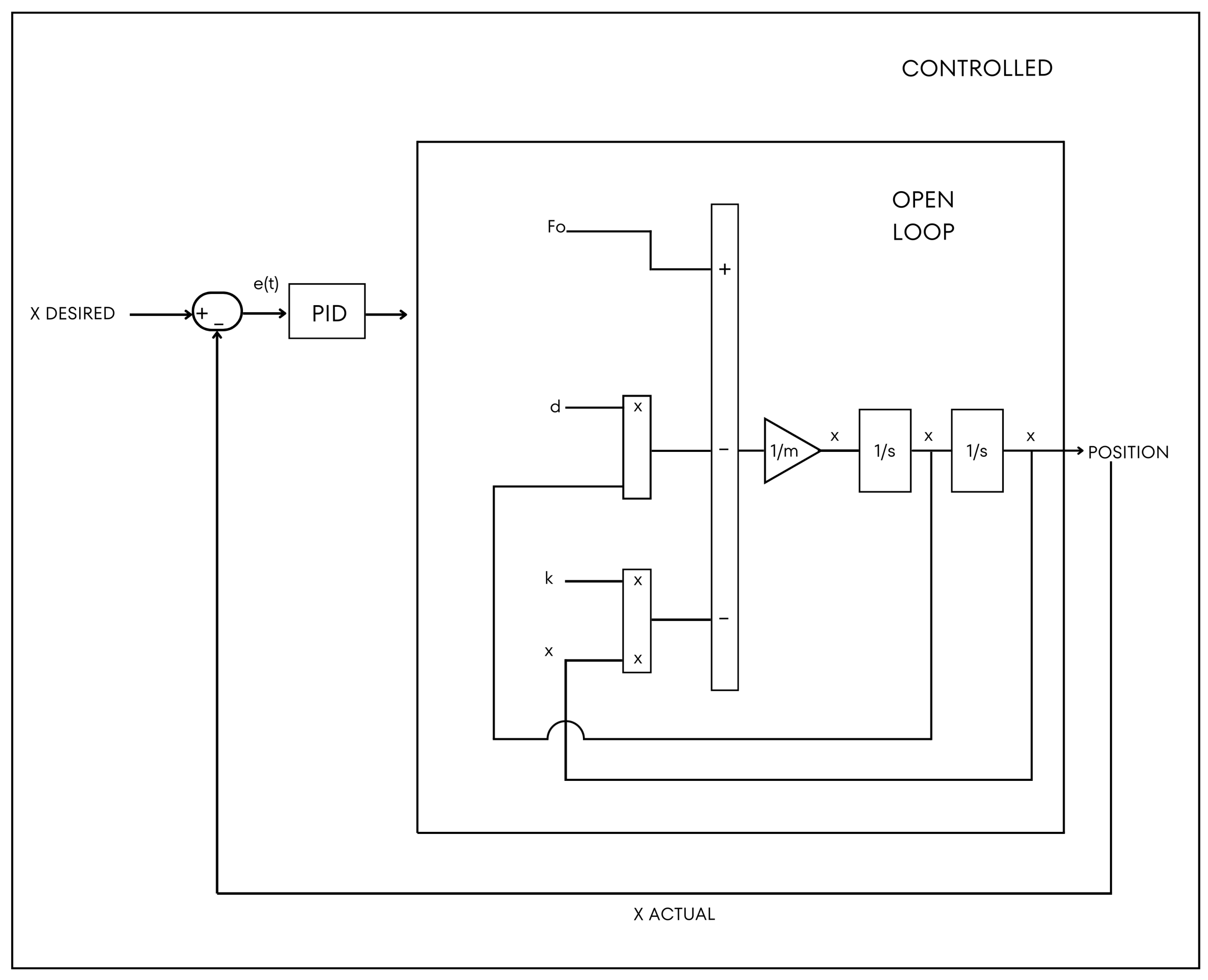
2.2. Numerical Implementation
2.3. Stability Analysis
2.4. Statistical Framework for Performance Analysis
3. Results and Discussion
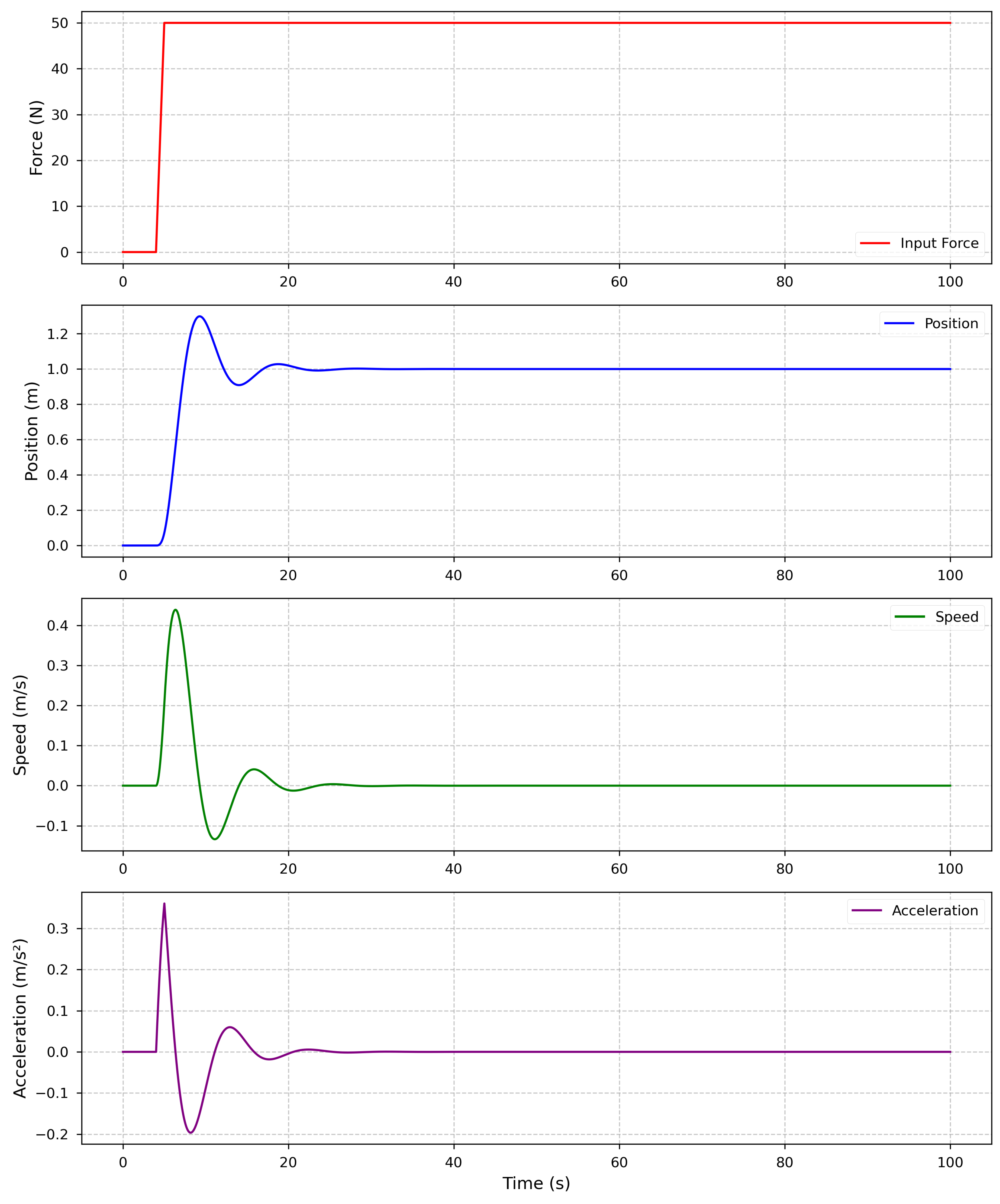
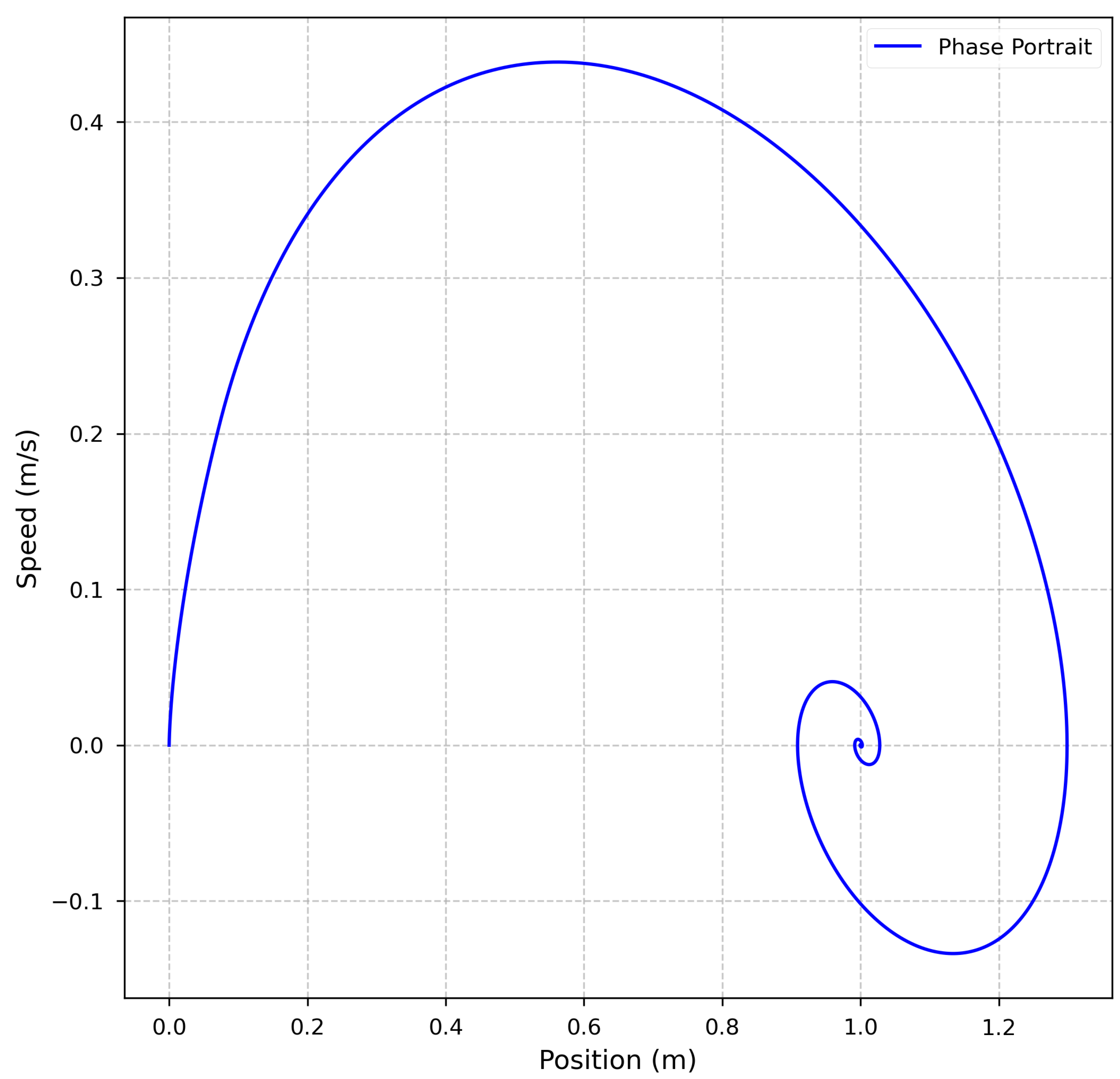
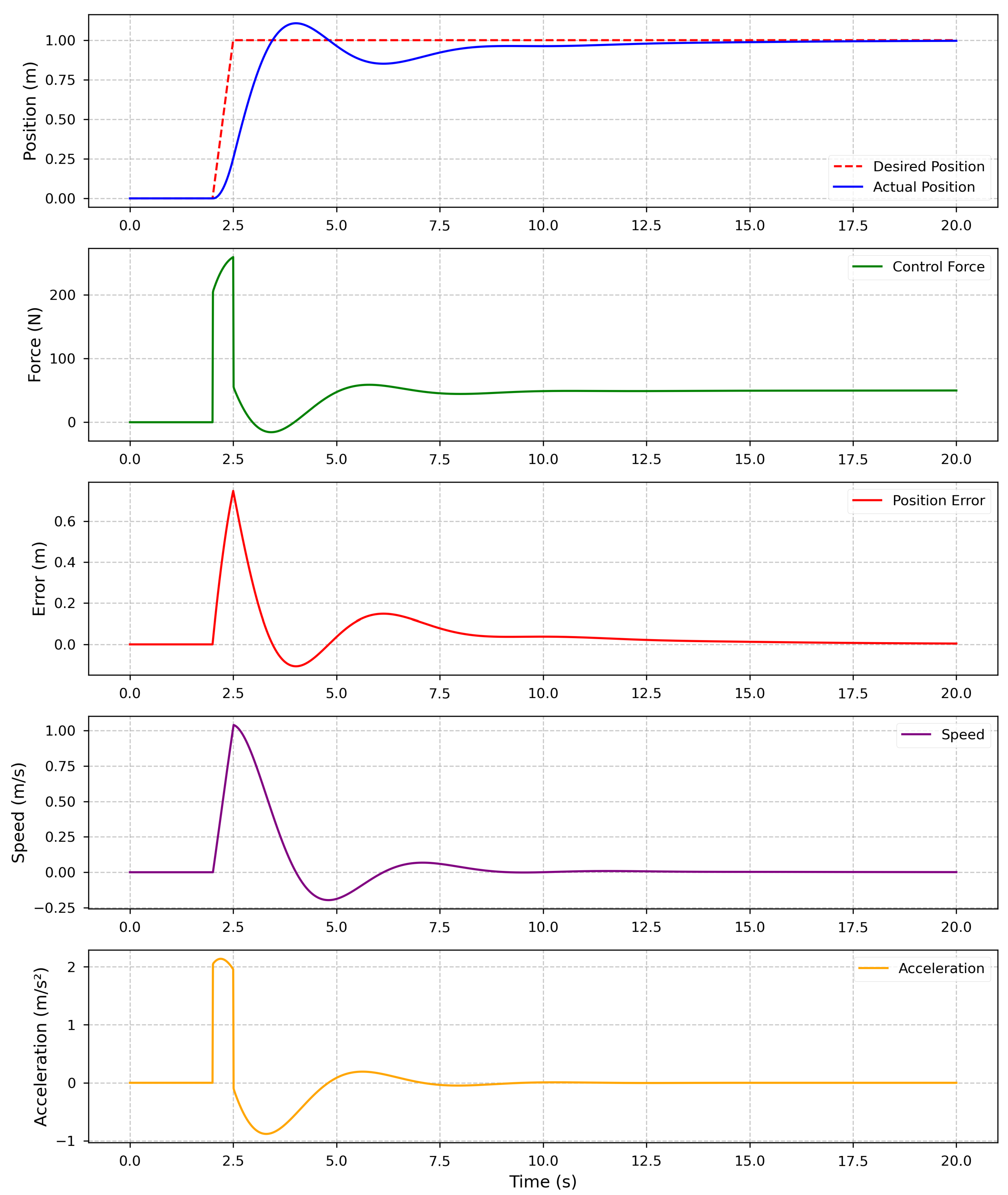
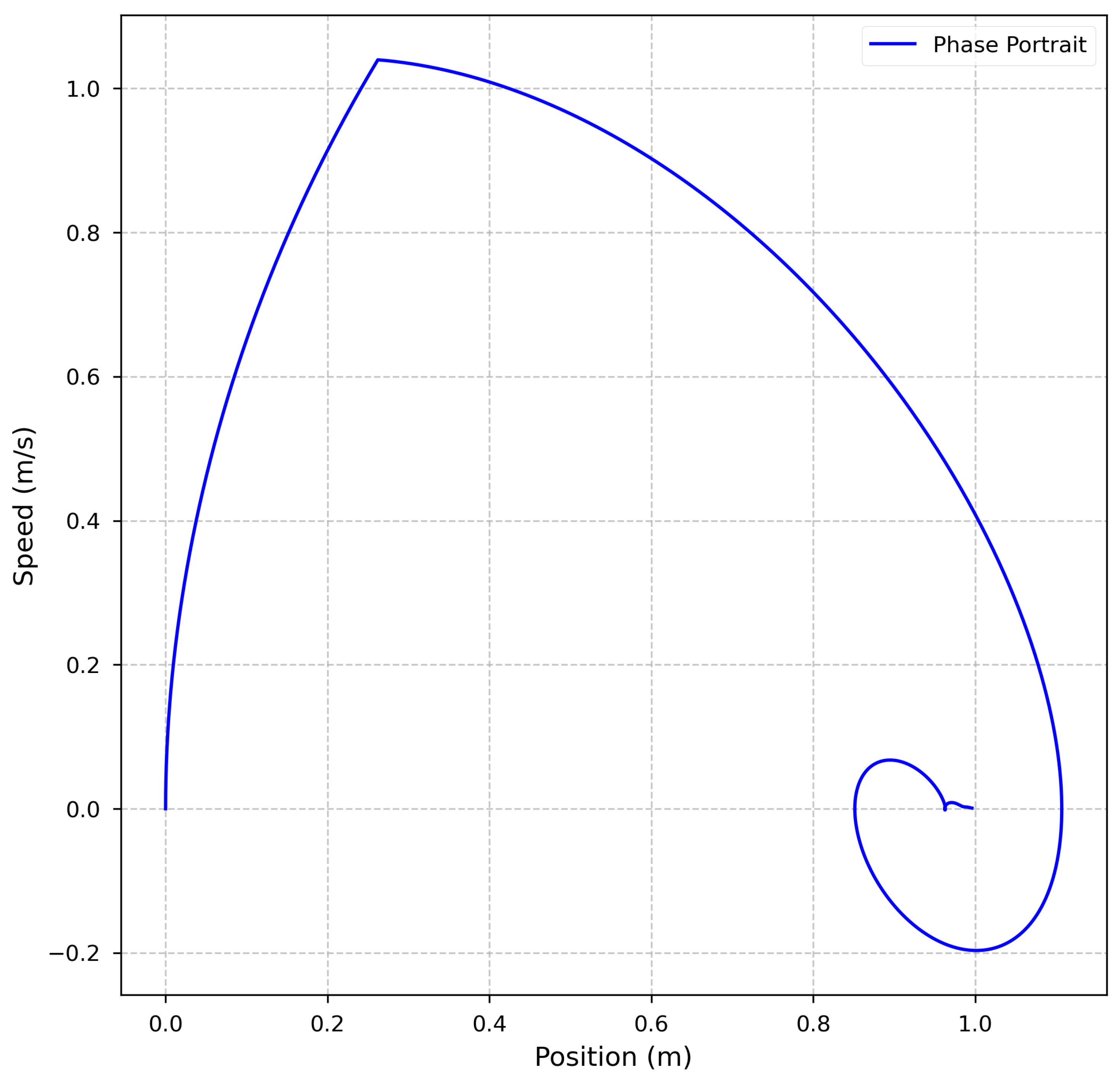
3.1. System Dynamics
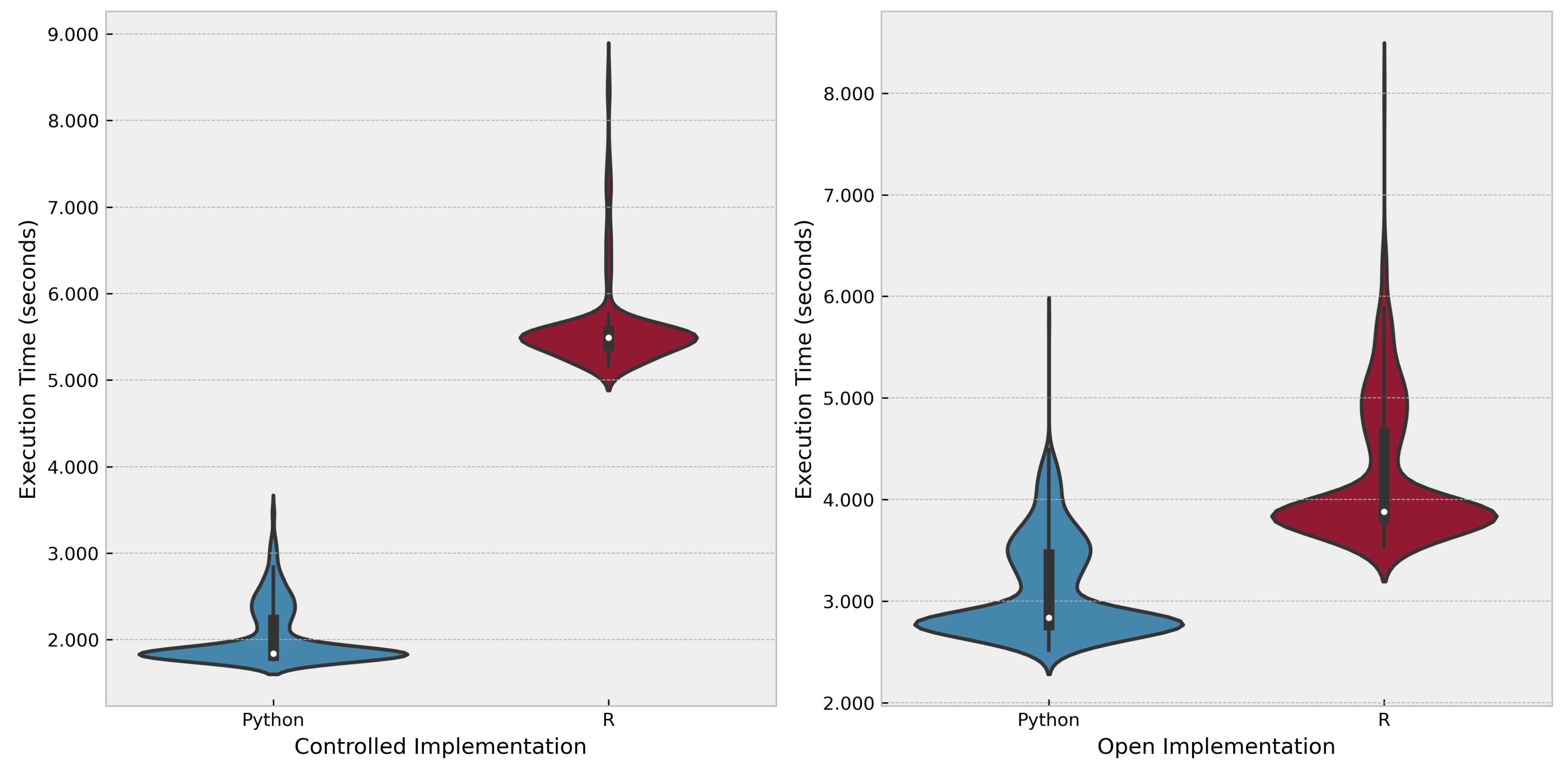
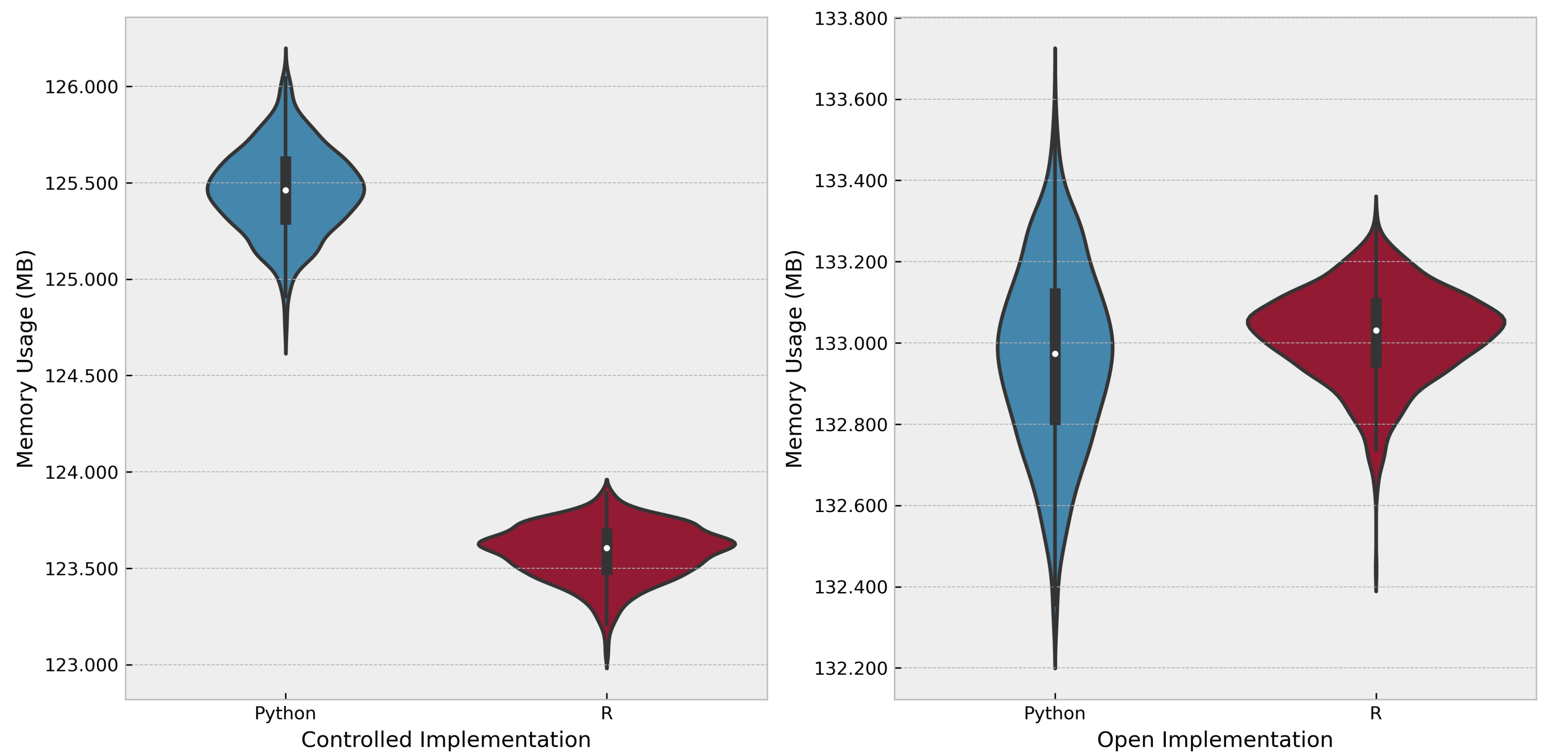
3.2. Performance Analysis
4. Conclusion
Declarations
References
- Irawan, D.E.; Pourret, O.; Besançon, L.; Herho, S.H.S.; Ridlo, I.A.; Abraham, J. Post-Publication Review: The Role of Science News Outlets and Social Media. Annals of Library and Information Studies 2024, 71, 465–474. [Google Scholar] [CrossRef]
- Fraser, N.; Brierley, L.; Dey, G.; Polka, J.K.; Pálfy, M.; Nanni, F.; Coates, J.A. The evolving role of preprints in the dissemination of COVID-19 research and their impact on the science communication landscape. PLoS Biology 2021, 19, e3000959. [Google Scholar] [CrossRef] [PubMed]
- Sugimoto, C.R.; Work, S.; Larivière, V.; Haustein, S. Scholarly use of social media and altmetrics: A review of the literature. Journal of the Association for Information Science and Technology 2017, 68, 2037–2062. [Google Scholar] [CrossRef]
- Harris, C.; Millman, K.; van der Walt, S.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.; et al. Array Programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nature Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the Proceedings of the 9th Python in Science Conference; pp. 201051–56. [CrossRef]
- Soetaert, K.; Petzoldt, T.; Setzer, R.W. Solving Differential Equations in R: Package deSolve. Journal of Statistical Software 2010, 33, 1–25. [Google Scholar] [CrossRef]
- Wickham, H.; Averick, M.; Bryan, J.; Chang, W.; McGowan, L.D.; François, R.; Grolemund, G.; Hayes, A.; Henry, L.; Hester, J.; et al. Welcome to the Tidyverse. Journal of Open Source Software 2019, 4, 1686. [Google Scholar] [CrossRef]
- Ogata, K. Modern Control Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Khalil, H.K. Nonlinear Systems; Prentice Hall: Upper Saddle River, New Jersey, USA, 2002. [Google Scholar]
- Dorf, R.C.; Bishop, R.H. Modern Control Systems; Prentice Hall: Upper Saddle River, NJ, USA, 2011. [Google Scholar]
- Nise, N.S. Control Systems Engineering; John Wiley & Sons: New York City, NY, USA, 2020. [Google Scholar]
- Franklin, G.F.; Powell, J.D.; Emami-Naeini, A. Feedback Control of Dynamic Systems; Pearson: Upper Saddle River, NJ, USA, 2015. [Google Scholar]
- Åström, K.J.; Murray, R.M. Feedback Systems: An Introduction for Scientists and Engineers; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Chen, C.T. Linear System Theory and Design; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Waskom, M.L. Seaborn: Statistical Data Visualization. Journal of Open Source Software 2021, 6, 3021. [Google Scholar] [CrossRef]
- Georges, A.; Buytaert, D.; Eeckhout, L. Statistically Rigorous Java Performance Evaluation. ACM SIGPLAN Notices 2007, 42, 57–76. [Google Scholar] [CrossRef]
- Thompson, S.K. Sampling; Wiley Series in Probability and Statistics: New York City, NY, USA, 2012. [Google Scholar] [CrossRef]
- Herho, S.; Anwar, I.; Herho, K.; Dharma, C.; Irawan, D. COMPARING SCIENTIFIC COMPUTING ENVIRONMENTS FOR SIMULATING 2D NON-BUOYANT FLUID PARCEL TRAJECTORY UNDER INERTIAL OSCILLATION: A PRELIMINARY EDUCATIONAL STUDY. Indonesian Physical Review 2024, 7, 451–468. [Google Scholar] [CrossRef]
- Herho, S.; Fajary, F.; Herho, K.; Anwar, I.; Suwarman, R.; Irawan, D. Reappraising Double Pendulum Dynamics across Multiple Computational Platforms. Preprints 2024. [Google Scholar] [CrossRef]
- Herho, S.; Kaban, S.N.; Irawan, D.E.; Kapid, R. Efficient 1D Heat Equation Solver: Leveraging Numba in Python. Eksakta : Berkala Ilmiah Bidang MIPA. [CrossRef]
- Jain, R. The Art of Computer Systems Performance Analysis: Techniques for Experimental Design, Measurement, Simulation, and Modeling; John Wiley & Sons: New York, USA, 1991. [Google Scholar]
- Brown, R.J.C.; Brown, R.F.C. Statistical Analysis of Measurement Data; Royal Society of Chemistry: London, United Kingdom, 1998. [Google Scholar]
- Hoaglin, D.C.; Mosteller, F.; Tukey, J.W. Understanding Robust and Exploratory Data Analysis; Wiley-Interscience: Hoboken, NJ, USA, 2000. [Google Scholar]
- Mostafavi, S.; Hakami, V.; Paydar, F. Performance Evaluation of Software-Defined Networking Controllers: A Comparative Study. Computer and Knowledge Engineering 2020, 2, 63–73. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: New York City, NY, USA, 2017. [Google Scholar]
- Bulmer, M.G. Principles of Statistics; Dover Publications: New York, USA, 1979. [Google Scholar]
- Razali, N.M.; Wah, Y.B. Power Comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling Tests. Journal of Statistical Modeling and Analytics 2011, 2, 21–33. [Google Scholar]
- Siegel, S. Nonparametric Statistics for the Behavioral Sciences; McGraw-Hill: New York City, NY, USA, 1956. [Google Scholar]
- Wilcoxon, F. Individual Comparisons by Ranking Methods. Biometrics Bulletin 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Levene, H. Robust Tests for Equality of Variances. In Contributions to Probability and Statistics; Olkin, I., Ed.; Stanford University Press: Stanford, California, USA, 1960; pp. 278–292. [Google Scholar]
- Brown, M.B.; Forsythe, A.B. Robust Tests for the Equality of Variances. Journal of the American Statistical Association 1974, 69, 364–367. [Google Scholar] [CrossRef]
- Sullivan, G.M.; Feinn, R. Using Effect Size—or Why the P Value is Not Enough. Journal of Graduate Medical Education 2012, 4, 279–282. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences; Routledge: New York City, NY, USA, 1988. [Google Scholar] [CrossRef]
- Sawilowsky, S.S. New Effect Size Rules of Thumb. Journal of Modern Applied Statistical Methods 2009, 8, 597–599. [Google Scholar] [CrossRef]
- Iglewicz, B.; Hoaglin, D.C. Volume 16: How to Detect and Handle Outliers; ASQC Quality Press: Milwaukee, WI, USA, 1993. [Google Scholar]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly Detection: A Survey. ACM Computing Surveys 2009, 41, 1–58. [Google Scholar] [CrossRef]
- Rousseeuw, P.J.; Croux, C. Alternatives to the Median Absolute Deviation. Journal of the American Statistical Association 1993, 88, 1273–1283. [Google Scholar] [CrossRef]
- Tukey, J.W. Exploratory Data Analysis; Addison-Wesley: Reading, MA, USA, 1977. [Google Scholar]
- Aggarwal, C.C. Outlier Analysis; Springer: New York City, NY, USA, 2013. [Google Scholar] [CrossRef]
- Mytkowicz, T.; Diwan, A.; Hauswirth, M.; Sweeney, P.F. Producing Wrong Data Without Doing Anything Obviously Wrong! ACM SIGARCH Computer Architecture News 2009, 37, 265–276. [Google Scholar] [CrossRef]
- Altman, D.G.; Machin, D.; Bryant, T.N.; Gardner, M.J. Statistics with Confidence: Confidence Intervals and Statistical Guidelines; BMJ Books: London, UK, 2013. [Google Scholar]
- Masini, S.; Bientinesi, P. High-Performance Parallel Computations Using Python as High-Level Language. In Proceedings of the Euro-Par 2010 Parallel Processing Workshops; Guarracino, M.R.; Vivien, F.; Träff, J.L.; Cannatoro, M.; Danelutto, M.; Hast, A.; Perla, F.; Knüpfer, A.; Di Martino, B.; Alexander, M., Eds., Berlin, Heidelberg; 2011; pp. 541–548. [Google Scholar] [CrossRef]
- Raschka, S.; Patterson, J.; Nolet, C. Machine Learning in Python: Main Developments and Technology Trends in Data Science, Machine Learning, and Artificial Intelligence. Information 2020, 11, 193. [Google Scholar] [CrossRef]
- Watson, A.; Babu, D.S.V.; Ray, S. Sanzu: A data science benchmark. In Proceedings of the 2017 IEEE International Conference on Big Data (Big Data); 2017; pp. 263–272. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).




