Submitted:
10 January 2025
Posted:
10 January 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Composite Signal’s Distribution and the Dataset
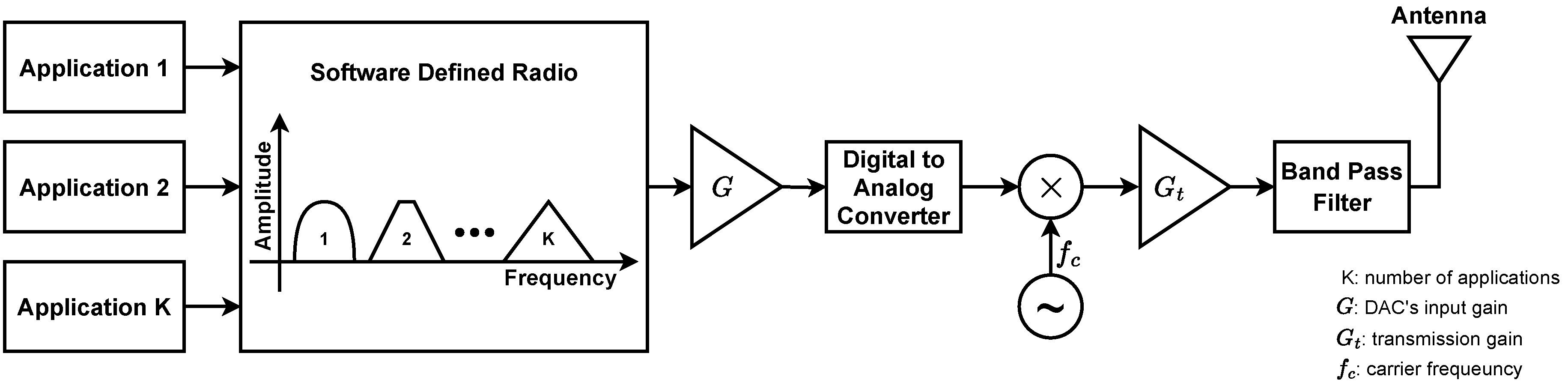
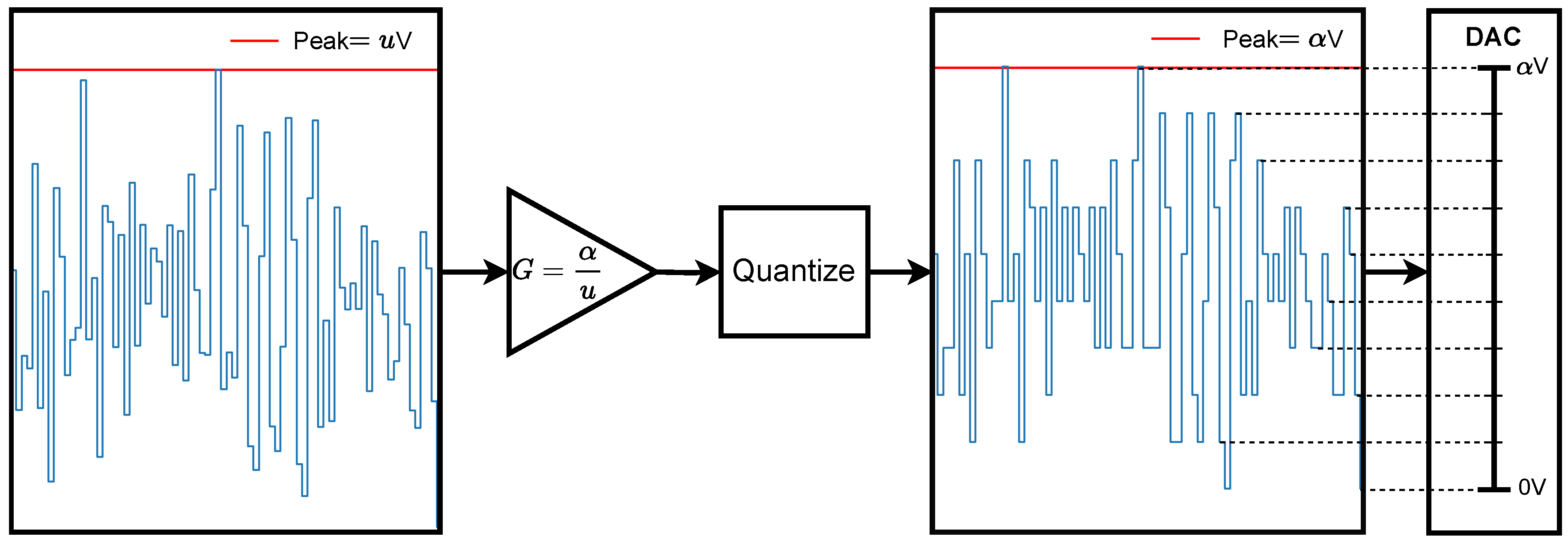
2.1. Composite Signal
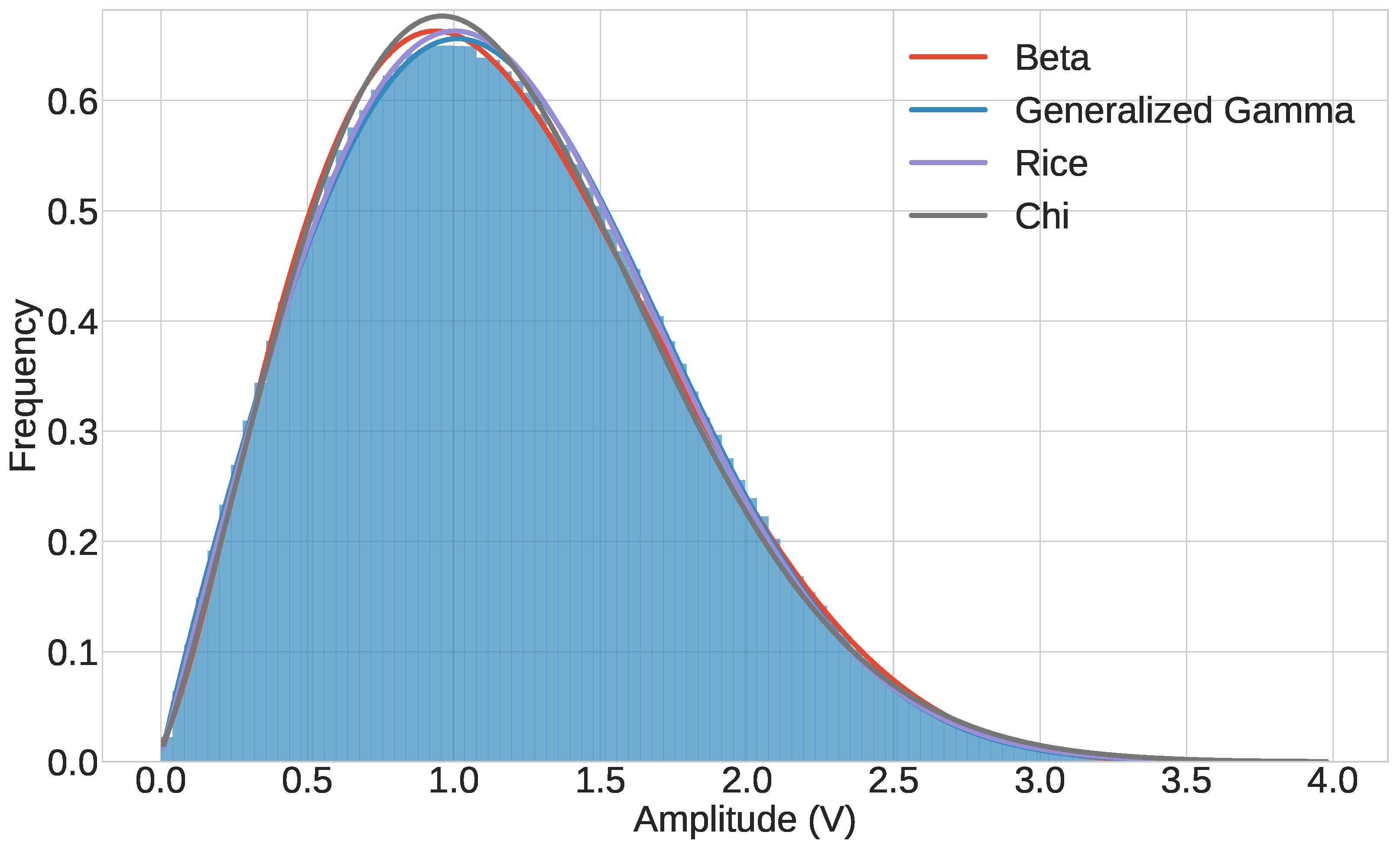
2.2. Distribution Fitting
2.3. Dataset
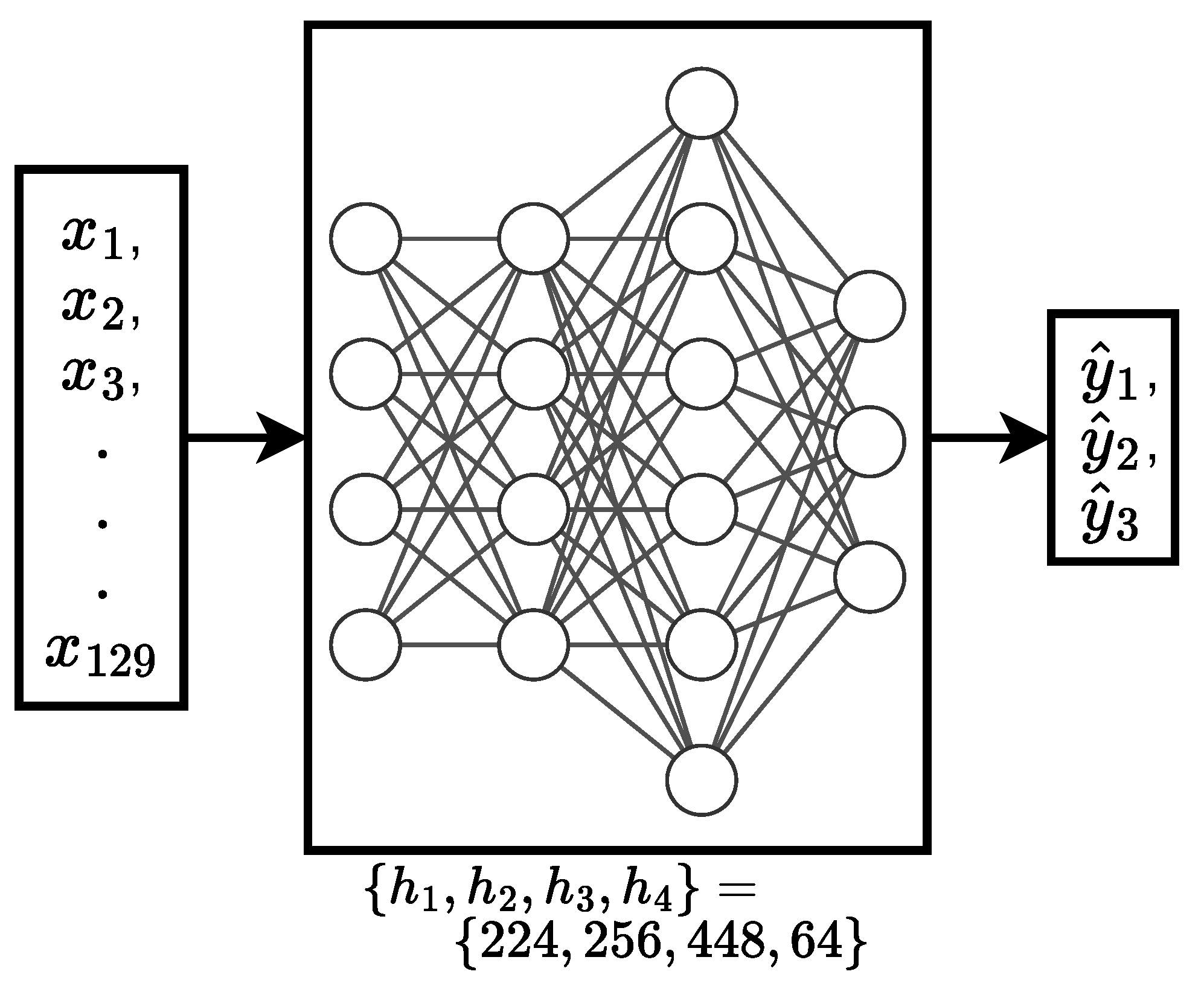
3. DNN Regression
4. Experiments, Results, and Analysis
4.1. K-Fold Cross Validation
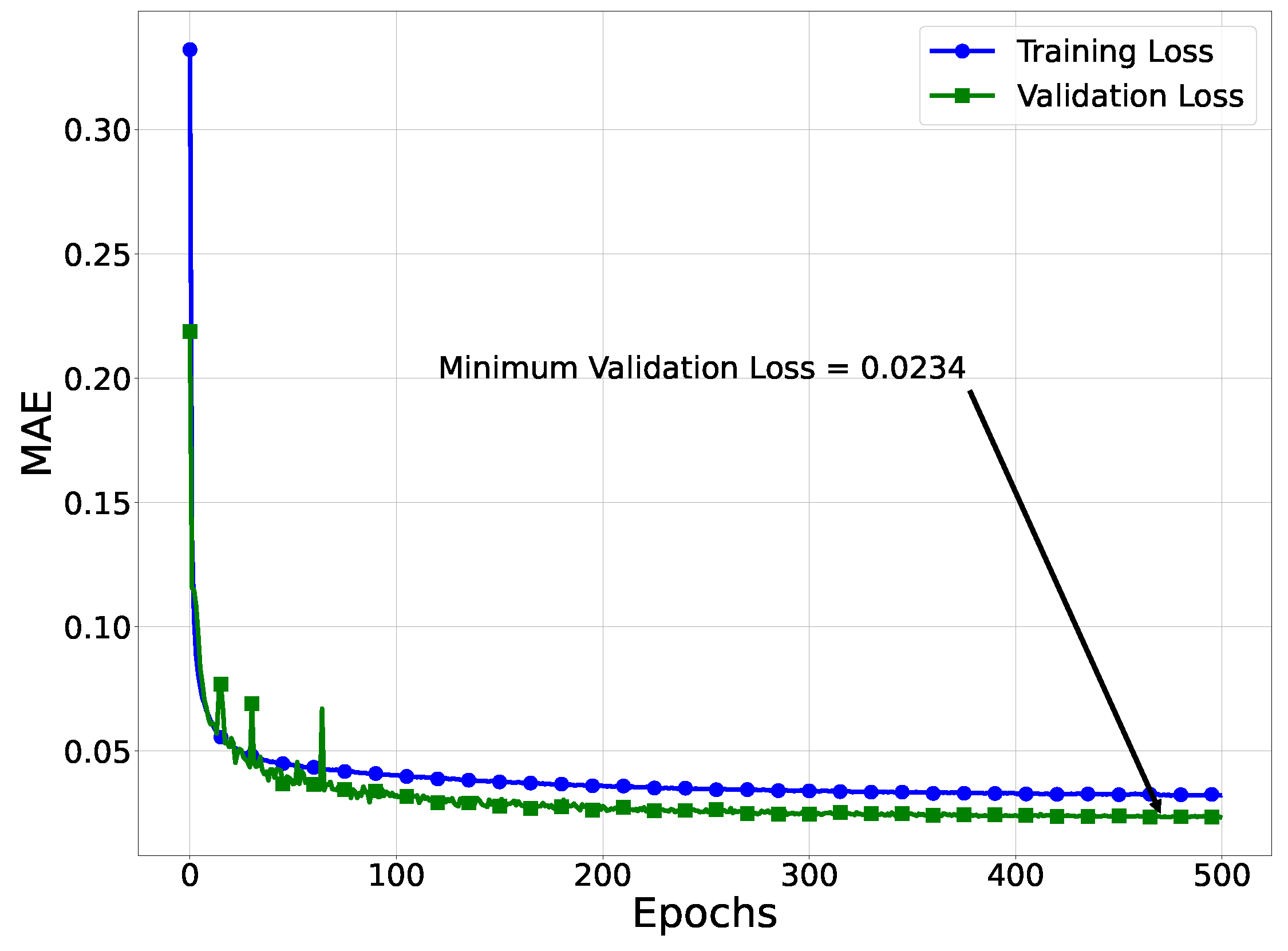
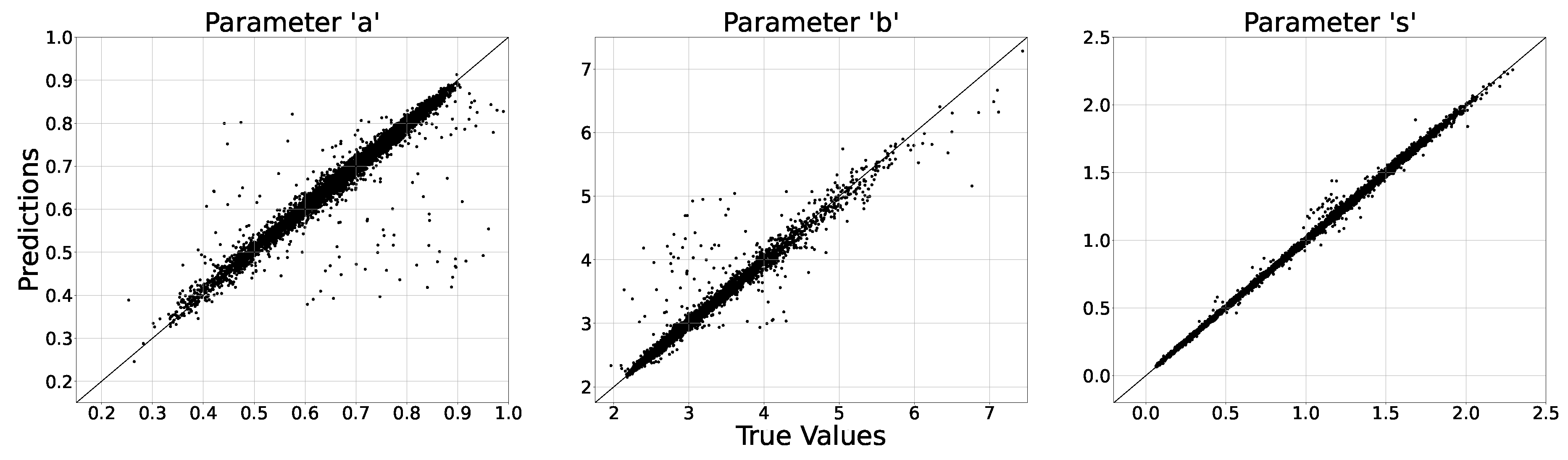
4.2. Performance of the DNN
4.3. Model Interpretability
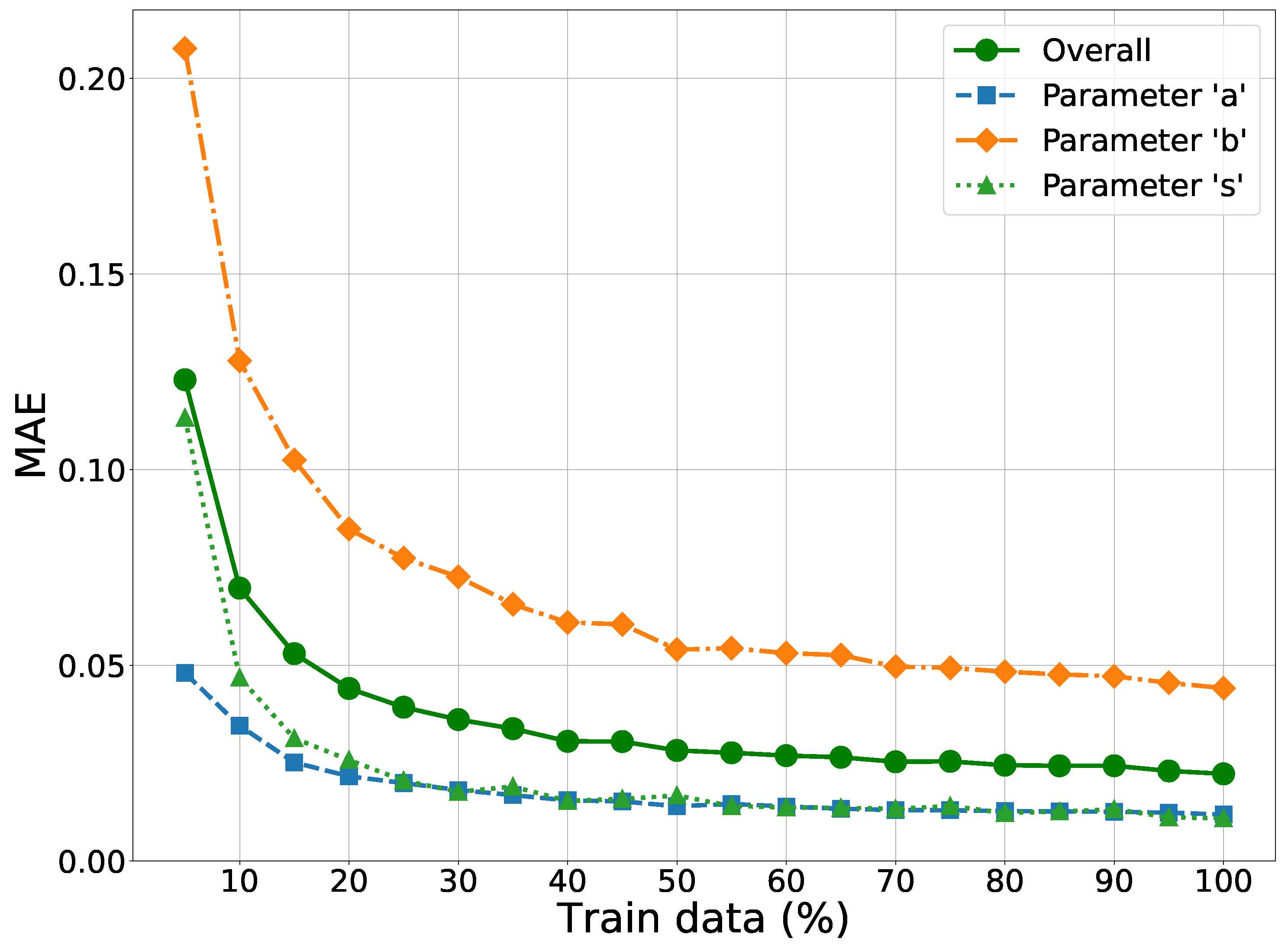
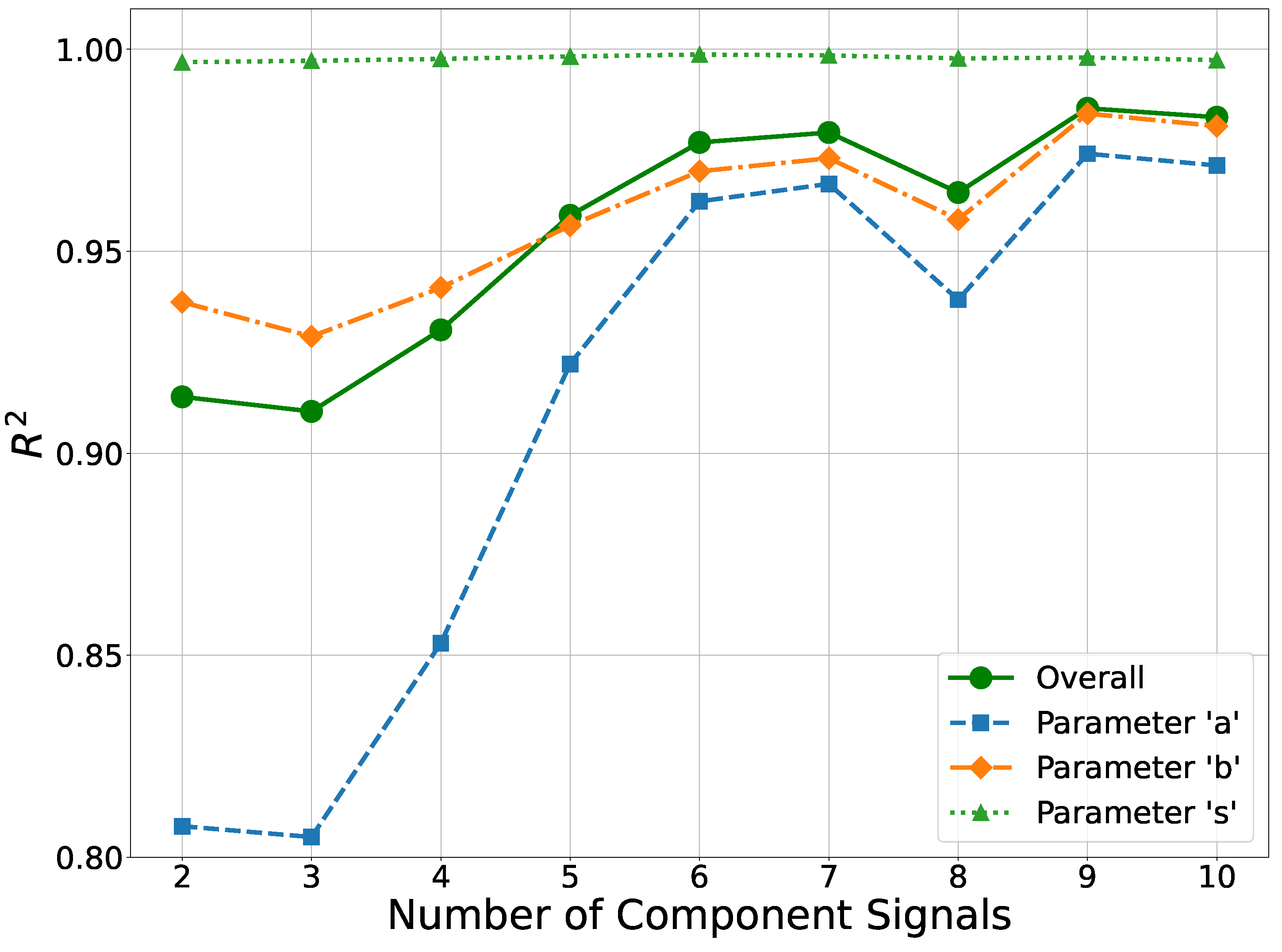
4.4. Performance as Number of SDR Applications Increase
4.5. Small DNN
4.6. Implementation Details, Computational Resources, and Model Complexity
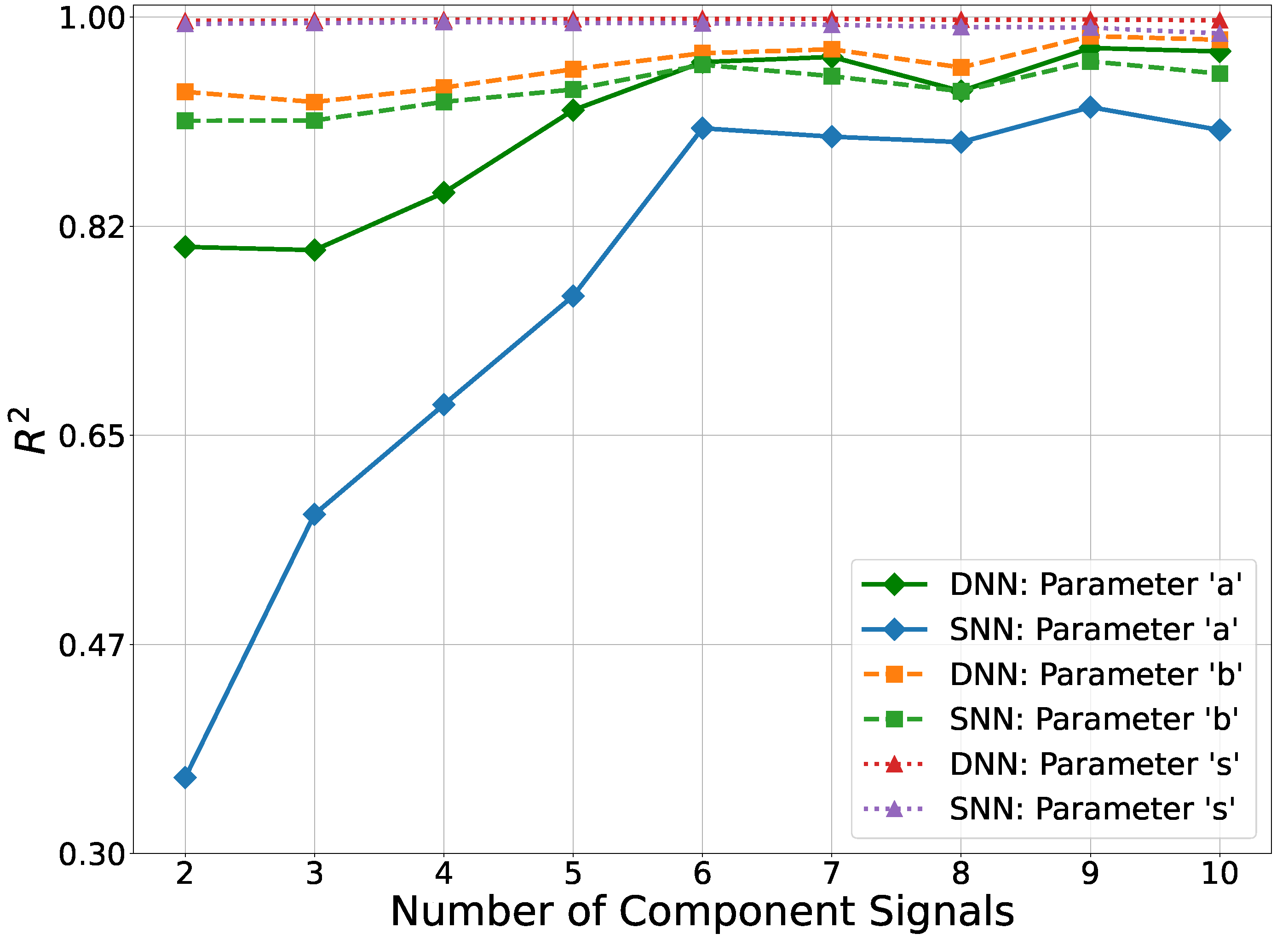
4.7. Comparison with Other Techniques
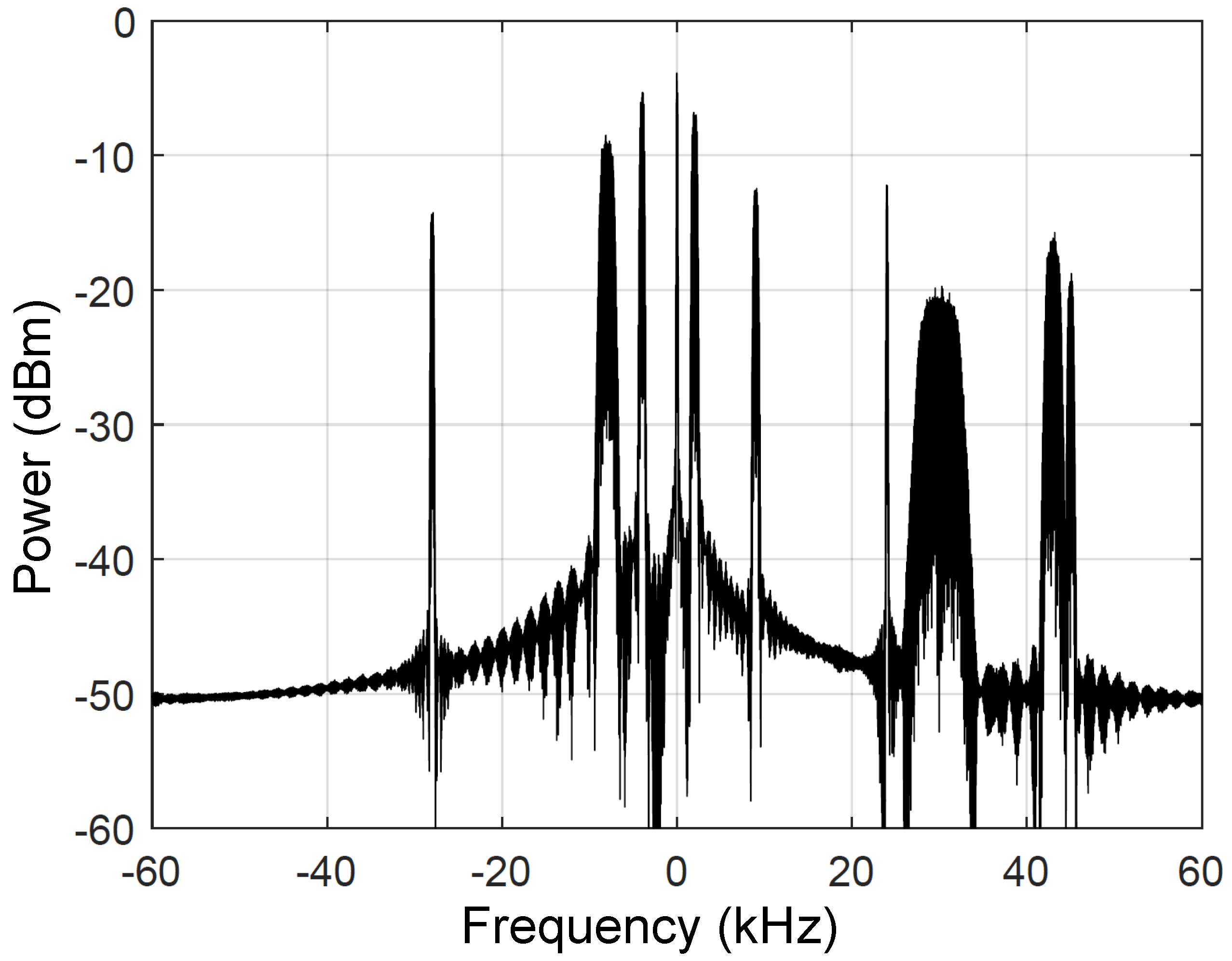
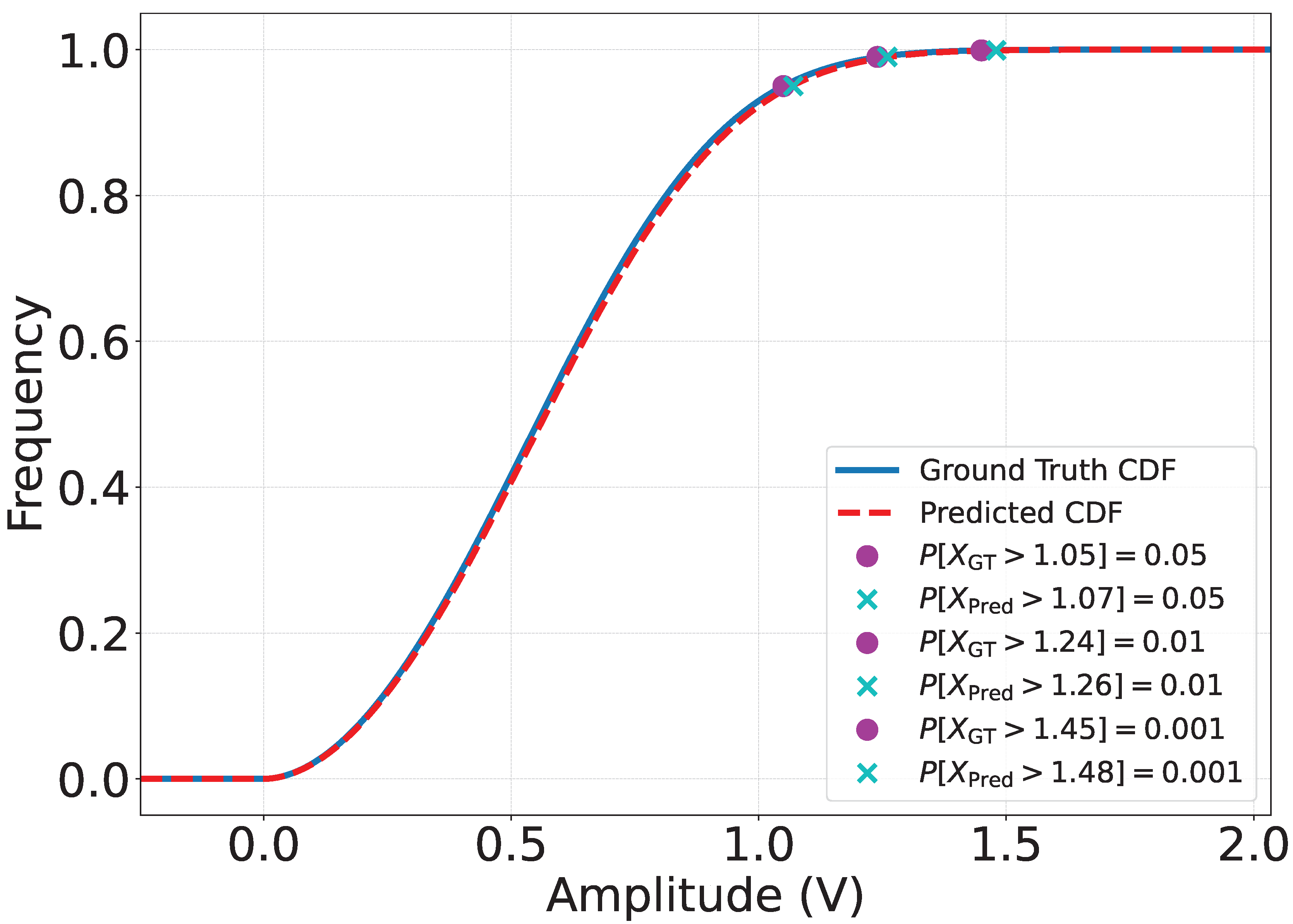
4.8. Typical Example
5. Conclusion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SDR | Software Defined Radio |
| DAC | Digital to Analog Converter |
| RF | Radio Frequency |
| GGD | Generalized Gamma Distribution |
| DL | Deep Learning |
| DNN | Deep neural network |
| MQAM | M-ary Quadrature Amplitude Modulated |
| RSS | Residual Sum of Squares |
| KL | Kullback-Leibler |
| Probability Density Function | |
| CDF | Cumulative Density Function |
| S-DNN | Small-Deep Neural Network |
| MAE | Mean Absolute Error |
| MSE | Mean Squared Error |
| SHAP | SHapley Additive exPLanations |
| FLOP | Floating Point OPeration |
| LR | Linear Regression |
| K-NR | K-Neighbors Regression |
| DTR | Decision Tree Regression |
| RFR | Random Forest Regression |
| GBRT | Gradient Boosted Regression Trees |
| SVR | Support Vector Regression |
References
- Gajjar, V.K. Machine Learning Applications in Plant Identification, Wireless Channel Estimation, and Gain Estimation for Multi-User Software-Defined Radio. Doctoral dissertation, Missouri University of Science and Technology, 2022.
- Baltaci, A.; Dinc, E.; Ozger, M.; Alabbasi, A.; Cavdar, C.; Schupke, D. A survey of wireless networks for Future Aerial Communications (FACOM). IEEE Communications Surveys & Tutorials 2021, 23, 2833–2884. [Google Scholar] [CrossRef]
- Furse, C.; Haupt, R. Down to the wire [aircraft wiring]. IEEE Spectrum 2001, 38, 34–39. [Google Scholar] [CrossRef]
- Sámano-Robles, R.; Tovar, E.; Cintra, J.; Rocha, A. Wireless avionics intra-communications: Current trends and design issues. In Proceedings of the Eleventh ICDIM, Porto, Portugal; 2016; pp. 266–273. [Google Scholar]
- Amrhar, A.; Kisomi, A.A.; Zhang, E.; Zambrano, J.; Thibeault, C.; Landry, R. Multi-Mode reconfigurable Software Defined Radio architecture for avionic radios. In Proceedings of the ICNS, Herndon, VA, USA; 2017; pp. 2D1–1–2D1–10. [Google Scholar]
- Price, N.; Kosbar, K. Decoupling hardware and software concerns in aircraft telemetry SDR systems. In Proceedings of the Proc. ITC, Glendale, AZ, USA; 2018; pp. 474–483. [Google Scholar]
- Pouyanfar, S.; Sadiq, S.; Yan, Y.; Tian, H.; Tao, T.; Reyes, M.P.; Shyu, M.; Chen, S.; Iyenger, S.S. A survey on deep learning: Algorithms, techniques, and applications. ACM Computing Surveys (CSUR) 2019, 51, 1–36. [Google Scholar] [CrossRef]
- Dong, S.; Wang, P.; Abbas, K. A survey on deep learning and its applications. Computer Science Review 2021, 40. [Google Scholar] [CrossRef]
- França, R.P.; Monteiro, A.; Arthur, R.; Iano, Y. An overview of deep learning in big data, image, and signal processing in the modern digital age. In Trends in Deep Learning Methodologies; Academic Press, 2020; pp. 63–87. [Google Scholar]
- Dai, L.; Jiao, R.; Adachi, F.; Poor, H.V.; Hanzo, L. Deep learning for wireless communications: An emerging interdisciplinary paradigm. IEEE Wireless Communications 2020, 27, 133–139. [Google Scholar] [CrossRef]
- Peng, S.; Jiang, H.; Wang, H.; Alwageed, H.; Zhou, Y.; Sebdani, M.M.; Yao, Y. Modulation classification based on signal constellation diagrams and deep learning. IEEE Transactions on Neural Networks and Learning Systems 2019, 30, 718–727. [Google Scholar] [CrossRef] [PubMed]
- Meng, F.; Chen, P.; Wu, L.; Wang, X. Automatic modulation classification: A deep learning enabled approach. IEEE Transactions on Vehicular Technology 2018, 67, 10760–10772. [Google Scholar] [CrossRef]
- Nambisan, A.; Gajjar, V.; Kosbar, K. Scalogram Aided Automatic Modulation Classification. In Proceedings of the Proc. ITC, Glendale, AZ, USA.
- Soltani, M.; Pourahmadi, V.; Mirzaei, A.; Sheikhzadeh, H. Deep learning-based channel estimation. IEEE Communications Letters 2019, 23, 652–655. [Google Scholar] [CrossRef]
- Luo, C.; Ji, J.; Wang, Q.; Chen, X.; Li, P. Channel State Information Prediction for 5G Wireless Communications: A Deep Learning Approach. IEEE Transactions on Network Science and Engineering 2020, 7, 227–236. [Google Scholar] [CrossRef]
- Luan, D.; Thompson, J. Attention Based Neural Networks for Wireless Channel Estimation. In Proceedings of the 2022 IEEE 95th Vehicular Technology Conference: (VTC2022-Spring); 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Ye, H.; Li, G.Y.; Juang, B.H. Power of Deep Learning for Channel Estimation and Signal Detection in OFDM Systems. IEEE Wireless Communications Letters 2018, 7, 114–117. [Google Scholar] [CrossRef]
- O’Shea, T.J.; Clancy, T.C.; McGwier, R.W. Recurrent Neural Radio Anomaly Detection. arXiv 2016, arXiv:cs.LG/1611.00301. [Google Scholar]
- Ma, H.; Zheng, X.; Yu, L.; Zhou, X.; Chen, Y. A novel end-to-end deep separation network based on attention mechanism for single channel blind separation in wireless communication. IET Signal Processing 2023, 17, e12173. [Google Scholar] [CrossRef]
- Jiang, C.; Zhang, H.; Ren, Y.; Han, Z.; Chen, K.C.; Hanzo, L. Machine learning paradigms for next-generation wireless networks. IEEE Wirel. Commun. 2017, 24, 98–105. [Google Scholar] [CrossRef]
- Sun, H.; Chen, X.; Shi, Q.; Hong, M.; Fu, X.; Sidiropoulos, N.D. Learning to Optimize: Training Deep Neural Networks for Interference Management. IEEE Transactions on Signal Processing 2018, 66, 5438–5453. [Google Scholar] [CrossRef]
- Donohoo, B.K.; Ohlsen, C.; Pasricha, S.; Xiang, Y.; Anderson, C. Context-aware energy enhancements for smart mobile devices. IEEE Trans. Mob. Comput. 2014, 13, 1720–1732. [Google Scholar] [CrossRef]
- Gajjar, V.; Kosbar, K. CSI estimation using artificial neural network. In Proceedings of the Proc. ITC, Las Vegas, NV, USA; 2019; pp. 413–422. [Google Scholar]
- Gajjar, V.; Kosbar, K. Rapid gain estimation for multi-user software defined radio applications. In Proceedings of the Proc. ITC, Las Vegas, NV, USA.
- Stacy, E.W. A generalization of the gamma distribution. Ann. Math. Stat. 1962, 33, 1187–1192. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R. On information theory and sufficiency. The Annals of Mathematical Statistics 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Continuous Statistical Distributions — SCIPY V1.13.0 Manual.
- Borchani, H.; Varando, G.; Bielza, C.; Larranaga, P. A survey on multi-output regression. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery 2015, 5, 216–233. [Google Scholar] [CrossRef]
- Brochu, E.; Cora, V.M.; de Freitas, N. Tutorial on Bayesian Optimization of Expensive Cost Functions, with Application to Active User Modeling and Hierarchical Reinforcement Learning. CoRR 2010, abs/1012.2599, [1012.2599].
- Ojala, M.; Garriga, G.C. Permutation tests for studying classifier performance. Journal of machine learning research 2010, 11. [Google Scholar]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Proceedings of the Proceedings of the 31st International Conference on Neural Information Processing Systems, Red Hook, NY, USA; 2017. NIPS’17. pp. 4768–4777. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems, 2015. Software available from tensorflow.org.
- Chollet, F.; et al. Keras. https://keras.io, 2015.
- Montgomery, D.C.; Peck, E.A.; Geoffrey, G.G. Multiple linear regression. In Introduction to Linear Regression Analysis, 6 ed.; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2021; pp. 72–85. [Google Scholar]
- Kramer, O. K-Nearest Neighbors; Springer: Berlin, Germany, 2013; pp. 13–23. [Google Scholar]
- Dea’th, G. Multivariate regression trees: A new Technique for modelling species-environment relationships. Ecology 2002, 83, 1105–1117. [Google Scholar] [CrossRef]
- Segal, M.R. Machine learning benchmarks and random forest regression 2004.
- Prettenhofer, P.; Louppe, G. Gradient Boosted Regression Trees in Scikit-Learn. 23 February 2014.
- Brudnak, M. Vector-valued support vector regression. In Proceedings of the IEEE Int. Joint Conf. on Neural Network Proc., Vancouver, BC, Canada; 2006; pp. 1562–1569. [Google Scholar]

| Parameter | Range |
|---|---|
| Modulation order | |
| Data rate | kbps |
| Power level | dBm |
| Nomalized frequency | kHz |
| Number of component signals |
| Distribution | RSS | KL Divergence Score |
|---|---|---|
| Beta | 0.2637±0.3544 | 0.0020±0.0018 |
| Chi | 0.5200±0.6494 | 0.0065±0.0047 |
| Generalized Gamma | 0.0922±0.2189 | 0.0007±0.0009 |
| Rice | 0.2342±0.4192 | 0.0025±0.0031 |
| Parameter | Explained Variance |
MAE | MSE | |
| a | 0.9358 | 0.9358 | 0.0119 | 0.0008 |
| b | 0.9664 | 0.9664 | 0.0442 | 0.0133 |
| s | 0.9985 | 0.9985 | 0.0109 | 0.0003 |
| Overall | 0.9669 | 0.9669 | 0.0223 | 0.0048 |
| Parameter | Feature Groups (%) | ||||
| Modulation Order |
Data Rate | Power Level |
Normalized Frequency |
Number of Component Signals |
|
| a | 42.55 | 1.57 | 46.67 | 1.80 | 7.40 |
| b | 49.94 | 0.68 | 39.35 | 0.75 | 9.28 |
| s | 38.96 | 0.12 | 48.87 | 0.11 | 11.95 |
| Overall | 44.42 | 0.63 | 44.30 | 0.70 | 9.95 |
| Model | Training Time (s) | FLOPs |
| DNN | 596 | 459548 |
| S-DNN | 407 | 17096 |
| Method | a | b | s | Overall |
| LR | 0.4926 | 0.4484 | 0.6994 | 0.5468 |
| K-NR | 0.4795 | 0.5297 | 0.4447 | 0.4846 |
| DTR | 0.5578 | 0.7218 | 0.9400 | 0.7398 |
| RFR | 0.7651 | 0.8527 | 0.9745 | 0.8641 |
| GBRT | 0.8381 | 0.8982 | 0.9928 | 0.9097 |
| SVR | 0.5908 | 0.6814 | 0.9142 | 0.7288 |
| S-DNN | 0.8311 | 0.9548 | 0.9952 | 0.9270 |
| DNN | 0.9358 | 0.9664 | 0.9985 | 0.9669 |
| Modulation Order |
Data rate (bps) |
Power level (dBm) |
Normalized Frequency (kHz) |
| 64 | 6753 | -23.65 | -9 |
| 32 | 5566 | -23.05 | -44 |
| 4 | 1460 | -26.23 | -21 |
| 8 | 5518 | -22.09 | 37 |
| 16 | 9751 | -10.05 | 28 |
| 256 | 7993 | -5.43 | 14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





