Submitted:
07 December 2024
Posted:
09 December 2024
You are already at the latest version
Abstract
Keywords:
MSC: 62E10; 62N99
1. Introduction
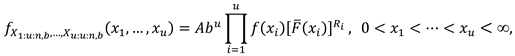
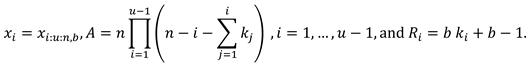
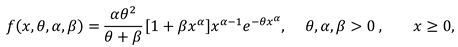
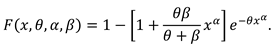
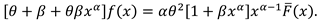
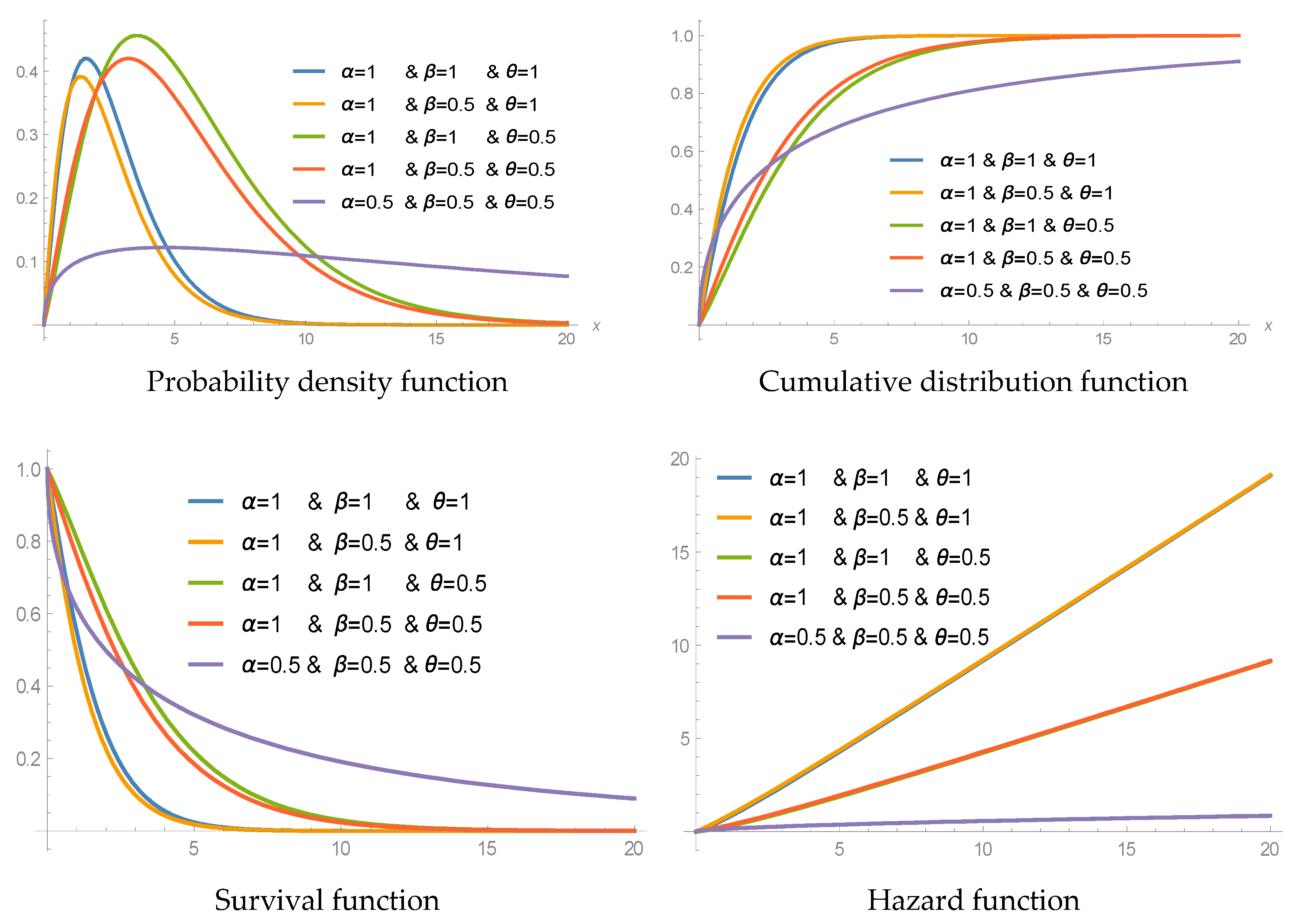
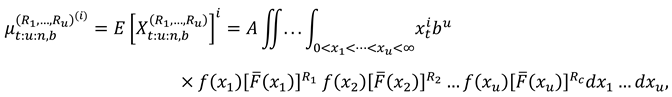
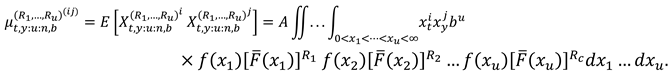
2. Recurrence Relations for SMs and PMs
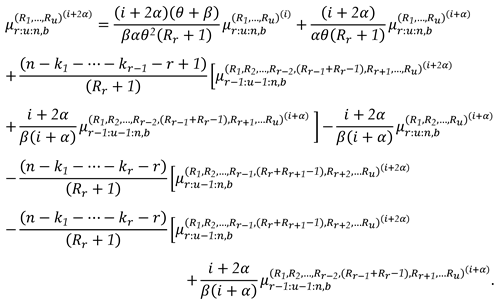
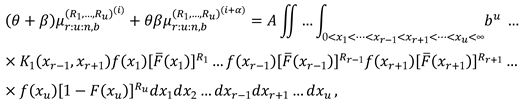
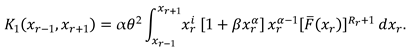
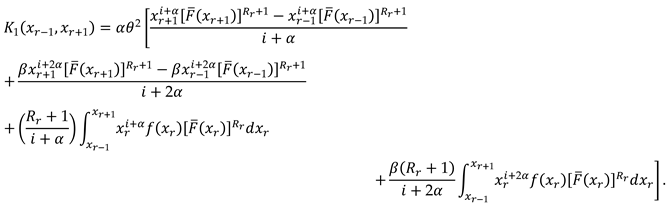
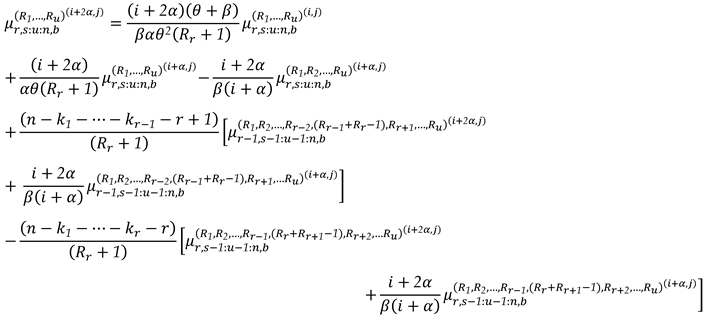
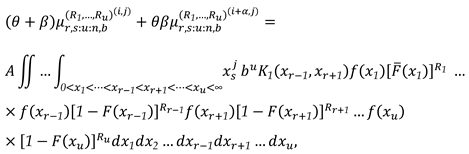
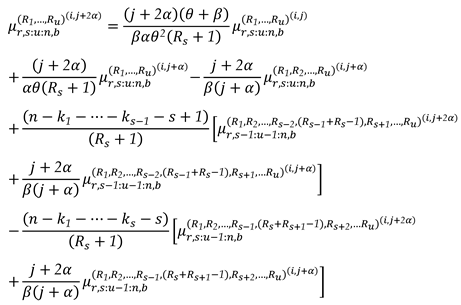
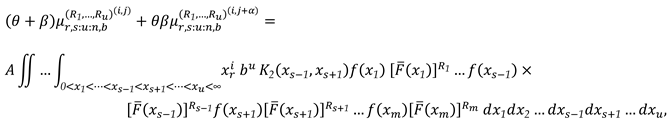
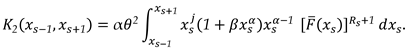
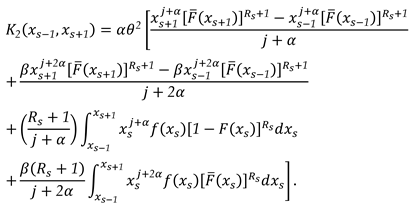
3. The Characterizations
3.1. Characterization via differential equation for the extended power Lindley distribution
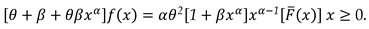
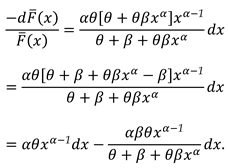
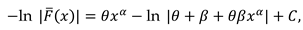
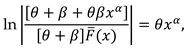
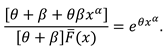
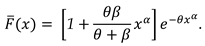
3.2. Characterization via RRs for SMs
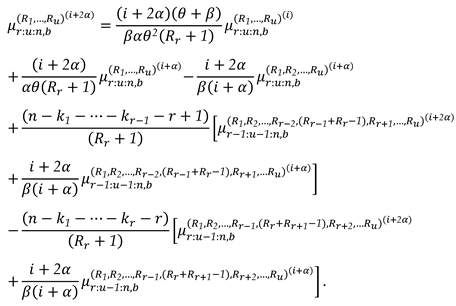
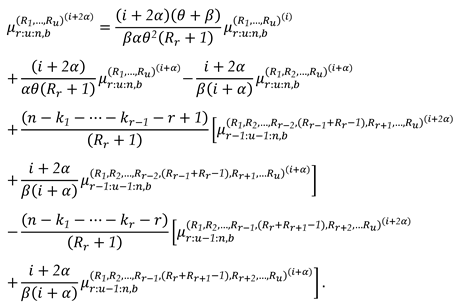
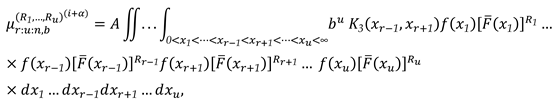
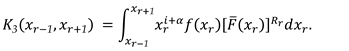
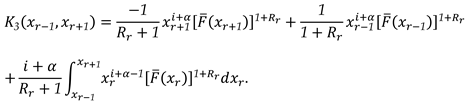

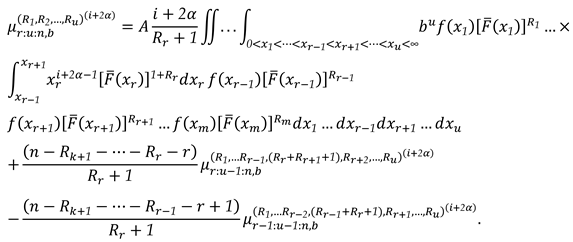
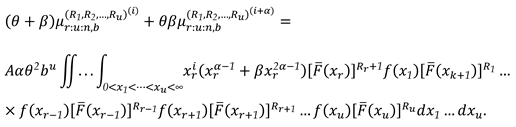
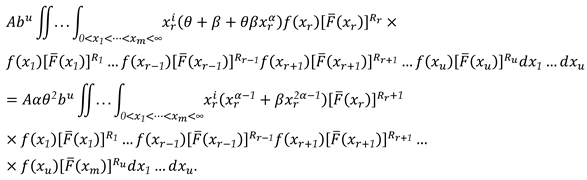
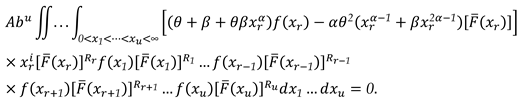
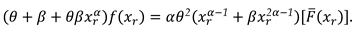
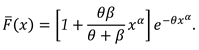
3.3. Characterization via RRs for PMs
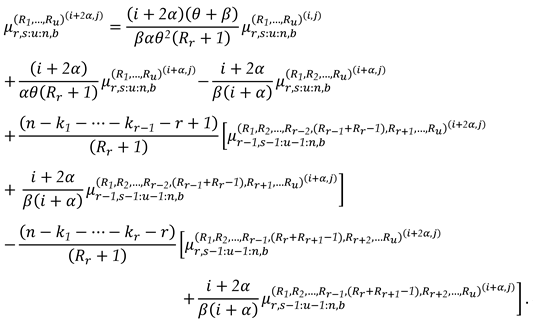
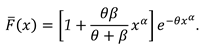
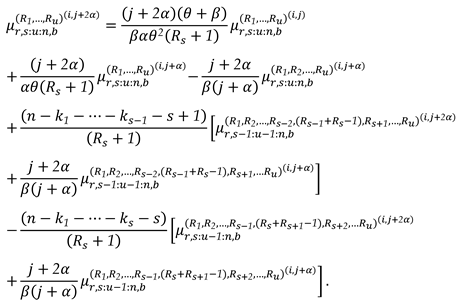
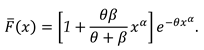
Author contributions
Conflict of interest
References
- Balakrishnan, N.; Cramer, E.; Kamps, U.; Schenk, N. Progressive type II censored order statistics from exponential distributions. Statistics: A Journal of Theoretical and Applied Statistics 2001, 35, 537–556. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Sandhu, R.A. Best linear unbiased and maximum likelihood estimation for exponential distributions under general progressive type-II censored samples. Sankhyā: The Indian Journal of Statistics, Series B 1996, 1–9. https://www.jstor.org/stable/25052923.
- Davis, H.T.; Feldstein, M.L. The generalized Pareto law as a model for progressively censored survival data. Biometrika 1979, 66, 299–306. [Google Scholar] [CrossRef]
- Singh, S.K.; Singh, U.; Kumar, M.; Vishwakarma, P.K. Classical and Bayesian inference for an extension of the exponential distribution under progressive type-II censored data with binomial removals. Journal of Statistics Applications & Probability Letters 2014, 1, 75–86. [Google Scholar] [CrossRef]
- Aggarwala, R.; Balakrishnan, N. Recurrence relations for single and product moments of progressive Type-II right censored order statistics from exponential and truncated exponential distributions. Annals of the Institute of Statistical Mathematics 1996, 48, 757–771. [Google Scholar] [CrossRef]
- Athar, H.; Akhter, Z.; Saran, J. Moments of progressive Type-II right censored order statistics from Lindley distribution. Statistics Research Letters 2014, 3, 01–06. [Google Scholar]
- Mohie El-Din, M.M.; Sharawy, A.; Abu-Moussa, M.H. E-Bayesian estimation for the parameters and hazard function of Gompertz distribution based on progressively type-II right censoring with application. Quality and Reliability Engineering International 2023, 39, 1299–1317. [Google Scholar] [CrossRef]
- Kotb, M.S.; Sharawy, A.; El-Din, M.M.M. E-Bayesian Estimation for Kumaraswamy Distribution Using Progressive First Failure Censoring. Mathematical Modelling of Engineering Problems 2021, 8, 8.–content. [Google Scholar] [CrossRef]
- Abu-Moussa, M.H.; Alsadat, N.; Sharawy, A. On Estimation of Reliability Functions for the Extended Rayleigh Distribution under Progressive First-Failure Censoring Model. Axioms 2023, 12, 680. [Google Scholar] [CrossRef]
- Sharawy, A. Recurrence Relations for Moment Generating Function of Progressive First Failure Censoring and Characterizations of Right Truncated Exponential Distribution. ERU Research Journal 2024, 3, 781–790. [Google Scholar] [CrossRef]
- Alsadat, N.; Abu-Moussa, M.; Sharawy, A. On the study of the recurrence relations and characterizations based on progressive first-failure censoring. AIMS Mathematics 2024, 9, 481–494. [Google Scholar] [CrossRef]
- Alkarni, S.H. Extended power lindley distribution: A new statistical model for non-monotone survival data. European J. of Statist. and Probability 2015, 3, 19–34. [Google Scholar]
- El-Din, M.M.; Sadek, A.; El-Din MM, M.; Sharawy, A. Characterization for Gompertz distribution based on general progressively type-ii right censored orderstatistics. International Journal of Advanced Statistics and Probability 2017, 5, 52–56. [Google Scholar] [CrossRef]
- Hwang, J.S.; Lin, G.D. Extensions of Müntz-Szász theorem and applications. Analysis 1984, 4, 143–160. [Google Scholar] [CrossRef]
| Case | Parameters | Distribution |
| 1 | Power Lindley | |
| 2 | Lindley | |
| 3 | Weibull | |
| 4 | Rayleigh | |
| 5 | Exponential | |
| 6 | Modified Gamma | |
| 7 | Modified Rayleigh | |
| 8 | Extended Lindley |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





