About Stabilization of the Controlled Inverted Pendulum under Stochastic Perturbations of the Type of Poisson's Jumps

1. Introduction

The problem of stabilization for the mathematical model of the controlled inverted pendulum is very popular among the researchers during many years (see, for instance, [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]). The nonlinear model of the controlled inverted pendulum has the form of nonlinear differential equation of the second order

$$\ddot{x}\left(t\right)-asinx\left(t\right)=u\left(t\right),a>0,t\ge 0,$$

(1)

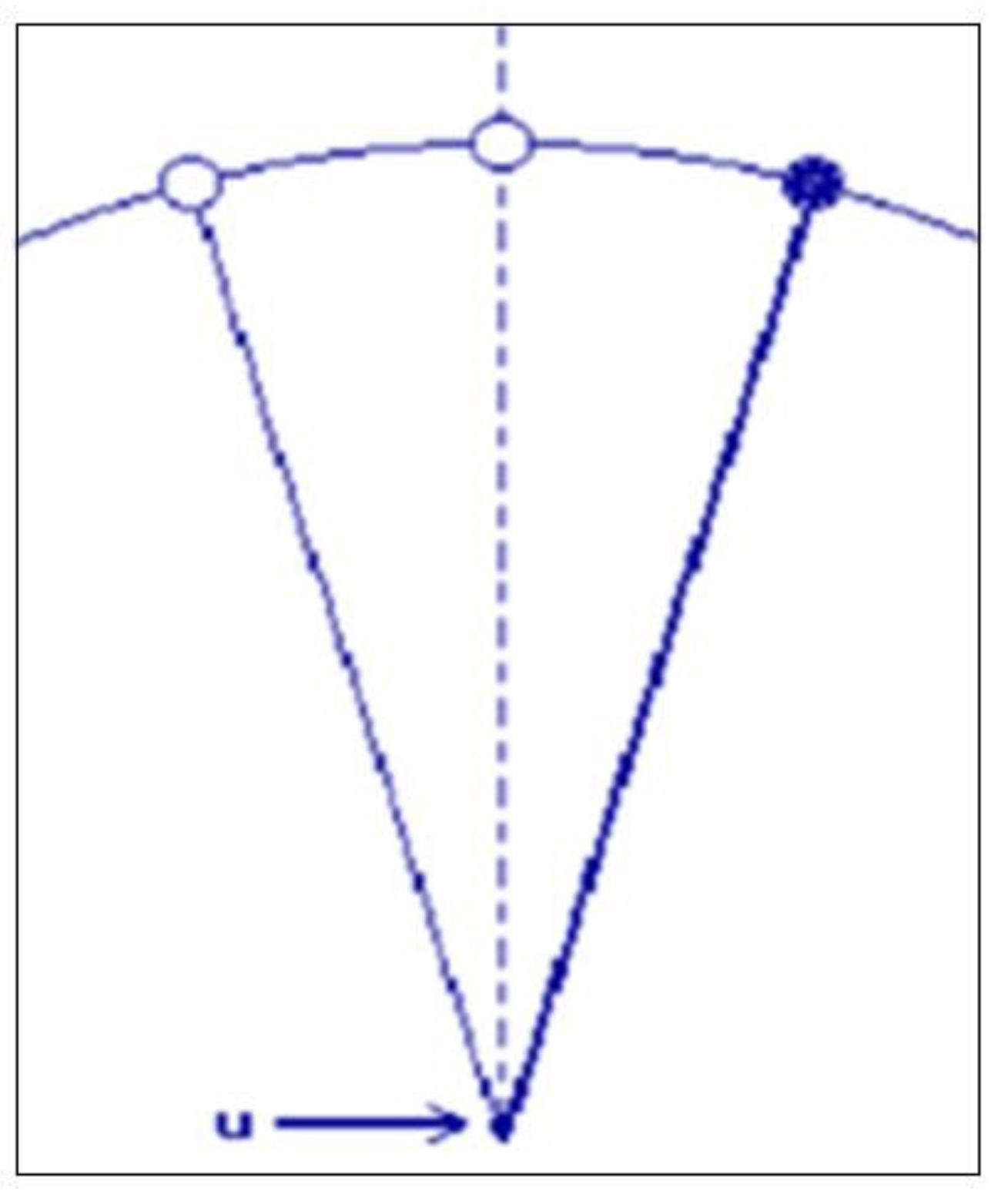
where $x\left(t\right)$ measures the angle between the rod and the upward vertical (Figure 1). The linearized mathematical model of the controlled inverted pendulum can be described by the linear differential equation of the second order

$$\ddot{x}\left(t\right)-ax\left(t\right)=u\left(t\right),a>0,t\ge 0.$$

(2)

The classical way of stabilization [7] for the equation (1) or (2) uses the control $u\left(t\right)$, which is a linear combination of the state and velocity of the pendulum, i.e.,

$$u\left(t\right)=-b_{1}x\left(t\right)-b_2\dot{x}\left(t\right),b_1>a,b_2>0.$$

But this type of control, which represents instantaneous feedback, is quite difficult to realize because usually it is necessary to have some finite time to make measurements of the coordinates and velocities, to treat the results of the measurements and to implement them in the control action.

Unlike of the classical way of stabilization another way of stabilization is proposed in [4,5,19]. It is supposed that only the trajectory of the pendulum is observed and the control $u\left(t\right)$ does not depend on the velocity, but depends on the previous values of the trajectory $x\left(s\right)$, $s\le t$, and is given in the form

$$u\left(t\right)={\int }_0^{\infty }dK\left(\tau \right)x(t-\tau ),$$

(3)

where the kernel $K\left(\tau \right)$ is a continuous from the right function of bounded variation on $[0,\infty )$ and the integral is understood in the Stieltjes sense. It means, in particular, that both distributed and discrete delays can be used depending on the concrete choice of the kernel $K\left(\tau \right)$.

In addition, it is supposed that the pendulum is under influence of stochastic perturbations, so, the considered stabilization problem is a problem of the theory of stochastic functional differential equations [19,20,21,22,23,24,25].

The initial conditions for the system (1), (3) or (2), (3) are

$$x\left(s\right)=\varphi \left(s\right),\dot{x}\left(s\right)=\dot{\varphi }\left(s\right),s\le 0,$$

(4)

where $\varphi \left(s\right)$ is a given continuously differentiable function.

1.1. Stability Conditions in the Deterministic Case

Substituting (3) into (2), putting $x_1\left(t\right)=x\left(t\right)$, $x_2\left(t\right)=\dot{x}\left(t\right)$ and using (4), we obtain the system of linear differential equations with delay

$$\begin{array}{l}{\dot{x}}_1\left(t\right)=x_2\left(t\right),\\ {\dot{x}}_2\left(t\right)=a{x}_1\left(t\right)+{\int }_0^{\infty }dK\left(\tau \right)x_1(t-\tau ),\\ x_1\left(s\right)=\varphi \left(s\right),x_2\left(s\right)=\dot{\varphi }\left(s\right),s\le 0.\end{array}$$

(5)

Put

$$k_i={\int }_0^{\infty }{\tau }^{i}dK\left(\tau \right),i=0,1,k_2={\int }_0^{\infty }{\tau }^2\left|dK\left(\tau \right)\right|.$$

(6)

By virtue of the general method of Lyapunov functionals construction in [19] the following statements have been proven.

Theorem 1. 

Let be

$$a_1=-(a+k_0)>0,k_1>0,k_2<{\displaystyle \frac{4}{1+\sqrt{1+4a_1{k}_1^{-2}}}}.$$

(7)

Then the zero solution of the system (5) is asymptotically stable.

Remark 1. 

Note that two first inequalities (7) are necessary conditions for asymptotic stability of the zero solution of the system (5), the third inequality (7) is a sufficient condition only.

Remark 2. 

Note that the third inequality (7) can be represented in the form

$$k_1>k_2\sqrt{{\displaystyle \frac{a_1}{2(2-k_2)}}},k_2<2.$$

(8)

Remark 3. 

Note that the inverted pendulum cannot be stabilized by a control that depends on the velocity only, i.e., $u\left(t\right)={\int }_0^{\infty }dK\left(\tau \right)\dot{x}(t-\tau )$ or on the acceleration only, i.e., $u\left(t\right)={\int }_0^{\infty }dK\left(\tau \right)\ddot{x}(t-\tau )$.

1.2. Transformation to a System of Differential Equations of Neutral Type

From the first equation of (5) we have

$${\int }_{t-\tau }^t{x}_2\left(s\right)ds={\int }_{t-\tau }^t{\dot{x}}_1\left(s\right)ds=x_1\left(t\right)-x_1(t-\tau ).$$

(9)

Putting

$$\begin{array}{c}G(t,x_{2t})={\int }_0^{\infty }dK\left(\tau \right){\int }_{t-\tau }^t(s-t+\tau )x_2\left(s\right)ds,\\ a_1=-(a+k_0),z\left(t\right)=x_2\left(t\right)-G(t,x_{2t}),\end{array}$$

(10)

from (10), (6) and (9) we obtain

$${\displaystyle \frac{d}{dt}}G(t,x_{2t})=k_1{x}_2\left(t\right)-{\int }_0^{\infty }dK\left(\tau \right){\int }_{t-\tau }^t{x}_2\left(s\right)ds$$

and

$$\begin{array}{cc}\hfill {\int }_0^{\infty }dK\left(\tau \right)x_1(t-\tau )& =k_0{x}_1\left(t\right)-{\int }_0^{\infty }dK\left(\tau \right){\int }_{t-\tau }^t{x}_2\left(s\right)ds\hfill \\ & =k_0{x}_1\left(t\right)-k_1{x}_2\left(t\right)+{\displaystyle \frac{d}{dt}}G(t,x_{2t}).\hfill \end{array}$$

(11)

Substituting (11) into the second equation of (5) and using (10), let us transform the system (5) to the form of the system of differential equations of neutral type [19,23,24]

$$\begin{array}{cc}\hfill {\dot{x}}_1\left(t\right)& =x_2\left(t\right),\hfill \\ \hfill \dot{z}\left(t\right)& =-a_1{x}_1\left(t\right)-k_1{x}_2\left(t\right).\hfill \end{array}$$

(12)

2. Stabilization of the Zero Solution Under Stochastic Perturbations

Linear and nonlinear models of the controlled inverted pendulum under stochastic perturbations of the type of white noise are studied in [19], where the zero and a stationary nonzero solutions are investigated analytically and via numerical simulations. Here both these mathematical models of the controlled inverted pendulum are considered under a combination of both types of stochastic perturbations: the white noise and Poisson’s jumps.

Let $\{\mathsf{\Omega },\mathfrak{F},\mathbf{P}\}$ be a complete probability space, $\{{\mathfrak{F}}_t,t\ge 0\}$ be a nondecreasing family of sub-$\sigma$-algebras of $\mathfrak{F}$, i.e., ${\mathfrak{F}}_s\subset {\mathfrak{F}}_t$ for $s<t$, $\mathbf{E}$ be the mathematical expectation with respect to the probability $\mathbf{P}$.

Let $w\left(t\right)$ and $\nu \left(t\right)$ be respectively ${\mathfrak{F}}_t$-measurable the Wiener and the Poisson processes, $\mathbf{E}\nu \left(t\right)=\lambda t$, $\lambda >0$ , $\tilde{\nu }\left(t\right)=\nu \left(t\right)-\lambda t$ [20,21,26,27],

$$\xi \left(t\right)=\sigma w\left(t\right)+\gamma \tilde{\nu }\left(t\right).$$

(13)

2.1. Linear Model

Supposing that the parameter a in the second equation of the system (5) is under the influence of stochastic perturbations $\dot{\xi }\left(t\right)$, we obtain

$${\dot{x}}_2\left(t\right)=(a+\dot{\xi }\left(t\right))x_1\left(t\right)+{\int }_0^{\infty }dK\left(\tau \right)x_1(t-\tau ),a>0,t\ge 0.$$

In this case instead of the system (12) we obtain the system of stochastic differential equations of the neutral type [19,20,21]

$$\begin{array}{cc}\hfill d{x}_1\left(t\right)& =x_2\left(t\right)dt,\hfill \\ \hfill dz\left(t\right)& =(-a_1{x}_1\left(t\right)-k_1{x}_2\left(t\right))dt+\sigma x_1\left(t\right)dw\left(t\right)+\gamma x_1\left(t\right)d\tilde{\nu }\left(t\right),\hfill \\ \hfill x_1\left(s\right)& =\varphi \left(s\right),x_2\left(s\right)=\dot{\varphi }\left(s\right),s\le 0,\hfill \end{array}$$

(14)

where $z\left(t\right)$ is defined in (10).

Putting

$$\eta \left(t\right)=\left[\begin{array}{c}{x}_1\left(t\right)\\ z\left(t\right)\end{array}\right],x\left(t\right)=\left[\begin{array}{c}{x}_1\left(t\right)\\ x_2\left(t\right)\end{array}\right],A=\left[\begin{array}{cc}0& 1\\ -a_1& -k_1\end{array}\right],B=\left[\begin{array}{cc}0& 0\\ \sigma & 0\end{array}\right],C=\left[\begin{array}{cc}0& 0\\ \gamma & 0\end{array}\right],$$

(15)

let us represent the system (14) in the matrix form

$$d\eta \left(t\right)=Ax\left(t\right)dt+Bx\left(t\right)dw\left(t\right)+Cx\left(t\right)d\tilde{\nu }\left(t\right).$$

(16)

Definition 1. 

The zero solution of the equation (16) is called:

-

stable in probability if for any ${\epsilon }_1>0$ and ${\epsilon }_2>0$ there exists $\delta >0$ such that the solution $x\left(t\right)$ of Eq. (16) satisfies the condition $\mathbf{P}\{\underset{t\ge 0}{sup}\left|x\left(t\right)\right|>{\epsilon }_1\}<{\epsilon }_2$ for any initial condition $\mathbf{P}\left\{\underset{s\le 0}{sup}\right|\varphi \left(s\right)|<\delta \}=1$;

-

mean square stable if for each $\epsilon >0$ there exists a $\delta >0$ such that ${\mathbf{E}\left|x\left(t\right)\right|}^2<\epsilon$, $t\ge 0$, provided that $\underset{s\le 0}{sup}\mathbf{E}{\left|\varphi \left(s\right)\right|}^2<\delta$;

-

asymptotically mean square stable if it is mean square stable and $\underset{t\to \infty }{lim}\mathbf{E}{\left|x\left(t\right)\right|}^2=0$ for each initial function $\varphi \left(s\right)$.

Lemma 1. 

[19] Let the matrix A is defined in (15). The matrix equation

$$PA+A^{\prime }P=-Q,Q=\left[\begin{array}{cc}q& 0\\ 0& 1\end{array}\right],q>0,$$

has the positive definite solution $P=\left[\begin{array}{cc}{p}_{11}& p_{12}\\ p_{12}& p_{22}\end{array}\right]$ with the elements

$$p_{11}=k_1{p}_{12}+a_1{p}_{22},p_{12}={\displaystyle \frac{q}{2a_1}},p_{22}={\displaystyle \frac{p}{2a_1}},p={\displaystyle \frac{q+a_1}{k_1}}.$$

(17)

Theorem 2. 

Let be

$$\begin{array}{l}{a}_1=-(a+k_0)>0,k_1>0,k_2<2,\\ \rho ={\sigma }^2+\lambda {\gamma }^2<2a_1\left(k_1-k_2\sqrt{{\displaystyle \frac{a_1}{2(2-k_2)}}}\right),\end{array}$$

(18)

where $k_i$, $i=0,1,2$, are defined in (6). Then the zero solution of the equation (16) (and the system (14)) is asymptotically mean square stable.

Proof. 

Following the general method of Lyapunov functionals construction [19], consider the functional $V=V_1+V_2$, where $V_1\left(x_t\right)={\eta }^{\prime }\left(t\right)P\eta \left(t\right)$, $\eta \left(t\right)$ is defined in (15), elements of the matrix P are defined in (17), the additional functional $V_2$ will be chosen below.

Let L be the generator of the equation (16) [19,20,21,26,27]. Then

$$\begin{array}{cc}\hfill L{V}_1\left(x_t\right)& =2{\eta }^{\prime }\left(t\right)PAx\left(t\right)+x^{\prime }\left(t\right)B^{\prime }PBx\left(t\right)\hfill \\ & +\lambda [V_1(\eta \left(t\right)+Cx\left(t\right))-V_1\left(\eta \left(t\right)\right)-2{\eta }^{\prime }\left(t\right)PCx\left(t\right)]\hfill \\ & =2{\eta }^{\prime }\left(t\right)PAx\left(t\right)+x^{\prime }\left(t\right)B^{\prime }PBx\left(t\right)+\lambda x^{\prime }\left(t\right)C^{\prime }PCx\left(t\right).\hfill \end{array}$$

(19)

Note that via (15) and (10) we have

$$\begin{array}{cc}\hfill 2{\eta }^{\prime }\left(t\right)PAx\left(t\right)& =2\left[\begin{array}{cc}{x}_1\left(t\right)& z\left(t\right)\end{array}\right]\left[\begin{array}{cc}{p}_{11}& p_{12}\\ p_{12}& p_{22}\end{array}\right]\left[\begin{array}{cc}0& 1\\ -a_1& -k_1\end{array}\right]\left[\begin{array}{c}{x}_1\left(t\right)\\ x_2\left(t\right)\end{array}\right]\hfill \\ & =2\left[\begin{array}{cc}{x}_1\left(t\right)& z\left(t\right)\end{array}\right]\left[\begin{array}{cc}{p}_{11}& p_{12}\\ p_{12}& p_{22}\end{array}\right]\left[\begin{array}{c}{x}_2\left(t\right)\\ -a_1{x}_1\left(t\right)-k_1{x}_2\left(t\right)\end{array}\right]\hfill \\ & =2\left[\begin{array}{cc}{x}_1\left(t\right)& z\left(t\right)\end{array}\right]\left[\begin{array}{c}{p}_{11}{x}_2\left(t\right)-a_1{p}_{12}{x}_1\left(t\right)-k_1{p}_{12}{x}_2\left(t\right)\\ p_{12}{x}_2\left(t\right)-a_1{p}_{22}{x}_1\left(t\right)-k_1{p}_{22}{x}_2\left(t\right)\end{array}\right]\hfill \\ & =2p_{11}{x}_1\left(t\right)x_2\left(t\right)-2a_1{p}_{12}{x}_1^2\left(t\right)-2k_1{p}_{12}{x}_1\left(t\right)x_2\left(t\right)\hfill \\ & +2(p_{12}{x}_2\left(t\right)-a_1{p}_{22}{x}_1\left(t\right)-k_1{p}_{22}{x}_2\left(t\right))(x_2\left(t\right)-G(t,x_{2t}))\hfill \\ & =-2a_1{p}_{12}{x}_1^2\left(t\right)-2(k_1{p}_{22}-p_{12})x_2^2\left(t\right)\hfill \\ & +2(p_{11}-k_1{p}_{12}-2a_1{p}_{22})x_1\left(t\right)x_2\left(t\right)\hfill \\ & +2a_1{p}_{22}{x}_1\left(t\right)G(t,x_{2t})+2(k_1{p}_{22}-p_{12})x_2\left(t\right)G(t,x_{2t}).\hfill \end{array}$$

From (17) it follows that $2a_1{p}_{12}=q$, $2(k_1{p}_{22}-p_{12})=1$, $p_{11}-k_1{p}_{12}-2a_1{p}_{22}=0$, $2a_1{p}_{22}=p$. So,

$$2{\eta }^{\prime }\left(t\right)PAx\left(t\right)=-q{x}_1^2\left(t\right)-x_2^2\left(t\right)+(p{x}_1\left(t\right)+x_2\left(t\right))G(t,x_{2t}).$$

(20)

Note also that via (15)

$$\begin{array}{cc}\hfill x^{\prime }\left(t\right)C^{\prime }PCx\left(t\right)& =\left[\begin{array}{cc}{x}_1\left(t\right)& x_2\left(t\right)\end{array}\right]\left[\begin{array}{cc}0& \gamma \\ 0& 0\end{array}\right]\left[\begin{array}{cc}{p}_{11}& p_{12}\\ p_{12}& p_{22}\end{array}\right]\left[\begin{array}{cc}0& 0\\ \gamma & 0\end{array}\right]\left[\begin{array}{c}{x}_1\left(t\right)\\ x_2\left(t\right)\end{array}\right]\hfill \\ & =\left[\begin{array}{cc}{x}_1\left(t\right)& x_2\left(t\right)\end{array}\right]\left[\begin{array}{cc}{\gamma }^2{p}_{22}& 0\\ 0& 0\end{array}\right]\left[\begin{array}{c}{x}_1\left(t\right)\\ x_2\left(t\right)\end{array}\right]={\gamma }^2{p}_{22}{x}_1^2\left(t\right)\hfill \end{array}$$

(21)

and similarly

$$x^{\prime }\left(t\right)B^{\prime }PBx\left(t\right)={\sigma }^2{p}_{22}{x}_1^2\left(t\right).$$

(22)

Using (6), for arbitrary $\mu >0$ we have

$$\begin{array}{cc}\hfill x_1\left(t\right)G(t,x_{2t})& ={\int }_0^{\infty }dK\left(\tau \right){\int }_{t-\tau }^t(s-t+\tau )x_1\left(t\right)x_2\left(s\right)ds\hfill \\ & \le {\displaystyle \frac{1}{2}}{\int }_0^{\infty }|dK\left(\tau \right)|{\int }_{t-\tau }^t(s-t+\tau )\left(\mu x_1^2\left(t\right)+{\displaystyle \frac{1}{\mu }}{x}_2^2\left(s\right)\right)ds\hfill \\ & ={\displaystyle \frac{1}{4}}\mu k_2{x}_1^2\left(t\right)+{\displaystyle \frac{1}{2\mu }}{\int }_0^{\infty }\left|K\left(\tau \right)\right|{\int }_{t-\tau }^t(s-t+\tau )x_2^2\left(s\right)ds\hfill \end{array}$$

(23)

and similarly

$$\begin{array}{cc}\hfill x_2\left(t\right)G(t,x_{2t})& ={\int }_0^{\infty }dK\left(\tau \right){\int }_{t-\tau }^t(s-t+\tau )x_2\left(t\right)x_2\left(s\right)ds\hfill \\ & \le {\displaystyle \frac{1}{2}}{\int }_0^{\infty }|dK\left(\tau \right)|{\int }_{t-\tau }^t(s-t+\tau )(x_2^2\left(t\right)+x_2^2\left(s\right))ds\hfill \\ & ={\displaystyle \frac{1}{4}}{k}_2{x}_2^2\left(t\right)+{\displaystyle \frac{1}{2}}{\int }_0^{\infty }\left|dK\left(\tau \right)\right|{\int }_{t-\tau }^t(s-t+\tau )x_2^2\left(s\right)ds.\hfill \end{array}$$

(24)

From (23), (24) we obtain

$$(p{x}_1\left(t\right)+x_2\left(t\right))G(t,x_{2t})\le {\displaystyle \frac{1}{4}}p\mu k_2{x}_1^2\left(t\right)+{\displaystyle \frac{1}{4}}{k}_2{x}_2^2\left(t\right)+\alpha {\int }_0^{\infty }\left|dK\left(\tau \right)\right|{\int }_{t-\tau }^t(s-t+\tau )x_2^2\left(s\right)ds,$$

(25)

where

$$\alpha ={\displaystyle \frac{1}{2}}\left(1+{\displaystyle \frac{p}{\mu }}\right).$$

(26)

As a result from (19), (20), (21), (22), (18), (25) it follows that

$$\begin{array}{cc}\hfill L{V}_1\left(\eta \left(t\right)\right)& =-q{x}_1^2\left(t\right)-x_2^2\left(t\right)+(p{x}_1\left(t\right)+x_2\left(t\right))G(t,x_{2t})+\rho {\displaystyle \frac{p}{2a_1}}{x}_1^2\left(t\right)\hfill \\ & \le -\left(q-{\displaystyle \frac{p}{4}}\mu k_2-\rho {\displaystyle \frac{p}{2a_1}}\right)x_1^2\left(t\right)-\left(1-{\displaystyle \frac{1}{4}}{k}_2\right)x_2^2\left(t\right)\hfill \\ & +\alpha {\int }_0^{\infty }\left|dK\left(\tau \right)\right|{\int }_{t-\tau }^t(s-t+\tau )x_2^2\left(s\right)ds.\hfill \end{array}$$

(27)

Put now

$$V_2(t,x_{2t})={\displaystyle \frac{\alpha }{2}}{\int }_0^{\infty }\left|dK\left(\tau \right)\right|{\int }_{t-\tau }^t{(s-t+\tau )}^2{x}_2^2\left(s\right)ds.$$

Then via (6)

$$L{V}_2(t,x_{2t})={\displaystyle \frac{\alpha k_2}{2}}{x}_2^2\left(t\right)-\alpha {\int }_0^{\infty }\left|dK\left(\tau \right)\right|{\int }_{t-\tau }^t(s-t+\tau )x_2^2\left(s\right)ds.$$

(28)

From (27), (28) and (26) for the functional $V(t,x_t)=V_1\left(\eta \left(t\right)\right)+V_2(t,x_{2t})$ we obtain

$$\begin{array}{cc}\hfill LV(t,x_t)& \le -\left(q-\rho {\displaystyle \frac{p}{2a_1}}-{\displaystyle \frac{p}{4}}\mu k_2\right)x_1^2\left(t\right)-\left(1-{\displaystyle \frac{1}{4}}{k}_2-{\displaystyle \frac{\alpha k_2}{2}}\right)x_2^2\left(t\right)\hfill \\ & =-\left(q-\rho {\displaystyle \frac{p}{2a_1}}-{\displaystyle \frac{p}{4}}\mu k_2\right)x_1^2\left(t\right)-\left(1-{\displaystyle \frac{1}{2}}{k}_2-{\displaystyle \frac{p{k}_2}{4\mu }}\right)x_2^2\left(t\right).\hfill \end{array}$$

(29)

From the condition of positivity of the expressions in the brackets before $x_1^2\left(t\right)$ and $x_2^2\left(t\right)$ we have

$${\displaystyle \frac{4}{p{k}_2}}\left(q-\rho {\displaystyle \frac{p}{2a_1}}\right)>\mu >{\displaystyle \frac{p{k}_2}{2(2-k_2)}},p={\displaystyle \frac{q+a_1}{k_1}}.$$

So, if

$${\displaystyle \frac{4}{p{k}_2}}\left(q-\rho {\displaystyle \frac{p}{2a_1}}\right)>{\displaystyle \frac{p{k}_2}{2(2-k_2)}}$$

(30)

then there exists $\mu >0$ such that the Lyapunov functional $V(t,x_t)$ satisfies the condition

$$LV(t,x_t)\le -c{\left|x\left(t\right)\right|}^2,c>0.$$

(31)

It is well known (see [19,22,23,24,25,29]) that the existence of a Lyapunov functional $V(t,x_t)$ satisfying the condition (31) ensures the asymptotic mean square stability of the zero solution of the considered equation.

It remains to show that the inequality (30) for some $p>0$ coincides with the inequality (18) for $\rho$. Really, from (30) it follows that

$$\rho <{\displaystyle \frac{2a_1}{p}}\left(q-{\displaystyle \frac{p^2{k}_2^2}{8(2-k_2)}}\right)$$

or via $q=p{k}_1-a_1$

$$\rho <2a_1\left(k_1-f\left(p\right)\right),f\left(p\right)={\displaystyle \frac{a_1}{p}}+{\displaystyle \frac{p}{b}},b={\displaystyle \frac{8(2-k_2)}{k_2^2}}.$$

(32)

Note that the function $f\left(p\right)$ has a minimum for $p_m=\sqrt{a_{1}b}$ and

$$f\left(p_m\right)=2\sqrt{{\displaystyle \frac{a_1}{b}}}=k_2\sqrt{{\displaystyle \frac{a_1}{2(2-k_2)}}}.$$

From this and (32) the inequality (18) for $\rho$ follows. The proof is completed. □

Remark 4. 

Note that by $\rho =0$ the last condition (18) coincides with (8).

2.2. Nonlinear Model

Consider now the nonlinear equation (1) with the control (3) and similarly to (5) represent it in the form of the system of nonlinear differential equations

$$\begin{array}{l}{\dot{x}}_1\left(t\right)=x_2\left(t\right),\\ {\dot{x}}_2\left(t\right)=asin{x}_1\left(t\right)+{\int }_0^{\infty }dK\left(\tau \right)x_1(t-\tau ).\end{array}$$

(33)

Supposing that the parameter a in (33) is influenced by stochastic perturbations $\dot{\xi }\left(t\right)$ (13), i.e., $a\to a+\dot{\xi }\left(t\right)$, we obtain

$$\begin{array}{l}{\dot{x}}_1\left(t\right)=x_2\left(t\right),\\ {\dot{x}}_2\left(t\right)=(a+\dot{\xi }\left(t\right))sin{x}_1\left(t\right)+{\int }_0^{\infty }dK\left(\tau \right)x_1(t-\tau ).\end{array}$$

or

$$\begin{array}{cc}\hfill d{x}_1\left(t\right)& =x_2\left(t\right)dt,\hfill \\ \hfill d{x}_2\left(t\right)& =\left(asin{x}_1\left(t\right)+{\int }_0^{\infty }dK\left(\tau \right)x_1(t-\tau )\right)dt\hfill \\ & \hspace{1em}+sin{x}_1\left(t\right)(\sigma dw\left(t\right)+\gamma d\tilde{\nu }\left(t\right)).\hfill \end{array}$$

(34)

From here and (11) it follows

$$\begin{array}{cc}\hfill d{x}_1\left(t\right)& =x_2\left(t\right)dt,\hfill \\ \hfill dz\left(t\right)& =(-a_1{x}_1\left(t\right)-k_1{x}_2\left(t\right)-af\left(x_1\left(t\right)\right))dt\hfill \\ & +(x_1\left(t\right)-f\left(x_1\left(t\right)\right))(\sigma dw\left(t\right)+\gamma d\tilde{\nu }\left(t\right)),\hfill \end{array}$$

(35)

where $f\left(x\right)=x-sinx$, $a_1$, $k_1$ and $z\left(t\right)$ are defined in (6), (10).

Note that the system (14) is the linear part of the system (35) and $\left|f\left(x\right)\right|\le {\displaystyle \frac{1}{6}}{x}^3$, i.e., the order of nonlinearity of the system (35) is higher than one. It is known [19] that if the order of nonlinearity of the nonlinear system under consideration is higher than one then the sufficient condition for asymptotic mean square stability of the zero solution of the linear part of this system is at the same time the sufficient condition for stability in probability of the zero solution of the initial nonlinear system. Thus, we obtain the following

Theorem 3. 

If the conditions (18) hold then the zero solution of the system (35) is stable in probability.

3. Nonzero Equilibrium

To get the nonzero equilibrium of the nonlinear system (33) let us suppose that ${\dot{x}}_1\left(t\right)\equiv 0$, ${\dot{x}}_2\left(t\right)\equiv 0$. Then $x_1\left(t\right)\equiv \widehat{x}\ne 0$ and $x_2\left(t\right)\equiv 0$. From (33) and (6) it follows that $\widehat{x}$ is a root of the equation

$$asin\widehat{x}+k_0\widehat{x}=0$$

(36)

or

$$S\left(\widehat{x}\right)=0,$$

(37)

where

$$S\left(x\right)={\displaystyle \frac{sinx}{x}}+{\displaystyle \frac{k_0}{a}}.$$

The function $S\left(x\right)$ we will call "the characteristic function of the system (33)".

Let us note the following statements [19].

Remark 5. 

The statements "$\widehat{x}$ is an equilibrium of the system (33)" and "$\widehat{x}$ is a root of the equation (37)" are equivalent.

Remark 6. 

For all $x\ne 0$

$$-\alpha \le {\displaystyle \frac{sinx}{x}}<1,$$

where $0.217233<\alpha <0.217234$. Therefore, if

$$-\alpha \le -{\displaystyle \frac{k_0}{a}}<1$$

or

$$0<a+k_0\le (1+\alpha )a$$

(38)

then there exists at least one nonzero root of the equation (37).

Remark 7. 

The condition (38) contradicts to the necessary condition $a_1=-(a+k_0)>0$ (7) for asymptotic stability of the zero solution of the linear system (5). Thus, by the condition (38) the zero solution of the linear system (5) is unstable.

Theorem 4. 

Let $\widehat{x}$ be a positive root of the equation (37).

-

If $\widehat{x}$ is a point of stable equilibrium of the system (33) then $\dot{S}\left(\widehat{x}\right)<0$, i.e., $\widehat{x}$ is a point of the decreasing of the characteristic function $S\left(x\right)$.

-

If $\widehat{x}$ is a point of the increasing of the characteristic function $S\left(x\right)$, i.e., $\dot{S}\left(\widehat{x}\right)>0$, then $\widehat{x}$ is a point of unstable equilibrium of the system (33).

Remark 8. 

Let $\widehat{x}$ be a point of an extremum of the characteristic function $S\left(x\right)$. In this case $\dot{S}\left(\widehat{x}\right)=0$ and $\widehat{x}$ is a point of one-sided stable of equilibrium of the system (33). It means that if the system stays in a point x from small enough neighborhood of $\widehat{x}$ and $\dot{S}\left(x\right)<0$ then the solution converges to $\widehat{x}$. But if the system stays in a point x from small enough neighborhood of $\widehat{x}$ and $\dot{S}\left(x\right)>0$ then the solution goes away from $\widehat{x}$.

Remark 9. 

Since the function $S\left(x\right)$ is an even function then for negative roots of the equation (37) the pictures are symmetrical.

3.1. Stochastic Perturbations and Linearization

Let us suppose that the second equation of the system (33) is influenced by additive stochastic perturbations of the form $(x_1\left(t\right)-\widehat{x})\dot{\xi }\left(t\right)$, where $\widehat{x}$ is a nonzero root of the equation (37) and $\xi \left(t\right)$ is defined in (13). Then similarly to (34) we obtain:

$$\begin{array}{l}d{x}_1\left(t\right)=x_2\left(t\right)dt,\\ d{x}_2\left(t\right)=\left(asin{x}_1\left(t\right)+{\int }_0^{\infty }dK\left(\tau \right)x_1(t-\tau )\right)dt+(x_1\left(t\right)-\widehat{x})d\xi \left(t\right).\end{array}$$

(39)

Putting $x_1\left(t\right)=\widehat{x}+y_1\left(t\right)$, $x_2\left(t\right)=y_2\left(t\right)$ and using (6), (36), let us transform the second equation of the system (39) by the following way

$$\begin{array}{cc}\hfill d{y}_2\left(t\right)& =\left(asin(\widehat{x}+y_1\left(t\right))+{\int }_0^{\infty }dK\left(\tau \right)(\widehat{x}+y_1(t-\tau ))\right)dt+y_1\left(t\right)d\xi \left(t\right)\hfill \\ & =\left(asin(\widehat{x}+y_1\left(t\right))+k_0\widehat{x}+{\int }_0^{\infty }dK\left(\tau \right)y_1(t-\tau )\right)dt+y_1\left(t\right)d\xi \left(t\right)\hfill \\ & =\left(a[sin(\widehat{x}+y_1\left(t\right))-sin\left(\widehat{x}\right)]+{\int }_0^{\infty }dK\left(\tau \right)y_1(t-\tau )\right)dt+y_1\left(t\right)d\xi \left(t\right).\hfill \end{array}$$

Using elementary trigonometric transformations and linearization

$$\begin{array}{cc}\hfill sin(\widehat{x}+y_1\left(t\right))& =sin\left(\widehat{x}\right)cos\left(y_1\left(t\right)\right)+cos\left(\widehat{x}\right)sin\left(y_1\left(t\right)\right)\hfill \\ & =sin\left(\widehat{x}\right)+cos\left(\widehat{x}\right)y_1\left(t\right)+o\left(y_1\left(t\right)\right),\hfill \\ \hfill sin(\widehat{x}+y_1\left(t\right))& -sin\left(\widehat{x}\right)=cos\left(\widehat{x}\right)y_1\left(t\right)+o\left(y_1\left(t\right)\right),\hfill \end{array}$$

we obtain

$$\begin{array}{cc}\hfill d{y}_1\left(t\right)& =y_2\left(t\right)dt,\hfill \\ \hfill d{y}_2\left(t\right)& =\left(acos\left(\widehat{x}\right)y_1\left(t\right)+{\int }_0^{\infty }dK\left(\tau \right)y_1(t-\tau )\right)dt\hfill \\ & +y_1\left(t\right))(\sigma dw\left(t\right)+\gamma d\tilde{\nu }\left(t\right)).\hfill \end{array}$$

(40)

or similarly to (11), (14) in the form of the system of neutral type differential equations

$$\begin{array}{cc}\hfill d{y}_1\left(t\right)& =y_2\left(t\right)dt,\hfill \\ \hfill dz\left(t\right)& =(-a_2{y}_1\left(t\right)-k_1{y}_2\left(t\right))dt+\sigma y_1\left(t\right)dw\left(t\right)+\gamma y_1\left(t\right)d\tilde{\nu }\left(t\right),\hfill \end{array}$$

(41)

where

$$\begin{gathered} a_2=-(acos\left(\widehat{x}\right)+k_0),z\left(t\right)=y_2\left(t\right)-G(t,y_{2t}), \\ G(t,y_{2t})={\int }_0^{\infty }dK\left(\tau \right){\int }_{t-\tau }^t(s-t+\tau )y_2\left(s\right)ds. \end{gathered}$$

(42)

Note that the system (41), (42) has the form of the system (14). So, using Theorems 2 and 3 we obtain the following

Theorem 5. 

Let be

$$\begin{gathered} a_2=-(acos\left(\widehat{x}\right)+k_0)>0,k_1>0,k_2<2, \\ \rho ={\sigma }^2+\lambda {\gamma }^2<2a_2\left(k_1-k_2\sqrt{{\displaystyle \frac{a_2}{2(2-k_2)}}}\right), \end{gathered}$$

(43)

where $k_i$, $i=0,1,2$, are defined in (6). Then the nonzero equilibrium $\widehat{x}$ of the system (39) is stable in probability.

4. Numerical Simulation

4.1. Difference Analogue of the System (34)

Put in (34)

$$dK\left(\tau \right)=(b_1\delta (\tau -h_1)+b_2\delta (\tau -h_2))d\tau ,$$

(44)

where $h_1>0$, $h_2>0$, and $\delta \left(\tau \right)$ is the Dirac delta-function. Then

$${\int }_0^{\infty }dK\left(\tau \right)x_1(t-\tau )=b_1{x}_1(t-h_1)+b_2{x}_1(t-h_2)$$

(45)

and the system (34) takes the form

$$\begin{array}{l}d{x}_1\left(t\right)=x_2\left(t\right)dt,\\ d{x}_2\left(t\right)=[asin{x}_1\left(t\right)+b_1{x}_1(t-h_1)+b_2{x}_1(t-h_2)]dt\\ +sin{x}_1\left(t\right)[\sigma dw\left(t\right)+\gamma d\tilde{\nu }\left(t\right)].\end{array}$$

(46)

Similarly to [16,18,28], consider the difference analogue of the system (46) in the form

$$\begin{array}{l}{x}_{1,i+1}=x_{1i}+\Delta x_{2i},\\ x_{2,i+1}=x_{2,i}+\Delta [asin{x}_{1,i}+b_1{x}_{1,i-m_1}+b_2{x}_{1,i-m_2}]\\ +sin{x}_{1,i}[\sigma (w_{i+1}-w_i)+\gamma ({\nu }_{i+1}-{\nu }_i-\lambda \Delta )],\end{array}$$

(47)

where

$$\begin{gathered} x_{ki}=x_k\left(t_i\right),m_k=h_k/\Delta ,k=1,2, \\ {w}_i=w\left(t_i\right),{\nu }_i=\nu \left(t_i\right),t_i=\Delta i,\Delta >0,i=0,1,.... \end{gathered}$$

(48)

Remark 10. 

In the case (44) the conditions (6) and (7) are respectively

$$a_1=-a-k_0=-a-(b_1+b_2),k_1=b_1{h}_1+b_2{h}_2,k_2=|b_1|h_1^2+\left|b_2\right|h_2^2,$$

and

$$k_0=b_1+b_2<-a<0,k_1=b_1{h}_1+b_2{h}_2>0,k_2=|b_1|h_1^2+\left|b_2\right|h_2^2<2.$$

(49)

Note that if, for instance, $b_2=0$ then from the first inequality (49) it follows that $b_1<0$, but from the second one it follows that $b_1>0$. This means that stabilization by control of the form $u\left(t\right)=b_1{x}_1(t-h_1)$ is impossible.

4.2. Difference Analogue of the System (39)

Using (45) for the system (39), we obtain

$$\begin{array}{l}{\dot{x}}_1\left(t\right)=x_2\left(t\right),\\ {\dot{x}}_2\left(t\right)=asin{x}_1\left(t\right)+b_1{x}_1(t-h_1)+b_2{x}_1(t-h_2)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+(x_1\left(t\right)-\widehat{x})[\sigma dw\left(t\right)+\gamma d\tilde{\nu }\left(t\right)].\end{array}$$

(50)

Similarly to (47), (48), the difference analogue of the system (50) has the form

$$\begin{array}{l}{x}_{1,i+1}=x_{1i}+\Delta x_{2i},\\ x_{2,i+1}=x_{2,i}+\Delta [asin{x}_{1,i}+b_1{x}_{1,i-m_1}+b_2{x}_{1,i-m_2}]\\ +(x_{1,i}-\widehat{x})[\sigma (w_{i+1}-w_i)+\gamma ({\nu }_{i+1}-{\nu }_i-\lambda \Delta )].\end{array}$$

(51)

4.3. Examples

Below two examples are considered, where the difference analogues (47) and (51) are used for numerical simulation of solutions of the systems (46) and (50). Similarly to [26,27], for numerical simulation of the Poisson process ${\nu }_i$ the continuous random variable $\zeta$ is used, uniformly distributed on the interval $(0,1)$: ${\nu }_{i+1}-{\nu }_i=1$ if $\zeta <\lambda \Delta$ and ${\nu }_{i+1}-{\nu }_i=0$ in the contrary case. A special algorithm for numerical simulation of the standard Wiener process and examples with stochastic perturbations of the white noise type are described in detail in [19], so, below it is supposed that $\sigma =0$. In both examples one can see that some trajectories have discontinuities, that is a consequence of the Poisson process jumps.

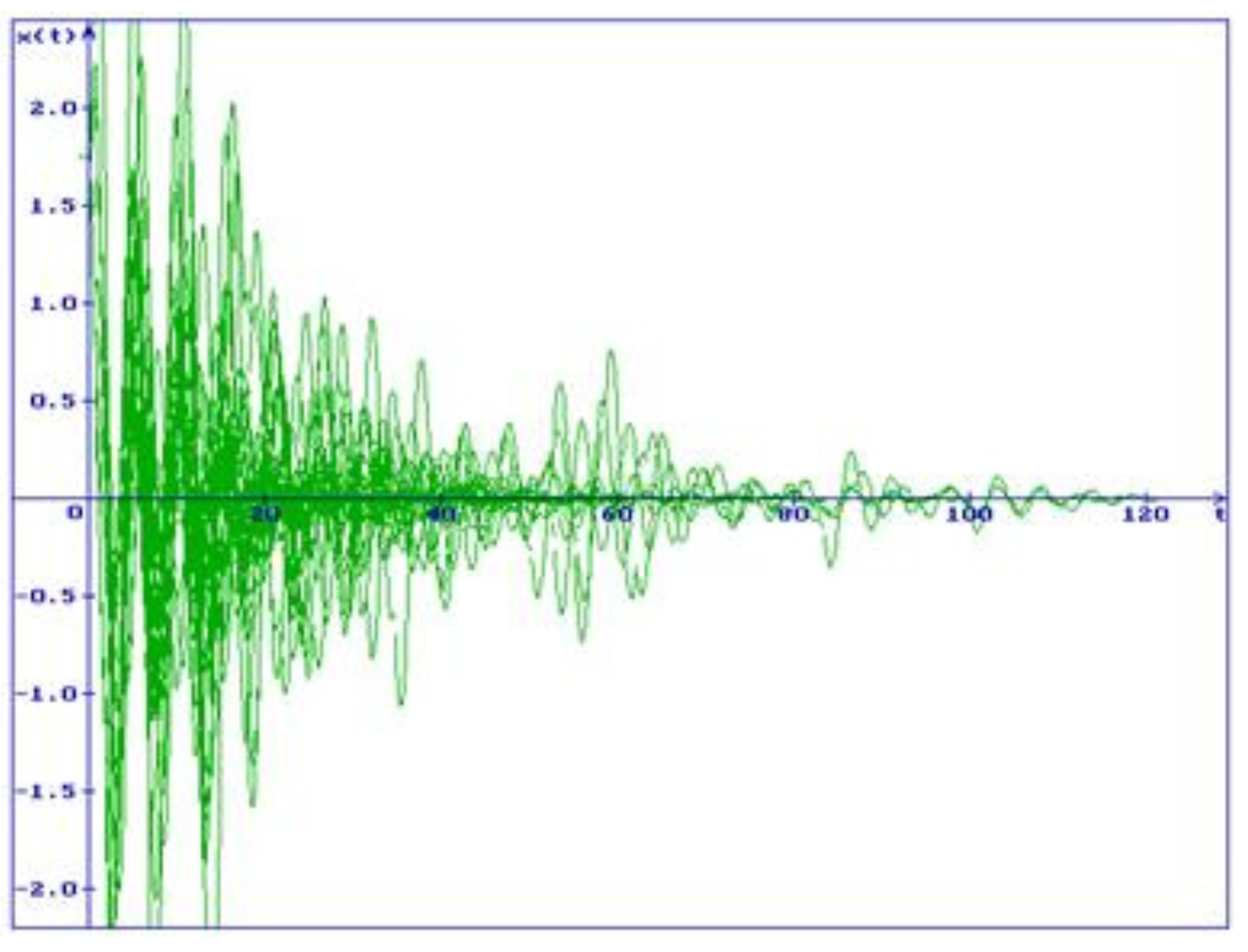
Example 1. 

Consider the system (46) with $a=0.3$, $b_1=1$, $b_2=-2.5$, $h_1=0.6$, $h_2=0.1$, $\sigma =0$, $\lambda =0.15$, $\gamma =0.25$ and the initial conditions $x\left(s\right)=1.75$, $s\le 0$. By this $k_0=-1.5$, $k_1=0.35$, $k_2=0.385$, $a_1=1.2>0$, the conditions (18) hold, the zero solution of the system (46) is stable in probability (Theorem 3), all trajectories converge to the zero (Figure 2).

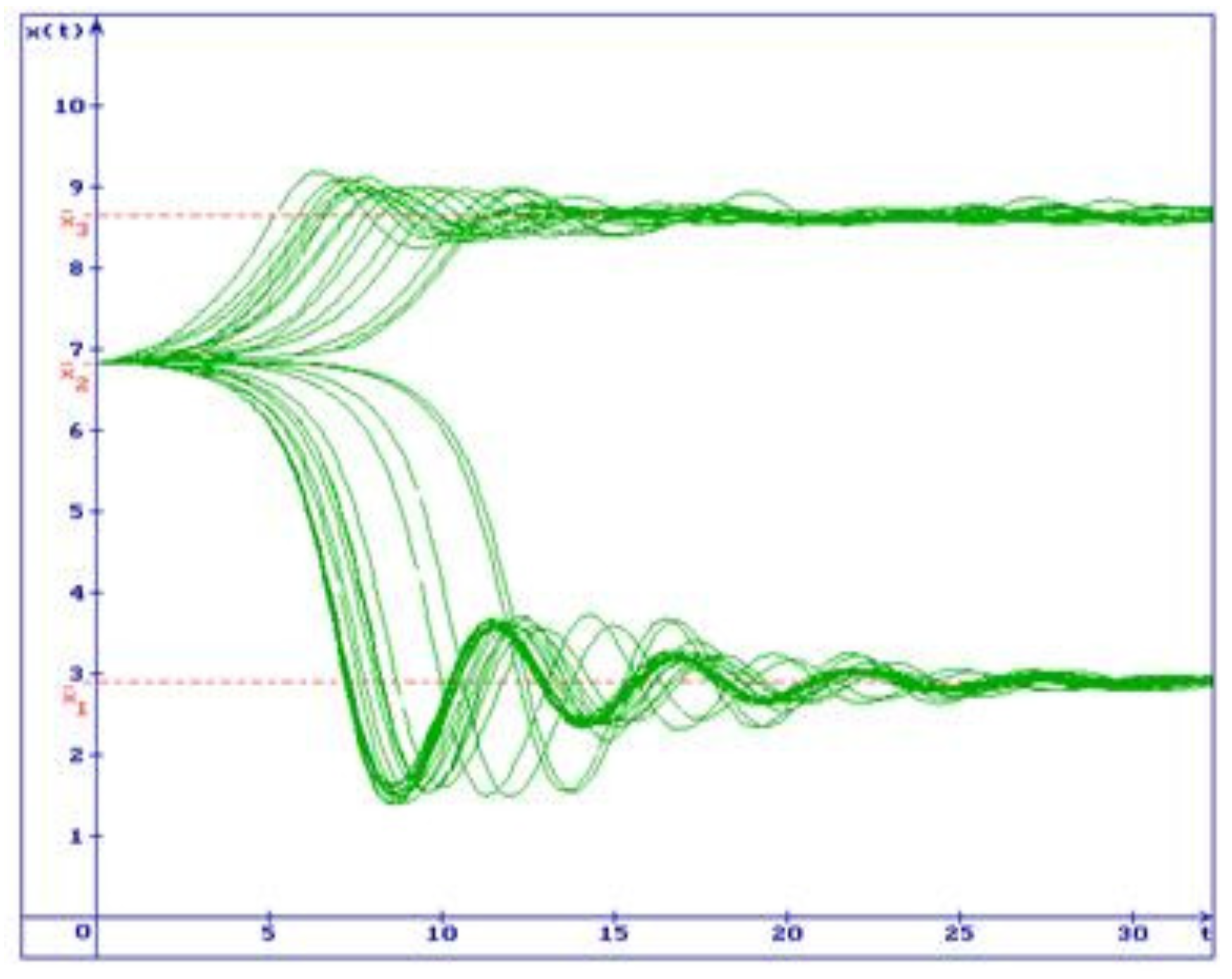
Example 2. 

Consider the system (50) with $a=1$, $b_1=1$, $b_2=-1.08$, $h_1=0.8$, $h_2=0.3$, $\sigma =0$, $\lambda =0.2$, $\gamma =0.1$. In this case $k_0=-0.08$, $k_1=0.476$, $k_2=0.7372$ and $a_1=-(a+k_0)=-0.92<0$. Thus, the first condition (7) does not hold and, consequently, the zero solution of the system (35) is unstable. By that, the equation (37) has three positive roots: ${\widehat{x}}_1=2.907$, ${\widehat{x}}_2=6.865$, ${\widehat{x}}_3=8.659$, which are equilibria of the system (33) (Remark 5). For these equilibria we have respectively: $cos\left({\widehat{x}}_1\right)=-0.973$, $a_2>0$; $cos\left({\widehat{x}}_2\right)=0.836$, $a_2<0$; $cos\left({\widehat{x}}_3\right)=-0.721$, $a_2>0$. Besides, $\dot{S}\left({\widehat{x}}_1\right)<0$, $\dot{S}\left({\widehat{x}}_2\right)>0$, $\dot{S}\left({\widehat{x}}_3\right)<0$. From Theorems 4 and 5 it follows that the equilibria ${\tilde{x}}_1$ and ${\tilde{x}}_3$ are stable in probability, the equilibrium ${\tilde{x}}_2$ is unstable. In Fig.3 50 trajectories of the system (50) solution are shown with the initial condition $x_1\left(s\right)={\tilde{x}}_2$, $x_2\left(s\right)=0$, $s\le 0$. One can see that all trajectories go out from the unstable equilibrium ${\tilde{x}}_2$. By that, a part of the trajectories converges to the stable equilibrium ${\tilde{x}}_1$, while another one converges to the stable equilibrium ${\tilde{x}}_3$.

5. Conclusions

In this paper the classical problem of stabilization for the inverted pendulum is considered under stochastic perturbations of the type of Poisson’s jumps. The linear and nonlinear models are studied, stability conditions for the zero and nonzero equilibria are investigated. The obtained results are illustrated by numerical simulation of solutions of the equations under consideration. The proposed here research method can be used for detail investigation of many other nonlinear mathematical models in different applications.