Regeneration Filter: Enhancing Mosaic Algorithm for Near Salt & Pepper Noise Reduction

1. Introduction

Although classified as a fundamental element of multimedia, the digital image, when viewed through the prism of digital signal processing, exhibits characteristics similar to those of other signal types. In every stage, be it generation, transmission, or processing, digital signals invariably incur a certain degree of noise. Thus, regardless of the conditions under which an image is created, it inherently contains some level of noise. This intrinsic noise presents a significant challenge within the field of Digital Image Processing (DIP), as it necessitates effective methods to mitigate or eliminate noise to an acceptable level. A prevalent type of noise encountered in digital images is Salt & Pepper (S&P) noise, which manifests as extreme pixel intensity values, specifically at 0 and 255 on the grayscale. The occurrence of S&P noise in images is spatially random, with affected pixels following a stochastic distribution, where the density of noise is quantified as a percentage. Initially, nonlinear filters were employed to address this type of noise; however, these filters indiscriminately processed all pixels within the image, including those unaffected by noise, which led to a reduction in image quality due to unnecessary processing of clean pixels.

Fundamentals of Nonlinear Digital Filtering is the first book to comprehensively explore and evaluate algorithms and applications in nonlinear digital filtering [1]. This seminal work serves as a reference handbook and textbook, catering to professors, researchers, engineers, and students alike. It establishes a foundational understanding of nonlinear filtering techniques and their practical implications, laying the groundwork for subsequent research endeavors. Impulse noise, particularly prevalent in image processing applications, presents a formidable obstacle to traditional filtering approaches. Paper [2] introduces innovative adaptive median filters designed to effectively remove impulses while preserving image sharpness. These algorithms demonstrate superior performance compared to conventional algorithms, offering promising solutions to the challenges posed by impulse noise corruption. Building upon the advancements in adaptive filtering, paper [3] proposes a novel decision-based algorithm for restoring images heavily corrupted by impulse noise. The algorithm exhibits remarkable efficacy in noise removal, surpassing the capabilities of standard median filters and adaptive schemes, while preserving image edges and details, even at high noise spatial density. Paper [4] presents an improved decision-based detail-preserving variational algorithm tailored for the removal of random-valued impulse noise. By integrating adaptive center weighted median filters and fast iteration strategies, the proposed algorithm outperforms existing algorithms in both qualitative and quantitative evaluations, offering expedited denoising solutions for practical applications. In parallel, the integration of infrared thermography instruments for PCB inspection underscores the interdisciplinary nature of noise reduction techniques. Paper [5] establishes a thermal model for PCB fault detection, leveraging advanced reconstruction algorithms to enhance temperature field quality. This approach showcases the versatility of noise mitigation strategies across diverse domains, highlighting their potential for real-world applications beyond traditional image processing contexts. Another research of impulse noise removal, paper [6] introduces a modified decision-based unsymmetrical trimmed median filter algorithm tailored for grayscale and color image restoration. This algorithm exhibits superior performance compared to conventional median filters, offering enhanced peak signal-to-noise ratios and image enhancement factors across various test scenarios. Paper [7] presents an effective noise removal algorithm utilizing switching median filtering techniques. By incorporating boundary discriminative noise detection, the proposed algorithm demonstrates superior noise suppression capabilities compared to traditional median filters, validating its efficacy through extensive simulation studies. Similarly, paper [8] introduces a novel switching median filter enhanced by boundary discriminative noise detection for denoising highly corrupted images. This algorithm achieves remarkable noise detection accuracy, outperforming existing algorithms while maintaining computational efficiency, thereby facilitating seamless integration into practical applications. Expanding the scope of noise removal beyond impulse noise, paper [9] proposes an efficient architecture for median filtering in image denoising applications. Leveraging decision filters and area-efficient designs, the proposed approach achieves significant improvements in denoising speed and peak signal-to-noise ratios, demonstrating its viability for real-world deployment. Paper [10] introduces a thresholding and regularization-based algorithms for salt and pepper noise removal, showcasing superior denoising performance compared to existing techniques. By leveraging total variation regularization and tailored noise detection strategies, the proposed algorithm offers robust solutions for noise reduction in large-scale image datasets. In parallel, paper [11] addresses limitations in switching median filters through innovative modifications to the boundary discriminative noise detection algorithm. Experimental evaluations highlight the effectiveness of these modifications in producing sharper images with enhanced noise suppression capabilities. Paper [12] presents a graph signal reconstruction-based approach for salt and pepper noise removal, offering a novel framework for image restoration. By modeling noise removal as a graph signal reconstruction problem, the proposed algorithm achieves superior denoising performance compared to state-of-the-art algorithms, demonstrating its potential for practical applications. Paper [13] introduces a two-step salt and pepper noise removal algorithm, combining median-type filtering with adaptive nonlocal bilateral filtering. By addressing errors inherent in median-type filtering, the proposed algorithm achieves superior noise reduction while preserving image details, offering a compelling solution for challenging noise removal scenarios. Although all the aforementioned solutions for reducing S&P noise have their advantages and contribute significantly to the field of digital image processing, they are not yet ideal solutions. Nearly all proposed models fail to produce satisfactory results beyond 30% noise. This manuscript provides insight into a novel filter solution for S&P noise reduction based on spatial domain processing, with a particular emphasis on statistical processing of numerical data (pixel values), which can be reliably utilized even in reducing images with 70% noise spatial density. Additionally, it is noteworthy that by reusing images, there is no loss in quality, thus enabling the reconstruction of images even with a 90% noise spatial density.

In defining special conditions, in this case, a hybrid algorithm of edge detection will not be used at the very beginning, as it is stated in the original form of the mosaic algorithm [14]. When it comes to noise reduction, it is inadequate to detect edges first because noise would also be detected as an edge, assuming that the image already contains a high degree of noise. Therefore, the first step starts with the segmentation and definition of submatrices for analysis. The complete Regeneration filter algorithm, as described in this paper, has been implemented using the R programming language. R language was chosen as an ideal tool for image processing in such methodologies. This choice was made because the proposed filter manipulates a large amount of numerical data, as digital images are represented through a model of pixel values per horizontal and vertical dimensions, across three components (RGB). Using R language for implementing this algorithm also provides advantages in terms of integration with other packages and tools for image and data processing available in the R ecosystem. For example, researchers can easily combine the Regeneration filter with other existing filters or image processing techniques in R language, or integrate it into larger data processing workflows or analytical pipelines. Moreover, the R programming language is well-suited for image processing since for a 1-megapixel image across three R, G, and B components, there are 3 million pixels, or 3 million numerical data points that are highly amenable to statistical processing. This approach to image processing represents a novel paradigm. Near Salt & Pepper (nS&P) noise is a specific type of digital image noise characterized by near extreme pixel values, typically at the grayscale levels of 0 (black) and 255 (white). This noise appears as sparse white and black pixels distributed randomly throughout the image. The presence of nS&P noise can significantly degrade image quality, making it challenging to accurately process and analyze the affected images. Traditional filters often struggle with effectively removing this noise without affecting the uncorrupted pixels. Advanced algorithms, such as the Regeneration Filter, are designed to selectively target and reconstruct the noisy pixels, ensuring the integrity of the image is preserved even at high noise levels. This manuscript addresses the challenge of reducing nS&P noise, particularly focusing on the noise that occurs in the vicinity of these near extreme values, as well as the extreme values themselves.

This paper is organized as follows: Section 2 provides a detailed description of the methodology behind the implementation of the Regeneration filter, including the algorithm for detecting and restoring pixels affected by near Salt & Pepper (nS&P) noise. Section 3 addresses specific processing conditions, while Section 4 presents the mathematical formalization of the filter, including the algorithmic approach for image restoration. Finally, Section 5 reports the simulation results and discussions, with a comparison against existing noise reduction methods. In Section 6, we conclude the paper and outline potential future research directions.

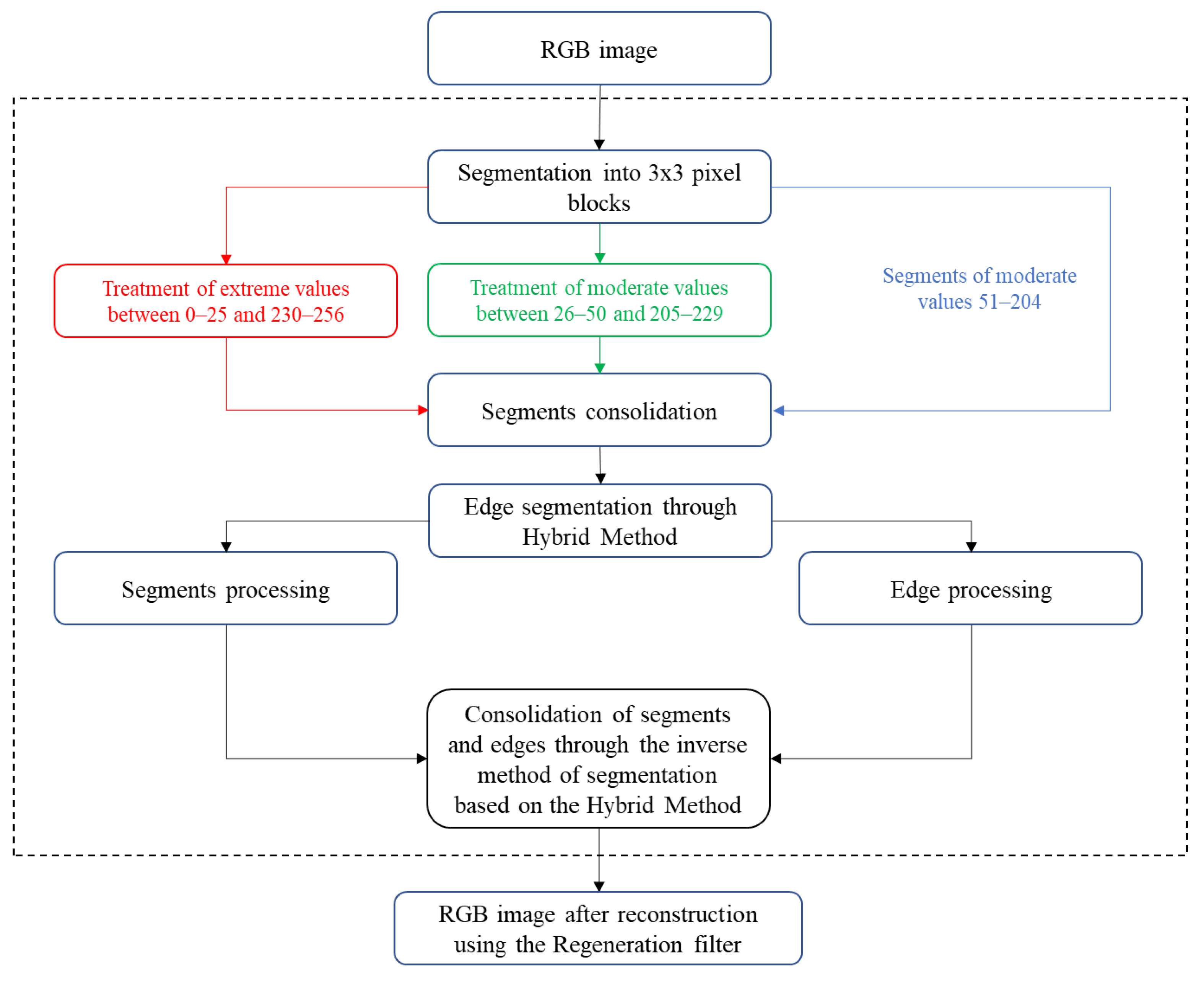
2. Implementation Methodology

The Regeneration filter represents a novel approach to the removal of nS&P noise from digital images. Aptly named after its property of "regenerating" the image, this filter selectively processes only the pixels affected by extreme values, characteristic of this type of noise, reconstructing them based on the "healthy" surrounding pixels. This eliminates the potential for damage to the parts of the image that are not affected by noise, providing an effective solution for images with high levels of spatial densities, without compromising quality.

Samples for analysis by the proposed filter were based on the images:

• Different resolutions (using processing of sub-matrices with repetition gives additional precision of the filter. Regardless of the square sub-matrix, the quality of processing does not depend on the resolution. Test resolutions covered the range from 262144 P to 48 MP.);
• Different bit depths (a test of this type provided confirmation that the filter gives very good results with both 24-bit and 32-bit recording);
• Different formats, to determine the quality, regardless of the type of compression;
• Generated for computer animation – to determine the quality of images created in special conditions;
• Generated CCD and CMOS sensors – real images from cameras / mobile phones, to show the quality of filters in various real situations in which images are taken and
• Characteristic images in the field of digital image processing, so that the results are measurable with other filters designed for this type of noise.

Figure 1 shows the part of the sample that was subjected to the processing process, while the entire database of test images was taken from the address: https://www.imageprocessingplace.com/root_files_V3/image_databases.htm. Regeneration filter as one of the results of the mosaic algorithm, presents it in full light and shows all the advantages of the proposed algorithm. Precisely with its ability to adapt to the needs of digital image processing, the mosaic algorithm provides very good results in almost all areas, as well as in this situation when reducing nS&P noise. It’s important to note that all images in this manuscript are standard images commonly utilized in works related to digital image processing, ensuring the measurability of this filter’s results against similar studies in this field. Samples of original images of various resolutions were subjected to the addition of nS&P noise using the established function within the R programming language. The original image underwent noise corruption by implementing the command for adding 1% nS&P noise, transitioning from Figure 1 to Figure 2. Subsequently, the process was iterated across the sample with incremental additions of nS&P noise spatial densities: 2%, 3%, 4%, 5%, 7.5%, 10%, 30%, 40%, 50%, 70%, 80%, and 90%. Figure 2 displays the resulting samples with noise additions ranging from 1% to 90%. Additionally, each sample with added noise serves to demonstrate the effects of varying spatial density of noise on image quality and the performance of the Regeneration filter.

Regeneration filter is applied over all images with added noise. The input to the filter is an image that contains noise, and the result of processing by the filter is an image of the same format and resolution as the input over which it was applied in the Regeneration filter. All images utilized in the analysis were stored in TIFF format for the purpose of mitigating the influence of compression on visual and numerical outcomes. The output image was compared with the original image without noise in order to determine the quality of the proposed filter.

3. Defining Special Processing Conditions

A new model of partial filtering in the implementation of algorithms for edge detection and digital image segmentation - mosaic algorithm, allows the image, using a hybrid model of edge detection (using a modified Weighted filter, image negative and providing the user to define the detection threshold) segments (parts of a mosaic) whereby the desired processing can be applied over each segment of the image with different or the same parameters.

Just as defined in the block diagram of the mosaic algorithm (Figure 3), the processing segments in this case will be submatrices 3x3. As explained in papers dealing with filter design [14,15]. When it comes to this type of problem, it is best to work with square submatrices. Vector analysis, where the pixels of a digital image are processed row by row, practically eliminates the connection of the surrounding columns with those that are processed, which can cause rough transitions in the images, and leads to an error in edge detection. The 3x3 processing matrix is the optimum on which more than 90% of the noise reduction filter is based [16]. If, for example, 2x2 submatrices are used and it is assumed that the reconstruction is done only on the basis of one "correct" pixel, it is possible to reconstruct the image up to a maximum of 75% of the damage. On the other hand, if it is a 3x3 matrix processing, and an attempt is made to reconstruct an image with a minimum of one "correct" pixel, we are talking about a potential reconstruction of approximately 90%. Another advantage of this model is the center pixel, with a position of five in that array of nine pixels. The median and all derivatives of this filter base their work on processing in relation to the value of the central pixel. Other 4x4 or 5x5 matrices give a higher degree of error, so they are not used often. Thus, for a 4x4 processing matrix, 16 pixels are processed at the same time, or for a 5x5 matrix, 25 pixels are processed at the same time. Such processing algorithms are used at extremely high noise spatial densities, while at low spatial densities they give a higher degree of error.

Another very important item in this part is the overlap of submatrices in processing. If a 3x3 matrix is used, the process involves processing 9 pixels. Processing without overlapping 18 pixels would be processed through two independent 3x3 iterations, while in the case of overlapping 18 pixels it would be processed through four independent iterations. The number of independent operations in one image processing has been doubled. This fact significantly increases the complexity of this algorithm, but on the other hand increases the efficiency of the filter. Thus, for example, if the noise spatial density in the figure is 90%, it can also be assumed that in the observed submatrix 3x3 at least one pixel is not covered by noise, so that based on one pixel, a "new" environment of that pixel can be reconstructed. This extreme example with a noise spatial density of 90% is the best explanation why the 3x3 pixel submatrix was chosen. But if by chance it happens that all the pixels of the first submatrix are detected as noise, already in the next step 6 pixels of the first submatrix will be found in the processing, which increases the efficiency of the proposed filter. The next step in the processing is the synchronization of the intermediate results of the submatrix processing. It often happens that there are extremely large differences between the pixel values after processing the submatrix. Therefore, spline interpolation is used to regulate the transition, due to the low degree of error, because lower degrees of polynomials are applied. "Fine transitions" between pixels should be used to replace pixels that are "damaged" by noise. Only in the next step over such an image is a hybrid model of edge detection used in order to further emphasize the edges. This procedure is performed by summing the detection results with the image. After the mentioned procedure, through a series of parameters for assessing the quality of the digital image, the obtained results are described.

The algorithm traverses all pixels of the image and treats only those pixels with extreme values using the algorithm, as indicated in Figure 3, performing this process in four directions to remove noise from all parts of the image. This selective processing of pixels with extreme values represents a key optimization of the proposed Regeneration filter compared to traditional approaches that process all pixels indiscriminately. First, the algorithm iterates through all pixels in the horizontal direction (rows), checking whether the value of each pixel exceeds a threshold of 254 or falls below a threshold of 2, indicating the presence of nS&P noise. If a pixel is affected by noise, its value is replaced with the value of a "healthy" pixel in the same row. This process is repeated for each row, except for the first row which lacks preceding pixels for reference. Next, the same procedure is applied in the vertical direction (columns), where noise-affected pixels are replaced with values of "healthy" pixels, except for the first column. Subsequently, the algorithm moves on to the third processing direction, replacing noise-affected pixels with values of pixels located to their right in the same row. The fourth and final direction involves replacing noise-affected pixels with values of pixels below them in the same column. Such a four-directional approach ensures that each noise-affected pixel is treated and replaced with an appropriate value based on surrounding "healthy" pixels, achieving effective noise removal from all parts of the image. The key advantage over traditional filters is that the processing focuses solely on noise-affected pixels, leaving unaffected pixels untouched. The entire algorithm is implemented using standard R functions for image loading (readTIFF), matrix manipulation (multidimensional arrays representing images), and saving the resulting image (writeTIFF). This implementation in the R programming language, which is widely used and has an active user community, facilitates result reproduction and further study of the algorithm by other researchers. Using R for implementing this algorithm also provides advantages in terms of integration with other packages and tools for image and data processing available in the R ecosystem. For example, researchers can easily combine the Regeneration filter with other existing filters or image processing techniques in R, or integrate it into larger data processing workflows or analytical pipelines.

4. Mathematical Framework

Near Salt & Pepper (nS&P) noise is a specific type of noise that affects not only the extreme pixel values (0 or 255), but also those in their immediate vicinity, i.e., pixels whose values are near these extremes. Formally, this noise can be described as a set of pixels with values within the intervals [0, $T_1$] and [$T_2,255$], where $T_1$ and $T_2$ are predefined thresholds that define the range of values close to the minimum and maximum intensities.

4.1. Formalizing Noise

Let $I(x,y)$ be the pixel intensity at position $(x,y)$ in the image I. Pixels affected by nS&P noise can be formally defined as:

$$I_{noisy}(x,y)=\left\{\begin{array}{cc}I(x,y),\hfill & \mathrm{with}\mathrm{probability}1-p\hfill \\ u\in [0,T_1],\hfill & \mathrm{with}\mathrm{probability}p/2\hfill \\ v\in [T_2,255],\hfill & \mathrm{with}\mathrm{probability}p/2\hfill \end{array},\right.$$

(1)

where $T_1$ and $T_2$ are thresholds near the minimum and maximum pixel values, and p represents the noise density. In this model, pixels u take values near 0, while pixels v take values near 255. This allows the nS&P noise model to include pixels close to the extreme values, not just those exactly at 0 and 255.

4.2. Noise Detection

The detection of pixels affected by nS&P noise is carried out using a binary mask $M(x,y)$ which marks pixels that fall within the noise region. Formally, the mask is defined as:

$$M(x,y)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}I(x,y)\in [0,T_1]\cup [T_2,255]\hfill \\ 0,\hfill & otherwise\hfill \end{array}.\right.$$

(2)

This mask differentiates "noisy" pixels from "healthy" pixels in the image. Pixels with $M(x,y)=1$ are treated as affected by noise, while those with $M(x,y)=0$ remain unchanged.

4.3. Pixel Restoration Algorithm

Pixels marked as noisy are restored based on their neighboring "healthy" pixels. The regeneration algorithm uses a local window $N(x,y)$ the pixel’s neighborhood—to calculate the restored pixel value. The neighborhood $N(x,y)$ is defined as a matrix of size kxk, where k is the window size (e.g., k=3 for a 3×3 window):

$$N(x,y)=\left\{I\right(i,j),i\in [x-k,x+k],I(i,j),j\in [y-k,y+k\left]\right\}.$$

(3)

For each pixel $I(x,y)$ marked by $M(x,y)=1$, its intensity is restored based on the pixels in its neighborhood $N(x,y)$ that are not affected by noise. We define the subset $N^{\prime }(x,y)$ of neighboring pixels that are not affected by noise as:

$$N^{\prime }(x,y)=\{I(i,j),I(x,jy)\in [0.T_1]\cup [T_2,255],(i,j)\in N(x,y)\}.$$

(4)

Unlike traditional filters, the Regeneration filter does not use median filtering. Instead, the restoration of each noisy pixel is based on a specific algorithmic strategy that analyzes the available pixel values in the neighborhood. For each noisy pixel $I(x,y)$ the algorithm examines the neighboring pixels within $N(x,y)$. These neighboring pixels are evaluated to determine whether they are free from noise (i.e., if $M(i,j)=0$. In the Regeneration filter, the restoration of noisy pixels involves averaging the values of neighboring, non-noisy pixels using a set of weights $w_{i,j}$, where $(i,j)$ represents the coordinates of the neighboring pixels. These weights determine how much influence each neighboring pixel has on the restoration of the noisy pixel, often assigning higher weights to closer or more relevant pixels.

The restoration of a noisy pixel $I(i,j)$ based on its non-noisy neighbors is done by calculating a weighted average. This process consists of two main steps:

• Sum the contributions of all neighboring pixels that are not affected by noise:

  $$S(x,y)=\sum _{(i,j)\in N(x,y),M(i,j)=0}{\omega }_{i,j}·I(i,j),$$

  (5)

  where $S(x,y)$ represents the sum of the weighted pixel values in the neighborhood $N(x,y)$. Here, ${\omega }_{x,y}$ is the weight assigned to pixel $I(i,j)$ and $M(i,j)=0$ ensures that only non-noisy pixels are included in the sum.
• Normalize the sum by dividing it by the sum of the weights:

  $$I_{new}(x,y)={\displaystyle \frac{S(x,y)}{{\sum }_{(i,j)\in N(x,y),M(i,j)=0}{\omega }_{i,j}}},$$

  (6)

  where the denominator ensures that the sum is properly scaled according to the total weight of the valid neighboring pixels. This step results in the final restored value $I_{new}(x,y)$.

This two-step process allows the algorithm to take into account the varying importance of each neighboring pixel during the restoration of the noisy pixel. The weights ${\omega }_{i,j}$ can be uniform (i.e., ${\omega }_{i,j}=1$ for all neighboring pixels) or they can vary depending on the distance of each neighboring pixel $(i,j)$ from the pixel being restored $(x,y)$. For example, a common choice for non-uniform weights is the Gaussian weight function, which assigns higher weights to pixels closer to $(x,y)$. The Gaussian weight function is given by:

$${\omega }_{i,j}=e^{-{\displaystyle \frac{d^2(i,j)}{2{\sigma }^2}}},$$

(7)

where $d(i,j)$ represents the Euclidean distance between pixel $(i,j)$ and $(x,y)$, and $\sigma$ is the standard deviation that controls the spread of the weights.

The restoration of noisy pixels in the Regeneration filter involves a two-step process: first, summing the weighted contributions of valid neighboring pixels, and second, normalizing the sum by the total weight of those neighbors. If no valid neighbors are available in the immediate vicinity, the algorithm expands the neighborhood and uses interpolation to restore the pixel values. This approach ensures that the restored pixel values are both accurate and contextually sensitive to the surrounding image structure.

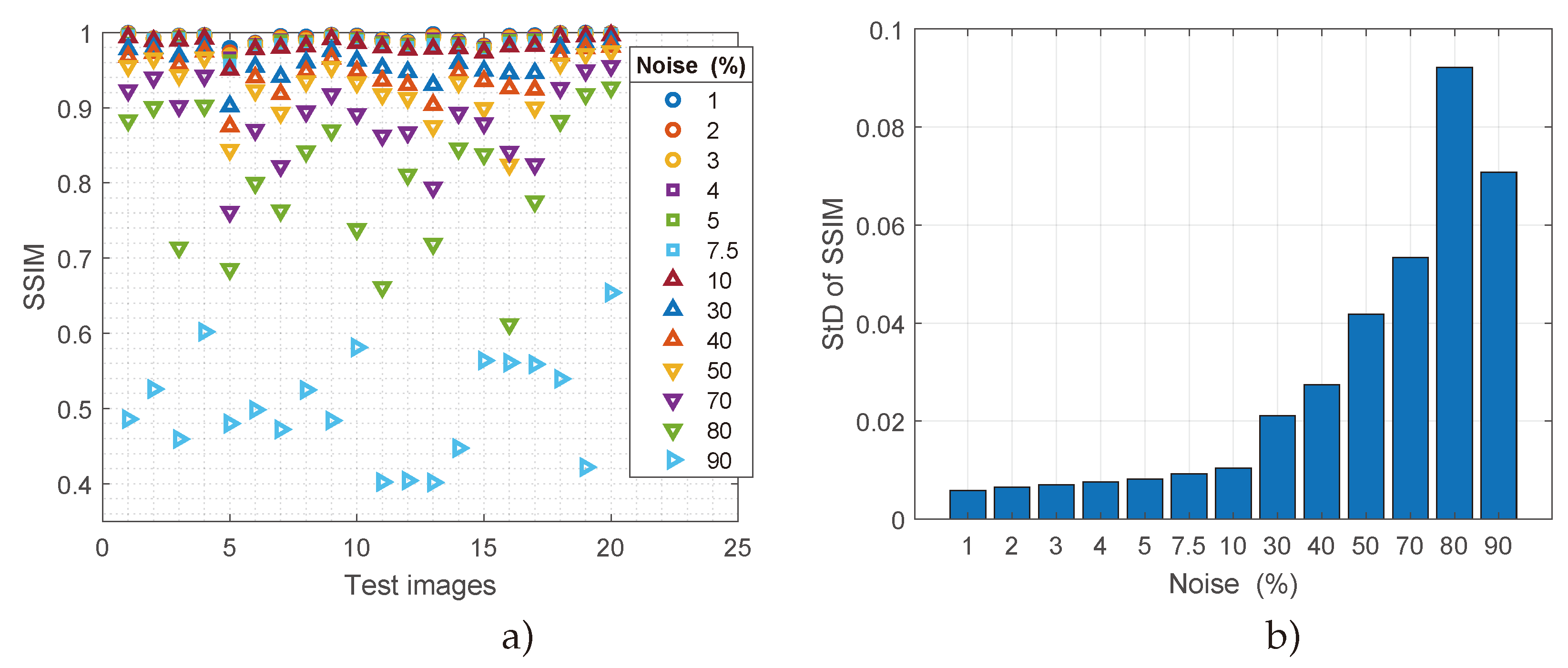
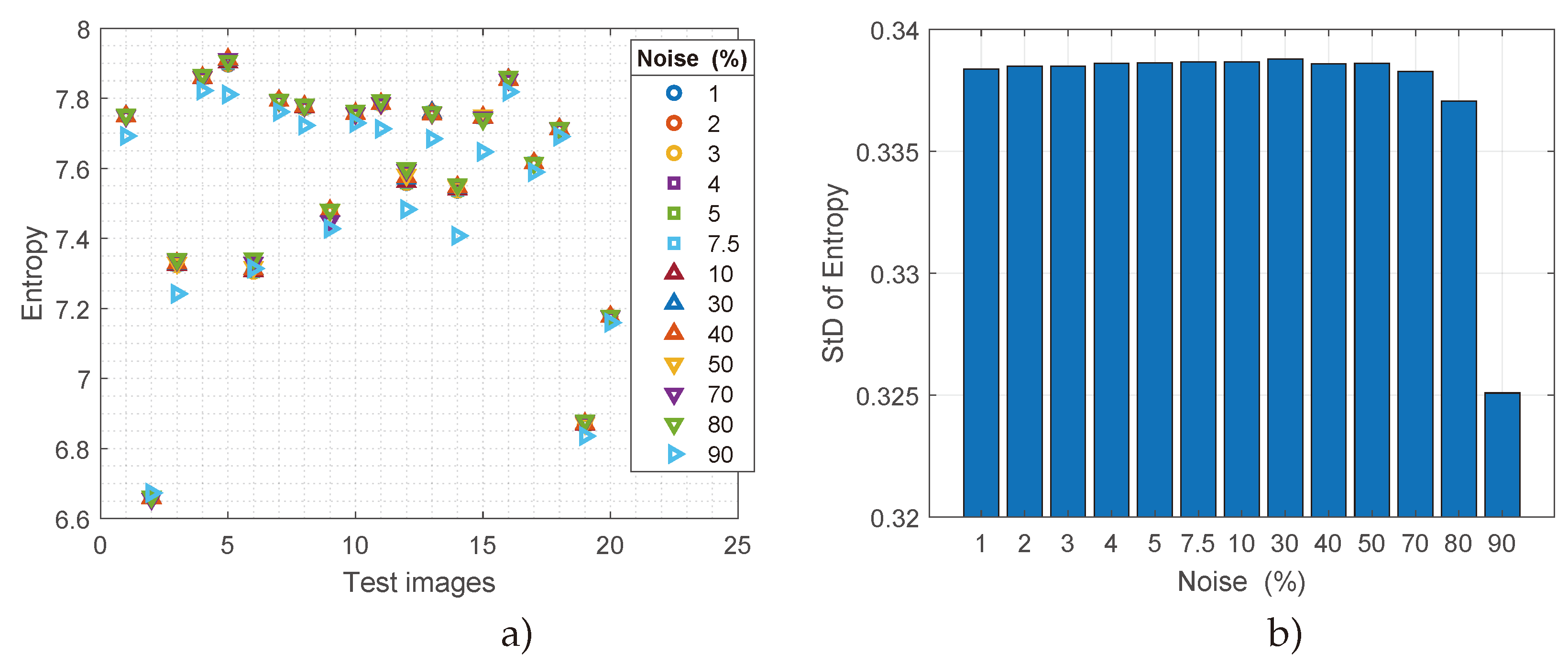
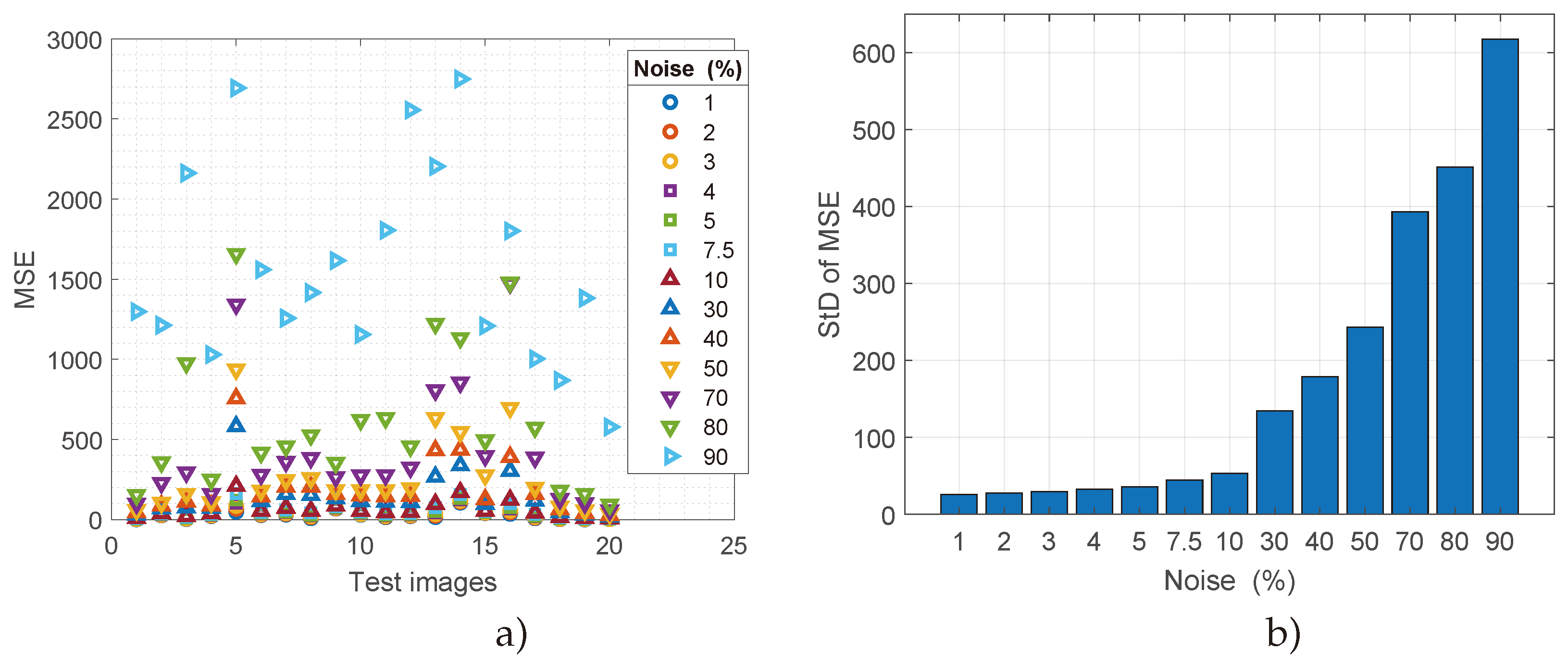
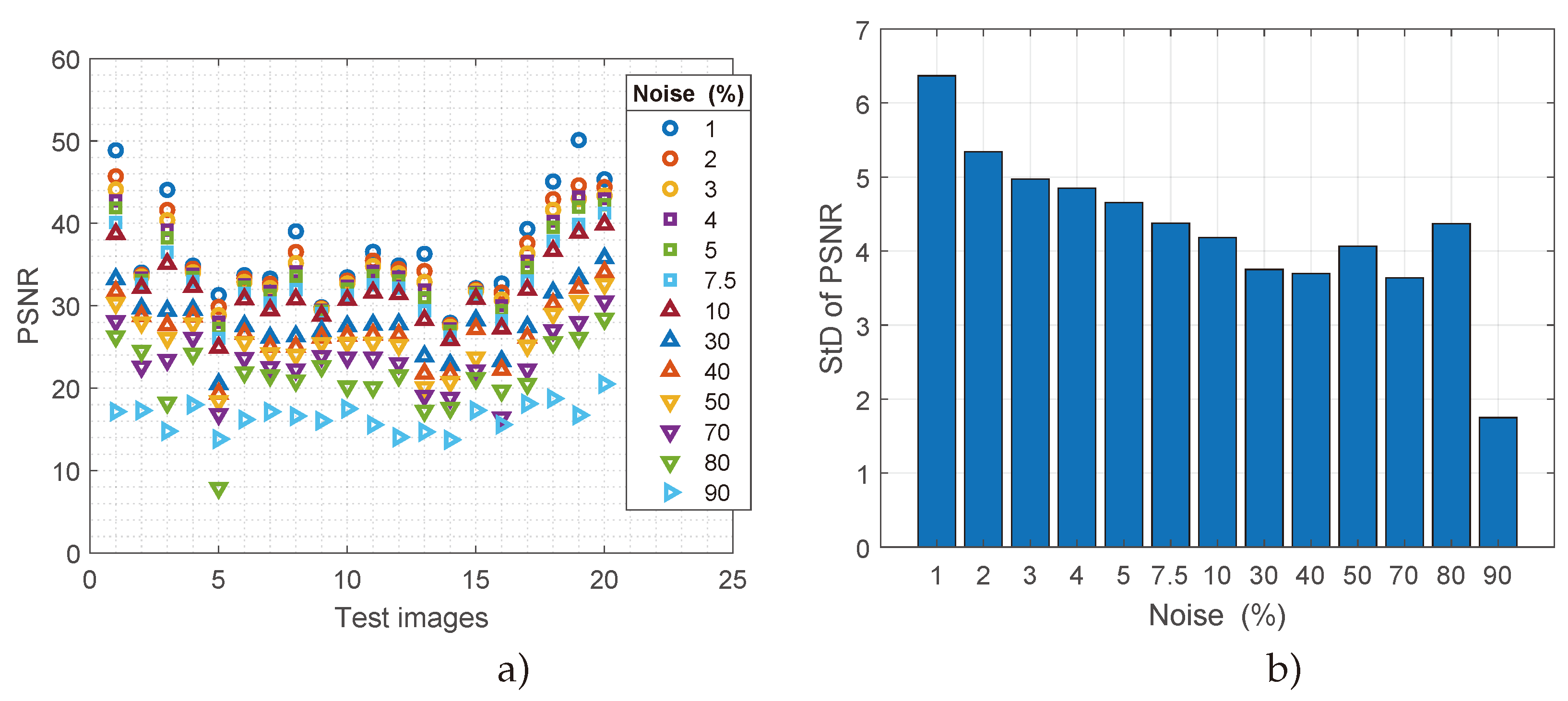
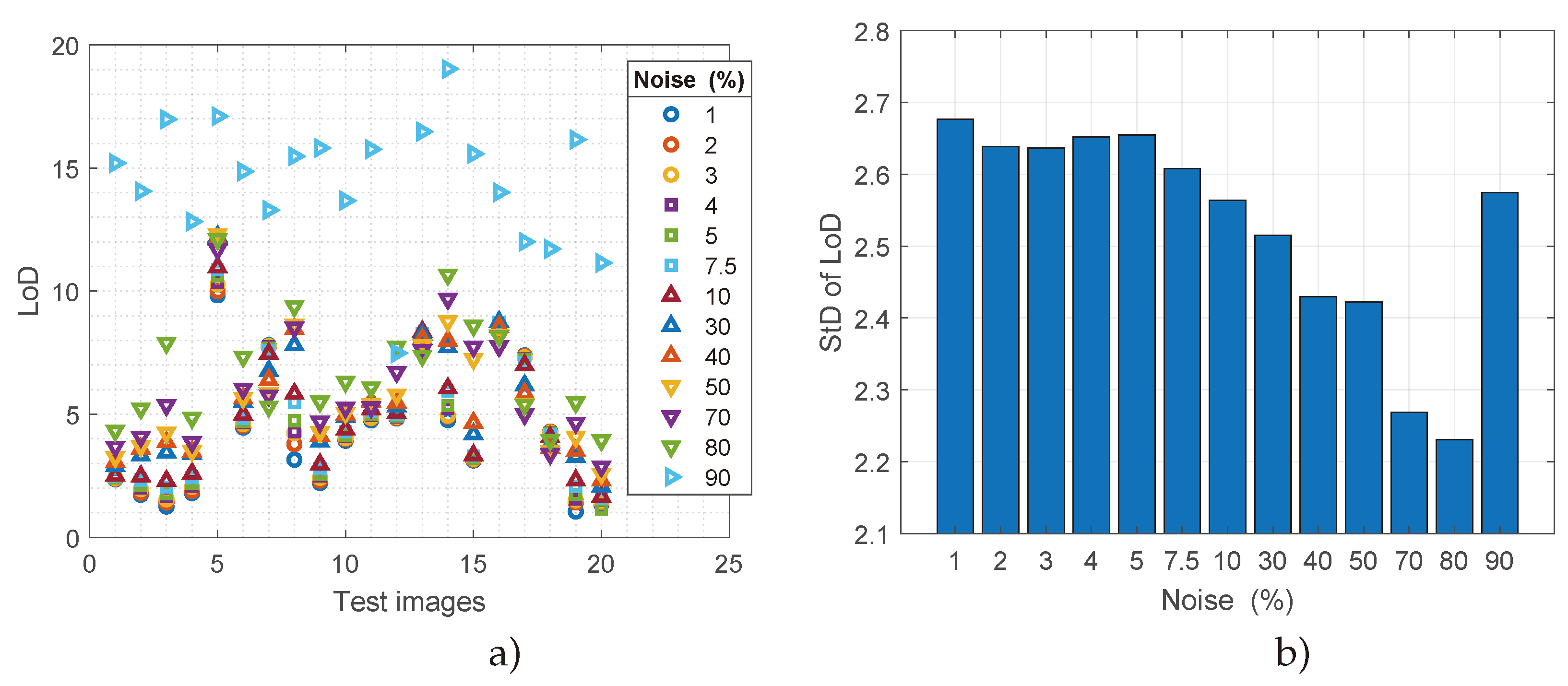
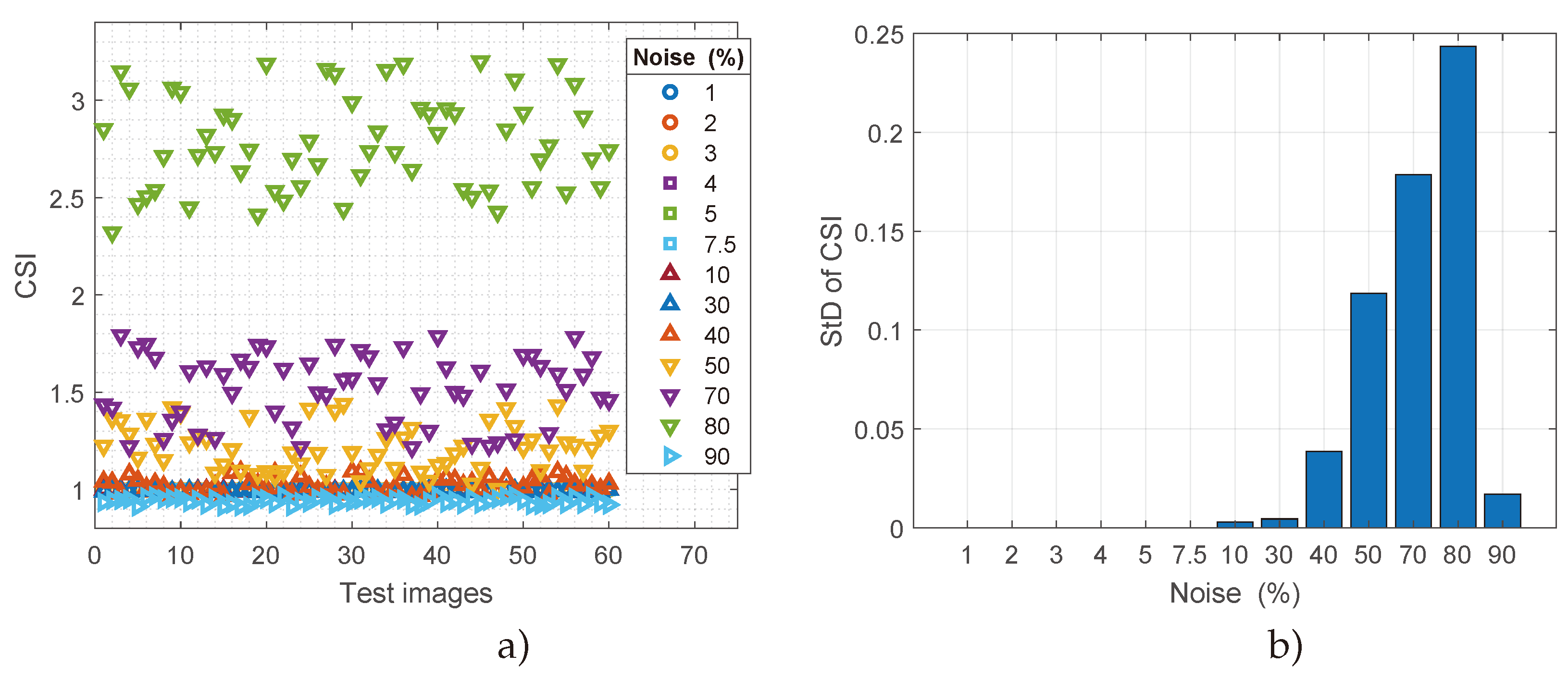
5. Results and Discussion

5.1. Results

The analysis of the results was carried out through the analysis of each parameter separately, where the filter will be evaluated according to the quality in relation to the processed images. On the other hand, each parameter was treated through a standard deviation of images with the same degree of damage. The StD parameter will assess the stability of the filter for various spatial densities.

The assessment of the structural similarity (SSIM) of the original and the reconstructed image is given in Figure 4.a. Samples are presented horizontally, and the degree of similarity according to SSIM is presented vertically. Different colors on the chart indicate different noise spatial densities, from 1% (0.01 on the chart) to 90% (0.9 on the chart). As can be seen from the graph, the degree of similarity of the reconstructed images to the noise percentage of 70% (0.7 on the x-axis of the graph) is over 80% on the y-axis of the graph) of similarity according to SSIM. For a noise spatial density of up to 50%, the percentage of reconstruction and similarity with the original image is over 90%. This is the first proof of the high quality of the proposed filter. Figure 4.b gives the average value of the standard deviation per certain noise level (x-axis) in relation to the average degree of similarity according to SSIM (y-axis). An increase in the degree of noise causes an increase in the standard deviation for the processed images. However, up to a degree of noise spatial density of up to 10%, the level of standard deviation is practically unchanged. In these situations, the proposed filter gives the best results in all observed conditions, so the average deviation is up to 10% noise, 1% difference compared to the original images. From 30% damage to 70% damage, this deviation is up to 5.2% compared to the original images. This relationship between the degree of noise and the similarity reconstructed with the original image unequivocally indicates a high degree of stability of the proposed filter in all conditions. When it comes to 80% damage, the degree of change of the standard deviation is 9.1% (on the y-axis between 0.08 and 0.1) and here is the largest deviation of the proposed filter. This noise spatial density when processing a 9-pixel submatrix contains a maximum of 1–3 pixels that are not affected by nS&P noise.

Theoretically, in an ideal distribution with a noise spatial density of 90%, each submatrix would ideally contain at least one pixel devoid of noise, thus enabling reconstruction based on it. However, in practice, this situation will almost never happen, so the processing is based on overlapping matrices. During this analysis, the noise density was of such spatial density that at 80% damage, the range of submatrices containing at least one noise-free pixel varied from 54 to 67% in the samples. The degree of damage of 90% provides reconstruction according to SSIM from 40 to 65%, so the degree of standard deviation for this degree of noise is 5.03%. The degree of noise is so high that the analysis must contain another repetition of the whole process, only then the standard deviation has values of 13.07%.

All original images have an entropy of 8 or approximately 8 bits before any processing. Figure 5.a shows the entropy values after image processing with added S&P noise. A higher degree of entropy corresponds to a higher "potential" of the image for later processing. All images that were subjected to analysis have a degree of entropy over 6.6 bits, which in theory is considered a very high value. Another confirmation of the stability of the attached filter can be found in Figure 5.b. The changes in entropy levels for the complete analysis to which the Regeneration filter was subjected are very low, practically negligible up to 80% of the damage to the image by nS&P noise.

The mean square error (MSE) error provides the ratio of how much noise the image generated after processing. Since the noise-reducing filter is analyzed, values that weigh zero are acceptable on the scale. Figure 6.a shows that for the largest percentage of processed images, MSE values are below 1000 dB, which is almost negligible information for high-resolution images, which were the object of processing. Below 500 dB MSE is almost 87% of the processed images, which confirms the claim of measurement by the algorithm of structural similarity. For StD measurement for MSE the same conclusion can be taken as for StD for SSIM, as seen in Figure 6.b. The deviation to the noise level of 30% is almost negligible. StD values for MSE from 40 to 90% of the noise spatial density are below the statistical error level for this parameter. Also, as in previous analysis situations for StD, the Regeneration filter shows exceptional stability in operation.

The peak signal-to-noise ratio (PSNR) is not an absolute relevant parameter for quality assessment, but when it comes to describing a new filter, it gives a complete picture. In the theoretical considerations that can be read in [17,18], the desirable ratio between the original and the processed image is between 20–50 dB. As can be seen from the attached Figure 7.a, approximately 87% of the processed images meet the theoretical requirements of high quality. Taking into account that there is no initial value for PSNR, the results of the change of StD for PSNR do not exceed 6.2, which can be seen in Figure 7.b. On the other hand, very low StD oscillations ranging from 1.8 to 6.2 also favor the stability of the Regeneration filter.

The level of details according to DCT (LoD DCT), as shown in Figure 8.a, shows that as the noise in the image increases, so does the level of detail in it. Although increasing the level of details is treated as a positive effect (the image is clearer, the edges are clearer, etc.), here it cannot be taken as a positive side, because the increase in noise spatial density in the image causes an increase in details. That is why almost all image samples at a noise spatial density of 30% and more fall into the category of images with an extremely high level of details. StD changes for DCT are given in Figure 8.b. The graph shows that all analyzed samples from extremely high levels of values were reduced to medium or low level of details, which coincides with the original images.

The comparison of CSI parameters is a comparison of the similarity of each component separately, the original sample with its pair in the reconstructed image [14]. Thus, the R component of a sample of an image will be compared with the R component of the reconstructed image, respectively for the G and B channels. That is why Figure 9.a shows 120 comparisons grouped according to the degree of noise. The ideal situation is when the original and the reconstructed image have a value of 1 because it indicates the complete similarity of these two images in the structure of the component. Values above 1, in this case, indicate a certain degree of noise that is in the image after reconstruction. The results of CSI factor measurements indicate that a slight increase above 1 can be observed in the reconstructed images above 40% of the added noise. This leads to the conclusion that the success of Regeneration filters up to 40% of the added noise is almost 100%. The changes in the CSI parameter (Std of CSI) shown in Figure 9.b once again confirm the stability in operation under all conditions up to a noise spatial density of 40%. As in the previous analysis with the SSIM parameter, so with the standard deviation for the CSI parameter, the level of standard deviation increases with noise growth. A similar conclusion can be drawn as for StD for SSIM at a noise spatial density of 90%. The noise level is so high that another iteration of the Regeneration filter is necessary to further remove some of the noise. After another iteration, the value of the standard deviation is 0.

Specifically, Figure 10.a and Figure 10.c depict the outcome of the initial treatment by the Regeneration filter, following the addition of 90% noise spatial densities to images from Figure 1.l and Figure 1.h. Conversely, Figure 10.b and Figure 10.d show case the results after the second interaction with the Regeneration filter. It is evident from Figure 10.b and Figure 10.d that there is no loss of image quality after the repeated use of the filter, and the results indicate further noise reduction.

The final presentation result is shown in Figure 11, where the processing by the Regeneration filter of all images with noise spatial densities as indicated in Figure 2 is presented. In addition to numerous numerical data, Figure 11 provides visual confirmation of the quality of the proposed filter across different noise spatial densities.

5.2. Discussion

In research conducted over the past five years, various approaches have been explored to reduce noise, with a particular focus on salt-and-pepper (S&P) noise. For instance, Quan et al. [19] developed an algorithm aimed at enhancing image resolution during rapid scanning through filtering, effectively removing S&P noise and increasing the spatial resolution of SICM scanning. This method combines a median filter with the Canny edge detection algorithm and edge interpolation to further sharpen the image. Zhou and colleagues [20] proposed a second-generation method for mixed noise removal in remote sensing, which combines extended convolution and an adaptive median filter to eliminate S&P noise while preserving image details. Lee and Jeong developed the Noise2Kernel algorithm [21], utilizing dilated convolution and a customized kernel for self-supervised learning without requiring clean/noisy image pairs, thus reducing dependency on masking during training. Feng et al. [22] explored vein feature extraction from finger images under S&P noise, employing principal component analysis and locality-preserving projections to improve recognition accuracy. Kwon et al. [23] developed a neural denoiser for PPG signals, leveraging deep generative models with transformers, while Fayaz and collaborators [24] integrated DWT and CNN for MRI image noise removal, employing a median filter to prepare high-density noisy images. Francis and team [25] applied a robust tensor methodology using simultaneous noise reduction through image decomposition, effectively removing high levels of S&P noise. Maleki et al. [26] used CDL and combined filtering to enhance agricultural surface data, allowing for improved segmentation and reduced S&P noise in CDL data. Li and colleagues [27] utilized SAR data for sugarcane mapping by applying time-series filtering to reduce speckle and S&P noise, thereby enhancing large-area pattern mapping. Liu et al. [28] applied LCAS-DetNet for ship detection in SAR images, using multi-local attention to reduce S&P noise and improve ship detection accuracy, while Wang and collaborators [29] employed ResNet-18 for concrete crack detection, reducing the impact of S&P noise with deep learning algorithms. Cao and Liu [30] proposed an enhanced median filter with entropy adaptation for high-intensity grayscale images affected by S&P noise, while Qin and team [31] used phase reconstruction combined with wavelet regularization for denoising complex noise types. Fajardo-Delgado [32] used genetic programming to remove impulsive noise from color images by applying pixel detection across color channels. Ilyin [33] utilized a hybrid Boltzmann model for nonlinear diffusion and S&P noise removal, and Zhang [34] applied a time-series and SNIC multi-scale segmentation-based method to reduce noise in crop structure extraction. Xue et al. [35] used Google Earth Engine for crop classification, reducing S&P noise and improving classification through radar image time-series. Wang and team [36] developed an iterative denoising method using mask symmetry to enhance the efficiency of S&P noise removal in grayscale images.

The proposed Regeneration filter offers several key differences compared to the approaches mentioned above for salt-and-pepper (S&P) noise reduction. Firstly, unlike most conventional methods that use median filtering as the basis for noise reduction, the Regeneration filter avoids using median or any other standard filtering technique. This provides a significant advantage because, while effective in removing noise, median filters tend to blur edges and reduce image sharpness, especially at higher noise levels. In contrast, the Regeneration filter is designed to process only noise-affected pixels, leaving untouched pixels unaltered. This approach preserves the original structure and details in the image, which is particularly important for applications requiring precise edge and texture retention, such as medical imaging and biometrics. A second important feature is the filter’s ability to selectively restore pixels based on local noise density, which enables high adaptability to different noise intensities. For instance, many of the described algorithms, such as methods using dilated convolutions (e.g., Noise2Kernel), genetic programming, or wavelet transforms, require predefined settings and specific models to optimize performance for particular noise types. These models often rely on pre-trained parameters and are difficult to generalize to noise that varies in spatial intensity. By contrast, the Regeneration filter employs adaptive pixel selection, where each pixel is evaluated based on its local environment. When high noise intensity is detected in a given area, the filter adjusts its processing approach to ensure more precise image reconstruction. A third major advantage is the modularity of the Regeneration filter, allowing it to be applied multiple times without degrading image quality. With most other methods, multiple applications of a filter can lead to further loss of detail or additional image blurring. However, the Regeneration filter is designed to support an iterative processing approach without additional quality loss, making it suitable for applications where high noise intensity is present. This is especially useful for very high noise levels, up to 97% spatial distribution. In such cases, most traditional methods have limitations regarding the maximum noise density they can effectively remove. The Regeneration filter has proven to be an effective solution even in extreme cases, thanks to its ability to adapt the processing range depending on noise density in the image. The fourth characteristic that sets the Regeneration filter apart from other methods is its focus on the noise’s immediate vicinity (near S&P, nS&P), enabling it to handle not only pixels with extreme values (0 or 255) but also those close to these limits. This approach further enhances reconstruction accuracy by enabling noise filtering in cases where extreme noise levels are present, while preserving subtle image details close to boundary values. Conventional methods, such as adaptive median filters, usually rely on fixed thresholds to determine noisy pixels, which can result in a loss of detail in surrounding areas, whereas the Regeneration filter uses customized algorithms that recognize fine noise nuances and adjust the processing accordingly. Another important distinction is the Regeneration filter’s flexibility and applicability across various contexts. Many approaches that use convolutional networks, dilated convolutions, or specialized processing methods are designed for narrow applications, such as crack detection in concrete or biometric signal processing. In contrast, the Regeneration filter offers a universal architecture that can be applied easily across diverse fields, including medical imaging, biometrics, satellite imaging, and other applications where preserving fine details is crucial. Its adaptive nature enables users to apply the filter across a wide range of images and noise densities without requiring specialized settings. At the end, the Regeneration filter is advantageous in terms of ease of application and processing, as it does not require model pre-training or complex configurations for each specific application. This makes it significantly easier to implement in real-time monitoring systems and resource-limited applications that require fast response times. Its ability to maintain image quality and details, even at high noise levels, positions it as one of the most effective solutions for S&P noise reduction across a broad spectrum of applications.

6. Conclusions

In this study, we present a Regeneration filter, an effective method for reducing near Salt-and-Pepper (nS&P) noise in images that overcomes the limitations of conventional filters. The approach, based on localized analysis, enables selective noise treatment exclusively in affected pixels, without impacting unaffected parts of the image, thereby preserving edges and details essential for high-resolution applications. Our iterative processing method allows for multiple applications of the filter, where additional iterations do not degrade the image quality achieved after the first filtration, even at noise levels up to 97% spatial distribution. The filter’s performance was evaluated using standard image quality assessment metrics such as SNR, CSI, Entropy, PSNR, and SSIM to ensure that the results are measurable and comparable with other methods. Experimental results across various image databases confirm that our filter consistently maintains high image quality. The code was implemented in the R programming language, and both the data and code used in the research are available in a public repository, enabling full replication and verification of the results. Future research may focus on optimizing the filter for specific applications and extending the approach to other types of noise to further enhance the method’s applicability and efficiency.