1. Introduction
The perovskite crystal structure has garnered significant attention due to its unique properties and potential applications. One of the key compounds within this family is Yttrium titanate (YTiO3) which has been a subject of interest, with studies focusing on the use of molecular dynamics simulations to explore the crystal symmetry and oxygen-ion transport in perovskite materials, shedding light on their behavior at different temperatures [1] . YTiO3 is a ferromagnetic Mott insulator with strong electron correlation effects and orbital ordering [2,3] . High-quality epitaxial YTiO3 thin films have been synthesized using pulsed laser deposition and molecular beam epitaxy [2,4] . The electronic structure of YTiO3 is characterized by a Mott-Hubbard band gap of ~1.5 eV and a lower Hubbard band at 1.1 eV below the Fermi level [2] . Both structural distortions and multiorbital electron interactions contribute to orbital polarization in YTiO3 [3] . Doping with La or Ca significantly affects the electronic and optical properties of YTiO3, including spectral weight transfer and changes in the band structure and optical conductivity [3,5] . Furthermore, YTiO3 has been studied for its potential applications in energy storage, electronic devices, and sensors [6] One study investigated the metal-insulator transition at YTiO3/LaTiO3 interfaces grown by the soft chemical method [7] . The researchers aimed to understand the behavior of the interface between YTiO3 and LaTiO3, shedding light on potential applications in electronics and optoelectronics. Additionally, a computational study explored the use of YTiO3±δ as cathode materials in solid oxide fuel cells (SOFCs) [8] . This study delved into the native defects and oxygen diffusion within YTiO3, providing valuable insights for the development of advanced SOFC technologies. In another study, Yttrium-doped SrTiO3 (SYT) demonstrated high electrical conductivity, structural stability, and chemical compatibility with YSZ and LSGM, making it a promising anode material for solid oxide fuel cells, achieving a maximum power density of 58 mW/cm² at 900 °C [9] . Furthermore, investigations on functional properties of Al0.8EuyLa0.2-yTiO3 (y = 0.01 - 0.04) nanoparticles synthesized by the hydrothermal method have also been conducted [10] . The research focused on the potential applications of these nanoparticles and their unique properties for specific electronic or optical devices. The effect of high-temperature annealing on the phase transformations of the perovskite YTiO3−x system was also explored, providing important insights into the structural characteristics of YTiO3-based materials [11] . Measurement of elastic modulus in YTiO3 suggests the appearance of the magnetostriction effect [12] .
Additionally, the magnetic properties of YTiO3 have been studied extensively in the literature, revealing several intriguing phenomena. Gossling et al. [13] investigated optical excitations in Mott-Hubbard insulators YTiO3 and SmTiO3, observing absorption bands and peak anomalies attributed to charge-neutral quasibound states. Akimitsu et al. [14] used the polarized neutron diffraction technique to directly observe the orbital ordering in ferromagnetic YTiO3. Additionally, a study by Zhou et al. [15] explored the magnetic properties and electronic structures of YTiO3-based superlattices, revealing unexpected magnetic orders and electronic behavior at the interfaces. In a different approach, a joint refinement model for the spin-resolved one-electron reduced density matrix of YTiO3 was proposed by Gueddida et al. [16] , which provided insights into the magnetic properties of YTiO3 using magnetic structure factors and magnetic Compton profiles data. Chae et al. [17] investigated epitaxial growth and the magnetic properties of orthorhombic YTiO3 thin films, revealing ferromagnetic transitions and the influence of substrate-induced atomic arrangements. Moreover, the transition from orbital liquid to the Jahn-Teller insulator in orthorhombic perovskites RTiO3, including YTiO3, was examined by Cheng et al. [18] , demonstrating a spin/orbital transition at a magnetic transition temperature. Furthermore, a first-principles study by Weng et al. [19] investigated electron doping of SmNiO3 / YTiO3 via interfacial charge transfer and its effects on the electronic and magnetic properties, highlighting the complex interplay between different materials. An interesting work by An et al. [20] explored the possibility of ferrimagnetism and ferroelectricity in half-substituted rare-earth titanates, including Y0.5La0.5TiO3.
In this study, we investigate the effect of doping Sr into YTiO3 with different ratios (0.01, 0.10, 0.50, 0.99). Our investigation covers elastic and electronic properties. The outline of this article is as follows. In the next section, the main methods are explained. The investigation results are given in the Results and Discussion section. Lastly, the outcomes of this research are given in the conclusion.
2. Materials and Methods
Y
1-xSr
xTiO
3 in Pm
m space group is doped by Sr by various ratios (x=0.01, 0.10, 0.50, 0.99). In
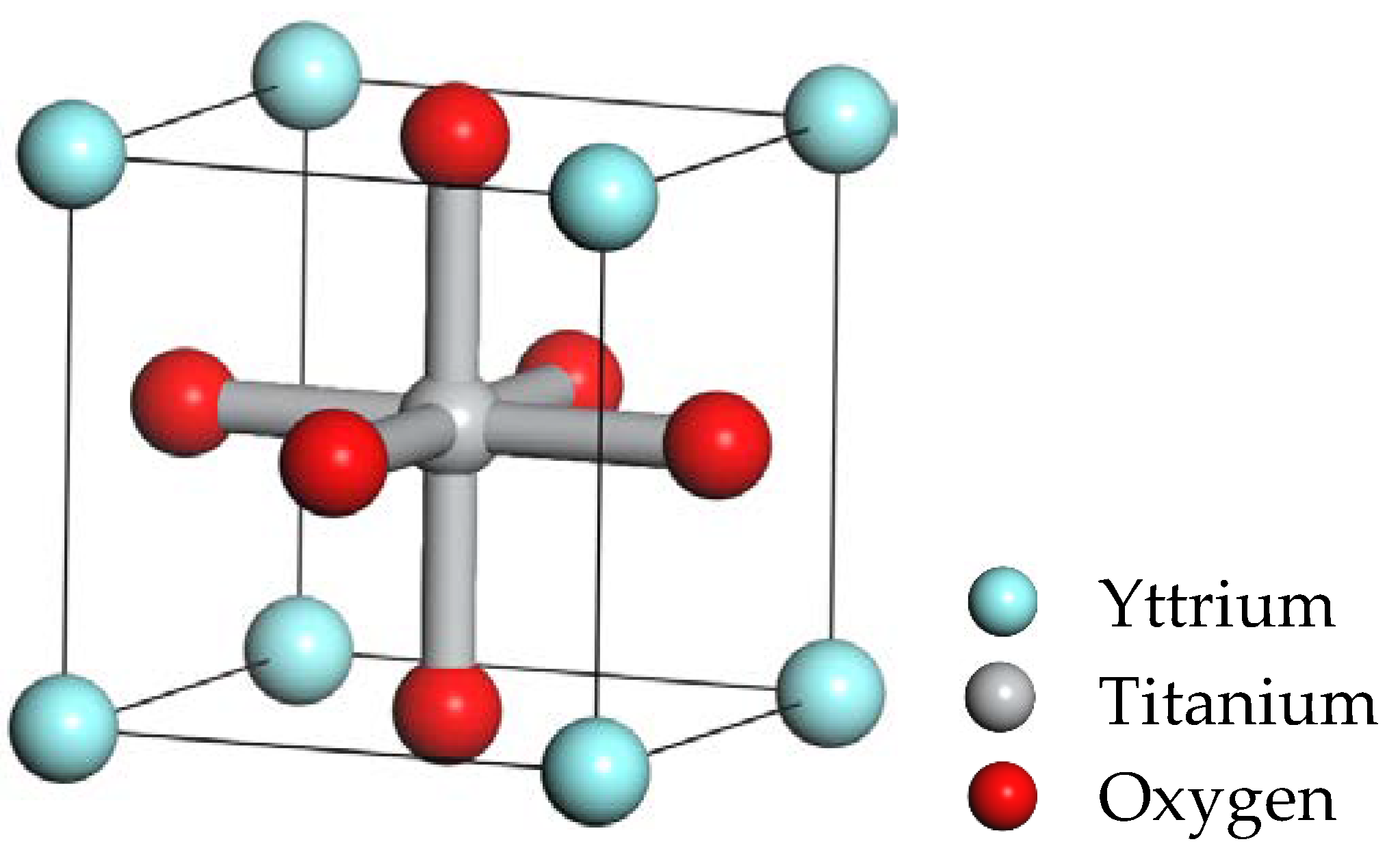
Figure 1, the initial structure of YTiO
3 is given with the lattice constant a=3.88Å. The geometry computation is completed with GGA-PBE, and cutoff energy is 630 eV which is defined based on used pseudopotentials and finite basis set correction [21] . The Monkhorst–Pack scheme was utilized to perform special k-points sampling integration across the Brillouin zone with the 6×6×6 mesh [22] .
Our DFT calculations are performed using the projector-augmented wave approach as implemented in the CASTEP [23,24] . We described the exchange and correlation potential using the GGA-PW91 functional, and the electron-core interactions with the ultrasoft pseudopotential [25] . The energy convergence tolerance was set at , the maximum force was set at , the maximum stress was set at , and the maximum displacement was set at The Perdew-Burke-Ernzorhof generalized gradient approximation was used to solve the Kohn-Sham equations [26] . The crystal structures underwent complete relaxation using the Broyden-Fletcher-Goldfarb-Shanno (BFGS) minimization method [27] .
The elastic properties are determined by the CASTEP through the application of the finite strain theory [28] . This theory allows for the calculation of elastic constants, which are the coefficients that relate the applied strain to the resulting stress, . The polycrystalline bulk modulus B and shearmodulus G are then evaluated using the Voigt-Reuss-Hill approximation based on the obtained values [29] .
3. Results and Discussion
In this study, we investigated the structural, elastic, and electronic properties of Y1-xSrxTiO3 (x=0, 0.01, 0.1, 0.5, 0.99) perovskites using density functional theory (DFT). The materials exhibit a cubic structure (Pmm) with optimized lattice constants. Elastic properties, including bulk modulus, shear modulus, and Young's modulus, confirm mechanical stability in accordance with the Born-Huang criteria. Electronic properties, examined through band structure and partial density of states (PDOS), reveal significant alterations in band structure due to Sr doping; however, no bandgap is observed, and the metallic nature of the materials is retained, with notable contributions from p and d orbitals.
3.1. Structural Properties
The structural properties and geometries of Y
1-xSr
xTiO
3 (x=0, 0.01, 0.1, 0.5, and 0.99) perovskites were examined using density functional theory (DFT) (See
Figure 1). The materials were found to have cubic structures with the space group Pm
m (no. 221). The states of complete relaxation in the structures are achieved through the optimization of its geometry, taking into account the lattice constants and internal atomic positions. This process involves adjusting the arrangement of atoms within the structure to minimize any residual stress or strain. By optimizing these parameters, the structure can achieve a more stable and energetically favorable configuration. Wyckoff spaces of Y, Ti, and O are respectively (0, 0, 0), (1/2, 1/2, 1/2), and (1/2, 1/2, 0). The optimized lattice constants, obtained from the unit cell optimization for the ground state stable atomic configuration, are presented in
Table 1 . To ascertain the stability of perovskite materials, we employ a computational approach to calculate and present the elastic constants in the subsequent sections, providing comprehensive details.
3.2. Elastic Properties
The study of the elastic properties of materials is essential prior to their practical use, as many device features depend on the elastic properties of the materials used in their manufacturing. Therefore, materials with superior elastic properties are highly valuable for incorporation into various devices. The elastic constant serves as a mathematical link between the mechanical and dynamical characteristics of materials, playing a crucial role in determining their properties and how they respond to external forces. Based on the principles of cubic symmetry, the elastic tensor consists of three distinct elastic components, namely , , and . The bulk modulus (BM) calculates the stress needed to change a material's volume, whereas the shear modulus (SM) describes how resistant a material is to shear stress-induced deformation. The forces per unit cross sectional area needed for an elongation or shortening dimensional change are measured by the Young modulus (YM).
The obtained values for these elastic constants are presented in
Table 2 and are evaluated against the Born-Huang generalized stability criteria [
31] as defined in equation (1) for the Pm
m structure. Therefore, it can be concluded that compounds exhibit mechanical stability.
Table 2 displays the findings of our study on the elastic properties under no pressure conditions. Based on the computation results, elastic stability is confirmed.
3.3. Electronic Properties
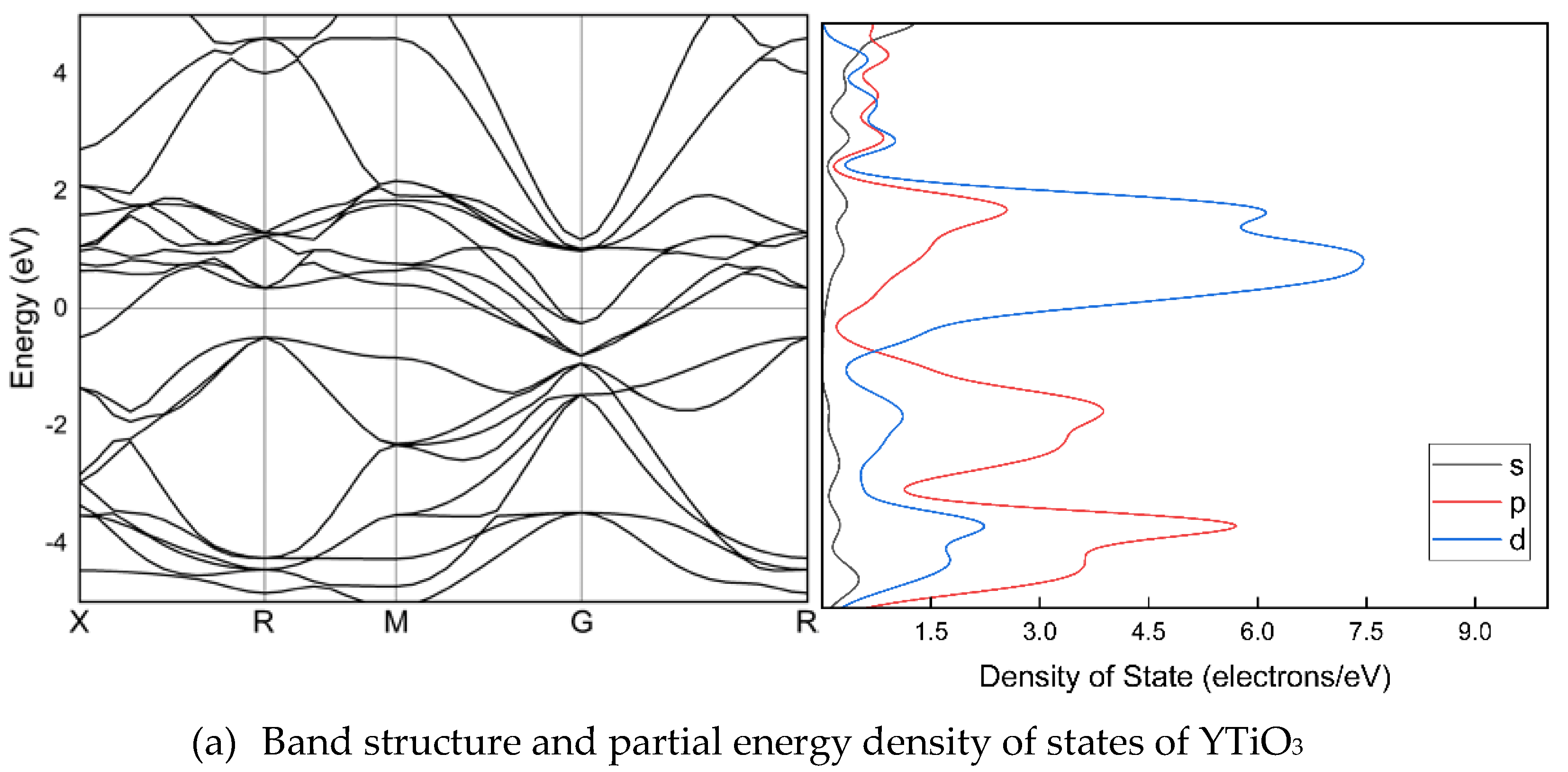
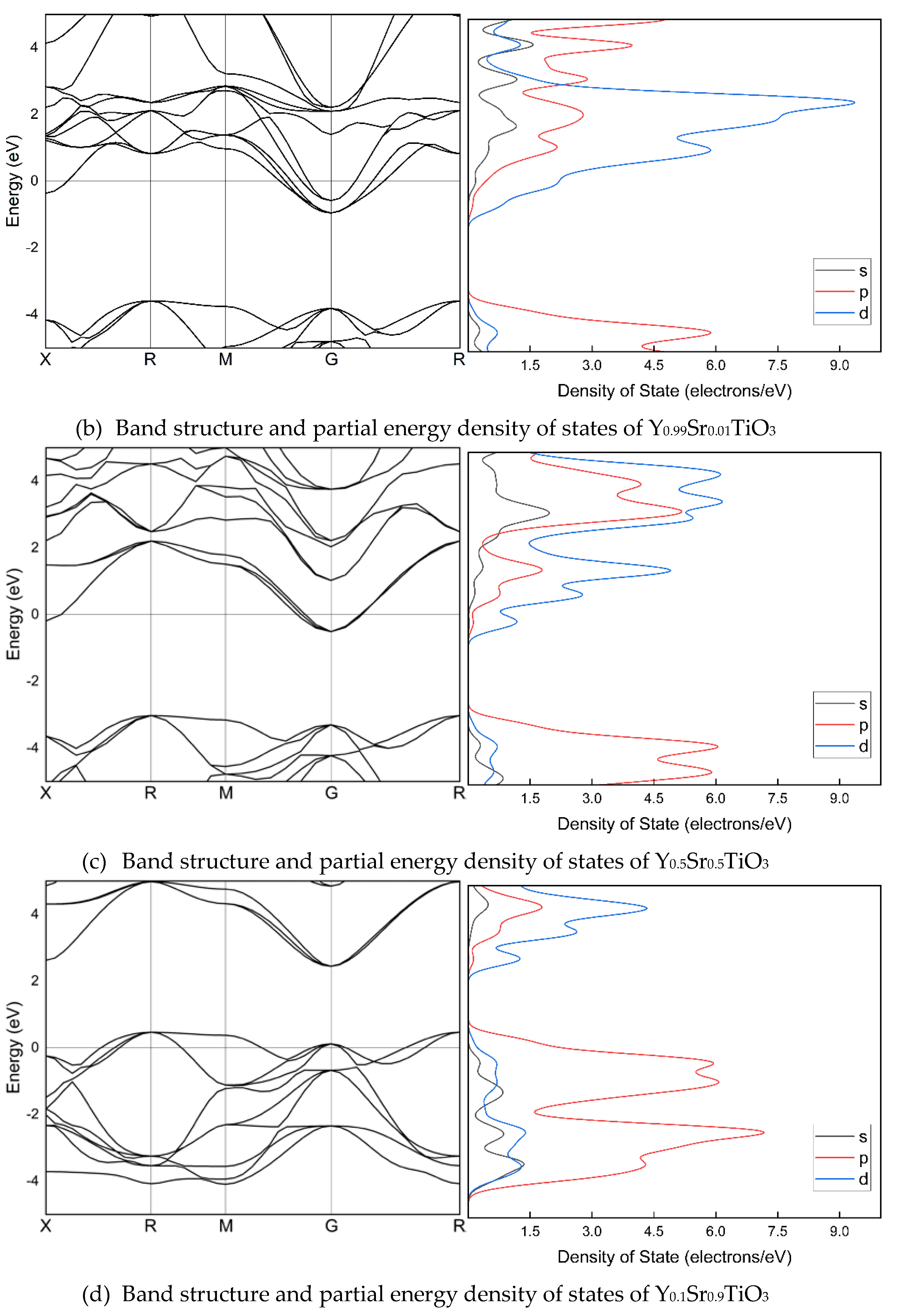
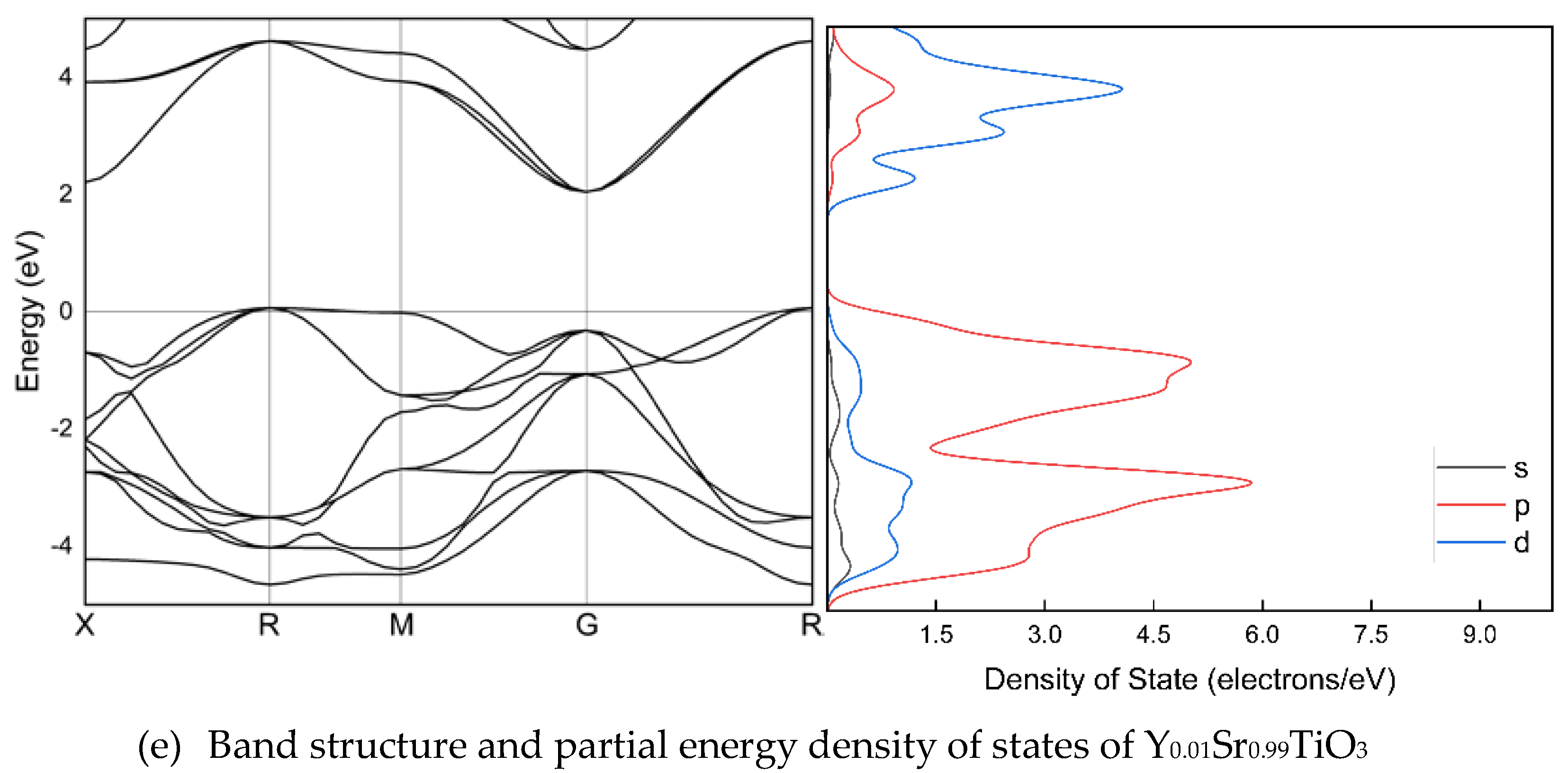
Figure 2 illustrates the band arrangement and PDOS of Y
1-xSr
xTiO
3 (x=0, 0.01, 0.1, 0.5, and 0.99), where the lattice parameters have been optimized along the high symmetry directions within the first Brillouin zone. The electronic band structure helps to identify the valence band and the area empty of electrons. The possible energies of electrons are explained by the conduction band. The conduction and valence bands are distinguished by the E
F. The valence bands are seen behind the E
F, while the conduction band is located above it. The findings indicate that, despite a considerable alteration in band structures due to Sr doping, there is no bandgap. The valence and conduction band spacing is expanding in doped crystals, but the metal nature of the crystals is preserved. In the band structure, p and d orbitals are particularly stronger than s orbitals.
4. Conclusion
In conclusion, the structural, elastic, and electronic properties of Y1-xSrxTiO3 (x=0.01, 0.10, 0.50, 0.99) perovskites within the Pmm space group were thoroughly investigated using density functional theory (DFT). The initial geometry optimizations, performed with the GGA-PBE functional, revealed stable configurations with varying Sr doping levels. Detailed elastic property calculations confirmed the mechanical stability of these compounds, with significant variations in elastic constants attributed to Sr doping. The electronic structure analysis, including band structure and partial density of states (PDOS), indicated that despite changes in the band structures, the materials retained their metallic nature, dominated by p and d orbitals. These findings underscore the potential of Sr-doped YTiO3 perovskites for applications that demand superior mechanical properties and highlight the influence of Sr doping on the materials' structural and electronic characteristics.
Author Contributions
The author confirms being the sole contributor of this work.
Funding
This research received no funding
Data Availability Statement
No data are available for this study.
Acknowledgments
The author would like to thank Adiyaman University for providing the necessary facilities and support for this research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Robens, E.; Rauschen, R.; Kaub, J.; Parras, J.P.; Kemp, D.; Freeman, C.L.; Souza, R.A.D. Perovskite crystal symmetry and oxygen-ion transport: A molecular-dynamics study of perovskite. Journal of Materials Chemistry A 2021. [Google Scholar] [CrossRef]
- Yue, J.; Quackenbush, N.F.; Laraib, I.; Carfagno, H.; Hameed, S.; Prakash, A.; Thoutam, L.R.; Ablett, J.M.; Lee, T.-L.; Greven, M.; et al. Electronic structure and small-hole polarons in YTiO3. arXiv: Materials Science, 2020. [Google Scholar]
- Craco, L.; Leoni, S.; Müller-Hartmann, E. Hidden orbital fluctuations in the solid solution Y1-xLaxTiO3 (x < 0.2). Physical Review B 2006, 74, 155128-–155121-155128-155125. [Google Scholar]
- Cao, Y.; Shafer, P.; Liu, X.; Meyers, D.; Kareev, M.; Middey, S.; Freeland, J.W.; Arenholz, E.A.; Chakhalian, J. Magnetism and electronic structure of YTiO3 thin films. Applied Physics Letters 2015, 107, 112401. [Google Scholar] [CrossRef]
- Sai, G.; Wang, Y.-H.; Na, Z.; Duan, Y.-F. First-Principles Study of Electronic and Optical Properties of Y1−xCaxTiO3 (x = 0, 0.25, 0.5, 0.75). Chinese Physics Letters 2010, 27, 037103. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, J.; Saito, N.; Yang, X.; Zhang, Z.; Yang, L.; Hirano, S. Layered Perovskite Lithium Yttrium Titanate as a Low-Potential and Ultrahigh-Rate Anode for Lithium-Ion Batteries. Advanced Energy Materials 2022, 12. [Google Scholar] [CrossRef]
- Tolentino Cabral, A.C.; Tafur Tanta, U.M.; Simões, A.Z.; Bastos, W.; Moreno, H.; Ramirez, M.A.; Ponce, M.A.; Moura, F. Unveiling the Metal-Insulator Transition at Ytio3/Latio3 Interfaces Grown by the Soft Chemical Method. SSRN Electronic Journal 2023. [Google Scholar] [CrossRef]
- Martins, N.R.; Borges, D.D.; Borges, P.D. Computational study of native defects and oxygen diffusion in the YTiO3±δ as cathode materials in SOFCs. Journal of Solid State Chemistry 2023. [Google Scholar] [CrossRef]
- Hui, S.; Petric, A. Evaluation of yttrium-doped SrTiO3 as an anode for solid oxide fuel cells. Journal of the European Ceramic Society 2002, 22, 1673–1681. [Google Scholar] [CrossRef]
- S, D.; Lakshmaiah, M.V.; Manjunath, V.; Nallabala, N.K.R.; Ravi, N.; Dhanalakshmi, M.; Kukkambakam, C.; Krishnaiah, K.V.; Minnam Reddy, V.R. Investigations on functional properties of Al0.8EuyLa0.2-yTiO3 (y = 0.01 - 0.04) nanoparticles synthesized by hydrothermal method. Surface Review and Letters, 2022. [Google Scholar]
- Mustakhieva, D.A.; Zhumataeva, I.Z.; Kozlovsky, A.L.; Kadyrzhanov, K.K. The effect of high-temperature annealing on the phase transformations of the perovskite YTiO3−x system. Eurasian Journal of Physics and Functional Materials 2019. [Google Scholar] [CrossRef]
- Suzuki, T. Elastic properties of ferromagnetic Mott insulator YTiO3. Physica B: Condensed Matter 2003, 329-333, 868–869. [Google Scholar] [CrossRef]
- Gossling, A.; Schmitz, R.; Roth, H.; Haverkort, M.W.; Lorenz, T.; Mydosh, J.A.; Muller-Hartmann, E.; Gruninger, M. Mott-Hubbard exciton in the optical conductivity of YTiO3 and SmTiO3. Physical Review B 2006, 78, 075122. [Google Scholar] [CrossRef]
- Akimitsu, J.; Ichikawa, H.; Eguchi, N.; Miyano, T.; Nishi, M.; Kakurai, K. Direct Observation of Orbital Ordering in YTiO3 by Means of the Polarized Neutron Diffraction Technique. Journal of the Physical Society of Japan 2001, 70, 3475–3478. [Google Scholar] [CrossRef]
- Zhou, P.X.; Liu, H.; Yan, Z.; Dong, S.; Liu, J. Magnetic properties and electronic structures of (YTiO3)2/(BaTiO3)n superlattices. Journal of Applied Physics 2014, 115. [Google Scholar] [CrossRef]
- Gueddida, S.; Yan, Z.; Kibalin, I.; Voufack, A.B.; Claiser, N.; Souhassou, M.; Lecomte, C.; Gillon, B.; Gillet, J.M. Joint refinement model for the spin resolved one-electron reduced density matrix of YTiO3 using magnetic structure factors and magnetic Compton profiles data. The Journal of chemical physics 2018, 148 16, 164106. [Google Scholar] [CrossRef]
- Chae, S.C.; Chang, Y.J.; Seo, S.S.A.; Noh, T.W.; Kim, D.-W.; Jung, C.U. Epitaxial growth and the magnetic properties of orthorhombic YTiO3 thin films. Applied Physics Letters 2006, 89, 182512. [Google Scholar] [CrossRef]
- Cheng, J.-G.; Sui, Y.; Zhou, J.-S.; Goodenough, J.; Su, W.h. Transition from orbital liquid to Jahn-Teller insulator in orthorhombic perovskites RTiO3. Physical review letters 2008, 101 8, 087205. [Google Scholar] [CrossRef]
- Weng, Y.; Long, F.; Chen, Y.; Miao, F.; Li, J.; Cheng, J.; Li, X.a. Electron doping of SmNiO3 via interfacial charge transfer: A first-principles study. Journal of Applied Physics 2023. [Google Scholar] [CrossRef]
- An, M.; Zhang, H.; Weng, Y.; Zhang, Y.; Dong, S. Possible ferrimagnetism and ferroelectricity of half-substituted rare-earth titanate: A first-principles study on Y0.5La0.5TiO3. Frontiers of Physics 2015, 11, 1–6. [Google Scholar]
- Francis, G.P.; Payne, M.C. Finite basis set corrections to total energy pseudopotential calculations. Journal of Physics: Condensed Matter 1990, 2, 4395–4404. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Physical Review B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Clark, S.; Segall, M.; Pickard, C.; Hasnip, P.; Probert, M.; Refson, K.; Payne, M. First principles methods using CASTEP. Zeitschrift für Kristallographie 2005, 220. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Physical Review 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Physical review B 1981, 23, 5048. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Physical Review 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Pfrommer, B.G.; Cote, M.; Louie, S.G.; Cohen, M.L. Relaxation of crystals with the quasi-Newton method. Journal of Computational Physics 1997, 131, 233–240. [Google Scholar] [CrossRef]
- Murnaghan, F. Finite deformation of an elastic solid. Bull. Am. Math. Soc 1952, 58, 577–579. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proceedings of the Physical Society. Section A 1952, 65, 349. [Google Scholar] [CrossRef]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Materials 2013, 1. [Google Scholar] [CrossRef]
- Mouhat, F.; Coudert, F.-X. Necessary and sufficient elastic stability conditions in various crystal systems. Physical Review B 2014, 90, 224104. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).