Global-Local-Structure Collaborative Approach for Cross-Domain Reference-Based Image Super-Resolution

1. Introduction

Remote sensing images are useful for collecting spatial information and have been extensively used in land resource survey, urban planning, agricultural monitoring, ecological protection, military reconnaissance, and disaster assessment [1]. High resolution remote sensing images have rich textures and sharp geometric details. They can be used in downstream tasks like land cover classification, semantic segmentation, and object detection. The remote sensing image exhibits several degradation issues such as low sensor resolution, clouds, blur, and compression loss. In such a case, the image can suffer from low resolution, noise, texture, and blurry edges. These deep degradation factors drastically affect the detection of small-scale ground objects (e.g. narrow roads, building barriers, farmland grids) and severely compromise the robustness of higher level intelligent analysis. Therefore, developing effective techniques for high quality remote sensing SISR in complex degradation scenarios is an important research challenge in remote sensing processing.

Limitations of traditional methods. Early attempts at image superresolution relied mainly on interpolation-based techniques (e.g., bicubic interpolation [2], Lanczos interpolation) or sparse coding and dictionary learning approaches [3,4]. While these methods can deliver modest improvements under low upscaling factors, their reliance on over-simplified priors makes them incapable of accurately recovering high-frequency details and complex structural information. As a result, the reconstructed images often suffer from excessive blurring and artificial artifacts. In remote sensing, the images often contain mixed noise. They also show textures at different scales and suffer from multiple types of degradation. These issues make the limitations more obvious and show the need for better methods.

Advances and challenges of deep learning. The advent of deep learning has revolutionized image restoration tasks, with convolutional neural networks (CNNs) [5,6] becoming the dominant paradigm in super-resolution. Some well-known works such as Enhanced Deep Residual Network (EDSR) [7] and Residual Channel Attention Network (RCAN) [8] use deep residual connections and attention techniques for improving pixel quality and structural consistency. Most recently, transformer-based models, such as SwinIR [9] or Uformer [10], have been able to model long-range dependencies, achieving perceptually good reconstructions. However, implementing these models directly to remote sensing images remains challenging due to complex degradation and large variability on spatial scales. While CNNs naturally prefer local feature extraction, they usually fail to capture global semantic consistency, Transformers do not achieve good global modeling, or even can fail to recover fine-grained textures and fine-grain geometry [11]. This highlights a persistent bottleneck which is, to address, the mismatch between local detail preservation and global structural consistency of RSISR.

Diffusion models: Possibles and limitations. Over the last years, diffusion models are rapidly emerging in generative modeling due to their strong distributional learning and sampling capabilities. By repeatedly adding and removing noise, diffusion model can keep them stable, higher than GANs [12,13] and VAEs. They can also perform well in image generation, inpainting, and super-resolution. Recent works like SinSR [14], RefDiff [15], and EDiffSR [16] are able to apply diffusion models to natural image super-resolved and achieve high perceptual quality and diversity. However, when applied to remote sensing images, diffusion-model has several drawbacks [17]. First, most of the existing formulations model ideal degradation models but do not consider the complexity inherent for multi source degradations of RS data. Second, traditional single-decoder pipelines suffer either from detail oversmoothing or semantic distortion in difficult scenes. Third, no explicit structural priors are available, resulting in undesirable artifacts or spatial inconsistency, which limits the usability of the output.

Motivation and Contributions. In order to address these issues, we propose a multi-module environment for remote sensing image super-resolution. It handles different degradations more efficiently. It also keeps the structure information accurate and accurate. Our vision is to exploit the benefits of degradation modeling, hybrid decoding and structural regularization in a multi diffusion framework. In particular, we design a degradation-aware modeling (DAM) module. It takes lightweight convolutions and channel attention to extract different types of degradation features, and inject them into the diffusion, enabling the model to adapt to mixed and complex degradation found in real remote sensing images. We propose a dual decoder recursive generation strategy, where a local convolutional decoder is combined with a global Transformer decoder. We also introduce temporal and residual recursion. This model allows the model iteratively refine the image from coarse geometry to high-frequency details, ensuring recovery of small geometric boundaries and preserving semantic consistency at different spatial scales. Moreover, we implement a static regularization guidance (SRG) in the diffusion latent space, embedding total variation and gradient consistency priors and controlling their effect via a temporal decay schedule, which effectively removes edge blur and structural distortion. These modules enable for enhanced perceptual realism and stability of reconstructed images. By incorporating these modules, our framework provides a natural way of connecting low-level degradation modeling with high-level semantic reconstruction. It provides a new solution for generating high-quality remote sensing images under complex and non-ideal degradations.

The major contributions of this work are summarized as follows:

• We introduce a degradation-aware modeling module to explicitly encode multi-source, multi-scale degradations as priors guiding the diffusion process.
• We propose a dual-decoder recursive generation mechanism that balances local detail restoration with global semantic consistency.
• We design a static regularization guidance strategy to stabilize structural preservation and enhance perceptual realism.
• We conduct extensive experiments on three widely used remote sensing benchmarks (UCMerced, AID), where our method consistently surpasses state-of-the-art approaches under both idealized and realistic degradations, demonstrating superior robustness, generalization, and adaptability to cross-domain scenarios.

2. Related Work

2.1. Remote Sensing Image Super-Resolution

The objective of RSISR is to reconstruct high-resolution data from low-resolution image to increase spatial resolution and semantic recognition. This provides reliable input for subsequent tasks such as land cover classification, building extraction, object detection, and environmental change monitoring [18,19]. Early methods mainly used interpolation, such as nearest neighbor, bilinear, and bicubic interpolation. These methods are simple and easy to use. However, they often cause texture blurring and edge distortion, and they cannot meet the high-precision needs of remote sensing applications [3]. Subsequently, sparse representation and dictionary learning methods (e.g., K-SVD and its variants) improved detail reconstruction to some extent through sparsity constraints. However, their reliance on fixed dictionaries limits adaptability, especially under multi-scale, multi-class, and complex degradation conditions in remote sensing imagery [4].The rise of deep learning has greatly advanced super-resolution research, especially the widespread use of CNNs in RSISR. Typical methods such as EDSR improve reconstruction accuracy via deep residual structures, RCAN enhances detail representation using channel attention, and SAN and HAN further incorporate non-local attention to model long-range dependencies [20]. Meanwhile, Transformer architectures have been gradually introduced into super-resolution tasks: SwinIR leverages hierarchical Swin Transformer for efficient global modeling, and Uformer combines U-Net with Transformer to balance cross-scale structural representation and local detail reconstruction.

However, RSISR in remote sensing scenarios still faces significant challenges. Complex degradation: remote sensing images are often affected by blur, noise, compression artifacts, and spectral differences, while most existing methods rely on idealized degradation assumptions, limiting generalization [21]; Scene diversity: the spatial structure varies widely from urban areas to farmland, making it difficult for models to maintain global semantic consistency while preserving local texture fidelity; High upscaling factor challenges: at ×4 or higher magnifications, edges can be blurred, textures unnatural, and geometric structures misaligned. To address these challenges, several improvement strategies have been proposed. Multi-scale feature extraction and fusion: capturing both global and local information via multi-scale convolutions and attention mechanisms; Generative models to enhance visual quality: GANs and diffusion models show promising performance in texture and detail restoration; Degradation-aware modeling: modeling the image degradation process to improve adaptation to real low-resolution remote sensing images; Hybrid Transformer and convolution structures: combining local convolutional features with global Transformer capabilities to enhance reconstruction in complex scenes. With the advancement of algorithms and hardware, future RSISR research will increasingly focus on robustness at high upscaling factors, adaptability to complex degradations, and cross-modal information fusion, providing higher-quality high-resolution inputs for remote sensing image analysis.

2.2. Applications of Diffusion Models in Super-Resolution

Diffusion Models have recently emerged as a research frontier in generative modeling. Their core principle is to progressively add noise to an image in the forward process and gradually denoise it in the reverse process, thereby mapping a Gaussian distribution to the real image distribution. This step-by-step approximation ensures stable training and for diffusion models to outperform the previous generation quality and diversity [22,23,24,25]. There are two advantages with diffusion models in super-resolution tasks. First,enhanced perceptual quality: due to their accurate modeling of image distributions, diffusion-based results can generally outperform CNN- and GAN-based approaches on perceptual measurements (e.g., LPIPS and FID) in terms of details and textures [26,27,28]. Second, conditional control and generalization: diffusion models can flexibly incorporate conditional inputs (low resolution images, degradation parameters, reference images) which are highly adaptable in cross-domain and high degradation situations [29,30].

Recent works introduce diffusion models into super-dimension: SinSR proposed a single step inference strategy, which substantially reduce inference cost while maintaining high perceptual quality; RefDiff utilized reference images as conditions to guide the diffusion, which has structural consistency in cross image detail transfer; EDiffSR applied diffusion models for remote sensing and used perceptual and structural constraints to improve reconstruction in complex ground objects; Other works including Implicit Diffusion Models [31] and DiT-SR explored latent implicit modeling and Transformer-based diffusion to trade global representation and fine-grained detail recovery. Nevertheless, existing diffusion-based SR approaches in remote sensing still face limitations such as oversimplified degradation assumptions [32], insufficient structural consistency [33], and limited generation stability [23,25]. Thus, achieving adaptive degradation modeling, structural preservation, and stable generation within diffusion frameworks remains a pressing challenge.

2.3. Degradation Modeling

Degradation modeling is responsible for super-resolution, which aims at capturing low-resolution image generation and providing reliable priors of reconstruction models. The majority of the previous suggestions assume LR images are generated from HR images by fixed down-sampling operators (e.g. bicubic). However, these ideal assumptions may not apply to remote sensing images [32]. In practice degradation is affected by spatial blur, additive noise, compression artifacts, spectral artifacts and atmospheric scattering [30].

Recent work focuses on more flexible degradation modeling. Explicit degradation modeling: Explicit degradation modelling may estimate degradation parameter (like blur kernel, noise distributions, or spectral shifts) of SR reconstruction e.g., joint blind deblurring and kernel estimation [34] may partially recover image structure. Due to heterogeneous degradation pattern and sensors in remote sensing, estimation of such parameter often requires high computation and is limited generalization. Implicit degradation modeling- Deep networks learn degradation representations and represent them as low dimensional condition vectors of SR models. A famous method is DASR [35], which performs well for blind SR tasks. For cross domain, multi-sensor or high complex problems, these models are still not flexible and thus suffer from structural misalignment or texture loss. Furthermore, degradation modeling is important for reconstruction performance, as well as robustness and generalization performance. In realistic remote sensing cases, LR images might exhibit multi-scale and multi-modal degradation properties simultaneously [30], which makes it challenging for the existing explicit or implicit approaches.

2.4. Regularization and Structural Consistency

Regularization restrictions are necessary to maintain stability and structure in generative results. Total variance regularization: suppressing high-frequency artifacts and oscillations, but poor TV may cause texture loss. Invariant consistency loss: retaining consistency between reconstructed and reference images for edge and gradient regions, especially in difficult boundary and transition regions [33,36]. Perceptual regularization; limiting generation based on features from pre-trained networks that are more consistent with human visual perception [26]. Recent results indicated that incorporating structural priors in diffusion models makes generation stability and artifact and edge blurring more reliable [23,25,37]. To overcome the shortcomings of static constraints, this paper proposed a Static Regularization-Guided (SRG) module with time-decay mechanism to dynamically adjust regularization strength. This method provides both structural stability and perceptual realism in latent diffusion space and facilitates quality and robustness of remote sensing SR results.

3. Methodology

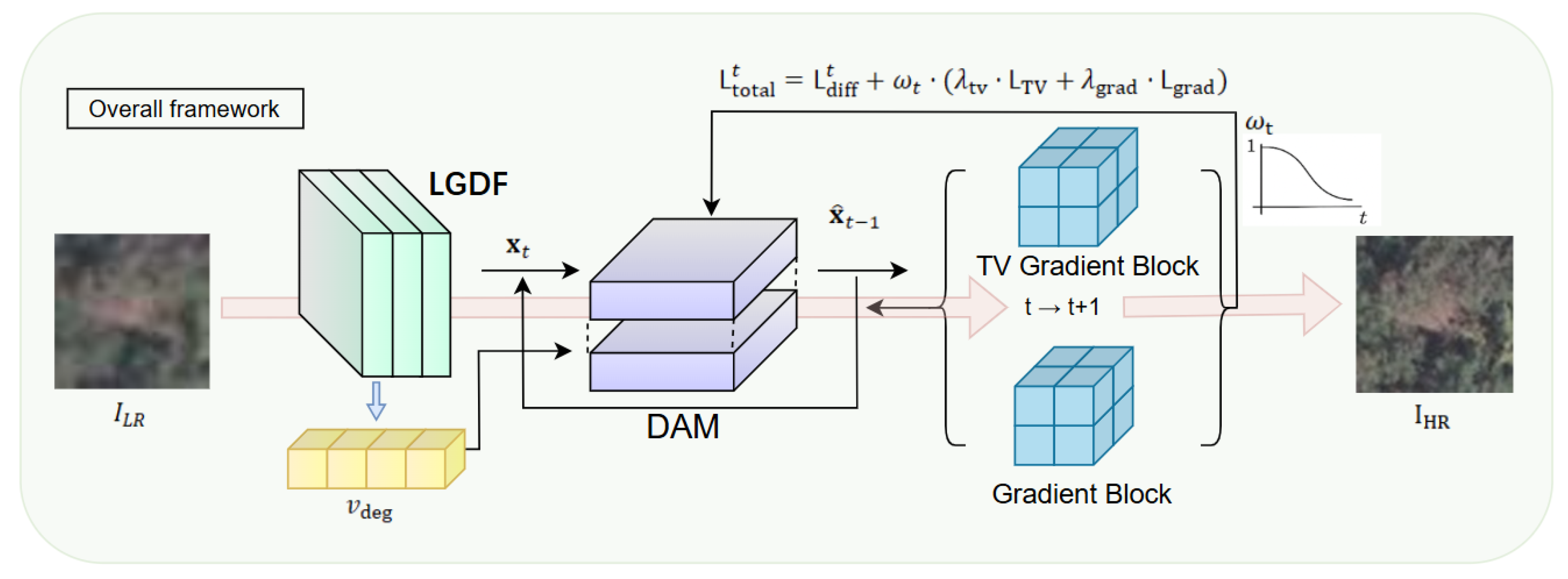
3.1. Overall Framework

As shown in Figure 1, we develop a multi-module collaborative modeling module for remote sensing image super-resolution to address detailed loss and structural blur of the degraded images, which includes three complementary modules: Degradation-Aware Modeling module, Dual-Decoder Recursive Generation module and Static Regularization-Guided Generation module. Degradation Aware Modeling considers multi-source degradations and cross-scale blurs of the remote sensing images. It extracts degradation vectors through lightweight CNNs with channel attention and introduces them in the diffusion latent space as priors [32,35]. Dual-decoder Rec recursive Generation introduces local convolutional layers and global Transformer structures to model fine-grained textures and long-range semantics. By introducing recursion over timesteps and residual domain corrections [33,36], this module establishes a progressive reconstruction line from coarse structures to fine details to obtain semantic consistency and geometric accuracy. Static Regularizing-Guiding Generation also introduces priors such as Total Variation and Gradient Consistency [26,37] into the diffusion hidden space to control edge preservation and texture detail. The module adaptively adjusts regularization strength to stabilize stability and structural awareness during the generation. In general, our framework models fine degradation with local detail recovery and global structural awareness. It achieves high reconstruction quality and generalization ability [27,28,30], which makes it suitable for multi-scene and multi-modal remote sensing super-resolution tasks.

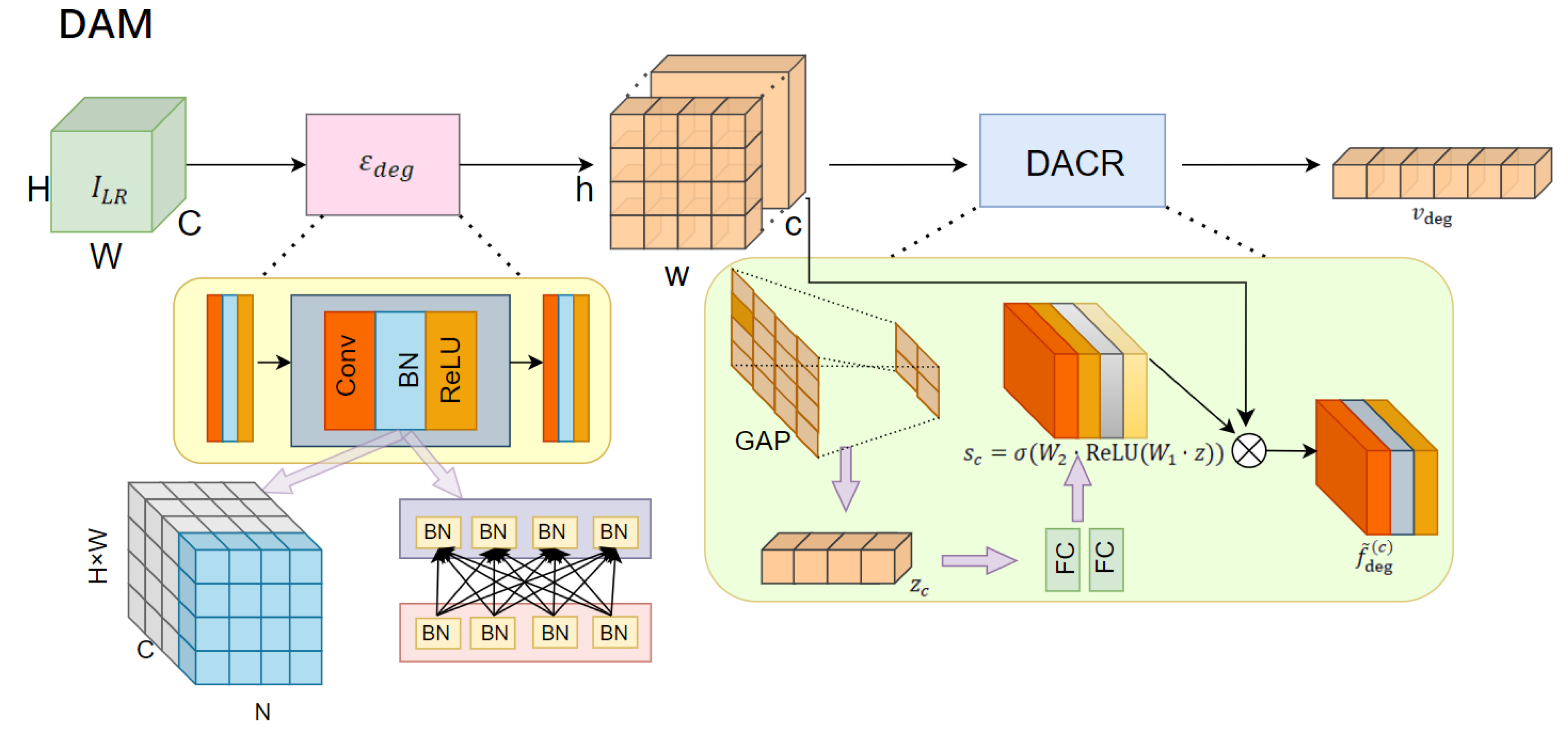
3.2. Degradation-Aware Modeling Module

Remote sensing images suffer from multiple-source and multiple-scale degradations during acquisition, including spatial blur, compression noise, color blur, cloud occlusion etc [38,39,40]. These degradation are challenging, heterogeneous, and generally do not have accurate annotations. Building a generalizable degradation modeling mechanism is a key prerequisite for improving super-resolution quality and stability [41,42]. In that, we propose degradative-aware modeling module(DAM) that first analyzes the input image with a light convolutional structure, extracting degradation features [43,44]. The features are combined using a channel attention algorithm in the form of a degradation vector $v_{\mathrm{deg}}$ that encodes both the type and severity of degradatory effects, which is illustrated in Figure 2. The vector is injected as a priori into the diffusion model to steer the super-scratching to a more reasonable solution distribution [45,46].

3.2.1. Lightweight Feature Extractor

Given an input low-resolution remote sensing image $I_{\mathrm{deg}}\in {\mathbb{R}}^{H\times W\times C}$, we create a lightweight convolutional neural network ${\epsilon }_{\mathrm{deg}}$ which extracts degradation-related features. Our low-fidelity convolution layer consists of three light convolution layers with a $3\times 3$ convolution kernel, batch normalization (BN), and ReLU activations:

$$f^{\left(i\right)}=\mathrm{ReLU}\left(\mathrm{BN}\left({\mathrm{Conv}}_{3\times 3}\left(f^{(i-1)}\right)\right)\right),i=1,2,3$$

(1)

where $f^{\left(0\right)}=I_{\mathrm{LR}}$. Finally, we obtain the degradation-aware feature map $f_{\mathrm{deg}}\in {\mathbb{R}}^{h\times w\times c}$.

The BN layer is important for training and convergence.The idea is to normalize the mean and variance of each channel in a mini-batch to reduce internal covariate shift. Specifically, for each channel c, BN performs:

$${\widehat{x}}_{n,c,h,w}={\displaystyle \frac{x_{n,c,h,w}-{\mu }_c}{\sqrt{{\sigma }_c^2+ϵ}}}$$

(2)

where ${\mu }_c$ and ${\sigma }_c^2$ denote the mean and variance of channel c, respectively, and $ϵ$ is a small constant for numerical stability. Then, BN applies a learnable linear transformation with scaling and shifting parameters ${\gamma }_c$ and ${\beta }_c$:

$$y_{n,c,h,w}={\gamma }_c{\widehat{x}}_{n,c,h,w}+{\beta }_c$$

(3)

This stabilizes the feature distributions across the network layers, removes vanishing or exploding gradients, and facilitates generalisation and training.

3.2.2. Degradation-Aware Channel Recalibration

To effectively capture the channel-wise response differences of multiple degradation types in remote sensing images, we propose a Degradation-Aware Channel Recalibration(DACR) mechanism. This module enhances the model’s capability to represent degradation-sensitive regions through an adaptive channel weighting strategy. DACR is based on Squeeze-and-Excitation idea. It adjusts intermediate features along the channel dimension and emphasizes features closely associated with degradation patterns. Specifically, given the degradation-aware feature map $f_{\mathrm{deg}}\in {\mathbb{R}}^{h\times w\times c}$, a global average pooling is first applied to each channel to extract its statistical descriptor:

$$z_c={\displaystyle \frac{1}{h\times w}}\sum _{i=1}^h\sum _{j=1}^w{f}_{\mathrm{deg}}^{\left(c\right)}(i,j)$$

(4)

The aggregated descriptor $z\in {\mathbb{R}}^c$ is then fed into a nonlinear transformation module consisting of two fully connected (FC) layers to model inter-channel dependencies and generate the attention weights $s_c\in {\mathbb{R}}^c$:

$$s_c=\sigma \left(W_2·\mathrm{ReLU}(W_1·z)\right)$$

(5)

where $W_1\in {\mathbb{R}}^{c/r\times c}$ and $W_2\in {\mathbb{R}}^{c\times c/r}$ are the dimensionality-reduction and expansion matrices, r denotes the channel reduction ratio, and $\sigma (·)$ is the Sigmoid activation function.

Subsequently, the generated attention weights are used to reweight the original feature map channels, producing the degradation-enhanced features:

$${\tilde{f}}_{\mathrm{deg}}^{\left(c\right)}=s_c·f_{\mathrm{deg}}^{\left(c\right)}$$

(6)

The enhanced feature map is then flattened and projected into a low-dimensional degradation vector:

$$v_{\mathrm{deg}}=W_f·\mathrm{vec}\left({\tilde{f}}_{\mathrm{deg}}\right)+b_f$$

(7)

where $\mathrm{vec}(·)$ denotes the flattening operation, $W_f\in {\mathbb{R}}^{d\times hwc}$ and $b_f\in {\mathbb{R}}^d$ are the parameters of a fully connected layer.

The resulting degradation vector $v_{\mathrm{deg}}$ semantically encodes multi-type and multi-scale degradation information within the image, demonstrating strong discriminative and transferable capabilities. When added as an external prior, $v_{\mathrm{deg}}$ guides the diffusion model at each noise prediction step. It helps the model focus on important degraded regions. This improves the super-resolution quality and cross-domain performance under complex degradations.

3.2.3. Degradation-Aware Conditional Injection

The degradation vector $v_{\mathrm{deg}}$, denoted as v hereafter, is injected into the diffusion network as a conditional guidance term, providing targeted degradation priors during each noise prediction step. In practice, this conditional injection enriches the diffusion process with explicit knowledge of the degradation type and severity [47,48]. As a result, the model not only achieves higher accuracy in reconstructing images degraded by blur, noise, or low contrast, but also maintains robustness under heterogeneous degradation conditions [49,50].More importantly, this mechanism demonstrates strong transferability in remote sensing applications. Since remote sensing images exhibit diverse spatial resolutions, sensor characteristics, and complex degradation patterns, super-resolution models trained solely on natural images often struggle to generalize. By incorporating the degradation-aware conditional injection, our model effectively leverages intrinsic degradation cues, bridging the gap between natural image pretraining and remote sensing image applications [51,52]. In this way, the proposed approach enables cross-modal and cross-task generalization, which is crucial for practical deployment in real-world remote sensing scenarios.

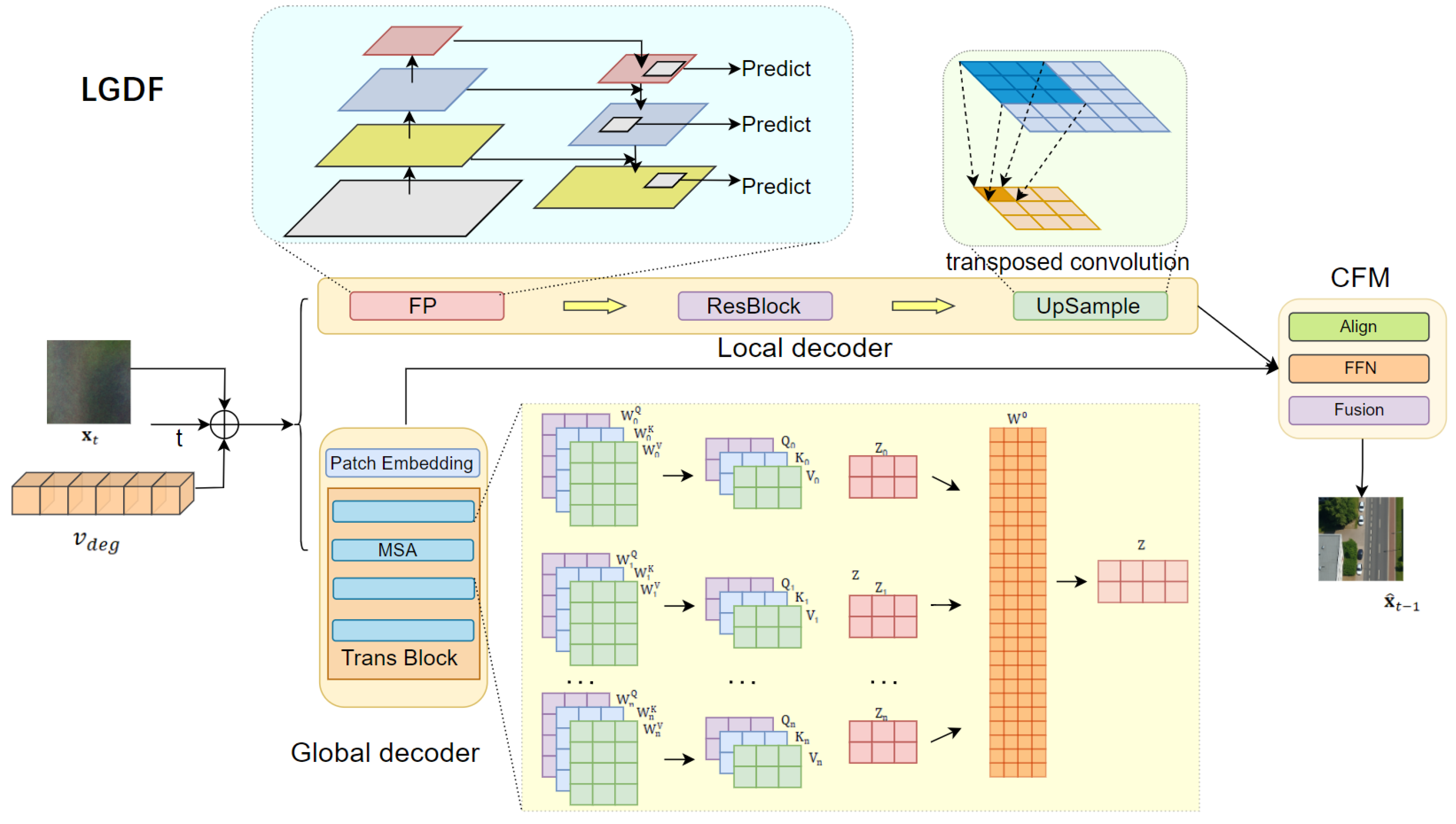
3.3. Dual-Decoder Design and Recursive Generation

In single-scale conditional diffusion modeling, we propose structure-aware dual-decoder design and cross-time recursive generation by progressive reconstruction from coarse structures to fine fine details [53]. The model is capable of capturing high-frequency structures and edges in remote sensing images. It works well for reconstructing complex textures and handling various degradations. Specifically, the proposed module integrates multi-stage recursion along the temporal dimension (Time-wise Recursion) with layer-wise residual refinement in the residual domain, thereby achieving progressive optimization from structure to texture [54].

3.3.1. Dual-Decoder Design

In classical diffusion models, the decoder is usually implemented as a single architecture such as U-Net, which iteratively denoises the Gaussian corrupted image $x_T$ into a clean target. However, single-decoder structures often struggle with complex degradations in remote sensing images, such as non-uniform blur, occluded structures, and multi-scale texture damage. This can cause missing local details and inconsistent semantics. To solve this problem, we propose a Local-Global Decoding Framework (LGDF), shown in Figure 3. It is integrated into the single-scale conditional diffusion process. The goal is to jointly optimize global semantic modeling and local detail restoration. It consists of two parallel decoding branches: a local decoder ${\mathsf{D}}_L$ responsible for fine-grained structure reconstruction, and a global decoder ${\mathsf{D}}_G$ responsible for long-range semantic consistency.

(1) Decoding Output Formulation

The general reverse diffusion objective is defined as:

$${\widehat{\mathbf{x}}}_{t-1}={\mathbf{x}}_t-{ϵ}_{\theta }({\mathbf{x}}_t,t\mid \mathbf{v})$$

(8)

where ${ϵ}_{\theta }(·)$ is the noise predictor and $\mathbf{v}$ is the degradation condition vector. In LGDF the noise estimation term is obtained by fusing the outputs of the two decoders:

$${ϵ}_{\theta }({\mathbf{x}}_t,t\mid \mathbf{v})=\alpha ·{\mathsf{D}}_L({\mathbf{x}}_t,t,\mathbf{v})+(1-\alpha )·{\mathsf{D}}_G({\mathbf{x}}_t,t,\mathbf{v})$$

(9)

where $\alpha \in [0,1]$ is a learnable fusion coefficient that adaptively balances the contributions of the two branches.

3.3.1.2. (2) Local Decoder

Local branch ${\mathsf{D}}_L$ adopts a U-Net to enhance local detail reconstruction. Features pyramids, residual connections, and upsampling modules are fused across-scale. The overall state of the local decoding is:

$${\mathsf{D}}_L({\mathbf{x}}_t,t,\mathbf{v})=\mathrm{UpSample}\circ \mathrm{ResBlock}\circ \mathrm{FP}({\mathbf{x}}_t\oplus \varphi \left(t\right)\oplus \mathbf{v})$$

(10)

where $\varphi \left(t\right)$ denotes the temporal embedding vector, and ⊕ represents channel-wise concatenation. ResBlock introduces local residual learning to improve the representation of edges and textures [55].The feature pyramid $\mathrm{FP}(·)$ is constructed as:

$$F_{\mathrm{fp}}=\sum _{k=1}^K{\mathrm{Conv}}_k\left(F_0\right)$$

(11)

where ${\mathrm{Conv}}_k$ denotes the convolution operator at scale k for processing hierarchical features, and K is the total number of scales [56]. The upsampling using transposed convolution is used to update the features to high resolution.

The final result is high-frequency details and geometric consistency which supports local details recovery for the entire decoder and leads to local sharpness and texture quality in degraded areas. The same works for global branch. So, the decoder produces consistent semantics and better quality images.

3.3.1.3. (3) Global Decoder

The global branch ${\mathsf{D}}_G$ is based on multiple Transformer blocks to capture long-range dependencies and global consistency [57]. The branch first compiles the input features into a patch by Patch Embedding and then applies a Multi-Head Self-Attention (MSA) to model global feature.The overall process is formulated as:

$${\mathsf{D}}_G({\mathbf{x}}_t,t,\mathbf{v})=\mathrm{MSA}\circ \mathrm{PatchEmbed}({\mathbf{x}}_t\oplus \varphi \left(t\right)\oplus \mathbf{v})$$

(12)

where $\varphi \left(t\right)$ denotes the temporal embedding vector, and ⊕ represents channel-wise concatenation.

In the global decoder, the main operation is MSA. In this case, all input features are first projected to the token sequence $\mathbf{z}$ with Patch Embedding. For each attention head, different linear projection matrices $W^Q$, $W^K$, and $W^V$ generate the query (Q), key (K), and value (V) representations, each head computes a weighted output to capture global dependencies across subspaces. The multi-head outputs are concatenated and linearly projected using $W^O$ to produce the fused contextual representation $\mathbf{z}$.

Each Transformer block integrates an MSA module with a residual connection, defined as:

$${\mathbf{z}}^{\prime }=\mathrm{MSA}\left(\mathbf{z}\right)+\mathbf{z}$$

(13)

where $\mathbf{z}$ denotes the input token sequence.

This global branch focuses on modeling structural and semantic consistency, effectively addressing non-local degradation issues such as large-area occlusion, geometric distortion, and artifacts. By providing macro-level semantic constraints, it complements the local decoder and contributes to achieving both global coherence and perceptually faithful reconstruction.

(4) Complementary Fusion Module

In order to combine the structure features of convolutional local decoder ${\mathsf{D}}_L$ with semantic features of Transformer global decoder ${\mathsf{D}}_G$, we design a Complementary Fusion Module(CFM). CFM consists of three types of features alignment, feature fusion, and nonlinear interaction modeling.

Feature alignment stage. Since the outputs of ${\mathsf{D}}_L$ and ${\mathsf{D}}_G$ differ in channel dimension and semantic distribution, we first apply linear mappings to align feature spaces:

$$F_L^{\mathrm{align}}=W_L{F}_L+b_L,F_G^{\mathrm{align}}=W_G{F}_G+b_G$$

(14)

Feature fusion stage. The aligned local and global features are concatenated:

$$F_{\mathrm{fusion}}=\mathrm{Concat}(F_L^{\mathrm{align}},F_G^{\mathrm{align}})$$

(15)

Nonlinear interaction stage. A lightweight feed-forward network (FFN) is introduced to enhance semantic interactions across channels:

$${\widehat{F}}_{\mathrm{fusion}}=F_{\mathrm{fusion}}+\mathrm{FFN}\left(F_{\mathrm{fusion}}\right),\mathrm{FFN}\left(x\right)=W_2·\sigma (W_{1}x+b_1)+b_2$$

(16)

where $\sigma (·)$ is activation. Finally, we use the last fused representation ${\widehat{F}}_{\mathrm{fusion}}$ for subsequent reconstruction, which gives much richer expressivity for multi-level structures and semantic details.

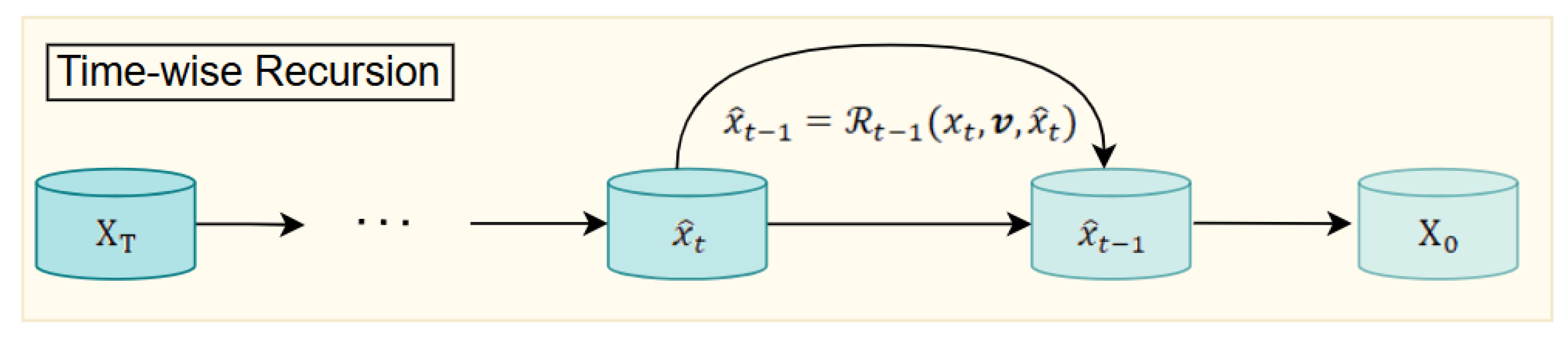
3.3.2. Recursive Generation Mechanism

We also propose a recursive generation function that iteratively improves from two perspectives. First, time-wise recursion performs progressive denoising of several timesteps, Second, residual correction recursion optimizes structural residuals to better edge and texture. The two mechanisms provide complementary models, time recursion improves global stability and semantic coherence and residual recursion enhances local detail quality [58]. Both of them lead to high perceptual quality and local readability [59].

(1) Time-wise Recursion

The fundamental idea of diffusion models is to progressively generate a clean image from pure noise through a reverse denoising process. Based on this result, we introduce a cross-timestep recursive mechanism where the result of a reconstruction at the current timestep is fed back as a prior for a next timesteps. The structure is shown in Figure 4. This enables a coarse-to-fine progressive generation process. The mechanism can be formally expressed as:

$${\widehat{\mathbf{x}}}_{t-1}={\mathcal{R}}_{t-1}\left({\mathbf{x}}_t,\mathbf{v},{\widehat{\mathbf{x}}}_t\right)$$

(17)

where ${\widehat{\mathbf{x}}}_t$ is the estimated image at timesteps t, $\mathbf{v}$ is the degradation vector, and ${\mathcal{R}}_{t-1}(·)$ is the recursive restore function based on the current estimate and the degradation prior between timestep t and $t-1$. We define the recursive function as follows:

$${\mathcal{R}}_{t-1}({\mathbf{x}}_t,\mathbf{v},{\widehat{\mathbf{x}}}_t)=f_{\theta }({\mathbf{x}}_t,{\widehat{\mathbf{x}}}_t,\varphi \left(\mathbf{v}\right))$$

(18)

where $f_{\theta }$ denotes the recursive restoration network, and $\varphi \left(\mathbf{v}\right)$ is the embedded representation of the degradation vector. Roughly, if we can update this formulation, a high quality image can be modelled in steps as:

$${\widehat{\mathbf{x}}}_0={\mathcal{R}}_0\left({\mathcal{R}}_1(\dots {\mathcal{R}}_{T-1}\left({\mathbf{x}}_T\right))\right)$$

(19)

Step-by-step recursion, starting from ${\mathbf{x}}_T\sim \mathcal{N}(0,I)$, reflects the time evolution behavior of diffusion models. In a multi-step network, such recursive dynamics are shown to yield more accurate detail recovery and uncertainty model.

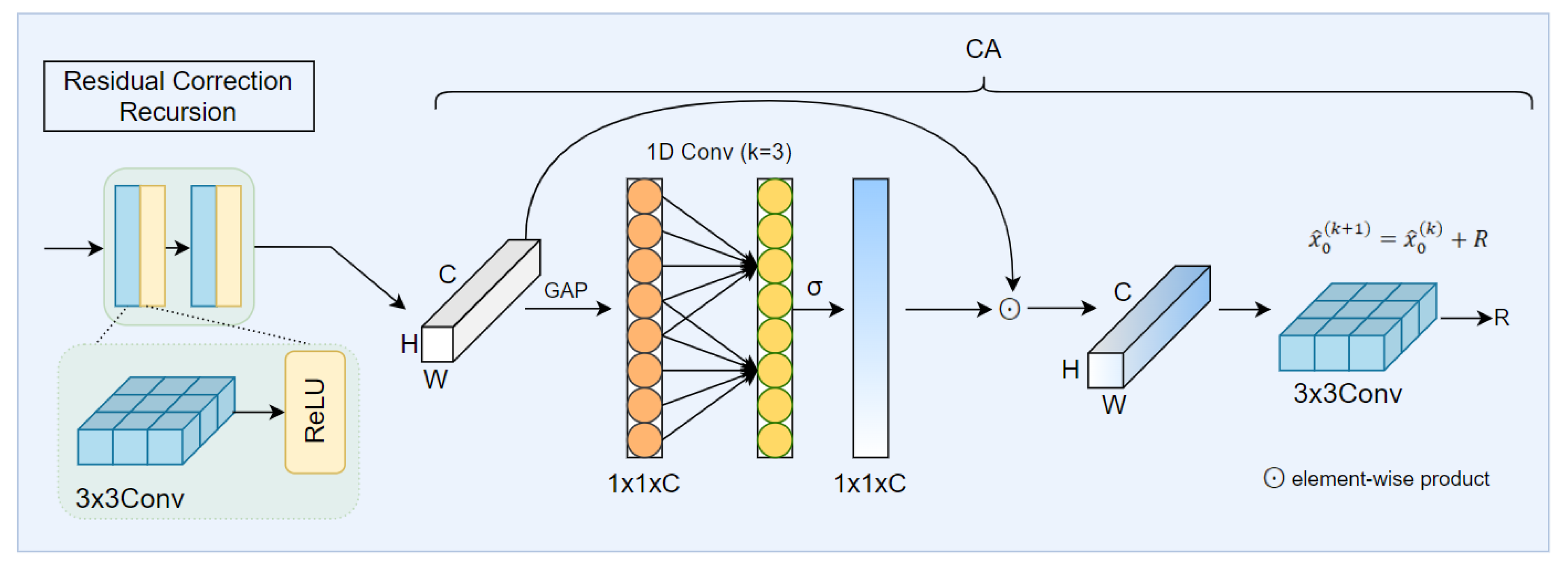
(2) Residual Correction Recursion

Although the primary diffusion-based reconstruction path can generate high-quality preliminary images, reconstruction deficiencies still exist in complex object boundaries and weak texture regions of remote sensing imagery. Therefore, as shown in the Figure 5, we introduce a structural residual correction mechanism. Specifically, based on the reconstructed image from the main diffusion path, a lightweight residual prediction network $\mathcal{C}(·)$ is employed to model and compensate for the residual components:

$${\widehat{x}}_0^{final}={\widehat{x}}_0+\mathcal{C}({\widehat{x}}_0,v)$$

(20)

Here, $\mathcal{C}(·)$ consists of a shallow convolutional feature extraction module and a channel attention enhancement module (CA), which jointly estimate the structural residual information using both the reconstructed image and the degradation vector [60]. The shallow convolutional feature extraction part focuses on learning local structural features and texture variations within the residual, implemented through two consecutive $3\times 3$ convolutional layers with ReLU activations:

$$F_{conv}=\mathrm{ReLU}\left({\mathrm{Conv}}_{3\times 3}\left(\mathrm{ReLU}\left({\mathrm{Conv}}_{3\times 3}\left(F_{in}\right)\right)\right)\right)$$

(21)

The channel attention enhancement module introduces a lightweight cross-channel interaction design to replace conventional fully connected attention structures. This mechanism applies a 1D convolution to the channel descriptor vector from global average pooling. It captures local relationships between channels without changing the feature dimension. This improves feature discrimination while keeping computation efficient. The process is formulated as follows:

$$z=\mathrm{GAP}\left(F_{conv}\right)\in {\mathbb{R}}^{1\times 1\times C}$$

(22)

$$w=\sigma \left(\mathrm{Conv}1\mathrm{D}\right(z\left)\right)$$

(23)

$$F_{att}=F_{conv}\odot w$$

(24)

where ⊙ denotes channel-wise multiplication. A final $3\times 3$ convolution is then used to transform the weighted features into a structural residual map:

$$R={\mathrm{Conv}}_{3\times 3}\left(F_{att}\right)$$

(25)

which is added to the current reconstruction result to complete one correction step:

$${\widehat{x}}_0^{(k+1)}={\widehat{x}}_0^{\left(k\right)}+R$$

(26)

The recursive correction process can be repeated several times, forming:

$${\widehat{x}}_0^{(k+1)}={\widehat{x}}_0^{\left(k\right)}+\mathcal{C}({\widehat{x}}_0^{\left(k\right)},v),k=0,1,\dots ,K-1$$

(27)

This mechanism introduces an adaptable optimizer at the network level which progressively optimizes the reconstruction with recursive residual compensation. Compared to static post-processing or one-shot prediction, the recursive correction mechanism is more flexible and sensitive to structure, it better reproduces geometric consistency and sharpness of the details in remote sensing image reconstruction.

3.4. Static Regularization Guidance

Edge structures and texture details play a major role in remote sensing image super resolution tasks for perceptual quality and semantic discrimination. Although diffusion models can fit data distributions well and generate diverse results, they often blur boundaries and lose details. This is especially true in transition areas between land cover types, such as building-to-ground or water-to-vegetation. Introducing static structural priors not only enhances the structural perception ability of the generated images but also significantly improves texture representation and edge sharpness in natural regions such as water, forest, and roads. Prior studies (e.g., DPS [61], IDDPM [62]) have demonstrated that incorporating prior knowledge into the diffusion process can improve both convergence stability and controllability of generation [63].

Based on this idea, we add a static structural prior regularization. It explicitly constrains the structure of generated images. This improves the model’s sensitivity and accuracy for edges and textures. During each reconstruction stage ${\widehat{I}}_t^{SR}$ of the diffusion process, the static regularization terms are integrated into the optimization objective to balance structural preservation and detail reconstruction at different time steps. Specifically, two types of regularization are included: Total Variation (TV) regularization and Gradient Consistency Loss.

3.4.1. Overall Loss Function

On top of the primary diffusion reconstruction loss, we incorporate the structural regularization to construct the following joint optimization objective:

$${\mathcal{L}}_{\mathrm{total}}^t={\mathcal{L}}_{\mathrm{diff}}^t+{\omega }_t·\left({\lambda }_{tv}·{\mathcal{L}}_{TV}+{\lambda }_{grad}·{\mathcal{L}}_{grad}\right),$$

(28)

where ${\mathcal{L}}_{\mathrm{diff}}^t$ denotes the reconstruction loss in the diffusion process, including L1 loss and perceptual loss; ${\mathcal{L}}_{TV}$ is the TV regularization term that suppresses local artifacts and oscillations [64]; ${\mathcal{L}}_{grad}$ is the gradient consistency loss enforcing similarity in the gradient domain between generated images and high-resolution references [65]. The hyperparameter ${\lambda }_{tv}$ and ${\lambda }_{grad}$ control the relative weights of each regularizer, with ${\lambda }_{tv}=0.1$ and ${\lambda }_{grad}=1.0$ in our experiments.

To adaptively adjust the influence of structural regularization across different diffusion time steps, we design a dynamic weighting factor ${\omega }_t$. It balances the strength of structural guidance between the early and late stages of the diffusion process. Specifically, ${\omega }_t\in [0,1]$ decreases over time. First of all, it imposes strong structural constraints for robust coarse reconstruction. Then the constraints are weaker in order to maintain fine details and avoid smoothing. We adopt a cosine scheduling strategy, formally defined as:

$${\omega }_t=cos\left({\displaystyle \frac{\pi t}{2T}}\right),$$

(29)

where T is the number of diffusion steps and $t\in [0,T]$ is the total number of steps that are made. With this scheduling, regularization strength is smoothly decay, and the structure stability is complemented with detail, yielding high quality and visual realism.

3.4.2. Total Variation Regularization

Total variation is a classical image smoothing and denoising technique to enhance the structural sharpness at edges. It is defined as:

$${\mathcal{L}}_{TV}=\sum _{i,j}\left(\left|{\nabla }_x{\widehat{I}}_{i,j}^{SR}\right|+\left|{\nabla }_y{\widehat{I}}_{i,j}^{SR}\right|\right),$$

(30)

where ${\widehat{I}}^{SR}$ is the current image and ${\nabla }_x,{\nabla }_y$ is a first order gradient operator in horizontal and vertical directions. It is calculated on the final output ${\widehat{I}}_0^{SR}$ of the diffusion and added as a regularization to the main loss. It guides the generation in structural consistency and edge clarity. It minimizes high-frequency oscillatory artifacts and avoids smoothing.

3.4.3. Gradient Consistency Loss

In order to further facilitate structural alignment between generated images and high resolution ground truth, we present a gradient consistency loss:

$${\mathcal{L}}_{grad}={∥\nabla {\widehat{I}}^{SR}-\nabla I^{HR}∥}_1,$$

(31)

where $I^{HR}$ denotes the high-resolution reference image and ∇ represents the Sobel gradient operator. This loss maintains consistency both in edge direction and intensity, especially in transition regions (e.g., blurred borders, blurred textures). This loss has the effect of making the fine details more consistent.

4. Experiment

4.1. Datasets and Evaluation Metrics

UCMerced LandUse Dataset

The UCMerced LandUse dataset [66] contains 21 classes of typical land-use categories, including residential areas, farmland, forest, rivers, etc., with a total of 2,100 aerial remote sensing images. Each image has a spatial resolution of $256\times 256$ pixels, exhibiting rich texture and structural features across diverse natural and man-made scenes. The dataset can be used to evaluate the quality of restoration of details. In our experiments, 1,800 images are used for training, 300 for validation, and the remaining 300 for testing.

AID Dataset

The AID dataset [67] contains 30 representative remote sensing scene categories containing 10,000 aerial images.The image resolution ranges from $600\times 600$ to $1000\times 1000$ pixels. Due to the large number of scenes and large scale variability, this information may be used to evaluate model robustness in difficult situations. To unify input resolutions, we crop the original images into $256\times 256$ patches, resulting in 8,000 training samples, 1,000 validation samples, and 1,000 test samples.

Evaluation Metrics

The reconstructed results are compared based on accuracy (PSNR, SSIM), perceptual quality (LPIPS), error magnitude (RMSE) [68] and fidelity (VIF) [69]. The first two metrics assess the closeness of the reconstructed images to the ground truth at the pixel and perceptual levels, respectively. RMSE quantifies the pixel-wise error magnitude, while VIF evaluates the fidelity of information content. Together, these metrics comprehensively reflect the performance of different methods in remote sensing image super-resolution tasks and correspond directly to the experimental results presented in the tables.

4.2. Comparison with Existing Methods

Experimental Setup

To comprehensively evaluate the performance of the proposed method, we selected several representative methods for comparison in remote sensing image super-resolution tasks. The diffusion-based methods include SinSR, EDiffSR, and RefDiff, while the non-diffusion-based methods include EDSR [7], RCAN [8], SwinIR [9], and Uformer [10]. The experiments cover three upscaling factors ($\times 2$, $\times 3$, $\times 4$) and two types of degradation scenarios. The first is Bicubic degradation, where low-resolution inputs are generated solely via bicubic downsampling for benchmark evaluation. The second is Blind degradation, in which, in addition to downsampling, multiple degradation factors such as Gaussian blur, additive noise, and optional JPEG compression are applied. All degradation parameters are randomly sampled within reasonable ranges to better simulate the degradation process of real remote sensing images.

All methods are evaluated under the same data splits, training epochs, and hardware environment, strictly following official implementations or publicly released training configurations. Training uses the Adam optimizer with an initial learning rate of $2\times {10}^{-4}$, decayed via a cosine annealing schedule. The batch size is 16, and all models are trained for 500 epochs on an NVIDIA RTX 4090 GPU (CUDA 12.2). The UCMerced LandUse and AID datasets are tested.PSNR, SSIM, LPIPS, RMSE, VIF evaluate pixel accuracy, perceptual quality, and information fidelity of the reconstructed images.

Quantitative Results Analysis The overall quantitative results are shown in Table 1 and Table 2. Each method performed in different data sets (UCMerced and AID) and degradation conditions. The main conclusions are:

Ideal degradation: The proposed method generally achieves comparable or comparable performance to state-of-the-art methods (e.g., RCAN [8], SwinIR [9]) in terms of PSNR and SSIM, especially on the $\times 2$ low-scale task, indicating high pixel-level fidelity.For perceptual quality of LPIPS, the proposed method outperforms non-diffusion methods and compares to diffusion methods such as SinSR [14] and RefDiff [15], for maintaining perceptual quality at mild degradation. It is also found to achieve low RMSE and high VIF, for reconstruction error and high information quality, while preserving structural and edge information.

Non-ideal degradation: Non-diffusion-based methods (EDSR [7], RCAN [8], SwinIR [9]) are less able to produce higher performance. PSNR and SSIM shrinks by around 1-2 dB, LPIPS shrinks, RMSE shrinks and VIF drops with poor pixel accuracy, perception quality, and information fidelity. Diffusion-based methods retain advantages in perceptual metrics, but some (e.g., RefDiff [15]) exhibit suboptimal RMSE and VIF. In contrast, the proposed method demonstrates robust performance across all metrics, with PSNR/SSIM significantly improved (approximately +1.3 dB PSNR and +0.018 SSIM compared with RCAN [8] for $\times 2$–$\times 4$ tasks), LPIPS reduced by 10%–20%, lower RMSE, and notably higher VIF. Structural and edge information are better preserved. The advantages are especially pronounced under high upscaling ($\times 4$) and strong noise degradation, further validating the effectiveness of the degradation-aware modeling module (DAM), which enables the model to adapt reconstruction strategies according to degradation type while maintaining structural integrity.

Qualitative Results and Analysis

As shown in Figure 6 and Figure 7, we further verify the visual reconstruction quality of the proposed model. Figure 6 presents the results under ideal bicubic degradation based on the UCMerced dataset, while Figure 7 illustrates the results under blind degradation conditions using the AID dataset. Under the ideal degradation setting, all methods are able to recover the overall structure to a certain extent; however, existing CNN- or Transformer-based baselines (such as RCAN [8], SwinIR [9], and Uformer [10]) still suffer from over-smoothed textures and blurred edges. In contrast, our method reconstructs fine-grained textures more effectively, such as building edges, tennis court lines, and vehicle contours, resulting in sharper boundaries and higher visual fidelity. In the harder non-ideal degradation case, our approach is better than others. Some diffusion methods (e.g. RefDiff [15], EDiffSR [16]) produce artifacts or structural inconsistencies when dealing with more than one blur and noise mix. Because of our proposed degradation aware modeling and fixed regularization guided generation, our model still maintains accurate details and geometric consistency when dealing in high-level scenes such as cities, vegetation, and dense building areas. Overall, our method produces improved perceptual sharpness and structural accuracies, with strong robustness and cross-dataset generalization.

All in all, if the degradations are ideal, our method performs well in general. When the distortions are not optimal, the perceptual quality of our method improves due to the multi-level detail refinement of the dual decoder recursive generation. The structural consistency (EPI) of our technique improves due to a smooth geometry of the multiple decoder recurrent generation, which results in fewer common distortions and artifacts in diffusion models. Overall, our model yields stable and strong performance in remote sensing image super resolution due to complicated degradation, different upscaling factors, and different scenes.

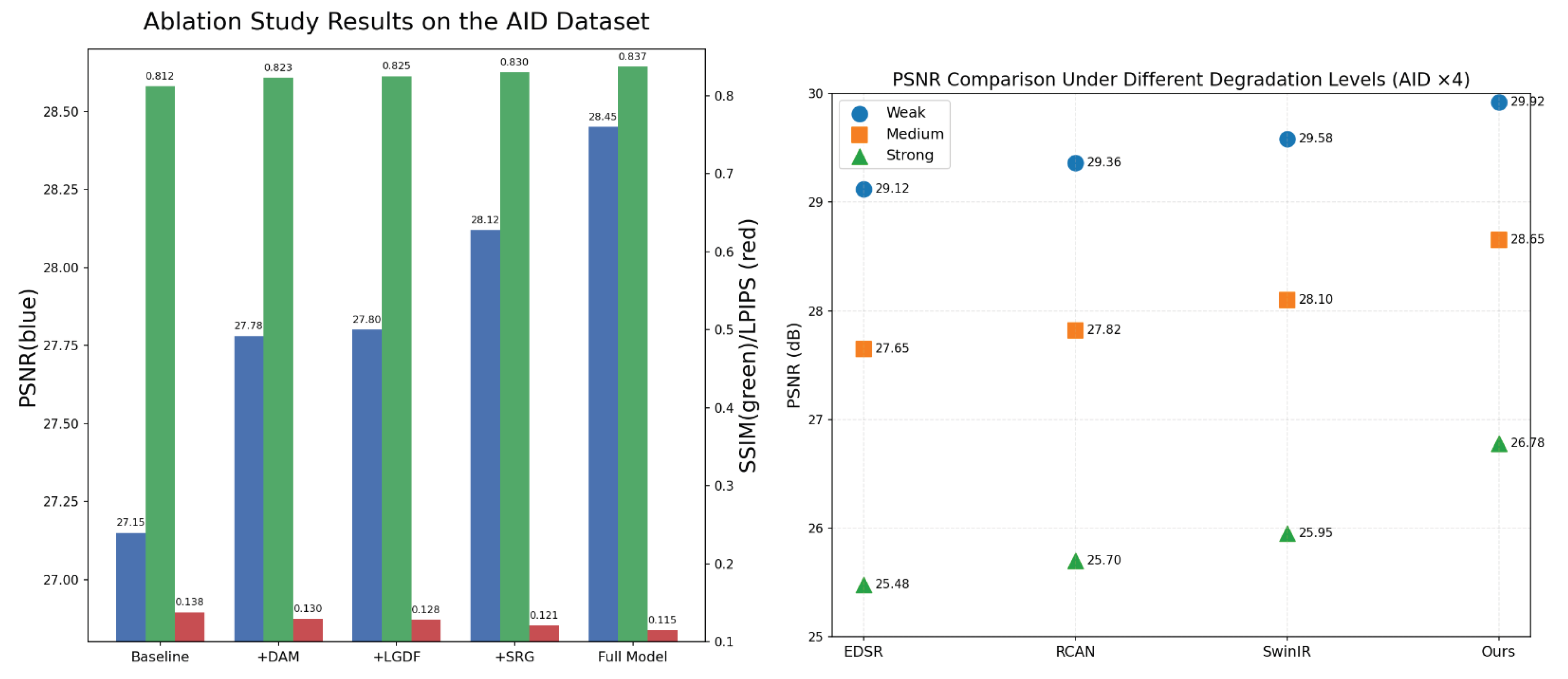
4.3. Ablation Study

In order to validate the contributions and benefits of the other core modules proposed here, we conducted an ablation study on the AID remote sensing data. Our hierarchical multi-task restoration network consists of three modules (DAM, LGDF and SRG). We started from a baseline network (Base) and progressively added one module to quantify the performance improvements at each stage. The model configurations are as follows.Base: The baseline model, which only includes the basic UNet encoder-decoder structure; Base + DAM: The baseline model augmented with the DAM to extract degradation features; Base + DAM + LGDF: Further addition of the LGDF to enable complementary convolutional and Transformer decoding; Base + DAM + LGDF + SRG (Full Model): The complete network, including the SRG module.

As shown in Table 3 and Figure 8, our model improves continuously with added modules. The DAM results in a 0.63 dB increase in PSNR and a 0.011 improvement in SSIM, showing that it can learn the degradation properties of low-resolution images better by recovering structures in blurry or noisy scenes. Further incorporating LGDF increases PSNR to 28.05 dB, while reducing LPIPS by 0.007. This indicates that the convolutional and Transformer decoders can achieve global structural consistency and local textures. Finally, the addition of SRG yields the optimal performance, with PSNR reaching 28.45 dB, SSIM 0.837, and LPIPS 0.115. The static regularization constraint based on structural priors and gradient consistency can suppress artifacts and improve edges and textures. Overall, our performance shows that each module can achieve the same degree of effectiveness and benefits.DAM provides degradation priors, LGDF combines semantic and detail information and SRG stabilizes generation and preserve structural consistency. Together, these three modules can enable our model to achieve higher pixel-level accuracies and perceptual quality in remote sensing image super-resolution tasks.

4.4. Further Analysis: Robustness Under Different Degradation Levels

We evaluated the robustness of the proposed method against varying degradation conditions on the AID dataset, for the weak degradation(low noise and mild blur), medium degradation(moderate noise and blur), and strong degradation(high noise and severe blur). We compared the proposed approach with several representative super-resolution models such as EDSR, RCAN and SwinIR and measured PSNR variations under the $\times 4$ upscaling task. Table 4 summarizes the experimental data. Overall, each method gets a small drop in performance. Our method gets smaller declines compared to competing approaches. For example, when a degradation goes from weak to strong, EDSR drops 3.64 dB and our method drops 3.14 dB in PSNR. This indicates that our DAM can adaptively model degradation properties and achieve good restoration performance with complex degradations.

Moreover, the scatter plots in Figure 8 show the degradation trends more clearly. Competing methods drop sharply as degradation increases. In contrast, our method stays more stable, showing lower sensitivity and better robustness. Overall, the proposed method consistently outperforms others under different degradation levels. This further confirms the adaptive ability and generalization of the DAM module for handling complex degradations.

5. Conclusions

In this work, we proposed a model for remote sensing image super-resolution based on degradation-aware modeling, a dual-decoder structure, and static regularization-guided generation. The degradation-explicit module adapts to different and complex degradations in remote sensing data. It provides prior information for reconstruction. The dual-constructed structure improves both structural accuracy and texture details. The static regularisation algorithm provides stable training and consistent results at scales and for degradation levels.Extensive studies on multiple benchmark datasets are performed where our method outperforms state-of-the-art methods in both objective and visual quality. Ablation studies show that we need each module and how they work together to improve robustness at various degradation levels respectively. We look forward to working on two major directions. One is to extend our framework to more challenging real world remote sensing tasks, like multispectral and hyperspectral super-resolution. The other is to use cross-modal priors like geographic information and semantic labels in order to improve the realism and structural consistency of reconstruction.We believe that the presented work provide a solid theoretical and methodological basis to achieve high-quality and robust remote sensing images.