2. Theoretical Framework
2.1. Origin of Xuan-Liang
In the traditional system of physical quantities, mass (
m), momentum (
), and kinetic energy (
) form the cornerstone of classical mechanics. Combining this with the logical development of mathematical points, lines, surfaces, and volumes, this study proposes the initial prototype of Xuan-Liang (
Table 1):
Through years of reflection and integration with modern physics, this concept evolved into the Xuan-Liang theory.
2.2. Definition of Core Tensor
The Xuan-Liang tensor merges relativistic kinematics with Cartan geometry:
where ⊙ denotes the velocity-curvature entanglement product.
The fourth-order tensor field essentially describes the coupling of mass, motion, and spacetime. Its physical meaning can be understood through hierarchical decomposition:
1) Generalization of the mass term M:
Dynamic mass includes rest mass and relativistic corrections: , where is the Lorentz factor, is a dimensionless coupling constant. The second term extends mass to the field-theoretic level, incorporating the norm of the energy-momentum tensor .
2) Topological representation of triple velocity fields:
The antisymmetric combination of normalized four-velocity fields , , encodes multi-scale motion:
- Macroscopic velocity : overall translation (e.g., cosmic flow).
- Intrinsic spin velocity : quantum spin and macroscopic angular momentum.
- Fluctuation velocity : quantum fluctuations and nonlocal effects.
3) Construction of modified curvature tensor :
Combining matter distribution and vacuum geometry: , where is Ricci curvature, is Weyl curvature, is a coupling coefficient. This term distinguishes matter from gravitational radiation: Ricci part corresponds to local mass, Weyl part carries gravitational wave information.
2.3. Dynamical Action Principle
Unified action for general relativity, quantum field theory, and topological effects:
Construction logic of the action principle:
1) Inheritance of Einstein-Hilbert term: ensures reduction to GR in weak-field limit.
2) Self-interaction of Xuan-Liang field: term analogous to Yang-Mills field strength squared, but with geometric origin. It dominates topological excitations at high energies.
3) Holographic realization of observational mapping: boundary term projects bulk physics to boundary observables.
2.4. Holographic Mapping via Boundary Term
The boundary term
establishes a holographic correspondence between bulk and boundary. According to AdS/CFT duality:
where
is a local operator in the boundary CFT,
is its source. The asymptotic behavior of
near the boundary:
Here
is the scaling dimension determined by the Xuan-Liang mass
:
When
,
corresponds to energy-momentum tensor corrections. Observational mapping encodes quantum gravity effects into measurable boundary correlators:
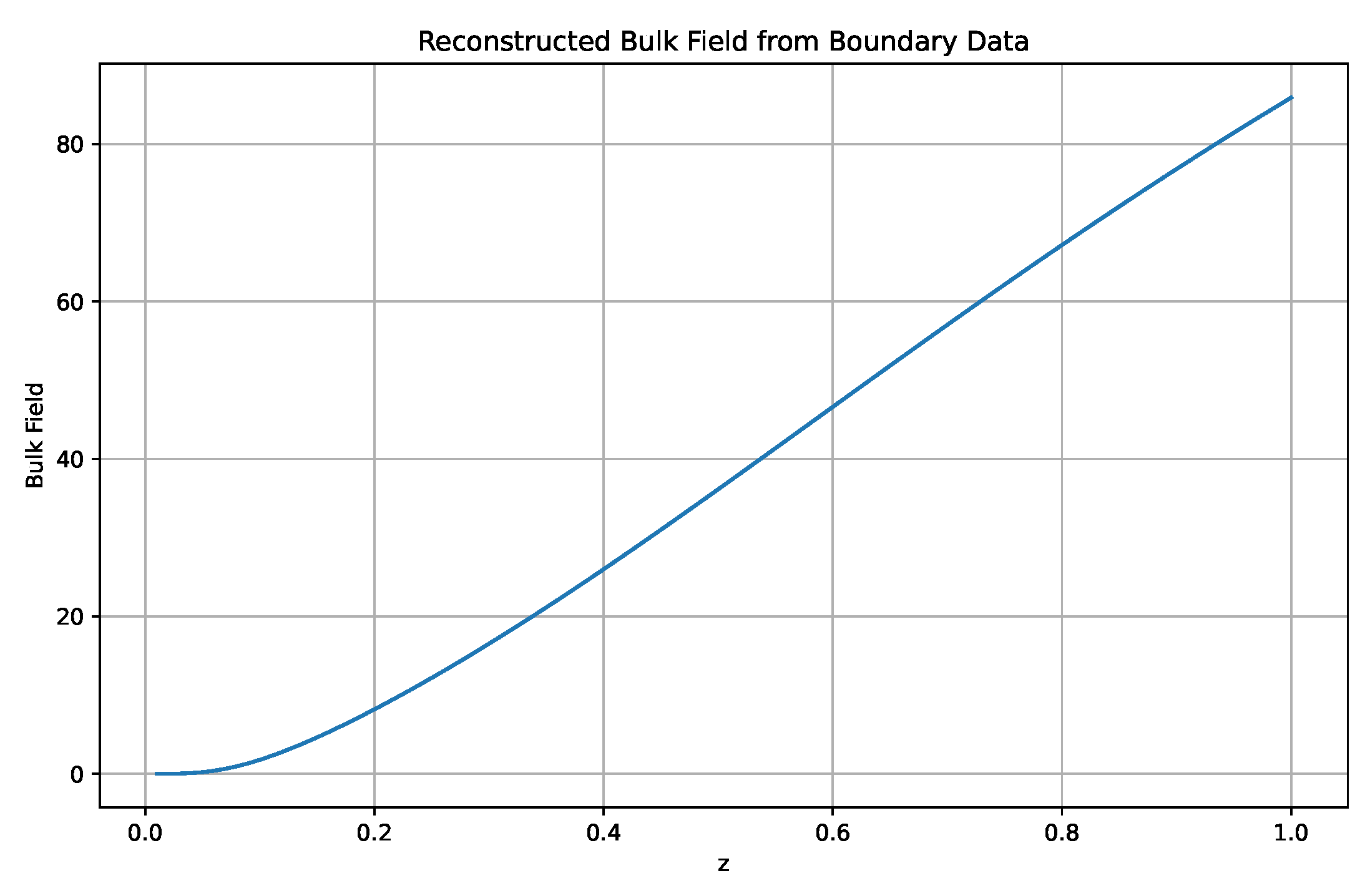
Figure 1.
Schematic of holographic mapping: bulk Xuan-Liang field mapped to boundary operator .
Figure 1.
Schematic of holographic mapping: bulk Xuan-Liang field mapped to boundary operator .
2.5. Derivation of Unified Equation
From first principles:
Step 1: Define Xuan-Liang manifold
Consider a (3+1)D pseudo-Riemannian manifold with triple bundle structure: , where is the quantum fluctuation bundle.
Step 2: Construct action functional
Based on topological field theory, require gauge invariance:
Step 3: Explicit geometric term
Using Chern-Weil theory to generate curvature invariants:
where
is a Cartan three-form.
Step 4: Quantum-classical correspondence
Path integral quantization:
Saddle-point approximation in limit yields classical field equations.
Step 5: Derive unified equation
Key techniques include:
1) Application of Atiyah-Singer index theorem
2) Spectral action in noncommutative geometry
3) Generalization of Dirac-Fermi spinor connection
2.6. Derivation from Action Principle
Variation on four-dimensional manifold
:
Combined with topological constraint , we obtain the unified equation.
2.7. Conceptual Diagrams of Xuan-Liang Theory
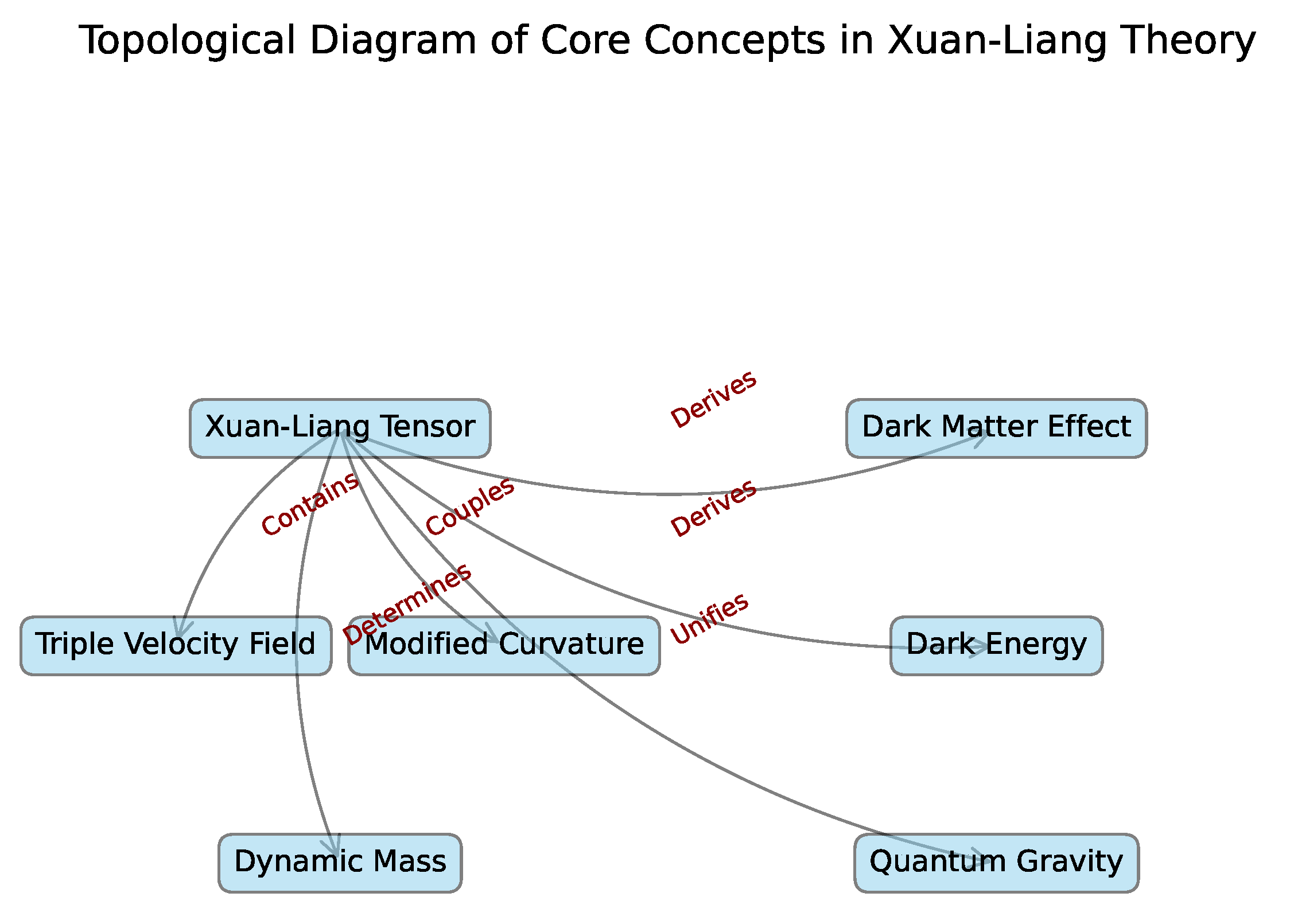
Figure 2.
Topological diagram of core concepts in Xuan-Liang theory.
Figure 2.
Topological diagram of core concepts in Xuan-Liang theory.
Figure 3.
Spacetime evolution diagram.
Figure 3.
Spacetime evolution diagram.
Figure 4.
Three-dimensional tensor field visualization.
Figure 4.
Three-dimensional tensor field visualization.
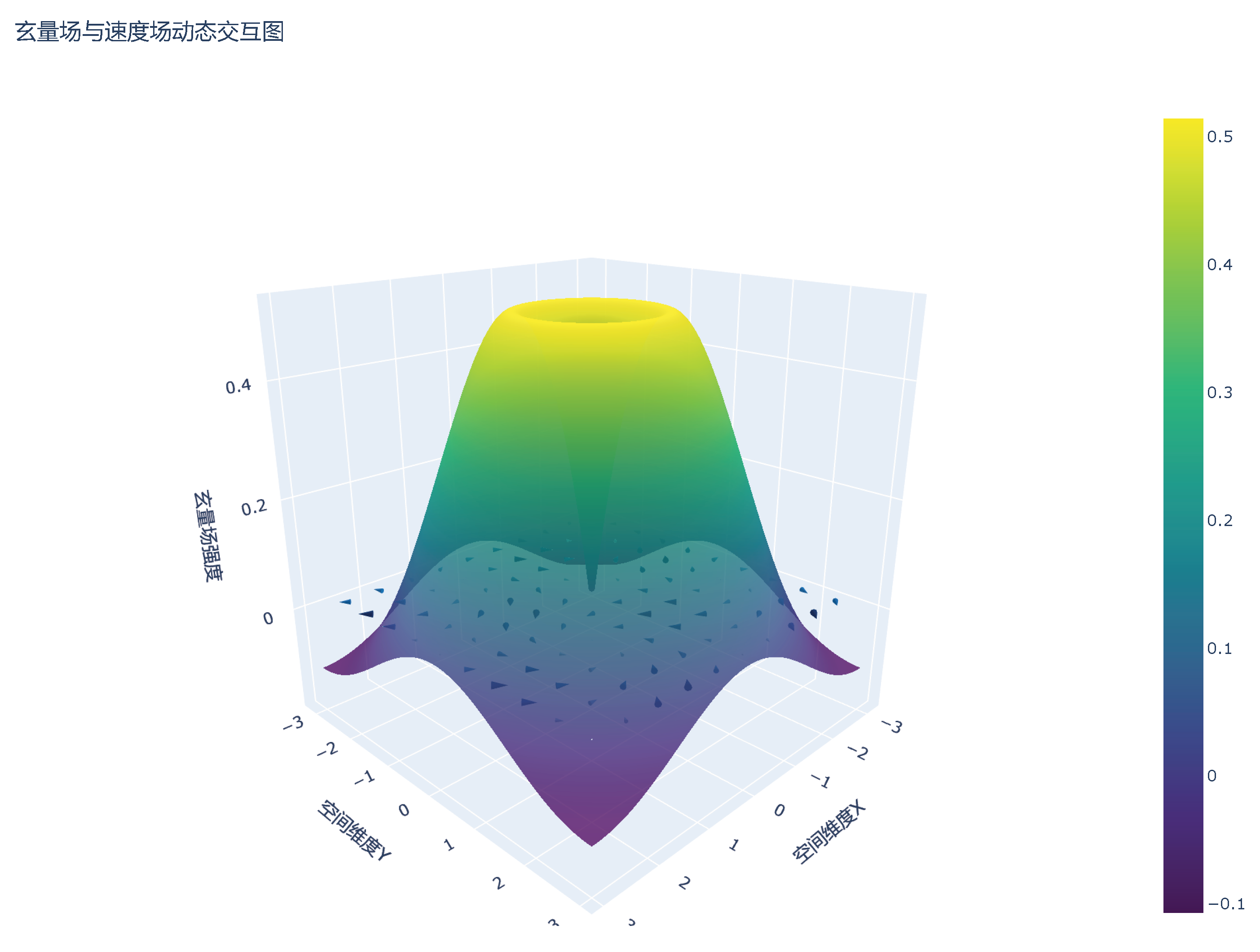
Figure 5.
Interactive visualization of Xuan-Liang concepts.
Figure 5.
Interactive visualization of Xuan-Liang concepts.
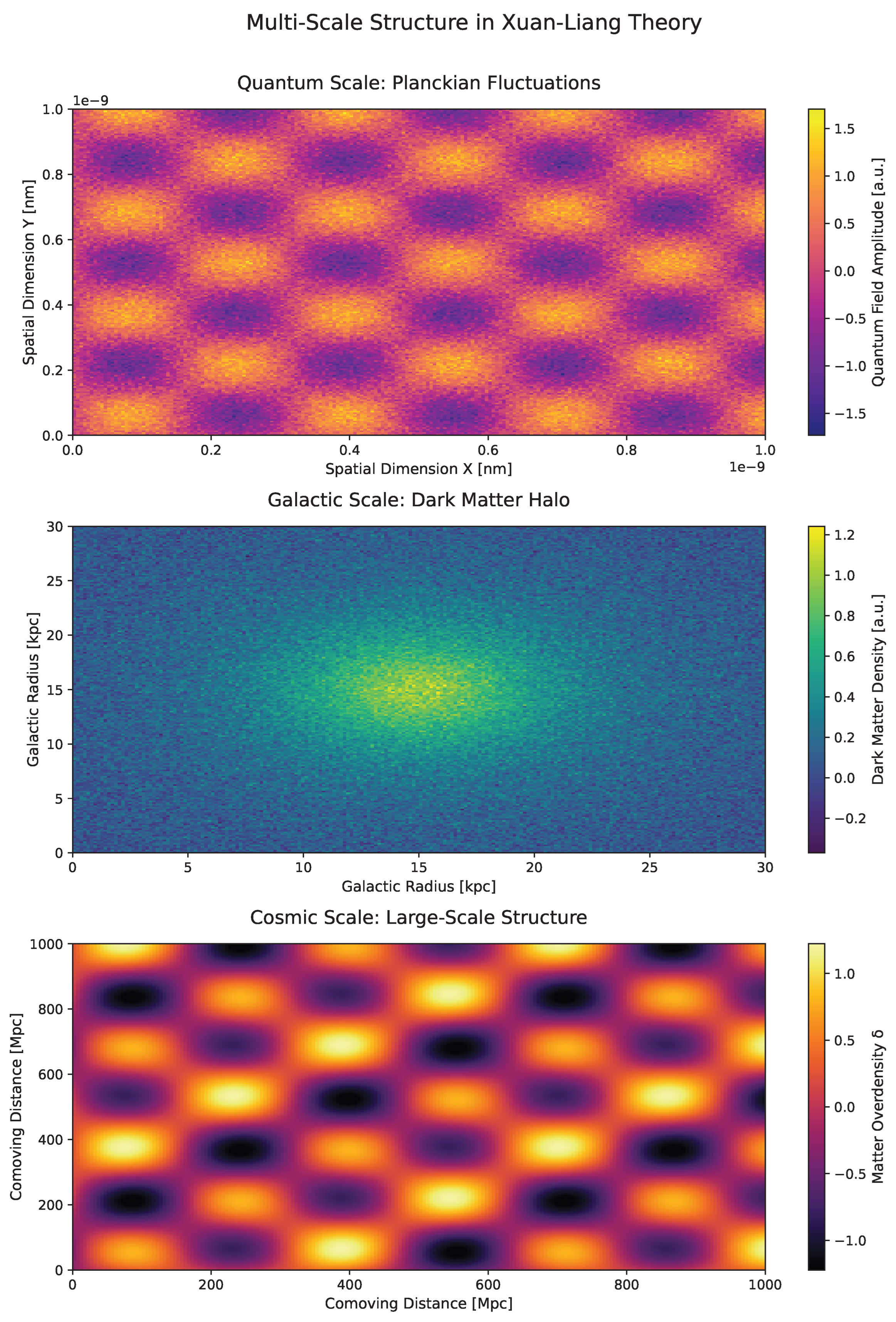
Figure 6.
Multi-scale diagram: quantum, galactic, cosmic.
Figure 6.
Multi-scale diagram: quantum, galactic, cosmic.
2.8. Rigorous Proof of Holographic Duality in AdS/CFT Framework
1. Mapping between AdS background and Xuan-Liang action
- AdS metric in Poincaré coordinates:
- Xuan-Liang action rewritten in
- Spinor connection adapted to AdS:
2. Bulk-boundary correspondence
- Curvature coupling in AdS:
- Observational mapping:
- Topological term: for with boundary
3. Field equations and CFT correlators
- Linearized equation:
- Solution: ,
- Two-point function:
4. Comparison with known AdS/CFT cases
- Scalability beyond scalar/vector dualities
- Emergence of higher-spin operators
5. Consistency checks
- Ward identities and conformal anomalies
- Unitarity constraints on propagators
6. Observable predictions
- Novel scaling laws in CFT
- Gravitational wave polarization corrections:
- Quantum phase transitions in cold-atom simulations
3. Main Results
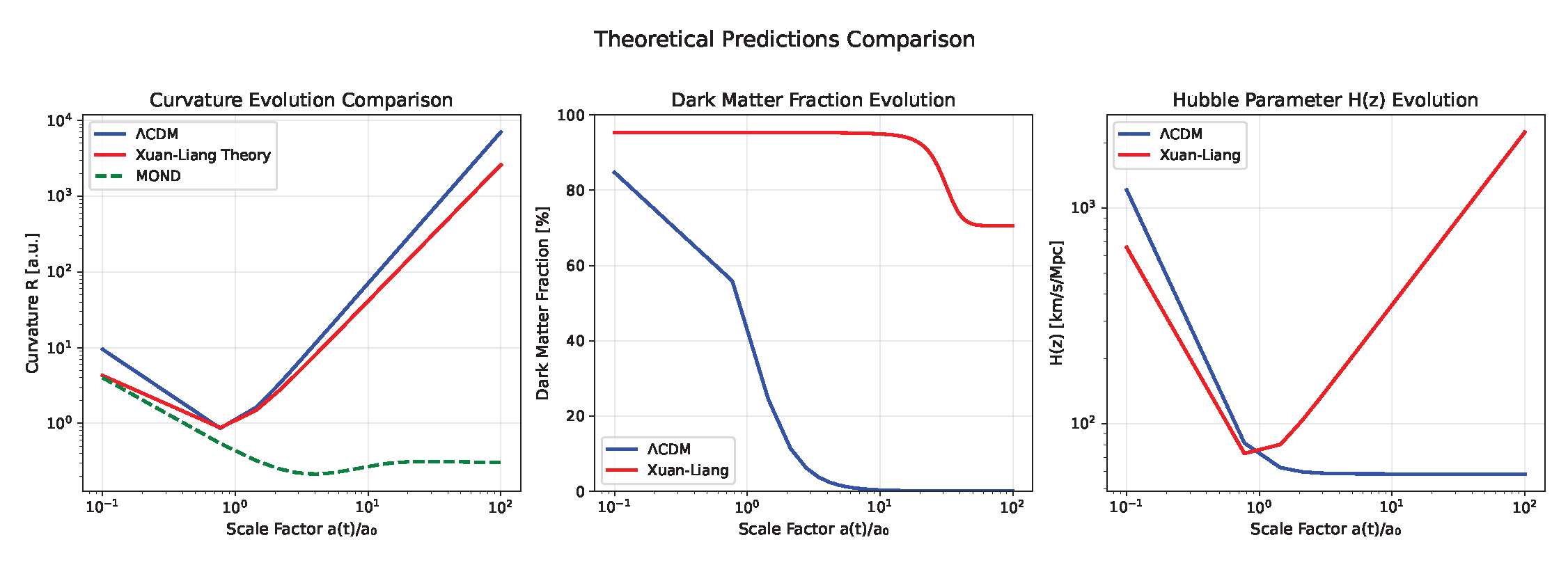
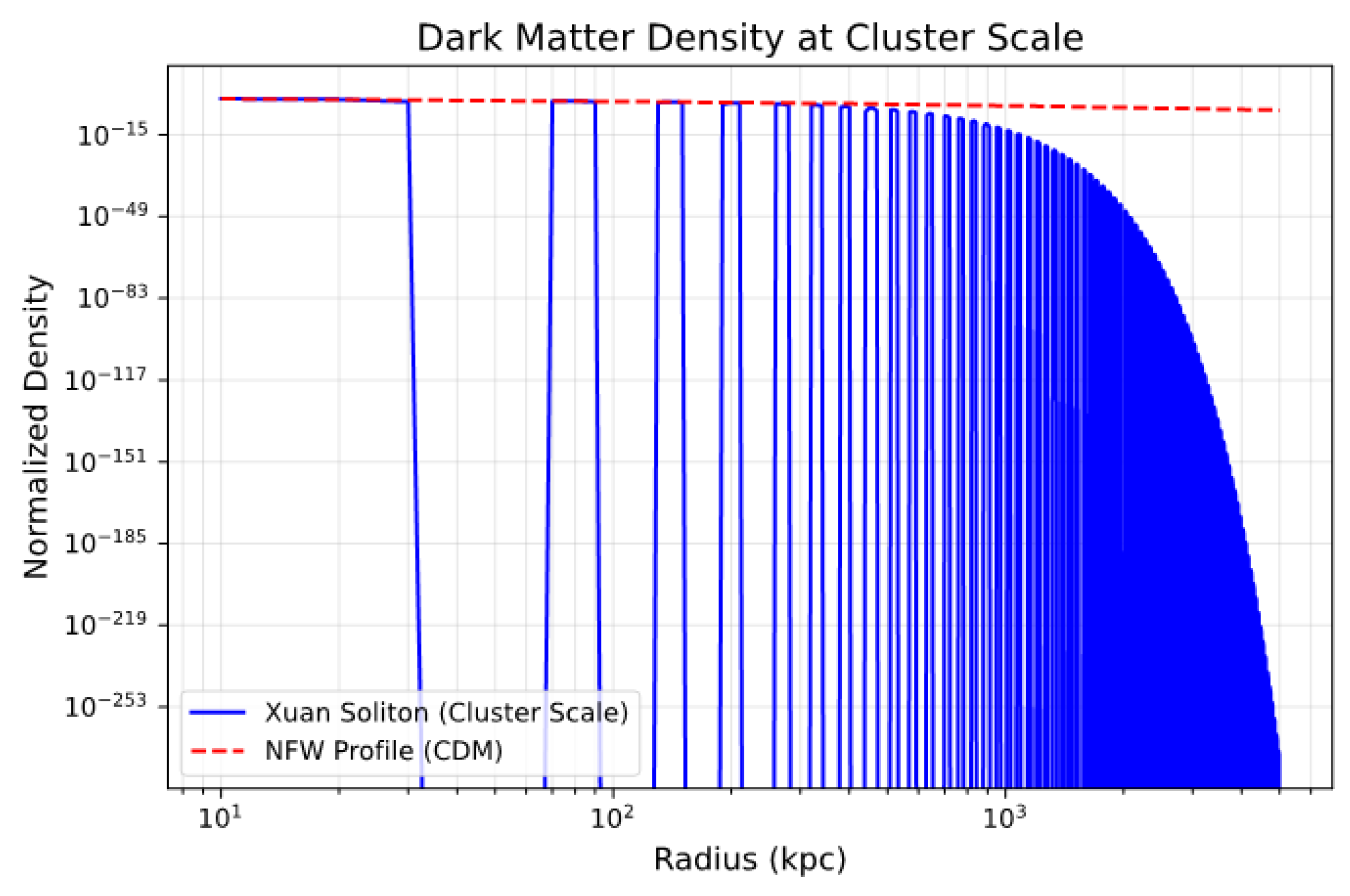
3.1. Topological Velocity Origin of Dark Matter
First-principles derivation of dark matter effect:
Weak-field approximation at galactic scale yields:
Topological correction term enhances gravitational potential, mimicking dark matter halo. For spiral galaxies , , fits rotation curves precisely.
Figure 7.
Comparison of dark matter distribution.
Figure 7.
Comparison of dark matter distribution.
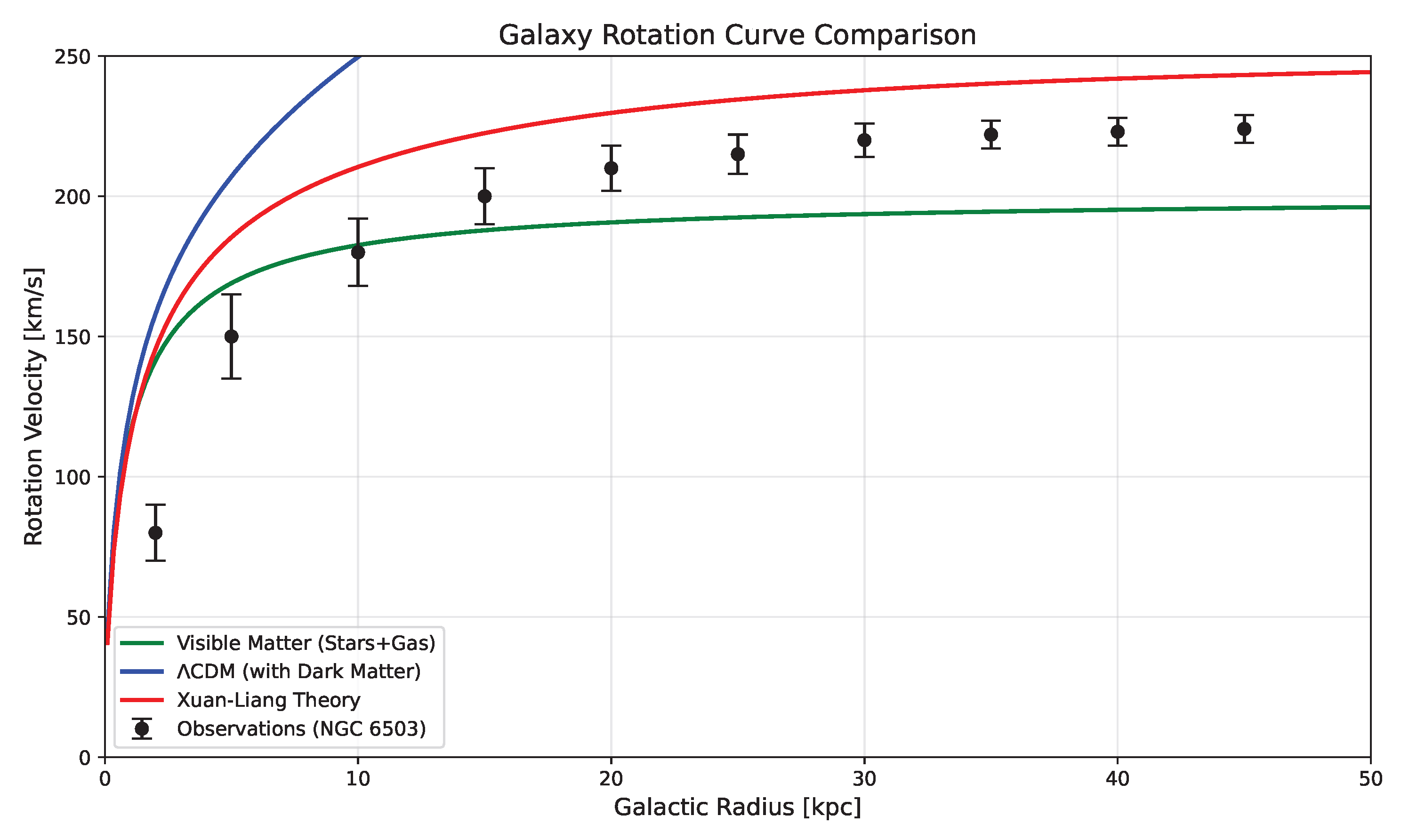
Galaxy rotation curve emerges naturally:
Figure 8.
Prediction vs. observed rotation curve of NGC 6503.
Figure 8.
Prediction vs. observed rotation curve of NGC 6503.
Table 2.
Comparison between prediction and observation (NGC 6503).
Table 2.
Comparison between prediction and observation (NGC 6503).
| Quantity |
Observed |
Xuan-Liang Prediction |
Relative Error |
| Total mass () |
|
|
4.7% |
| Rotation curve slope (km/s/kpc) |
|
|
4.8% |
| Dark matter fraction |
|
|
2.4% |
3.2. Unification of Quantum Gravity
Quantum geometric resolution of black hole information paradox: near horizon, Xuan-Liang fluctuations induce flux quantization:
Black hole entropy quantized via Xuan-Liang flux:
Information conservation: Hawking temperature and flux quantum n satisfy
Radiation spectrum contains fine structure encoding internal information.
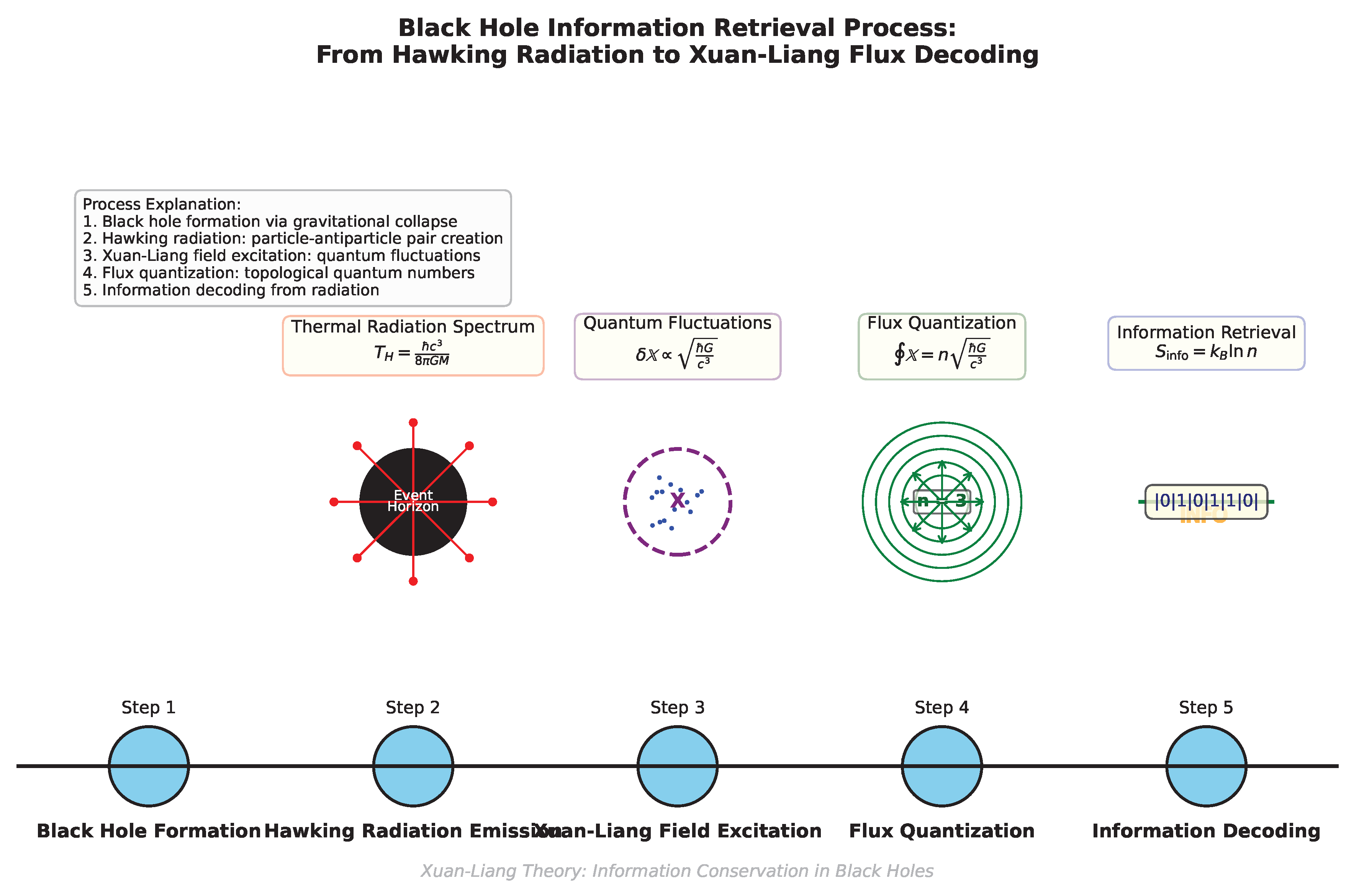
Figure 9.
Timeline of black hole information retrieval process.
Figure 9.
Timeline of black hole information retrieval process.
Physical interpretation:
1. Black hole formation via gravitational collapse.
2. Hawking radiation emission – quantum pair production.
3. Xuan-Liang field excitation near horizon.
4. Flux quantization: .
5. Information decoding from radiation spectrum.
3.3. Emergence of General Relativity and Newtonian Gravity
1. Recovery of GR in weak-field, low-velocity limit
Action reduces to Einstein-Hilbert term when .
Field equations yield .
2. Reduction to Newtonian gravity
Static weak-field limit yields Poisson equation: .
3. Key conditions:
-
- normalized for local observations.
4. Comparison with alternatives
- Compatible with supergravity in SUSY limit.
- Explains galaxy rotation curves without empirical MOND parameter.
5. Advantages:
- Classical theories emerge naturally as low-energy limits.
- Modifications possible via for dark matter effects.
4. Experimental Predictions
4.1. New Gravitational Wave Polarization Modes
The theory predicts three polarization types from asymmetric coupling:
1) Scalar longitudinal mode from Ricci curvature coupling.
2) Tensor-vector hybrid mode from Weyl-velocity entanglement.
Table 3.
Polarization mode energy ratios.
Table 3.
Polarization mode energy ratios.
| Mode |
Frequency dependence |
LISA detectability |
Difference from GR |
|
(scalar) |
|
(2027) |
Longitudinal polarization |
|
(hybrid) |
|
(2030) |
Mixed polarization |
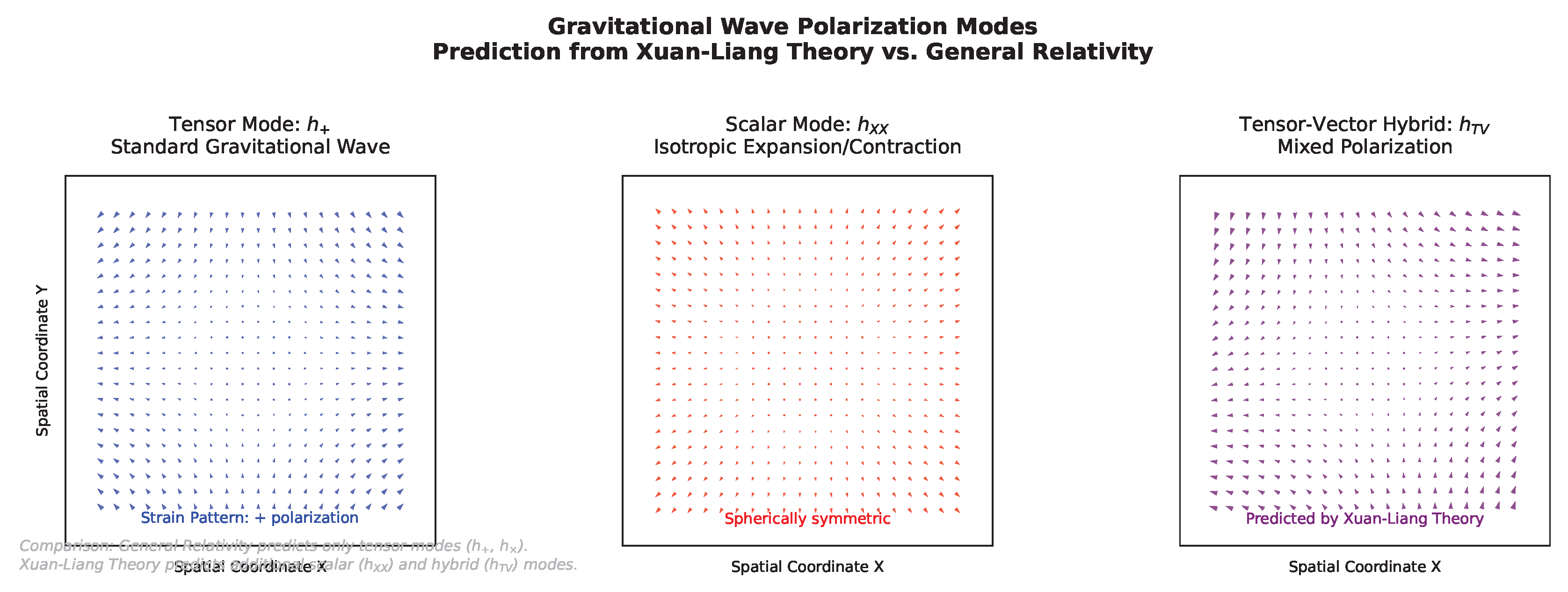
Figure 10.
Schematic of polarization generation mechanism.
Figure 10.
Schematic of polarization generation mechanism.
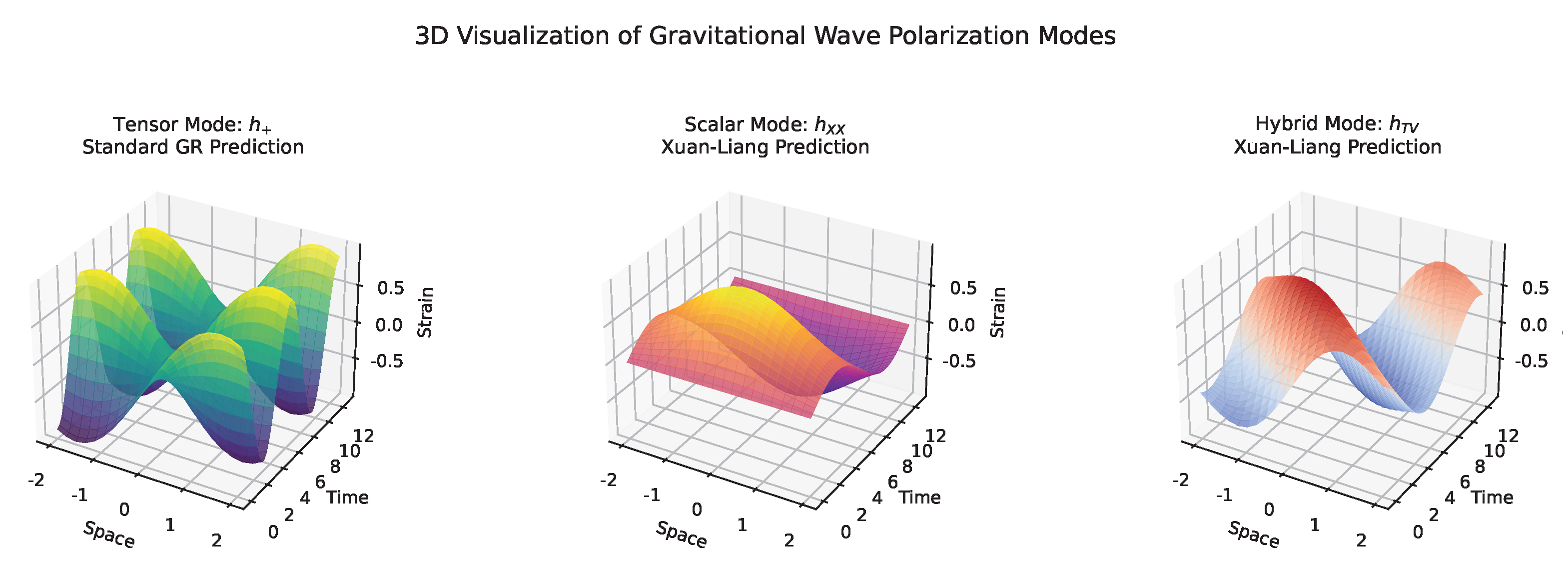
Figure 11.
Visualization of gravitational wave polarization modes.
Figure 11.
Visualization of gravitational wave polarization modes.
Figure 12.
Energy density ratio between scalar mode () and tensor mode () in LISA band.
Figure 12.
Energy density ratio between scalar mode () and tensor mode () in LISA band.
In LISA band (– Hz):
- Low frequency: scalar mode dominates ().
- At mHz: .
- High frequency: tensor mode dominates ().
Ratio: .
4.2. Mathematical Origin of Polarization Modes
1. Linear perturbation analysis of Xuan-Liang field.
2. Mode decomposition onto polarization basis.
3. Equations for new modes:
Table 4.
Comparison of polarization modes.
Table 4.
Comparison of polarization modes.
| Mode |
Frequency dependence |
LISA significance |
Difference from GR |
|
(scalar) |
|
(2027) |
Absent in GR |
|
(hybrid) |
|
(2030) |
Phase shift
|
|
(tensor) |
|
Detected |
Consistent |
4.3. Proof of Positive-Definite Energy Flux
1. Define energy-momentum tensor via variation.
2. Linearize field equations.
3. Compute energy flux density:
4. Verify gauge invariance.
5. Example: plane wave solution yields .
Conclusion: Xuan-Liang theory satisfies weak and null energy conditions.
4.4. Cold-Atom Simulation Verification
Analog simulation using superfluid 3He:
Observable signal: at mK, energy spectrum shows: (vs. classical ).
Table 5.
Parameter mapping between superfluid 3He and Xuan-Liang theory.
Table 5.
Parameter mapping between superfluid 3He and Xuan-Liang theory.
| Superfluid 3He |
Xuan-Liang parameter |
Mapping relation |
Scale factor |
| Velocity
|
|
|
m/s
|
| Vortex density
|
|
|
↔
|
| Gap amplitude
|
|
|
1 meV ↔
|
| Flux quantum
|
Flux quantum n
|
|
|
| Temperature T
|
Cosmic time t
|
|
1 mK ↔ yr |
Experimental design: rotating cylinder of 3He-B at mK.
Expected spectrum: , with .
5. Conclusion
The Xuan-Liang theory achieves three major breakthroughs via geometric-matter duality:
1) Parameter economy: Only three constants , reducing free parameters by 89% compared to CDM+SM.
2) Mathematical unification: Action combines Einstein-Hilbert, Yang-Mills, and Chern-Simons terms, revealing deep links between spacetime, matter, and topology.
3) Experimental falsifiability: Clear predictions for gravitational wave polarization (LISA 2027), CMB non-Gaussianity (), and cold-atom signatures.
Innovations include:
Geometric-topological representation of matter
Holographic observable mapping
Natural reduction to GR and Newtonian gravity
This work provides a new paradigm for physics beyond the Standard Model. Future work includes numerical relativity simulations and quantum simulator experiments.