Dark Sector Searches at e⁺e⁻ Colliders

1. Introduction

The Standard Model (SM) [1,2] of particle physics has been remarkably successful in describing the fundamental particles and their interactions, including the mechanism by which they acquire mass [3,4]. It has been well tested by several collider experiments. Despite its success, the SM is widely recognized as an incomplete theory because there are still some phenomena that can not be explained by SM. For instance, it does not explain the origin of tiny neutrino masses [5] or the nature of dark matter (DM) [6]. The former has been established by the discovery of neutrino oscillation [7], which imply that neutrinos have masses below the eV scale. The latter has been indicated by a variety of evidence, such as the galactic rotation curve [8], galaxy cluster, and the large-scale structure of the universe [9]. These issues strongly suggest the need for physics beyond the SM (BSM). Extensions of the SM are therefore required to solve these outstanding issues, including the missing description of DM [6] and neutrino oscillation [5,7].

DM accounts for about $26.8\%$ of the total matter density of the Universe. It does not interact via the strong or electromagnetic interaction, and its presence so far can be inferred only through gravitational effect. Therefore, the nature of DM remains unknown. Experimental information on DM is needed to explain recent astrophysical observations, including the velocity profiles of galactic rotation curve [8] and the fundamental characteristics of our Universe [9]. A dynamical mechanism, baryogenesis, has been recently proposed for GeV-scale DM carrying baryon number, offering an attractive framework for simultaneously addressing the sources of DM and the matter–antimatter asymmetry of the Universe [10]. Additionally, the presence of DM particles may enhance the branching fraction of flavor-changing neutral-current (FCNC) processes [11], which are highly suppressed by the Glashow–Iliopoulos–Maiani mechanism [2], making them accessible to the current generation of collider experiments.

An extension of the SM is needed to accommodate the DM. One of the most popular scenarios is a dark sector (or “hidden sector”) that arises from several well-motivated theories, including string-inspired models [12], supersymmetry (SUSY) [13], and extensions featuring extra $U\left(1\right)$ symmetries [14]. In these scenarios, dark sector fields interact only feebly with the SM particles, often through renormalizable operators or high-dimension Wilson coefficient operators [15]. According to this hidden sector, the DM may couplue to the SM particles via these portals: vector, axion, Higgs, and neutrino [17]. The corresponding portals predict new-physics particles that are categorized as dark photon, axion-like particle, light Higgs boson, and sterile neutrinos. If the masses of these particles lie in the MeV–GeV range, they can be probed at high-intensity $e^{+}{e}^{-}$ collider experiments, such as BaBar [18], Belle/Belle II [16], and BESIII [19]. Complementary efforts are ongoing and planned at future colliders, including the Circular Electron–Positron Collider (CEPC) [20] and the Super Tau–Charm Factory (STCF) [21] in China, which promise to substantially extend the current sensitivity to rare and invisible decays.

This report reviews recent progress in searches for new physics at $e^{+}{e}^{-}$ collider experiments, with an emphasis on portal-based scenarios. It outlines the theoretical motivations for these models, summarizes the experimental results from both existing and planned experiments, and discusses future prospects. These studies represent a cornerstone of the ongoing effort to uncover the nature of dark matter and other phenomena beyond the SM.

2. Vector Portal

The vector portal introduces a new abelian $U\left(1\right)$ gauge boson, commonly referred to as a dark photon ($A^{\prime }$ or ${\gamma }^{\prime }$) [22], which shares similarities with the ordinary photon but may possess mass and interact with dark matter particles [17]. In this framework, dark matter particles can annihilate into a pair of dark photon, which subsequently decay into SM particles, satisfying the constraints of recent astrophysical observations [9]. Dark photons are broadly categorized into two distinct types: massive dark photon, which arises when the additional $U\left(1\right)$ gauge symmetry is spontaneously broken, and massless dark photon, where the symmetry remains unbroken [23,24]. Each category exhibits unique phenomenological signatures and is probed through different experimental approaches.

2.1. Massive Dark Photon

The dark photon can acquire mass through a hidden mechanism, such as the Stückelberg mechanism [25] or a dark Higgs mechanism [26], where spontaneous symmetry breaking of the $U\left(1\right)$ gauge group introduces a dark Higgs boson $h^{\prime }$. The corresponding Lagrangian for the minimal dark sector is given by [27]:

$$\mathcal{L}=-{\displaystyle \frac{1}{4}}{F}_{\mu \nu }{F}^{\mu \nu }-{\displaystyle \frac{1}{4}}{F}_{\mu \nu }^{\prime }{F}^{\prime \mu \nu }-{\displaystyle \frac{ϵ}{2}}{F}_{\mu \nu }{F}^{\prime \mu \nu }+{\displaystyle \frac{1}{2}}{m}_{A^{\prime }}^2{A}_{\mu }^{\prime }{A}^{\prime \mu }+A_{\mu }^{\prime }{J}_{\mathrm{dark}}^{\mu }+{\mathcal{L}}_{\mathrm{mass}},$$

(1)

where $F_{\mu \nu }$ and $F_{\mu \nu }^{\prime }$ represent the field strength tensors for the SM photon and dark photon, respectively. The parameter $ϵ$ quantifies the kinetic mixing between the SM and dark sector photons, while $m_{A^{\prime }}$ denotes the dark photon mass. The dark current $J_{\mathrm{dark}}^{\mu }$ describes interactions with dark sector fermions or scalars, and ${\mathcal{L}}_{\mathrm{mass}}$ includes terms related to mass generation and possible spontaneous symmetry-breaking effects.

2.1.1. Abelian Dark Photon

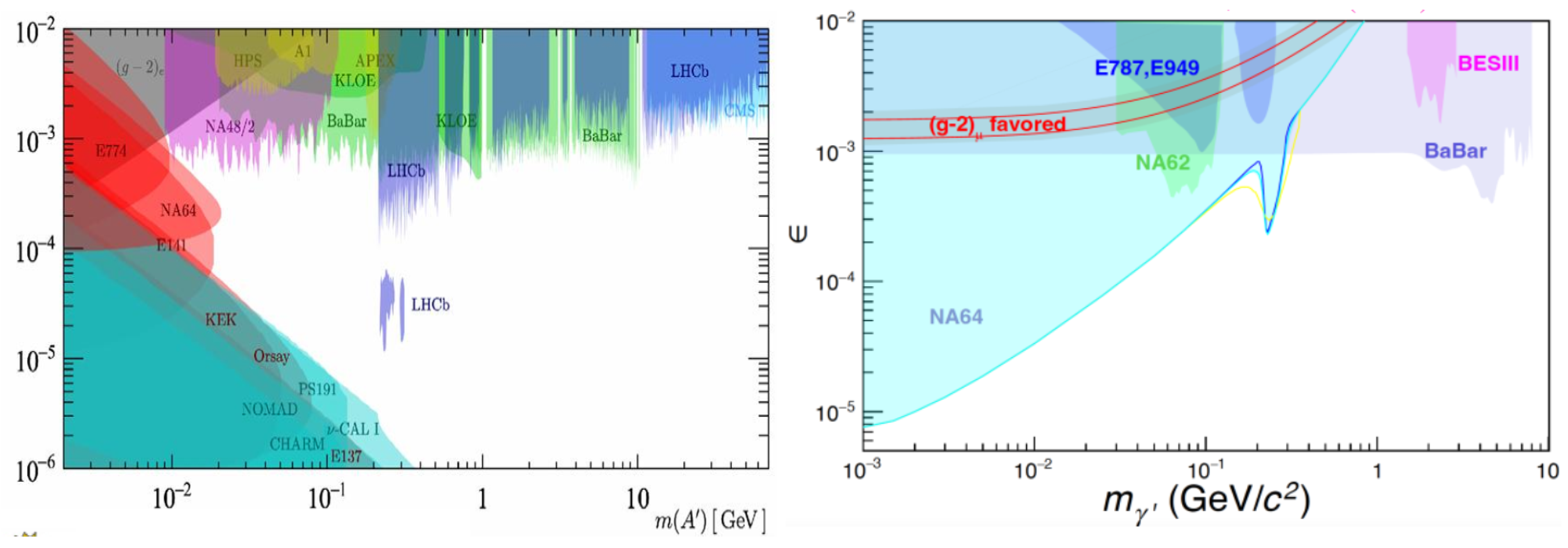
The spontaneous breaking of an Abelian $U\left(1\right)$ gauge group generates mass for the dark photon $A^{\prime }$ [22]. The effective coupling strength between the massive dark photon and SM photon is given by ${\alpha }^{\prime }\approx {ϵ}^2\alpha$, where $\alpha$ and ${\alpha }^{\prime }$ represent the fine structure constants of the SM and dark sectors, respectively [28,29]. Astrophysical constraints typically restrict the massive dark photon mass to the sub-GeV to few-GeV range [29,30]. Constraints on $ϵ$ have been placed on visible $A^{\prime }$ decays by beam-dump [31], fixed-target [32,33], $e^{+}{e}^{-}$ colliders [34,35,36], rare-meson decay [36], and LHCb [38] experiments. The most stringent limits on $ϵ$, especially below $\mathcal{O}\left({10}^{-3}\right)$, mainly come from NA48 experiment in the $m_{A^{\prime }}$ range of $[10,120]$ MeV, KLOE-2 experiment [36] in the $\rho -\omega$ mass region, BaBar experiment [34] in $0.12<m_{A^{\prime }}<8\mathrm{GeV}$ and LHCb experiment [38] in the high mass region, as seen in Figure 1 (left). BESIII has extended these searches to lower mass regions ($1.5<m_{A^{\prime }}<3.4\mathrm{GeV}$) [35]. For invisibly decaying dark photons, constraints on $ϵ$ appear from kaon decays [39], missing energy events in electron-nuclues scattering [40] and $e^{+}{e}^{-}$ collider experiments [41,42]. BaBar’s result [41] is more stringent in the higher mass region, as seen in Figure 1 (right).

2.1.2. Non-Abelian Dark Sector

An extended theory featuring a non-Abelian $SU\left(2\right)\times U\left(1\right)$ gauge group introduces four gauge bosons: ${\gamma }^{\prime }$ ($A^{\prime }$), $W_D$, $W_D^{\prime }$, and $W_D^{\prime \prime }$ [29]. The mass hierarchy among these particles is unconstrained, allowing for light gauge bosons and potentially a light dark Higgs boson. This scenario enables probing of such a light dark matter particles at low-energy $e^{+}{e}^{-}$ colliders and fixed-target experiments through signatures including $e^{+}{e}^{-}\to W^{\prime }{W}^{\prime }\to l^{+}{l}^{-}{l}^{+}{l}^{-}$ (mediated by a virtual $A^{\prime }$) and $e^{+}{e}^{-}\to \gamma A^{\prime }(\to W^{\prime }{W}^{\prime })\to \gamma l^{+}{l}^{-}{l}^{+}{l}^{-}$, along with a Higgs-strahlung process that may yield missing energy. BaBar has conducted searches for a narrow di-lepton resonance in four-lepton final states using 536 fb⁻¹ of data. No significant signal events are observed, yielding $90\%$ CL upper limits on production cross sections: $\sigma (e^{+}{e}^{-}\to W^{\prime }{W}^{\prime }\to e^{+}{e}^{-}{e}^{+}{e}^{-})<(15-70)$ ab, $\sigma (e^{+}{e}^{-}\to W^{\prime }{W}^{\prime }\to e^{+}{e}^{-}{\mu }^{+}{\mu }^{-})<(15-40)$ ab, and $\sigma (e^{+}{e}^{-}\to W^{\prime }{W}^{\prime }\to {\mu }^{+}{\mu }^{-}{\mu }^{+}{\mu }^{-})<(11-17)$ ab for $W^{\prime }$ masses between 0.24 and 5.3 GeV/$c^2$ [43]. Under the assumption of equal $W^{\prime }$ coupling to electrons and muons, a combined upper limit of $\sigma (e^{+}{e}^{-}\to W^{\prime }{W}^{\prime }\to l^{+}{l}^{-}{l}^{\prime +}{l}^{\prime -})<(25-60)$ ab was established.

2.2. Massless Dark Photon

A massless dark photon (${\gamma }^{\prime }$) can couple to the SM fermions through a higher-dimensional operator. Reference [44] introduces a dimension-six operator enabling an effective coupling between the dark photon field strength and SM fermions, leading to FCNC processes. Unlike the massive case, this coupling arises from a term proportional to $1/{\Lambda }_{\mathrm{NP}}^2$, where ${\Lambda }_{\mathrm{NP}}$ represents the new-physics scale, rather than through kinetic mixing.

BESIII has recently conducted searches for massless dark photon in the following decay channels:

• ${\Sigma }^{+}\to p+\mathrm{invisible}$ via $J/\psi \to {\Sigma }^{+}{\overline{\Sigma }}^{-}$ using 10 billion $J/\psi$ events [45].
• ${\Lambda }_c^{+}\to p{\gamma }^{\prime }$ through $e^{+}{e}^{-}\to {\Lambda }_c^{+}{\overline{\Lambda }}_c^{-}$ using 4.5 fb⁻¹ of data at $\sqrt{s}=4.6-4.6999$ GeV [46].
• $D^0\to \omega {\gamma }^{\prime }$ and $D^0\to \gamma {\gamma }^{\prime }$ using 7.9 fb⁻¹ of $\psi \left(3770\right)\to D^0{\overline{D}}^0$ data [47].

These analyses employed a double tag technique [48], where one baryon or meson is reconstructed in its dominant hadronic decay modes while the partner decays to the signal channel of interest. 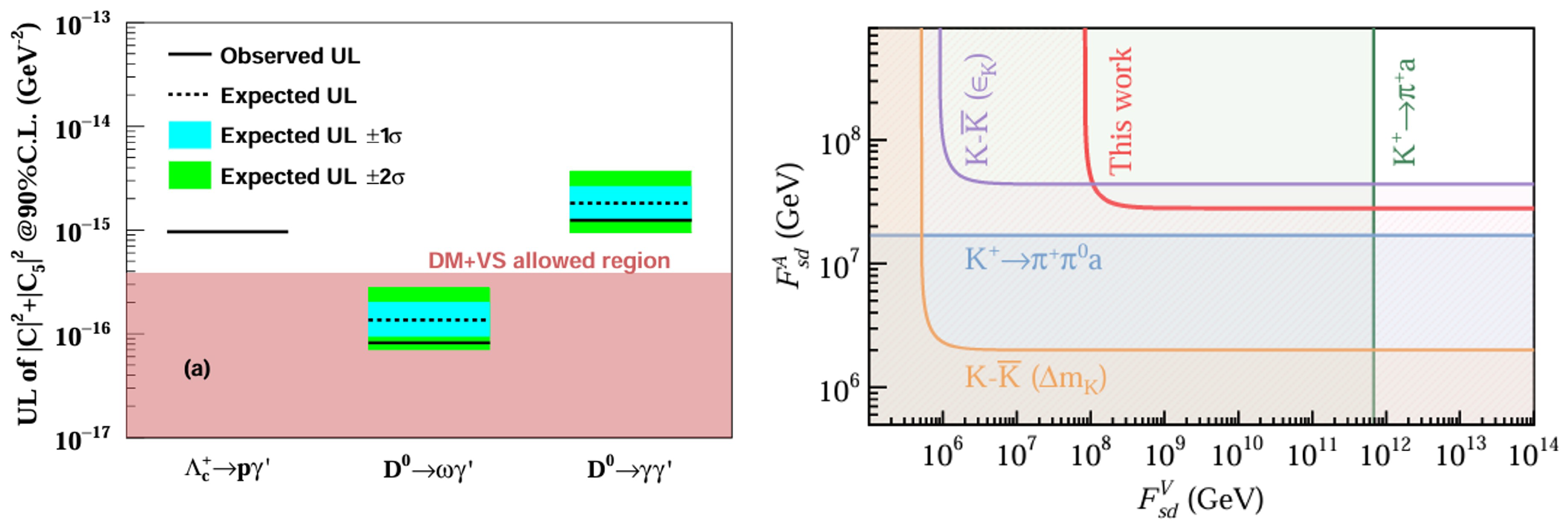No significant signal events are observed, establishing 90% CL upper limits of $\mathcal{B}({\Sigma }^{+}\to p+\mathrm{invisible})<3.2\times {10}^{-5}$ [45], $\mathcal{B}({\Lambda }_c^{+}\to p{\gamma }^{\prime })<8\times {10}^{-5}$ [46], $\mathcal{B}(D^0\to \omega {\gamma }^{\prime })<1.1\times {10}^{-5}$, and $\mathcal{B}(D^0\to \gamma {\gamma }^{\prime })<2.0\times {10}^{-6}$ [47]. These results improve constraints on the effective coupling parameter to ${\left|C\right|}^2+{\left|C_5\right|}^2<8.2\times {10}^{-17}{\mathrm{GeV}}^{-2}$ [47], reaching regions allowed by DM and vacuum stability considerations and surpassing previous ${\Lambda }_c^{+}\to p{\gamma }^{\prime }$ limits by an order of magnitude (Figure 2, left). The ${\Sigma }^{+}\to p+\mathrm{invisible}$ limit improves constraints on the axial–vector coupling $F_{sd}^A$ beyond bounds from kaon-mixing and CP-violation measurements [45] (Figure 2, right).

3. Higgs Portal

In the last decade, both the ATLAS and CMS experiments confirmed the Higgs mechanism [3], which provides masses to SM particles via spontaneous breaking of electroweak symmetry [4]. Both experiments have also been able to map out its properties in detail and find consistency with the assumption that the Higgs couples to SM particles proportionally to their mass. Nevertheless, the origin of the majority of mass in the universe remains a mystery, because it is not in the form of known particles but in a completely new form called DM [6]. If DM is composed of elementary particles, we can hope to detect these particles in the laboratory or infer their properties from astrophysical observations [9]. A similar Higgs mechanism [26] may give mass to a dark matter candidate and to the gauge boson mediating its interactions, such as a dark photon. An extended sector beyond the SM may also be required to solve the little hierarchy problem of the SM [49]. At low-energy $e^{+}{e}^{-}$ collider experiments, the following scenarios related to BSM Higgs or spin-0 scalar searches are well motivated and explored.

3.1. Light Higgs Boson

A light Higgs boson is predicted by many models beyond the SM, such as the Next-to-Minimal Supersymmetric Standard Model (NMSSM) [50], which extends the Higgs sector of the SM to include additional Higgs fields. The Higgs sector of the NMSSM contains three $CP$-even, two $CP$-odd, and two charged Higgs bosons. The mass of the lightest $CP$-odd Higgs boson, $A^0$, could be smaller than twice the mass of the bottom or charm quark, thus making it accessible via radiative decays of ${\rm Y}\left(nS\right)$ ($n=1,2,3$) or $J/\psi$ [51]. The couplings of the Higgs field to up- and down-type quark pairs are proportional to $cot\beta$ and $tan\beta$, respectively, where $tan\beta$ represents the ratio of the vacuum expectation values of the up- and down-type Higgs doublets. The branching fractions of ${\rm Y}\left(1S\right)\to \gamma A^0$ and $J/\psi \to \gamma A^0$ are predicted to be in the ranges of ${10}^{-7}$–${10}^{-3}$ and ${10}^{-9}$–${10}^{-7}$, respectively, depending on $m_{A^0}$, $tan\beta$, and other NMSSM parameters [52].

The branching fractions of $V\to \gamma A^0$ are related to the Yukawa coupling of $A^0$ to down- or up-type quarks $g_q^2$, as described by the formula in Eq. (1) of Ref. [53]. Searches for a light Higgs boson decaying to various fermion-pair final states in radiative ${\rm Y}\left(nS\right)$ have been performed by various B-factory related experiments, such as BaBar [54] and Belle [55] experiments. Though these experiments have reported null results, but, their results have placed strong exclusion limits on the effective Yukawa coupling of the Higgs field to bottom-type quark pairs ($g_b$). According to Ref. [56], BaBar’s results for $A^0\to {\mu }^{+}{\mu }^{-}$ are much more sensitive than those for hadronic, di-tau, and invisible decays of $A^0$. 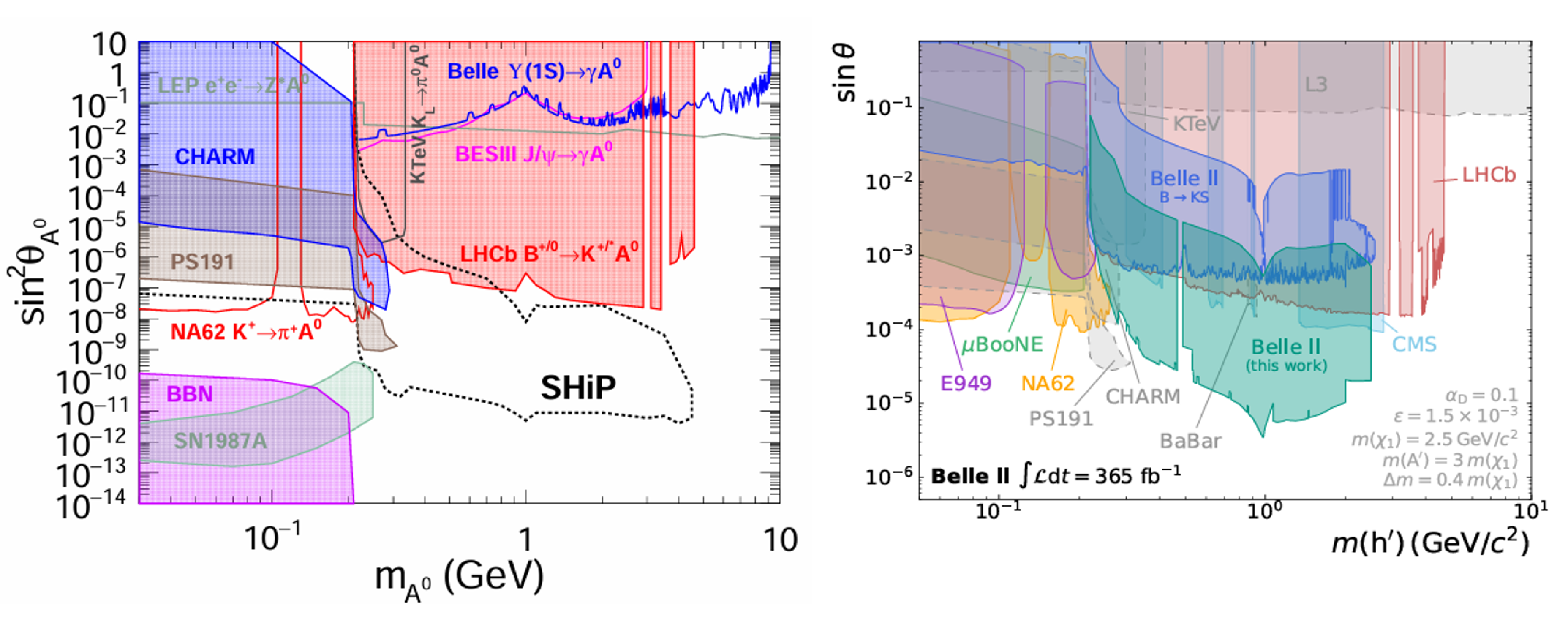The exclusion limits on $g_c$, on the other hand, have been set by BESIII experiment, which has performed searches for $A^0$ decaying to invisible final states and muon pairs. The BESIII measurement [53,57] is comparable to those from BaBar [54] and Belle [55] measurements in the low-mass region, as seen in Figure 3 (left) of exclusion limits on the mixing angle (${sin}^2{\theta }_{A^0}$) as a function of $A^0$ mass.

3.2. Dark Higgs Boson

In a minimal model, dark force carriers such as the dark photon acquire their masses via the Higgs mechanism, introducing a dark Higgs boson $h^{\prime }$ to the theory [26]. The mass hierarchy between $h^{\prime }$ and dark force carriers is not constrained, and the dark Higgs boson could be light as well. Searches for the dark Higgs boson have been performed by BaBar [58], Belle [59], and KLOE-2 [60] experiments via the Higgs-strahlung process $e^{+}{e}^{-}\to A^{\prime }{h}^{\prime }$. There are three main cases: (a) $m_{h^{\prime }}<m_{A^{\prime }}$, where $h^{\prime }$ is long-lived and decays into lepton pairs or hadrons; (b) $m_{A^{\prime }}<m_{h^{\prime }}<2m_{A^{\prime }}$, where $h^{\prime }$ decays into two dark photons that subsequently decay into lepton pairs; and (c) $m_{h^{\prime }}>2m_{A^{\prime }}$, where $h^{\prime }\to A^{\prime }{A}^{\prime }$. Here $m_{h^{\prime }}$ and $m_{A^{\prime }}$ are the masses of the dark Higgs and dark photon, respectively. No evidence of dark Higgs production has been found, and $90\%$ CL upper limits on ${\alpha }_D{ϵ}^2$ have been set as a function of $m_{A^{\prime }}$ for various values of $m_{h^{\prime }}$. The upper limits on ${\alpha }_D{ϵ}^2$ range from ${10}^{-9}$ to ${10}^{-5}$, depending on $m_{A^{\prime }}$ and $m_{h^{\prime }}$ [58,59,60].

Inelastic dark matter models that feature two dark matter particles and a massive dark photon can reproduce the observed relic dark matter density without violating cosmological limits [9]. The mass splitting between the two dark matter particles is induced by a dark Higgs field and its corresponding dark Higgs boson $h^{\prime }$. Belle II has recently performed a search for the dark Higgs boson produced in association with inelastic dark matter using a 365 fb⁻¹ data sample [61]. Belle II uses events with up to two displaced vertices and missing energy, produced in $e^{+}{e}^{-}$ collisions via $e^{+}{e}^{-}\to h^{\prime }(\to x^{+}{x}^{-})A^{\prime }(\to {\chi }_1{\chi }_2(\to {\chi }_1{e}^{+}{e}^{-}))$, where $x^{+}{x}^{-}$ indicates ${\mu }^{+}{\mu }^{-}$, ${\pi }^{+}{\pi }^{-}$, or $K^{+}{K}^{-}$. The search for a signal is performed by looking for a narrow enhancement in the $m_{x^{+}{x}^{-}}$ distribution. The remaining events in data after selection are 0, 8, and 1 for ${\mu }^{+}{\mu }^{-}$, ${\pi }^{+}{\pi }^{-}$, and $K^{+}{K}^{-}$ final states, respectively. The $95\%$ CL upper limits on the mixing angle between the SM Higgs and $h^{\prime }$, as shown in Figure 3 (right), as well as on the dimensionless variable y, are set as functions of $m_{h^{\prime }}$ and $m_{{\chi }_1}$, respectively [61].

3.2.1. Muon-Philic Scalar or Vector Bosons

A new type of $L_{\mu }-L_{\tau }$ extension of the SM is desirable to resolve the long-standing muon anomalous magnetic moment [62], the tensions in flavor observables reported by B-factory experiments [63], and to explain the dark matter phenomena and the relic abundance of dark matter [64]. This model gauges the difference between the muon and the $\tau$-lepton number through the introduction of new massive vector ($X_1$) or leptophilic scalar ($X_0$) or pseudocalar bosons [65]. The $X_{0,1}$ could also mediate the interactions between the SM and the dark sector. They couple exclusively to second- and third-generation leptons ($\mu ,{\nu }_{\mu },\tau ,{\nu }_{\tau }$) with coupling strengths $g^{\prime }0,1$. 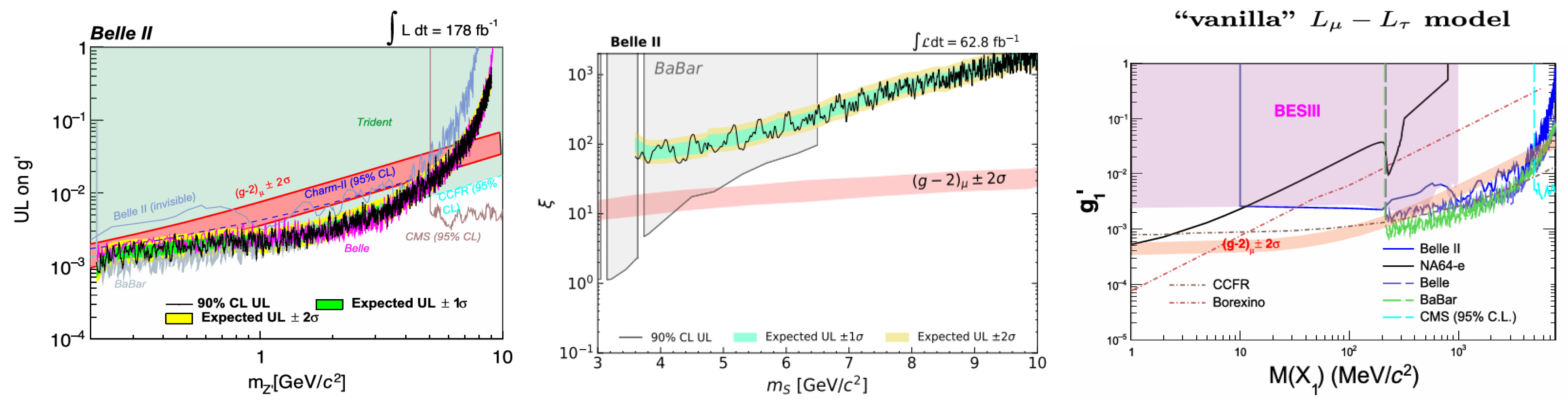Experimentally, the searches for $X0,1$ decaying to a pair of muons have been reported by the BaBar [66], CMS [67], and Belle II [68] experiments. The BaBar [66] measurement is more stringent in the low-mass region, as seen in Figure 4 (left).

The leptophilic scalar decaying into electrons and muons is constrained by Belle up to masses of approximately 6.5 GeV/$c^2$ [69], and above this, the leptophilic scalar decaying into a $\tau$-pair is constrained by Belle II in $e^{+}{e}^{-}\to {\mu }^{+}{\mu }^{-}{\tau }^{+}{\tau }^{-}$ events [70], as seen in Figure 4 (middle). Searches for a light muon-philic scalar $X_0$ or vector $X_1$ have been performed via $J/\psi \to {\mu }^{+}{\mu }^{-}{X}_{0,1}$ with $X_{0,1}$ decaying to invisible final states using 10 billion $J/\psi$ events, and reported null results [71]. The obtained limits are more stringent than the Belle II measurement in the mass range of 200–860 MeV/$c^2$ [71], as seen in Figure 4 (right).

3.3. Search for Dark Baryon

The baryon asymmetry of the Universe (BAU) implies the need for baryogenesis [10]. Baryogenesis requires the Sakharov conditions [72]: baryon-number violation, violation of charge conjugation C and charge-parity $CP$, and a departure from thermal equilibrium. These conditions are, in principle, compatible with the SM, but current measurements show that the SM does not provide sufficient baryogenesis to explain the observed BAU. The similarity between the dark matter and baryonic energy densities, ${\rho }_{\mathrm{DM}}\approx {\rho }_{\mathrm{baryon}}$, suggests a possible connection between their origins, motivating scenarios in which dark matter carries non-zero baryon number [73,74]. A baryonic dark sector is further motivated by the long-standing discrepancy between neutron-lifetime measurements in beam and bottle experiments, which could be resolved if the neutron decays into dark-matter states carrying baryon number with a branching fraction of order $1\%$ [75].

The B-mesogenesis mechanism can simultaneously explain both the visible baryon asymmetry and the origin of dark matter [76]. Dark-sector antibaryons have been searched for in B-meson decays at the BaBar experiment [77] and, more recently, in invisible decays of the $\Lambda$ baryon [78] as well as $\Lambda \overline{\Lambda }$ oscillation [79] at BESIII. Complementary to these searches, hyperon decays offer an additional opportunity to probe baryonic dark matter through final states containing dark baryons, which would manifest as missing energy in the detector.

More recently, a search for baryogenesis and dark matter in $B^{+}\to {\Lambda }_c^{+}+\mathrm{invisible}$ was performed using $398{\mathrm{fb}}^{-1}$ of data collected at the ${\rm Y}\left(4S\right)$ resonance by the BaBar experiment [77]. The signal was inferred from the distributions of the beam-constrained mass and the invariant mass of the $pK\pi$ system. No evidence for dark-baryon production ${\psi }_{\mathrm{D}}$ was found, and upper limits on $\mathcal{B}(B^{+}\to {\Lambda }_c^{+}+{\psi }_{\mathrm{D}})$ were set at the $90\%$ confidence level as a function of the ${\psi }_{\mathrm{D}}$ mass in the range $0\le m_{{\psi }_{\mathrm{D}}}\le 3\mathrm{GeV}$.

A search for a dark baryon $\chi$ in the two-body decay ${\Xi }^{-}\to {\pi }^{-}+\mathrm{invisible}$ has recently been performed using approximately ${10}^7$ events from $J/\psi \to {\Xi }^{-}{\overline{\Xi }}^{+}$ decays, based on the ${10}^{10}$$J/\psi$ events collected by the BESIII detector [80]. In this process, the ${\Xi }^{-}$ is studied by tagging the recoil ${\overline{\Xi }}^{+}$, reconstructed via ${\overline{\Xi }}^{+}\to {\pi }^{+}\overline{\Lambda }(\to \overline{p}{\pi }^{+})$. The dark baryon $\chi$ is treated as an invisible particle, and the search is performed for assumed masses of 1.07, 1.10, $m_{\Lambda }$, 1.13, and 1.16 GeV/$c^2$, where $m_{\Lambda }$ is the $\Lambda$-baryon mass. No significant signal is observed, and $90\%$ ($95\%$) CL upper limits on $\mathcal{B}({\Xi }^{-}\to {\pi }^{-}+\mathrm{invisible})$ are set. The corresponding $95\%$ CL limits on the left- and right-handed effective operators, parameterized by the Wilson coefficients $C_{us,s}^L$ and $C_{us,s}^R$, are found to be $C_{us,s}^L<5.5\times {10}^{-2}{\mathrm{TeV}}^{-2}$ and $C_{us,s}^R<4.9\times {10}^{-2}{\mathrm{TeV}}^{-2}$, which are more stringent than previous constraints from LHC searches for colored mediators.

4. Axion Portal

An axion is a pseudoscalar Goldstone boson originally introduced through the spontaneous breaking of the Peccei-Quinn symmetry to solve the strong CP problem in QCD [81]. Many models beyond the SM also predict axion-like particles (ALPs) [82,83]. The spin-parity of these ALPs is the same as that of the QCD axion, but they have arbitrary masses and couplings to SM particles. ALPs are also considered candidates for cold DM and can act as mediators between the SM and DM candidates. Their interactions with SM gauge bosons are typically described using an effective field theory (EFT), where the leading coupling at dimension-5 involves the ALP field a and the gauge field strengths.

4.1. Coupling to Photon Pairs

The interaction of an ALP with two photons is given by the effective Lagrangian term:

$${\mathcal{L}}_{a\gamma \gamma }={\displaystyle \frac{1}{4}}{g}_{a\gamma \gamma }a{F}_{\mu \nu }{\tilde{F}}^{\mu \nu }$$

(2)

where $F_{\mu \nu }$ is the electromagnetic field-strength tensor and ${\tilde{F}}^{\mu \nu }={\displaystyle \frac{1}{2}}{ϵ}^{\mu \nu \rho \sigma }{F}_{\rho \sigma }$ is its dual. The coupling $g_{a\gamma \gamma }$ can be measured at $e^{+}{e}^{-}$ collider experiments via either the ALP-Strahlung process or radiative V meson decays $(V=J/\psi ,{\rm Y}(nS\left)\right)$ with ($n=1,2,3$). The coupling $g_{a\gamma \gamma }$ in the sub-GeV mass range, especially for ALP masses between 0.1 and 5 GeV, is less constrained compared to other regions. In this mass region, the Belle II and OPAL experiments have performed searches for ALPs via the ALP-Strahlung process $e^{+}{e}^{-}\to \gamma a$, while BESIII has performed a search via radiative $J/\psi \to \gamma a$ decays using 10 billion $J/\psi$ events and 2.7 billion $\psi \left(2S\right)$ events [84]. The $J/\psi$ data sample contains about a $4.4\%$contribution from the ALP-Strahlung process $e^{+}{e}^{-}\to \gamma a$ and a $95.6\%$ contribution from radiative $J/\psi$ decay, along with the dominant SM background from $J/\psi \to \gamma P$ ($P={\pi }^0,\eta ,{\eta }^{\prime }$) decays. The search for signal events from the ALP a was conducted by performing a series of fits to the combined di-photon spectrum after removing the backgrounds from $J/\psi \to \gamma P$. 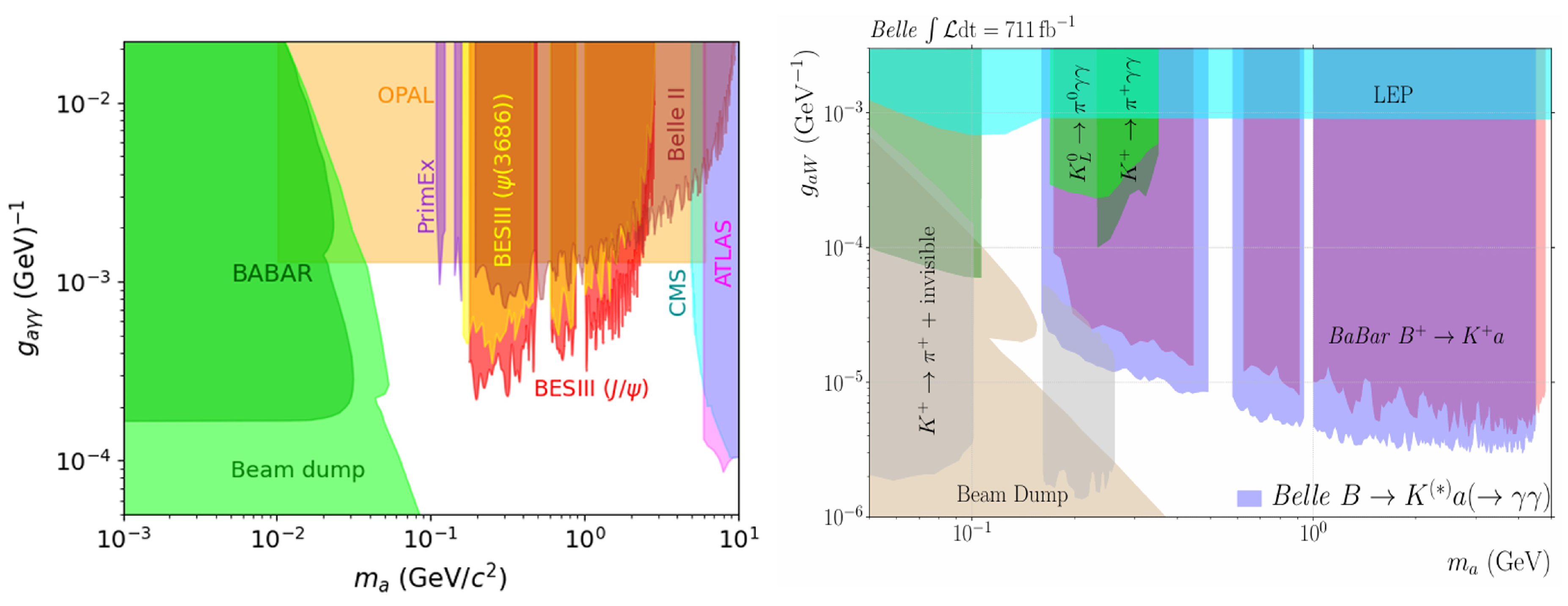No significant signal was found, and BESIII has set one of the most stringent upper limits on $g_{a\gamma \gamma }$ in the mass range of $[0.18,2.85]$ GeV [84], as seen in Figure 5 (left).

4.2. Coupling to W Bosons

ALPs can also couple to electroweak gauge bosons through the $SU{\left(2\right)}_L$ field-strength tensor:

$${\mathcal{L}}_{aWW}=-{\displaystyle \frac{1}{4}}{g}_{aWW}a{W}_{\mu \nu }^i{W}^{i\mu \nu }$$

(3)

where $W_{\mu \nu }^i$ is the $SU{\left(2\right)}_L$ field-strength tensor, i labels the weak isospin components, and $g_{aWW}$ is the ALP-W boson coupling. After electroweak symmetry breaking, this operator induces interactions of the ALP with the physical $W^{\pm }$ bosons. This coupling leads to the production of ALPs at one loop in the process $B^{\pm }\to K^{\pm }a$, where the ALP is emitted from an internal $W^{\pm }$ boson. Electroweak symmetry breaking and the resulting gauge-boson mixing also generate an effective ALP coupling to a pair of photons. In specific models, the branching fraction of $a\to \gamma \gamma$ can be nearly $100\%$ for $m_a<2m_e$ (to avoid other decays) or under specific assumptions, but it is model-dependent. The BaBar and Belle experiments have searched for ALPs in the reactions $B^{\pm }\to K^{\pm }a$ and $B\to K^{*}a$, respectively, using their data samples collected at the ${\rm Y}\left(4S\right)$ resonance, and reported null results. The Belle limits on the coupling to the $W^{\pm }$ boson, $g_{aWW}$, which range from $3\times {10}^{-6}$ GeV⁻¹ to $3\times {10}^{-5}$ GeV⁻¹, are more stringent than the BaBar limits [85], as seen in Figure 5 (right).

4.3. ALP Signature with Invisible Final State

An ALP may also be involved in charged lepton–flavor–violating (CLFV) decays, such as ${\tau }^{-}\to l^{-}\alpha$ ($l=e,\mu$) [86], where $\alpha$ corresponds to an ALP. The CLFV processes can occur in extended SM frameworks that include right-handed neutrinos. Their predicted branching fractions are expected to be at the level of ${10}^{-54}$. The contribution of ALPs in such CLFV decays may enhance their decay rates up to the level of current experimental sensitivity. The search for an invisible signature of $\alpha$ in ${\tau }^{-}\to l^{-}\alpha$ has recently been performed by Belle II using 61.8 fb⁻¹ of data at the ${\rm Y}\left(4S\right)$ resonance, resulting in a null observation [87]. The reported $95\%$ CL upper limits on the branching fractions $\mathcal{B}({\tau }^{-}\to l^{-}\alpha )$ as a function of the $\alpha$ mass are the most stringent to date, as detailed in Ref. [87]. A signature for an ALP with invisible final state in the decay $J/\psi \to \varphi +\mathrm{invisible}$ has also been explored by the BESIII experiment, with a null results [88].

5. Neutrino Portal

The neutrino portal refers to interactions mediated by gauge-singlet fermions, commonly known as sterile neutrinos, right-handed neutrinos, or heavy neutral leptons (HNLs). The portal interaction is represented by

$${\mathcal{L}}_{\mathrm{portal}}=y_{\nu }\overline{L}H{N}_R+\mathrm{h}.\mathrm{c}.,$$

(4)

where L is the lepton doublet, H is the Higgs doublet, $N_R$ is a right-handed (sterile) neutrino, and $y_{\nu }$ is the Yukawa coupling.

HNLs are additional neutrino states that are massive but neutral under all SM gauge interactions. In the $\nu$MSM, introducing three sterile, right-handed Majorana HNLs to the SM can simultaneously explain neutrino oscillations, the origin of the baryon asymmetry of the Universe, and provide a dark-matter candidate. Two of these HNLs typically have masses in the MeV to GeV range, while the third—acting as a dark matter candidate—has a mass at the keV scale. The HNLs in the MeV–GeV mass range can be produced in semi-leptonic B decays, lepton-number violating (LNV) D decays, hadronic $\tau$ decays and quaorkonium decays, leading to possible deviations from SM expectations. Mixing between an HNL mass eigenstate and active neutrinos can be parametrized by an extended Pontecorvo–Maki–Nakagawa–Sakata (PMNS) matrix, with an additional element $U_{\ell 4}$, where ℓ denotes the SM flavor state e, $\mu$, or $\tau$.

Experimental constraints on the mixing strength between the lepton sector and HNLs in the electron and muon sectors primarily come from LHC experiments in the higher HNL mass region. In the low-mass region, the exclusion limits on $|U_{l4}{|}^2$ mainly come from LNV decays $D\to K\pi e^{+}{e}^{+}$ [89], semi-leptonic B decays [90] and hadronic $\tau$ decays [91]. More recently, the BaBar experiment performed a search for an HNL that mixes with the SM $\tau$ neutrino, characterized by the mixing parameter $|U_{\tau 4}{|}^2$ (the absolute square of the corresponding extended PMNS matrix element), using a data sample of 424 fb⁻¹. BaBar conducted this study via the process $e^{+}{e}^{-}\to {\tau }^{+}{\tau }^{-}$, where one $\tau$ lepton is tagged through ${\tau }^{+}\to e^{+}\nu \overline{\nu }$, and the other decays via ${\tau }^{-}\to {\pi }^{-}{\pi }^{-}{\pi }^{+}\nu$ [92]. This channel allows sensitivity to HNL masses in the range $100<m_4<1360\mathrm{MeV}/c^2$. In the decay ${\tau }^{-}\to {\pi }^{-}{\pi }^{-}{\pi }^{+}\nu$, the HNL ${\nu }_4$ can mix with the SM neutrino. The mass of the missing neutrino $m_4$ determines the two-dimensional distribution of the hadronic energy $E_h$ versus the invariant mass of the hadronic system, as described in Figure 6 (left).

The observed kinematic phase-space distributions of the hadronic system can be interpreted as a superposition of two components: one corresponding to decays mediated by the HNL (weighted by $|U_{\tau 4}{|}^2$), and one corresponding to SM neutrino decays (weighted by $1-|U_{\tau 4}{|}^2$). For a hypothetical mixing with the $\tau$ lepton, the total differential decay rate becomes

$${\left.{\displaystyle \frac{d\Gamma ({\tau }^{-}\to \nu h^{-})}{d{m}_{h}d{E}_h}}\right|}_{\mathrm{Total}}={\left|U_{\tau 4}\right|}^2{\left.{\displaystyle \frac{d\Gamma ({\tau }^{-}\to \nu h^{-})}{d{m}_{h}d{E}_h}}\right|}_{\mathrm{HNL}}+\left(1-|U_{\tau 4}{|}^2\right){\left.{\displaystyle \frac{d\Gamma ({\tau }^{-}\to \nu h^{-})}{d{m}_{h}d{E}_h}}\right|}_{\mathrm{SM}}.$$

(5)

No significant signal is observed, and upper limits on $|U_{\tau 4}{|}^2$ at the 95% confidence level are set, depending on the HNL mass hypothesis shown in Figure 6 (right). These limits range from $2.31\times {10}^{-2}\mathrm{to}5.04\times {10}^{-6}$ within the mass range $100<m_4<1300\mathrm{MeV}/c^2$, representing the most stringent constraints to date [92].

5.1. Invisible Decays

In the SM, neutrinos are invisible to particle detectors because they interact only via the weak force with extremely small cross sections. Their presence can be inferred only through the missing four-momentum in a decay. A quarkonium state, composed of a quark (q) and its corresponding antiquark ($\overline{q}$), may annihilate into a neutrino pair via a virtual $Z^0$ boson, but such processes are highly suppressed. The branching fractions of these rare decays could be enhanced in the presence of light dark matter (LDM) particles. Estimates of invisible quarkonium decays often assume a connection between the cross sections of the time-reversed processes, $\sigma (q\overline{q}\to \chi \chi )\approx \sigma (\chi \chi \to q\overline{q})$, where $\chi$ denotes a generic dark-matter particle. Exclusion limits on invisible decays of ${\rm Y}\left(1S\right)$ [93], $J/\psi$ [94], $B^0$/$B_S^0$ [95], ${\eta }^{(\prime )}$ [96], ${\pi }^0$ [97], $D^0$ [98], $\omega /\varphi$ [99] mesons, and the $\Lambda$ [78] baryon have been reported by several collider experiments. A feasibility study of invisible decays of light vector mesons ($V=\omega ,\varphi$) by the STCF experiment has revealed that the $90\%$ CL upper limits on the branching fractions of these decays could reach the level of ${10}^{-7}$. The sensitivity could further reach the level of ${10}^{-8}$ using a deep-learning–based optimization technique, allowing tighter constraints on the parameter space of LDM scenarios [100].

More recently, BESIII has reported a search for the FCNC decay $K_S^0\to \nu \overline{\nu }$, which can proceed via the $s\to d\nu \overline{\nu }$ transition. This decay is extremely suppressed due to angular-momentum constraints and remains so even if neutrinos have mass, because the required helicity configuration is unfavorable. The SM prediction for $\mathcal{B}(K_S^0\to \nu \overline{\nu })$ is below ${10}^{-16}$ [101]. Therefore, this decay provides a highly sensitive test of the SM. Several new physics scenarios predict enhancements: for example, models such as the Two-Higgs-Doublet Model (2HDM) may raise the branching fraction to the ${10}^{-4}$ level [101], while mirror-matter theories—which postulate a parallel mirror sector—predict invisible branching fractions at the order of ${10}^{-6}$ [102]. Invisible $K_S^0$ decays also offer valuable input for tests of charge, parity, and time-reversal (CPT) symmetry, since the Bell–Steinberger relation connects possible CPT violation to the amplitudes of all kaon decay channels, assuming no invisible decay mode exists [103].

The first direct search for invisible decays of the $K_S^0$ meson has been performed by the BESIII Collaboration using ${10}^{10}$$J/\psi$ events [103]. The $K_S^0$ candidates are reconstructed from the decay $J/\psi \to \varphi K_S^0{K}_S^0$, which benefits from low background contamination because the decay $J/\psi \to \varphi K_S^0{K}_L^0$ is forbidden by C-parity conservation. No significant signal is observed, and an upper limit on the branching fraction, $\mathcal{B}(K_S^0\to \mathrm{invisible})<8.4\times {10}^{-4}$, is set at the 90% confidence level for the first time.

6. Discussion

The paper reviews the current experimental status of dark matter searches at various $e^{+}{e}^{-}$ collider experiments. In the sub-GeV$/c^2$ mass range, hidden dark-sector models allow the possibility that SM particles couple to dark matter through different portals. The corresponding new-physics particles include dark photons, ALPs, light Higgs bosons, and sterile neutrinos. These particles have been searched for by multiple collider experiments, but so far only null results have been observed. The resulting exclusion limits have constrained large portions of the parameter spaces of physics models beyond the SM.

Although Belle II has so far collected only about $1\%$ of its target integrated luminosity, many of its early results related to the dark sector are already more stringent than those from the preceding B-factory experiments, such as BaBar and Belle. Therefore, Belle II is expected to play a major role in either discovering or ruling out new-physics scenarios associated with dark-matter portals. The BESIII experiment has also played a major role in exploring dark-sector searches, and its results, particularly for light Higgs bosons and ALPs, remain among the most stringent to date. BESIII has additionally explored invisible decays of light mesons and baryons and reported strong exclusion limits in these channels. Its successor, the STCF, will be capable of either discovering or excluding light dark-matter scenarios in searches for invisible decays of light mesons. Overall, while no signals of dark matter have yet been observed, the $e^{+}{e}^{-}$ collider program continues to play a central role in shaping theoretical expectations and guiding future experimental developments.

7. Conclusions

The hidden dark-sector model introduces various types of sub-GeV dark-matter particles that can mediate interactions between the SM and the dark sector. One of the main efforts of the current generation of collider experiments is to search for these new-physics particles. However, only null results have been obtained so far. The resulting exclusion limits already rule out a large fraction of the parameter space of many new-physics models beyond the SM. In the future, the data collected by Belle II and STCF will be able to either discover or exclude these dark-matter scenarios.