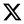Submitted:
02 December 2025
Posted:
04 December 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Layout of the Main Directions of the Route
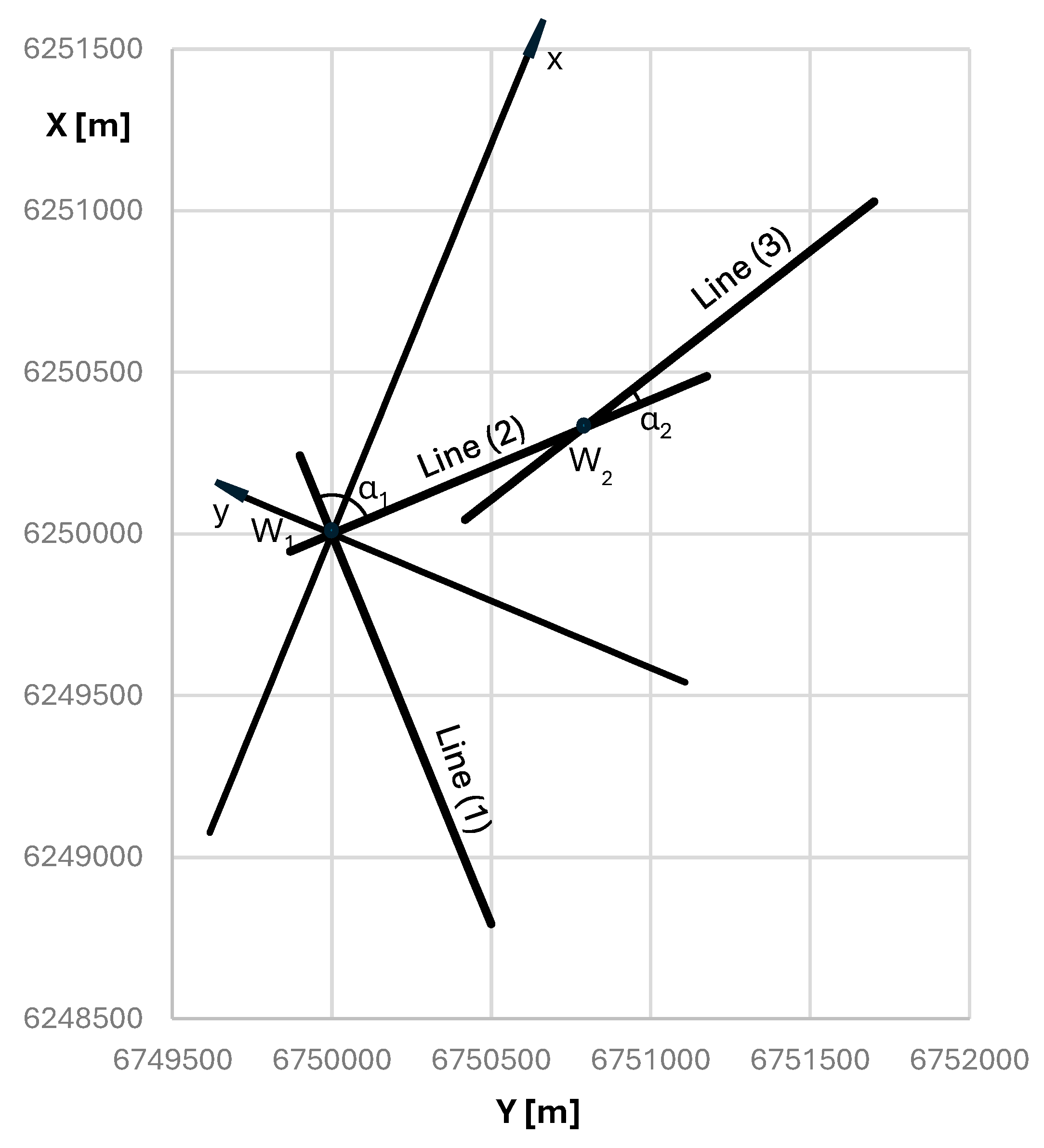
3. Local Coordinate System
- for Line 1: , ,
- for Line 2: , ,
- , .
4. Reverse Arcs Radii
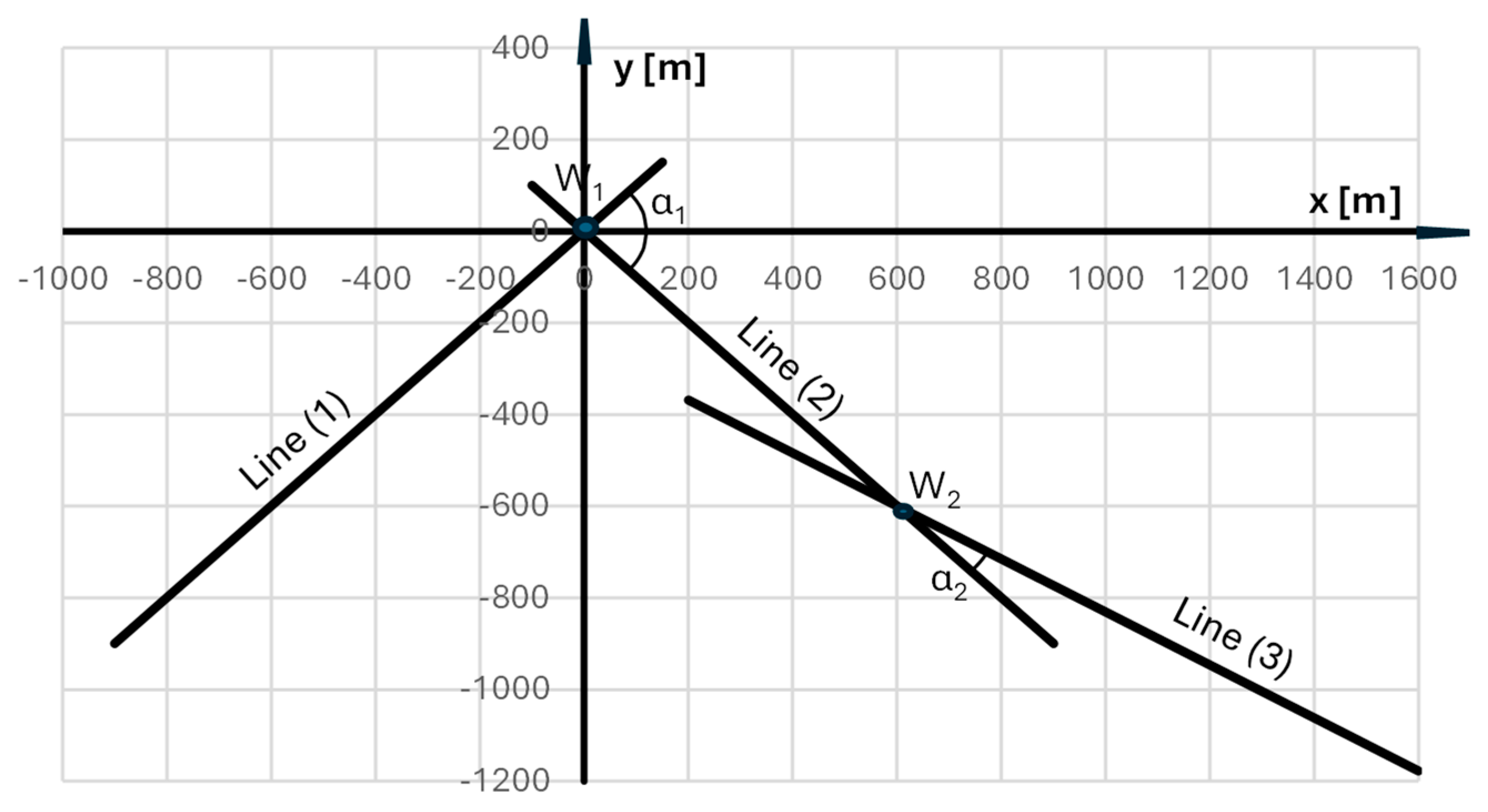
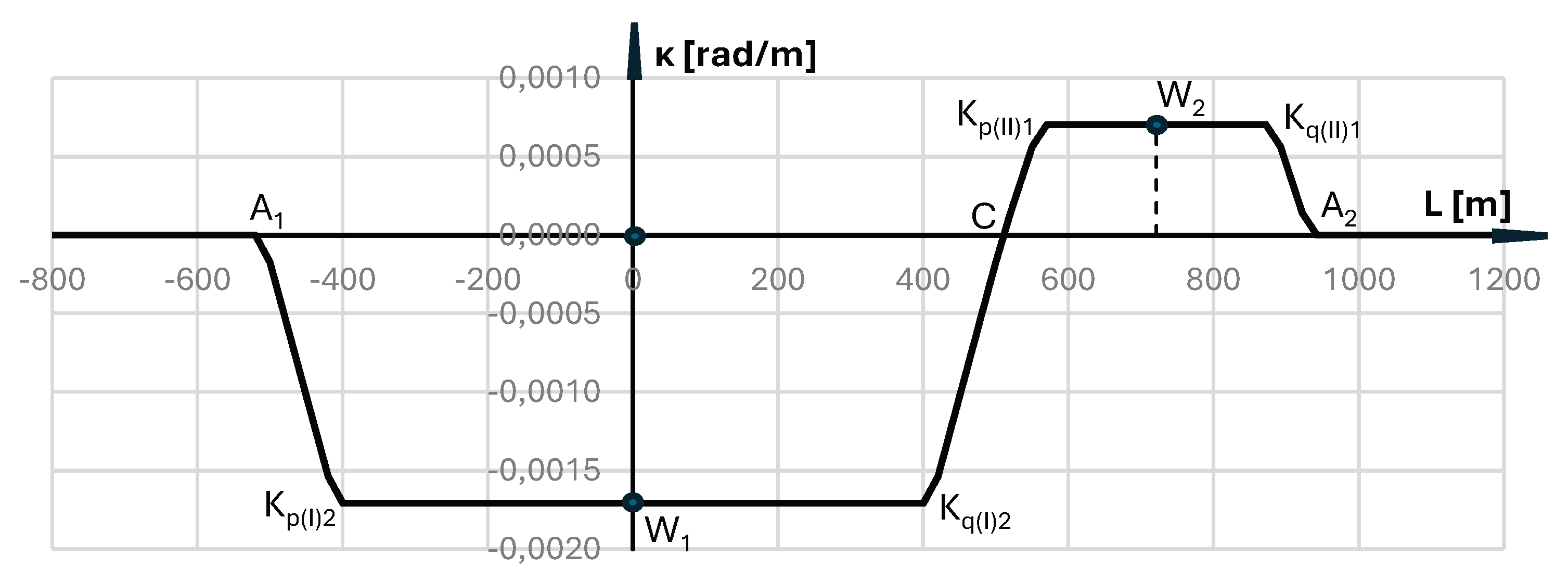
5. Curvature of the Primary Reverse Arc System
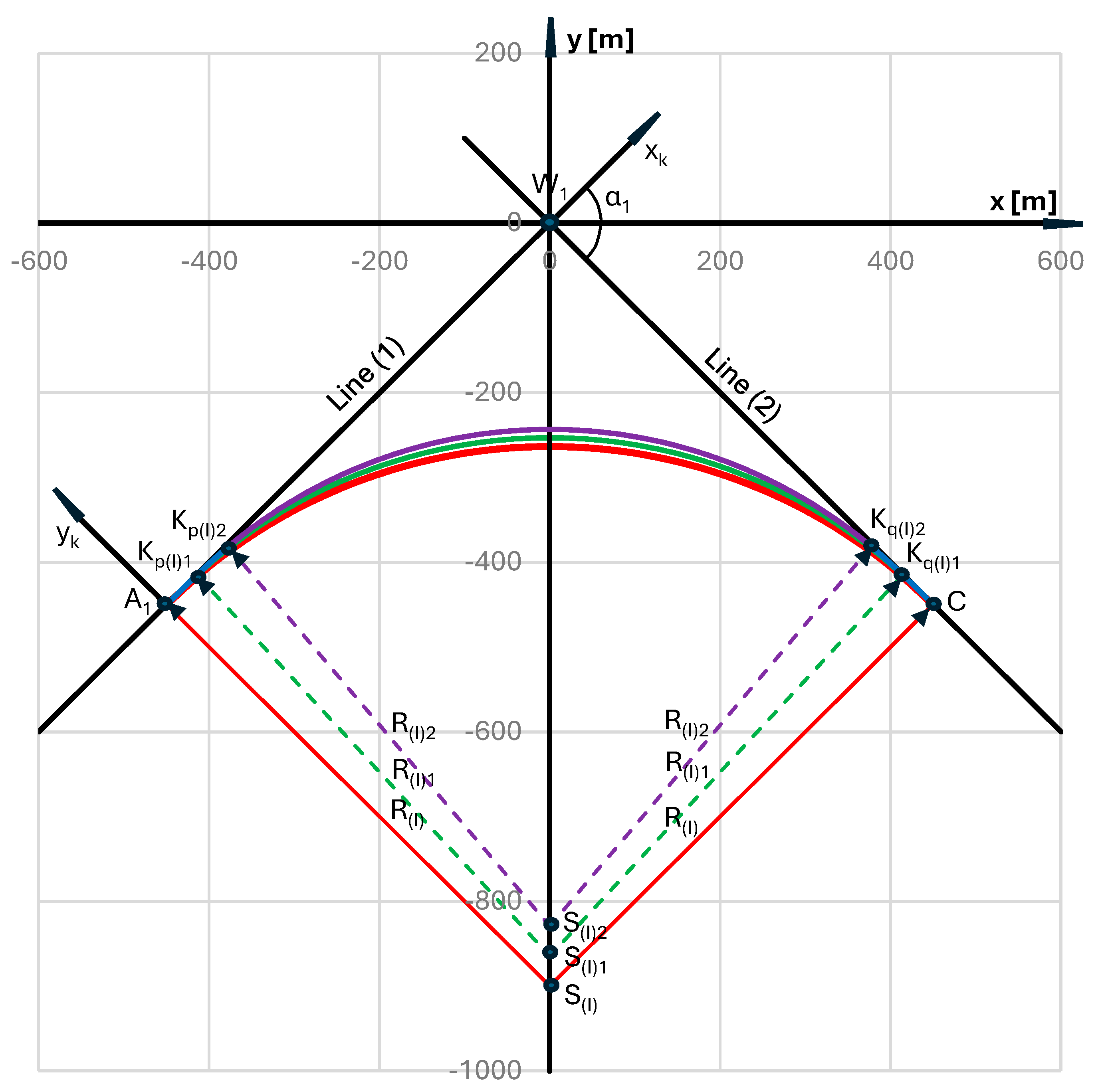
6. Applying Transition Curves for the First Circular Arc
-
for , that is,,where
- for , where xKq(I)i = – xKp(I)i
- for , that iswhere
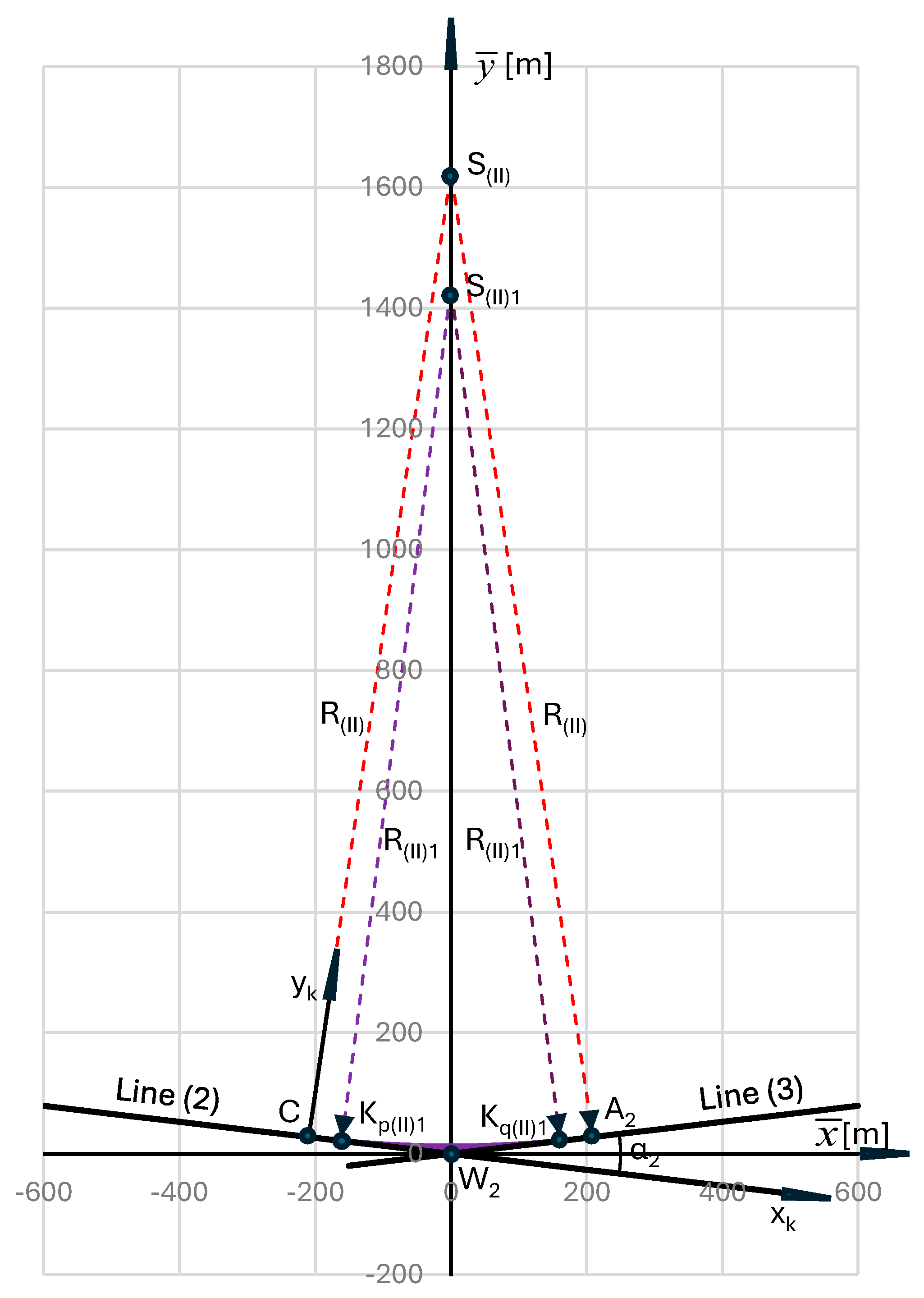
7. Applying Transition Curves for the Second Circular Arc
- for , that iswhere
- for , where
- for , that iswhere
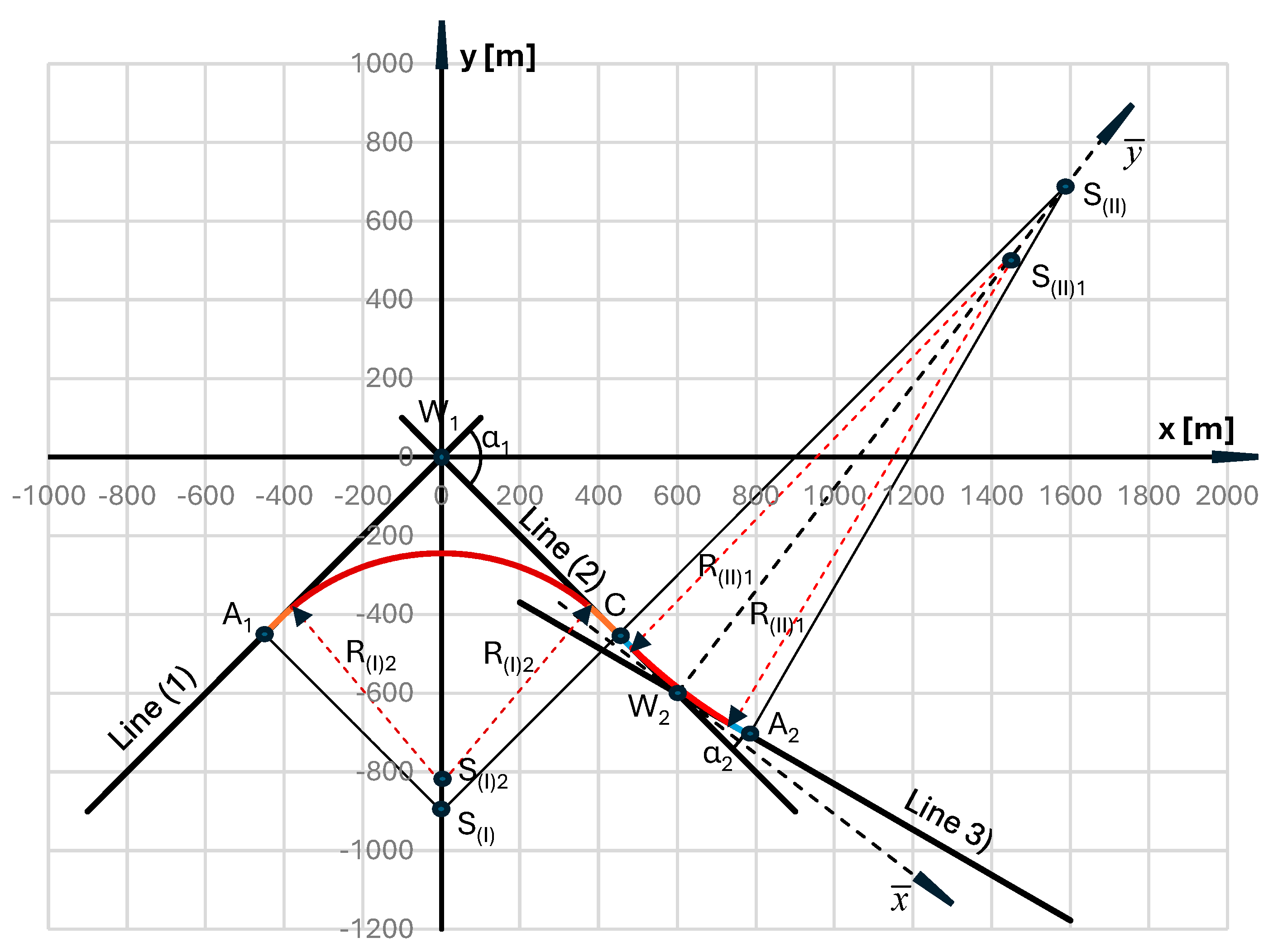
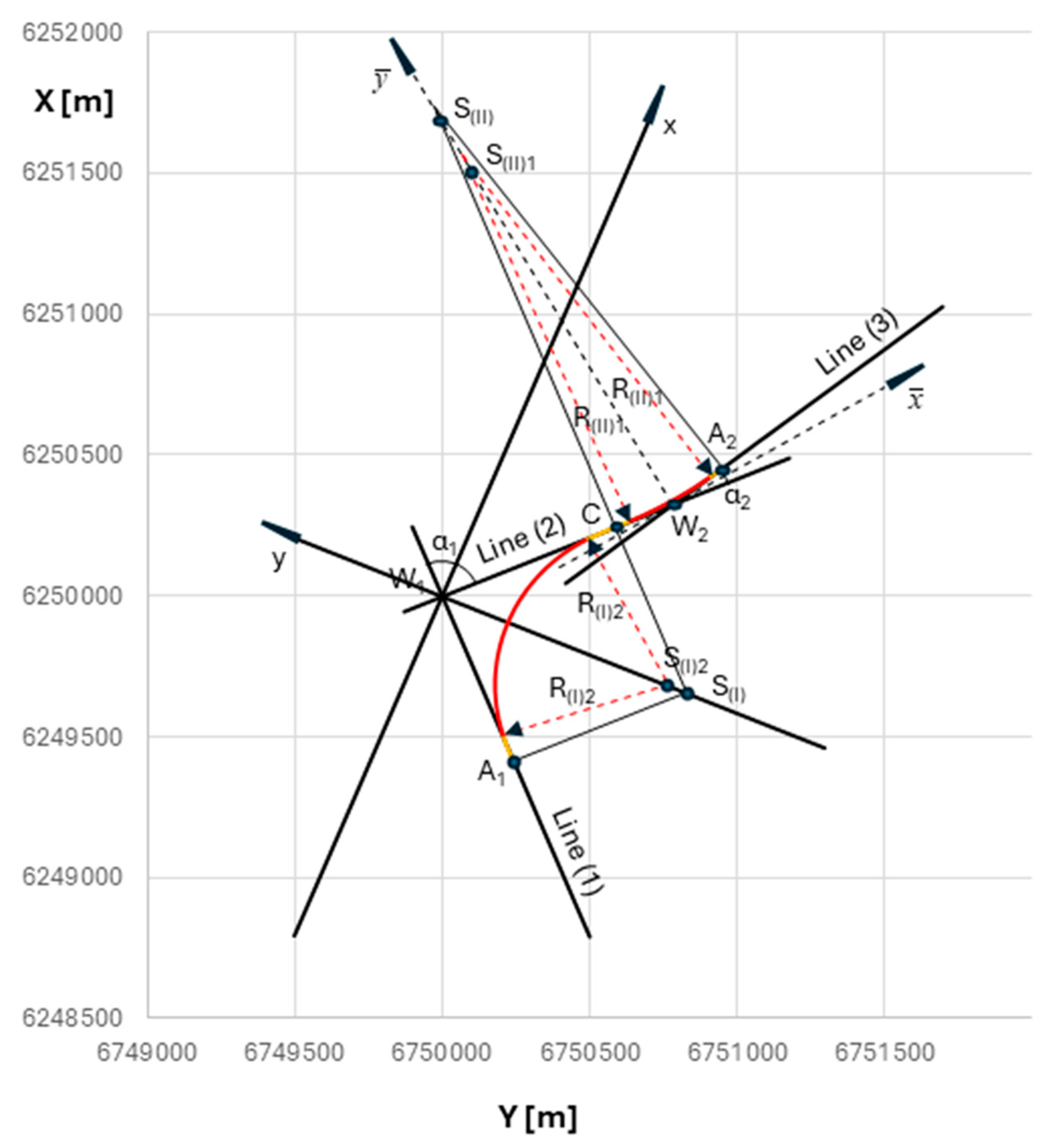
8. The Resulting Geometric Arrangement of Reverse Curves
9. Evaluation of the Obtained Solution
10. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Arc I | Marking the first circular arc |
| Arc II | Marking the second circular arc |
| A1 | Designation of the starting point of a geometric system |
| A2 | Designation of the end point of a geometric system |
| am1 | Unbalanced acceleration on Arc I |
| am2 | Unbalanced acceleration on Arc II |
| aper | Permissible value of unbalanced acceleration |
| C | Destination of the assumed connection point of reverse arc |
| Distance between points C and W2 | |
| f1 | Lifting speed of the rolling stock on the gradient due to cant for Arc I |
| f2 | Lifting speed of the rolling stock on the gradient due to cant for Arc II |
| g | Acceleration of gravity (g = 9.81 m/s2) |
| h1 | Track cant on Arc I |
| h2 | Track cant on Arc II |
| Kp(I)i | End of the assumed transition curve before Arc I |
| Kp(I)1 | End of the transition curve before Arc I for its assumed length L(I)1 |
| Kp(I)2 | End of the transition curve before Arc I for its assumed length L(I)2 |
| Kq(I)i | End of the assumed transition curve after Arc I |
| Kq(I)1 | End of the transition curve after Arc I for its assumed length L(I)1 |
| Kq(I)2 | End of the transition curve after Arc I for its assumed length L(I)2 |
| Kp(II)i | End of the assumed transition curve before Arc II |
| Kp(II)1 | End of the transition curve before Arc II for its assumed length L(II)1 |
| Kq(II)i | End of the assumed transition curve after Arc II |
| Kq(II)1 | End of the transition curve after Arc II for its assumed length L(II)1 |
| l | Transition curve parameter (distance from the beginning of the curve) |
| lb | Length of the rigid wagon base |
| LCS | Local coordinate system |
| Line 1 | Marking the first main direction of the route |
| Line 2 | Marking the second main direction of the route |
| Line 3 | Marking the third main direction of the route |
| L(I)i | Assumed lengths of the transition curves for Arc I |
| L(I)1 | The first assumed length of the transition curve for Arc I |
| L(I)2 | The second assumed length of the transition curve for Arc I |
| L(II)i | Assumed lengths of the transition curves for Arc II |
| L(II)1 | The first assumed length of the transition curve for Arc II |
| p | Marking the transition curve before the circular arc |
| PL-2000 | The Polish national spatial reference system |
| q | Marking the transition curve after the circular arc |
| R(I) | Initial value of Arc I radius |
| R(I)i | Corrected Arc I radius |
| R(I)1 | Value of corrected Arc I radius after introducing a transition curve of length L(I)1 |
| R(I)2 | Value of corrected Arc I radius after introducing a transition curve of length L(I)2 |
| R(II) | Initial value of Arc II radius |
| R(II)i | Corrected Arc II radius |
| R(II)1 | Value of corrected Arc II radius after introducing a transition curve of length L(II)1 |
| s | Centre distance of rails (on standard gauge lines s = 1500 mm) |
| s1 | Slope tangent Line 1 in the LCS |
| s2 | Slope tangent Line 2 in the LCS |
| s3 | Slope tangent Line 3 in the LCS |
| S(I) | Center of the primary Arc I |
| S(I)i | Corrected Arc I center |
| S(I)1 | Corrected Arc I center after introducing a transition curve of length L(I)1 |
| S(I)2 | Corrected Arc I center after introducing a transition curve of length L(I)2 |
| S(II) | Center of the primary Arc II |
| S(II)i | Corrected Arc II center |
| S(II)1 | Corrected Arc II center after introducing a transition curve of length L(II)1 |
| t1 | Value of the tangent to Arc I |
| t2 | Value of the tangent to Arc II |
| V | Train speed |
| Vmax | Maximum speed of trains on the route |
| W1 | Intersection point of the first and second main directions of the route |
| W2 | Intersection point of the second and third main directions of the route |
| Distance between points W1 and C | |
| Distance between points W1 and W2 | |
| X | North coordinate of the PL-2000 coordinate system |
| XW1 | Ordinate of point W1 in the PL-2000 coordinate system |
| XW2 | Ordinate of point W2 in the PL-2000 coordinate system |
| x | Abscissa of the local coordinate system |
| Abscissa of the auxiliary coordinate system | |
| xA1 | Abscissa of point A1 in the LCS |
| xA2 | Abscissa of point A2 in the LCS |
| auxiliary coordinate system | |
| xC | Abscissa of point C in the LCS |
| auxiliary coordinate system | |
| xk | Abscissa in the transition curve coordinate system |
| xKp(I)i | Abscissa of the end of the transition curve before Arc I in the LCS |
| xKq(I)i | Abscissa of the end of the transition curve after Arc I in the LCS |
| auxiliary coordinate system | |
| auxiliary coordinate system | |
| auxiliary coordinate system | |
| auxiliary coordinate system | |
| xS(I) | Abscissa of the center of the primary Arc I in the LCS |
| xS(I)i | Abscissa of corrected Arc I center in the LCS |
| xS(I)1 | Abscissa of corrected Arc I center in the LCS after introducing a transition curve of length L(I)1 |
| xS(I)2 | Abscissa of corrected Arc I center in the LCS after introducing a transition curve of length L(I)2 |
| xS(II) | Abscissa of the center of the primary Arc II in the LCS |
| coordinate system | |
| xW2 | Abscissa of point W2 in the LCS |
| Y | Easting coordinate of the PL-2000 coordinate system |
| YW1 | Abscissa of point W1 in the PL-2000 coordinate system |
| YW2 | Abscissa of point W2 in the PL-2000 coordinate system |
| y | Ordinate of the local coordinate system |
| Ordinate of the auxiliary coordinate system | |
| yA1 | Ordinate of point A1 in the LCS |
| yA2 | Ordinate of point A2 in the LCS |
| auxiliary coordinate system | |
| yC | Ordinate of point C in the LCS |
| auxiliary coordinate system | |
| yk | Ordinate in the transition curve coordinate system |
| yKp(I)i | Ordinate of the end of the transition curve before Arc I in the LCS |
| yKq(I)i | Ordinate of the end of the transition curve after Arc I in the LCS |
| auxiliary coordinate system | |
| auxiliary coordinate system | |
| auxiliary coordinate system | |
| auxiliary coordinate system | |
| yS(I) | Ordinate of the center of the primary Arc I |
| yS(I)i | Ordinate of corrected Arc I center in the LCS |
| yS(I)1 | Ordinate of corrected Arc I center in the LCS after introducing a transition curve of length L(I)1 |
| yS(I)2 | Ordinate of corrected Arc I center in the LCS after introducing a transition curve of length L(I)2 |
| yS(II) | Ordinate of the center of the primary Arc II |
| auxiliary coordinate system | |
| yW2 | Ordinate of point W2 in the LCS |
| α1 | Turning angle of the route at point W1 |
| α2 | Turning angle of the route at point W2 |
| β | Rotation angle of the PL-2000 system when transformed to the LCS |
| γ | system when it is transformed to the LCS |
| κ | Curvature of the track axis |
| Θ | Inclination angle at the end of the transition curve in the LCS |
| Ф1 | Inclination angle of Line 1 in the PL-2000 coordinate system |
| Ф2 | Inclination angle of Line 2 in the PL-2000 coordinate system |
| Ф3 | Inclination angle of Line 3 in the PL-2000 coordinate system |
| Φx | Angle of inclination of the x-axis in the PL-2000 coordinate system |
| Φy | Angle of inclination of the y-axis in the PL-2000 coordinate system |
| Θk | Angle of inclination of the tangent at the end of the transition curve in xk, yk system |
| ΘKp(I)i | Inclination angle at the end of the transition curve before Arc I in the LCS |
| ΘKq(I)i | Inclination angle at the end of the transition curve after Arc I in the LCS |
| Angle of inclination of the tangent at the end of transition curve before Arc II in the coordinate system | |
| Angle of inclination of the tangent at the end of transition curve of length L(II)1 before Arc II in the coordinate system | |
| Angle of inclination of the tangent at the end of transition curve after Arc II in the coordinate system | |
| Angle of inclination of the tangent at the end of transition curve of length L(II)1 after Arc II in the | |
| φ1 | Inclination angle of Line 1 in the LCS |
| φ2 | Inclination angle of Line 2 in the LCS |
| φ3 | Inclination angle of Line 3 in the LCS |
| ψ | Acceleration increase |
| ψ1 | Acceleration increase on the transition curve for Arc I |
| ψ2 | Acceleration increase on the transition curve for Arc II |
| ψper | Permissible value of acceleration increase |
References
- Beria, P.; Grimaldi, R.; Albalate, D.; Bel, G. Delusions of success: Costs and demand of high-speed rail in Italy and Spain. Transp. Policy 2018, 68, 63–79. [Google Scholar] [CrossRef]
- Yang, X.; Lin, S.; Zhang, J.; He, M. Does high-speed rail promote enterprises productivity? Evidence from China. J. Adv. Transp. 2019, 2019, 1, 1279489. [Google Scholar] [CrossRef]
- De Rus, G. The economic rationale for high-speed rail. In International Encyclopedia of Transportation, Elsevier, 2021.
- Xiao, F.; Wang, J.; Du, D. High-speed rail heading for innovation: The impact of HSR on intercity technology transfer. Area Dev. Policy 2022, 7, 293–311. [Google Scholar] [CrossRef]
- Chen, H.; Zhu, T.; Zhao, L. High-speed railway opening, industrial symbiotic agglomeration and green sustainable development – empirical evidence from China. Sustainability 2024, 16(5), 2070. [Google Scholar] [CrossRef]
- Bigi, F.; Bosi, T.; Pineda-Jaramillo, J.; Viti, F. Long-term fleet management for freight trains: Assessing the impact of wagon maintenance through simulation of shunting policies. J. Rail Transp. Plann. Manag. 2024, 29, 100430. [Google Scholar] [CrossRef]
- Wang, Q.; Jiang, X.; Zeng, J.; Mao, R.; Wei, L. , Wu, S. Innovative method for high-speed railway carbody vibration control caused by hunting instability using underframe suspended equipment. JVC 2024, 31, 3245–3257. [Google Scholar]
- Zhang, M.; Hu, R.; Mo, J.; Xiang, Z.; Zhou, Z. A cross-domain state monitoring method for high-speed train brake pads based on data generation under small sample conditions. Measurement 2024, 226, 114074. [Google Scholar] [CrossRef]
- Qazi, A.; Yin, H.; Sebès, M.; Chollet, H.; Pozzolini, C. A semi-analytical numerical method for modelling the normal wheel-rail contact. Veh. Syst. Dyn. 2022, 60, 1322–1340. [Google Scholar] [CrossRef]
- Fang, C.; Jaafar, S.A.; Zhou, W.; Yan, H.; Chen, J.; Meng, X. Wheel-rail contact and friction models: A review of recent advances. Proc. Inst. Mech. Eng. F J. Rail Rapid Transit 2023, 237, 1245–1259. [Google Scholar] [CrossRef]
- Wu, B.; Yang, Y.; Xiao, G. A transient three-dimensional wheel-rail adhesion model under wet condition considering starvation and surface roughness. Wear 2024, 540–541, 205263. [Google Scholar] [CrossRef]
- Kasimu, A.; Zhou, W.; Yan, H.; Wang, Y.; Shen, C. Evaluation of the vehicle-cargo and vehicle-trackside clearance of long and big railway freight vehicles. Alex. Eng. J. 2025, 119, 22–34. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, B.; Wu, S.; Wen, Z. Effects of wheel tread hollow wear on wheel-rail adhesion under wet condition. Tribology International 2025, 211, 110927. [Google Scholar] [CrossRef]
- AutoCAD Civil 3D: Design, Engineering and Construction Software. Available online: http://www.autodesk.pl/products/civil-3d (accessed on 31 August 2025).
- Bentley Rail Track: Rail Infrastructure Design and Optimization. Available online: https://www.bentley.com/software/rail-design (accessed on 31 August 2025).
- Koc, W. Elements of Track Systems Design Theory (In Polish); Gdansk University of Technology Publishing House: Gdansk, Poland, 2004. [Google Scholar]
- Hodas, S. Design of railway track for speed and high-speed railways. Procedia Eng. 2014, 91, 256–261. [Google Scholar] [CrossRef]
- Aghastya, A.; Prihatanto, R.; Rachman, N.F.; Adi, W.T.; Astuti, S.W.; Wirawan, W.A. A new geometric planning approach for railroads based on satellite imagery. AIP Conf. Proc. 2023, 2671, 50005. [Google Scholar] [CrossRef]
- Guerrieri, M. Fundamentals of railway design, Chapter: The alignment design of ordinary and high-speed railways, 2023, pp. 21-56, Springer Link.
- Tasci, L.; Kuloglu, N. Investigation of a new transition curve. Balt. J. Road Bridge Eng. 2011, 6, 23–29. [Google Scholar] [CrossRef]
- Kobryn, A. Universal solutions of transition curves. J. Surv. Eng. 2016, 142, 4016010. [Google Scholar] [CrossRef]
- Koc, W. New transition curve adapted to railway operational requirements. J. Surv. Eng. 2019, 145, 4019009. [Google Scholar] [CrossRef]
- Zboinski, K.; Woznica, P. Optimum railway transition curves for different circular arc radii. Arch. Civ. Eng. 2022, 68, 111–125. [Google Scholar] [CrossRef]
- Palsson, B.A. Design of optimization of switch rails in railway turnouts. Veh. Sys. Dyn. 2013, 51, 1610–1639. [Google Scholar] [CrossRef]
- Ping, W. Design of High-Speed Railway Turnouts; Theory and Applications; Elsevier Science & Technology: Oxford, UK, 2015. [Google Scholar]
- Koc, W. Analytical method of connecting parallel tracks located in a circular arc using curved turnouts. J. Transp. Eng. Part A Syst. 2020, 146, 4019081. [Google Scholar] [CrossRef]
- Hamarat, M.; Papaelias, M.; Kaewunruen, S. Fatigue damage assessment of complex railway turnout crossings via Peridynamics-based digital twin. Sci. Rep. 2022, 12, 14377. [Google Scholar] [CrossRef]
- Tonias, E.C.; Tonias, C.N. Compound and reversed curves. In Geometric Procedures for Civil Engineers; Springer International Publishing AG: Cham, Germany, 2016; pp. 185–242. [Google Scholar]
- Koc, W. : Design of reverse curves adapted to the satellite measurements. Adv. Civ. Eng. 2016, 2016, 6503962. [Google Scholar] [CrossRef]
- Koc, W. Design of rail-track geometric systems by satellite measurement. J. Transp. Eng. 2012, 138, 113–122. [Google Scholar] [CrossRef]
- Koc, W. Analytical method of modelling the geometric system of communication route. ReMPE 2014, 679817. [Google Scholar] [CrossRef]
- Koc, W. The analytical design method of railway route’s main directions intersection area. Open Eng. 2016, 6, 1–9. [Google Scholar] [CrossRef]
- Regulation of the Council of Ministers of 15 October 2012 on the national spatial reference system (in Polish). Journal of Laws of the Republic of Poland, 2012; position 1247.
- Koc, W. : Determination of track axis coordinates in the analytical method of designing railway route geometry. EJAS 2024, 12(5), 339–362. [Google Scholar] [CrossRef]
- Koc, W. Modeling of compound curves on railway lines. Geomatics 2025, 5, 21. [Google Scholar] [CrossRef]
- Korn, G.A.; Korn, T.M. Mathematical Handbook for Scientists and Engineers, 1st ed.; McGraw–Hill Book Company: New York, NY, USA, 1968. [Google Scholar]
- Technical Standards – detailed technical conditions for the modernization or construction of railway lines up to a speed of Vmax ≤ 250 km/h. Volume I – Railroad – Appendix ST-T1-A6 – Geometric layouts of tracks (in Polish). PKP Polish Railway Lines S.A., Warszawa 2021.
- Regulation of the Minister of Transport and Maritime Economy of 10 September 1998 on the technical conditions to be met by railway structures and their location (in Polish). Journal of Laws of the Republic of Poland 1998, 151, 987.

| Abscissa xC [m] |
Ordinate yC [m] |
Tangent t1 [m] |
Radius R(I) [m] |
Tangent t2 [m] |
Radius R(II) [m] |
|---|---|---|---|---|---|
| 350 | – 350 | 494.075 | 494.975 | 353.553 | 2685.505 |
| 375 | – 375 | 530.330 | 530.330 | 318.198 | 2416.954 |
| 400 | – 400 | 565.685 | 565.685 | 282.843 | 2348.404 |
| 425 | – 425 | 601.041 | 601.041 | 247.487 | 1879.853 |
| 450 | – 450 | 636.396 | 636.396 | 212.132 | 1611.303 |
| 475 | – 475 | 671.751 | 671.751 | 176.777 | 1342.752 |
| 500 | – 500 | 707.107 | 707.107 | 141.421 | 1074.202 |
| Train speed V [km/h] |
Radius R(I) [m] |
Acceleration am1 [m/s2] |
Radius R(II) [m] |
Acceleration am2 [m/s2] |
Sum of accelerations am1 + am2 [m/s2] |
Acceleration increase ψ [m/s3] |
|---|---|---|---|---|---|---|
| 50 | 636.396 | 0.303115 | 1611.303 | 0.119718 | 0.422833 | 0.293634 |
| 55 | 636.396 | 0.366769 | 1611.303 | 0.144858 | 0.511627 | 0.390827 |
| 60 | 636.396 | 0.436486 | 1611.303 | 0.172393 | 0.608879 | 0.507399 |
| 65 | 636.396 | 0.512264 | 1611.303 | 0.202323 | 0.714587 | 0.645113 |
| 70 | 636.396 | 0.594105 | 1611.303 | 0.234646 | 0.828752 | 0.805731 |
| Radius R(I)1 [m] |
Abscissa xk(L(I)1) [m] |
Ordinate yk(L(I)1) [m] |
Angle Θk(L(I)1) [rad] |
Abscissa xKp(I)1 [m] |
Ordinate yKp(I)1 [m] |
Angle ΘKp(I)1 [rad] |
Abscissa xS(I)1 [m] |
Ordinate yS(I)1 [m] |
|---|---|---|---|---|---|---|---|---|
| 611.230 | 49.99164 | -0.68160 | 0.0409 | -414.169 | -415.133 | 0.744497 | 0.002060594 | -864.649 |
| 611.229 | 49.99164 | -0.68161 | 0.0409 | -414.169 | -415.133 | 0.744497 | 0.001353681 | -864.648 |
| 611.228 | 49.99164 | -0.68161 | 0.0409 | -414.169 | -415.133 | 0.744497 | 0.000646768 | -864.647 |
| 611.227 | 49.99164 | -0.68161 | 0.0409 | -414.169 | -415.133 | 0.744497 | -0.00006014 | -864.647 |
| 611.226 | 49.99164 | -0.68161 | 0.0409 | -414.169 | -415.133 | 0.744497 | -0.00076706 | -864.646 |
| 611.225 | 49.99164 | -0.68161 | 0.0409 | -414.169 | -415.133 | 0.744497 | -0.00147397 | -864.645 |
| 611.224 | 49.99164 | -0.68161 | 0.0409 | -414.169 | -415.133 | 0.744497 | -0.00218088 | -864.644 |
| 611.223 | 49.99164 | -0.68161 | 0.0409 | -414.169 | -415.133 | 0.744497 | -0.00288780 | -864.644 |
| 611.222 | 49.99164 | -0.68161 | 0.0409 | -414.169 | -415.133 | 0.744496 | -0.00359471 | -864.643 |
| Radius R(I)2 [m] |
Abscissa xk(L(I)2) [m] |
Ordinate yk(L(I)2) [m] |
Angle Θk(L(I)2) [rad] |
Abscissa xKp(I)2 [m] |
Ordinate yKp(I)2 [m] |
Angle ΘKp(I)2 [rad] |
Abscissa xS(I)2 [m] |
Ordinate yS(I)2 [m] |
|---|---|---|---|---|---|---|---|---|
| 585.694 | 99.92715 | -2.84415 | -0.08537 | -377.330 | -381.352 | 0.700029 | -0.00213926 | -829.304 |
| 585.695 | 99.92715 | -2.84414 | -0.08537 | -377.330 | -381.352 | 0.700029 | -0.00143299 | -829.305 |
| 585.696 | 99.92715 | -2.84414 | -0.08537 | -377.330 | -381.352 | 0.700030 | -0.00072671 | -829.306 |
| 585.697 | 99.92715 | -2.84413 | -0.08537 | -377.330 | -381.352 | 0.700030 | -0.00002043 | -829.306 |
| 585.698 | 99.92715 | -2.84413 | -0.08537 | -377.330 | -381.352 | 0.700030 | 0.00068585 | -829.307 |
| 585.699 | 99.92715 | -2.84412 | -0.08537 | -377.330 | -381.352 | 0.700030 | 0.00139212 | -829.308 |
| 585.700 | 99.92715 | -2.84412 | -0.08537 | -377.330 | -381.352 | 0.700030 | 0.00209840 | -829.309 |
| Radius R(II)1 [m] |
Abscissa xk(L(II)1) [m] |
Ordinate yk(L(II)1) [m] |
Angle Θk(L(II)1) [rad] |
Abscissa [m] |
Ordinate [m] |
Angle [rad] |
Abscissa [m] |
Ordinate [m] |
|---|---|---|---|---|---|---|---|---|
| 1421,341 | 49.99845 | 0,293144 | 0.017589 | -160,708 | 21,453 | -0,11331 | 0,000449570 | 1433,680 |
| 1421,340 | 49.99845 | 0,293144 | 0.017589 | -160,708 | 21,453 | -0,11331 | 0,000314437 | 1433,679 |
| 1421,339 | 49.99845 | 0,293144 | 0.017589 | -160,708 | 21,453 | -0,11331 | 0,000183918 | 1433,678 |
| 1421,338 | 49.99845 | 0,293145 | 0.017589 | -160,708 | 21,453 | -0,11331 | 0.000053398 | 1433,677 |
| 1421,337 | 49.99845 | 0,293145 | 0.017589 | -160,708 | 21,453 | -0,11331 | -0.00007712 | 1433,676 |
| 1421,336 | 49.99845 | 0,293145 | 0.017589 | -160,708 | 21,453 | -0,11331 | -0.00020764 | 1433,675 |
| 1421,335 | 49.99845 | 0,293145 | 0.017589 | -160,708 | 21,453 | -0,11331 | -0.00033816 | 1433,674 |
| 1421,334 | 49.99845 | 0,293145 | 0.017589 | -160,708 | 21,453 | -0,11331 | -0.00046868 | 1433,673 |
| 1421,333 | 49.99845 | 0,293145 | 0.017589 | -160,708 | 21,453 | -0,11331 | -0.00059920 | 1433,672 |
| Arc with radius R(I)2 | Arc with radius R(II)1 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| V [km/h] |
R(I)2 [m] |
L(I)2 [m] |
am1 [m/s2] |
ψ1 [m/s3] |
V [km/h] |
R(II)1 [m] |
L(II)1 [m] |
am2 [m/s2] |
ψ2 [m/s3] |
| 60 | 585.697 | 100 | 0.47427 | 0.10945 | 90 | 1421.338 | 50 | 0.43973 | 0.30443 |
| 65 | 585.697 | 100 | 0.55661 | 0.13915 | 95 | 1421.338 | 50 | 0.48994 | 0.35804 |
| 70 | 585.697 | 100 | 0.64553 | 0.17380 | 100 | 1421.338 | 50 | 0.54287 | 0.41759 |
| 75 | 585.697 | 100 | 0.74105 | 0.21376 | 105 | 1421.338 | 50 | 0.59852 | 0.48342 |
| 80 | 585.697 | 100 | 0.84314 | 0.25943 | 110 | 1421.338 | 50 | 0.65688 | 0.55582 |
| 85 | 585.697 | 100 | 0.95183 | 0.31118 | 115 | 1421.338 | 50 | 0.71795 | 0.63511 |
| 90 | 585.697 | 100 | 1.06711 | 0.36938 | 120 | 1421.338 | 50 | 0.78174 | 0.72160 |
| 95 | 585.697 | 100 | 1.18897 | 0.43443 | 125 | 1421.338 | 50 | 0.84824 | 0.81561 |
| 100 | 585.697 | 100 | 1.31741 | 0.50670 | 130 | 1421.338 | 50 | 0.91745 | 0.91745 |
| 105 | 585.697 | 100 | 1.45249 | 0.58657 | 135 | 1421.338 | 50 | 0.98939 | 1.02744 |
| 110 | 585.697 | 100 | 1.59407 | 0.67441 | 140 | 1421.338 | 50 | 1.06403 | 1.14588 |
|
h1 [mm] |
V [km/h] |
R(I)2 [m] |
L(I)2 [m] |
am1 [m/s2] |
ψ1 [m/s3] |
f1 [mm/s] |
|---|---|---|---|---|---|---|
| 120 | 105 | 585,697 | 100 | 0,66765 | 0,26963 | 35,00000 |
| 120 | 110 | 585,697 | 100 | 0,80927 | 0,34238 | 36,66667 |
| 120 | 115 | 585,697 | 100 | 0,95748 | 0,42350 | 38,33333 |
| 120 | 120 | 585,697 | 100 | 1,11228 | 0,51336 | 40,00000 |
| 130 | 105 | 585,697 | 100 | 0,60225 | 0,24322 | 37,91667 |
| 130 | 110 | 585,697 | 100 | 0,74387 | 0,31471 | 39,72222 |
| 130 | 115 | 585,697 | 100 | 0,89208 | 0,39457 | 41,52778 |
| 130 | 120 | 585,697 | 100 | 1,04688 | 0,48317 | 43,33333 |
| 130 | 125 | 585,697 | 100 | 1,20826 | 0,58089 | 45,13889 |
| 140 | 110 | 585,697 | 100 | 0,67847 | 0,28705 | 42,77778 |
| 140 | 115 | 585,697 | 100 | 0,82668 | 0,36565 | 44,72222 |
| 140 | 120 | 585,697 | 100 | 0,98148 | 0,45299 | 46,66667 |
| 140 | 125 | 585,697 | 100 | 1,14286 | 0,54945 | 48,61111 |
| 140 | 130 | 585,697 | 100 | 1,31083 | 0,65541 | 50,55556 |
| 145 | 110 | 585,697 | 100 | 0,64577 | 0,27321 | 44,30556 |
| 145 | 115 | 585,697 | 100 | 0,79398 | 0,35118 | 46,31944 |
| 145 | 120 | 585,697 | 100 | 0,94878 | 0,43790 | 48,33333 |
| 145 | 125 | 585,697 | 100 | 1,11016 | 0,53373 | 50,34722 |
|
h2 [mm] |
V [km/h] |
R(II)1 [m] |
L(II)1 [m] |
am2 [m/s2] |
ψ2 [m/s3] |
f2 [mm/s] |
|---|---|---|---|---|---|---|
| 20 | 105 | 1421,338 | 50 | 0,46772 | 0,37777 | 11,66667 |
| 20 | 110 | 1421,338 | 50 | 0,52608 | 0,44514 | 12,22222 |
| 20 | 115 | 1421,338 | 50 | 0,58715 | 0,51940 | 12,77778 |
| 20 | 120 | 1421,338 | 50 | 0,65094 | 0,60086 | 13,33333 |
| 20 | 125 | 1421,338 | 50 | 0,71744 | 0,68984 | 13,88889 |
| 20 | 130 | 1421,338 | 50 | 0,78665 | 0,78665 | 14,44444 |
| 20 | 135 | 1421,338 | 50 | 0,85859 | 0,89161 | 15,00000 |
| 30 | 110 | 1421,338 | 50 | 0,46068 | 0,38980 | 18,33333 |
| 30 | 115 | 1421,338 | 50 | 0,52175 | 0,46155 | 19,13337 |
| 30 | 120 | 1421,338 | 50 | 0,58554 | 0,54050 | 20,00000 |
| 30 | 125 | 1421,338 | 50 | 0,65204 | 0,62696 | 20,83333 |
| 30 | 130 | 1421,338 | 50 | 0,72125 | 0,72125 | 21,66667 |
| 30 | 135 | 1421,338 | 50 | 0,79319 | 0,82369 | 22,50000 |
| 30 | 140 | 1421,338 | 50 | 0,86783 | 0,93459 | 23,33333 |
| 40 | 115 | 1421,338 | 50 | 0,45635 | 0,40369 | 25,55556 |
| 40 | 120 | 1421,338 | 50 | 0,52014 | 0,48013 | 26,66667 |
| 40 | 125 | 1421,338 | 50 | 0,58664 | 0,56408 | 27,77778 |
| 40 | 130 | 1421,338 | 50 | 0,65585 | 0,65585 | 28,88889 |
| 40 | 135 | 1421,338 | 50 | 0,72779 | 0,75578 | 30,00000 |
| 40 | 140 | 1421,338 | 50 | 0,80243 | 0,86416 | 31,11111 |
| 40 | 145 | 1421,338 | 50 | 0,87979 | 0,98130 | 32,22222 |
| 45 | 115 | 1421,338 | 50 | 0,42365 | 0,37477 | 28,75000 |
| 45 | 120 | 1421,338 | 50 | 0,48744 | 0,44994 | 30,00000 |
| 45 | 125 | 1421,338 | 50 | 0,55394 | 0,53263 | 31,25000 |
| 45 | 130 | 1421,338 | 50 | 0,62315 | 0,62315 | 32,50000 |
| 45 | 135 | 1421,338 | 50 | 0,69509 | 0,72182 | 33,75000 |
| 45 | 140 | 1421,338 | 50 | 0,76973 | 0,82894 | 35,00000 |
| 45 | 145 | 1421,338 | 50 | 0,84709 | 0,94483 | 36,25000 |
| 45 | 150 | 1421,338 | 50 | 0,92716 | 1,06980 | 37,50000 |
| 50 | 115 | 1421,338 | 50 | 0,39095 | 0,34584 | 31,94444 |
| 50 | 120 | 1421,338 | 50 | 0,45454 | 0,41976 | 33,33333 |
| 50 | 125 | 1421,338 | 50 | 0,52124 | 0,50119 | 34,72222 |
| 50 | 10 | 1421,338 | 50 | 0,59045 | 0,59045 | 36,11111 |
| 50 | 135 | 1421,338 | 50 | 0,66239 | 0,68786 | 37,50000 |
| 50 | 140 | 1421,338 | 50 | 0,73703 | 0,79372 | 38,88889 |
| 50 | 145 | 1421,338 | 50 | 0,81439 | 0,90836 | 40,27778 |
| 50 | 150 | 1421,338 | 50 | 0,89446 | 1,03207 | 41,66667 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).