1. Introduction
Jets are fluid streams formed by the discharge of fluid through an orifice or nozzle into a surrounding medium, resulting in a momentum-driven flow that entrains and interacts with the ambient fluid. Due to their ability to deliver high momentum fluid, jets are widely employed in practical applications across various engineering domains (
Figure 1). They play a pivotal role in propulsion systems including aircraft engines, rocket propulsion, and marine thrusters (
Figure 1a) where high velocity fluid ejection generates thrust [
1]. Jets are also extensively used in heat and mass transfer applications, such as impinging jets for localized cooling, spray cooling in electronics, and industrial drying processes (
Figure 1b), where enhanced convective transport is critical [
2]. Additionally, they are used in flow control and mixing to improve combustion efficiency, reduce noise, and mitigate pollution (
Figure 1c) by actively manipulating flow fields and enhancing fluid mixing [
3,
4,
5].
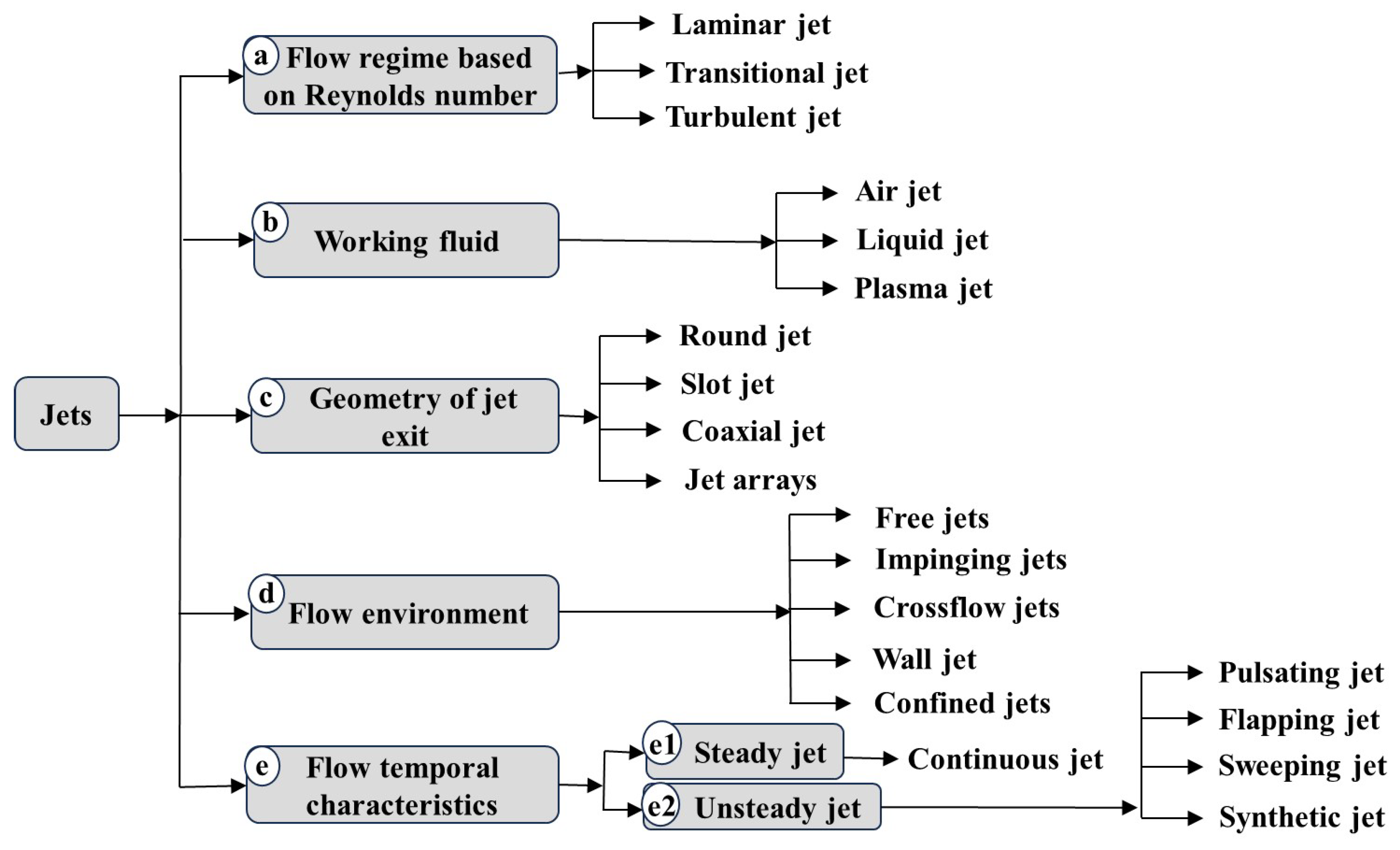
Jets can be broadly classified based on different criteria, as shown in
Figure 2. Depending on the flow regime, jets can be classified as laminar, transitional, or turbulent, with each regime distinguished primarily by the Reynolds number (
Figure 2a). Laminar jets exhibit smooth flow [
6,
7], transitional jets show emerging instabilities [
8], and turbulent jets display chaotic motion with strong mixing [
9,
10]. Classifications based on working fluid (
Figure 2b) are air jets [
11], liquid jets [
12], and plasma jets [
13]. Each type varies in fluid properties and energy requirements, influencing their suitability for specific thermal and flow control applications. Jet classification based on exit geometry (
Figure 2c) includes round jets [
14], slot jets [
15], coaxial jets [
16], and jet arrays [
17]. Each geometry produces distinct flow patterns and spatial coverage, affecting mixing efficiency and heat transfer characteristics. Jets, based on the surrounding flow environment (
Figure 2d), can also be categorized into free jets [
18], impinging jets [
19], crossflow jets [
20], wall jets [
21], and confined jets [
22]. These categories reflect differences in boundary interactions and flow confinement, which significantly influence jet behavior and performance. Additionally, jets based on their temporal characteristics (
Figure 2e) can be classified as steady jets maintaining continuous flow (
Figure 2e1) [
18] and unsteady jets (
Figure 2e2). The latter includes pulsating [
23], flapping [
24], sweeping [
25], and synthetic jets (SJs) [
26]. Steady jets provide consistent flow conditions, while unsteady jets exhibit time-varying dynamics that enhance mixing and flow control capabilities [
27].
Among unsteady jets, synthetic jets are unique in generating periodic vortices through alternating suction and blowing without net mass input [
26]. Their compact design [
19], non-requirement of external fluid to form the jet [
26], precise control over operating parameters [
16], energy efficiency [
28], and easy integration into complex circuits [
29] make synthetic jets well-suited for a wide range of engineering applications.
Figure 2.
Jet classification based on various criteria.
Figure 2.
Jet classification based on various criteria.
1.1. Overview of Synthetic Jets
Over the last two decades, SJs, also referred to as zero-net-mass-flux (ZNMF) actuators [
26], have gained significant attention as an innovative approach in the fields of fluid mechanics [
30,
31] and aerodynamics [
32,
33]. Unlike conventional jet systems that rely on mechanical components such as rotors or blades, SJs operate without any physically moving parts, eliminating issues related to wear and tear [
34]. This inherent characteristic enhances their reliability and extends their operational lifespan compared to traditional mechanical systems [
28].
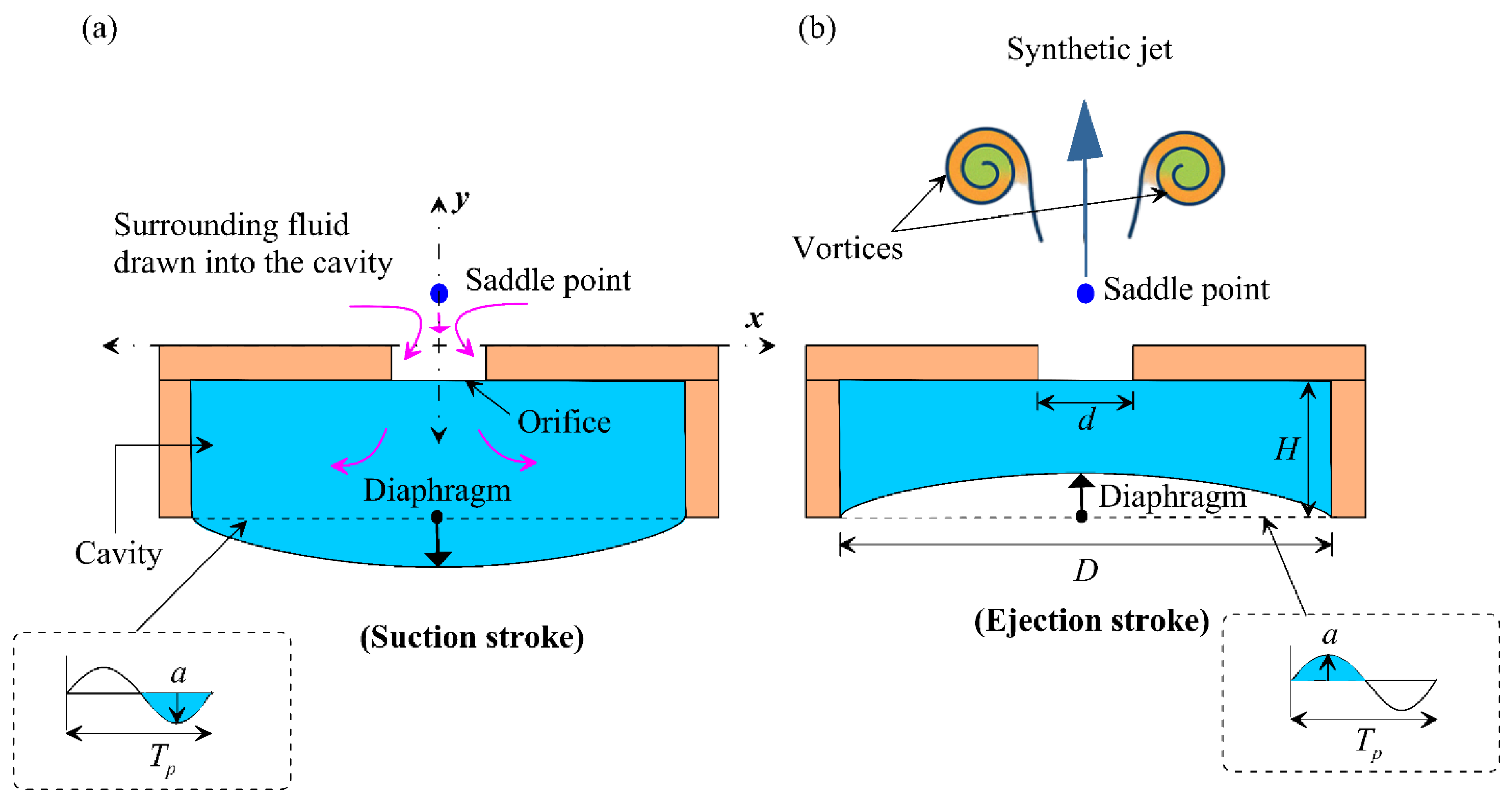
Synthetic jets are typically generated using a fluidic device called a synthetic jet actuator (SJA) (
Figure 3), which consists of a cavity enclosed by a vibrating membrane on one side and an orifice on the other [
26]. The vibrating medium can be a piston-cylinder arrangement [
35], a speaker [
36], or a diaphragm [
16]. When an alternating current (AC) is applied, the diaphragm undergoes oscillatory motion, drawing surrounding fluid into the cavity during the suction stroke (
Figure 3a) and ejecting fluid along with a pair of counter rotating vortices during the ejection stroke (
Figure 3b). This cyclic process generates a series of vortex rings, which collectively form the synthetic jet [
37]. Typically, the ejection phase produces a high velocity jet that dominates the region downstream of the orifice, while the suction phase induces inward flow toward the orifice. These opposing phases create distinct flow regions, with a saddle point often observed near the orifice exit, separating the suction-influenced zone from the ejection-dominated region (
Figure 3). The resulting SJs exhibit high-momentum [
38] and turbulent characteristics [
29].
1.2. Comparative Analysis of Synthetic Jets and Continuous Jets
Unlike continuous jets (CJs), which require an external fluid source, SJAs utilize the surrounding fluid, eliminating the need for additional airflow [
29]. For a given Reynolds number (
Re), synthetic jets exhibit stronger entrainment of the surrounding fluid [
18,
29], leading to a wider and more rapidly spreading jet (
Figure 4a) compared to continuous jets (
Figure 4b). Hot-wire anemometry and Schlieren visualizations confirm that these vortex structures dominate the early development of SJs before transitioning into turbulence downstream [
26,
39]. Under identical operating conditions, SJs generate approximately 1.414 times higher eddy viscosity than CJs, promoting stronger momentum transfer and enhanced mixing due to their pulsatile nature [
27].
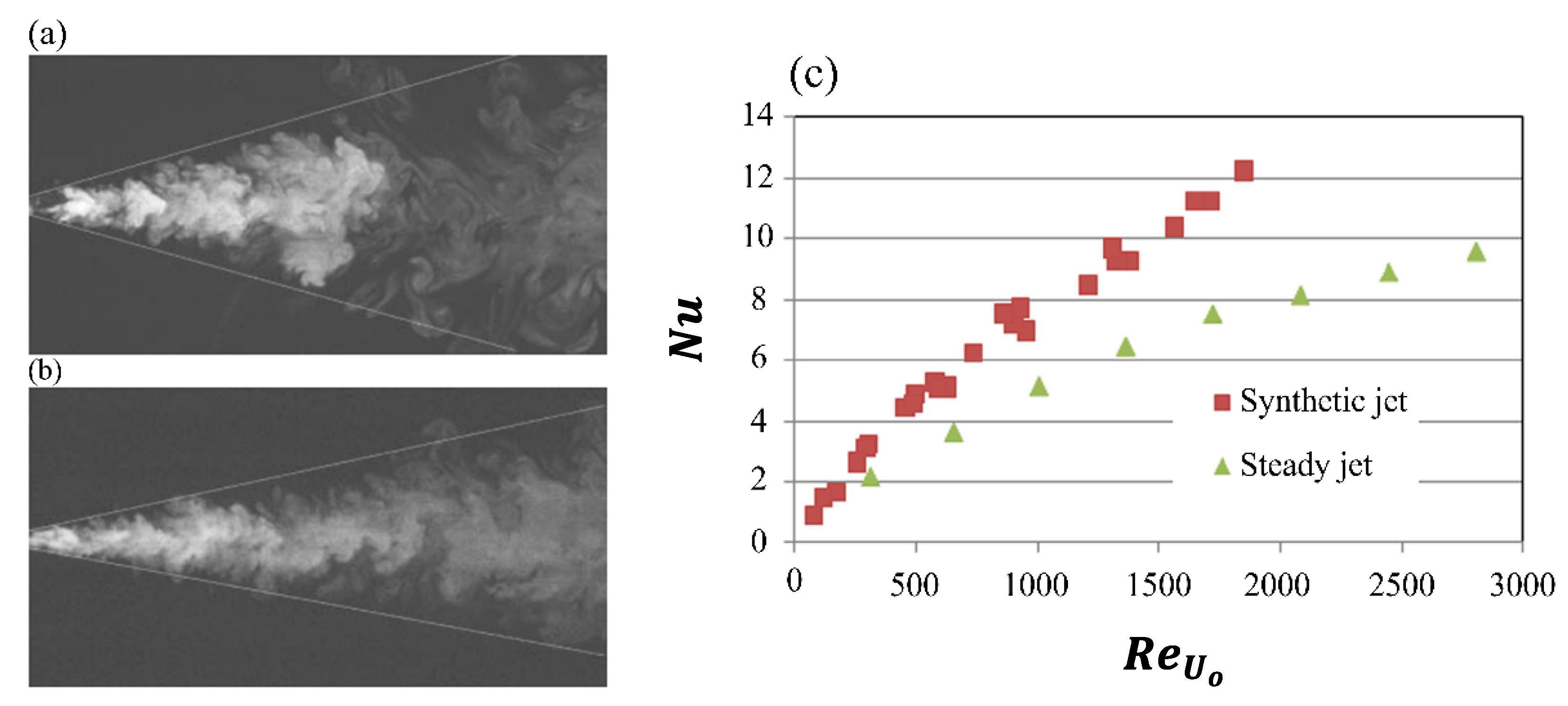
In terms of thermal performance, SJs produce broader and more uniform thermal distributions during impingement cooling. Under identical flow conditions (
≈ 1700), the Nusselt number for SJs exceeded that of CJs by approximately 34% (
Figure 4c), with the improvement attributed to the dynamic entrainment and mixing characteristics of jets [
40]. The enhancement in Nusselt number remains significant across a range of
[
41]. Additional studies support these findings, consistently demonstrating improved convective cooling by SJs relative to CJs under similar operational regimes [
42,
43]. The enhanced entrainment and increased eddy viscosity make synthetic jets a compelling alternative to continuous jets.
Figure 4.
Evolution of synthetic and continuous jets along with their heat transfer characteristics. Flow development of (a) synthetic jets and (b) continuous jets, reproduced with permission from [
18]; (c) variation of Nusselt number with Reynolds number at a jet-to-heated-plate distance of
Y = 10 for both jet types, reproduced with permission from [
40].
Figure 4.
Evolution of synthetic and continuous jets along with their heat transfer characteristics. Flow development of (a) synthetic jets and (b) continuous jets, reproduced with permission from [
18]; (c) variation of Nusselt number with Reynolds number at a jet-to-heated-plate distance of
Y = 10 for both jet types, reproduced with permission from [
40].
1.3. Applications of Synthetic Jets in Various Fields
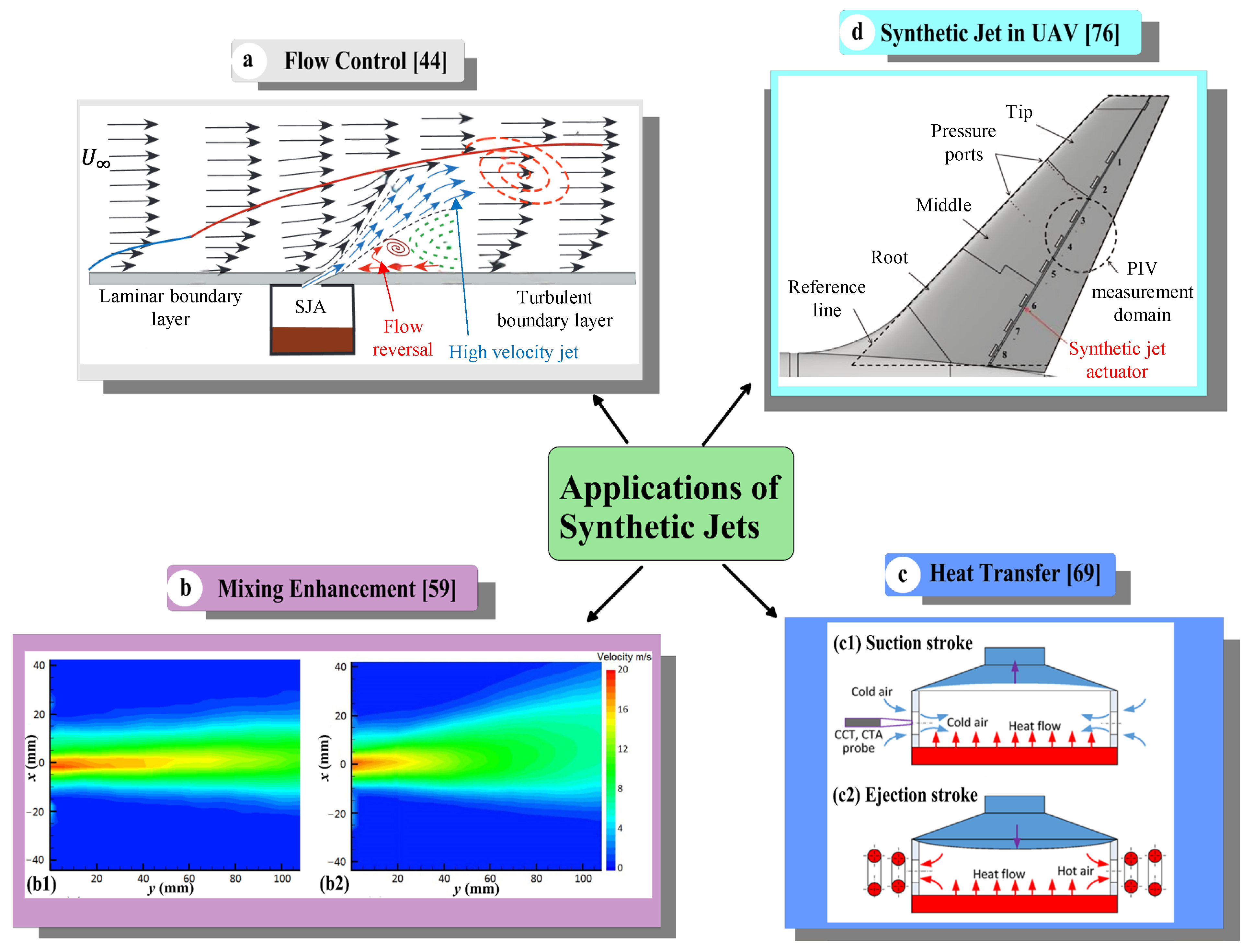
Due to their unique design and operational advantages discussed earlier, synthetic jets have progressed beyond laboratory investigations and are increasingly utilized in various engineering applications. The major applications of synthetic jets are illustrated in
Figure 5. One of the most prominent areas is flow control (
Figure 5a), where synthetic jets inject momentum into the boundary layer, energizing near-wall fluid, generating coherent vortices, and suppressing flow separation. This leads to enhanced lift, reduced drag, and improved maneuverability in aerospace systems [
31,
38,
44,
45,
46,
47,
48,
49,
50,
51,
52,
53,
54,
55,
56,
57,
58]. Synthetic jets are widely used to enhance mixing by introducing unsteady disturbances that intensify turbulence and promote entrainment. This is demonstrated in
Figure 5b, which shows the coaxial jet without synthetic jet actuation (
Figure 5b1) and with actuation (
Figure 5b2). The synthetic jets disrupt the potential core and broaden the shear layer, leading to a thickened outer shear layer and a reduced radial velocity gradient, clear indicators of enhanced entrainment (
Figure 5b2) compared to the case without synthetic jet actuation (
Figure 5b1) [
59]. The enhanced mixing leads to improved combustion efficiency and reduced emissions [
60,
61,
62,
63,
64,
65,
66,
67,
68]. They are also widely adopted in thermal management applications, where their unsteady nature disrupts thermal boundary layers and enhances convective heat transfer [
69]. During the cyclic operation of synthetic jets, the suction stroke draws in cool ambient air (
Figure 5c1), while the ejection stroke expels hot air (
Figure 5c2). This periodic jetting action improves entrainment, increases near-wall turbulence, and significantly enhances convective heat removal from the surface. This is particularly effective for cooling electronic components such as CPUs and GPUs [
15,
22,
43,
70,
71,
72,
73,
74]. Additionally, synthetic jets are employed in unmanned aerial vehicles (UAVs) (
Figure 5d), where their compactness and controllability contribute to aerodynamic efficiency and flight control [
75,
76,
77,
78].
Together with these major areas, synthetic jets have also been explored for underwater propulsion and maneuvering in marine robotics, offering a compact and efficient solution for submerged environments [
75,
77,
78,
79,
80]. These diverse implementations highlight the versatility of synthetic jets and their potential to impact a wide spectrum of engineering domains.
Figure 5.
Applications of synthetic jets in (a) flow control, reproduced with permission from [
44]; (b) mixing enhancement, figure reproduced from [
59], licensed under CC BY 4.0; (c) heat transfer, reproduced with permission from [
69]; and (d) unmanned aerial vehicles (UAVs), reproduced with permission from [
76].
Figure 5.
Applications of synthetic jets in (a) flow control, reproduced with permission from [
44]; (b) mixing enhancement, figure reproduced from [
59], licensed under CC BY 4.0; (c) heat transfer, reproduced with permission from [
69]; and (d) unmanned aerial vehicles (UAVs), reproduced with permission from [
76].
1.4. Review Scope and Objectives
As discussed previously, SJs exhibit strong potential for flow control and thermal management applications, owing to their compact design, ZNMF, ease of integration into miniaturized systems, and independence from external fluid sources. However, a detailed review of the literature highlights three fundamental limitations affecting the practical deployment of synthetic jets, namely restricted jet formation, limited spanwise coverage, and rapid loss of momentum and coherence in the far field due to vortex diffusion. These core issues remain largely unaddressed in existing literature, where most studies focus on specific performance aspects without identifying or correlating the underlying challenges with specific design strategies. This review is the first to explicitly define these inherent drawbacks and systematically assess the technological advancements.
The review categorizes and evaluates four major SJ configurations, namely dual cavity jets, single actuator multi-orifice jets, coaxial jets, and synthetic jet arrays, based on their ability to mitigate these limitations. Each configuration is analyzed in terms of momentum delivery, spatial coverage, and vortex structure sustainability. Performance improvements through design modifications, actuator arrangements, and control of operating parameters are critically examined alongside unresolved challenges. By establishing a clear link between the observed limitations in single actuator configurations and the functional enhancements achieved through more advanced arrangements, this review offers a solid foundation for future research and design optimization. This assessment is crucial due to the rising demand for compact, efficient flow control along with thermal management solutions in miniaturized electronics, aerospace, and next-generation energy systems.
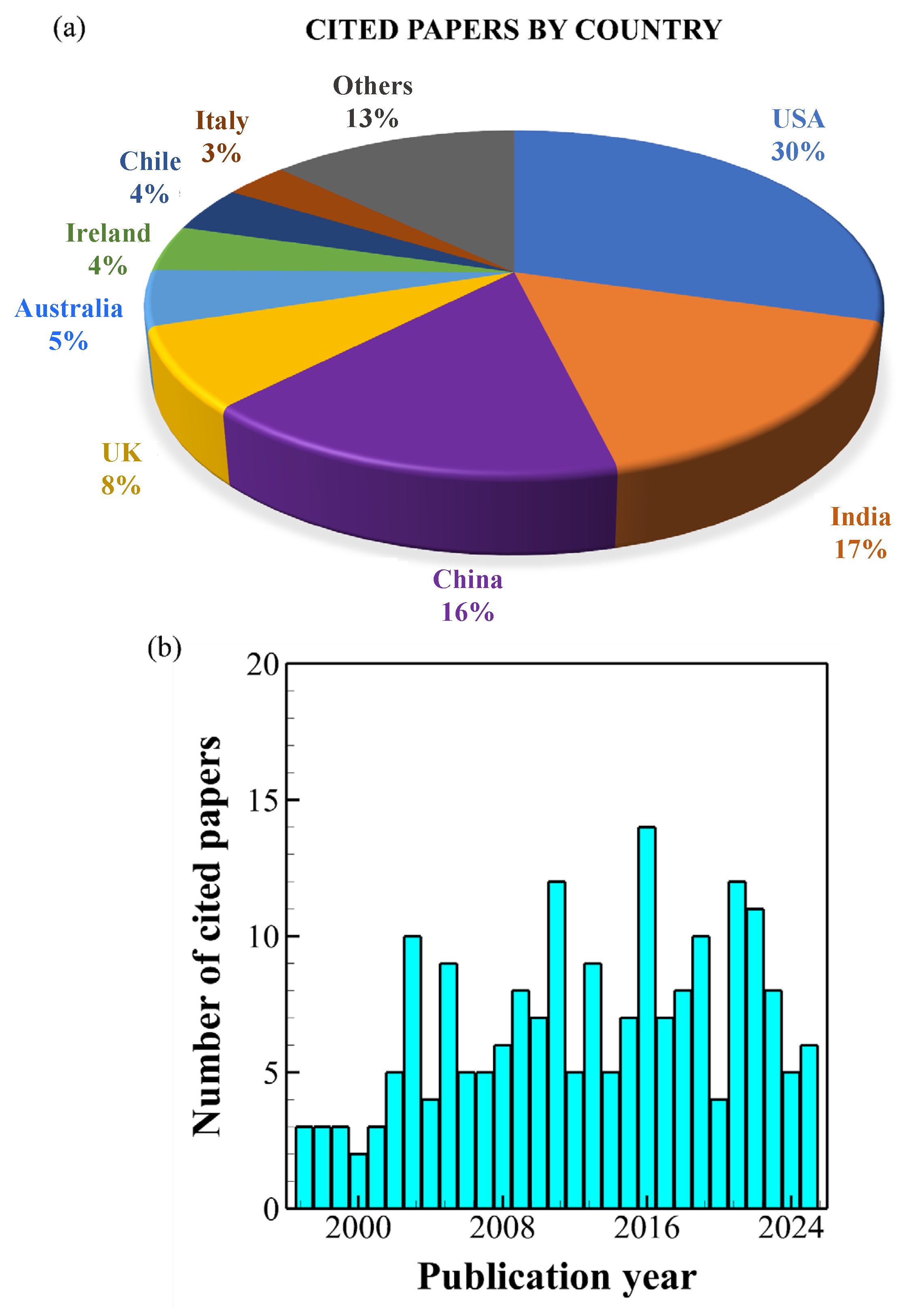
To provide a quantitative overview of the literature surveyed in this review,
Figure 6 presents the distribution of cited papers by country (a) and by year of publication (b). This illustrates the geographical spread and temporal evolution of research in synthetic jet technologies, highlighting growing international interest and increasing publication trends over the past two decades. In recent years, greater emphasis has been placed on the practical implementation of synthetic jets in cooling and flow control applications, reflecting a shift toward real-world applicability and system-level integration. This review offers a comprehensive synthesis of existing knowledge that not only clarifies key challenges and technological progress but also provides a valuable foundation for guiding future research and development efforts toward more effective and practical synthetic jet solutions.
2. Key Parameters Governing Flow and Heat Transfer in Synthetic Jets
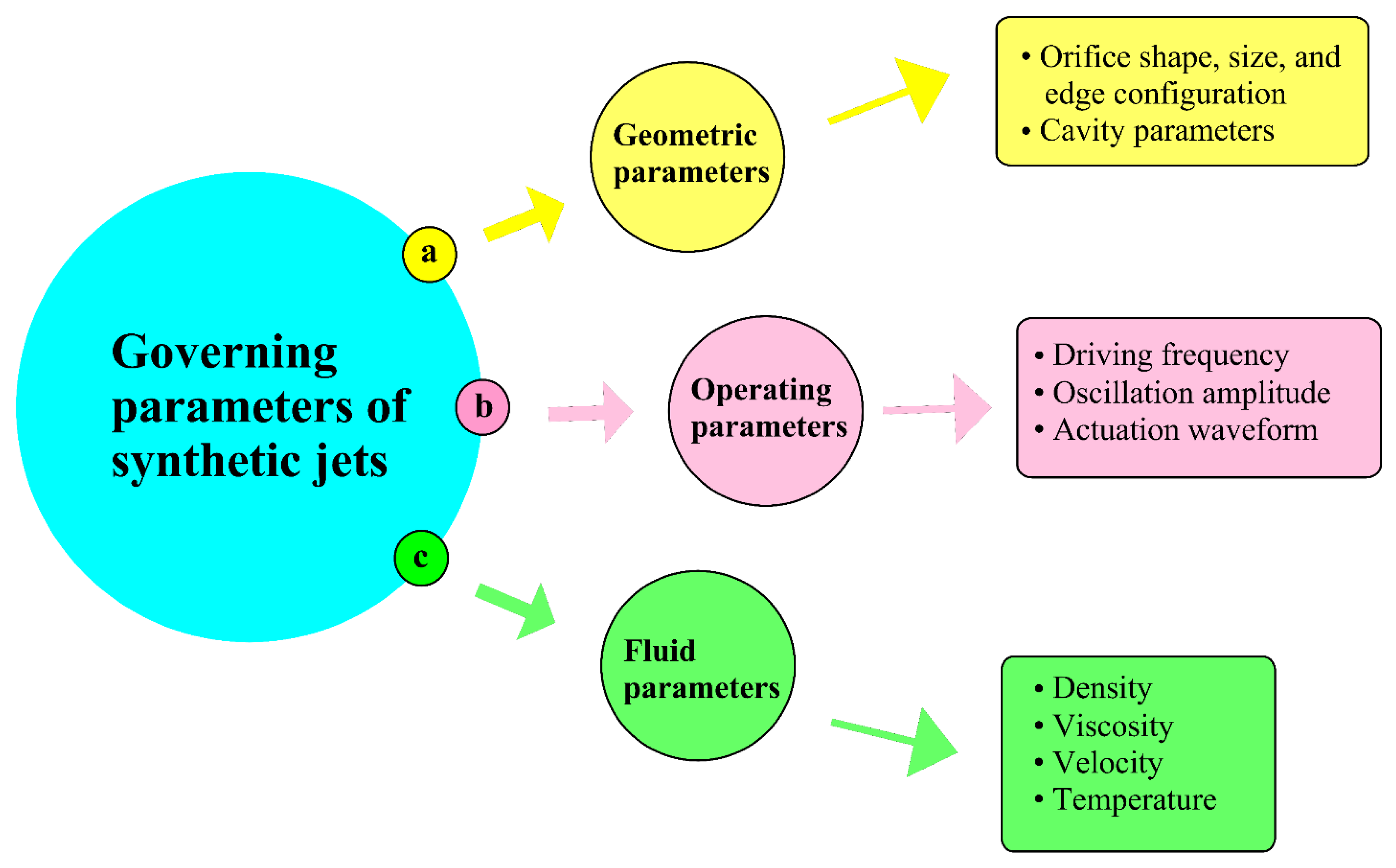
The performance of synthetic jets, encompassing both flow dynamics and heat transfer, is strongly governed by a combination of geometric, operational, and fluid parameters (
Figure 7). Additionally, various non-dimensional numbers (
Figure 8) are critical in describing the development and interaction of synthetic jets with the surrounding flow and thermal fields. This section outlines the key parameters that influence the overall behavior and effectiveness of synthetic jets.
2.1. Geometric Parameters of SJA
The geometry of an SJA plays a crucial role in defining its flow behavior and performance. Two primary geometric aspects govern this behavior, namely the orifice configuration, referring to its shape, size, and edge, and the cavity parameters (
Figure 7a). The orifice shape, size, and edge configuration directly influence the exit jet's velocity profile, directionality, and coherence [
81]. Circular, rectangular, and slit-shaped orifices generate distinct vortex structures and entrainment characteristics. Smaller orifices produce faster, more focused jets due to concentrated momentum, while larger ones yield slower, higher-volume jets with broader coverage [
82]. However, an increase in peak jet velocity resulting from a reduced orifice size does not necessarily lead to a proportional increase in Reynolds number or entrainment capability [
83]. The orifice edge configuration significantly affects vortex formation and jet performance; sharp edges enhance vortex roll-up and momentum flux, while rounded edges improve entrainment and mixing but reduce axial velocity and impingement strength [
84,
85].
The cavity parameters largely affect the actuator's resonant behavior and energy transfer efficiency. Together with the orifice, the cavity forms a system that closely resembles a Helmholtz resonator, where the air inside the cavity acts as a compressible spring, and the slug of air oscillating through the orifice behaves as an inertial mass [
86]. A larger cavity volume enhances compressibility, lowering the natural oscillation frequency, while a larger orifice area reduces inertial resistance, thereby raising the frequency [
87]. Optimal actuator performance typically occurs near the resonant frequency, where stronger vortex formation and higher jet velocities enhance flow control and heat transfer [
88].
2.2. Operating Parameters of SJA
A critical aspect of synthetic jet actuator operation is the membrane oscillation. The key input parameters controlling this oscillation include the driving frequency, oscillation amplitude, and actuation waveform (
Figure 7b), which govern jet formation and vortex dynamics, and influence both flow control and heat transfer performance.
2.2.1. Driving frequency ()
The actuation frequency of the oscillating membrane determines the rate at which SJs are produced during each oscillatory cycle. An increase in frequency typically leads to higher jet velocities and the formation of stronger vortex structures, which can be beneficial in applications requiring rapid and dynamic flow control. In contrast, lower frequencies tend to generate more stable jets with reduced turbulence, making them more suitable for conditions where steady flow behavior is desired [
87].
2.2.2. Oscillation amplitude ()
Amplitude reflects the extent of membrane displacement during each oscillation cycle. A larger amplitude typically induces greater fluid movement, resulting in stronger jet formation. This parameter significantly influences the evolution and spreading characteristics of the jet [
89]. Moreover, variations in amplitude influence the formation and spreading of vortices within the flow, which directly impacts the mixing efficiency and heat transfer performance of the jet.
2.2.3. Actuation Waveform
Synthetic jet actuators can be operated using various waveforms, including sinusoidal, square, and triangular signals. The choice of waveform influences the jet’s temporal behavior, leading to differences in velocity profiles and vortex dynamics. These waveforms affect the rate of diaphragm acceleration and deceleration during each cycle, which in turn alters the strength and structure of the expelled vortices. Square waveforms tend to produce sharper transitions and more abrupt vortex shedding, whereas sinusoidal signals generate smoother, more continuous flow development [
90,
91]. These variations affect the balance between suction and expulsion phases, altering the jet's symmetry, strength, and temporal characteristics, which collectively impact its overall performance. By modifying the waveform, the thermal and momentum transport characteristics of the jet can be adjusted to meet specific application requirements [
92].
2.3. Fluid Parameters in SJA
The thermophysical properties of the working fluid, including density, viscosity, velocity, and temperature, play a critical role in shaping the behavior of synthetic jets (
Figure 7c). These properties govern the momentum and heat transport mechanisms that influence the formation, evolution, and stability of vortical structures during each actuation cycle, particularly under varying thermal conditions [
31]. Density determines the inertial response and penetration capability of the flow [
13]. Viscosity affects the rate of vorticity diffusion, thereby influencing the coherence and dissipation of the jet [
93]. Fluid velocity contributes directly to the jet momentum and the vortex strength [
26,
94]. Temperature variations not only modify the intrinsic properties of fluid but also influence key dimensionless numbers, such as the Reynolds and Prandtl numbers, which are critical to both flow dynamics and thermal transport [
95]. These effects become increasingly significant in applications involving strong thermal gradients, where precise control of jet behavior is essential for optimal performance.
2.4. Characteristics of Dimensionless Numbers Governing Synthetic Jet Behavior
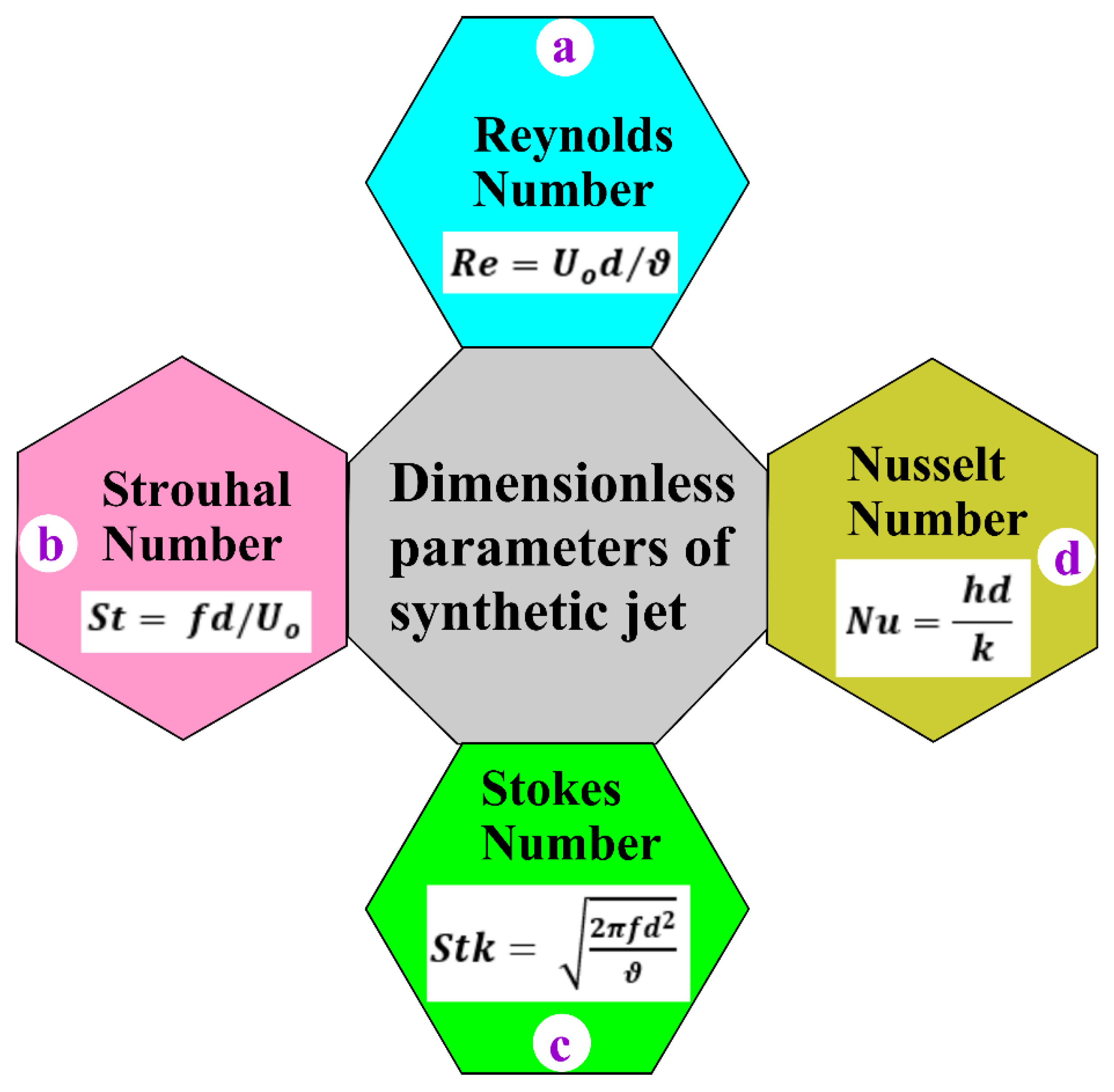
The dimensionless parameters simplify the influence of operating conditions and fluid properties into meaningful quantities that help understand patterns in vortex motion, jet development, and heat transfer. Various key dimensionless quantities, such as the Reynolds number (
), Strouhal number (
), Stokes number (
), and Nusselt number (
), as illustrated in
Figure 8, provide insight into the fundamental physics governing jet behavior and thermal transport.
Figure 8.
Nondimensional parameters governing the flow and heat transfer characteristics of synthetic jets.
Figure 8.
Nondimensional parameters governing the flow and heat transfer characteristics of synthetic jets.
2.4.1. Reynolds Number ()
The Reynolds number is a fundamental dimensionless parameter that characterizes the flow behavior of SJs (
Figure 8a). It indicates the nature of the flow regime, distinguishing whether the flow remains laminar or transitions to turbulence. In SJ applications, the Reynolds number affects vortex formation, jet penetration, and overall mixing behavior [
37].
The Reynolds number is defined as [
26]
where
is the time-averaged jet velocity during the ejection stroke,
is the orifice diameter or slot width, and
is the kinematic viscosity of the working fluid. The
is related to the stroke length and actuation frequency as
where
The denotes the stroke length, representing the effective displacement of the jet during the blowing half-cycle. The is the instantaneous centerline velocity at the orifice exit, and represents the period of one complete actuation cycle, where is the diaphragm frequency.
To account for the distributed nature of the exit velocity, Utturkar et al. [
96] later proposed a Reynolds number formulation based on the average velocity over time and space across the orifice area, i.e.,
where
is defined as
In this formulation,
represents the local velocity at the orifice exit as a function of time and transverse coordinate
, and
is the orifice area. The two velocity scales are related as
Both definitions are commonly used, depending on the experimental approach or modelling requirements. A higher Reynolds number typically correlates with increased jet momentum, enhanced vortex strength, and improved mixing and heat transfer performance [
97].
2.4.2. Strouhal Number ()
The Strouhal number (
Figure 8b) is a dimensionless quantity that governs the relationship between actuation frequency, orifice dimension, and time-averaged jet velocity. It can be expressed as [
26]
This parameter characterizes the interaction between periodic actuation and the inertia of the fluid, which plays a significant role in shaping the formation and spacing of vortical structures. It influences the generation of discrete vortex pairs during each actuation cycle by relating the actuation frequency and orifice geometry to the resulting fluid motion. According to Smith and Glezer [
26], the
is the inverse of the nondimensional stroke length and controls the axial distance from the orifice where vortex pairs or rings are shed. Experimental results indicate that at lower
values, vortex rings form farther apart, reducing mutual interaction and shifting the breakdown location downstream [
37]. On the other hand, high
values prevent proper vortex separation, resulting in flow being drawn back into the cavity during the suction phase, thereby disrupting jet formation. The vortex formation condition that incorporates the combined effects of Reynolds number,
, and Stokes number (
) was introduced by Holman et al. [
98]. For jets issuing from planar orifices, formation is observed when
and for axisymmetric jets, the corresponding criterion is
These expressions define the minimum conditions required for effective vortex roll-up and sustained jet formation during the ejection phase.
2.4.3. Stokes Number ()
The Stokes number (
Figure 8c) is another important parameter that influences the evolution of vortices in synthetic jet flows. It captures the combined effects of actuation frequency, orifice size, and fluid viscosity on the unsteady behavior of the flow near the orifice. For synthetic jets, the Stokes number is defined as [
99]
This quantity plays a crucial role in determining whether coherent vortices can form and separate from the orifice. Earlier investigations reported that the strength of the vortex roll-up mechanism diminishes as
decreases [
99]. Experimental results showed that when the
falls below 7, the shear layer cannot produce well-defined vortex structures [
99]. Generally, a Stokes number around or above 10 is considered necessary to ensure the formation of distinct vortex rings that can detach and propagate downstream, contributing to effective SJ formation.
2.4.4. Nusselt Number ()
The Nusselt number (
Figure 8d) is a key parameter for evaluating the convective heat transfer performance of SJs. It is defined as
where
is the convective heat transfer coefficient and
represents the thermal conductivity of the working fluid.
The area-average Nusselt number (
) can be expressed as:
Here, is the surface area of the heated object.
Synthetic jets enhance convective heat transfer by periodically ejecting and ingesting fluid, disrupting the thermal boundary layer and promoting vortex-induced mixing. The resulting Nusselt number is governed by vortex strength, actuation frequency, oscillation amplitude, and the orifice-to-surface spacing. Several studies [
11,
88,
100] have shown that careful adjustment of these operating conditions can significantly increase both local and average Nusselt numbers. This makes SJs particularly effective for thermal management applications.
3. Flow Characteristics of Synthetic Jets
A comprehensive overview of the geometric configurations, operating conditions, fluid properties, and non-dimensional parameters influencing synthetic jet behavior has been presented earlier. This section reviews key experimental and numerical studies that examine the effects of these factors on vortex dynamics and flow characteristics. In addition to offering deeper insight into the relevant flow phenomena, the discussion also highlights limitations and challenges related to synthetic jets, particularly in engineering applications with specific performance requirements.
3.1. Influence of Geometric Parameters on SJ Flow Characteristics
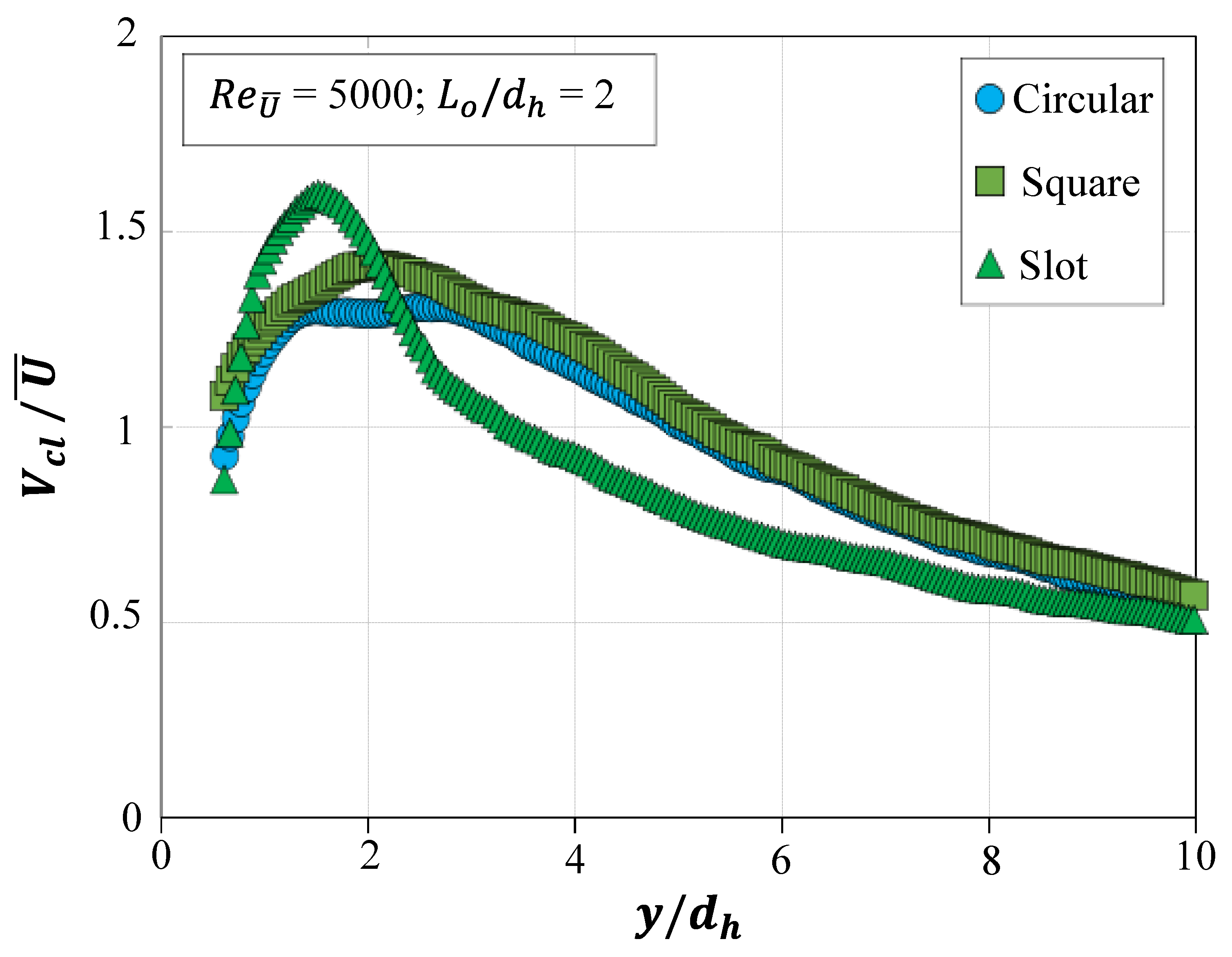
The geometric configuration of SJA exerts a critical influence on jet formation, flow development, and downstream momentum transfer. For the same orifice area, actuation frequency, and actuation amplitude, a comparison of circular, square, slot, and triangular orifices revealed that the triangular orifice performs best in terms of peak centerline velocity (
) [
82]. The percentage enhancement of peak
for the triangular orifice is approximately 6%, 24%, and 31% compared to the circular, slot, and square orifices, respectively. However, the triangular orifice exhibits the highest decay in
among all the orifice shapes. For instance, the triangular orifice shows a decay of approximately 42% in
between
1 (where
reaches its peak) and
4 [
82]. Here,
is the hydraulic diameter, defined as
= 4 × orifice area / perimeter. This significant reduction in
is attributed to the pronounced weakening of jet strength in the downstream direction [
82]. A similar drastic reduction in
for circular, square, and slot orifices can also be observed in
Figure 9, indicating that all orifice shapes experience substantial weakening of jet strength with downstream distance [
101]. Moreover, studies have shown that rectangular orifices generate broader vortex structures and enhanced lateral spreading; however, rapid diffusion of vortex strength in the far field remains a significant drawback [
82,
102].
The design of the orifice edge adds an additional dimension to the aerodynamic behavior. Sharp orifice edges typically facilitate stronger vortex roll-up and higher momentum flux [
84], whereas rounded or beveled edges tend to suppress flow separation and enhance lateral entrainment [
85]. Although the latter improves mixing, it often reduces axial velocity and impingement strength. Further insights from Smith and Swift [
103], Shuster and Smith [
37], and Cater and Soria [
18] revealed that orifice edge design affects vortex roll-up and propagation during the expulsion phase. Nani and Smith [
104] quantified the impact of inner edge rounding, showing that it reduces acoustic power input up to a radius of 0.5
. Beyond this threshold, power consumption increases due to loss of wall attachment and suction inefficiency.
Figure 9.
Variation of jet centerline velocity (
) along the streamwise direction (
) for different orifice shapes. Figure reproduced from [
101], licensed under CC BY 4.0.
Figure 9.
Variation of jet centerline velocity (
) along the streamwise direction (
) for different orifice shapes. Figure reproduced from [
101], licensed under CC BY 4.0.
Internal cavity dimensions further modulate jet characteristics, especially through their interaction with the acoustic response of the actuator. A reduced cavity height strengthens vortex shedding and improves near-field momentum transfer [
85,
105,
106,
107]. Conversely, under resonance conditions, larger cavities can support enhanced jet velocities by amplifying acoustic oscillations [
108]. This resonance-based performance improvement has been extensively documented [
87,
109,
110], and is often associated with peak output occurring at or near the actuator’s Helmholtz frequency [
86,
111]. These studies collectively highlight the importance of tuning cavity dimensions to balance jet strength, frequency response, and energy efficiency.
Along with poor far field performance, another primary limitation of single actuator configurations is that the generated stroke volume is inherently constrained by physical displacement and chamber size of the actuator. As a result, the time-averaged mass flow rate remains relatively low when considered for various engineering applications [
21,
112,
113,
114].
3.2. Effect of Non-Dimensional Parameters on SJ Flow Dynamics
As discussed earlier, the flow characteristics of synthetic jets are governed by several dimensionless parameters, including the Reynolds number, , and , along with that is inherently related to both Reynolds number (Equations 1 and 2) and (Equation 7) through its dependence on . These dimensionless parameters encapsulate the effects of actuation frequency, oscillation amplitude, and fluid properties, thereby governing jet flow behaviors.
Operation of the SJA at low
limits SJ formation by preventing vortices from moving far enough from the orifice during the blowing phase. This causes stronger suction effects that disrupt coherent vortex development, resulting in weaker jets and reduced fluid mixing, which are major drawbacks restricting effective jet formation [
21]. As
increases, the spacing between successive vortices grows, significantly affecting the jet's spatial development. In rectangular configurations, a higher
enhances lateral spreading but causes a transition from a discrete vortex train to a more continuous jet flow, resulting in a weakened jet due to increased vortex diffusion [
27]. The best performance occurs in the range 4 ≤
< 8, where a balance is achieved between vortex strength and stability. In contrast, for
8, the primary vortices become unstable and eventually lose coherence, giving rise to trailing jets that dominate the downstream flow [
115].
A higher
produces stronger and more stable vortex rings, thereby enhancing momentum flux [
116]. However, as the jet propagates away from the orifice, vortex diffusion causes a rapid decay in jet velocity. For example, Shuster and Smith [
37] showed that synthetic jets operating at
= 10
4 experience a 33% drop in peak streamwise velocity between
= 2 and 5, and nearly a 50% reduction between
= 5 and 10, highlighting the significant impact of vortex diffusion in the far field. In flow control applications, moderate Reynolds numbers combined with a low-frequency actuation have shown improved flow reattachment using less momentum input than high-frequency strategies [
117]. Nonetheless, maintaining jet effectiveness at higher Reynolds numbers remains challenging due to enhanced turbulence and diffusion losses in the far field.
The
St integrating actuation frequency, flow velocity, and jet size (Equation 7) characterizes jet formation and behavior. In two-dimensional and axisymmetric jets, the
ratio governs the onset of vortex shedding and the development of coherent flow structures [
96,
98]. Operating outside the optimal
range can inhibit the formation of discrete vortex rings or lead to unstable and ineffective flow regimes. For instance, in high Reynolds number impinging jets, lower Strouhal numbers shift the flow dominance from the primary jet to trailing jets, thereby weakening the actuator control capability and effectiveness [
118]. Additionally, spanwise instabilities and secondary flow structures, such as rib-like vortices, emerge under certain operating conditions, further contributing to the decay of jet strength. The
plays a pivotal role in dictating the onset, scale, and evolution of these flow features, as it influences both the initial vortex formation and the subsequent development of three-dimensional instabilities [
119].
The Stokes number has emerged as a particularly important nondimensional parameter for evaluating synthetic jet coherence. Coherent jets typically form only when the Stokes number exceeds a critical threshold, often around 8.5, and when the stroke length ratio is greater than 4 [
99]. Below these values, vortex formation is weak or suppressed entirely, leading to low-momentum jets incapable of effective flow control or heat transfer. As the jet moves downstream, the increasing Kolmogorov length scale reflects vortex breakdown and reduced mixing efficiency [
49]. Research has shown that counter-rotating vortex pairs near the orifice dissipate rapidly, becoming indistinct beyond one wavelength and causing significant velocity decay beyond
10, thereby highlighting challenges to long-range jet effectiveness [
120]. This rapid jet diffusion in the far field has also been demonstrated earlier (
Figure 4a) by Cater and Soria [
18].
While appropriate values of , , , and enhance near-field entrainment and vortex coherence, these advantages progressively weaken downstream due to vortex breakdown and diffusion. The combined limitations of insufficient jet formation and reduced jet strength beyond the near field represent fundamental challenges to employing SJs in applications demanding sustained and spatially extensive flow control.
3.3. Impact of Waveform on Flow Dynamics of SJs
The shape of the actuation waveform directly impacts the dynamic response of SJs, influencing the suction and ejection of fluid through oscillatory membrane motion. This, in turn, affects vortex formation and the momentum of the jet. In the region close to the wall, sine wave excitation typically leads to optimal performance, as it facilitates smoother transitions between the suction and blowing cycles, supporting stable vortex formation [
68]. However, as the jet moves farther from the orifice, square waves prove more effective in delivering momentum due to their higher power input, enhancing jet strength. On the other hand, triangular waveforms fail to effectively stabilize the flow, resulting in weaker jet performance and a higher tendency for wake unsteadiness [
68].
The type of actuator used further affects the jet velocity. With piezoelectric actuators, square and pulse waveforms generate stronger jets compared to sine wave excitations, which produce lower peak velocities [
14]. The way the waveform is modulated also plays a significant role. Dual sine waves, when modulated at low frequencies and voltages, result in higher velocity ratios than single sine inputs at higher voltages, providing a more energy-efficient approach to generating momentum [
121]. Similarly, square and sawtooth waveforms enhance the velocity profiles, with square waveforms producing the most robust jets in terms of peak output [
122,
123].
4. Heat Transfer Characteristics of Synthetic Jets
Here, we focus on the heat transfer behavior of SJs under various geometric and nondimensional configurations, providing a comprehensive understanding of the mechanisms through which SJs enhance heat transfer. Additionally, the effectiveness of SJs in various cooling applications is examined, along with the challenges and limitations associated with their use for thermal enhancement.
4.1. Influence of Geometric Parameters on Synthetic Jet Heat Transfer Characteristics
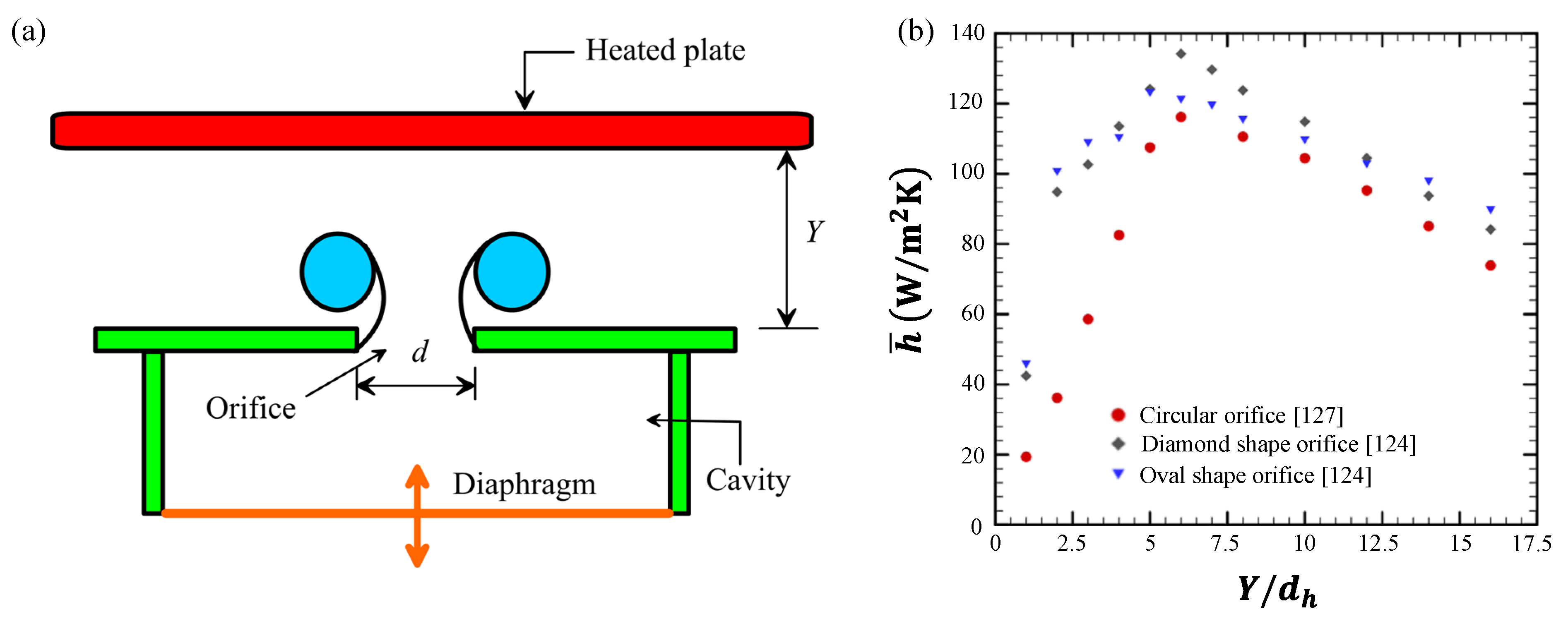
A synthetic jet impingement configuration illustrating the jet-to-surface spacing (
) is shown in
Figure 10(a). Among the common orifice shapes, such as circular, square, and rectangular, square orifices exhibit strong heat transfer performance in the near field but experience a significant decline as
increases, showing approximately a 46% drop in
between
6 (where heat transfer peaks) and
20 [
81]. This significant drop in heat transfer is attributed to the drastic loss of jet strength at larger spacings [
81]. A similar trend is observed for circular and rectangular orifices, where thermal enhancement diminishes noticeably with increasing
[
81]. Nonconventional orifice shapes, such as diamond and oval, have demonstrated superior thermal performance compared to the traditional circular configuration (
Figure 10b). At 200 Hz, diamond orifices provide up to 17% higher area-average heat transfer coefficient (
) than circular ones (
Figure 10b). However, a significant decline of approximately 40% in thermal performance is observed as the jet-to-surface distance increases from
6 to
16 [
124]. Oval orifices perform better at smaller
and are particularly effective in compact configurations (
Figure 10b), but like others, their efficiency deteriorates with
[
124]. When orifice shapes with equal exit areas are compared, rectangular geometries offer slightly better stagnation point performance, while circular ones yield more uniform heat distribution, especially at larger spacings. Despite variations in geometry, the overall trend remains a consistent decline in thermal performance with increasing
[
41].
The roles of orifice diameter, aspect ratio, and cavity depth are equally significant. Among these, the aspect ratio significantly influences near-wall behavior and jet development. Elliptical orifices with moderately low aspect ratios around 1.4 have been shown to enhance heat transfer at smaller
(<6) [
125]. Increasing the aspect ratio tends to produce elongated vortex structures that improve mixing and momentum exchange near the surface compared to circular jets, thereby further enhancing heat transfer. However, increasing the aspect ratio beyond a certain threshold does not necessarily yield further improvement. In fact, doubling the aspect ratio has been associated with a decline in heat transfer performance by approximately 15%, highlighting that the geometric advantage is limited to specific operating conditions [
125]. Similarly, increased cavity depth and hydraulic diameter contribute positively to heat transfer, with maximum Nusselt numbers typically occurring around
= 6 [
126]. Additionally, optimizing the cavity design to operate at the actuator’s resonance frequency can significantly enhance heat transfer; however, this improvement diminishes as the jet-to-surface spacing increases beyond an optimal range [
127]. These findings are consistent with previous studies showing that, although geometric optimization can significantly enhance thermal performance in the near field, the rapid decay of jet strength and coherence at greater distances remains a fundamental limitation [
128,
129,
130,
131].
Extensive investigations into orifice shape, size, and cavity configuration have demonstrated that thermal performance can be optimized under specific conditions. However, a consistent pattern emerges across the literature as synthetic jets are fundamentally limited by a rapid decline in momentum and vortex structure beyond the near field. This leads to a marked drop in heat transfer performance, typically in the range of 40% – 46% as spacing increases. The degradation is due to vortex diffusion, which disrupts the coherence of the jet and limits its effectiveness in the far field.
4.2. Influence of Dimensionless Parameters on Heat Transfer
The thermal performance of SJs is closely tied to their unsteady vortex dynamics and governed by , , , and . These parameters collectively influence the formation, strength, and coherence of vortex structures, thereby modulating both local and global heat transfer behavior.
4.2.1. Nondimensional Stroke Length
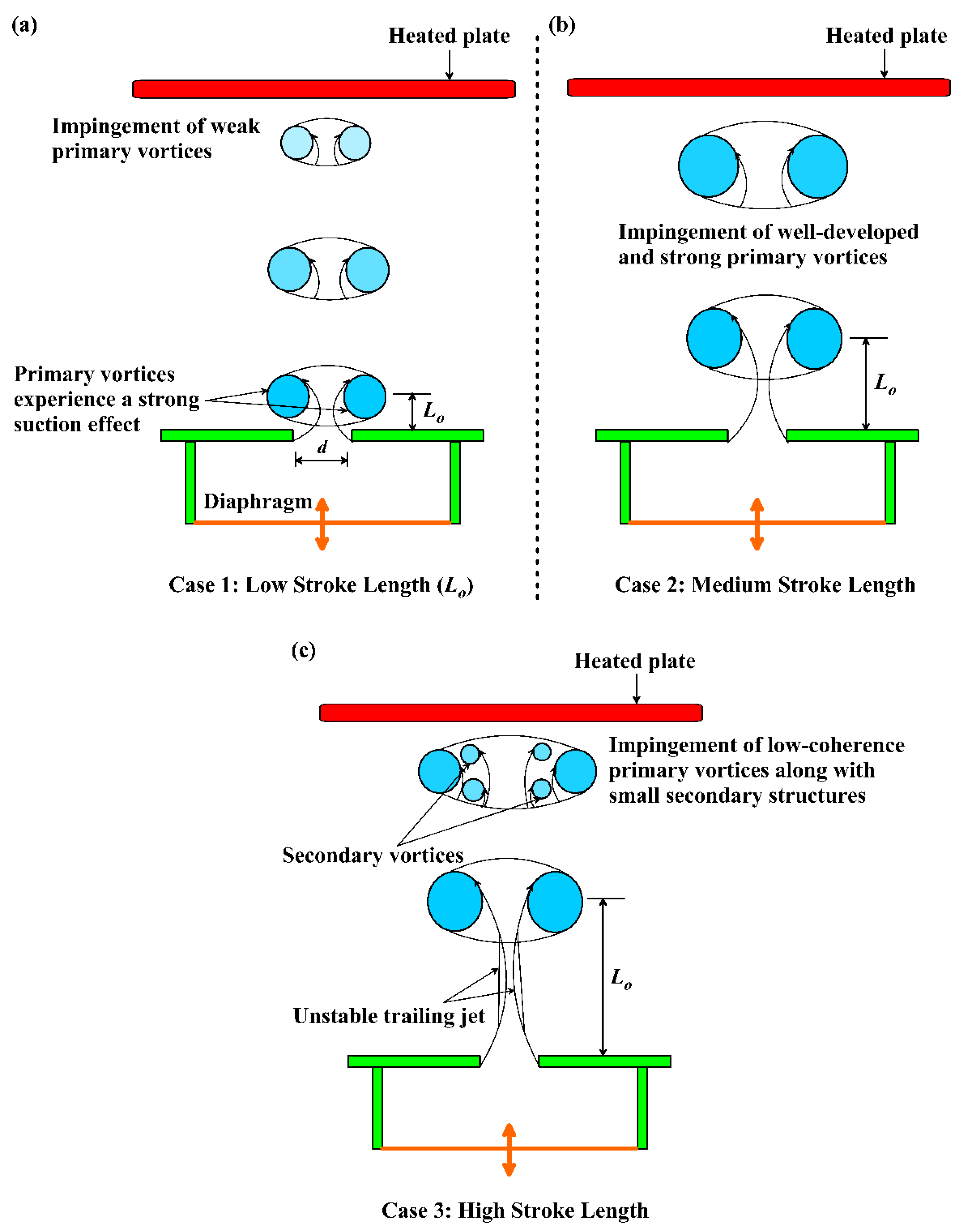
The
serves as a governing parameter for the thermal performance of SJs by regulating the formation, strength, and propagation of vortex rings. The dynamics of the vortices and the impingement heat transfer behavior of the synthetic jet operated at low, moderate and high
are illustrated in
Figure 11. At low values of
4 (
Figure 11a), the strong suction effect during the suction stroke disrupts vortex formation, resulting in underdeveloped primary vortices that dissipate rapidly. This leads to weak impingement and limited heat transfer enhancement (
Figure 11a) [
115]. As
increases to a moderate range between 6 and 8, coherent vortex structures develop, enabling more effective momentum transfer and improved convective transport (
Figure 11b). Within this regime, a marked increase in heat transfer at the stagnation region is observed, consistent with phase-resolved measurements that identify a transition in vortex behavior around
5 [
100]. However, at higher
values (
Figure 11c), the unstable trailing jet promotes vortex instabilities and the formation of small secondary vortical structures, which reduce the coherence of the primary vortices before they impinge on the heated surface, leading to diminished thermal performance [
115].
Experimental findings further support this trend, showing an enhancement of approximately 105% in the peak
at
2 when the stroke length ratio is reduced from
= 13.75 to 7.86 [
127]. However, even at the optimal
7.86, a substantial 64% drop in
is observed between the near field (
2 corresponding to the peak) and the far field (
14), which is attributed to the pronounced reduction in jet strength with increasing
. This decline in far-field performance, despite operating at the optimal
, aligns with findings reported by other researchers [
127,
132]. Ineffective heat transfer in the far field was also observed by Chaudhari et al. [
127] for synthetic jets operating within a Reynolds number (
) range of 1500 to 4200. A similar trend was reported by Persoons et al. [
133] across varying Strouhal numbers (
= 0.15 − 0.35), indicating that the diminished thermal performance in the far field is largely insensitive to changes in these parameters.
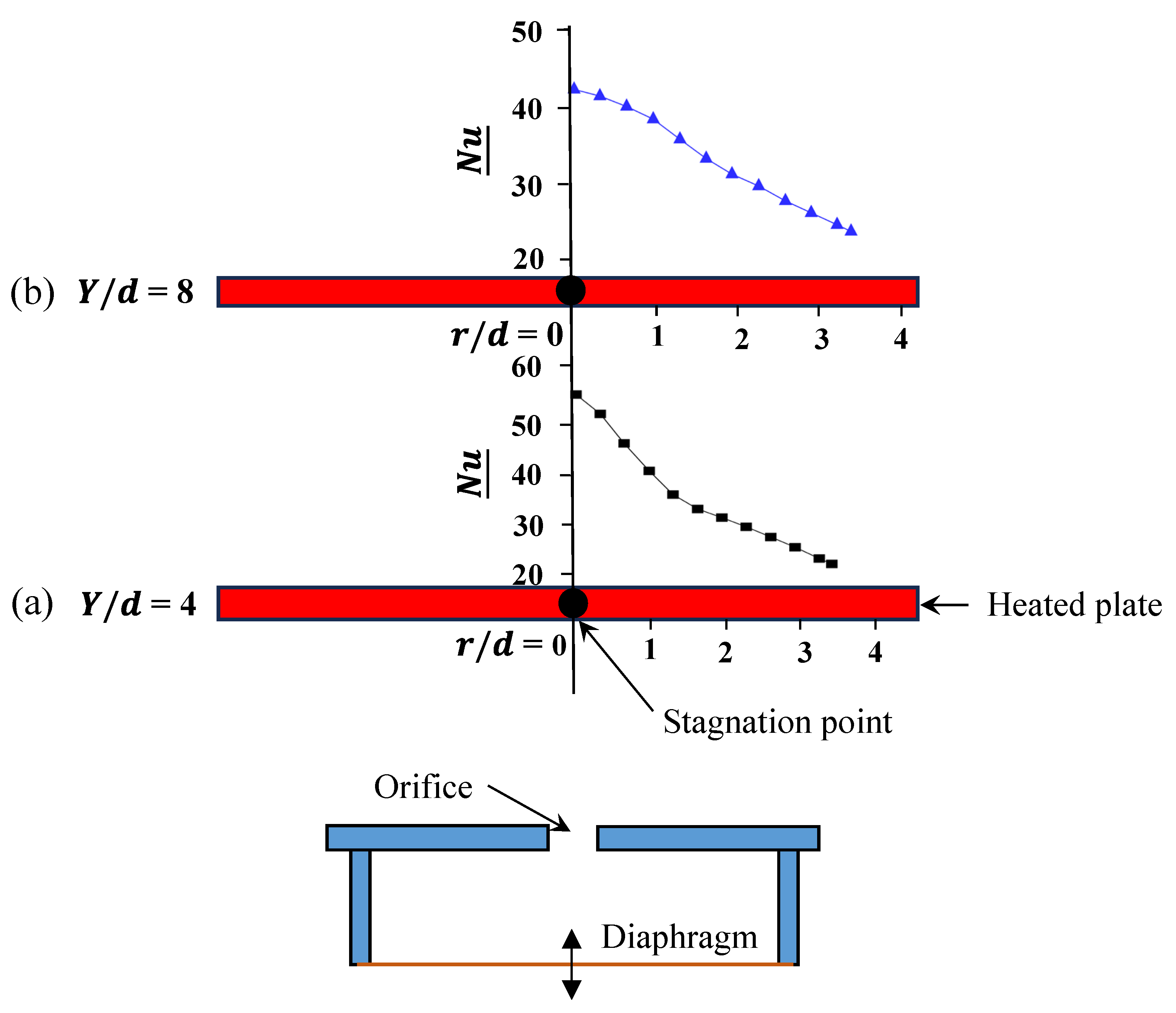
Even when operated at a moderate
(= 10), synthetic jets exhibit another primary drawback, namely limited spanwise coverage (
Figure 12). The radial distribution (
) of the time averaged Nusselt number (
) at
5250 demonstrates a consistent decline in heat transfer intensity away from the jet centreline [
134]. Regardless of
(
Figure 12), the heat transfer performance reduces noticeably with increasing radial distance. For instance, at
4,
decreases by approximately 52% between
0 and 3.5 (
Figure 12a), indicating a significant loss in thermal effectiveness across the surface. This observation reflects the concentrated nature of vortex-induced momentum transfer in synthetic jets, which remains dominant near the core but weakens rapidly with lateral distance. As a result, the inability to maintain strong radial coverage limits the suitability of synthetic jets for applications requiring broad and uniform thermal control [
134]. This limitation is further highlighted in the work of Rylatt and O’Donovan [
135], where thermal enhancement was predominantly confined to the core region.
Although operating at optimal stroke lengths enhances near-field heat transfer due to coherent vortex formation, SJs exhibit poor thermal performance in the far field as jet strength rapidly deteriorates with distance. Moreover, the spanwise coverage remains limited, as the influence of coherent structures is largely confined near the jet axis, restricting the effective cooling of large surface areas.
Figure 12.
Radial distribution of time-averaged Nusselt number (
) for the synthetic jet operated at
5250,
= 10 at (a)
= 4 and (b)
= 8, derived from data in [
134].
Figure 12.
Radial distribution of time-averaged Nusselt number (
) for the synthetic jet operated at
5250,
= 10 at (a)
= 4 and (b)
= 8, derived from data in [
134].
4.2.2. Influence of Oscillation Frequency
Frequency, though dimensional, is often characterized by dimensionless parameters like the Stokes number (Equation 10), which relates frequency, orifice diameter, and fluid viscosity. SJAs perform optimally when operating near resonant frequencies, including mechanical or diaphragm resonance frequency (
) and fluidic or Helmholtz resonance frequency (
). The diaphragm resonance is primarily determined by the physical properties of the actuator membrane and its geometry [
134], while Helmholtz resonance is influenced by cavity and orifice dimensions [
136]. At these resonant conditions, membrane displacement and pressure oscillations are maximized, thereby enhancing the volume and strength of fluid ejection [
86,
87,
88]. Previous studies have reported that for both circular and square orifices, the heat transfer increases with excitation frequency and reaches a maximum at the Helmholtz resonant frequency, after which it begins to decline [
81,
127]. However, even at the optimal resonant frequency, the area-averaged heat transfer coefficient in the far field (
= 20) shows a substantial decrease, with a reduction of about 40% for the circular orifice and about 45% for the square orifice compared with their respective peak values (
6.25 for both orifices) [
81,
127]. Similarly, SJAs operated under different Reynolds numbers and heat flux conditions reveal that although resonance improves local mixing and impingement, the strength of the vortices deteriorates rapidly with increasing axial distance [
11].
The frequency of oscillation significantly influences the near-field, far-field, and overall performance of SJAs [
137,
138]. Even beyond the resonance frequency (>
), SJAs demonstrate enhanced heat transfer in the near field (
≈ 5) at a higher excitation frequency. This improvement is attributed to the more rapid generation and accumulation of coherent vortices near the orifice, which impinge collectively and enhance local mixing [
137]. Ghaffari et al. [
138] made a similar observation and further reported that the high frequency leads to increased power consumption and noise. This, in turn, reduces the coefficient of performance (COP), particularly in configurations operating above the diaphragm or Helmholtz resonance. Despite marginal gains in convective enhancement, the associated energy inefficiency and acoustic penalties make such operating conditions less favorable for practical applications [
138]. Moreover, these densely packed vortices lose coherence rapidly as they propagate downstream, breaking into smaller, less effective structures, and consequently diminishing far-field performance [
137,
139]. In contrast, at lower frequencies, the spacing between successive vortex rings is larger, allowing each vortex to impinge independently on the target surface. This improves coherence retention and leads to better heat transfer further downstream [
137].
To extend synthetic jet functionality beyond conventional frequency limits, operating in the ultrasonic regime (above 20 kHz) has shown promise in enhancing heat transfer by generating densely packed vortices that behave like a quasi-steady jet [
19]. Piezoelectric-driven ultrasonic SJAs offer compactness and low noise, making them well-suited for micro-scale thermal applications [
140,
141]. Even with these advantages, far-field ineffectiveness in heat transfer is still observed due to the rapid decay of jet momentum downstream [
19]. Together with this, excessively short stroke lengths at ultrasonic frequencies can limit net fluid displacement and volumetric flow rate [
142], while thermal loading and material fatigue pose additional reliability concerns. Although operating SJAs at optimal (resonant) or ultrasonic frequencies enhances near-field performance, the steep decline in far-field effectiveness remains a concern for synthetic jets.
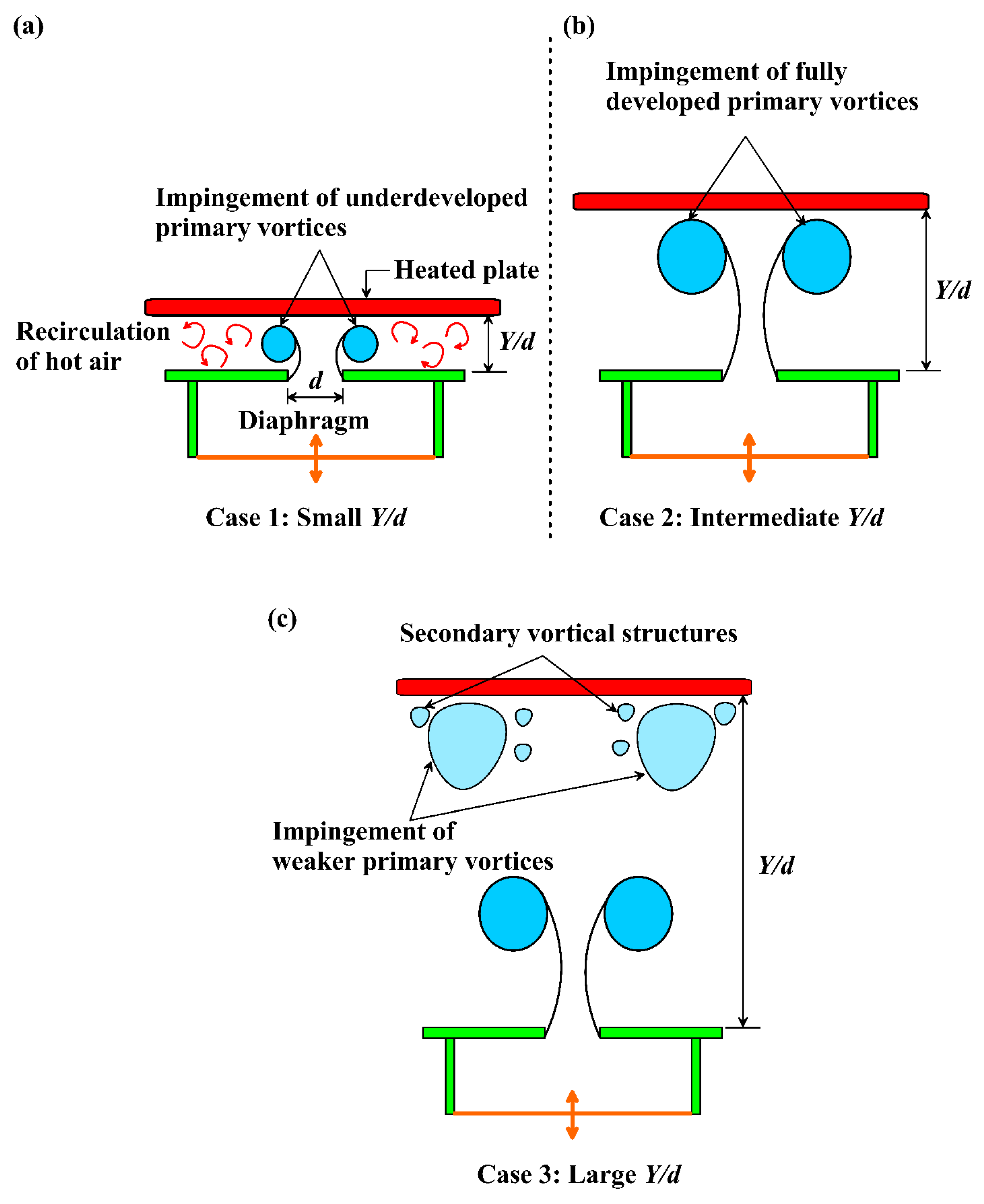
4.2.3. Jet-to-Heated Plate Distance ()
The behavior of synthetic jets at different
values has been extensively studied, revealing distinct regions of performance [
11,
23,
40,
42,
100,
128,
133,
137,
143,
144,
145,
146]. Based on previous findings [
127], the relationship between heat transfer and
can be classified into three stages: increasing heat transfer (
< 5), maximum heat transfer (
= 5 – 9), and decreasing heat transfer (
> 9). These three trends are linked to three stages of jet development: prematured (small
), matured (intermediate
), and over-matured (large
) as explained in
Figure 13.
When
is small, the limited spacing between the orifice and the target surface prevents the vortices from fully developing before reaching the surface. In addition, the confined spacing traps hot air and promotes recirculation (
Figure 13a). The heat transfer thus increases with increasing
in this regime [
71,
132]. The intermediate values of
(
Figure 13b) allow for the full development of the primary vortices, with the impingement of coherent vortical structures on the surface resulting in the highest heat transfer [
11]. On the other hand, when
is large (
Figure 13c), the primary vortices lose significant coherence and even break into small vortical structures before impingement, leading to a sharp decline in cooling performance. Such behavior is consistently reported across multiple studies [
81,
127,
137,
138,
146,
147,
148,
149]. Gillespie et al. [
11] noted up to a 36% drop in heat transfer between
= 18 (intermediate) and
= 23 (large).
In addition to heat transfer decay with increasing
, synthetic jets suffer from significant limitations in spanwise coverage. For the single-orifice SJA at
= 6, a pronounced reduction in heat transfer is observed across the span, with the Nusselt number dropping by approximately 58% from the stagnation point (
= 0) to the outer region (
= 4) [
150]. This is attributed to the rapid spanwise decay in jet strength [
150].
5. Technological Advancements of Synthetic Jets
A detailed flow and heat transfer study identified three fundamental drawbacks of SJs: (a) limited jet formation, particularly when driven by a single actuator; (b) reduced spanwise effectiveness, which limits their applicability in scenarios requiring wide area coverage; and (c) diminished far field performance due to the rapid decay of jet strength caused by strong vortex diffusion. Collectively, these limitations constrain the practical implementation of synthetic jets in real-world applications. Here, various technological advancements aimed at addressing these limitations are discussed in detail, with a focus on their effectiveness in enhancing SJ performance.
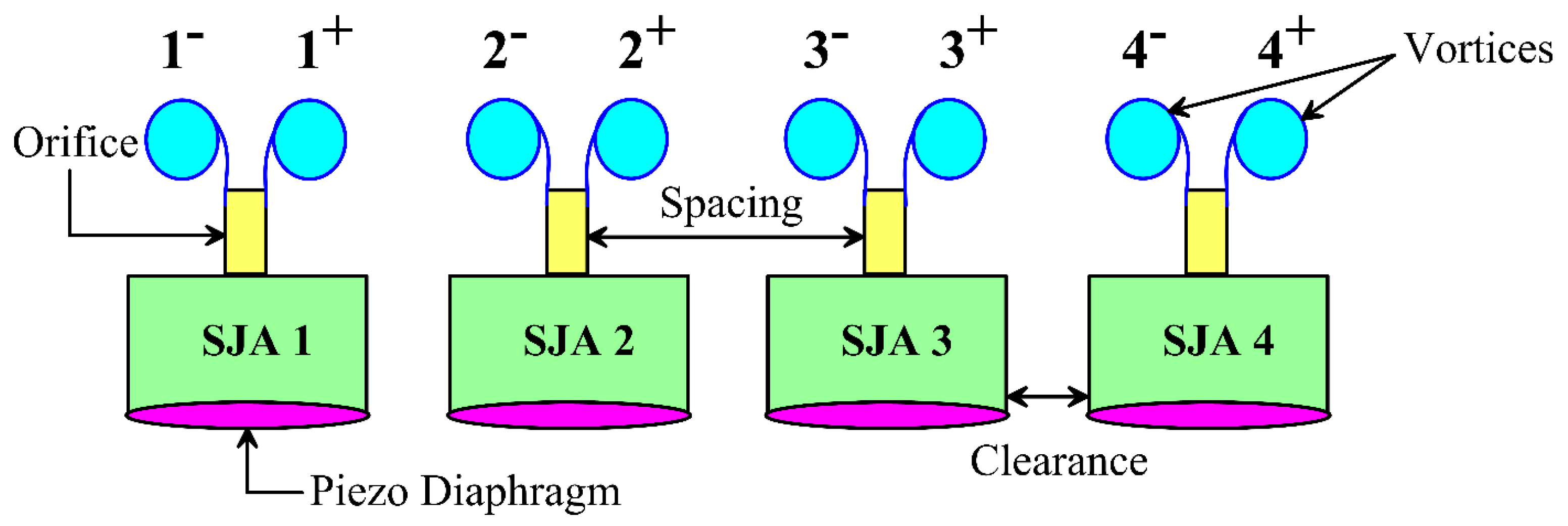
5.1. Dual Cavity Synthetic Jets (DSJs)
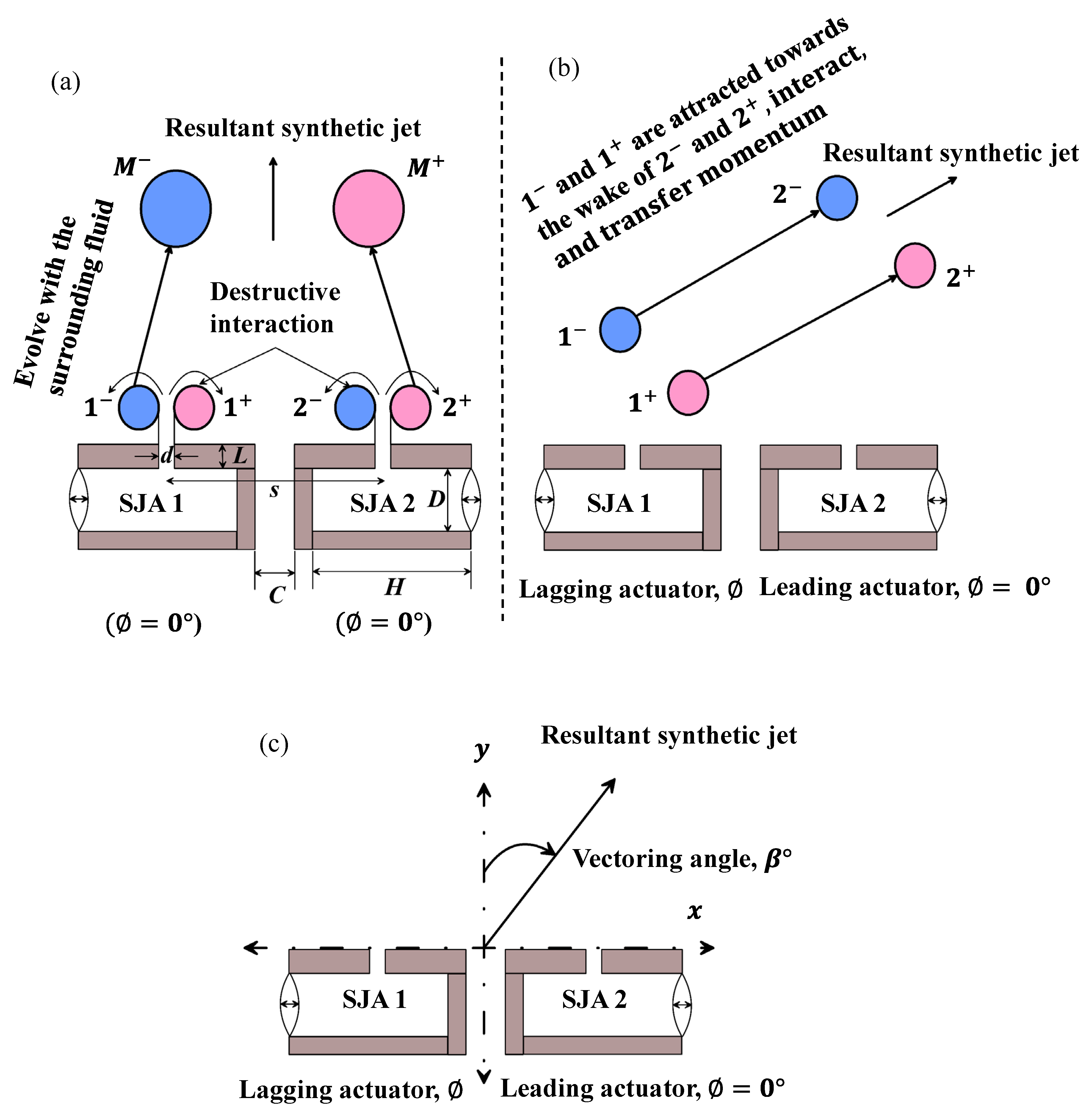
Dual synthetic jets (
Figure 14), consisting of two actuators adjacent to each other and operating either in phase or out of phase, offer greater control over vortex interactions compared to a single SJ [
112]. When the DSJ operates in phase (
0°), each actuator generates a pair of counter rotating vortices, namely vortices
and
from SJA 1, and
and
from SJA 2 (
Figure 14a). Due to their opposite sense of rotation, the inner vortices (
and
) undergo destructive interaction near the centerline, while the outermost vortices (
and
) evolve through interaction with the ambient fluid to form merged vortices, denoted as
and
, respectively (
Figure 14a). These merged vortices convect in a straight downstream direction (
Figure 14a and a). Studies have reported that under in-phase operation, the volume flow rate produced by the DSJ is approximately twice that of a single synthetic jet actuator (
Figure 15c) [
112].
In contrast, when a phase difference (
) is introduced between the actuators (
Figure 14b), with SJA 2 leading SJA 1, vortices
and
form earlier and convect with their self-induced velocities. The wake generated by the leading vortices entrains the lagging vortices
and
, which share the same rotational direction. This interaction leads to momentum transfer from the lagging to the leading vortices, which in turn causes vectoring of the resultant jet toward the leading actuator (
Figure 14b and b). This directional control, or vectoring, was later attributed to a mechanism known as the "attract impact causing deflection" (AICD) [
151]. The vectoring angle (
) is typically measured as the angle between the vertical axis (
= 0) and the direction of convection of the resultant jet (
Figure 14c and
Figure 15b). The angle is considered positive when the jet vectors toward the leading actuator and negative when it vectors toward the lagging actuator [
114]. Further studies have shown that the vectoring angle increases with increasing phase difference [
112,
152].
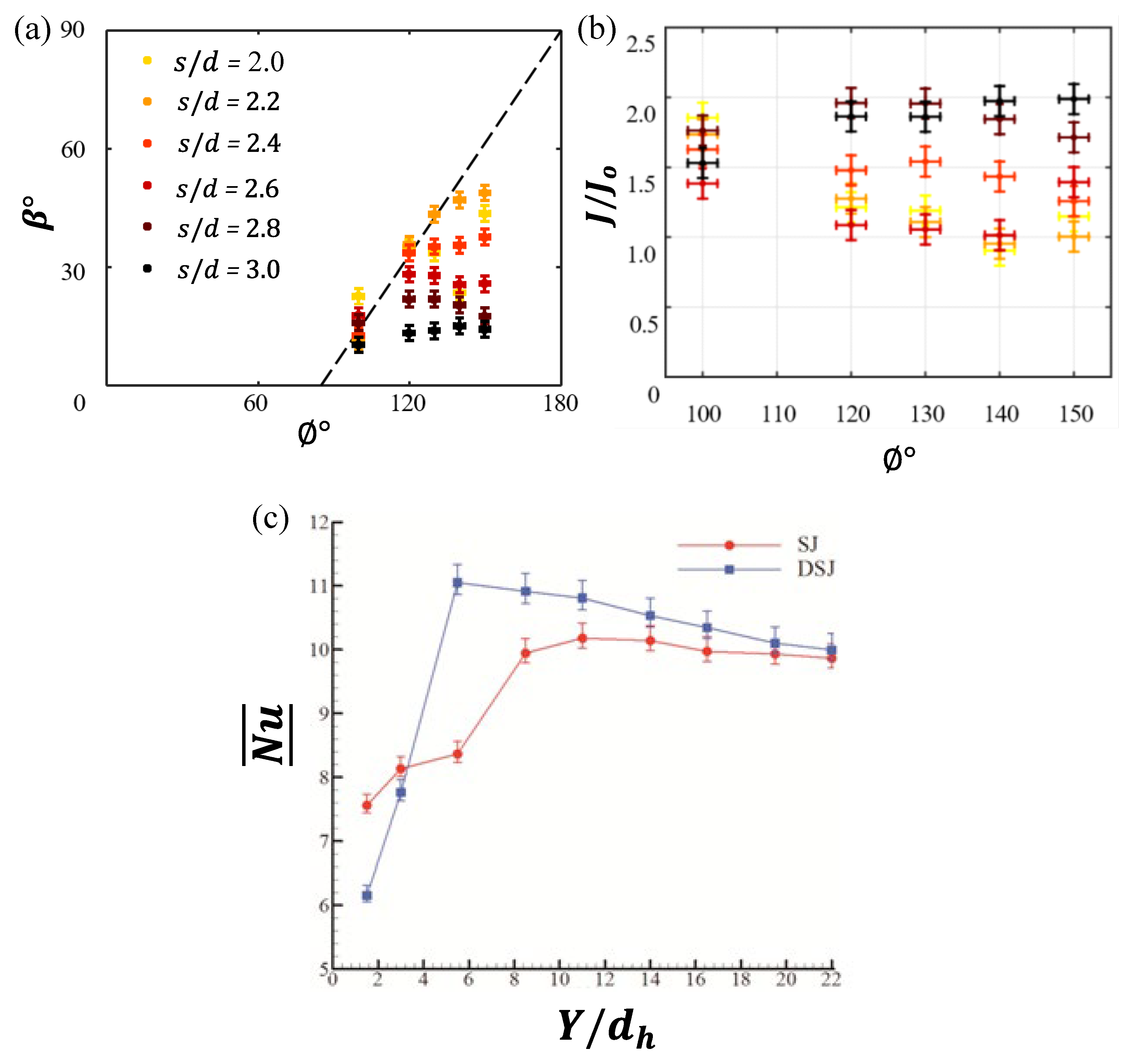
Figure 14.
Schematic representation showing (a) dual synthetic jets operated in phase (), (b) DSJ operated with a phase difference where SJA 2 leads SJA 1, and (c) demonstration of vectoring angle () calculation.
Figure 14.
Schematic representation showing (a) dual synthetic jets operated in phase (), (b) DSJ operated with a phase difference where SJA 2 leads SJA 1, and (c) demonstration of vectoring angle () calculation.
DSJs offer advantages over single-actuator SJs by generating multiple vortices that entrain more surrounding fluid, thereby increasing the volume flow rate [
112]. Additionally, their vectoring capability enables wider spanwise coverage [
112,
152,
153]. However, far-field ineffectiveness remains a key drawback of DSJs. For
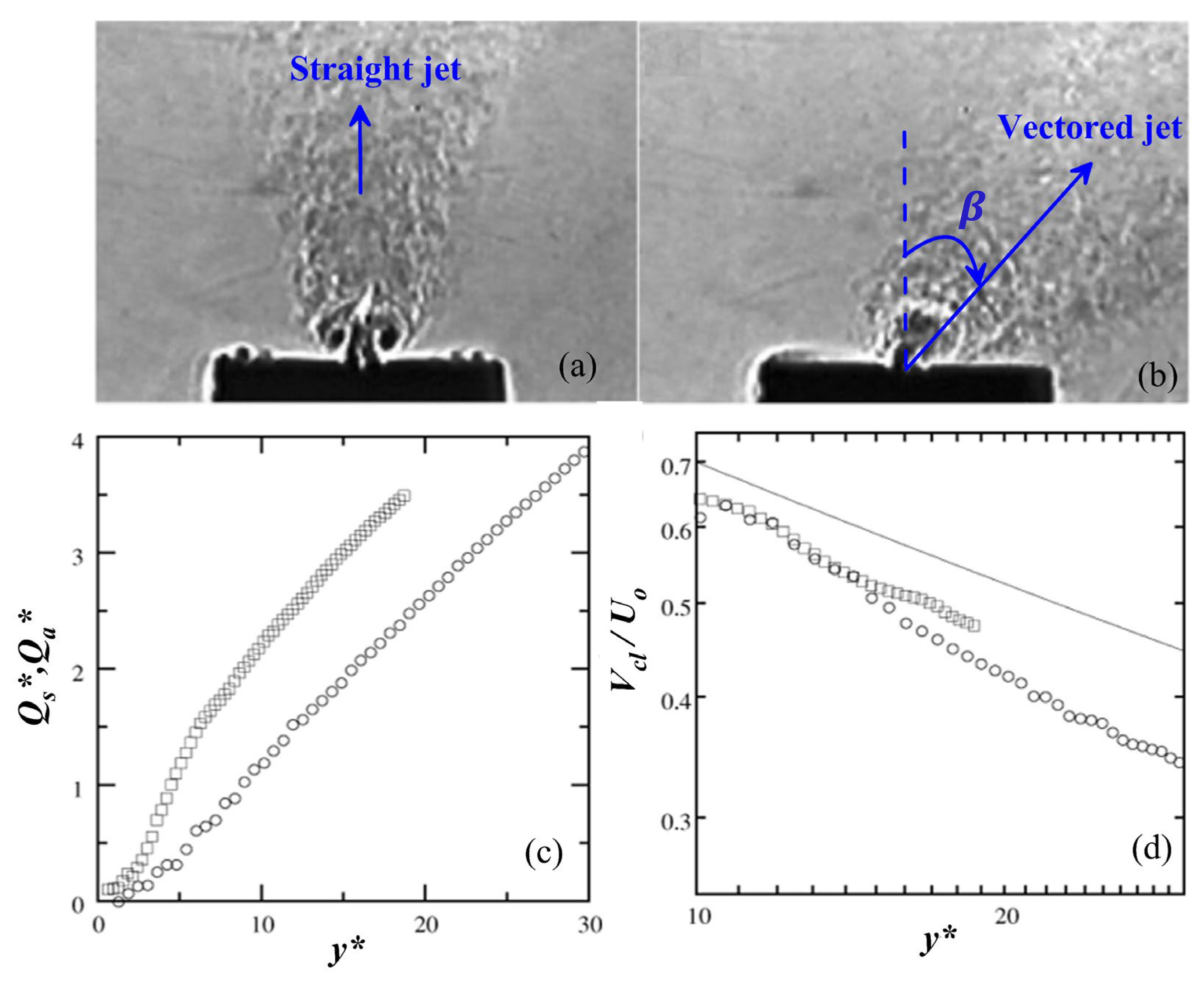
0° (
Figure 14a), the counter-rotating inner vortices (1⁺ and 2⁻) lead to significant destructive interference in the near field. This interaction diminishes vortex coherence and results in a noticeable reduction in jet strength downstream [
112]. The centerline velocity decay (
), plotted against the non-dimensional streamwise distance (
), is shown in
Figure 15d. For the single SJA,
, whereas for the DSJ,
2
, where 2
represents the total orifice width of the dual configuration. This scaling is adopted to enable a direct comparison of the streamwise evolution of the single jet and the merged jet pair based on their respective total exit widths [
112]. It can be interpreted from
Figure 15d that, beyond
15, although the DSJs retain a modest advantage in velocity magnitude over the single SJs, both configurations exhibit significant decay.
Figure 15.
Schlieren visualization of DSJ operated at (a)
and (b)
. (c) Streamwise variation (
y*) of normalized volume flow rate for single (
, ○) and DSJs (
, □). (d) Decay of centerline velocity (
) for a single synthetic jet (○) and DSJs (□) operated at
. The solid line shows the
decay law. Reproduced with permission from [
112].
Figure 15.
Schlieren visualization of DSJ operated at (a)
and (b)
. (c) Streamwise variation (
y*) of normalized volume flow rate for single (
, ○) and DSJs (
, □). (d) Decay of centerline velocity (
) for a single synthetic jet (○) and DSJs (□) operated at
. The solid line shows the
decay law. Reproduced with permission from [
112].
Berk et al. [
154] investigated effects of
(171 – 856), Strouhal number (
= 0.02 – 0.12), orifice spacing (
= 2 – 3), and phase difference (
= 100°– 150°) on the flow behavior of DSJs, while maintaining a fixed aspect ratio (
= 13). While the Reynolds number showed limited influence on vectoring, greater
amplified jet deflection. For smaller orifice spacings (
2.2 and 2.4), the vectoring angle increases noticeably with higher phase differences (
Figure 16a). However, these conditions also intensified vortex interactions, diminishing jet momentum. For example, at
= 2.2 and
= 100°– 140°, jet vectoring angle increased by ~31° (
Figure 16a), but the normalized jet momentum flux (
) dropped by nearly 45% (
Figure 16b). Here, the jet momentum flux
is defined as [
154]
Here,
is the air density,
is the normal velocity,
is the radial distance from the origin, and
is the angle measured from the vertical axis. The momentum flux is normalized by
, the reference momentum flux, which is calculated using the time-averaged velocity at the orifice exit. This decline in normalized momentum flux is attributed to enhanced vortex interaction, where destructive interference and the formation of smaller secondary vortices disrupt the primary flow structures [
154]. Similar reductions in jet strength due to strong inner vortex interactions have also been reported at small orifice spacings [
155], with the merged structure mimicking a single jet rather than two distinct sources. For DSJs, research has reported that while cavity geometry has minimal influence on jet dynamics, stroke length and Reynolds number play a crucial role in jet development and deflection [
152]. The influence of phase difference and actuator spacing on the vectoring and mixing characteristics of DSJs in both quiescent and crossflow environments has been extensively investigated [
20,
153,
156,
157,
158,
159,
160,
161,
162,
163,
164,
165,
166,
167,
168].
Figure 16.
(a) Vectoring angle (
) and (b) normalized momentum flux (
) as functions of phase difference at
and
, reproduced with permission from [
154]. (c) Comparison of time-averaged and area-averaged Nusselt number
variation with
between a single-actuator SJ and a DSJ, reproduced with permission from [
175].
Figure 16.
(a) Vectoring angle (
) and (b) normalized momentum flux (
) as functions of phase difference at
and
, reproduced with permission from [
154]. (c) Comparison of time-averaged and area-averaged Nusselt number
variation with
between a single-actuator SJ and a DSJ, reproduced with permission from [
175].
DSJs have proven effective in aerodynamic flow control applications due to their ability to generate synchronized or phase-shifted vortex pairs, which enables precise manipulation of boundary layer behavior [
169]. This makes them well suited for delaying flow separation, enhancing lift, and suppressing wake instabilities [
166,
167,
170]. In particular, DSJs have demonstrated greater control effectiveness in managing flow over airfoils and bluff bodies compared to single actuators, owing to enhanced momentum addition [
171].
In heat transfer applications, DSJs operated out of phase have demonstrated improved heat transfer performance compared to in-phase operation [
172,
173,
174]. Specifically, DSJs with phase differences between 60° and 120° show enhanced heat transfer compared to all other phase configurations, primarily due to the vectoring effect and improved mixing characteristics with the surrounding fluid [
174]. Furthermore, in applications requiring localized cooling, such as hot spot mitigation, phase differences between 135° and 180° have been found to be most effective [
174]. The heat transfer benefits of DSJs over single SJs have also been reported in the literature [
128,
175]. At
= 6, the heat transfer enhancement between the DSJ and single SJ is approximately 32% (
Figure 16c) [
175]. However, this enhancement drastically reduces to about 10% at
= 8, with further decrease in performance as
increases (
Figure 16c). This suggests that DSJs exhibit superior heat removal capabilities at lower jet-to-surface distances, facilitated by the formation of twin vortex rings and strong inter-jet interactions, a phenomenon also noted by other researchers [
128]. In the far downstream, DSJs resemble single SJs (
Figure 16c,
> 20), demonstrating their ineffectiveness in the far field. This decline in performance is attributed to extensive vortex diffusion, a phenomenon well documented in the literature [
128,
175].
5.2. Single Actuator Multi-Orifice Synthetic Jets
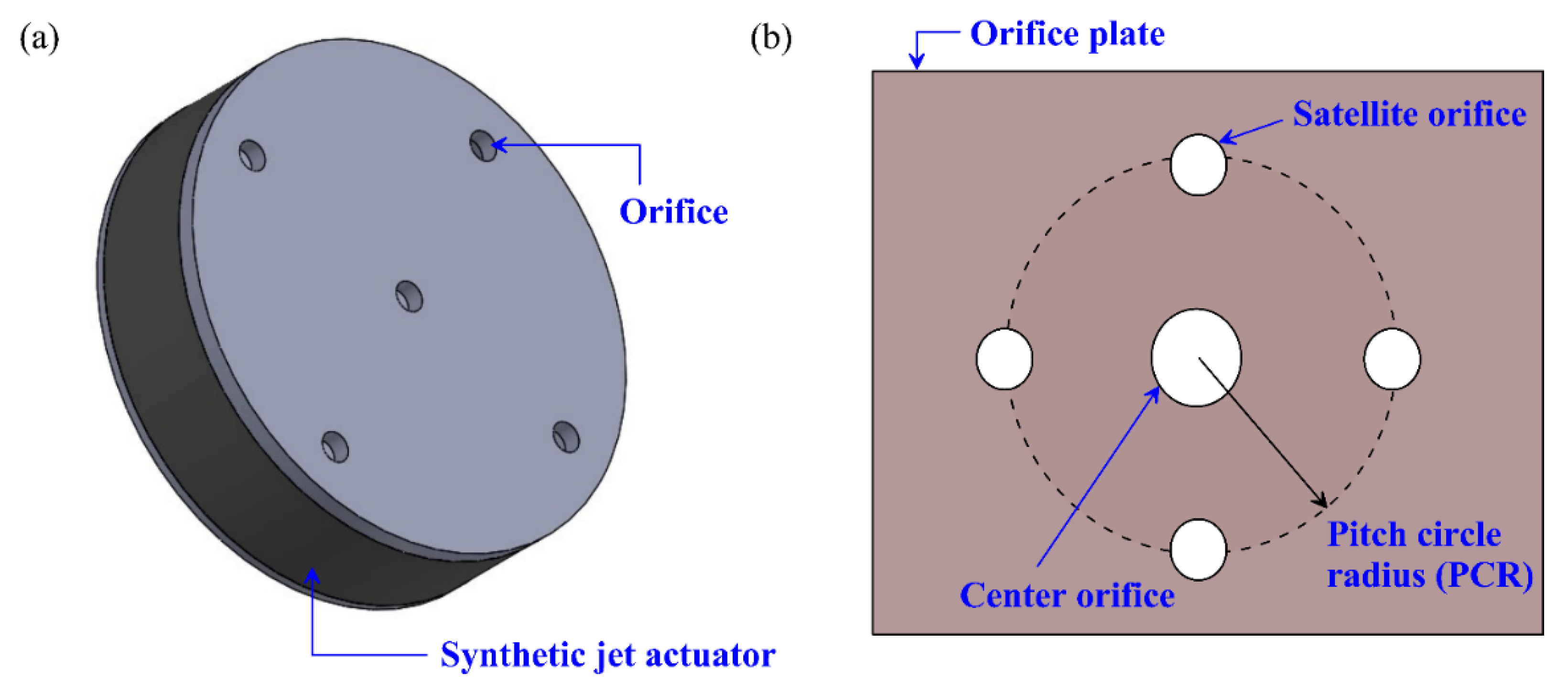
Another advancement in SJ technology is the single actuator multi-orifice configuration (
Figure 17a), in which a single actuator simultaneously drives multiple orifices [
176]. The multi-orifice design, typically featuring a central orifice encircled by satellite orifices (
Figure 17b), enhances fluid entrainment and mixing near the surface, thereby significantly improving convective heat transfer [
176].
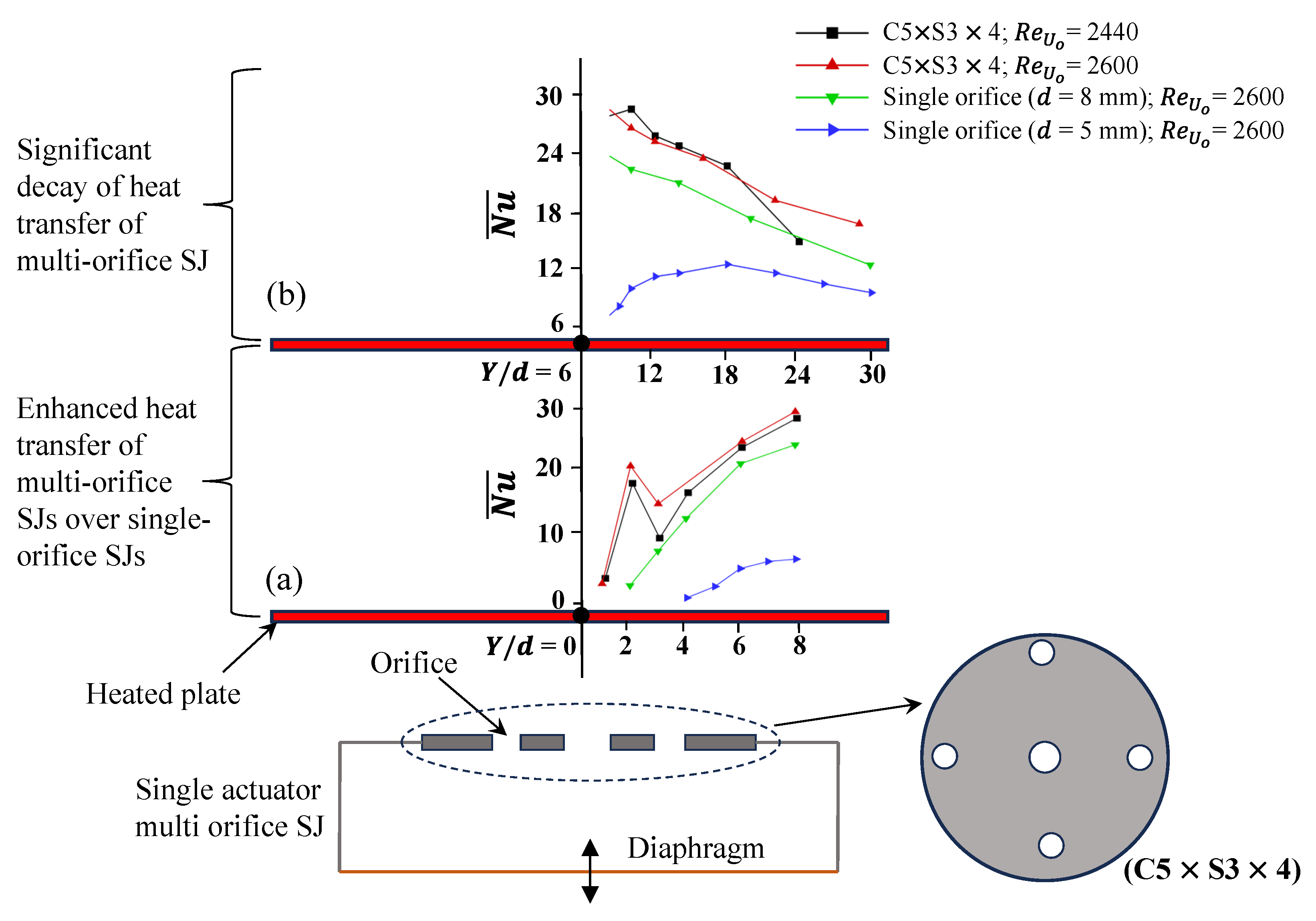
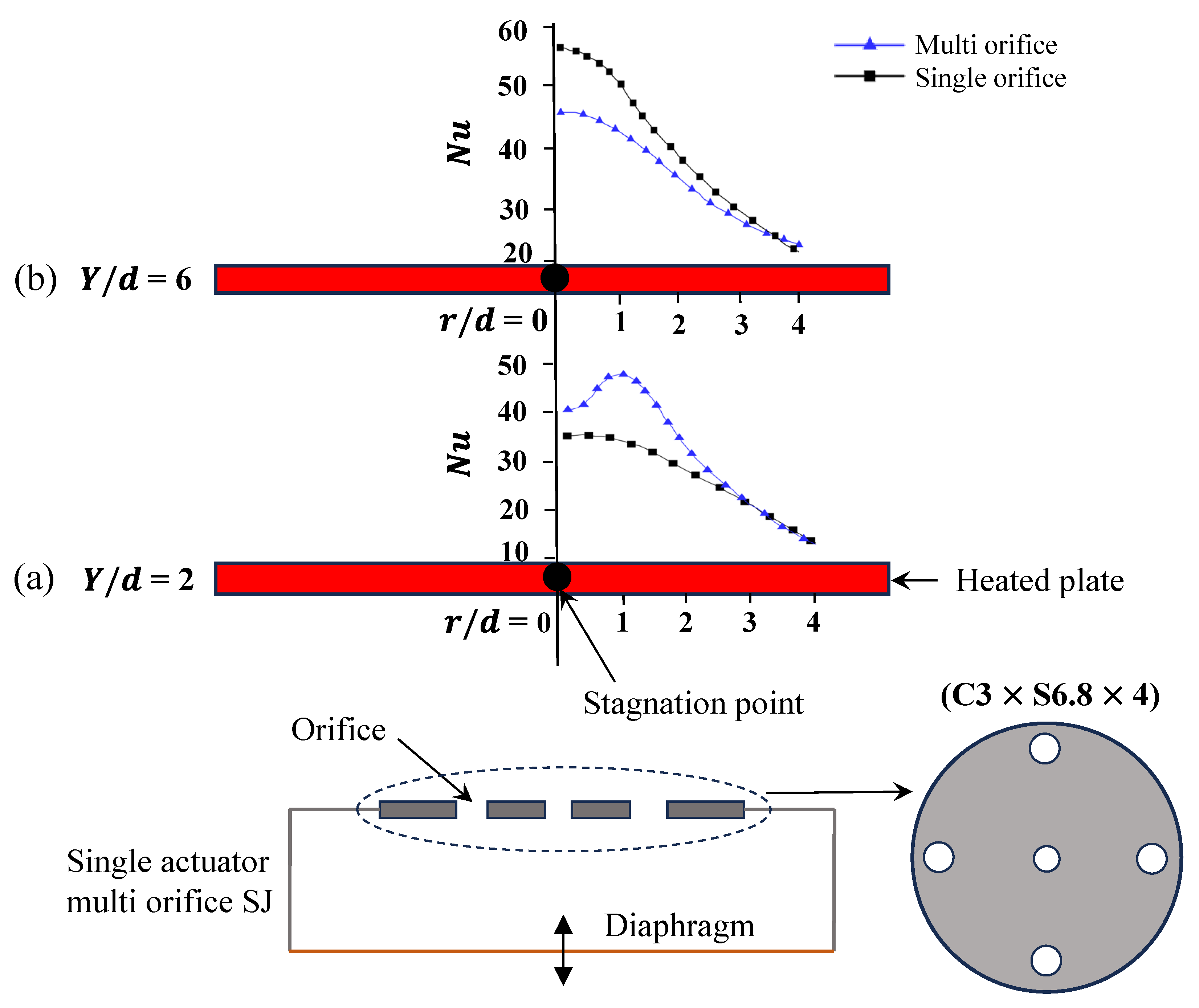
Uunder the same jet operating parameters (
= 2600), multi-orifice synthetic jets with the C5 × S3 × 8 configuration (where 5 mm is the diameter of the central orifice, 3 mm is the diameter of the satellite orifices, and 8 is the number of satellite orifices) achieve higher heat transfer than single-orifice synthetic jets (
Figure 18) [
176]. The heat transfer enhancement measured at
= 8 (
Figure 18a) for the C5 × S3 × 8 jets at
= 2600 is approximately 20% percent greater than that of conventional single-orifice synthetic jets with an 8 mm diameter under identical conditions (
= 2600) [
176]. For the same hydraulic diameter (
=
= 14 mm) and the same operating parameters (
= 125 Hz and
= 4 V), the heat transfer enhancement achieved with multi orifice synthetic jets, compared to a single orifice, is also observed along the spanwise direction in the near field (
= 2) (
Figure 19a) [
150]. Research has also reported that a configuration consisting of a central orifice surrounded by satellite orifices provides improved cooling performance for compact electronic components that require localized heat dissipation [
176]. Interestingly, such heat transfer enhancements occur without increasing input power. The multi-orifice configuration can slightly reduce power consumption compared to single-orifice actuators [
176].
Figure 17.
Schematic representation of a multi-orifice synthetic jet actuator: (a) 3D view of a synthetic jet actuator with five circular orifices, and (b) front view of the orifice plate illustrating the central and satellite orifices arranged along a defined pitch circle radius (PCR).
Figure 17.
Schematic representation of a multi-orifice synthetic jet actuator: (a) 3D view of a synthetic jet actuator with five circular orifices, and (b) front view of the orifice plate illustrating the central and satellite orifices arranged along a defined pitch circle radius (PCR).
Figure 18.
(a) Variation of
with
showing (a) heat transfer enhancement of multi-orifice synthetic jets over single-orifice, and (b) significant performance degradation of multi-orifice SJs in the far field. Data derived from [
176]. Configuration C5 × S3 × 4 denotes center orifice diameter × satellite orifice diameter × number of satellite orifices.
Figure 18.
(a) Variation of
with
showing (a) heat transfer enhancement of multi-orifice synthetic jets over single-orifice, and (b) significant performance degradation of multi-orifice SJs in the far field. Data derived from [
176]. Configuration C5 × S3 × 4 denotes center orifice diameter × satellite orifice diameter × number of satellite orifices.
When integrated into electronic cooling systems such as heat sinks, multi-orifice synthetic jets have demonstrated superior thermal performance [
17,
177]. During impingement on the heat sink surface, these jets showed a 12% increase in the maximum heat transfer coefficient compared to single-orifice jets, and an overall heat transfer enhancement nearly six times greater than that achieved by natural convection [
177]. Despite these benefits, multi-orifice jets, like single-orifice SJs, exhibit ineffective performance in the far field [
176]. For example, the
for satellite orifices (C5
3
4) at
= 2440 decreases by approximately 50% between
= 10 and 24 (
Figure 18b), which Chaudhari et al. [
176] attributed to rapid vortex diffusion in the far downstream region. This decline in far field performance has been observed across various multi-orifice shapes, including circular, oval, and diamond configurations, as well as different waveforms [
91,
178,
179,
180]. It is worth mentioning that the spanwise heat transfer enhancement of the multi orifice synthetic jets, compared to the single orifice jet observed in the near field (
= 2) (
Figure 19a), is no longer present at
= 6 (
Figure 19b) [
150]. At
= 6, the interaction between the central and satellite vortices breaks into smaller vortical structures before they can fully develop [
150]. As a result, the radial cooling advantage of multi orifice jets diminishes and becomes comparable to, or even weaker than, that of single orifice configurations (
Figure 19b). This suggests that the performance benefits of multi orifice arrangements are primarily limited to the near field [
150].
Figure 19.
Comparison of local Nusselt number distribution along the radial direction between multi-orifice synthetic jets and single-orifice SJs with the same hydraulic diameter of 14 mm, operated at 125 Hz frequency and 4 V amplitude, at (a)
= 2 and (b)
= 6, based on data from [
150].
Figure 19.
Comparison of local Nusselt number distribution along the radial direction between multi-orifice synthetic jets and single-orifice SJs with the same hydraulic diameter of 14 mm, operated at 125 Hz frequency and 4 V amplitude, at (a)
= 2 and (b)
= 6, based on data from [
150].
5.3. Coaxial Synthetic Jets (CSJs)
Coaxial synthetic jets, another technological advancement based on their structural configuration and actuation method, are categorized into three types: (a) double acting synthetic jets with concentric cavities driven by a common actuator (
Figure 20); (b) concentric orifice single-actuator synthetic jets, which use one actuator to supply multiple concentric orifices (
Figure 22); and (c) independently controlled coaxial synthetic jets, featuring separate actuators for each element (
Figure 23).
5.3.1. Double Acting Synthetic Jets (DASJs)
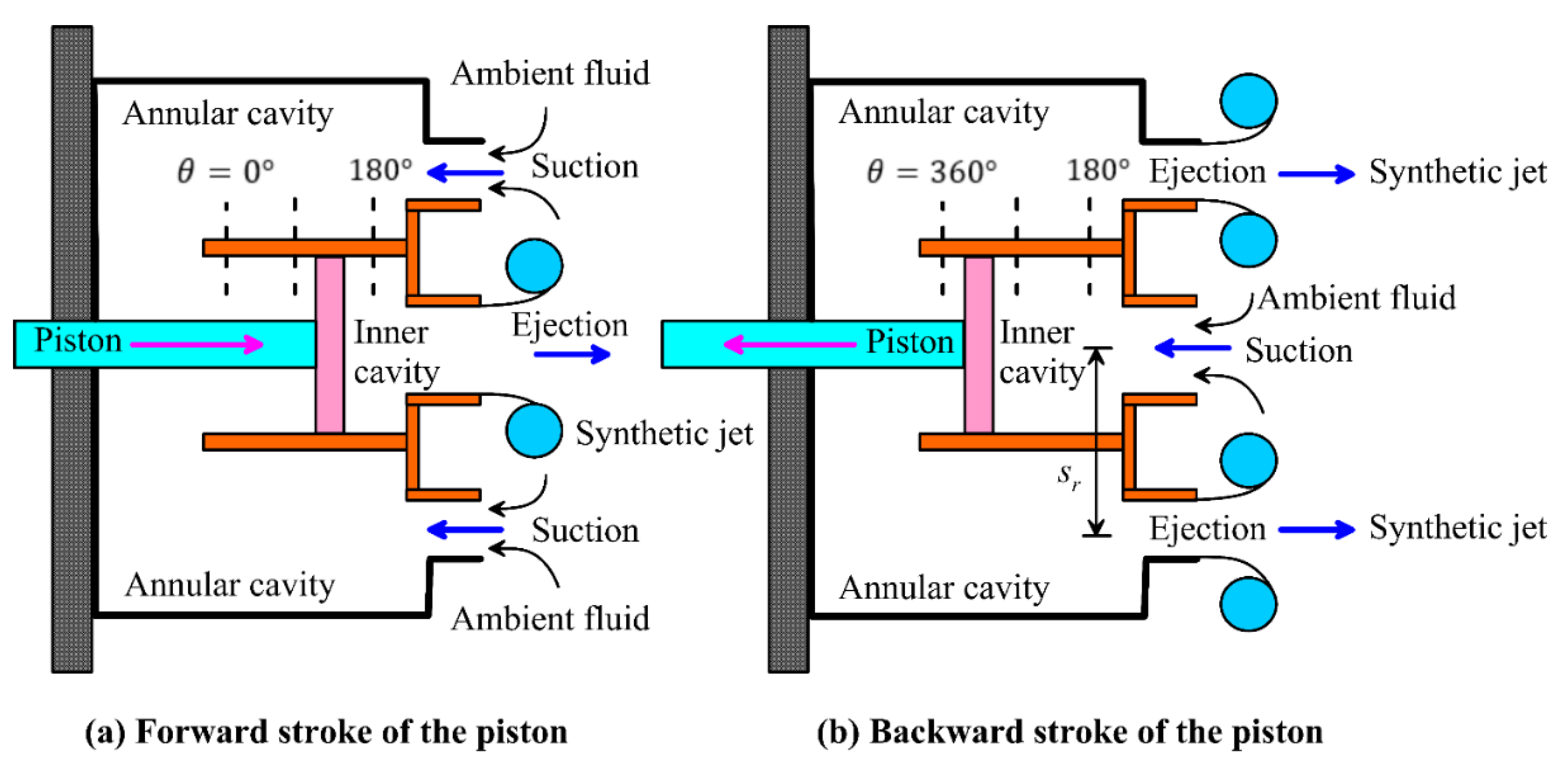
In the DASJ configuration, both the inner and annular cavities are actuated by a common mechanism operating in anti-phase (∅ = 180°). During one half-cycle, the inner cavity expels fluid while the annular cavity simultaneously draws it in (
Figure 20a). This flow pattern reverses in the subsequent half-cycle, with the annular cavity ejecting fluid and the inner cavity inducing suction (
Figure 20b). The phase-opposed operation induces dynamic interactions between the core flow and surrounding vortical structures, substantially influencing the jet development [
12].
Figure 20.
Operating principle of a DASJs showing (a) ejection from the inner cavity and suction into the annular cavity during the forward stroke, and (b) suction from the inner cavity and ejection from the annular cavity during the backward stroke.
Figure 20.
Operating principle of a DASJs showing (a) ejection from the inner cavity and suction into the annular cavity during the forward stroke, and (b) suction from the inner cavity and ejection from the annular cavity during the backward stroke.
DASJs produce significantly higher vorticity than single jets while exhibiting a noticeably narrower jet profile [
12]. The velocity field remains strongly centered along the axis a result of increased inward entrainment induced by the annular flow component, which sharpens the jet and helps maintain its coherence further downstream [
12]. Therefore, despite the enhanced jet strength, the narrower profile of DASJs may limit their effectiveness in applications requiring broader surface coverage. To address this limitation, researchers modified the geometric configuration of DASJs [
181]. Ahmed and Bangash [
181] reported that for DASJs, when the radial spacing (
) between the inner orifice and the outer annular opening (as shown in
Figure 20b) is maintained at 1
, the jet width is significantly enhanced compared to a single orifice SJ. This demonstrates a strong potential to mitigate the confinement effect typically observed in single actuator synthetic jets, which are characterized by narrower jet profiles [
181]. Further studies revealed that DASJ performance is highly sensitive to the operating parameters of the actuators [
181,
182].
While manipulating the design and operating parameters of DSJs enhances jet spreading [
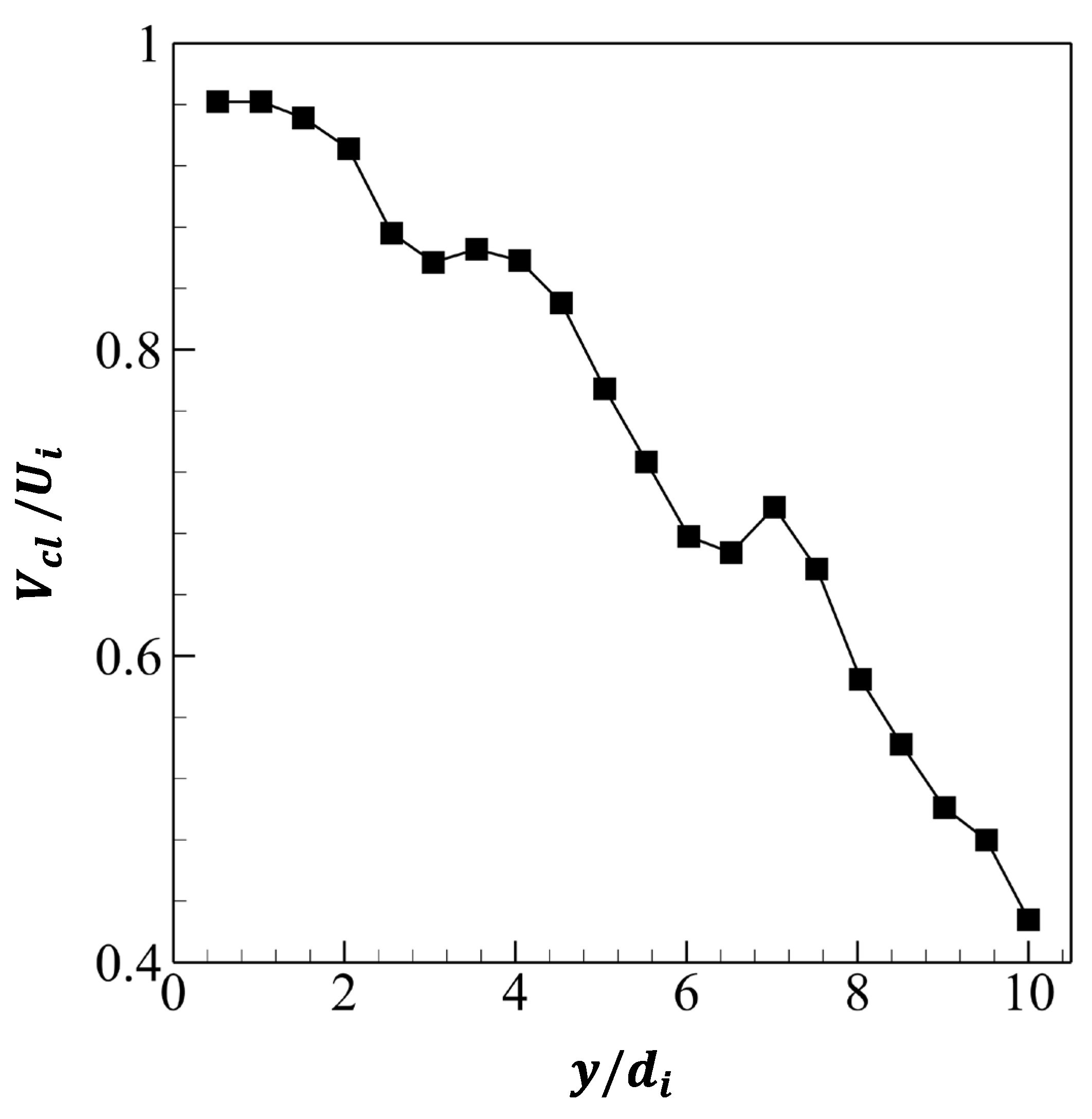
181], this improvement often comes at the expense of a significant reduction of the centerline velocity (
Figure 21) [
59]. Specifically, the centerline velocity
decreases by approximately 56% between
= 0.5 and
= 10 (
Figure 21), where
and
are the time-averaged velocity and diameter measured at the inner orifice exit, respectively [
59]. This reduction is due to the weakening of vortex structures downstream [
59,
181].
5.3.2. Concentric Orifices Single-Actuator Synthetic Jets (COSASJs)
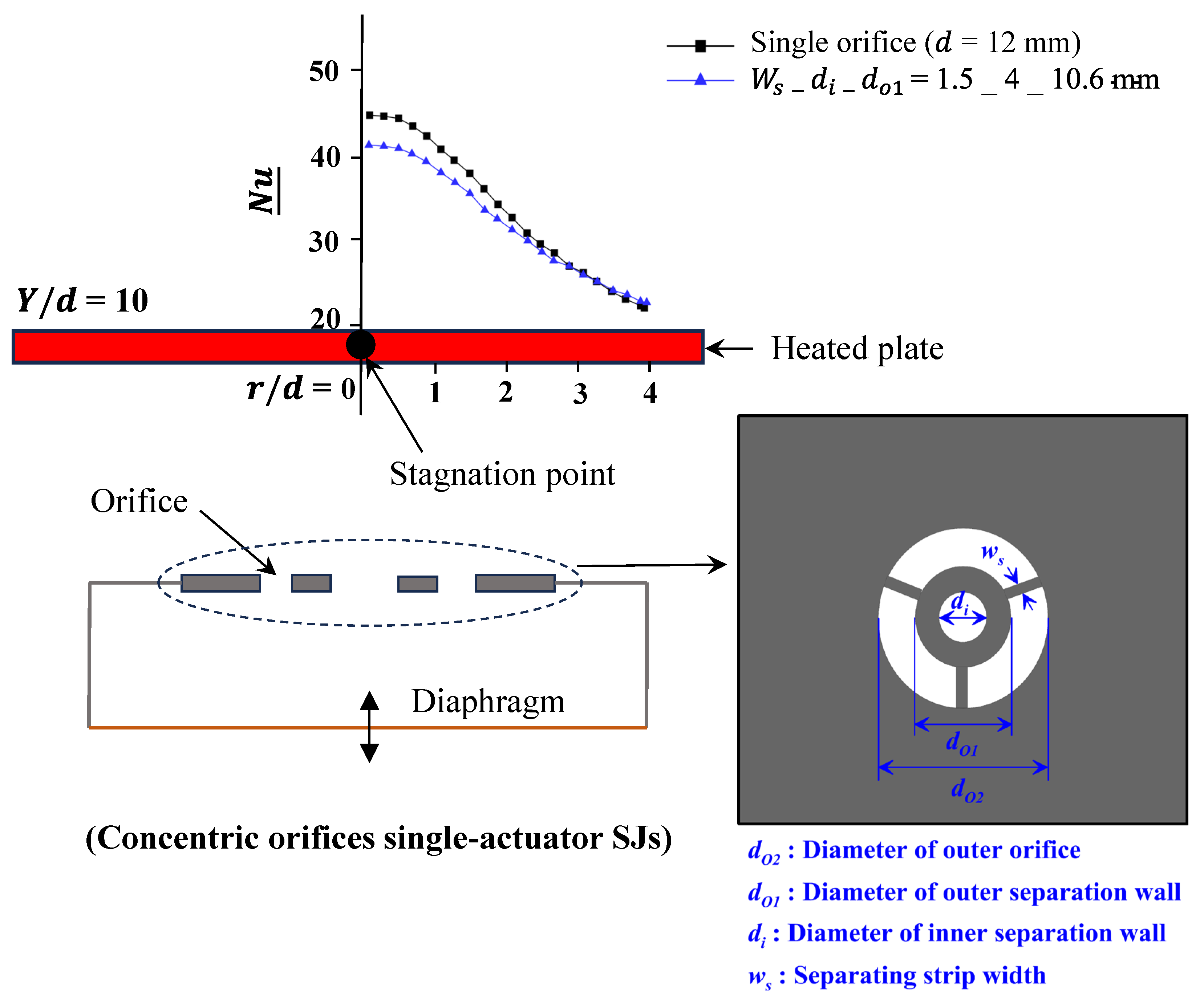
In the COSASJs configuration (
Figure 22), both the inner and outer orifices operate simultaneously, generating coordinated vortex structures that enhance jet formation and increase the overall flow volume [
183]. Studies employing infrared thermography and smoke wire visualization across various Reynolds numbers, actuation amplitudes, and orifice-to-surface spacings have demonstrated significant improvements in convective heat transfer when this configuration operates in close proximity to the heated surface [
183]. Research reported that at smaller spacings (
= 2), the COSASJ configuration with dimensions 1.5_4_10.6 (where
= 1.5 mm,
= 4 mm, and
= 10.6 mm) achieves an approximately 20% increase in the time- and area-averaged Nusselt number (
) compared to conventional single-orifice synthetic jets of 12-mm diameter [
183]. The equivalent diameter
used for normalization is defined such that the total discharge area of the coaxial configuration equals the area of a 12-mm single orifice [
183]. The enhancement in
for the COSASJ at
= 2 is primarily attributed to independent vortex generation from the inner and outer orifices, which strengthens local mixing, disrupts the thermal boundary layer, and suppresses hot-air recirculation near the heated surface [
183].
However, for
≥ 6, the thermal performance of COSASJs begins to deteriorate, becoming lower than that of single-orifice jets [
183]. This decline is attributed to rapid vortex energy dissipation, which weakens momentum transport in the far field and reduces the effectiveness of jet-surface interaction [
183]. A similar trend is observed in the radial distribution of heat transfer (
Figure 22), where COSASJs demonstrate inferior performance compared to single-orifice jets at
= 10 [
183].
Figure 22.
Comparison of time-averaged Nusselt number distribution along the radial direction between COSASJs and single-orifice SJs with the same hydraulic diameter of 12 mm, operated at
5830 at
= 10, based on data from [
183].
Figure 22.
Comparison of time-averaged Nusselt number distribution along the radial direction between COSASJs and single-orifice SJs with the same hydraulic diameter of 12 mm, operated at
5830 at
= 10, based on data from [
183].
5.3.3. Independently Controlled Coaxial Synthetic Jets (IC-CSJs)
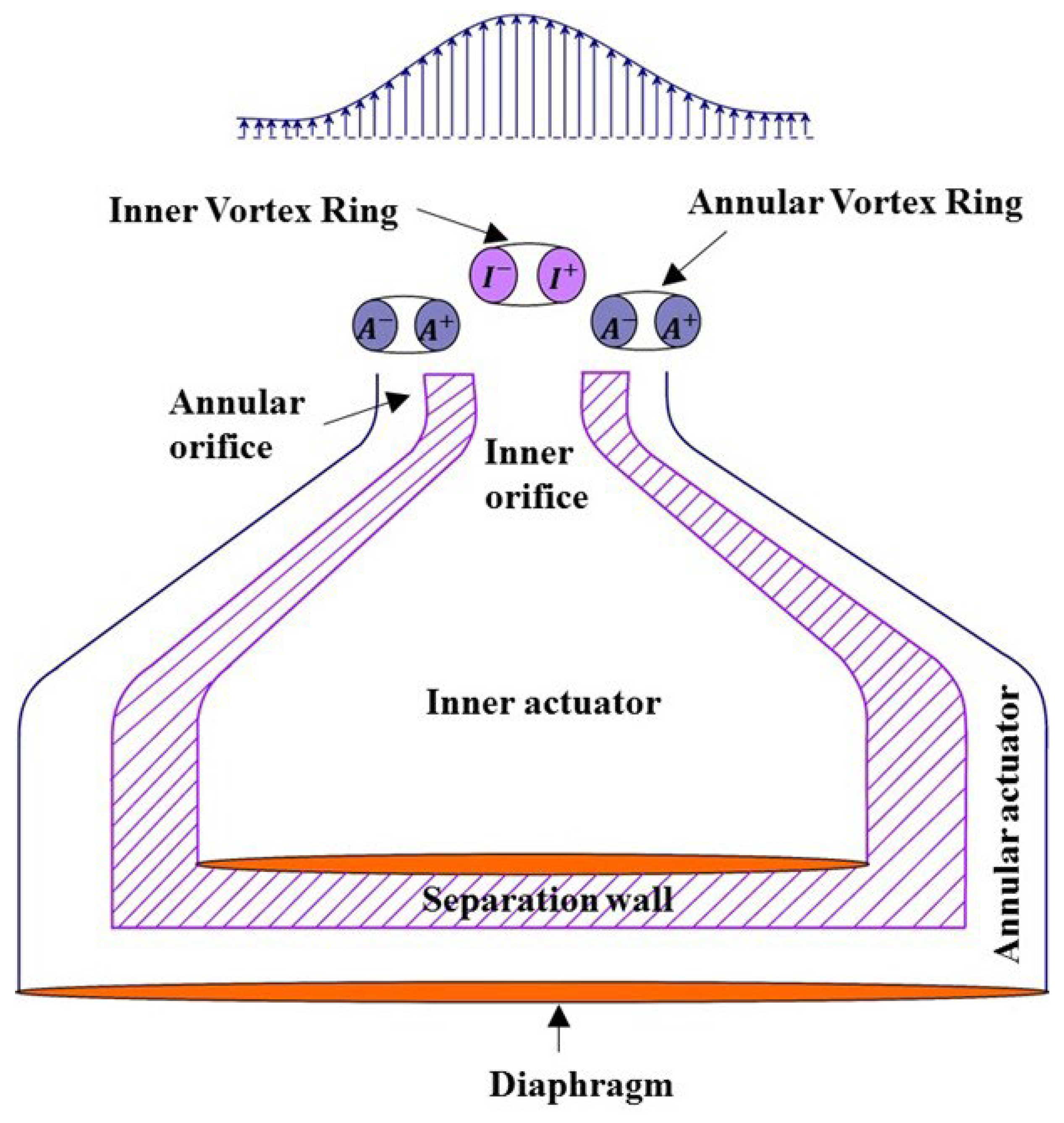
Among all coaxial synthetic jet configurations, independently controlled coaxial synthetic jets (
Figure 23) stand out for their ability to precisely regulate frequency, amplitude, and phase of each actuator separately, enabling fine-tuned control over jet behavior [
184]. Such independent control enables precise modulation of vortex interactions, leading to more efficient momentum transfer and enhanced entrainment [
16,
184]. The flow dynamics of IC-CSJs involve the formation, evolution, and interaction of the inner vortex ring (IVR) generated by the inner actuator and the annular vortex ring (AVR) formed by the annular actuator [
184,
185]. In a two-dimensional representation, the annular actuator produces a pair of counter-rotating vortices, denoted as
and
, corresponding to anticlockwise and clockwise rotations, respectively, while the inner actuator generates vortices
and
with the same rotational convention (
Figure 23). The dynamics of these vortex structures under varying jet operating conditions have been extensively reported in the literature [
184,
185].
Figure 23.
Schematic of IC-CSJs illustrating key components.
Figure 23.
Schematic of IC-CSJs illustrating key components.
A crucial parameter governing IC-CSJ behavior is the mass flux ratio (
), defined as the ratio of the mass flux of the inner jet (
) to that of the annular jet (
) [
184]. The mass flux for each jet is expressed as
=
and
=
, where
and
are the time-averaged velocities of the inner and annular jets, respectively. This ratio is typically varied by modifying the annular jet's frequency and amplitude of oscillation [
184]. Panda et al. [
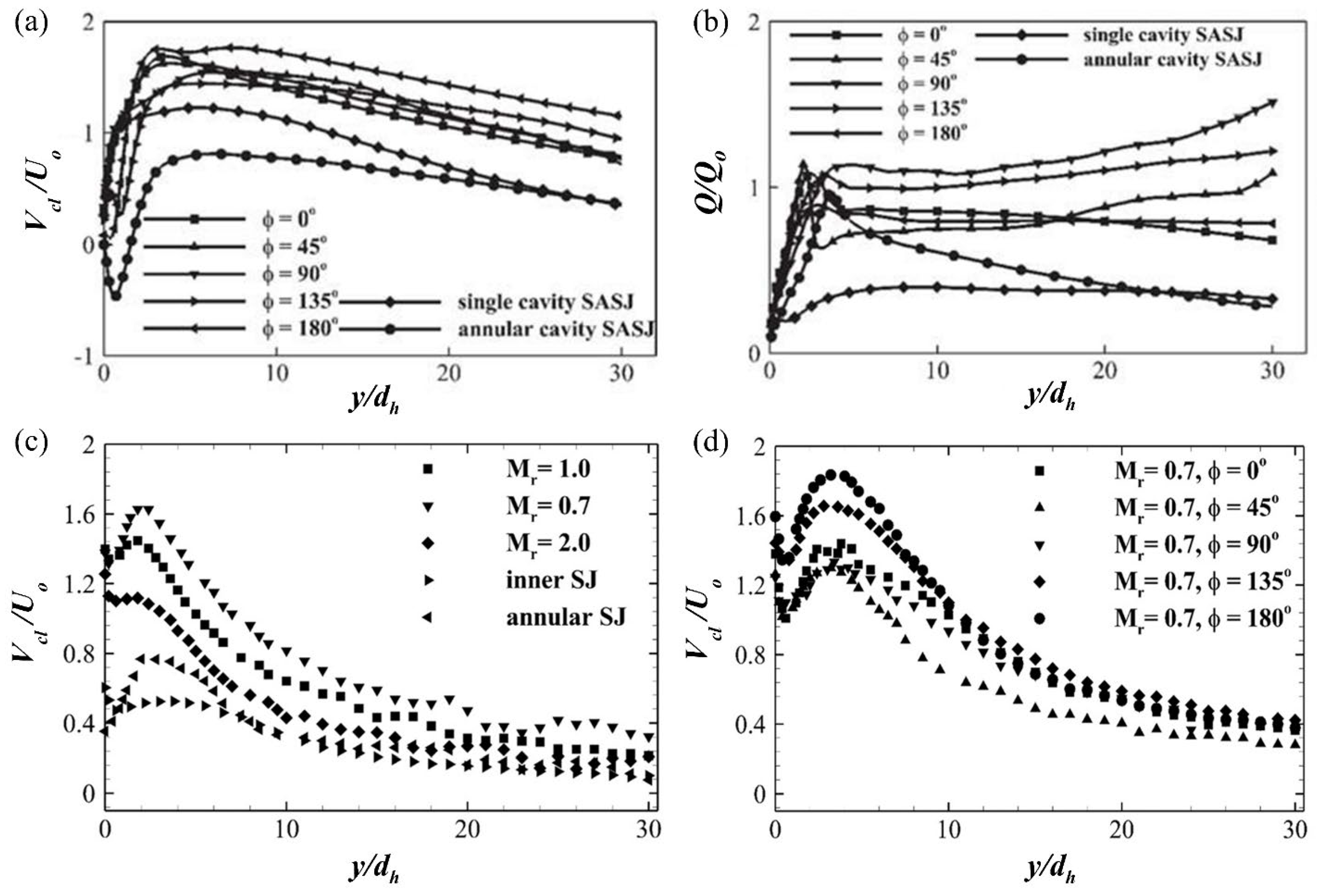
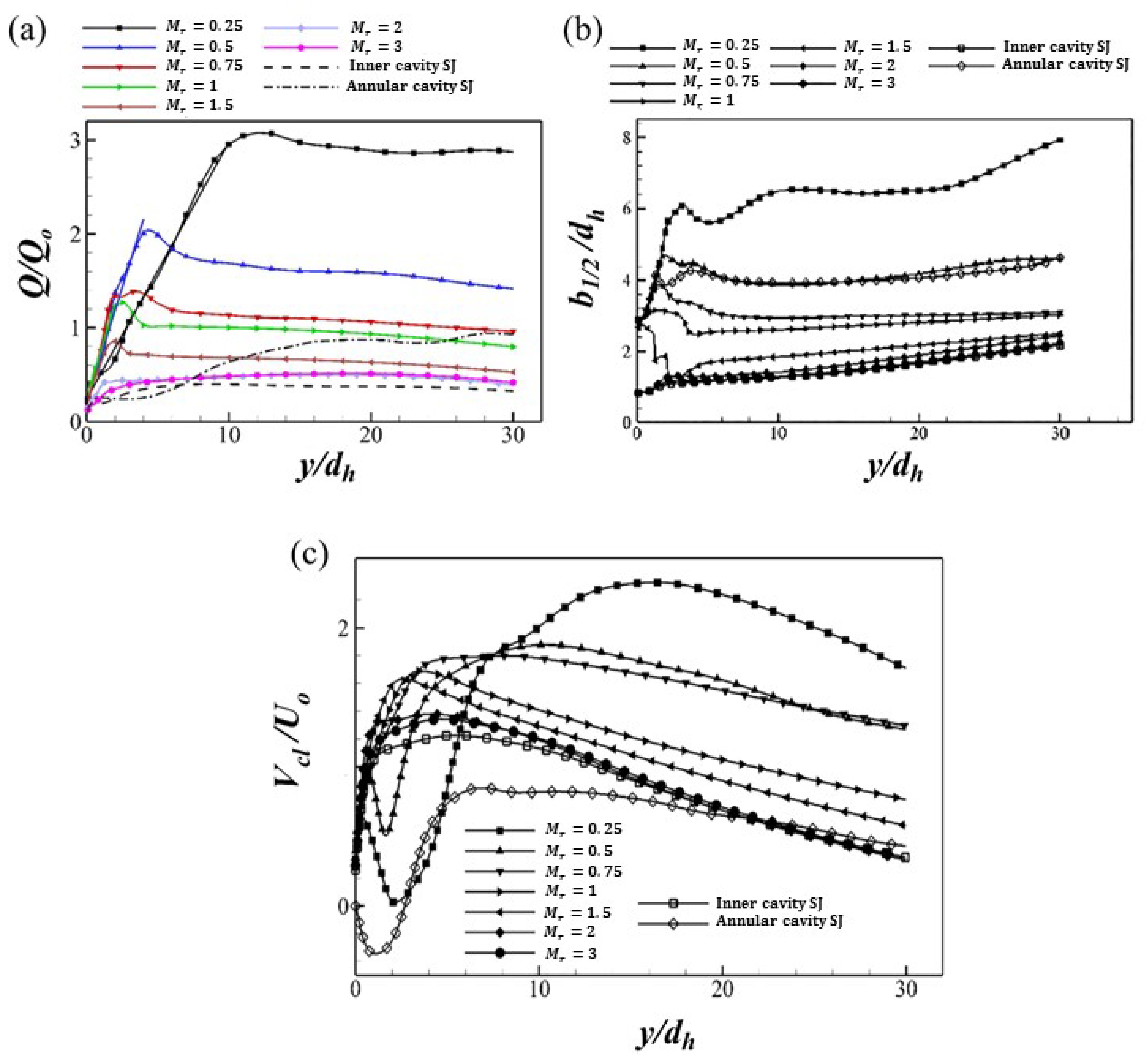
184] performed a detailed numerical investigation at
= 150 to examine the influence of mass flux ratio (
0.25
3) on the flow behaviour of IC-CSJ and compared the results with those of independently operated inner and annular actuators. According to their findings, when the IC-CSJ is operated at the lower end of this range (
0.25), the resulting jet exhibits superior flow characteristics compared to other mass flux ratios, as well as to the inner and annular jets operating individually (
Figure 24). Specifically, the jet maintains a stronger volume flux (
) throughout the streamwise domain (
Figure 24a), a wider half-width (
) (
Figure 24b), and a significantly higher centerline velocity (
Figure 24c). For the three-dimensional simulated case, the detailed methodology for estimating the volume flux and jet half-width has been comprehensively documented in the literature [
184]. Here, the hydraulic diameter (
) is maintained at 1.5 mm for both the inner and annular orifices [
184]. The enhanced volume flux corresponds to the generation of a larger flow rate, while the wider jet half-width and higher centerline velocity indicate greater spanwise coverage and sustained jet strength in the far field, respectively, for IC-CSJs compared to single-actuator synthetic jets [
184]. The enhanced performance of the IC-CSJ at the lower mass flux ratio (
0.25) arises from an effective interaction between the strong annular jet momentum and the inner jet, which promotes intensified vortex interactions, improved mixing, and a coherent, sustained jet structure [
184].
This advantage becomes even more pronounced when the phase difference between the actuators is varied [
185]. Introducing a phase difference between the inner and annular jets, where the annular jet leads in phase relative to the inner jet, facilitates constructive vortex interactions [
185]. For instance, at
180°, vortex pairing enhances the coherence and strength of the jet core, while intermediate phase differences such as
90° and 135° induce azimuthal instabilities that enhance entrainment and volumetric growth [
185]. The progressive increase in centerline velocity and jet volume flux with increasing
is evident in
Figure 25(a) and (b), respectively. These trends underscore the critical role of phase control in optimizing the full potential of IC-CSJ configurations [
185].
When operated at
= 1100, the IC-CSJ configuration demonstrates superior performance compared to single-actuator counterparts, as revealed through hotwire anemometry measurements (
Figure 25c, d) [
16]. The study considered
0.7, 1, and 2. At the lower
0.7), the centerline velocity attains a peak value that exceeds those of the inner and annular jets by 184% and 113%, respectively (
Figure 25c). Furthermore, introducing a phase difference of 180° produces a 28.5% increase in peak centerline velocity compared with the in-phase case (
Figure 25d) [
16].
In thermal applications, IC-CSJ performance exhibits a similar trend with changes in
0.5, 1, and 2) and phase difference (
0°
180°) [
186]. Maximum heat transfer rates were achieved at the smaller
0.5) with
135°, indicating that the flow behavior strategies observed at lower
for momentum transfer also contribute to enhanced thermal transport [
186].
Figure 25.
Streamwise variation of independently controlled coaxial synthetic jets: (a) Normalized centerline velocity (
) and (b) normalized jet volume flux (
) for different phase differences (
, 45
, 90
, 135
, 180
) at
= 150, reproduced with permission from [
185]. (c) Influence of mass flux ratio (
0.7, 1.0, and 2.0) and (d) effect of phase difference (
, 45
, 90
, 135
, 180
) at
0.7 on centreline velocity at
= 1100, reproduced with permission from [
16].
Figure 25.
Streamwise variation of independently controlled coaxial synthetic jets: (a) Normalized centerline velocity (
) and (b) normalized jet volume flux (
) for different phase differences (
, 45
, 90
, 135
, 180
) at
= 150, reproduced with permission from [
185]. (c) Influence of mass flux ratio (
0.7, 1.0, and 2.0) and (d) effect of phase difference (
, 45
, 90
, 135
, 180
) at
0.7 on centreline velocity at
= 1100, reproduced with permission from [
16].
However, a comparison between the numerical and experimental results offers additional insights into Reynolds number sensitivity. Despite similar trends in flow structure and jet enhancement across both studies, the decay rate of normalized centerline velocity
is significantly higher in the experimental case (
Figure 25c). The numerical simulations, conducted at
= 150, exhibit a more gradual decay (
Figure 24c), while the experimental study at
= 1100 reveals a steeper decline (
Figure 25c). This difference is attributed to increased vorticity diffusion and turbulence intensity at higher Reynolds numbers, which accelerate the breakdown of vortex rings and cause earlier momentum dissipation in the far field [
16,
185]. Such behavior can constrain the far-field effectiveness of IC-CSJs, especially under high Reynolds number conditions.
5.4. Synthetic Jet Array (SJ Array)
The synthetic jet array (
Figure 26) is composed of multiple independently controlled actuators placed adjacent to each other. Unlike multi-orifice SJs driven by a common diaphragm with uniform operating conditions [
176], the SJ array allows individual control over frequency, amplitude, and phase difference for each actuator [
114]. This precise control facilitates spatial and temporal modulation of the flow field, which enhances jet interaction and offers greater flexibility for flow manipulation and thermal management [
114,
187].
5.4.1. Vectoring of Jets
Controlling the direction of synthetic jet propagation through phase manipulation has emerged as an effective strategy for achieving broader surface coverage compared to single-actuator synthetic jets [
114]. Research has shown that when the actuators in a synthetic jet array operate in phase (∅ = 0°) (Case 1,
Figure 29a), the resulting jet remains symmetric and directed along the streamwise axis (
Figure 27). However, introducing a uniform linear phase difference between the actuators (Case 2,
Figure 29a) causes the jet to deflect toward the actuator leading in phase [
114] (
Figure 27), with the extent of deflection strongly dependent on the operating Strouhal number [
114]. In this configuration, the actuators from SJA 1 to SJA 4 operate with progressively increasing phase lag (Case 2,
Figure 29a). At a low Strouhal number (
= 0.028) and a phase difference of 90° (
Figure 27a), the jet attained its maximum vectoring angle of 78°. At an intermediate Strouhal number (
= 0.086), the vectoring angle was observed to vary with changes in the phase difference (
Figure 27c). Notably, for
= 0.086, a 90°phase difference produced a vectoring angle of 36°, while at
180°, the jet curved toward the lagging actuator (
10°), demonstrating the reversibility of jet direction based on phase configuration (
Figure 27c) [
114].
The effectiveness of jet vectoring for bluff body flow control has been extensively investigated by Mittal and Arumuru [
188]. A pronounced peak in
near the cylinder reflects the influence of SJ actuation, in contrast to the case without actuation (
Figure 28) [
188]. Compared to all other operated phase differences, at ∅ = 60°, where the vectoring effect is most prominent, two distinct peaks appear (
Figure 28), which Mittal and Arumuru [
188] identified as indicative of asymmetric vortex shedding from the upper and lower shear layers. This asymmetry, induced by the vectoring effect, modifies the vortex formation length and alters the wake structure, highlighting the ability of jet vectoring to manipulate shear layer dynamics and improve flow control effectiveness [
188].
From a thermal management perspective, vectoring significantly improves heat transfer performance [
189]. Maximum vectoring, achieved at a phase difference of 90°, results in a substantially larger cooling surface area on the heated plate compared to the in-phase operation (∅ = 0°) of the SJ array [
189]. The phenomenon of enhanced heat transfer when the SJ array is operated out of phase has also been reported in the literature [
190]. This demonstrates that phase control can be strategically employed to target and cool specific surface regions based on application requirements. Together with this, the multiple vortices generated by each actuator interact with the surrounding fluid as they propagate outward, promoting greater entrainment and enhancing overall jet formation [
114,
191].
Figure 28.
Streamwise variation of cross-stream velocity fluctuations along the square cylinder centerline, reproduced with permission from [
188].
Figure 28.
Streamwise variation of cross-stream velocity fluctuations along the square cylinder centerline, reproduced with permission from [
188].
5.4.2. Focusing of Jets
While the use of independently controlled SJ array and jet vectoring effectively addresses the primary limitations of single actuator SJs, such as restricted jet formation [
114,
191] and limited spanwise coverage [
114,
189,
192], the degradation of jet strength in the far field remains a significant challenge [
191]. When the synthetic jet array operates in phase (
0°), the inner counter-rotating vortices in the near field interact destructively, similar to the behavior observed in dual synthetic jets in
Figure 15a [
191,
193,
194]. This interaction breaks the primary vortices into smaller secondary structures, which dissipate rapidly as they convect downstream, resulting in a pronounced reduction in jet momentum [
191,
195]. To address this issue, a novel focusing technique has been introduced, where a nonlinear phase delay, specifically a trapezoidal distribution (Case 3,
Figure 29a), is applied across the actuators. In this configuration, the inner actuators (SJA 2 and SJA 3) lead in phase compared to the outer actuators (SJA 1 and SJA 4) (Case 3,
Figure 29a). This approach reduces destructive vortex interactions and promotes coherent vortex evolution along with constructive merging, thereby enhancing jet strength in the far field [
191,
196].
The study revealed that for the SJ array operated at
= 300, maximum focusing was achieved at an intermediate Strouhal number (
= 0.086) and a moderate nonlinear phase difference of 90° (
Figure 29b) [
191]. A quantitative assessment indicates that in the far field at
= 20
, maximum focusing (
90°) leads to an increase of approximately 52% in
compared to
0° (
Figure 29b). Additionally, under maximum focusing conditions,
, which also characterizes the jet strength measured in the far field (
= 20
), increased by nearly 35% compared to ∅ = 0° (
Figure 29c). Notably, contrary to the expectation that focusing would confine the flow near the centerline and reduce the jet width, the jet instead displayed lateral expansion (
Figure 29d). This broadening is attributed to the development of larger and more coherent vortical structures capable of entraining greater volumes of surrounding fluid [
191]. A further quantitative analysis revealed that maximum focusing at
90° led to a reduction of approximately 43% in destructive vortex interactions compared to the in-phase operation of the synthetic jet array [
191].
Figure 29.
(a) Schematic diagram showing the phase difference between actuators for the formation of straight, vectored, and focused jets. Focusing characteristics of SJ array operated at
= 300,
= 0.086, and varying non-linear phase differences: (b) directivity plot showing enhancement or reduction of
measured at
= 20 , (c) normalized jet momentum flux (
) variation, and (d) jet half-width, reproduced with permission from [
191].
Figure 29.
(a) Schematic diagram showing the phase difference between actuators for the formation of straight, vectored, and focused jets. Focusing characteristics of SJ array operated at
= 300,
= 0.086, and varying non-linear phase differences: (b) directivity plot showing enhancement or reduction of
measured at
= 20 , (c) normalized jet momentum flux (
) variation, and (d) jet half-width, reproduced with permission from [
191].
Flow control applications benefit considerably from this focusing effect [
188]. By delaying vortex shedding and shortening the vortex formation length, focused synthetic jets contribute to a more stable and narrower wake [
188]. These alterations promote earlier and stronger interactions with bluff body vortices, leading to reduced velocity fluctuations and suppression of turbulent structures. At optimal focusing (
90°), the root-mean-square values of both streamwise and transverse velocities reach their minimum, resulting in a 43% reduction in the drag coefficient (
) (
Figure 30a) [
188].
Thermal performance also benefits from this focused configuration [
187]. For the SJ array operated at Reynolds numbers (
= 600) and Strouhal number (
= 0.1), constructive merging of the leading and lagging vortices in a nonlinearly phased synthetic jet array significantly enhances convective heat transfer [
187]. The intermediate region (
= 14) exhibits enhanced heat transfer (
Figure 30b), with the peak
increasing by approximately 21% under maximum focusing (∅ = 120°), compared to the in-phase operation of the SJ array [
187]. Moreover, the drop in heat transfer from the intermediate region (
= 14) to the far field (
= 28) under maximum focusing (∅ = 120°) is only 17% (
Figure 30b) [
187], which represents a substantial improvement compared to a single actuator SJ operated at
= 396, where a drop of approximately 36% is observed between the intermediate field (
= 18) and the far field (
= 23) [
11]. These outcomes underscore that jet focusing, achieved through nonlinear phase delay, directly addresses the loss of jet coherence and strength in the far field [
187,
191].
Figure 30.
Effect of nonlinear phase delay (
) on (a) drag coefficient (
) for a bluff body with synthetic jet actuation, reproduced with permission from [
188] and (b)
distribution at various
values, reproduced with permission from [
187].
Figure 30.
Effect of nonlinear phase delay (
) on (a) drag coefficient (
) for a bluff body with synthetic jet actuation, reproduced with permission from [
188] and (b)
distribution at various
values, reproduced with permission from [
187].
Table 1 summarizes the fundamental drawbacks of single-actuator synthetic jets along with the effectiveness of various technological advancements in overcoming these limitations. While some configurations address one or two drawbacks, the synthetic jet array with independently controlled actuators emerges as the most promising solution, offering comprehensive improvement across all critical performance aspects.
6. Conclusions
Synthetic jets generate zero net mass flux through periodic suction and blowing, offering compactness, ease of integration, and eliminating the need for an external fluid supply. These features make them well-suited for applications such as flow control and heat transfer enhancement. Despite their promise, SJs are not without limitations. This review presents a detailed assessment of the primary limitations associated with single-actuator SJs and examines the technological developments that have emerged to overcome these challenges. Our findings reveal that key drawbacks such as restricted jet formation capacity, limited spanwise coverage, and diminished far field effectiveness significantly constrain their broader application in practical scenarios. To mitigate these limitations, several technological advancements have been proposed, including dual-cavity synthetic jets, single-actuator multi-orifice synthetic jets, coaxial synthetic jets, and synthetic jet arrays, each aiming to enhance the flow and thermal performance of SJ systems.
Dual-cavity synthetic jets, comprising two side-by-side actuators operated either in phase or with a phase difference, enable enhanced jet formation and controllable vectoring. When actuated in phase, the jet remains symmetric and convects straight downstream, while a phase difference causes deflection toward the leading actuator, allowing directional control. Experimental studies have shown that DSJs can nearly double the flow rate and expand the effective coverage area, addressing key limitations of conventional SJs related to restricted jet formation and limited spanwise influence. However, destructive interactions in the near field significantly degrade the far-field performance of DSJs.
Single-actuator multi-orifice synthetic jets, which utilize a single actuation chamber connected to multiple orifices, address the limitation of restricted jet formation observed in single-orifice designs by generating multiple coherent vortices. In this configuration, higher near-field heat transfer performance has been observed compared to conventional single orifice jets. Together with this, experimental studies have reported two distinct peaks in the average Nusselt number distribution, with the first occurring near the orifice exit ( = 2), highlighting the effectiveness of this configuration for localized or spot cooling applications. Despite these advantages, ineffective performance in the far field due to significant vortex diffusion remains a limiting factor for this configuration.
Among all coaxial synthetic jet configurations, independently controlled coaxial jets show the most promise, offering precise control over vortex dynamics through the modulation of frequency, amplitude, and phase. This configuration significantly enhances jet volume flux and promotes greater jet spreading. The resulting jets also retain their strength in the far field. However, at higher Reynolds numbers, intensified vortex diffusion limits their performance in the far field.
A synthetic jet array, comprising multiple independently controlled actuators, facilitates two powerful strategies: vectoring and focusing of jets. Formation of multiple vortices from the SJ array entrains more surrounding fluid, which enhances jet formation, and precise control of the jet direction using phase modulation increases spanwise coverage. Focusing, achieved through nonlinear phase delays, reduces destructive vortex interactions, allows the primary vortices to evolve effectively, and constructive merging between vortices enables them to retain their strength in the far field. These capabilities have demonstrated substantial improvements in both flow control and thermal management. Overall, the strategic use of phase modulation in the SJ array effectively addresses the key limitations of SJs, including limited jet formation, restricted surface coverage, and ineffective performance in the far field, making it a promising solution for advanced fluidic and thermal applications.
Author Contributions
For research articles with several authors, a short paragraph specifying their individual contributions must be provided. The following statements should be used “Conceptualization, J.P., M.M.A., and V.A.; methodology, J.P. and M.M.A.; software, J.P., M.M.A., and H.C.; validation, J.P., V.A., and H.C.; formal analysis, J.P. and M.M.A.; investigation, J.P. and M.M.A.; resources, M.M.A., V.A., H.C., and T.C.; data curation, J.P. and M.M.A.; writing—original draft preparation, J.P.; writing—review and editing, J.P., M.M.A., V.A., H.C., and T.C.; visualization, J.P. and M.M.A.; supervision, M.M.A. and T.C.; project administration, M.M.A. and T.C.; funding acquisition, M.M.A. and T.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under Grant 12472235.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors have no conflicts to disclose.
Nomenclature
| a |
Amplitude of diaphragm oscillation |
[mm] |
|
Area of foil |
[mm2] |
|
Jet half width |
[mm] |
|
Drag coefficient |
-- |
| d |
Slot width or diameter of the orifice |
[mm] |
|
Hydraulic diameter of the orifice |
[mm] |
| D |
Diameter of diaphragm |
[mm] |
|
Characteristic length of the square cylinder |
[mm] |
|
Diaphragm oscillating frequency |
[Hz] |
|
Mechanical frequency |
[Hz] |
|
Helmholtz frequency |
[Hz] |
|
Cavity height |
[mm] |
|
Area-average heat transfer coefficient |
W/m²·K |
|
Time-average heat transfer coefficient |
W/m²·K |
|
Time-averaged jet momentum flux for unit width of orifice |
[kg/Sec] |
| k |
Thermal conductivity of air |
[] |
|
Length of slot orifice |
[mm] |
| L |
Orifice neck length |
[mm] |
|
Stroke length |
[mm] |
|
Mass flux ratio |
-- |
|
Nusselt Number |
-- |
|
Area-averaged Nusselt Number |
-- |
|
Time-averaged Nusselt Number |
-- |
|
Area- and time-averaged Nusselt Number |
-- |
|
radial distance from the center of the jet orifice |
[mm] |
| Re |
Reynolds Number |
-- |
|
Stokes Number |
-- |
| s |
Spacing between two orifices |
[mm] |
|
Radial spacing between the orifice and the annulus |
[mm] |
| St |
Strouhal Number |
-- |
| t |
Time |
[Sec] |
|
Time period of oscillation |
[Sec] |
|
Ambient temperature |
[K] |
|
Wall temperature |
[K] |
| Uo |
Time-average velocity |
[m/s] |
|
Average velocity over time and space |
[m/s] |
|
Freestream velocity |
[m/s] |
|
Instantaneous jet centerline velocity measured at the orifice exit |
[m/s] |
|
Time averaged streamwise velocity |
[m/s] |
|
Streamwise centerline velocity |
[m/s] |
|
Normal velocity |
[m/s] |
|
Jet-to-plate distance |
[mm] |
| Ø |
Phase difference |
[degree] |
|
Vectoring angle |
[degree] |
|
Kinematic viscosity |
[m2/s] |
Abbreviations
| avg |
Average |
|
Aspect ratio |
| AVR |
Annular vortex ring |
| COP |
Coefficient of performance |
| COSASJ |
Concentric orifices single-actuator synthetic jets |
| CSJ |
Coaxial synthetic jet |
| DASJ |
Double acting synthetic jet |
| DSJ |
Dual synthetic jet |
| ICASJ |
Independently controlled actuators |
| IVR |
Inner vortex ring |
| PIV |
Particle image velocimetry |
| SJ |
Synthetic jet |
|
Synthetic jet actuator |
| SJ array |
Synthetic jet array |
| Subscripts |
|
|
Inner jet |
|
Annular jet |
| Superscripts |
|
|
Anti-clockwise rotation of vortex |
| + |
Clockwise rotation of vortex |
References
- Herschlag, G., & Miller, L. (2011). Reynolds number limits for jet propulsion: a numerical study of simplified jellyfish. Journal of Theoretical Biology, 285(1), 84-95.
- Shukla, A. K., & Dewan, A. (2017). Flow and thermal characteristics of jet impingement: comprehensive review. International Journal of Heat and Technology, 35(1), 153-166.
- Gad-el-Hak, M. (2001). Flow control: The future. Journal of Aircraft, 38(3), 402-418.
- Rastan, M. R., Sohankar, A., Doolan, C., Moreau, D., Shirani, E., & Alam, M. M. (2019). Controlled flow over a finite square cylinder using suction and blowing. International Journal of Mechanical Sciences, 156, 410-434.
- Wang, L., Alam, M. M., Rehman, S., & Zhou, Y. (2022). Effects of blowing and suction jets on the aerodynamic performance of wind turbine airfoil. Renewable Energy, 196, 52-64.
- Bergthorson, J. M., Sone, K., Mattner, T. W., Dimotakis, P. E., Goodwin, D. G., & Meiron, D. I. (2005). Impinging laminar jets at moderate Reynolds numbers and separation distances. Physical Review E—Statistical, Nonlinear, and Soft Matter Physics, 72(6), 066307.
- Bogey, C., & Bailly, C. (2010). Influence of nozzle-exit boundary-layer conditions on the flow and acoustic fields of initially laminar jets. Journal of Fluid Mechanics, 663, 507-538.
- Suresh, P. R., Srinivasan, K., Sundararajan, T., & Das, S. K. (2008). Reynolds number dependence of plane jet development in the transitional regime. Physics of Fluids, 20(4), 044105.
- Freund, J. B. (2001). Noise sources in a low-Reynolds-number turbulent jet at Mach 0.9. Journal of Fluid Mechanics, 438, 277-305.
- Dewan, A., Dutta, R., & Srinivasan, B. (2012). Recent trends in computation of turbulent jet impingement heat transfer. Heat Transfer Engineering, 33(4-5), 447-460.
- Gillespie, M. B., Black, W. Z., Rinehart, C., & Glezer, A. (2006). Local convective heat transfer from a constant heat flux flat plate cooled by synthetic air jets. Journal of Heat Transfer, 128(10), 990-1000.
- Hsu, S. S., Travnicek, Z., Chou, C. C., Chen, C. C., & Wang, A. B. (2013). Comparison of double-acting and single-acting synthetic jets. Sensors and Actuators A: Physical, 203, 291-299.
- Zong, H., & Kotsonis, M. (2017). Experimental investigation on frequency characteristics of plasma synthetic jets. Physics of Fluids, 29(11), 115107.
- Mossi, K., Mane, P., & Bryant, R. (2005). Velocity profiles for synthetic jets using piezoelectric circular actuators. In 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, pp. 2341.
- Miró, A., Soria, M., Cajas, J. C., Rodríguez, I., & Moulinec, C. (2021). Flow topology and heat transfer analysis of slotted and axisymmetric synthetic impinging jets. International Journal of Thermal Sciences, 164, 106847.
- Panda, S., Pasa, J., & Arumuru, V. (2023). Characterisation of an independently controlled coaxial synthetic jet. Sensors and Actuators A: Physical, 359, 114469.
- Yeom, T., Huang, L., Zhang, M., Simon, T., & Cui, T. (2019). Heat transfer enhancement of air-cooled heat sink channel using a piezoelectric synthetic jet array. International Journal of Heat and Mass Transfer, 143, 118484.
- Cater, J. E., & Soria, J. (2002). The evolution of round zero-net-mass-flux jets. Journal of Fluid Mechanics, 472, 167-200.
- Ghaffari, O., Solovitz, S. A., Ikhlaq, M., & Arik, M. (2016). An investigation into flow and heat transfer of an ultrasonic micro-blower device for electronics cooling applications. Applied Thermal Engineering, 106, 881-889.
- Jankee, G. K., &Ganapathisubramani, B. (2021). Interaction and vectoring of parallel rectangular twin jets in a turbulent boundary layer. Physical Review Fluids, 6(4), 044701.
- Jabbal, M., & Zhong, S. (2008). The near wall effect of synthetic jets in a boundary layer. International Journal of Heat and Fluid Flow, 29(1), 119-130.
- Lemanov, V. V., Pakhomov, M. A., Terekhov, V. I., & Travnicek, Z. (2022). Non-stationary flow and heat transfer in a synthetic confined jet impingement. International Journal of Thermal Sciences, 179, 107607.
- Utturkar, Y., Arik, M., Seeley, C. E., & Gursoy, M. (2008). An experimental and computational heat transfer study of pulsating jets, Journal of Heat Transfer, 130(6), 062201.
- Xu, M., Wu, M., & Mi, J. (2019). A new type of self-excited flapping jets due to a flexible film at the nozzle exit. Experimental Thermal and Fluid Science, 106, 226-233.
- Ostermann, F., Woszidlo, R., Nayeri, C. N., & Paschereit, C. O. (2018). Properties of a sweeping jet emitted from a fluidic oscillator. Journal of Fluid Mechanics, 857, 216-238.
- Smith, B. L., & Glezer, A. (1998). The formation and evolution of synthetic jets. Physics of Fluids, 10(9), 2281-2297.
- Krishnan, G., & Mohseni, K. (2009). An experimental and analytical investigation of rectangular synthetic jets, Journal of Fluids Engineering, 131(12), 121101.
- Walimbe, P., Agrawal, A., & Chaudhari, M. (2021). Flow characteristics and novel applications of synthetic jets: A review. Journal of Heat Transfer, 143(11), 112301.
- Smith, B., & Swift, G. (2001, June). Synthetic jets at large Reynolds number and comparison to continuous jets. In 15th AIAA Computational Fluid Dynamics Conference, pp. 3030.
- Shuster, J., & Smith, D. (2004). A Study of the Formation and Scaling of a Synthetic Jet. In 42nd AIAA Aerospace Sciences Meeting and Exhibit, pp. 90.
- Glezer, A., & Amitay, M. (2002). Synthetic jets. Annual Review of Fluid Mechanics, 34(1), 503-529.
- Amitay, M., Smith, B., & Glezer, A. (1998, January). Aerodynamic flow control using synthetic jet technology. In 36th AIAA Aerospace Sciences Meeting and Exhibit, pp. 208.
- Mallinson, S. G., Reizes, J. A., Hong, G., & Buttini, M. (1999, September). Synthetic jet actuators for flow control. In Electronics and Structures for MEMS, 3891, pp. 146-156.
- Tesař, V., Hung, C. H., & Zimmerman, W. B. (2006). No-moving-part hybrid-synthetic jet actuator. Sensors and Actuators A: Physical, 125(2), 159-169.
- Jacob, A., Shafi, K. A., & Roy, K. R. (2021). Heat transfer characteristics of piston-driven synthetic jet. International Journal of Thermofluids, 11, 100104.
- Kanase, M. M., Mangate, L. D., & Chaudhari, M. B. (2018). Acoustic aspects of synthetic jet generated by acoustic actuator. Journal of Low Frequency Noise, Vibration and Active Control, 37(1), 31-47.
- Shuster, J. M., & Smith, D. R. (2007). Experimental study of the formation and scaling of a round synthetic jet. Physics of Fluids, 19(4), 045109.
- Van Buren, T., Whalen, E., & Amitay, M. (2016). Achieving a high-speed and momentum synthetic jet actuator. Journal of Aerospace Engineering, 29(2), 04015040.
- Smith, B. L., & Swift, G. W. (2003). A comparison between synthetic jets and continuous jets. Experiments in Fluids, 34, 467-472.
- Arik, M., Sharma, R., Lustbader, J., & He, X. (2013). Steady and unsteady air impingement heat transfer for electronics cooling applications. Journal of Heat Transfer, 135(11), 111009.
- Tan, X. M., Zhang, J. Z., Yong, S., & Xie, G. N. (2015). An experimental investigation on comparison of synthetic and continuous jets impingement heat transfer. International Journal of Heat and Mass Transfer, 90, 227-238.
- Arik, M. (2007). An investigation into feasibility of impingement heat transfer and acoustic abatement of meso scale synthetic jets. Applied Thermal Engineering, 27(8-9), 1483-1494.
- Minichiello, A., Glezer, A., Hartley, J. G., & Black, W. Z. (1997). Thermal management of sealed electronic enclosures using synthetic jet technology. Advances in Electronic Packaging, 1997: Proceedings of the Pacific Rim/ASME International Intersociety Electronic & Photonic Packaging Converence, 19(2), 1809.
- Ramasamy, M., Wilson, J. S., & Martin, P. B. (2010). Interaction of synthetic jet with boundary layer using microscopic particle image velocimetry. Journal of Aircraft, 47(2), 404-422.
- Tadjfar, M., & Kamari, D. (2020). Optimization of flow control parameters over SD7003 airfoil with synthetic jet actuator. Journal of Fluids Engineering, 142(2), 021206.
- Smith, B. L., & Glezer, A. (2002). Jet vectoring using synthetic jets. Journal of Fluid Mechanics, 458, 1-34.
- Amitay, M., Washburn, A. E., Anders, S. G., & Parekh, D. E. (2004). Active flow control on the stingray uninhabited air vehicle: transient behaviour. AIAA Journal, 42(11), 2205-2215.
- Watson, M., Jaworski, A. J., & Wood, N. J. (2007). Application of synthetic jet actuators for the modification of the characteristics of separated shear layers on slender wings. The Aeronautical Journal, 111(1122), 519-529.
- Mallinson, S. G., Reizes, J. A., Hong, G., & Westbury, P. S. (2004). Analysis of hot-wire anemometry data obtained in a synthetic jet flow. Experimental Thermal and Fluid Science, 28(4), 265-272.
- Glezer, A. (2011). Some aspects of aerodynamic flow control using synthetic-jet actuation. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 369(1940), 1476-1494.
- Hong, M. H., Cheng, S. Y., & Zhong, S. (2020). Effect of geometric parameters on synthetic jet: A review. Physics of Fluids, 32(3), 031301.
- Tadjfar, M., & Kamari, D. (2020). Optimization of flow control parameters over SD7003 airfoil with synthetic jet actuator. Journal of Fluids Engineering, 142(2), 021206.
- Honohan, A. , Amitay, M., & Glezer, A. (2000). Aerodynamic control using synthetic jets. In Fluids 2000 Conference and Exhibit, pp. 2401.
- Lee, J., Lee, B., Kim, M., & Kim, C. (2016). Active flow control on a UCAV planform using synthetic jets. International Journal of Aeronautical and Space Sciences, 17(3), 315-323.
- Li, J., & Zhang, X. (2020). Active flow control for supersonic aircraft: A novel hybrid synthetic jet actuator. Sensors and Actuators A: Physical, 302, 111770.
- Feng, J., Lin, Y., Zhu, G., & Luo, X. (2019). Effect of synthetic jet parameters on flow control of an aerofoil at high Reynolds number. Sādhanā, 44(8), 1-10.
- Ja'fari, M., Jaworski, A. J., & Rona, A. (2022). Application of synthetic jet arrays for flow separation control on a circular “hump” model. Experimental Thermal and Fluid Science, 131, 110543.
- Ja’fari, M., Jaworski, A. J., & Rona, A. (2022). Numerical study of flow separation control over a circular hump using synthetic jet actuators. AIP Advances, 12(9), 095205.
- Zhang, B., Liu, H., Li, Y., Liu, H., & Dong, J. (2021). Experimental study of coaxial jets mixing enhancement using synthetic jets. Applied Sciences, 11(2), 803.
- Lord, W., MacMartin, D., & Tillman, G. (2000, June). Flow control opportunities in gas turbine engines. In Fluids 2000 Conference and Exhibit, pp. 2234.
- Tensi, J., Boué, I., Paillé, F., & Dury, G. (2002). Modification of the wake behind a circular cylinder by using synthetic jets. Journal of Visualization, 5(1), 37-44.
- Gilarranz, J. L., Traub, L. W., & Rediniotis, O. K. (2005). A new class of synthetic jet actuators—part II: application to flow separation control. Journal of Fluids Engineering, 127(2), 377-387.
- Gompertz, K. A., & Bons, J. P. (2011). Combined unsteady wakes and active flow control on a low-pressure turbine airfoil. Journal of Propulsion and Power, 27(5), 990-1000.
- De Giorgi, M. G., Traficante, S., De Luca, C., Bello, D., & Ficarella, A. (2012, June). Active flow control techniques on a stator compressor cascade: a comparison between synthetic jet and plasma actuators. In Turbo expo: power for land, sea, and air, The American Society of Mechanical Engineers, 44748, pp. 439-450.
- De Giorgi, M. G., De Luca, C. G., Ficarella, A., & Marra, F. (2015). Comparison between synthetic jets and continuous jets for active flow control: application on a NACA 0015 and a compressor stator cascade. Aerospace Science and Technology, 43, 256-280.
- Traficante, S., De Giorgi, M. G., & Ficarella, A. (2016). Flow separation control on a compressor-stator cascade using plasma actuators and synthetic and continuous jets. Journal of Aerospace Engineering, 29(3), 04015056.
- Zhang, H., Chen, S., Gong, Y., & Wang, S. (2019). A comparison of different unsteady flow control techniques in a highly loaded compressor cascade. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 233(6), 2051-2065.
- Ja'fari, M., Shojae, F. J., & Jaworski, A. J. (2023). Synthetic jet actuators: Overview and applications. International Journal of Thermofluids, 20, 100438.
- Gil, P. (2021). Experimental investigation on heat transfer enhancement of air-cooled heat sink using multiple synthetic jets. International Journal of Thermal Sciences, 166(106949), 10-1016.
- Thompson, M. R., Denny, D. L., Black, W. Z., Hartley, J. G., & Glezer, A. (1997). Cooling of microelectronic devices using synthetic jet technology. In 11th European Microelectronics Conference, pp. 362-366.
- Campbell, S. J., Black, W. Z., Glezer, A., & Hartley, J. G. (1998). Thermal management of a laptop computer with synthetic air microjets. In ITherm'Sixth Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems, (Cat. No. 98CH36208), pp. 43-50.
- Lasance, C. J., & Aarts, R. M. (2008). Synthetic jet cooling part I: overview of heat transfer and acoustics. In 2008 Twenty-fourth Annual IEEE Semiconductor Thermal Measurement and Management Symposium, pp. 20-25.
- Remsburg, R. , Lucas, T., & Binshtok, R. J. (2010). Practical CFD modeling of synthetic air jets for thermal management of electronics. In 2010 26th Annual IEEE Semiconductor Thermal Measurement and Management Symposium (SEMI-THERM), pp. 18-28.
- Plant, R. D., Friedman, J., & Saghir, M. Z. (2023). A review of jet impingement cooling. International Journal of Thermofluids, 17, 100312.
- Thomas, A. P., Milano, M., G'Sell, M. G., Fischer, K., & Burdick, J. (2005). Synthetic jet propulsion for small underwater vehicles. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, pp. 181-187.
- Rathay, N. W., Boucher, M. J., Amitay, M., & Whalen, E. (2014). Performance enhancement of a vertical tail using synthetic jet actuators. AIAA Journal, 52(4), 810-820.
- Krieg, M., Nelson, K., Eisele, J., & Mohseni, K. (2018). Bioinspired jet propulsion for disturbance rejection of marine robots. IEEE Robotics and Automation Letters, 3(3), 2378-2385.
- Wang, D., Zhang, F., Zhang, S., Liu, D., Li, J., Chen, W., ... & Liu, Y. (2024). Miniature Modular Reconfigurable Underwater Robot Based on Synthetic Jet. Advanced Science, 11(39), 2406956.
- Geng, L., Lin, Y., Hu, Z., Wang, C., Meng, L., & Li, D. (2016). A new concept spherical underwater robot propelled by thrust vector synthetic jet actuator. In OCEANS 2016-Shanghai, pp. 1-4.
- Geng, L., Hu, Z., & Lin, Y. (2018). Hydrodynamic characteristic of synthetic jet steered underwater vehicle. Applied Ocean Research, 70, 1-13.
- Chaudhari, M., Puranik, B., & Agrawal, A. (2010). Effect of orifice shape in synthetic jet based impingement cooling. Experimental Thermal and Fluid Science, 34(2), 246-256.
- Oren, L., Gutmark, E., Muragappan, S., & Khosla, S. (2009). Flow characteristics of non circular synthetic jets. In 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, p. 1309.
- Jain, M., Puranik, B., & Agrawal, A. (2011). A numerical investigation of effects of cavity and orifice parameters on the characteristics of a synthetic jet flow. Sensors and actuators A: Physical, 165(2), 351-366.
- Fugal, S. R., Smith, B. L., & Spall, R. E. (2005). Displacement amplitude scaling of a two-dimensional synthetic jet. Physics of Fluids, 17(4), 045103.
- Lee, C. Y., & Goldstein, D. B. (2002). Two-dimensional synthetic jet simulation. AIAA Journal, 40(3), 510-516.
- Gallas, Q., Holman, R., Nishida, T., Carroll, B., Sheplak, M., & Cattafesta, L. (2003). Lumped element modeling of piezoelectric-driven synthetic jet actuators. AIAA Journal, 41(2), 240-247.
- Chaudhari, M., Verma, G., Puranik, B., & Agrawal, A. (2009). Frequency response of a synthetic jet cavity. Experimental Thermal and Fluid Science, 33(3), 439-448.
- Tan, X. M., & Zhang, J. Z. (2013). Flow and heat transfer characteristics under synthetic jets impingement driven by piezoelectric actuator. Experimental Thermal and Fluid Science, 48, 134-146.
- Qayoum, A., Gupta, V., Panigrahi, P. K., & Muralidhar, K. (2010). Influence of amplitude and frequency modulation on flow created by a synthetic jet actuator. Sensors and Actuators A: Physical, 162(1), 36-50.
- Singh, P. K., Renganathan, M., Yadav, H., Sahu, S. K., Upadhyay, P. K., & Agrawal, A. (2022). An experimental investigation of the flow-field and thermal characteristics of synthetic jet impingement with different waveforms. International Journal of Heat and Mass Transfer, 187, 122534.
- Singh, P. K., Shah, A. K., Tripathi, S. N., Yadav, H., Upadhyay, P. K., & Sahu, S. K. (2022). Numerical investigation of the flow and thermal behavior of impinging single and multi-orifice synthetic jets with different waveforms. Numerical Heat Transfer, Part A: Applications, 83(6), 573-593.
- Zhang, Y., Li, P., & Xie, Y. (2018). Numerical investigation of heat transfer characteristics of impinging synthetic jets with different waveforms. International Journal of Heat and Mass Transfer, 125, 1017-1027.
- Yen, J., & Ahmed, N. A. (2013). Synthetic jets as a boundary vorticity flux control tool. AIAA Journal, 51(2), 510-513.
- Alam, M. M. (2023). Fluctuating forces on bluff bodies and their relationships with flow structures. Ocean Engineering, 273, 113870.
- Sharma, P., Singh, P. K., Sahu, S. K., & Yadav, H. (2022). A critical review on flow and heat transfer characteristics of synthetic jet. Transactions of the Indian National Academy of Engineering, 7(1), 61-92.
- Utturkar, Y., Holman, R., Mittal, R., Carroll, B., Sheplak, M., & Cattafesta, L. (2003, January). A jet formation criterion for synthetic jet actuators. In 41st Aerospace Sciences Meeting and Exhibit, pp. 636.
- Silva-Llanca, L., & Ortega, A. (2017). Vortex dynamics and mechanisms of heat transfer enhancement in synthetic jet impingement. International Journal of Thermal Sciences, 112, 153-164.
- Holman, R., Utturkar, Y., Mittal, R., Smith, B. L., & Cattafesta, L. (2005). Formation criterion for synthetic jets. AIAA Journal, 43(10), 2110-2116.
- Zhou, J., Tang, H., & Zhong, S. (2009). Vortex roll-up criterion for synthetic jets. AIAA Journal, 47(5), 1252-1262.
- Valiorgue, P., Persoons, T., McGuinn, A., & Murray, D. B. (2009). Heat transfer mechanisms in an impinging synthetic jet for a small jet-to-surface spacing. Experimental Thermal and Fluid Science, 33(4), 597-603.
- Smyk, E., Gil, P., Dančová, P., & Jopek, M. (2022). The PIV measurements of time-averaged parameters of the synthetic jet for different orifice shapes. Applied Sciences, 13(1), 328.
- Wang, L., Feng, L. H., Wang, J. J., & Li, T. (2018). Parameter influence on the evolution of low-aspect-ratio rectangular synthetic jets. Journal of Visualization, 21, 105-115.
- Smith, B. L., & Swift, G. W. (2003). Power dissipation and time-averaged pressure in oscillating flow through a sudden area change. The Journal of the Acoustical Society of America, 113(5), 2455-2463.
- Nani, D. J., & Smith, B. L. (2012). Effect of orifice inner lip radius on synthetic jet efficiency. Physics of Fluids, 24(11), 115110.
- Rizzetta, D. P., Visbal, M. R., & Stanek, M. J. (1999). Numerical investigation of synthetic- jet flowfields. AIAA Journal, 37(8), 919-927.
- Mane, P., Mossi, K., Rostami, A., Bryant, R., & Castro, N. (2007). Piezoelectric actuators as synthetic jets: Cavity dimension effects. Journal of Intelligent Material Systems and Structures, 18(11), 1175-1190.
- Jain, M., Puranik, B., & Agrawal, A. (2011). A numerical investigation of effects of cavity and orifice parameters on the characteristics of a synthetic jet flow. Sensors and actuators A: Physical, 165(2), 351-366.
- Jabbal, M., Tang, H., & Zhong, S. (2006). The effect of geometry on the performance of synthetic jet actuators. In ICAS-Secretariat - 25th Congress of the International Council of the Aeronautical Sciences 2006, 2, pp. 815-823.
- Chaudhari, M., Verma, G., Baramade, A., Puranik, B., & Agrawal, A. (2008). Near-field measurements and cavity design for synthetic jets. In 38th Fluid Dynamics Conference and Exhibit, pp. 4068.
- Lv, Y. W., Zhang, J. Z., Shan, Y., & Tan, X. M. (2014). Numerical investigation for effects of actuator parameters and excitation frequencies on synthetic jet fluidic characteristics. Sensors and Actuators A: Physical, 219, 100-111.
- Tang, H., & Zhong, S. (2005, June). Modelling of the characteristics of synthetic jet actuators. In 35th AIAA Fluid Dynamics Conference and Exhibit, pp. 4748.
- Smith, B. L., & Glezer, A. (2005). Vectoring of adjacent synthetic jets. AIAA Journal, 43(10), 2117-2124.
- Zhang, S., & Zhong, S. (2010). Experimental investigation of flow separation control using an array of synthetic jets. AIAA Journal, 48(3), 611-623.
- Pasa, J., Panda, S., & Arumuru, V. (2022). Influence of Strouhal number and phase difference on the flow behavior of a synthetic jet array. Physics of Fluids, 34(6), 065118.
- McGuinn, A., Farrelly, R., Persoons, T., & Murray, D. B. (2013). Flow regime characterisation of an impinging axisymmetric synthetic jet. Experimental Thermal and Fluid Science, 47, 241-251.
- Xu, Y., He, G., Kulkarni, V., & Wang, J. (2017). Experimental investigation of influence of Reynolds number on synthetic jet vortex rings impinging onto a solid wall. Experiments in Fluids, 58(1), 6. 58, 1, 6.
- Feero, M. A., Goodfellow, S. D., Lavoie, P., & Sullivan, P. E. (2015). Flow reattachment using synthetic jet actuation on a low-Reynolds-number airfoil. AIAA Journal, 53(7), 2005-2014.
- Greco, C. S., Cardone, G., & Soria, J. (2017). On the behaviour of impinging zero-net-mass-flux jets. Journal of Fluid Mechanics, 810, 25-59.
- Kotapati, R. B., Mittal, R., & Cattafesta Iii, L. N. (2007). Numerical study of a transitional synthetic jet in quiescent external flow. Journal of Fluid Mechanics, 581, 287-321.
- Kral, L., Donovan, J., Cain, A., Cary, A., Kral, L., Donovan, J., & Cary, A. (1997, June). Numerical simulation of synthetic jet actuators. In 4th Shear Flow Control Conference (p. 1824).
- Watson, M., Jaworski, A. J., & Wood, N. J. (2003). A study of synthetic jets from rectangular and dual-circular orifices. The Aeronautical Journal, 107(1073), 427-434.
- Mane, P. (2005). Experimental design and analysis of piezoelectric synthetic jets in quiescent air, M.Sc. dissertation, Virginia Commonwealth University.
- Ohanian, O. J. (2011). Ducted fan aerodynamics and modeling, with applications of steady and synthetic jet flow control, Doctoral dissertation, Virginia Tech, 2011.
- Mangate, L. D., & Chaudhari, M. B. (2015). Heat transfer and acoustic study of impinging synthetic jet using diamond and oval shape orifice. International Journal of Thermal Sciences, 89, 100-109.
- Bhapkar, U. S., Srivastava, A., & Agrawal, A. (2014). Acoustic and heat transfer characteristics of an impinging elliptical synthetic jet generated by acoustic actuator. International Journal of Heat and Mass Transfer, 79, 12-23.
- Lee, C. Y. Y., Woyciekoski, M. L., & Copetti, J. B. (2016). Experimental study of synthetic jets with rectangular orifice for electronic cooling. Experimental Thermal and Fluid Science, 78, 242-248.
- Chaudhari, M., Puranik, B., & Agrawal, A. (2010). Heat transfer characteristics of synthetic jet impingement cooling. International Journal of Heat and Mass Transfer, 53(5-6), 1057-1069.
- Greco, C. S., Ianiro, A., & Cardone, G. (2014). Time and phase average heat transfer in single and twin circular synthetic impinging air jets. International Journal of Heat and Mass Transfer, 73, 776-788.
- Silva-Llanca, L., Ortega, A., & Rose, I. (2015). Experimental convective heat transfer in a geometrically large two-dimensional impinging synthetic jet. International Journal of Thermal Sciences, 90, 339-350.
- Silva-Llanca, L. (2016). Replicating impinging synthetic jets as a train of consecutive viscous Lamb-Ossen vortex pairs. In 2016 15th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), pp. 930-938.
- Ikhlaq, M., Yasir, M., Demiroğlu, M., & Arik, M. (2021). Synthetic jet cooling technology for electronics thermal management—a critical review. IEEE Transactions on Components, Packaging and Manufacturing Technology, 11(8), 1156-1170.
- Ghaffari, O., Ikhlaq, M., & Arik, M. (2015). An experimental study of impinging synthetic jets for heat transfer augmentation. International Journal of Air-Conditioning and Refrigeration, 23(03), 1550024.
- Persoons, T., McGuinn, A., & Murray, D. B. (2011). A general correlation for the stagnation point Nusselt number of an axisymmetric impinging synthetic jet. International Journal of Heat and Mass Transfer, 54(17-18), 3900-3908.
- Greco, C. S., Paolillo, G., Ianiro, A., Cardone, G., & De Luca, L. (2018). Effects of the stroke length and nozzle-to-plate distance on synthetic jet impingement heat transfer. International Journal of Heat and Mass Transfer, 117, 1019-1031.
- Rylatt, D. I., & O'Donovan, T. S. (2014, July). The effects of stroke length and Reynolds number on heat transfer to a ducted confined and semi-confined synthetic air jet. In Journal of Physics: Conference Series, 525(1), pp. 012012.
- Gil, P., Wilk, J., & Korzeniowski, M. (2021). Helmholtz resonance frequency of the synthetic jet actuator. Applied Sciences, 11(12), 5666.
- Pavlova, A., & Amitay, M. (2006). Electronic cooling using synthetic jet impingement, Journal of Heat Transfer, 128, 897–907.
- Ghaffari, O., Solovitz, S. A., & Arik, M. (2016). An investigation into flow and heat transfer for a slot impinging synthetic jet. International Journal of Heat and Mass Transfer, 100, 634-645.
- Alam, M. M., Zhou, Y., & Wang, X. W. (2011). The wake of two side-by-side square cylinders. Journal of Fluid Mechanics, 669, 432-471.
- Wang, C. P. (2019). Thermal management for portable electronics using a piezoelectric micro-blower. IEEE Transactions on Device and Materials Reliability, 19(3), 563-567.
- Chovet, C., Lippert, M., Keirsbulck, L., & Foucaut, J. M. (2016). Dynamic characterization of piezoelectric micro-blowers for separation flow control. Sensors and Actuators A: Physical, 249, 122-130.
- Ikhlaq, M., Arik, M., Arshad, A., & Jabbal, M. (2021). Flow and Heat Transfer Characteristics of Piezoelectric-Driven Synthetic Jet Actuator with Respect to Their Stroke Length. In Advances in Heat Transfer and Thermal Engineering: Proceedings of 16th UK Heat Transfer Conference (UKHTC2019) (pp. 659-662). Springer Singapore.
- Hatami, M., Bazdidi-Tehrani, F., Abouata, A., & Mohammadi-Ahmar, A. (2018). Investigation of geometry and dimensionless parameters effects on the flow field and heat transfer of impingement synthetic jets. International Journal of Thermal Sciences, 127, 41-52.
- Kercher, D. S., Lee, J. B., Brand, O., Allen, M. G., & Glezer, A. (2003). Microjet cooling devices for thermal management of electronics. IEEE Transactions on Components and Packaging Technologies, 26(2), 359-366.
- Silva, L. A., & Ortega, A. (2013). Convective heat transfer in an impinging synthetic jet: a numerical investigation of a canonical geometry. Journal of Heat Transfer, 135(8), 082201.
- Silva, L., Ortega, A., & Rose, I. (2013). Experimental study of the convective heat transfer from a geometrically scaled up 2d impinging synthetic jet. In International Electronic Packaging Technical Conference and Exhibition, American Society of Mechanical Engineers, pp. V002T08A030–V002T08A030.
- Silva, L., & Ortega, A. (2011). CFD analysis of the vortex dynamics generated by a synthetic jet impinging on a heated surface. In ASME International Mechanical Engineering Congress and Exposition, American Society of Mechanical Engineers, pp. 217-225.
- Silva, L., & Ortega, A. (2011). Numerical simulation of local heat transfer and scaling of a synthetic impinging jet in a canonical geometry. In International Electronic Packaging Technical Conference and Exhibition, American Society of Mechanical Engineers, pp. 113-121.
- Silva, L., Ortega, A., & Ebrahim, M. (2012). Experiments and simulation of an impinging synthetic jet designed to eliminate actuator artifacts. In Heat Transfer Summer Conference, pp. 703-710.
- Kumar, R., Mirikar, D., Agrawal, A., & Yadav, H. (2024). Insights into the flow and heat transfer aspects of single and multi-orifice synthetic jets. International Journal of Heat and Mass Transfer, 231, 125897.
- Zhen-Bing, L., & Zhi-Xun, X. (2008). PIV measurements and mechanisms of adjacent synthetic jets interactions. Chinese Physics Letters, 25(2), 612.
- Alimohammadi, S., Fanning, E., Persoons, T., & Murray, D. B. (2016). Characterization of flow vectoring phenomenon in adjacent synthetic jets using CFD and PIV. Computers & Fluids, 140, 232-246.
- Guo, D., Cary, A.W., Agarwal, R.K. (2003). Numerical Simulation of the Interaction of Two Adjacent Synthetic Jet Actuators. In: Armfield, S.W., Morgan, P., Srinivas, K. (eds) Computational Fluid Dynamics 2002 (Springer, Berlin, Heidelberg), pp. 751-756.
- Berk, T., Gomit, G., & Ganapathisubramani, B. (2016). Vectoring of parallel synthetic jets: A parametric study. Journal of Fluid Mechanics, 804, 467-489.
- Watson, M., Jaworski, A. J., & Wood, N. J. (2003). Contribution to the understanding of flow interactions between multiple synthetic jets. AIAA Journal, 41(4), 747-749.
- Luo, Z. B., Xia, Z. X., & Liu, B. (2006). An adjustable synthetic jet by a novel PZT-driven actuator with a slide block. In Journal of Physics: Conference Series, 34, 487.
- Liu, Y., Wang, B., & Liu, S. (2009). Investigation of phase excitation effect on mixing control in coaxial jets. Journal of Thermal Science, 18, 364-369.
- Riazi, H., & Ahmed, N. (2011). Numerical investigation on two-orifice synthetic jet actuators of varying orifice spacing and diameter. In 29th AIAA Applied Aerodynamics Conference, pp. 3171.
- Smith, B., Trautman, M., & Glezer, A. (1999). Controlled interactions of adjacent synthetic jets. American Institute of Aeronautics and Astronautics, pp. 669.
- Holman, R., Gallas, Q., Carroll, B., & Cattafesta, L. (2003). Interaction of adjacent synthetic jets in an airfoil separation control application. In 33rd AIAA Fluid dynamics Conference and Exhibit, pp. 3709.
- He, W., Luo, Z. B., Deng, X., Peng, C., Liu, Q., Gao, T. X., ... & Peng, W. Q. (2023). Numerical study on the atomization mechanism and energy characteristics of synthetic jet/dual synthetic jets. Applied Energy, 346, 121376.
- Zhenbing, L., Zhixun, X., Xiong, D., Lin, W., Yujie, L., Yao, M., ... & Rui, Y. (2017). Research progress of dual synthetic jets and its flow control technology. Acta Aerodynamica Sinica, 35(2), 252-264. (.
- Luo, Z., Zhao, Z., Deng, X., Wang, L., & Xia, Z. (2022, July). Dual synthetic jets actuator and its applications—Part I: PIV measurements and comparison to synthetic jet actuator. In Actuators, 11 (8), 205.
- Liu, J. F., Luo, Z. B., Deng, X., Zhao, Z. J., Li, S. Q., Liu, Q., & Zhu, Y. X. (2022, July). Dual Synthetic jets actuator and its applications—Part II: Novel fluidic thrust-vectoring method based on dual synthetic jets actuator. In Actuators, 11(8), 209.
- Zhao, Z., Luo, Z., Deng, X., Zhang, J., Liu, J., & Li, S. (2023). Effects of dual synthetic jets on longitudinal aerodynamic characteristics of a flying wing layout. Aerospace Science and Technology, 132, 108043.
- Li, S., Luo, Z., Deng, X., Peng, W., & Liu, Z. (2021). Experimental investigation on active control of flow around a finite-length square cylinder using dual synthetic jet. Journal of Wind Engineering and Industrial Aerodynamics, 210, 104519.
- Wei, H. E., Songjiang, F. E. N. G., Zhenbing, L. U. O., Lurui, X. I. A., Xiong, D. E. N. G., Sen, L. I., & Sheng, X. U. (2025). Flow control mechanism of sprays using dual synthetic jets. Chinese Journal of Aeronautics, 38(3), 103362.
- He, W., Luo, Z. B., Deng, X., & Xia, Z. X. (2019). Experimental investigation on the performance of a novel dual synthetic jet actuator-based atomization device. International Journal of Heat and Mass Transfer, 142, 118406.
- Wang, Y., Cheng, P., Luo, Z., Liu, Q., Wang, H., & Yu, X. (2025). Flow field characteristics and crossflow interaction mechanisms of underwater dual synthetic jets. Physics of Fluids, 37(7), 075104.
- Li, S., Xia, M., Gao, T., Zhao, Z., & Luo, Z. (2025). Experimental Study of a Novel Circulation Control Device Based on Dual Synthetic Jets. Journal of Aerospace Engineering, 38(1), 04024111.
- Zhao, G., Zhao, Q., Gu, Y., & Chen, X. (2016). Experimental investigations for parametric effects of dual synthetic jets on delaying stall of a thick airfoil. Chinese Journal of Aeronautics, 29(2), pp. 346-35.
- Persoons, T., O’Donovan, T. S., & Murray, D. B. (2009). Heat transfer in adjacent interacting impinging synthetic jets. In Heat Transfer Summer Conference, The American Society of Mechanical Engineers, pp. 955-962.
- Fanning, E., Persoons, T., & Murray, D. B. (2012). Heat transfer characteristics of a pair of impinging synthetic jets: Effect of orifice spacing and impingement distance. In Journal of Physics: Conference Series, IOP Science, 395, 012025.
- Fanning, E., Persoons, T., & Murray, D. B. (2015). Heat transfer and flow characteristics of a pair of adjacent impinging synthetic jets. International Journal of Heat and Fluid Flow, 54, 153-166.
- Deng, X., Luo, Z. B., Xia, Z. X., & Gong, W. J. (2019). Experimental investigation on the flow regime and impingement heat transfer of dual synthetic jet. International Journal of Thermal Sciences, 145, 105864.
- Chaudhari, M., Puranik, B., & Agrawal, A. (2011). Multiple orifice synthetic jet for improvement in impingement heat transfer. International Journal of Heat and Mass Transfer, 54(9-10), 2056-2065.
- Mangate, L. D., & Chaudhari, M. B. (2016). Experimental study on heat transfer characteristics of a heat sink with multiple-orifice synthetic jet. International Journal of Heat and Mass Transfer, 103, 1181-1190.
- Yadav, H., Joshi, A., Chaudhari, M., & Agrawal, A. (2019). An experimental study of a multi-orifice synthetic jet with application to cooling of compact devices. AIP Advances, 9, 125108.
- Mangate, L., Yadav, H., Agrawal, A., & Chaudhari, M. (2019). Experimental investigation on thermal and flow characteristics of synthetic jet with multiple-orifice of different shapes. International Journal of Thermal Sciences, 140, 344-357.
- Gil, P. (2023). Flow and heat transfer characteristics of single and multiple synthetic jets impingement cooling. International Journal of Heat and Mass Transfer, 201, 123590.
- Ahmed, A., & Bangash, Z. A. (2009). Experimental investigation of axisymmetric coaxial synthetic jets. Experimental Thermal and Fluid Science, 33(8), 1142-1148.
- Broučková, Z., Trávníček, Z., & Šafařík, P. (2013). Active control of the jet in coaxial arrangement. In EPJ Web of Conferences, 45, 01016.
- Kumar, R., Kapadiya, Z., Mirikar, D., & Yadav, H. (2025). A comparative study of coaxial and conventional synthetic jet heat transfer. International Communications in Heat and Mass Transfer, 161, 108530.
- Panda, S., Gohil, T. B., & Arumuru, V. (2022). Influence of mass flux ratio on the evolution of coaxial synthetic jet. Physics of Fluids, 34(9), 093601.
- Panda, S., Gohil, T. B., & Arumuru, V. (2022). Evolution of flow structure from a coaxial synthetic jet. International Journal of Mechanical Sciences, 231, 107588.
- Sethi, C., Pasa, J., Panda, S., & Arumuru, V. (2024). Influence of mass flux ratio and phase difference on impingement heat transfer characteristics of coaxial synthetic jet. International Journal of Heat and Mass Transfer, 234, 126075.
- Pasa, J., Shathrughnu, N. V., & Arumuru, V. (2024). Impingement heat transfer enhancement by focusing the jet from synthetic jet array. International Communications in Heat and Mass Transfer, 152, 107306.
- Mittal, V., & Arumuru, V. (2024). Control of the von Kármán vortex street with focusing and vectoring of jet using synthetic jet array. Physics of Fluids, 36(10), 103630.
- McGuinn, A., Rylatt, D. I., & O’Donovan, T. S. (2016). Heat transfer enhancement to an array of synthetic air jets by an induced crossflow. Applied Thermal Engineering, 103, 996-1003.
- Pasa, J., & Arumuru, V. (2021). Impingement heat transfer enhancement by synthetic jet array. In Proceedings of the 26thNational and 4th International ISHMT-ASTFE Heat and Mass Transfer Conference December 17-20, 2021, IIT Madras, Chennai-600036, Tamil Nadu, India. (Begel House Inc.), pp. 277-2743.
- Pasa, J., Panda, S., & Arumuru, V. (2023). Focusing of jet from synthetic jet array using non-linear phase delay. Physics of Fluids, 35(5), 055141.
- Pasa, J., & Arumuru, V. (2025). Phase difference effects on synthetic jet array flow: A proper orthogonal decomposition study. Physics of Fluids, 37(1), 015123.
- Zheng, Q., & Alam, M. M. (2017). Intrinsic features of flow past three square prisms in side-by-side arrangement. Journal of Fluid Mechanics, 826, pp. 996-1033.
- Zhu, H., Li, Y., Zhou, T., & Alam, M. M. (2025). Single-freedom vortex-induced vibration and collision of two side-by-side circular cylinders subjected to power-law flow. Physics of Fluids, 37(3), 033128.
- Alam, M. M., & Zhou, Y. (2013). Intrinsic features of flow around two side-by-side square cylinders. Physics of Fluids, 25(8), 085106.
- Alam, M. M., Moriya, M., & Sakamoto, H. (2003). Aerodynamic characteristics of two side-by-side circular cylinders and application of wavelet analysis on the switching phenomenon. Journal of Fluids and Structures, 18(3-4), 325-346.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).