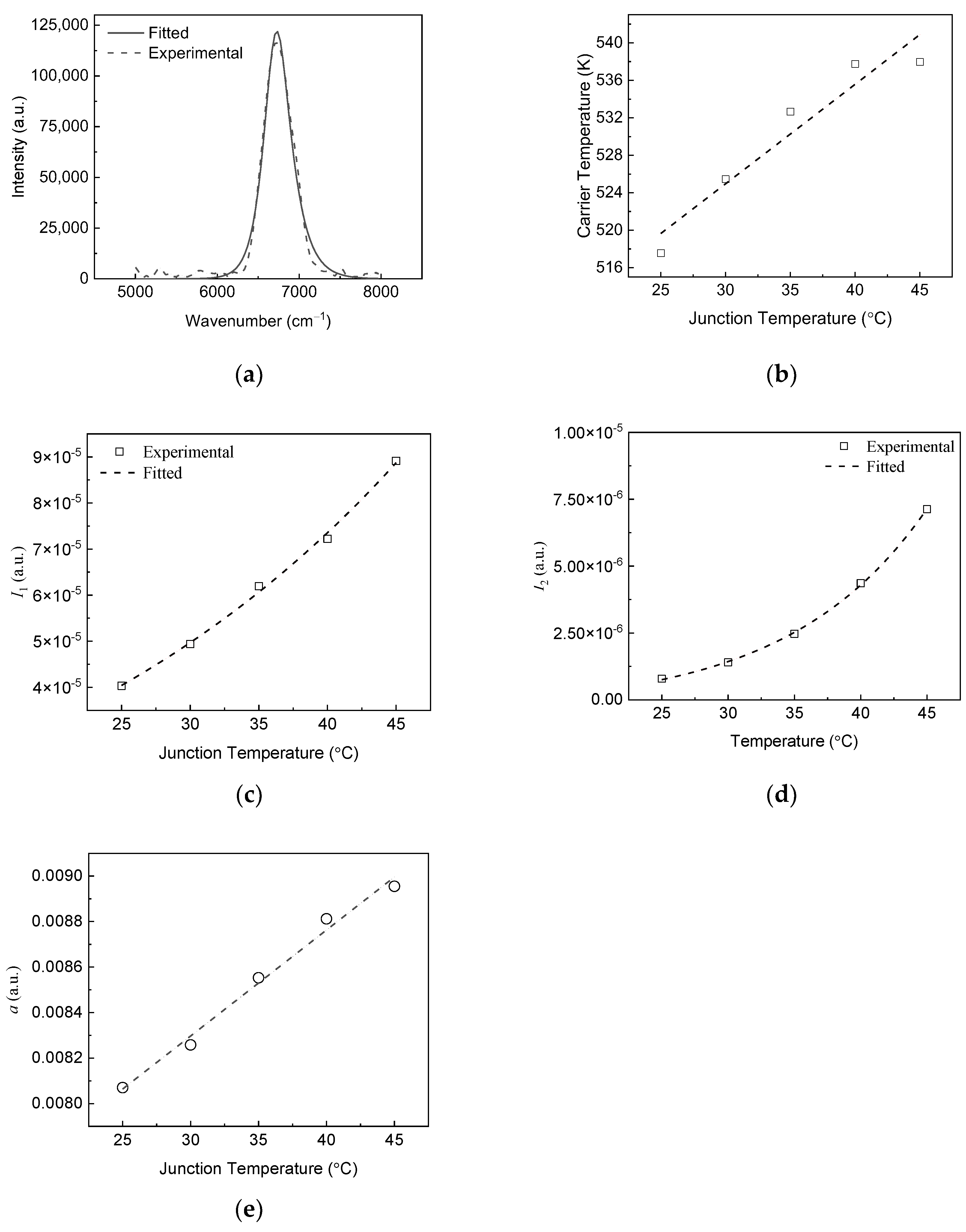Determination of Superluminescent Diode Junction Temperature via Static Modulated Fourier-Transform Spectrometer

1. Introduction

Super luminescent diodes are essential components widely used in various optical applications, ranging from optical coherence tomography to fiber-optic sensors [1,2]. For these devices, accurate modeling of spectral information is crucial, not only for understanding device performance but also for diagnosing internal physical processes, such as thermal behavior [3,4]. One of the most significant factors affecting the lifespan and stability of these diodes is the junction temperature, which is, however, challenging to measure directly during operation [5,6].

The spectral characteristics of these sources can be effectively estimated using Gaussian curve fitting techniques [3,7]. This modeling approach involves a reciprocal relationship: if the fitting parameters are precisely defined, the spectral characteristics can be accurately estimated; conversely, if the spectral information is acquired experimentally, the corresponding internal physical parameters of the Super luminescent diodes or light-emitting diodes can be inferred [8,9,10].

This work focuses on utilizing a generalized analytical expression based on spectral line components to model the measured spectra of a super luminescent diode. Specifically, we employ a modified static modulated Fourier-transform spectrometer to obtain rapid spectral data. It allows for relatively fast measurement (in the order of microseconds) compared to a conventional dynamic modulated Fourier transform spectrometer [11]. Due to the diverse structures of these diodes, directly measuring and monitoring the junction temperature of a super luminescent diode is often challenging and impractical [7,12]. Therefore, evaluating the performance of the super luminescent diode through its characteristics is a more effective and accurate method for assessment [13].

We then investigate the relationship between the fitting parameters obtained through the nonlinear least squares method and the device's operating conditions, specifically current and junction temperature [1,8,12]. Furthermore, this study establishes the quantitative connections between the extracted carrier temperature and external conditions, providing a robust method for non-invasive temperature estimation [5,14].

2. Methodology

Most commercially available spectrometers rely on a scanning mechanism. This design renders them inadequate for applications that require the monitoring of optical characteristics that vary rapidly with respect to changing operating conditions.

To address this limitation, the static modulated Fourier-transform spectrometer is employed. Unlike traditional scanning instruments, the static modulated Fourier-transform spectrometer generates an interferogram as a function of space, making it ideally suited for the real-time, instantaneous monitoring of the optical properties of light sources.

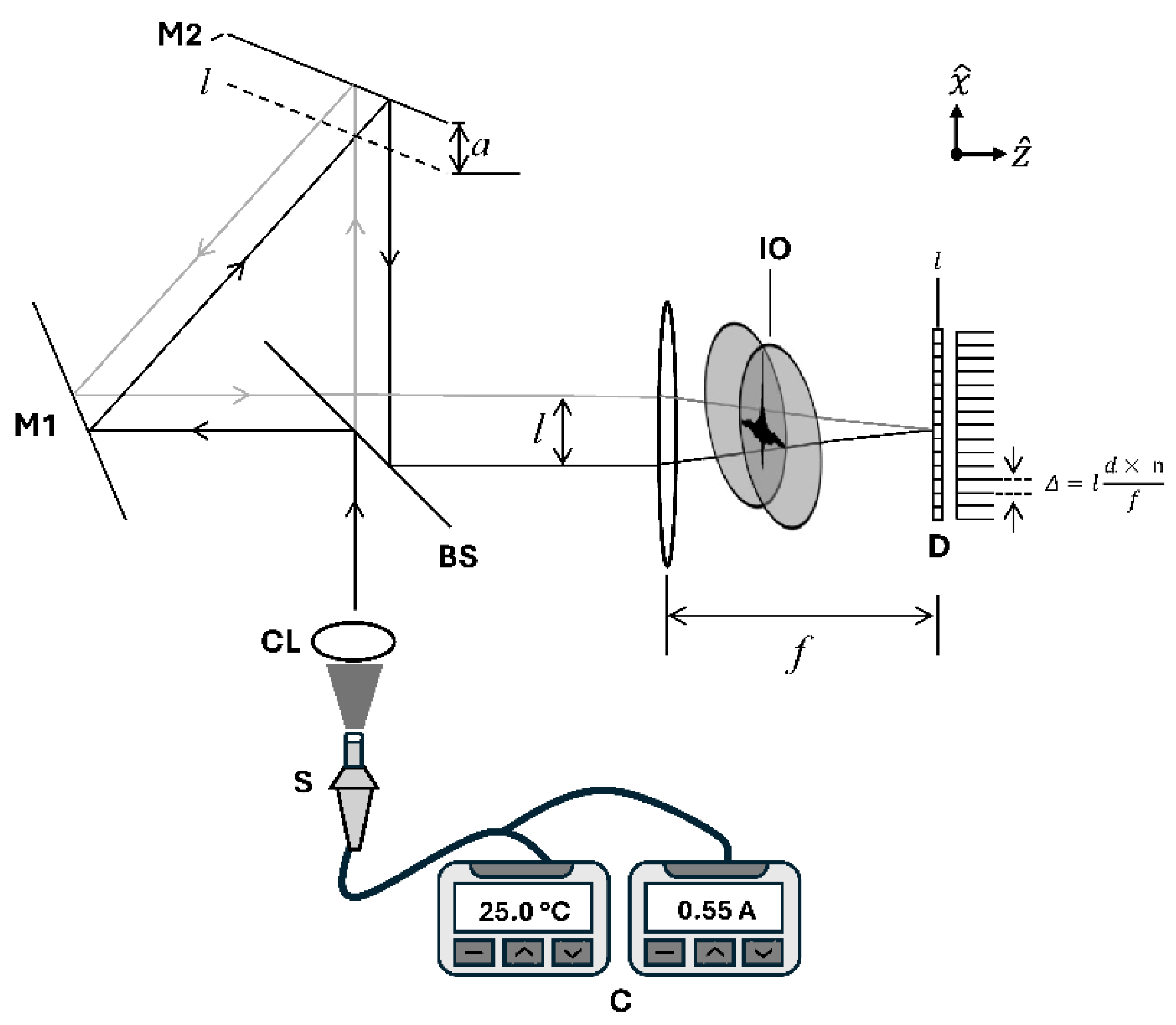
The static modulated Fourier-transform spectrometer comprising a modified Sagnac interferometer which is one of popular configurations. It consists of a beam splitter, two mirrors, a focusing lens, and a detector, as shown in Figure 1. Emission from the optical source is collected and collimated by the collective optics. The collected light enters the static modulated Fourier-transform spectrometer. It is split into two separate beams at the beam splitter. Since two mirrors are asymmetrically displaced from the beamsplitter, the separated beams travel different optical paths. The two beams are subsequently recombined at the beamsplitter. This difference in optical path difference causes the beams to interfere, generating a spatially distributed interferogram.

By performing a Fourier-transform on the measured interferogram, the corresponding spectral information is obtained. The resulting spectrum is substantially affected by changes in temperature and operating current. Analyzing these spectral changes provides insight into how the light-emitting diode is influenced by its operating conditions. The analytical expression for estimating the spectrum related to a light-emitting diode is given as:

$$\Phi ={\displaystyle \frac{1}{I_1\exp [-a(\nu -{\nu }_p)]+I_2\exp [-\frac{h}{k{T}_c}(\nu -{\nu }_p)]+I_3\exp [-{(\frac{\nu -{\nu }_G}{b})}^2]}},$$

(1)

where $\nu$ is a frequency of a light-emitting diode, ${\nu }_p$ is a peak frequency of a light-emitting diode, $h$ is the Planck constant, $k$ is the Boltzmann constant, $T_c$ is a carrier temperature, and $I_1$, $I_2$, $I_3$, ${\nu }_G$,$a$, and $b$ are fitting parameters. The numerator of the original frequency-based expression shows that the terms represent distinct spectral features: the first term represents a growing spectral line, the second term represents a decaying spectral line, and the third term is an additional component introduced to improve similarity.

In the static modulated Fourier-transform spectrometer, the obtained spectral information is a function of wavenumber, which can be converted from the frequency of the light source as follows:

$$\nu ={\displaystyle \frac{c}{\lambda }}=c\overline{\nu },$$

(2)

where $c$ is the speed of light, $\lambda$ is a wavelength corresponding to $\nu$, and $\overline{\nu }$ is a wavenumber corresponding to $\nu$. Equation (1) can be reformulated using Equation (2), as follows:

$$\Phi ={\displaystyle \frac{1}{I_1\exp [-a(\overline{\nu }-{\overline{\nu }}_p)]+I_2\exp [-\frac{1.44}{T_c}(\overline{\nu }-{\overline{\nu }}_p)]+I_3\exp [-{(\frac{\overline{\nu }-{\overline{\nu }}_G}{b})}^2]}},$$

(3)

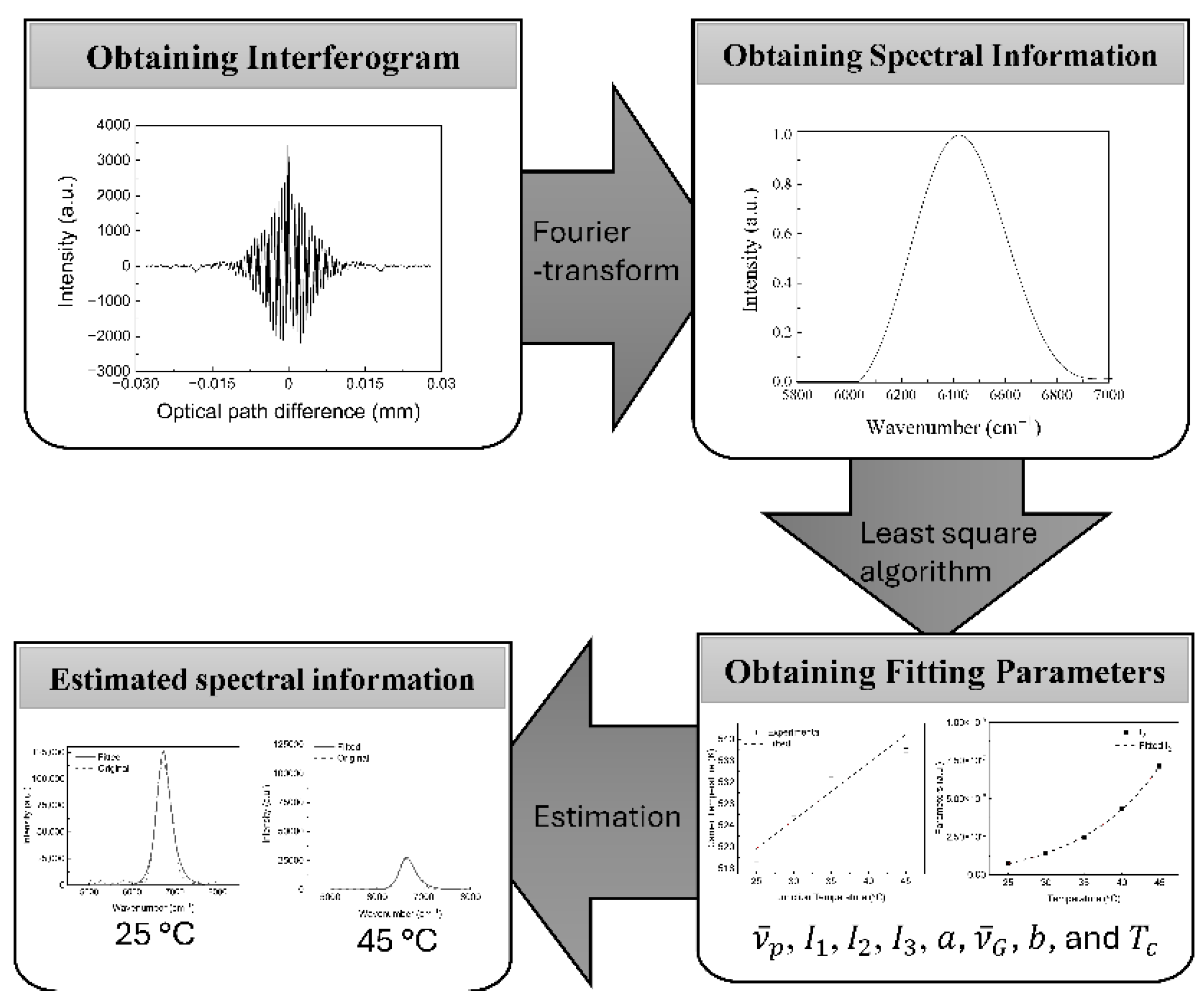
where ${\overline{\nu }}_p$ is the peak wavenumber corresponding to ${\nu }_p$ and ${\overline{\nu }}_G$ serves as a fitting parameter in the wavenumber domain. The advantage of this equation over Eq. (1) is that the parameter values are significantly larger, which allows for more accurate estimation. Equation (3) can be solved from the obtained spectral information using the least squares method. Specifically, information such as the peak wavenumber and junction temperature, along with the operating condition of the optical source, can be obtained. These parameters are then used to estimate the emission spectrum. The concept of this procedure is depicted in Figure 2.

The carrier temperature $T_c$ is expressed as a function of the junction temperature $T_j$. The carrier temperature is known to be typically higher than the junction temperature. The relationship between the carrier temperature and the junction temperature is modeled linearly using Equation (4).

$$T_c=m{T}_j+T_0,$$

(4)

where $T_0$ is expected to be related to electrical bias condition on materials, mainly influenced by current. The junction temperature is calculated using Eq. (4)

The intensity of emission from the source is expected to be related to three fitting parameters, $I_1$, $I_2$, and $I_3$. Given that the intensity varies exponentially, this relationship is expressed as follows:

$$I_n=M_n\exp (k_n{T}_j)+I_0,$$

(5)

where $I_n$ is the emission intensity, while $M_n$, $k_n$, and $I_0$ are fitting parameters determined via the method of the least squares.

3. Results and discussions

The parameters in Equation (3) are calculated using the nonlinear least squares method applied to the measured spectrum. This process allows for the estimation of spectral characteristics and, conversely, the inference of corresponding LED parameters given the spectral information. This process can also be used specifically to estimate the temperature from the spectrum.

Figure 3 shows the measured spectrum and the fitting results. In Figure 3a, a solid line shows the spectrum obtained using the static modulated Fourier-transform spectrometer, while a dashed line shows the fitted spectrum calculated using Equation (3).

For this experiment, a source current was fixed at 0.55 A, and the junction temperature was varied from 25 °C to 45 °C in increments of 5 °C. During the calculation, several parameters were held constant: $I_3$= 1, ${\overline{\nu }}_G$=${\overline{\nu }}_P$= 6422.11 cm⁻¹, and $b$= 0.1. When least square method is applied to extract the parameters from the spectrum at a temperature of 25°C, the results were: $I_1$ = 4.031×10⁻⁵, $I_2$=7.884×10⁻⁷, $a$ = 0.008066, $T_c$=244.4 °C.

Figure 3(b) shows carrier temperature as a function of junction temperature. The carrier temperature increases from 244.4 °C to 264.8 °C, while the junction temperature increases from 25 °C to 45 °C. The relationship between the carrier temperature and the junction temperature is calculated using Equation (4), which is depicted by the dashed line. Fitting parameters representing the intensity of emission are investigated, shown in Figure 3c,d. $I_3$ remains constant with respect to the junction temperature. As the junction temperature increases, parameters, $I_1$ and $I_2$, increase. At 45 °C, $I_1$ and $I_2$ are 8.915×10⁻⁵ and 7.127×10⁻⁶, respectively. The remaining fitting parameter, $a$, is analyzed as a function of junction temperature, as shown in Figure 3e. It is linearly related to the junction temperature and increases as the junction temperature rises. At 45 °C, $a$ is 0.008383.

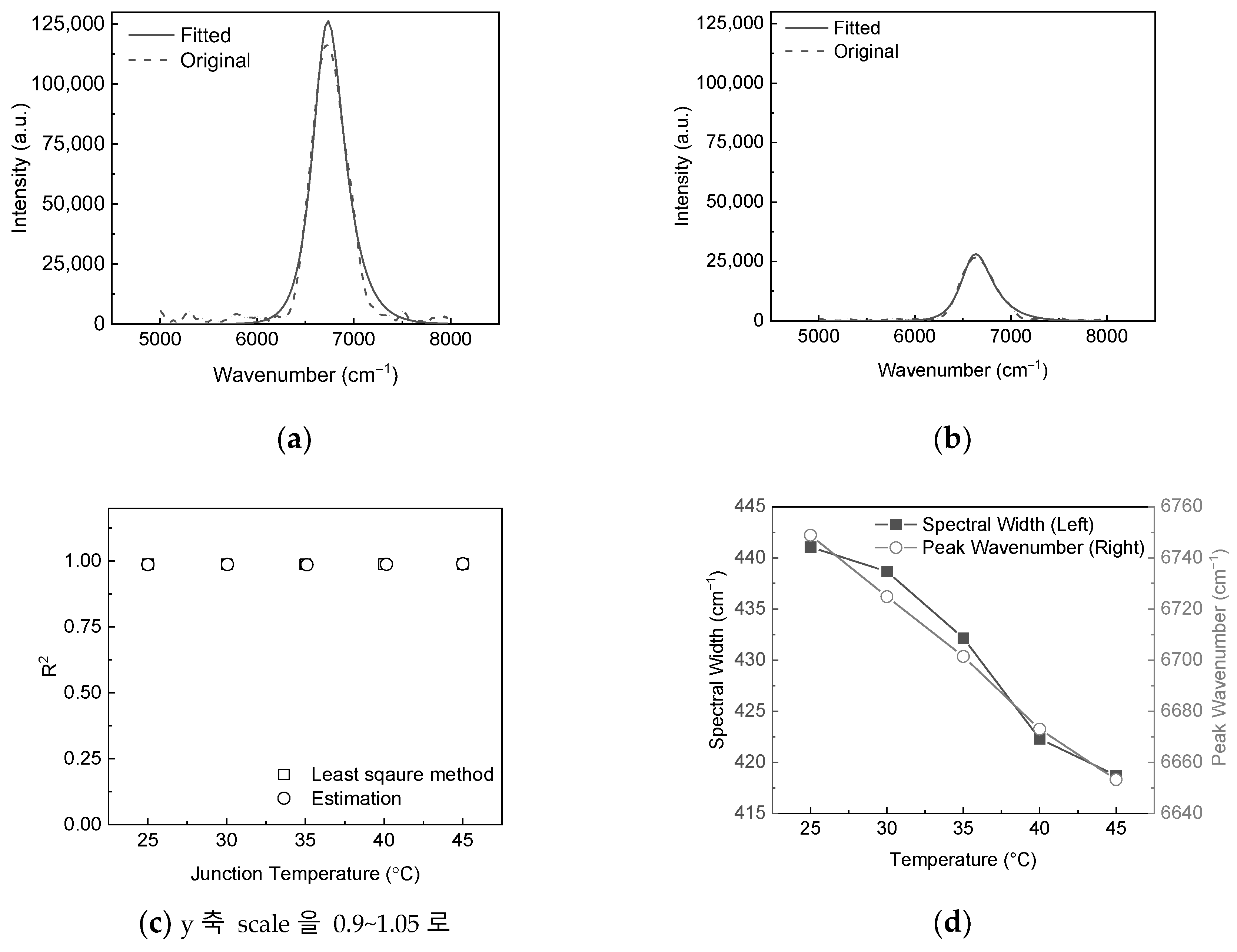
The spectrum is calculated using parameters obtained from Eq. (3). Figure 4 shows the estimated spectrum and optical characteristics at various temperatures. The estimated spectra at 25 °C and 45 °C are compared to those obtained using the static modulated Fourier-transform spectrometer, as shown in Figure 4a,b. To evaluate the accuracy of the estimated spectrum, the coefficient of determination R² is calculated, as shown in Figure 4c. Hollow rectangles represent the spectrum calculated using the least squares method, while the hollow circles represent the estimated spectrum calculated using the extracted parameters. In both cases, the average R² is 0.99, indicating high accuracy for both the extracted parameter and the estimated spectrum.

The variation of spectral width and peak wavenumber was investigated across the temperature range, as shown in Figure 4d. At 25 °C, the spectral width and the peak wavenumber are 441.06 cm⁻¹, and 6748.83 cm⁻¹, respectively. As the temperature rises, both the spectral width and the peak wavenumber decrease. At 45 °C, the spectral width and the peak wavenumber are 418.72 cm⁻¹, and 6653.24 cm⁻¹, respectively.

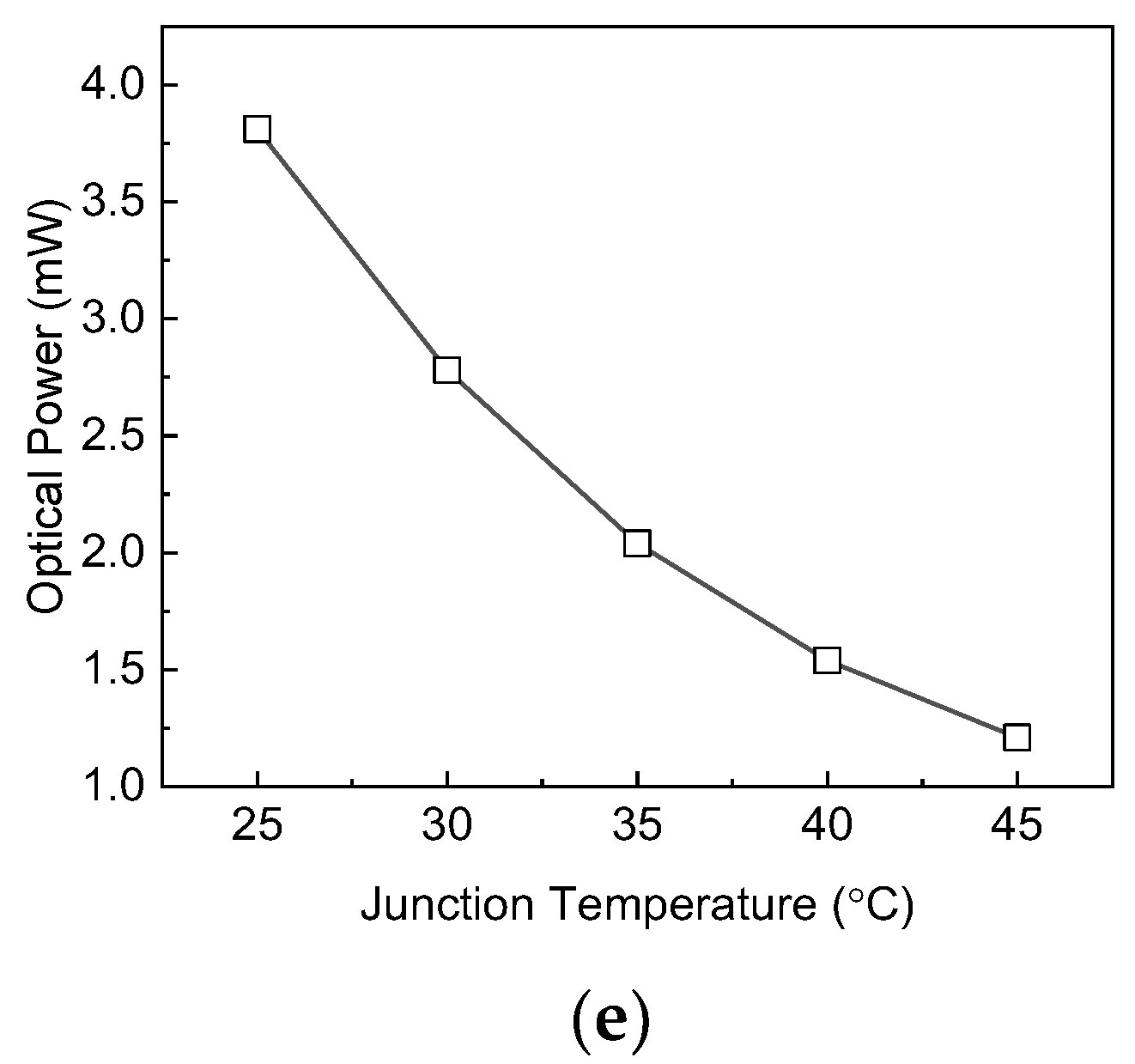
The optical power of the source was measured using a thermal detector, as shown in Figure 4e. It is noted that in super luminescent diodes, the optical power output is significantly affected by temperature variations, particularly at high operating currents. The optical power was measured to be 3.81 mW at 25 °C, while it dropped to 1.21 mW at 45 °C, representing a significant reduction.

4. Conclusions

We propose a novel approach to evaluate the super luminescent diode performance by combining a modified static modulated Fourier-transform spectrometer with Gaussian curve fitting method to rapidly obtain and estimate its spectral properties. The static modulated Fourier transform spectrometer allows for relatively fast measurement (in the order of microseconds) compared to a conventional dynamic modulated Fourier transform spectrometer [11]. This capability is key to addressing the challenges of impractical and inaccurate super luminescent diode evaluation often encountered due to their diverse internal structures.

This study also presented and validated an analytical expression utilizing Gaussian curve fitting components to estimate the spectral output of super luminescent diodes. The proposed model provides a highly accurate method for spectral estimation, achieving an average coefficient of determination R² of 0.99 across various operating currents and temperatures.

By applying the nonlinear least squares method to measured spectra from a static modulated Fourier-transform spectrometer, we successfully extracted key fitting parameters. The analysis revealed distinct physical correlations: the carrier temperature, $T_c$, and the spectral shape parameter, $a$, exhibited clear linear dependencies on the junction temperature. Additionally, the intensity parameters, $I_1$ and $I_2$, followed an exponential trend with rising temperature, while the optical power decreased significantly as expected.

These results demonstrate that the internal physical state of a super luminescent diode, specifically its junction and carrier temperatures, can be accurately inferred solely from its spectral shape. This approach offers a powerful, non-invasive tool for monitoring device health and thermal performance in real-time applications.