Hybrid Particle Swarm and Grey Wolf Optimization for Robust Feedback Control of Nonlinear Systems

1. Introduction

The Proportional–Integral–Derivative (PID) controller remains one of the most fundamental and widely adopted strategies in industrial automation, process control, and mechatronic systems. Its enduring popularity is attributed to its conceptual simplicity, robustness, and ease of implementation across diverse application domains. Despite its ubiquity, achieving optimal performance through appropriate tuning of the PID gains $(K_p,K_i,K_d)$ continues to be a challenging and active area of research. This challenge becomes particularly pronounced in nonlinear or time-varying systems, where conventional tuning rules derived from linearized models—such as the Ziegler–Nichols or Cohen–Coon methods—often result in degraded transient behavior, excessive overshoot, or even closed-loop instability. In safety-critical or high-precision industrial processes, such overshoot or oscillatory responses are often unacceptable, motivating the need for more advanced and adaptive tuning methodologies. The monograph by Åström and Hägglund [1] provides a detailed discussion of PID controller design and optimization for various types of systems, including nonlinear ones, with practical insights into tuning and implementation. Similarly, Nise [2] offers a comprehensive foundation for linear and nonlinear control design, while Ogata [3] presents an in-depth treatment of control system analysis and design principles encompassing both linear and nonlinear dynamics. A recent and comprehensive review of modern approaches to PID controller design, including nonlinear extensions, can be found in [4].

In recent decades, metaheuristic and evolutionary optimization techniques have emerged as powerful and flexible alternatives to traditional analytical tuning methods. These algorithms are particularly well-suited for solving highly nonlinear, nonconvex, and multimodal optimization problems without requiring gradient information or model simplification. A comprehensive survey of metaheuristic optimization algorithms, including 47 nature-inspired methods designed for load balancing in cloud computing, is presented in [5]. In contrast, the present work focuses on applying metaheuristic optimization techniques to parameter tuning in nonlinear dynamical systems, emphasizing their ability to balance convergence efficiency, robustness, and computational cost.

Among metaheuristic approaches, Particle Swarm Optimization (PSO) has demonstrated notable success due to its efficient local exploitation of promising regions. Originally developed by Kennedy and Eberhart [6,7,8], PSO draws inspiration from the collective movement of bird flocks and fish schools, iteratively refining candidate solutions.

The Grey Wolf Optimizer (GWO) [9], inspired by grey wolves’ social hierarchy and cooperative hunting, excels in global exploration and avoids local minima. Its simplicity and balanced exploration-exploitation behavior make it effective across diverse optimization tasks.

Hybrid strategies combining PSO and GWO leverage the strengths of both methods: PSO refines solutions locally, while GWO ensures thorough global search. Recent applications demonstrate their effectiveness, such as optimal reactive power dispatch [10] and smart grid reconfiguration [11], where the hybrid approach achieved reduced losses, stable voltage, and robust performance in high-dimensional, nonconvex scenarios.

In distributed generation planning, hybrid PSO–GWO strategies have demonstrated superior performance. Alyu [12] employed a hybrid GWO–PSO algorithm to determine the optimal placement and sizing of multiple photovoltaic distributed generators (PV-DGs), achieving reduced active and reactive power losses and improved voltage profiles compared to other metaheuristics such as WOA, SCA, and standalone PSO or GWO. Similarly, Aguila-Lopez [13] integrated a GWO-enhanced PSO into a Maximum Power Point Tracking (MPPT) controller, achieving up to 20% gains in energy extraction efficiency under varying irradiation, highlighting the hybrid algorithm’s adaptability and robustness.

The effectiveness of PSO–GWO hybridization extends to broader optimization contexts. For example, Bhandari et al. [14] applied it to reliability-redundancy optimization, showing that combining PSO’s exploitation with GWO’s exploration yields better solutions with fewer iterations. Likewise, Senel [15] confirmed the hybrid method’s superiority over standard and hybrid approaches on benchmark functions and real-world industrial problems, including process optimization and material nesting.

It is possible to find several publications that apply metaheuristic algorithms for the optimization of PID control systems. For instance, in [16], a hybrid PSO–GWO optimization algorithm was proposed for tuning a PID controller in an Automatic Voltage Regulator (AVR) system. The main objective of the study was to improve the transient response of the AVR by minimizing key performance indices such as rise time, settling time, peak overshoot, and peak time. Comparative analyses with other heuristic-based tuning methods available in the literature demonstrated that the proposed hybrid PSO–GWO approach provided superior performance and enhanced dynamic behavior. However, the considered system in this case is a linear time-invariant (LTI) process, where the underlying dynamics are relatively simple and predictable, and thus do not capture the complexities encountered in nonlinear systems.

A similar observation can be made in [17], which evaluates the performance and robustness of a metaheuristic-based PID controller for a First-Order with Time Delay (FOPTD) system. Like the AVR case, the FOPTD process represents a linear model analyzed through a transfer function framework, which is a well-established and elegant tool for LTI system analysis. Nevertheless, such methods cannot be directly applied to nonlinear systems, where the system behavior depends on the instantaneous state variables and the dynamic equations exhibit strong nonlinear coupling. Consequently, the use of transfer function-based approaches or linear metaheuristic tuning schemes is inherently limited in such contexts.

Despite these advances across diverse application areas—ranging from power systems and renewable energy to reliability engineering and industrial optimization—none of the aforementioned studies have addressed the problem of metaheuristic-based PID tuning for nonlinear dynamical systems. This gap is particularly significant, as strong nonlinearities, such as those present in pendulum-like or Duffing oscillators, introduce severe challenges for controller design and stability assurance. Consequently, extending hybrid metaheuristic frameworks such as PSO–GWO to the automatic tuning of PID controllers in nonlinear systems represents a novel and impactful research direction, which is the main focus of the present study.

In this work, three metaheuristic-based PID tuning strategies are systematically investigated for nonlinear control systems:

• PSO-based PID tuning, leveraging swarm intelligence for global parameter optimization;
• GWO-based PID tuning, employing hierarchical search to balance exploration and exploitation; and
• Hybrid PSO–GWO tuning, integrating both paradigms to accelerate convergence and enhance robustness under strong nonlinearities.

The proposed optimization framework is evaluated on representative second-order nonlinear benchmark systems, including pendulum-type, Duffing-type, and nonlinear damping models. The optimization objective combines integral-based performance indices–such as the Integral of Time-weighted Absolute Error (ITAE) and the Integral of Squared Overshoot (ISO)–to capture both transient accuracy and overshoot suppression. Particular attention is given to the influence of the ISO weighting coefficient $\alpha$, which provides an additional degree of freedom to regulate the trade-off between convergence speed and control smoothness.

Simulation results demonstrate that all three optimization methods effectively stabilize the considered nonlinear systems. While the hybrid PSO–GWO consistently achieves the lowest number of cost function evaluations, it may exhibit more aggressive transient dynamics, which can be mitigated by appropriate tuning of $\alpha$. These findings highlight the potential of metaheuristic-based PID tuning–especially in hybrid form–as a powerful and computationally efficient tool for nonlinear control system design.

The remainder of this paper is organized as follows. Section 2 presents the mathematical formulation of the nonlinear systems and the associated control structure. Section 3 describes the proposed optimization framework for PID tuning, including PSO, GWO, and hybrid PSO–GWO strategies. Section 4 introduces the benchmark nonlinear systems, evaluates the performance of the proposed approaches, and discusses the obtained results. A comparative performance analysis is provided in Section 5. In particular, Subsection 5.2 presents a robustness evaluation in which the hybrid PSO–GWO optimization scheme is applied to the Duffing oscillator under parameter conditions that induce chaotic dynamics. This challenging case highlights the algorithm’s capability to stabilize strongly nonlinear and aperiodic systems, demonstrating its robustness and adaptability in one of the most demanding control scenarios. Finally, Section 6 summarizes the key findings and outlines directions for future research.

2. Problem Formulation

Consider a general nth-order nonlinear dynamic system defined as

$$y^{\left(n\right)}\left(t\right)+f\left(t,y\left(t\right),y^{\prime }\left(t\right),\dots ,y^{(n-1)}\left(t\right)\right)=u\left(t\right),$$

(1)

over the interval $[0,\infty )$, with zero initial conditions

$$y\left(0\right)=y^{\prime }\left(0\right)=\dots =y^{(n-1)}\left(0\right)=0.$$

(2)

In the feedback control configuration shown in Figure 1, $u\left(t\right)$ represents the control signal generated by the PID controller and applied to the system input, while $y\left(t\right)$ denotes the process (or output) variable whose behavior is being regulated. Both $u\left(t\right)$ and $y\left(t\right)$ are assumed to be scalar functions defined on the interval $[0,\infty )$ and to possess the required degree of continuous differentiability on this interval.

The PID controller is expressed as

$$u\left(t\right)=K_{p}e\left(t\right)+K_i{\int }_0^{t}e\left(\tau \right)d\tau +K_d{\displaystyle \frac{de\left(t\right)}{dt}},$$

(3)

where $e\left(t\right)=r\left(t\right)-y\left(t\right)$ is the tracking error between the reference input $r\left(t\right)$ and the system output $y\left(t\right)$.

By analyzing the closed-loop signal flow in Figure 1, the dynamics of the nth-order nonlinear system under PID control can be written as

$$\begin{array}{cc}\hfill y^{\left(n\right)}\left(t\right)& +f\left(t,y\left(t\right),y^{\prime }\left(t\right),\dots ,y^{(n-1)}\left(t\right)\right)=u\left(t\right),\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill u\left(t\right)& =K_{p}e\left(t\right)+K_i{\int }_0^{t}e\left(\tau \right)d\tau +K_d{\displaystyle \frac{de\left(t\right)}{dt}},\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill e\left(t\right)& =r\left(t\right)-y\left(t\right).\hfill \end{array}$$

(6)

For numerical implementation and analysis, the system can be equivalently represented in an augmented first-order state-space form using the state vector

$$[Y_0,Y_1,\dots ,Y_{n-1},E_{\mathrm{int}}]=\left[y,y^{\prime },\dots ,y^{(n-1)},{\int }_0^{t}e\left(\tau \right)d\tau \right],$$

(7)

which evolves according to

$$\begin{array}{cc}\hfill Y_i^{\prime }\left(t\right)& =Y_{i+1}\left(t\right),i=0,1,\dots ,n-2,\hfill \\ \hfill Y_{n-1}^{\prime }\left(t\right)& =u\left(t\right)-f\left(t,Y_0\left(t\right),Y_1\left(t\right),\dots ,Y_{n-1}\left(t\right)\right)\hfill \\ \hfill & =K_{p}e\left(t\right)+K_i{\int }_0^{t}e\left(\tau \right)d\tau +K_d{\displaystyle \frac{de\left(t\right)}{dt}}\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & -f\left(t,Y_0\left(t\right),Y_1\left(t\right),\dots ,Y_{n-1}\left(t\right)\right),\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill E_{\mathrm{int}}^{\prime }\left(t\right)& =e\left(t\right)=r\left(t\right)-Y_0\left(t\right).\hfill \end{array}$$

(10)

In this study, we focus exclusively on second-order systems ($n=2$) with a unit-step reference input, defined as

$$r\left(t\right)=\left\{\begin{array}{cc}1,\hfill & t\ge 0,\hfill \\ 0,\hfill & t<0.\hfill \end{array}\right.$$

(11)

Second-order systems exhibit more complex transient behavior than first-order systems, including overshoot, oscillations, and slower settling times, providing a richer testbed for evaluating the effectiveness of different PID tuning strategies. The simulation setup examines the system’s transient response when the input undergoes a step change from zero to unity, allowing direct comparison of various optimization-based tuning methods under realistic nonlinear dynamics.

Figure 1. Schematic representation of the feedback control loop with reference input $r\left(t\right)$, controlled output $y\left(t\right)$, and control signal $u\left(t\right)$ generated by a PID controller.

Figure 1. Schematic representation of the feedback control loop with reference input $r\left(t\right)$, controlled output $y\left(t\right)$, and control signal $u\left(t\right)$ generated by a PID controller.

3. Optimization Framework

The objective of PID tuning is to determine the optimal controller gains $K_p$, $K_i$, and $K_d$ such that the closed-loop system achieves the desired transient performance while maintaining stability and minimizing overshoot. In essence, the PID controller continuously adjusts its control action to keep the actual process output $y\left(t\right)$ as close as possible to the reference signal $r\left(t\right)$. In this paper, the reference input is defined as a unit-step function. The unit-step signal is commonly employed in control system analysis and simulation because it effectively excites the system dynamics and provides a clear characterization of transient and steady-state behavior. Its simplicity allows for straightforward evaluation of key performance indicators such as rise time, settling time, and overshoot, which are critical for assessing control quality. Consequently, the step response serves as a standard benchmark for tuning and comparing PID control strategies across both linear and nonlinear systems.

To quantify this objective, we adopt a composite performance index that accounts for both the speed of response and the magnitude of undesirable deviations:

$$J(K_p,K_i,K_d)={\int }_0^T\left[t\left|e\left(t\right)\right|+\alpha {\left(max(0,-e(t\left)\right)\right)}^2\right]dt,$$

(12)

where $e\left(t\right)=r\left(t\right)-y\left(t\right)$ is the tracking error between the reference input $r\left(t\right)$ and system output $y\left(t\right)$. The first term, $\mathrm{ITAE}={\int }_0^{T}t\left|e\left(t\right)\right|dt$, represents the Integral of Time-weighted Absolute Error, which penalizes errors that persist over time, thereby promoting fast settling and reducing long-lasting deviations. The second term, $\mathrm{ISO}={\int }_0^T{\left(max(0,-e(t\left)\right)\right)}^{2}dt$, corresponds to the Integral of Squared Overshoot, which selectively penalizes overshoot in the system’s response, limiting the peak amplitude above the desired reference during transients.

The weighting factor $\alpha >0$ allows flexible tuning of the relative importance between minimizing prolonged error versus avoiding overshoot, providing a more nuanced evaluation of closed-loop performance. The finite time horizon T is selected to sufficiently capture both transient dynamics and steady-state behavior, ensuring that the resulting PID parameters yield a balance between rapid response, overshoot control, and long-term stability.

By employing this performance index as the objective function, metaheuristic optimization algorithms such as PSO, GWO, and hybrid PSO–GWO can systematically search the multidimensional space of $K_p$, $K_i$, and $K_d$ to identify near-optimal solutions without requiring explicit linearization or analytical design formulas. This approach enables robust PID tuning for nonlinear systems, accommodating complex dynamical behaviors that are challenging to handle using classical methods.

Particle Swarm Optimization (PSO)

In the context of PID controller optimization, the Particle Swarm Optimization (PSO) algorithm treats each particle in the swarm as a potential solution defined by a triplet of controller gains $(K_p,K_i,K_d)$. During the optimization process, particles iteratively adjust their positions in the search space based on both their individual best experiences and the collective knowledge of the swarm. The objective is to minimize the predefined performance index $J(K_p,K_i,K_d)$, typically expressed as a weighted combination of integral error measures such as the ITAE and ISO criteria defined in Equation (12). Due to its velocity-based update mechanism, PSO exhibits strong local search capability (exploitation), enabling fast convergence toward promising regions of the cost landscape. However, this characteristic also increases the risk of premature convergence in multimodal or highly nonlinear problems, where sufficient exploration of alternative regions is required [9].

Grey Wolf Optimizer (GWO)

The Grey Wolf Optimizer (GWO) is a nature-inspired metaheuristic based on the cooperative hunting behavior and hierarchical leadership structure observed in grey wolf packs. Within the context of PID controller tuning, each wolf represents a candidate set of controller gains $(K_p,K_i,K_d)$, while the search process is guided by three leading wolves–$\alpha$, $\beta$, and $\delta$–representing the best solutions found so far. The remaining wolves update their positions by mimicking the encircling and hunting behavior of the leaders, gradually refining their estimates toward the global optimum. In contrast to PSO, GWO exhibits stronger exploratory behavior, preserving population diversity and systematically scanning the search space through adaptive encircling and shrinking mechanisms [9]. By effectively balancing exploration and exploitation through this hierarchical mechanism, GWO achieves stable convergence and robustness in complex, nonconvex optimization landscapes.

Hybrid Strategy: PSO–GWO

The hybrid PSO–GWO algorithm combines the exploitation strength of PSO with the exploration capability of GWO. In this hybrid framework, the PSO component provides rapid local refinement by updating particle velocities and positions, ensuring efficient convergence in promising regions. Conversely, the GWO mechanism maintains global diversity and exploration by emulating the social hierarchy and cooperative hunting strategy of grey wolves. This complementary interaction allows the hybrid algorithm to dynamically balance global exploration and local exploitation throughout the optimization process [9]. When applied to PID tuning, the PSO–GWO hybrid typically achieves faster convergence, higher solution accuracy, and improved robustness against the multimodal and nonconvex nature of the cost landscape that characterizes strongly nonlinear control problems.

In practical implementation, the population is divided into two cooperative sub-swarms:

• The first sub-swarm updates positions using PSO velocity and position rules, enabling efficient local exploitation.
• The second sub-swarm evolves according to GWO’s hierarchical encircling and hunting behavior, ensuring effective global exploration.
• At each iteration, elite and global best information are exchanged between the sub-swarms to preserve diversity and guide convergence toward the global optimum.

This cooperative structure enhances the robustness and efficiency of the hybrid optimizer, making it particularly suitable for nonlinear and dynamically complex PID controller tuning tasks.

Expected Benefits of the Hybrid PSO–GWO Approach

• Complementary Search Dynamics: The PSO sub-swarm exploits rapid convergence in smooth regions, while the GWO sub-swarm ensures broad exploration in complex, multimodal areas.
• Robustness Against Local Minima: The hybrid structure mitigates premature convergence by leveraging PSO’s memory-guided exploitation and GWO’s stochastic encircling mechanisms.
• Enhanced Population Diversity: Periodic exchange of elite and global best information between sub-swarms maintains diversity and prevents stagnation.
• Improved Convergence Efficiency: Hybridization accelerates convergence by allowing PSO to refine promising regions discovered through GWO’s exploratory search.
• Flexibility in Multi-Objective Optimization: The framework can be extended to handle multiple conflicting objectives, such as minimizing both ITAE and overshoot.

Overall, the hybrid PSO–GWO algorithm leverages the complementary strengths of both metaheuristics, achieving faster, more reliable, and globally effective PID tuning for strongly nonlinear control systems.

The following section presents its implementation and performance evaluation on representative nonlinear benchmark models.

3.1. General Procedure

The overall PID tuning framework is implemented in Python, leveraging widely-used scientific computing and metaheuristic optimization libraries.

The general procedure for both PSO and GWO consists of the following steps:

• Initialization: Define the search space for PID parameters $K_p,K_i,K_d\in [0,10]$, generate the initial population (particles or wolves) randomly within these bounds, and initialize historical records for tracking cost evaluations.
• Simulation: For each candidate solution, simulate the second-order nonlinear system using the augmented first-order form of the dynamics, integrating the ODEs with a Runge–Kutta solver (RK45) over the simulation horizon.
• Cost Evaluation: Compute the performance index $J(K_p,K_i,K_d)$ as the sum of ITAE and ISO terms, storing each evaluation for convergence analysis.
• Position Update:
  • In PSO, update particle velocities and positions according to the standard PSO rules, taking into account inertia, cognitive, and social components.
  • In GWO, update wolf positions using the encircling, hunting, and attacking strategies defined by the leader hierarchy.
• Global Best Update: Identify the best-performing solution across the population (global best) and update personal or elite records as needed.
• Iteration and Convergence Check: Repeat simulation, evaluation, and update steps for the specified number of generations or until an early stopping criterion is satisfied (e.g., cost improvement below a threshold $\delta ={10}^{-5}$).
• Output: The optimal PID parameters $(K_p^{*},K_i^{*},K_d^{*})$, the associated cost $J(K_p^{*},K_i^{*},K_d^{*})$, and the total number of cost function evaluations are reported to quantify the performance and computational effort of each optimization strategy.

The hybrid PSO–GWO procedure combines the strengths of both algorithms, exploiting PSO’s local refinement capabilities and GWO’s global exploration through hierarchical hunting. The general workflow is as follows:

• Initialization: Define the search space for PID parameters $K_p,K_i,K_d\in [0,10]$. Initialize the PSO swarm and GWO population randomly within these bounds. Set personal bests for PSO particles and the leader hierarchy for GWO ($\alpha ,\beta ,\delta$). Initialize historical records for cost evaluations.
• Simulation: For each candidate solution (particle or wolf), simulate the second-order nonlinear system in augmented first-order form. Integrate the ODEs over the simulation horizon using a Runge–Kutta solver (RK45) to obtain the system response $y\left(t\right)$.
• Cost Evaluation: Compute the performance index $J(K_p,K_i,K_d)$ as the sum of ITAE and ISO terms. Store each evaluation in a history log for convergence analysis and potential CSV export.
• PSO Update: Update particle velocities and positions using the PSO formula:

  $$v\leftarrow wv+c_1{r}_1(p_{\mathrm{best}}-x)+c_2{r}_2(g_{\mathrm{best}}-x),x\leftarrow x+v$$
  Clip positions to remain within bounds. Update personal and global bests as necessary.
• GWO Iteration: Execute a single iteration of GWO for the current population. Evaluate costs, update positions based on encircling and hunting mechanisms guided by leaders $\alpha ,\beta ,\delta$, and identify the best GWO solution.
• Hybrid Global Best Update: Compare the global best solution from PSO and the best solution from GWO. Update the PSO global best if the GWO solution is superior.
• Iteration and Convergence Check: Repeat PSO and GWO update steps for the specified number of epochs or until the early stopping criterion is satisfied (e.g., improvement below $\delta ={10}^{-5}$).
• Output: Report the optimal PID parameters $(K_p^{*},K_i^{*},K_d^{*})$, the associated cost $J(K_p^{*},K_i^{*},K_d^{*})$, the total number of cost function evaluations, and the convergence history.

In practice, the PSO and GWO procedures share the same simulation and cost evaluation structure, differing only in the respective update rules. This uniformity facilitates hybrid strategies, in which subsets of the population are evolved using PSO rules while others follow GWO dynamics, enabling exchange of global best solutions and complementary search behavior.

The pseudocodes for the PSO, GWO, and hybrid PSO–GWO PID tuning procedures are provided in Appendices Appendix A, Appendix B and Appendix C, respectively.

4. Benchmark Nonlinear Systems and Simulation Results

4.1. Benchmark Nonlinear Systems

To evaluate the effectiveness of the proposed PID tuning strategies, we consider three representative second-order nonlinear systems. Each system is expressed in the standard form:

$$y^{\prime \prime }\left(t\right)+f(t,y,y^{\prime })=u\left(t\right),t\ge 0$$

(13)

where $y\left(t\right)$ is the system output, $u\left(t\right)$ is the control input, and $f(t,y,y^{\prime })$ encodes the system-specific nonlinear dynamics. The three benchmark systems considered in this study are as follows:

• System 1: Pendulum-like nonlinear system

  $$y^{\prime \prime }\left(t\right)+asin\left(y\left(t\right)\right)+b{y}^{\prime }\left(t\right)=u\left(t\right),$$

  (14)
  with parameters $a=2.0$, $b=0.4$. This system exhibits moderate nonlinearity and resembles the dynamics of a simple pendulum with damping (for $b>0$). It is suitable for testing the convergence and robustness of PID tuning algorithms.
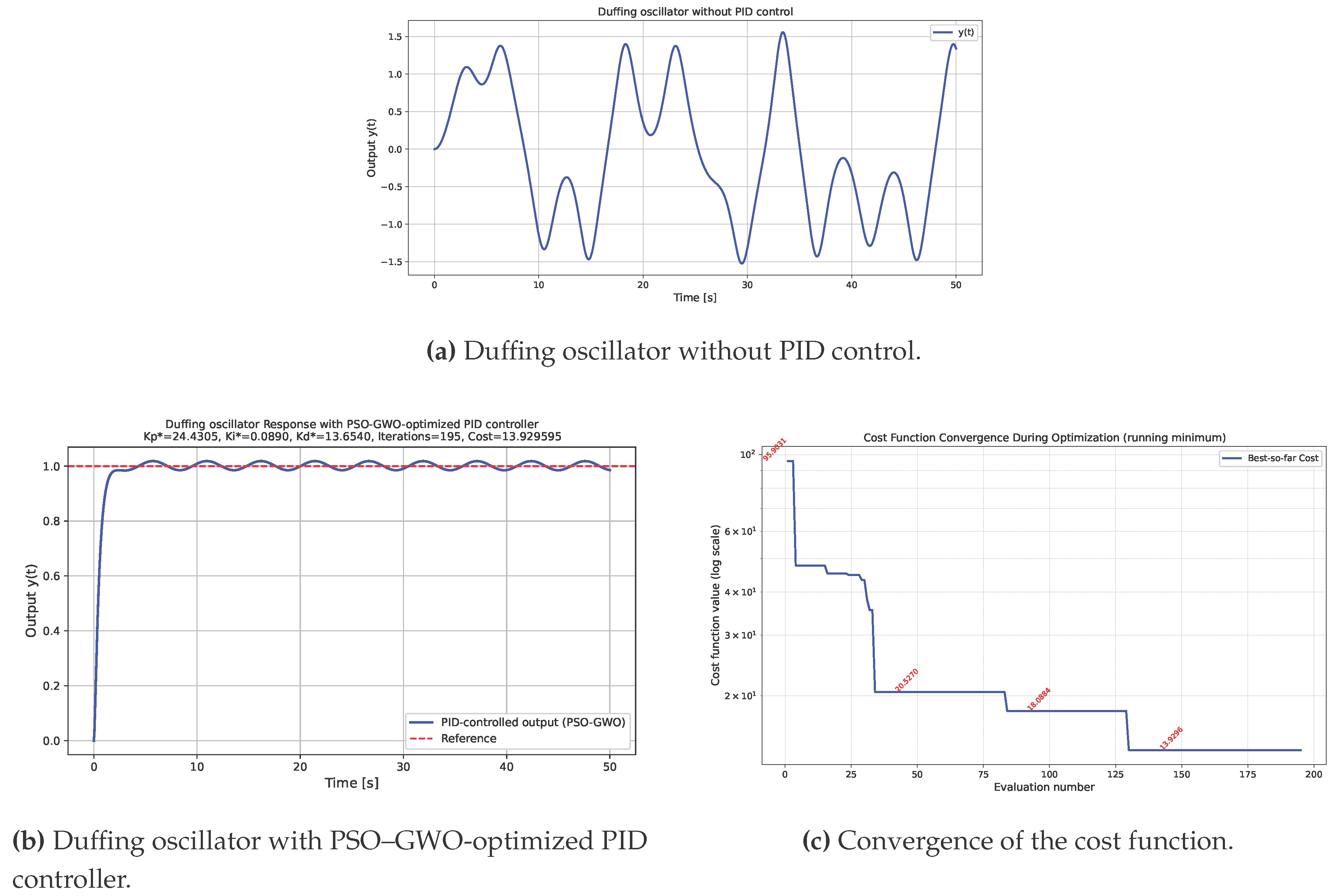
• System 2: Duffing oscillator

  $$y^{\prime \prime }\left(t\right)+\tilde{\delta }{y}^{\prime }\left(t\right)+\tilde{\alpha }y\left(t\right)+\tilde{\beta }{y}^3\left(t\right)=u\left(t\right),$$

  (15)
  with parameters $\tilde{\alpha }=-1.0$, $\tilde{\beta }=1.0$, $\tilde{\delta }=0.2$. This system is commonly used to test control strategies for stiff and highly nonlinear systems due to the cubic stiffness term, which can produce multiple equilibria and nonlinear oscillatory behavior.
• System 3: Nonlinear damping system

  $$y^{\prime \prime }\left(t\right)+{\tilde{c}}_1{y}^{\prime }\left(t\right)+{\tilde{c}}_{2}y\left(t\right)+{\tilde{c}}_{3}y\left(t\right)y^{\prime }\left(t\right)=u\left(t\right),$$

  (16)
  with parameters ${\tilde{c}}_1=0.5$, ${\tilde{c}}_2=2.0$, ${\tilde{c}}_3=1.0$. This system introduces a velocity-dependent nonlinear damping term $y{y}^{\prime }$, creating asymmetric transient responses and testing the adaptability of metaheuristic PID tuning.

These three benchmark systems collectively cover a range of nonlinear behaviors, including oscillatory, stiff, and asymmetric dynamics. They provide a meaningful testbed for comparing the performance of PSO, GWO, and hybrid PSO–GWO-based PID tuning strategies. The selection of additional systems may be performed in subsequent studies to further explore algorithmic robustness and generalizability.

4.2. PSO Parameters

The PSO algorithm is implemented using the pyswarm package with a swarm of $N=30$ particles, each representing a candidate set of PID parameters $(K_p,K_i,K_d)$. Particle velocities are updated using an inertia weight $\omega =0.7$ and cognitive and social acceleration coefficients $c_1=c_2=1.5$. The maximum number of iterations is set to 50 to ensure sufficient exploration while keeping the computational cost reasonable, as summarized in Table 1.

4.3. GWO Parameters

For GWO, we use the OriginalGWO class from mealpy-3.0.3 with a population of $N=30$ wolves representing candidate PID parameters $(K_p,K_i,K_d)$. The algorithm follows the standard hunting and encircling strategies, keeping the alpha, beta, and delta leadership weights at their default values ($\alpha =\beta =\delta =1.0$). The maximum number of epochs is set to 50 to ensure convergence while maintaining a computational cost comparable to PSO, as summarized in Table 2.

4.4. Hybrid PSO–GWO Parameters

For the hybrid PSO–GWO strategy, the same population size and algorithmic parameters are used as in the standalone PSO and GWO cases. However, the population is explicitly divided into two equal sub-swarms: 15 particles evolve according to PSO update rules, while the other 15, acting as wolves, follow the GWO dynamics. At each iteration, global best information and elite solutions are exchanged between the sub-swarms to exploit complementary search behaviors. This setup allows the hybrid approach to leverage both the exploration capability of GWO and the fast convergence of PSO, while maintaining the same total computational budget as the standalone algorithms.

For all simulations, unless stated otherwise, the cost function in (12) employs a weighting factor $\alpha =1.0$, assigning equal importance to the ITAE and ISO components. During each optimization run, we record and visualize the following outputs: the time-domain response of the controlled system $y\left(t\right)$, the evolution of the cost function values corresponding to candidate PID parameter sets $(K_p,K_i,K_d)$, the minimal achieved cost function value, and the total number of cost function evaluations required to reach the optimum. Additionally, an early stopping criterion is enforced: if two consecutive cost function values differ by less than ${10}^{-5}$, the optimization is terminated to prevent unnecessary computations while ensuring convergence.

4.5. Closed-Loop Response under PSO, GWO, and Hybrid PSO–GWO PID Control

In this section, we present the results of the closed-loop simulations for the three benchmark nonlinear systems introduced in Subsection 4.1. These results demonstrate the effectiveness of the PSO, GWO, and hybrid PSO–GWO PID tuning strategies in regulating second-order nonlinear systems. For each system, we provide graphical illustrations of the system output $y\left(t\right)$ under the optimized PID parameters, the evolution of the cost function $J(K_p,K_i,K_d)$ during optimization, and the trajectories of the PID gains $(K_p,K_i,K_d)$ as they converge to their optimal values. The achieved minimum of the cost function and the total number of function evaluations required to reach this optimum are reported, along with any early stopping criteria that were triggered. Early stopping is applied when the absolute difference between two consecutive cost function evaluations falls below ${10}^{-5}$. This ensures computational efficiency while maintaining accuracy in identifying the optimal PID parameters.

• System 1: Pendulum-like nonlinear system
  Figure 2 presents the simulation results obtained for the pendulum-like nonlinear system. The figure is organized into three rows and two columns. The left column illustrates the closed-loop time responses $y\left(t\right)$ to a unit-step reference input under the PID gains optimized by the PSO, GWO, and hybrid PSO–GWO algorithms, respectively. All three metaheuristic methods successfully stabilize the nonlinear system, while the hybrid PSO–GWO algorithm demonstrates faster convergence and a reduced overshoot compared to the individual approaches. The right column of Figure 2 illustrates the evolution of the cost function over successive evaluations, providing insight into the convergence behavior of each optimization strategy. For each case, the achieved minimum cost and the number of evaluations required to reach it are depicted graphically.

Figure 2. System 1 – Pendulum-like nonlinear system. Comparison of the system responses and convergence profiles for different optimization algorithms. The left column shows the closed-loop responses of the pendulum-like nonlinear system under PSO-, GWO-, and hybrid PSO–GWO-optimized PID gains, while the right column depicts the evolution of the cost function during the optimization process. Minimum cost values and the corresponding number of evaluations are indicated.

Figure 2. System 1 – Pendulum-like nonlinear system. Comparison of the system responses and convergence profiles for different optimization algorithms. The left column shows the closed-loop responses of the pendulum-like nonlinear system under PSO-, GWO-, and hybrid PSO–GWO-optimized PID gains, while the right column depicts the evolution of the cost function during the optimization process. Minimum cost values and the corresponding number of evaluations are indicated.

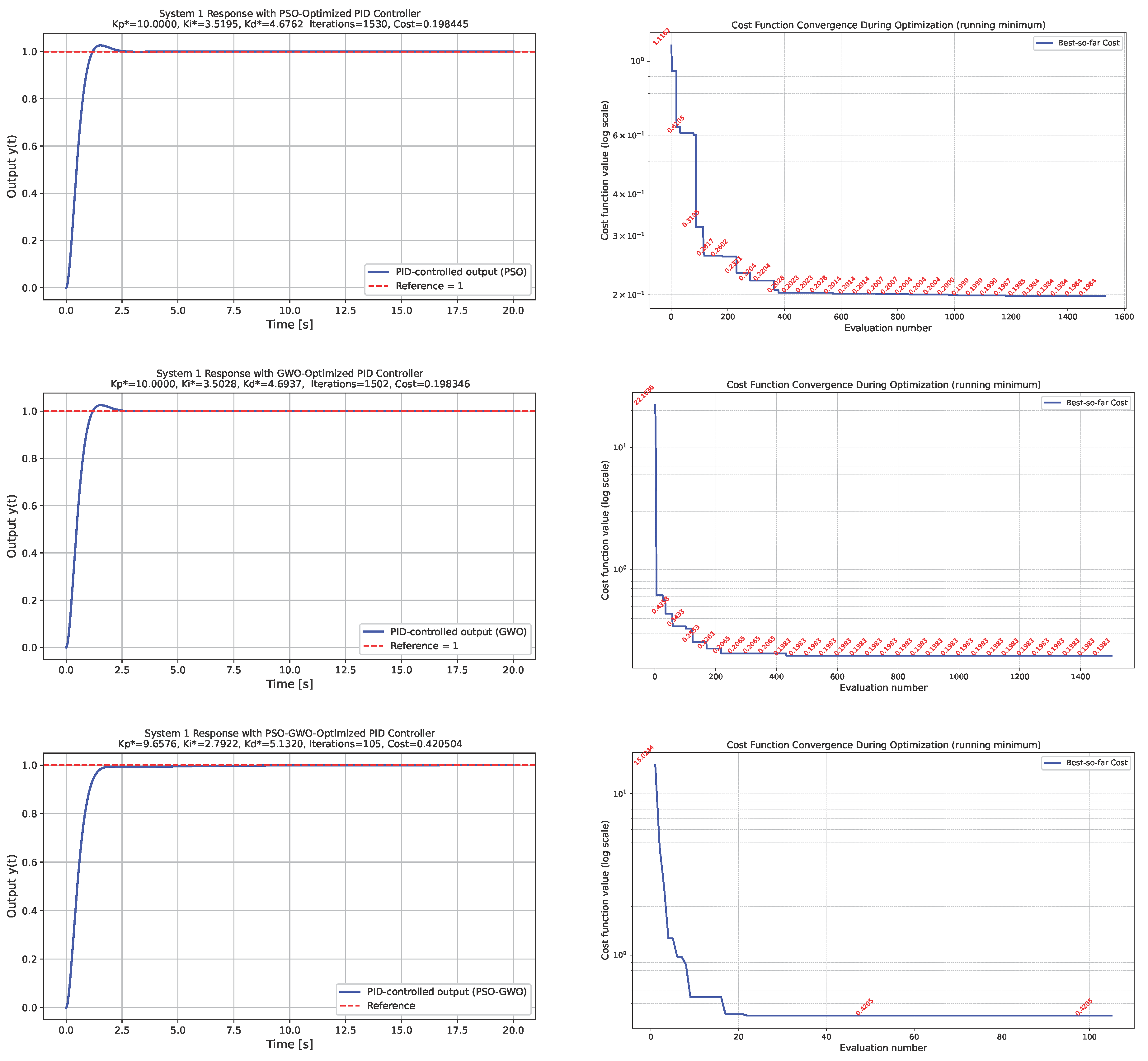
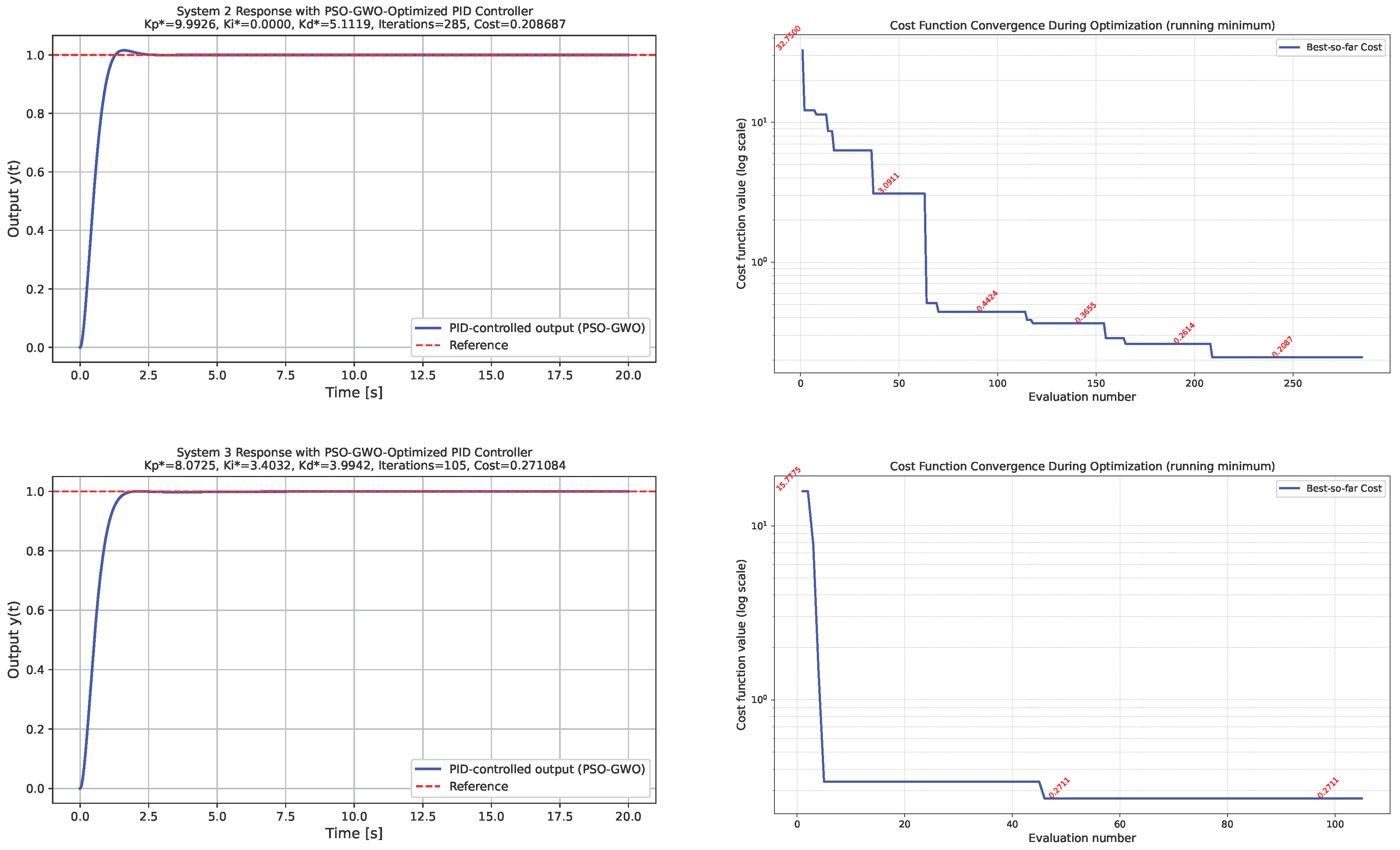
• System 2: Duffing oscillator
  The response of the Duffing oscillator is presented in Figure 3. Due to the presence of the cubic stiffness term, the system exhibits pronounced nonlinear and potentially oscillatory behavior. The left column of Figure 3 displays the time-domain responses of $y\left(t\right)$ obtained using PID gains optimized by the PSO, GWO, and hybrid PSO–GWO algorithms. All three controllers are able to regulate the system effectively; however, the hybrid PSO–GWO algorithm produces a noticeably higher overshoot compared to PSO and GWO. This behavior can be mitigated by increasing the weight of the ISO term in the performance function. For instance, when $\alpha =100$, a significant suppression of overshoot is observed, as illustrated in the first row of Figure 5. The right column of Figure 3 provides insights into the convergence of the cost function across iterations.

Figure 3. System 2 – Duffing oscillator. Comparison of the Duffing oscillator responses and optimization progress for different metaheuristic strategies. The left column illustrates the closed-loop behavior of the nonlinear oscillator, whereas the right column presents the evolution of the cost function, highlighting convergence differences among PSO, GWO, and the hybrid PSO–GWO approach. Minimum cost and evaluation count are annotated in the plots.

Figure 3. System 2 – Duffing oscillator. Comparison of the Duffing oscillator responses and optimization progress for different metaheuristic strategies. The left column illustrates the closed-loop behavior of the nonlinear oscillator, whereas the right column presents the evolution of the cost function, highlighting convergence differences among PSO, GWO, and the hybrid PSO–GWO approach. Minimum cost and evaluation count are annotated in the plots.

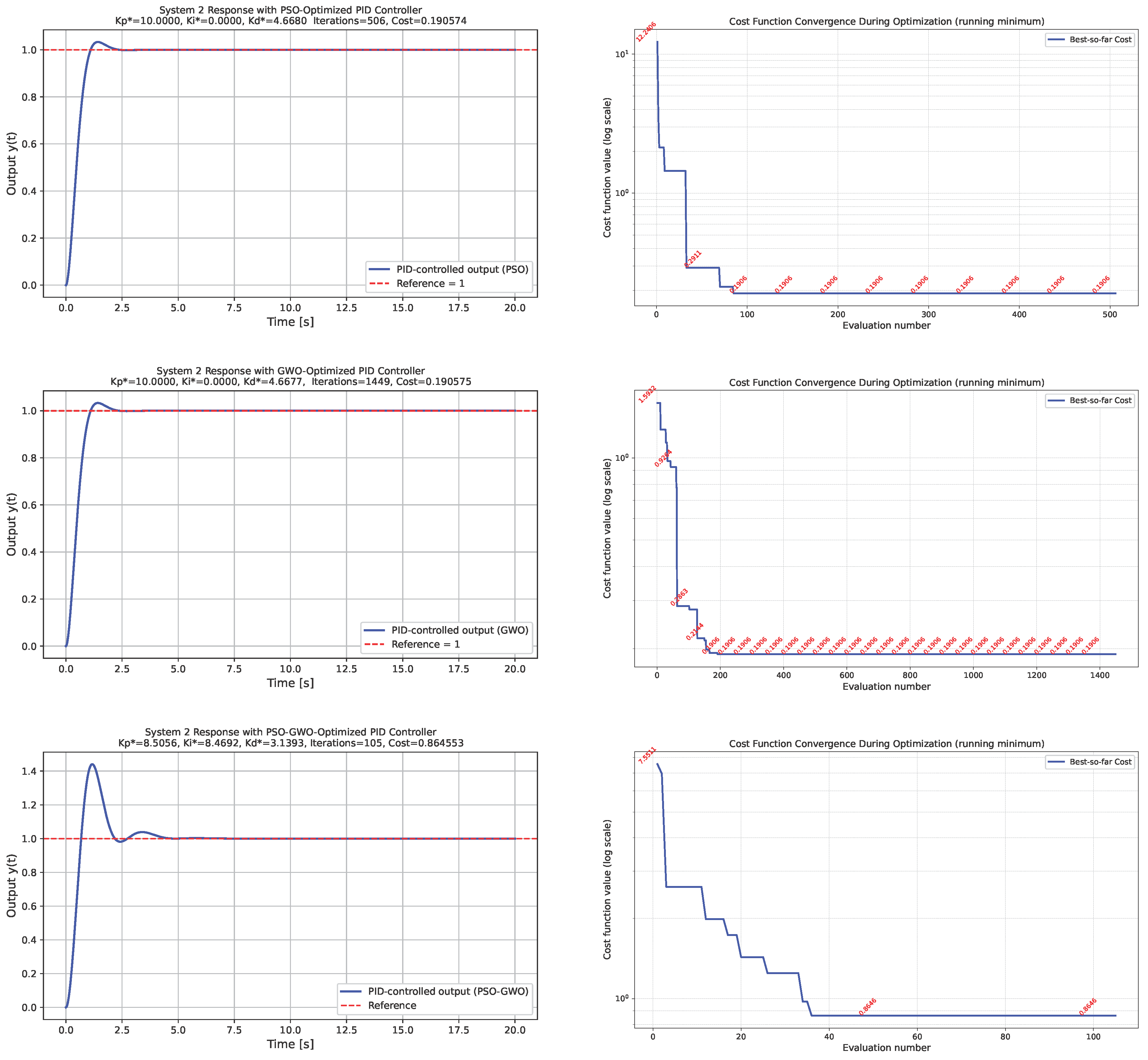
• System 3: Nonlinear damping system
  Figure 4 illustrates the closed-loop behavior of the nonlinear damping system for the PID controllers optimized by PSO, GWO, and the hybrid PSO–GWO algorithm. The left column shows the system responses $y\left(t\right)$ to a unit-step input. The presence of the velocity-dependent damping term $y{y}^{\prime }$ introduces asymmetric transient dynamics and nonlinear dissipation effects. All optimized PID controllers are capable of stabilizing the system; however, the hybrid PSO–GWO approach again exhibits a relatively higher overshoot compared to the standalone PSO and GWO methods. Nevertheless, this increased transient excitation occurs at a substantially lower number of cost function evaluations, indicating a more efficient search process. As in the case of the Duffing oscillator, this overshoot can be mitigated by appropriately increasing the weighting coefficient $\alpha$ of the ISO component in the performance index, as can be observed in the second row of Figure 5, thereby emphasizing steady-state accuracy. The right column of Figure 4 depicts the evolution of the cost function during the optimization process, further highlighting the convergence characteristics and trade-offs in exploration and exploitation among the three algorithms.

Figure 4. System 3 – Nonlinear damping system. Comparison of the nonlinear damping system responses and cost evolution across optimization algorithms. The left column displays the system output trajectories obtained using PID parameters tuned via PSO, GWO, and hybrid PSO–GWO, while the right column shows the convergence of the cost function.

Figure 4. System 3 – Nonlinear damping system. Comparison of the nonlinear damping system responses and cost evolution across optimization algorithms. The left column displays the system output trajectories obtained using PID parameters tuned via PSO, GWO, and hybrid PSO–GWO, while the right column shows the convergence of the cost function.

Figure 5. Hybrid PSO–GWO simulations for the Duffing and nonlinear damping systems with $\alpha =\mathbf{100}$. The plots demonstrate the effect of increasing the weighting coefficient $\alpha$ in the ISO term of the performance index. Compared to the previous simulations with $\alpha =1$, a substantial reduction in overshoot is observed, indicating improved damping and smoother transient behavior. This adjustment effectively mitigates the excessive aggressiveness of the hybrid optimizer observed in earlier cases.

Figure 5. Hybrid PSO–GWO simulations for the Duffing and nonlinear damping systems with $\alpha =\mathbf{100}$. The plots demonstrate the effect of increasing the weighting coefficient $\alpha$ in the ISO term of the performance index. Compared to the previous simulations with $\alpha =1$, a substantial reduction in overshoot is observed, indicating improved damping and smoother transient behavior. This adjustment effectively mitigates the excessive aggressiveness of the hybrid optimizer observed in earlier cases.

It should be noted that the convergence graph of the cost function $J(K_p,K_i,K_d)$ for the PSO-based PID tuning of System 1 (as well as for some other systems and algorithms) exhibits extreme values during the initial evaluations. These large cost values result from transient numerical instabilities caused by certain initial combinations of PID parameters that produce high initial errors.

To present the tuning process more clearly, only the running minimum of the cost function (the "best-so-far" value) is plotted, which effectively illustrates the progressive improvement of the PID parameters over successive evaluations. Selected cost values are annotated at specific intervals to provide quantitative insight while avoiding visual clutter in the figure.

This approach ensures that the graphical representation accurately reflects the optimization dynamics without being distorted by transiently unstable simulations.

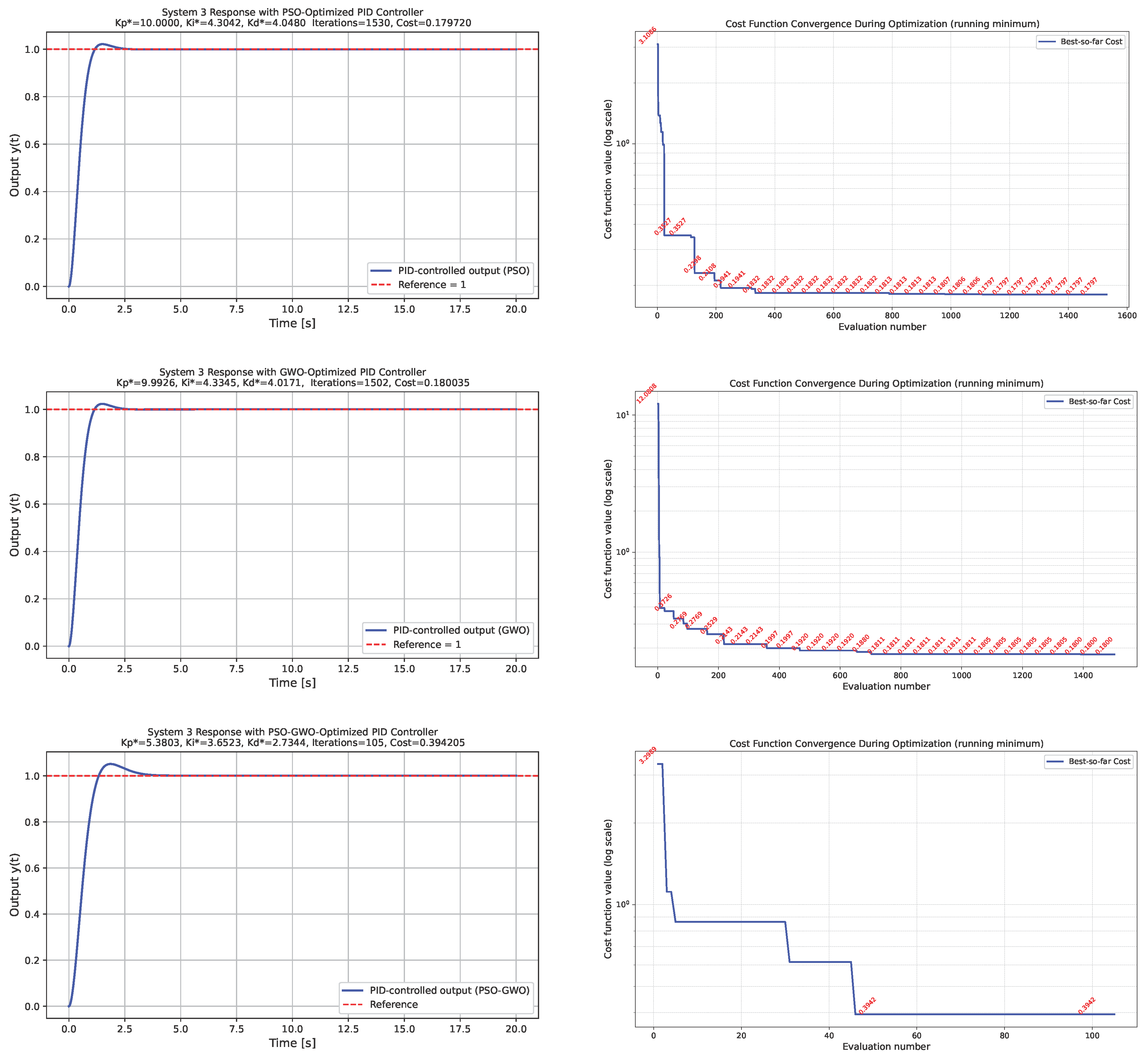
5. Discussion

For a better comparison and quantitative evaluation of the obtained results, the key performance metrics and optimal PID parameters are summarized in Table 3. This table consolidates the outcomes for all three nonlinear benchmark systems and provides insights into the convergence efficiency and stability characteristics of the tested optimization methods.

• Computational efficiency: The hybrid PSO–GWO algorithm achieves the target cost values with a substantially smaller number of cost function evaluations-approximately 10% of those required by standalone PSO or GWO. This remarkable reduction can be attributed to the synergy between the exploration capability of GWO and the exploitation behavior of PSO, which enables faster convergence toward promising regions of the search space. The hybrid structure effectively combines global and local search mechanisms, resulting in a rapid decrease in the cost function even in highly nonlinear conditions.
• System performance and overshoot behavior: Although the hybrid PSO–GWO demonstrates excellent convergence speed, its time-domain responses for Systems 2 and 3 exhibit pronounced overshoot and oscillations during the transient phase. This behavior suggests that the algorithm tends to generate aggressive control actions due to a strong emphasis on the integral and derivative gains during the optimization process. The observed overshoot can be mitigated by increasing the weighting factor $\alpha$ in the ISO term of the performance function. Numerical experiments show that setting $\alpha \approx 100$ effectively suppresses overshoot without significantly affecting the total number of cost function evaluations, indicating a favorable trade-off between control smoothness and optimization efficiency.
• Comparison of PSO and GWO: Both standalone PSO and GWO algorithms achieve stable control performance with low cost values, though at the expense of considerably higher computational effort. GWO, in particular, exhibits consistent but slower convergence, reflecting its exploratory nature. PSO maintains fast convergence and strong exploitation of promising regions, but requires more evaluations to achieve comparable performance to the hybrid approach.
• Sensitivity to the performance index parameters: The results further confirm that the design of the performance function, particularly the weighting of its integral and overshoot (ISO) components, plays a critical role in shaping controller behavior. For the hybrid PSO–GWO, an insufficiently penalized overshoot term (small $\alpha$) leads to aggressive transient responses, whereas larger $\alpha$ values produce smoother trajectories without degrading the convergence rate. Hence, the parameterization of the performance function directly governs the trade-off between control aggressiveness and robustness.

In summary, the hybrid PSO–GWO framework exhibits superior computational efficiency while maintaining satisfactory control accuracy across all considered nonlinear systems. However, the observed overshoot behavior indicates that careful tuning of the ISO weight $\alpha$ is necessary to balance rapid convergence with acceptable transient performance. These findings suggest that hybrid swarm-based metaheuristics are promising for real-time PID tuning, provided that the cost function formulation appropriately reflects the desired control objectives.

5.1. Remark on stochastic variability of optimization results.

During the simulation campaign, repeated runs of the same optimization algorithm–PSO, GWO, or the hybrid PSO–GWO–often converged to slightly different sets of controller parameters, even under identical initialization and stopping criteria (maximum iteration count and tolerance of ${10}^{-5}$). This variability arises from the stochastic nature of metaheuristic search, where random initialization and probabilistic update rules inherently influence the optimization trajectory.

In complex, nonlinear, and multimodal cost landscapes–such as those from chaotic dynamical systems–numerous local minima of comparable depth may exist. As a result, different runs can converge to distinct, yet nearly equivalent, optima that yield similar performance indices while corresponding to different PID parameter combinations. Such differences do not indicate algorithmic instability but rather reflect the multiplicity of acceptable solutions in a rugged landscape. For presentation, representative responses from the most frequently observed convergence patterns were selected.

This phenomenon is common in stochastic metaheuristics. Due to their inherent randomness, independent runs may converge to different local or quasi-global minima even under identical stopping criteria. The stochastic variability of these algorithms is well-documented [18,19], highlighting the importance of multiple independent runs and reporting statistical performance metrics to ensure fair and reproducible comparisons.

In the following subsection, the robustness and effectiveness of the proposed PSO–GWO-based PID tuning framework are rigorously evaluated on one of the most challenging nonlinear dynamic benchmarks–the chaotic Duffing oscillator.

5.2. Robustness Test on the Chaotic Duffing Oscillator

The Duffing oscillator represents one of the most challenging nonlinear dynamical systems to control due to its strong nonlinearity, sensitivity to initial conditions, and the presence of chaotic behavior under certain parameter regimes. Its dynamics can be described by the nonlinear second-order differential equation:

$$y^{\prime \prime }\left(t\right)+\tilde{\delta }{y}^{\prime }\left(t\right)+\tilde{\alpha }y\left(t\right)+\tilde{\beta }{y}^3\left(t\right)=\tilde{\gamma }cos\left(\tilde{\omega }t\right)+u\left(t\right),$$

(17)

where $\tilde{\delta }$ denotes the damping coefficient, $\tilde{\alpha }$ and $\tilde{\beta }$ are the linear and nonlinear stiffness parameters, $\tilde{\gamma }$ represents the amplitude of the external forcing, $\tilde{\omega }$ is its excitation frequency, and $u\left(t\right)$ is the control input generated by the PID controller.

For the selected parameter set $\tilde{\delta }=0.2$, $\tilde{\alpha }=-1.0$, $\tilde{\beta }=1.0$, $\tilde{\gamma }=0.5$, and $\tilde{\omega }=1.2$, the uncontrolled system ($u\left(t\right)=0$) exhibits aperiodic oscillations and extreme sensitivity to small perturbations-hallmarks of chaotic behavior. Such characteristics render conventional linear control strategies largely ineffective, as even minor variations in the control signal or in the system state may lead to significantly different trajectories. Consequently, the chaotic Duffing oscillator is frequently employed as a benchmark for evaluating the robustness, adaptability, and convergence properties of advanced control and optimization algorithms, particularly in the context of nonlinear and chaotic dynamics.

Figure 6 illustrates the contrasting responses of the Duffing oscillator without and with PID control, assuming zero initial conditions for the oscillator, $y\left(0\right)=0$ and $y^{\prime }\left(0\right)=0$. In the absence of control, the system exhibits irregular, chaotic oscillations that fail to settle to any equilibrium, demonstrating its highly unstable and unpredictable nature. In contrast, when the PID controller is tuned using the proposed hybrid PSO–GWO optimization method, the chaotic oscillations are effectively suppressed, and the system exhibits smooth, near-periodic behavior. Although small oscillations remain due to the periodic excitation term $cos\left(\tilde{\omega }t\right)$, the overall motion is significantly stabilized and follows the desired reference trajectory. This demonstrates the hybrid algorithm’s ability to handle strong nonlinearities and nonstationary dynamics, confirming both its robustness and adaptability in one of the most demanding nonlinear control scenarios.

6. Conclusions and Future Work

This study presented a comprehensive investigation of PID controller tuning for strongly nonlinear dynamic systems using swarm-based optimization techniques. The main objective was to design a direct, simulation-based optimization approach that does not rely on system linearization or analytical model simplification. Three representative nonlinear systems–pendulum-like, Duffing-type, and nonlinear damping models–were employed to evaluate the algorithms under comparable conditions.

The comparative analysis demonstrated that all tested metaheuristics (PSO, GWO, and the hybrid PSO–GWO) were capable of identifying PID parameters that ensure closed-loop stability and satisfactory dynamic performance. Among them, the hybrid PSO–GWO exhibited the fastest convergence and the lowest number of cost function evaluations, typically requiring less than 10% of the computational effort compared to the standalone algorithms. This superior efficiency stems from the hybrid algorithm’s ability to exploit the exploitation capabilities of PSO while leveraging the exploration power of GWO.

However, the hybrid method also showed a tendency toward aggressive control behavior, manifesting as higher overshoot and transient oscillations, particularly in the Duffing system. Such behavior can be effectively mitigated by adjusting the weighting coefficient $\alpha$ in the ISO component of the performance index (12), as higher $\alpha$ values penalize overshoot and yield smoother responses without significantly increasing computational cost.

The results further confirm that PID controllers, when properly tuned using modern swarm intelligence techniques, remain highly effective even for strongly nonlinear systems characterized by non-symmetric or amplitude-dependent dynamics. The combination of simplicity, adaptability, and high performance makes swarm-optimized PID control a viable solution for a wide range of nonlinear control problems.

Future research will focus on several directions:

• Incorporating adaptive or self-tuning strategies for real-time adjustment of PID gains based on system operating conditions.
• Extending the hybrid optimization framework to multi-objective formulations, balancing competing criteria such as energy consumption, robustness, and tracking precision.
• Applying the proposed approach to higher-order nonlinear and time-delay systems, and validating it through hardware-in-the-loop or real experimental platforms.
• Due to the inherent stochastic nature of metaheuristic optimization, incorporating statistical assessment across multiple independent runs to ensure robust evaluation of convergence characteristics and to quantify the distribution of attainable control performances in strongly nonlinear systems.

In summary, this study demonstrates that the synergy of swarm intelligence and classical PID control offers a powerful and computationally efficient approach to nonlinear system regulation, bridging the gap between heuristic optimization and practical control implementation.